 Open Access Article
Open Access ArticleQuantifying lattice vibrational modes and optical conductivity in mixed magnetite–maghemite nanoparticles†
Mireia
Sainz-Menchón
 a,
Iñigo
González de Arrieta
a,
Iñigo
González de Arrieta
 *a,
Telmo
Echániz
*a,
Telmo
Echániz
 b,
Karam
Nader
b,
Karam
Nader
 c,
Maite
Insausti
c,
Maite
Insausti
 cd,
Aurélien
Canizarès
cd,
Aurélien
Canizarès
 e,
Olivier
Rozenbaum
e,
Olivier
Rozenbaum
 e and
Gabriel A.
López
e and
Gabriel A.
López
 a
a
aPhysics Department, University of the Basque Country (UPV/EHU), E-48940 Leioa, Spain. E-mail: inigo.gonzalezdearrieta@ehu.eus
bApplied Mathematics, University of the Basque Country (UPV/EHU), E-48013 Bilbao, Spain
cDepartamento Química Orgánica e Inorgánica, Facultad de Ciencia y Tecnología, University of the Basque Country (UPV/EHU), Sarriena s/n, 48940 Leioa, Spain
dBCMaterials, Basque Center for Materials, Applications and Nanostructures, UPV/EHU Science Park, 48940 Leioa, Spain
eUniversité dOrléans, CNRS, CEMHTI UPR 3079, Orléans, France
First published on 28th March 2025
Abstract
Magnetite nanoparticles are an important nanomaterial with promising biomedical applications that depend crucially on their stoichiometry. Their tendency to oxidize and turn into isostructural maghemite means that discriminating between both oxides is a essential task that is difficult to achieve with conventional techniques. In this work, a novel methodology based on infrared spectroscopy is developed and tested with practically relevant magnetic nanoparticles. In contrast to Raman spectroscopy, which is prone to systematic errors and only offers a qualitative understanding of the vibrational properties, infrared spectroscopy is not only able to identify all the modes corresponding to magnetite and maghemite, but also capable of discriminating between two possible structural variants of maghemite. Additionally, the proposed approach also allows the acquisition of electrical conductivity, a property that is sensitive to the structure and stoichiometry of the particles. Together, vibrational mode modeling and conductivity quantification provide a detailed picture of the structure and properties of mixed iron oxide nanoparticles that is valuable towards an advanced characterization of magnetic nanomaterials in real biomedical applications.
1 Introduction
Iron oxide can be found in a vast diversity of species, whether naturally occurring or synthetically produced. Besides amorphous oxides and exotic compounds, it predominantly manifests in the following oxidation states: magnetite (Fe3O4), wüstite (FeO), maghemite (γ-Fe2O3), and hematite (α-Fe2O3), the last two being the most prevalent species within the Fe2O3 polymorphic family.1Over the past decade, magnetite nanoparticles (Fe3O4-NPs) have emerged as a versatile and interesting nanomaterial for a variety of applications in a wide range of scientific areas, including biomedicine, pharmacy, environmental chemistry, and optoelectronics. These nanoparticles are studied for their potential applications notably in magnetic drug targeting,2,3 tissue engineering,3,4 pollutant elimination in natural environments5,6 and ferrofluids for novel optoelectronic devices.7–9 Nevertheless, one of the primary applications of Fe3O4-NPs in modern biomedicine has been their implementation in magnetic hyperthermia treatments.
Among all their qualities, high magnetization saturation, magnetic anisotropy, and excellent biocompatibility are the properties that make ferrimagnetic Fe3O4-NPs an ideal candidate for hyperthermia applications.10–12 Furthermore, several studies were published exploring the transportation of these nanoparticles in biological environments by taking advantage of their ferrimagnetic nature.11,13 Emerging research indicates that the combination of efficient transportation and the precise spatial control of carcinogenic cell destruction make Fe3O4-NPs a promising tumor-selective material. This allows the development of an alternative to conventional cancer treatment techniques, which often lack selectivity and may affect the surrounding healthy tissues, as observed in radiation and microwave therapies.12
A strict control of the size and shape of the nanoparticles, together with a precise regulation of the stoichiometric ratios, is necessary to guarantee optimum hyperthermic behavior. Regarding size and shape control, several studies conducted over the last years worked on tailoring these properties to enhance the synthesis process.14,15 Controlling the synthesis to ensure high crystallinity and compositional homogeneity is not a trivial task, since a mixture of oxides can lead to degradation or loss of the distinctive magnetic properties, and, as previous studies have established, Fe3O4-NPs could easily suffer partial transformation to γ-Fe2O3 depending on the storing environment, temperature and atmosphere.16,17 Consequently, establishing a characterization technique able to accurately distinguish different iron oxides (particularly Fe3O4 and γ-Fe2O3) becomes crucial in order to develop novel synthesis routes. Additionally, a technique that is widely recognized, and does not demand extensive pre-training would be highly practical for scientists working on the area.
Nevertheless, a significant challenge arises as a result of the crystal structure similarity of both oxides. Fe3O4 exhibits an inverse spinel structure with a FCC lattice (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at ambient temperature. In this case, trivalent iron cations occupy tetrahedral sites, while octahedral sites are occupied with the same probability by trivalent and divalent cations, as described by the following structural formula:
m) at ambient temperature. In this case, trivalent iron cations occupy tetrahedral sites, while octahedral sites are occupied with the same probability by trivalent and divalent cations, as described by the following structural formula:
| (Fe3+)8 [Fe3+Fe2+]16O32 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) and [
) and [![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] represent tetrahedral and octahedral sites, respectively. Divalent cations are highly unstable in contact with atmospheric oxygen, which produces a migration to the surface of the material and introduces a population of vacancies in the crystal structure. As a result, Fe3O4 suffers a transformation to γ-Fe2O3, described by the following structural formula:
] represent tetrahedral and octahedral sites, respectively. Divalent cations are highly unstable in contact with atmospheric oxygen, which produces a migration to the surface of the material and introduces a population of vacancies in the crystal structure. As a result, Fe3O4 suffers a transformation to γ-Fe2O3, described by the following structural formula:| (Fe3+)8 [Fe5/63+□1/6]16O32 |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Partially ordered γ-Fe2O3 is related to a partial vacancy ordering, linked to a lower symmetry cubic space group P4332.18 Finally, fully ordered γ-Fe2O3 develops when the highest vacancy ordering is attained, generating the lowest symmetry structure described by the tetragonal space group P41212.19
m space group. Partially ordered γ-Fe2O3 is related to a partial vacancy ordering, linked to a lower symmetry cubic space group P4332.18 Finally, fully ordered γ-Fe2O3 develops when the highest vacancy ordering is attained, generating the lowest symmetry structure described by the tetragonal space group P41212.19
In this regard, discerning between the isostructural species Fe3O4 and fully disordered γ-Fe2O3 using X-ray diffraction (XRD) becomes a challenging task, as both exhibit very similar diffraction patterns. Mössbauer spectroscopy has been established as the standard technique for this purpose, since it allows the differentiation between divalent and trivalent iron cations based on their different isomer shifts. Nonetheless, for nanoparticles with diameters around d = 20 nm, thermal effects such as Brown and Néel relaxation may disturb the magnetic splitting at room temperature, making it only possible to characterize the composition of small nanoparticles applying strong magnetic fields (>5 T) or considerably low temperatures (<120 K),20,21 conditions that are not always available.
The resonant frequencies of fully disordered γ-Fe2O3 vibrational modes differ from those of Fe3O4 due to the structural modification caused by the distribution of vacancies and the different atomic bond strengths. Consequently, vibrational spectroscopic techniques, such as Raman and IR spectroscopy, become promising candidates for the identification of these species in mixed iron oxide materials. Both Fe3O4 and γ-Fe2O3 show a strong Raman vibrational band, located at distinct frequencies for each substance as a result of differences in the Fe–O bond strength and distance. Despite allowing a qualitative interpretation, Raman laser power can overheat the sample under study, causing a transformation from Fe3O4 to γ-Fe2O3 during the experiment. This technical problem prevents an adequate interpretation of the results, making it challenging to accurately index the Raman vibrational modes of these iron oxide species. This topic has been extensively discussed in literature, which evidenced the need of prior understanding and pre-training in order to apply a proper Raman laser power and perform a correct indexation of the vibrational modes.22,23 Furthermore, relating Raman signals to the concentration of different iron oxide phases becomes highly challenging, as the Raman response of a material varies depending on the laser wavelength used on the experiment, resulting on signals of different intensities.
Considering this, IR spectroscopy shows promise as a technique able to discern Fe3O4 from γ-Fe2O3 as it is able to detect the different vibrational modes coming from each material without the risk of sample overheating. However, not many detailed IR studies about iron oxides can be found in literature,24 in spite of the popularity and ease of use of the technique. Several qualitative studies focused on the indexation and characterization of surface species have been published over the years,5,25,26 but a detailed understanding of the complex vibrational nature of iron oxides is still lacking. Furthermore, the potential of IR spectroscopy is enhanced by combining it with a robust permittivity extraction model, which brings us closer to extract quantitative information such as the proportion of the constituent oxides or the conductivity of the sample. This proposal aligns with the current trend of developing permittivity extraction techniques and quantitative analysis based on IR spectroscopy of inorganic solids.27–29
2 Materials and methods
2.1 Synthesis
The selection of the samples was based on the need to develop a characterization technique for the materials that are commonly used in hyperthermia research. This choice links this rather academic study to social issues, enhancing its relevance and usefulness.The samples studied in this work were reported in ref. 14 and were synthesized by the thermal decomposition of iron(III) oleates. Briefly, different iron(III) oleates were synthesized varying synthesis conditions and the effect of the iron(III) chloride/sodium oleate molar ratio and the annealing time was studied. Then, thermal decomposition of iron(III) oleates dissolved in octadecene (10 mL), dibenzyl ether (5 mL) and oleic acid (3.2 mL) yield high-quality nanoparticles with diverse sizes (10 to 40 nm) and morphologies (cuboctahedral, octahedral, and spherical). After washing the samples by centrifugation 3 times, they were stored in chloroform at 4 °C. Nanoparticles obtained by this synthesis route are coated with oleic ligands, where the oxygen atoms are in contact with the magnetic core and the carbon chains are exposed outside, forming a brush-like structure with a hydrophobic character. For this reason, nanoparticles will be stable in non-polar or slightly polar solvents such as chloroform or THF.
The sample codes reflect their synthesis characteristics. The first part of the name corresponds to the molar ratio of the precursors (FeCl3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaOleate) and an additional letter is used to denote the annealing time (S stands for a shorter 21-h annealing, L for a longer 42-h one). The only exception to this code is the sample synthesized using oleylamine instead of oleate, which is given the code 40:115_S_OAm. To determine the percentage of organic matter in the samples, thermogravimetric analysis of 10 mg of well-dried nanoparticles was performed, and the following organic ligand (OL) proportions were obtained:14mOL,40:120_S = 18.8%, mOL,40:120_L = 23.4%, mOL,40:115_S = 29.6%, mOL,40:125_S = 31.6% and mOL,40:115_S_OAm = 11.8%.
NaOleate) and an additional letter is used to denote the annealing time (S stands for a shorter 21-h annealing, L for a longer 42-h one). The only exception to this code is the sample synthesized using oleylamine instead of oleate, which is given the code 40:115_S_OAm. To determine the percentage of organic matter in the samples, thermogravimetric analysis of 10 mg of well-dried nanoparticles was performed, and the following organic ligand (OL) proportions were obtained:14mOL,40:120_S = 18.8%, mOL,40:120_L = 23.4%, mOL,40:115_S = 29.6%, mOL,40:125_S = 31.6% and mOL,40:115_S_OAm = 11.8%.
TEM images of the samples studied in this work can be seen in Fig. 1. The samples present a monophasic composition and narrow size distribution. Histograms of size distributions are added as insets, together with Gaussian fits, which have been generated based on Feret diameter measurements from microscopy images using the image processing software ImageJ.30 For octahedral samples, the length of the longer diagonal was measured, while for cuboctahedral and spherical samples, the approximated diameter was evaluated. Additionally, images of selected nanoparticles are also found in insets. For spectroscopy experiments, the samples were allowed to dry, and the resulting nanoparticle powder was stored under vacuum conditions produced by a rotary pump. This ensured the elimination of the chloroform, allowing an adequate structural and spectroscopic characterization of the sample material.
2.2 Experimental methods
A set of experimental characterization techniques was employed to study the structural and vibrational properties of the samples. XRD experiments were performed to study the crystal structure of the samples, while Raman and specular IR spectroscopy provided insight into the vibrational behavior, optical properties and composition. A detailed description of the techniques is included in the following paragraphs.XRD measurements were performed with a four-circle Stoe Stadivari diffractometer with a Debye–Scherrer geometry and spinning stage for powder samples. In this equipment, the radiation originates from a microfocus X-ray tube with a Mo anode, monochromatized with a multilayer mirror. The wavelength of the radiation is Mo Kα = 0.71069 Å and the detector is a two-dimensional CMOS Dectris Pilatus-100K. While several studies from literature use a Cu Kα X-ray source (λ = 1.5418 Å) the Mo Kα source is more convenient for iron oxide samples, as they present fluorescence when exposed to Cu Kα radiation, causing a significant increase in background signal. This phenomenon decreases the signal-to-noise ratio and makes it difficult to detect low-intensity peaks.31
Raman spectroscopy measurements were performed using a Renishaw inVia Qontor spectrometer equipped with a 633 nm HeNe laser (20 mW), and a Renishaw inVia Reflex with a 514 nm (50 mW) Diode pumped Solid State Laser. In both cases, a grating of 1800 lines per mm was used to disperse the scattered light before being detected by the charged coupled device (CCD) camera. The spectra were obtained using an optical microscope Leica DM 2500 equipped with a long working distance 50× objective with a numerical aperture of 0.50. For analysis, a minimal laser excitation power (<1 mW) was used to avoid laser-induced heating.
To perform IR reflectance experiments, 5 mm diameter pellets were prepared by pressing the nanoparticle powder employing a die and a hydraulic press (compaction pressure of 2 t). To compute the filling factors of the pellets, the ratio between the pellet and compound densities was determined (f = ρpellet/ρnanoparticles), where ρpellet was computed by direct measurements of the mass and volume of the pellets. The volume of the pellets was obtained by direct measurement of their thickness using an optical microscope. The density of the nanoparticle compound was determinated using the density of Fe3O4 (assumed to be ρFe3O4 = 5.175 g cm−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32), and the density of oleic acid (ρOA = 0.895 g cm−3) to take into account the proportion of resting organic ligands. An estimated value of the density is required for our analysis, and using the value of Fe3O4 is the best approximation, even if subject to a small systematic error due to the γ-Fe2O3 fraction present in the nanoparticles exposed to atmospheric oxygen. This choice was made because the nanoparticles after synthesis consisted mainly of Fe3O4, and the density of γ-Fe2O3 (ργ-Fe2O3 = 4.9 g cm−3) is similar to that of Fe3O4.
32), and the density of oleic acid (ρOA = 0.895 g cm−3) to take into account the proportion of resting organic ligands. An estimated value of the density is required for our analysis, and using the value of Fe3O4 is the best approximation, even if subject to a small systematic error due to the γ-Fe2O3 fraction present in the nanoparticles exposed to atmospheric oxygen. This choice was made because the nanoparticles after synthesis consisted mainly of Fe3O4, and the density of γ-Fe2O3 (ργ-Fe2O3 = 4.9 g cm−3) is similar to that of Fe3O4.
Spectral reflectivity measurements were performed in the MIR and FIR wavelength ranges using a Bruker VERTEX 80v FT-IR spectrometer with a variable incident-angle specular reflectance accessory. This accessory allows changing the value of the incident angle, which for this study was chosen to be the closest to the normal that the apparatus permitted to obtain (15°). The MIR range (400 cm−1 to 7000 cm−1) was measured with a Deuterated L-alanine doped TriGlycine Sulphate (DLaTGS) detector, while a liquid He cooled bolometer was employed for the FIR range (100 cm−1 to 700 cm−1). Both ranges were measured with a 2 cm−1 spectral resolution. An aluminum mirror was used as a reference. The effect of spurious radiation sources due to the sample environment was corrected by substracting from each measurement the signal obtained with the Globar source turned away from the sample chamber.
2.3 IR modeling and permittivity extraction
 | (1) |
The extended Drude model is composed of two contributions corresponding to the Drude and Debye relaxation terms. The first term is related to the conventional electric transport, involving large delocalized polarons. Alternately, the second term describes the dielectric relaxation driven by the hopping transport of small polarons, a type of transport common in materials with disorder or defects that create localized energy states. This approach has been widely applied to study the infrared optical properties of diverse conducting oxides.33–35
Simple damped oscillators, known as Lorentzian functions or 3 parameter phonon functions, were used to model the contribution of phonon absorption bands in the spectra, which can be understood as the combination of harmonic oscillator terms:
 | (2) |
| εeff1/3 = fεi1/3 + (1 − f)εm1/3 | (3) |
Finally, the reflectivity at near normal incidence can be computed from εeff applying Fresnel's equation:
 | (4) |
 | (5) |
 | (6) |
 | (7a) |
 | (7b) |
3 Results and discussion
3.1 X-ray diffraction
The XRD patterns of the five samples studied in this work can be seen in Fig. 2. All samples present the peaks corresponding to the FCC spinel structure, and no other peaks from other oxides such as hematite are present. Due to the similar XRD patterns of Fe3O4 and the spinel γ-Fe2O3, and the widening of the diffraction peaks due to the nanoscale size of the crystal domains, it is not possible to accurately determine which oxide is present, or the composition of the mixture.17 | ||
| Fig. 2 Diffractograms of the samples measured with a molybdenum Kα source (λ = 0.71069 Å). The reflections corresponding to the inverse spinel cubic crystal structure was indicated by Miller indices. | ||
For determining the cell structure and refining the cell parameters the DICVOL04 method (also known as Louers method) was applied, which is a procedure for the automatic indexing of powder diffraction patterns based on the dichotomy principle.40 The method was implemented using the WinXPOW software.41 The refinement process indicated a consistent cubic crystal structure for all samples. The computed cell parameters can be seen in Table S1 from the ESI,† together with the parameters of pure magnetite42 and the ideal structure of fully disordered maghemite.24 The parameters of the five samples lie in between the values of ideal Fe3O4 and fully disordered γ-Fe2O3, which was related in literature to the coexistence of both oxides.43,44
Based on the information derived from the refinement, the indexing of the peaks to the crystalline planes was performed, as illustrated by their Miller indices in Fig. 2. The (210) and (211) diffraction peaks have been previously related to the presence of maghemite.45 In this case, these peaks appear simultaneously in samples 40:120_L, 40:125_S and 40:115_S_OAm, as can be better appreciated in Fig. S1 found in the ESI.† However, this presence is not sufficient or useful to discern between a single oxide or a mixture of oxides.
3.2 Raman spectroscopy
Fig. 3 shows the Raman spectra for the five samples measured with a laser wavelength of λ = 633 nm. The typical room temperature Raman spectrum of magnetite is characterized by a high-intensity band corresponding to the A1g mode, found at ∼660–670 cm−1, together with two low-intensity bands corresponding to Eg and T2g(3) modes, located around ∼300 and ∼530 cm−1, respectively. In the case of γ-Fe2O3, the A1g mode is located around ∼710 cm−1, blue-shifted compared to that of Fe3O4. A detailed discussion about the most accepted interpretation of the Raman vibrational modes can be found in the ESI,† together with a table containing peak positions (Table S2, ESI†), revealing that the position of the bands corresponds to the ones expected for the A1g modes of Fe3O4 and γ-Al2O3. In addition, these bands exhibit an almost purely Lorentzian profile. | ||
| Fig. 3 Baseline-corrected Raman spectra of the samples measured using a laser wavelength of λ = 633 nm. | ||
Regarding our results, the prominent Fe3O4 A1g mode centered around 665 cm−1 is present in all samples, appearing with a relatively higher intensity in samples 40:120_S, 40:120_L and 40:115_S. The γ-Fe2O3 A1g mode appears more notably in samples 40:125_S and 40:115_S_OAm, as a shoulder of the Fe3O4 A1g, and its presence is followed by a more noticeable presence of the bands located around 380, 460 and 530 cm−1. These bands can be related to the overlap of T2g(2) and T2g(3) modes of magnetite and weak modes related to maghemite,23,46 although it is difficult to estimate considering the low signal-to-noise ratio, especially in the sample 40:125_S.
To analyze in more detail the A1g bands for both oxides, the deconvolution of the peak structure was performed fitting the 660 and 710 cm−1 bands using pseudo-Voigt profiles for λ = 514 nm and λ = 633 nm Raman laser wavelengths (see Fig. 4). A phase quantification attempt was recently reported based on the ratio between the areas of the γ-Fe2O3 and Fe3O4 A1g bands (A(710 cm−1)/A(660 cm−1)).47 However, the relative intensity between these two bands for the same sample changes with the Raman laser wavelength, as seen in Fig. 4, proving that further standardization and a more robust analytical framework is needed to improve these quantitative estimations. The most prudent way to act in this case is to stick to the qualitative interpretation. All samples present to a greater or lesser extent the γ-Fe2O3 specific vibrational band at 710 cm−1. However, the relative area of this band compared to the A1g related to Fe3O4 changes from sample to sample, being more prominent for samples 40:125_S and 40:115_S_OAm. This tendency is observable for both Raman laser wavelengths.
 | ||
| Fig. 4 Deconvolution of the Raman spectra of the samples using pseudo-Voigt profiles. The spectra were measured using a laser wavelength of λ = 514 nm (a) and λ = 633 nm (b). | ||
These results indicate that Fe3O4 and γ-Fe2O3 coexist in all nanoparticle samples, albeit to varying degrees. This could be explained by partial Fe3O4 to γ-Fe2O3 transformation, probably caused by the exposition to atmospheric oxygen. Samples 40:125_S and 40:115_S_OAm exhibit a higher degree of transformation, as the ratio between the γ-Fe2O3 A1g band area to the Fe3O4 A1g band area is greater compared to other samples, for both Raman experiments. A greater presence of the γ-Fe2O3 A1g Raman band for these samples could be explained by the smaller particle size obtained using precursors with higher content of oleate or with a different ligand (oleylamine). The smaller size leads to a larger surface-to-volume ratio, and in presence with oxygen a greater Fe3O4 to γ-Fe2O3 A1g conversion occurs. This is in agreement with the more noticeable presence of the bands at 380, 460 and 530 cm−1 in samples 40:125_S and 40:115_S_OAm.
3.3 IR spectroscopy
The reflectance results from 200 to 7000 cm−1 for all samples can be seen in Fig. 5, together with insets highlighting the zoomed-in section of the spectra from 200 to 1000 cm−1. At first examination, all samples present a structure composed of two main bands in the FIR (from 200 cm−1 to 700 cm−1), followed by a pseudo-Christiansen wavenumber at ∼780 cm−1 which is defined as the wavenumber in which the real part of the refractive index of the material nearly matches that of the surrounding air and the imaginary part of the refractive index is small enough, producing a local reflectance minima. A monotonic decrease of the reflectance is seen from 1000 cm−1 onward for all samples, which is qualitatively consistent with studies for bulk samples.48,49 However, upon closer inspection on the 200 cm−1 to 700 cm−1 spectral range (see insets), it is easily noticeable that the two main bands are actually composed by several smaller features, which will be examined and discussed in detail further on this section. | ||
| Fig. 5 Reflectance spectrum for samples 40:120_S (a), 40:120_L (b), 40:115_S (c), 40:125_S (d) and 40:115_S_OAm (e) are shown by solid lines. The fitting curves obtained using the permittivity model presented in eqn (1) and applying the LLL EMT formula (eqn (3)) are represented by dashed lines. Zoomed-in plots of the FIR range were included as insets to allow a detailed observation of the spectral features in that range. | ||
The fit performed applying the model presented in Section 2.3.1 is represented by dashed line in Fig. 5. The modelization and fitting procedure was done using FOCUS, a curve-fitting software developed at CEMHTI-CNRS and available online.50 The imaginary part of the permittivity corresponding to the nanoparticles, obtained by applying eqn (1), can be seen in Fig. 6 (solid line). The filling factors used to link the effective permittivity (εeff) to the permittivity of the nanoparticles (εNP) are: f40:120_S = 0.681 ± 0.006, f40:120_L = 0.753 ± 0.005, f40:115_S = 0.52 ± 0.02 f40:125_S = 0.730 ± 0.008 and f40:115_S_OAm = 0.607 ± 0.006. The dispersion of filling factor values could be affected by the organic ligand amount of the samples, particle size and particle morphology, as all those factors affect their compaction.
Spectroscopic deconvolution procedures featuring a high number of fitting parameters are normally considered ill-conditioned problems, as small changes of the initial values may produce major alterations in the final results. This may lead to several combinations of parameter values yielding the same results. Taking into account that this challenge usually arises in IR fitting procedures, it is essential to gather as much prior spectral information as possible. Consequently, it is possible to delimit the value of some fitting parameters, such as the position and bandwidth of absorption bands, by referring to previous indexing works and theoretical studies.
Hence, in order to fit the absorption bands of the spectra, the contribution of both Fe3O4 and γ-Fe2O3 oxides was taken into account as their presence was confirmed for all samples by Raman spectroscopy. This choice is also supported by XRD results, which show an intermediate cell parameter and the presence of (210) and (211) γ-Fe2O3 peaks at small angles, suggesting the presence of both oxides in all samples. For modeling the spectral contribution of both oxides, 4 absorption bands were used for each one of them, as stated by group theory.51 The imaginary part of the permittivity bands corresponding to Fe3O4 and spinel γ-Fe2O3 phonon modes are shown in Fig. 6, and the parameters used to build each permittivity phonon band are shown in Tables 1 and 2. The widths of these bands corresponding to the same phonon were chosen to remain constant across all samples in order to constrain the parameter space, with the band intensity adjusted to fit the experimental spectra. Regarding the phonon bands related to Fe3O4, their position was chosen based on previous published works.46,48,52,53 The same approach was applied for assigning the position of the absorption modes of spinel γ-Fe2O3.24,46,53 These constraints are required to avoid over-fitting the spectra with an excessive number of parameters. Therefore, although the model has a limited capacity to capture all spectral features, it successfully reproduces the response of five samples with a single set of parameters with values consistent with literature ones.
| Phonon mode | Sample | ω (cm−1) | γ (cm−1) | Δε |
|---|---|---|---|---|
| T1u(1) | 40:120_S | 238 | 193 | 1.51 |
| 40:120_L | 234 | 193 | 0.40 | |
| 40:115_S | 236 | 193 | 3.54 | |
| 40:125_S | 244 | 193 | 0.39 | |
| 40:115_S_OAm | 235 | 193 | 0.32 | |
| T1u(2) | 40:120_S | 298 | 65 | 0.64 |
| 40:120_L | 301 | 65 | 0.20 | |
| 40:115_S | 296 | 65 | 1.76 | |
| 40:125_S | 299 | 65 | 0.28 | |
| 40:115_S_OAm | 300 | 65 | 0.61 | |
| T1u(3) | 40:120_S | 353 | 47 | 1.05 |
| 40:120_L | 359 | 50 | 0.26 | |
| 40:115_S | 344 | 47 | 1.62 | |
| 40:125_S | 348 | 47 | 0.16 | |
| 40:115_S_OAm | 345 | 47 | 0.35 | |
| T1u(4) | 40:120_S | 573 | 55 | 0.60 |
| 40:120_L | 586 | 58 | 0.27 | |
| 40:115_S | 564 | 47 | 0.58 | |
| 40:125_S | 583 | 47 | 0.11 | |
| 40:115_S_OAm | 582 | 47 | 0.33 |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) model of γ-Fe2O3
m) model of γ-Fe2O3
| Phonon mode | Sample | ω (cm−1) | γ (cm−1) | Δε |
|---|---|---|---|---|
| T1u(1) | 40:120_S | 204 | 193 | 0.68 |
| 40:120_L | 196 | 193 | 0.23 | |
| 40:115_S | 203 | 193 | 2.37 | |
| 40:125_S | 201 | 193 | 1.21 | |
| 40:115_S_OAm | 196 | 193 | 2.28 | |
| T1u(2) | 40:120_S | 388 | 65 | 1.00 |
| 40:120_L | 390 | 60 | 0.41 | |
| 40:115_S | 374 | 65 | 0.76 | |
| 40:125_S | 384 | 65 | 0.37 | |
| 40:115_S_OAm | 385 | 65 | 1.44 | |
| T1u(3) | 40:120_S | 444 | 45 | 0.29 |
| 40:120_L | 445 | 45 | 0.12 | |
| 40:115_S | 440 | 47 | 0.22 | |
| 40:125_S | 444 | 38 | 0.06 | |
| 40:115_S_OAm | 444 | 44 | 0.34 | |
| T1u(4) | 40:120_S | 551 | 45 | 0.26 |
| 40:120_L | 561 | 47 | 0.25 | |
| 40:115_S | 549 | 47 | 0.08 | |
| 40:125_S | 553 | 47 | 0.16 | |
| 40:115_S_OAm | 555 | 47 | 0.53 |
Ishii et al. studied the lattice vibrations of Fe3O4 using the GF matrix method, and related the 4 phonon modes to the following vibrational dynamics,54 listed from the lowest to the highest energetic vibrational mode: the motion of the Fe–Fe of the octahedral iron cations against the tetrahedral ones (T1u(1)), a bending vibrational mode of the O–Fe–O bond in the octahedral coordinations (T1u(2)), a stretching mode Fe–O for the iron cations in octahedral coordination (T1u(3)) and finally a stretching motion of the Fe–O bond in octahedral and tetrahedral coordination (T1u(4)).24,54 This interpretation was extended to other ferrites such as γ-Fe2O3.24
Samples 40:125_S and 40:115_S_OAm clearly present more intense Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m γ-Fe2O3 vibrational bands when compared to Fe3O4 bands. This can be linked to a larger γ-Fe2O3 content in these samples, as seen also in Raman spectroscopy, which can be related to a greater oleate concentration and the use of OAm as surfactant. Regarding samples 40:115_S and 40:120_S, the presence of vibrational bands corresponding to Fe3O4 is more significant in comparison with the Fd
m γ-Fe2O3 vibrational bands when compared to Fe3O4 bands. This can be linked to a larger γ-Fe2O3 content in these samples, as seen also in Raman spectroscopy, which can be related to a greater oleate concentration and the use of OAm as surfactant. Regarding samples 40:115_S and 40:120_S, the presence of vibrational bands corresponding to Fe3O4 is more significant in comparison with the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m γ-Fe2O3 bands. This is in agreement with Raman results, linking smaller maghemite contents to these samples synthesized with smaller oleate content. Finally, sample 40:120_L exhibits an anomalous behaviour from the overall one observed in the other samples. Taking into account the Raman data it can be said that the relative maghemite amounts in samples 40:120_S and 40:120_L are very similar. Therefore, the most probable explanation for the lower conductivity of the 40:120_L sample is the decrease in the intrinsic conductivity of the magnetite phase upon a longer annealing. Moreover, only the T1u(2) and T1u(4) maghemite bands are more intense than their magnetite counterparts. According to literature, T1u(2) and T1u(3) modes of Fe3O4 appear at smaller wavenumber compared to the same modes of other ferrites (T2(2) and T2(3) for γ-Fe2O3), as can be seen in our results. A plausible hypothesis is that the delocalized electrons present in Fe3O4 could screen the effective electrostatic potential between octahedral iron cations and oxygen, producing a weaker interaction potential compared to γ-Fe2O3, thus lowering the resonance frequency of some vibrational modes.24
m γ-Fe2O3 bands. This is in agreement with Raman results, linking smaller maghemite contents to these samples synthesized with smaller oleate content. Finally, sample 40:120_L exhibits an anomalous behaviour from the overall one observed in the other samples. Taking into account the Raman data it can be said that the relative maghemite amounts in samples 40:120_S and 40:120_L are very similar. Therefore, the most probable explanation for the lower conductivity of the 40:120_L sample is the decrease in the intrinsic conductivity of the magnetite phase upon a longer annealing. Moreover, only the T1u(2) and T1u(4) maghemite bands are more intense than their magnetite counterparts. According to literature, T1u(2) and T1u(3) modes of Fe3O4 appear at smaller wavenumber compared to the same modes of other ferrites (T2(2) and T2(3) for γ-Fe2O3), as can be seen in our results. A plausible hypothesis is that the delocalized electrons present in Fe3O4 could screen the effective electrostatic potential between octahedral iron cations and oxygen, producing a weaker interaction potential compared to γ-Fe2O3, thus lowering the resonance frequency of some vibrational modes.24
Furthermore, 4 additional phonon bands were included in the fitting (see Fig. 6). Even though these bands are not as intense as the previously described ones, their presence is essential to correctly reproduce the subtle spectral features found around 470–500 cm−1 and 620–680 cm−1, and they are present in all samples with a lesser or greater strength. The origin of these bands can be related to the symmetry lowering of a structural model of γ-Fe2O3 with partial vacancy ordering. Table S3 from the ESI† introduces more details about the IR active modes of the space groups related to γ-Fe2O3, showing an increasing number of vibrational modes with decreasing crystal symmetry. This change of symmetry induces new modes linked to the P4132 structure that are activated by the new selection rules. This structure has 18 modes, although in our case only the most intense of the new ones were detected. Moreover, Pecharroman et al. found that the high frequency bands located around 620–680 cm−1 only appeared for partially or totally ordered γ-Fe2O3 samples.24 These additional bands present a relatively low intensity compared to the bands related to Fe3O4 and Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m γ-Fe2O3 for all samples, which is probably correlated to the low degree of vacancy ordering.
m γ-Fe2O3 for all samples, which is probably correlated to the low degree of vacancy ordering.
Even if IR spectroscopy is usually applied qualitatively, thanks to data treatment procedures that allow permittivity extraction, the quantification of certain properties can be achieved. In this case, the permittivity of the nanoparticles (εNP) is related to the conductivity of the samples by the following equation (in Gaussian units):55
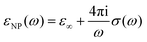 | (9) |
 | ||
| Fig. 7 DC conductivity of the samples computed from an extrapolation to zero frequency of eqn (9). | ||
Regarding conductivity results, it is important to highlight that the samples showing the most intense magnetite-specific absorption bands in relation to the maghemite-specific ones (40:120_S and 40:115_S) are those with the highest DC conductivity values. In contrast, the samples presenting the lowest conductivity values are related to more prominent maghemite-specific absorption bands (40:120_L, 40:125_S and 40:115_S_OAm). This relation is supported by the results obtained by Raman spectroscopy, where samples 40:125_S and 40:115_S_OAm showed the most intense γ-Fe2O3 A1g band. Considering this, it can be noted that, based on the conductivity values obtained from IR modeling, the samples with a greater γ-Fe2O3 proportion can be easily distinguished from those showing a lower content. Specifically, for samples 40:115_S, 40:120_S and 40:125_S an increase in oleate concentration during synthesis corresponds to a decrease in DC conductivity. Moreover, for different synthesis procedures (longer annealing time in the case of 40:120_L and the use of OAm as surfactant in the case of 40:115_S_OAm), the conductivity is further reduced. These decreases in conductivity can be attributed largely to higher maghemite contents, although the precise mechanism behind this correlation is beyond the scope of this paper.
Finally, the real and imaginary parts of the effective permittivity corresponding to the sample pellets can be seen in Fig. 8 (dashed lines), together with the Kramers–Kronig transform results derived directly from the experimental spectra (solid lines). Among all samples, the data related to those showing the best and worst overlap has been plotted (samples 40:115_S_Oam and 40:115_S, respectively). The spectra have been plotted from 200 to 7000 cm−1, as corresponding to the experimental spectral range, and from 0 to 1000 cm−1, highlighting the details of the curves in the range where the absorption bands are located.
 | ||
| Fig. 8 The real and imaginary parts of the effective permittivity of the samples computed using Kramers–Kronig analysis (solid lines) and obtained from the modelization (dashed lines), the best overlap was obtained for sample 40:115_S_Oam (FIR (a) and MIR (b)), and the worst for sample 40:115_S (FIR (c) and MIR (d)). The comparisons corresponding to the other samples can be found in Fig. S2 of the (ESI†). | ||
The Kramers–Kronig analysis aligns well with the model over the whole MIR range for all samples. Regarding the FIR range, while the overall tendency of the curves is well replicated, there is a slight discrepancy in the values, especially for samples 40:115_S and 40:120_L, and a small deviation observed for sample 40:120_S. Nonetheless, aside from these subtle differences, our model reflects well the spectral structure and behaviour shown by the Kramers–Kronig analysis. Examining the Kramers–Kronig spectra in more detail, the detailed spectral structure related to the additional bands is noticeable around 470–500 cm−1 and 620–680 cm−1, supporting the decision to include them in the model. This structure is more evident for samples 40:120_L and 40:115_S_OAm, agreeing with the fact that additional band intensities in the model are stronger for these samples.
In general, a good overlap is achieved for all samples, which enhances the plausibility of the model and indexation proposed in this work. These results, together with the consistency of a unique parameter set employed to model the optical behavior of all the samples, illustrate the significant reliability of the proposed methodology. Taking into account that the Kramers–Kronig analysis propagates the effect of small discrepancies to the whole spectral range, this comparison serves as a cross-check, and the agreement between both approaches reinforces the reliability of the fitting results.
4 Conclusions
This study demonstrated that IR spectroscopy-based methodologies show promise to retrieve detailed optical and structural insights about mixed magnetite–maghemite nanoparticles. The permittivity of practical-use samples was successfully extracted by fitting the reflectance spectra combining a permittivity model for conducting oxides, a effective medium theory applicable to high porosity systems and a precise band-indexation based on group theory and literature studies. The reliability of the model was tested by a comparison of the effective permittivity obtained and that derived using Kramers–Kronig analysis, for which a good overlapping was achieved. In addition, the same band parameter set was employed to model the spectral behavior of the different samples, kipping the width of the bands constant. This ensures consistency of band shape among samples, and strengthens the methodology.By applying this approach, the presence of both magnetite and maghemite was confirmed for all samples, as phonon bands related to both oxides needed to be included to accurately model the spectra. These findings corroborate the results obtained by Raman spectroscopy, and agree with the cell parameter computations from XRD experiments, as the derived cell parameter values lie in between those of pure Fe3O4 and ideal spinel γ-Fe2O3. Additionally, absorption bands related to the cation vacancy ordering in the maghemite lattice were identified, allowing the discrimination between two possible structural variants of maghemite. This proves that a combination of IR spectroscopy and an adequate modeling procedure could reveal detailed structural information about iron oxide nanomaterials. Furthermore, a quantitative estimation of the optical conductivity was also achieved, revealing that samples with a higher presence of magnetite, as indicated by more intense magnetite-specific absorption bands, show higher conductivity values.
New characterization techniques, along with the development of novel methodologies, are crucial for supporting the synthesis and application of novel magnetic nanomaterials. In this context, IR spectroscopy-based methodologies offer researchers the opportunity to obtain detailed compositional and structural information of nanoscale ferrites, while having the advantage of being widespread, easy-to-use and accessible. Regarding future perspectives, the methodology presented in this work could serve as a base for advanced analysis and phase quantification, which remains a relevant challenge.
Author contributions
M. Sainz-Menchón: investigation, data curation, formal analysis, writing – original draft; I. González de Arrieta: investigation, conceptualization, supervision, writing – review & editing; T. Echániz: supervision, writing – review & editing; K. Nader: resources; M. Insausti: resources; O. Rozenbaum: supervision, resources; A. Canizarès: resources; G. A. López: supervision, writing – review & editing.Data availability
The data contained in this article is available at Zenodo (https://doi.org/10.5281/zenodo.14744824).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by the Basque Government through research projects (IT-1714-22, IT1546-22 and Elkartek KK-2023/00041) and a Predoctoral grant (PRE-2022-1-0086). M. Insausti would like to acknowledge the Spanish Ministry of Science and Innovation for financial support under grant no. PID2022-136993OB-I00 (AEI/FEDER, UE), funded by MCIN/AEI/10.13039/501100011033 and, as appropriate, by “ERDF A way of making Europe”, by the “European Union”. M. Sainz-Menchón thanks the CEMHTI laboratory at CNRS Orléans for a research stay. Finally, the authors thank G. Madariaga and L. Cosson for assistance in the characterization of the materials.References
- K. G. Gareev, Magnetochemistry, 2023, 9, 119 CrossRef CAS
.
- E. Kianfar, J. Supercond. Novel Magn., 2021, 34, 1709–1735 CrossRef CAS
.
- M. C. Mañas Torres, C. Gila-Vilchez, F. J. Vazquez-Perez, P. Kuzhir, D. Momier, J.-C. Scimeca, A. Borderie, M. Goracci, F. Burel-Vandenbos and C. Blanco-Elices,
et al.
, ACS Appl. Mater. Interfaces, 2021, 13, 49692–49704 CrossRef
.
- C. Gila-Vilchez, L. Rodriguez-Arco, M. C. Mañas-Torres, L. Á. de Cienfuegos and M. T. Lopez-Lopez, Curr. Opin. Colloid Interface Sci., 2022, 62, 101644 CrossRef CAS
.
- M. Bielicka, J. Maliszewska, U. Klekotka, A. Wasilewska, E. Zambrzycka-Szelewa, D. Satuła and B. Kalska-Szostko, Environ. Nanotechnol., Monit. Manage., 2024, 22, 100958 Search PubMed
.
- H. Park, A. May, L. Portilla, H. Dietrich, F. Münch, T. Rejek, M. Sarcletti, L. Banspach, D. Zahn and M. Halik, Nat. Sustain., 2020, 3, 129–135 CrossRef
.
- D. Zhang, Y. Tian, S. Zou, J. Tang and Y. Li, Opt. Lett., 2019, 44, 2462–2465 CrossRef CAS PubMed
.
- P. Yang, H. Li, S. Zhang, L. Chen, H. Zhou, R. Tang, T. Zhou, F. Bao, Q. Zhang, L. He and X. Zhang, Nanoscale, 2016, 8, 19036–19042 RSC
.
- N. Dudchenko, S. Pawar, I. Perelshtein and D. Fixler, Materials, 2022, 15, 2601 CrossRef CAS PubMed
.
- A. Włodarczyk, S. Gorgoń, A. Radoń and K. Bajdak-Rusinek, Nanomaterials, 2022, 12, 1807 Search PubMed
.
- F. Oltolina, A. Peigneux, D. Colangelo, N. Clemente, A. DUrso, G. Valente, G. R. Iglesias, C. Jiménez-Lopez and M. Prat, Cancers, 2020, 12, 2564 CrossRef CAS PubMed
.
- M. Bañobre-López, A. Teijeiro and J. Rivas, Rep. Pract. Oncol. Radiother., 2013, 18, 397–400 CrossRef PubMed
.
- D. Gandia, L. Gandarias, I. Rodrigo, J. Robles-Garca, R. Das, E. Garaio, J. Á. Garca, M.-H. Phan, H. Srikanth and I. Orue,
et al.
, Small, 2019, 15, 1902626 CrossRef CAS PubMed
.
- K. Nader, I. Castellanos-Rubio, I. Orue, D. Iglesias-Rojas, A. Barón, I. G. de Muro, L. Lezama and M. Insausti, J. Solid State Chem., 2022, 316, 123619 CrossRef CAS
.
- I. Castellanos-Rubio, O. Arriortua, D. Iglesias-Rojas, A. Barón, I. Rodrigo, L. Marcano, J. S. Garitaonandia, I. Orue, M. L. Fdez-Gubieda and M. Insausti, Chem. Mater., 2021, 33, 8693–8704 CrossRef CAS PubMed
.
- M. Widdrat, M. Kumari, É. Tompa, M. Pósfai, A. M. Hirt and D. Faivre, ChemPlusChem, 2014, 79, 1225–1233 CrossRef CAS PubMed
.
- M. Stoia, R. Istratie and C. Păcurariu, J. Therm. Anal. Calorim., 2016, 125, 1185–1198 CrossRef CAS
.
- A. Shmakov, G. Kryukova, S. Tsybulya, A. Chuvilin and L. Solovyeva, J. Appl. Crystallogr., 1995, 28, 141–145 Search PubMed
.
- J.-E. Jørgensen, L. Mosegaard, L. E. Thomsen, T. R. Jensen and J. C. Hanson, J. Solid State Chem., 2007, 180, 180–185 CrossRef
.
- I. Dézsi, C. Fetzer, Á. Gombkötö, I. Szücs, J. Gubicza and T. Ungár, J. Appl. Phys., 2008, 103, 104312 CrossRef
.
- S. Singh and N. Goswami, J. Mater. Sci.: Mater. Electron., 2021, 32, 26857–26870 CrossRef CAS
.
- O. N. Shebanova and P. Lazor, J. Raman Spectrosc., 2003, 34, 845–852 CrossRef CAS
.
- D. L. De Faria, S. Venâncio Silva and M. T. de Oliveira, J. Raman Spectrosc., 1997, 28, 873–878 CrossRef CAS
.
- C. Pecharromán, T. Gonzalez-Carreno and J. E. Iglesias, Phys. Chem. Miner., 1995, 22, 21–29 CrossRef
.
- Y. Zhang, N. Kohler and M. Zhang, Biomaterials, 2002, 23, 1553–1561 CrossRef CAS PubMed
.
- B. Lesiak, N. Rangam, P. Jiricek, I. Gordeev, J. Tóth, L. Kövér, M. Mohai and P. Borowicz, Front. Chem., 2019, 7, 642 CrossRef CAS PubMed
.
- T. G. Mayerhöfer, A. K. Singh, J.-S. Huang, C. Krafft and J. Popp, Spectrochim. Acta, Part A, 2024, 305, 123549 CrossRef PubMed
.
- M. Sainz-Menchón, I. González de Arrieta, A. Zaki, F. Fayon and G. A. López, Appl. Spectrosc., 2024, 78, 209–216 CrossRef PubMed
.
- D. D. S. Meneses, M. Malki and P. Echegut, J. Non-Cryst. Solids, 2006, 352, 769–776 CrossRef
.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CAS
.
- Y. M. Mos, A. C. Vermeulen, C. J. Buisman and J. Weijma, Geomicrobiol. J., 2018, 35, 511–517 CAS
.
-
J. W. Anthony, R. A. Bideaux, K. W. Bladh and M. C. Nichols, Handbook of Mineralogy, Mineralogical Society of America, Chantilly, USA, 1988 Search PubMed
.
- F. Gervais, Mater. Sci. Eng., R, 2002, 39, 29–92 Search PubMed
.
- J.-F. Brun, L. Del Campo, D. De Sousa Meneses and P. Echegut, J. Appl. Phys., 2013, 114, 223501 Search PubMed
.
- I. González de Arrieta, L. González-Fernández, T. Echániz, L. del Campo, D. De Sousa Meneses and G. López, J. Appl. Phys., 2021, 130, 075105 Search PubMed
.
- H. Looyenga, Physica, 1965, 31, 401–406 CAS
.
- I. González de Arrieta, L. Del Campo and D. De Sousa Meneses, Phys. Chem. Chem. Phys., 2021, 23, 13095–13105 Search PubMed
.
- I. González de Arrieta, A. Zaki, A. Canizarès, E. Véron, C. Genevois, L. Del Campo, C. Blanchard and O. Rozenbaum, Spectrochim. Acta, Part A, 2023, 298, 122795 Search PubMed
.
- J.-F. Brun, D. de Sousa Meneses, B. Rousseau and P. Echegut, Appl. Spectrosc., 2001, 55, 774–780 CAS
.
- D. Louer and A. Boultif, et al., Ninth European Powder Diffraction Conference: Prague, September 2–5, 2004, 2006, pp. 225–230.
-
Stoie&Cie, WinXPOW, Stoe & Cie, Darmstadt, Germany, 2004 Search PubMed
.
- O. Lemine, K. Omri, B. Zhang, L. El Mir, M. Sajieddine, A. Alyamani and M. Bououdina, Superlattices Microstruct., 2012, 52, 793–799 CAS
.
- A. Cervellino, R. Frison, G. Cernuto, A. Guagliardi and N. Masciocchi, J. Appl. Crystallogr., 2014, 47, 1755–1761 CAS
.
- O. Shilova, A. Nikolaev, A. Kovalenko, A. Sinelnikov, G. Kopitsa and A. Baranchikov, Russ. J. Inorg. Chem., 2020, 65, 426–430 CAS
.
- W. Kim, C.-Y. Suh, S.-W. Cho, K.-M. Roh, H. Kwon, K. Song and I.-J. Shon, Talanta, 2012, 94, 348–352 CAS
.
- I. Chamritski and G. Burns, J. Phys. Chem. B, 2005, 109, 4965–4968 CrossRef CAS PubMed
.
- S. P. Schwaminger, C. Syhr and S. Berensmeier, Crystals, 2020, 10, 214 CrossRef CAS
.
- L. Gasparov, D. Tanner, D. Romero, H. Berger, G. Margaritondo and L. Forro, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 7939 CrossRef CAS
.
- J. Ebad-Allah, L. Baldassarre, M. Sing, R. Claessen, V. Brabers and C. A. Kuntscher, J. Phys.: Condens. Matter, 2012, 25, 035602 CrossRef PubMed
.
- D. De Sousa Meneses, Focus, https://www.cemhti.cnrs-orleans.fr/pot/software/focus.html.
- M. I. Aroyo, J. M. Perez-Mato, D. Orobengoa, E. Tasci, G. de la Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197 CAS
.
- L. Zheng, W. Su, Z. Qi, Y. Xu, M. Zhou and Y. Xie, Nanotechnology, 2011, 22, 485706 CrossRef PubMed
.
- J. F. Bell III, T. L. Roush and R. V. Morris, J. Geophys. Res.: Planets, 1995, 100, 5297–5307 CrossRef
.
- M. Ishii, M. Nakahira and T. Yamanaka, Solid State Commun., 1972, 11, 209–212 CrossRef CAS
.
-
M. Dressel and G. Grüner, Electrodynamics of solids: optical properties of electrons in matter, Cambridge University Press, 2002 Search PubMed
.
-
R. M. Cornell and U. Schwertmann, et al., The iron oxides: structure, properties, reactions, occurrences, and uses, Wiley-vch, Weinheim, 2003, vol. 664 Search PubMed
.
- B. Lorenz and D. Ihle, Phys. Status Solidi B, 1975, 69, 451–457 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00503e |
| This journal is © the Owner Societies 2025 |


