 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Analyzing spectral distributions of charge transfer character in ensembles: a case study on the reaction center of photosystem II†
Adam
Šrut
 a,
Sinjini
Bhattacharjee
a,
Sinjini
Bhattacharjee
 b,
Dimitrios A.
Pantazis
b,
Dimitrios A.
Pantazis
 *b and
Vera
Krewald
*b and
Vera
Krewald
 *a
*a
aTU Darmstadt, Department of Chemistry, Quantum Chemistry, Peter-Grünbegr-Straße, 64287 Darmstadt, Germany. E-mail: vera.krewald@tu-darmstadt.de
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Rühr, Germany. E-mail: dimitrios.pantazis@kofo.mpg.de
First published on 4th April 2025
Abstract
Understanding the primary charge separation events in Nature's photosynthetic reaction centers is a key step toward harnessing the microscopic processes of light conversion into chemical energy. Despite intense research efforts employing state-of-the-art spectroscopic and theoretical techniques, the precise nature of energy transfer and charge separation events in these systems are still insufficiently understood. Herein, we present a computational approach that enables analysis of the charge transfer character in excited electronic states with inclusion of thermal effects in ensembles. We showcase an application of this approach to the reaction center of photosystem II, focusing on the ChlD1PheoD1 and PD1PD2 pairs of pigments. We find that the ChlD1PheoD1 pair is a more likely candidate for the primary charge separation than the PD1PD2 pair. Our computational approach is transferable to other biological and man-made charge separation and charge transfer systems.
1. Introduction
The thorough understanding of energy and electron transfer mechanisms in photosynthetic pigment–protein complexes is essential for the knowledge-guided design of synthetic platforms and devices that will drive the energy transition. Photosystem II (PSII) of oxygenic photosynthesis1 is one of the most important potential blueprints for artificial light-driven charge-separating devices.2–4 The four chlorophyll and two pheophytin molecules that comprise the reaction center (RC) of PSII (Fig. 1) are able to convert with ultimate efficiency visible light to electron flow, powering water oxidation and plastoquinone reduction.5–7 Three main factors need to be elucidated for understanding the function of the PSII RC, each factor representing a substantial challenge for both experiment and theory: (a) the electronic structure of the pigments themselves, (b) the influence of the protein environment in terms of structure and electrostatics, and (c) the role that dynamic motion plays in modulating the electronic structure, absorption properties, and function of RC pigments. Since the initial charge separation is intimately tied to the light absorption process, the electronic structure analysis must encompass the ground state and the spectrum of low-lying excited states.Crucial advances have been made toward a reliable description of the electronic structure of chlorophylls using modern quantum chemical methods,8–11 while the influence of the protein environment on the PSII RC properties and function has also began to be reliably quantified in recent studies using hybrid quantum-mechanics/molecular-mechanics (QM/MM) approaches.12–15 Initial studies have also begun to consider how the flexibility of the protein environment affects the properties of RC pigments.16,17 On the other hand, the flexibility of the geometric structures of the pigments themselves is a crucial factor that remains unexplored, in part because the classical force fields used in typical molecular dynamics studies of PSII are not able to correctly sample the conformation flexibility of the photosynthetic macrocycles. This flexibility however can have important implications for the theoretical description of the primary RC function13 as well as for the charge separation processes that follow the initial photo-initiation.18–20
Methods for characterising excited states are well established.21,22 Specifically, the charge-transfer character of an excited state can be conveniently analysed with electron–hole correlation plots23 or natural transition orbitals.24 These methods represent both qualitative and quantitative ways to analyze the wavefunction of an excited state. A distinct challenge, however, is how to perform such analysis in an ensemble of distorted geometries, as it will be present in reality due to zero point vibrations, conformational flexibility and other effects. The electronic states will reorder and mix among each other upon distortion of the nuclear coordinates. Each member of the ensemble can thus possess a different set of electronic states. Herein, we present a new way to analyse a thermally populated nuclear ensemble. We solve the issue of reordering and mixing of the electronic states by calculating the electronic properties in a chosen set of reference states.25,26 Our method is rooted in the determination of wavefunction overlaps and is exemplified with the ChlD1PheoD1 and PD1PD2 pairs of Photosystem II. We expect the method to be generally applicable to electron transfer chains in enzymes as well as in synthetic charge-separating systems.
2. Methodology
The fundamental idea of the presented approach is to analyze an ensemble of distorted geometries in a unified basis of electronic states. The ensemble is generated only by sampling the individual pigment pairs in the frozen environment of the protein. The reference states, with respect to which the ensemble is analyzed, are the electronic states at Franck–Condon (FC) geometry. These states are well characterized by means of natural transition orbitals and charge transfer numbers.At each geometry in the ensemble, wavefunction overlaps of the excited states with the reference states are calculated. These are then collected into an overlap matrix with elements:
| Sij = 〈ψFCi|ψdistj〉 | (1) |
 | (2) |
In reality, however, the overlap matrix will deviate from orthogonality 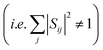 because of the displacement of basis functions, truncation of the wavefunction and interaction with external states.27 The overlap matrix can be, however, orthogonalized using Löwdin orthogonalization.27,28 The resulting matrix will then satisfy eqn (2). We further note that in case of extremely large structural changes the calculation of wavefunction overlaps might be too inaccurate and the orthogonalized matrix will deviate too much from the original one.
because of the displacement of basis functions, truncation of the wavefunction and interaction with external states.27 The overlap matrix can be, however, orthogonalized using Löwdin orthogonalization.27,28 The resulting matrix will then satisfy eqn (2). We further note that in case of extremely large structural changes the calculation of wavefunction overlaps might be too inaccurate and the orthogonalized matrix will deviate too much from the original one.
We wish to use the electronic states at the FC geometry as reference states (or the so-called diabatic basis) in the analysis of the ensemble. The quantity we thus need is the expectation value of a given operator for a system in a reference state ψFCα, but at a distorted geometry. The reference state can be written as an expansion of the electronic states at the distorted geometry using the overlap matrix:
 | (3) |
Inserting this expansion into the formula for an expectation value of a Hamiltonian operator Ĥ for a system in a state |ψFCα〉 will result in:
 | (4) |
 | (5) |
This approach is conceptually similar to the local diabatization scheme frequently used in non-adiabatic dynamics.29,30 Notably, this idea was recently employed for parameterization of vibronic coupling Hamiltonian for non-adiabatic quantum dynamics of the PSII RC.31
The transition dipole moments and charge transfer characters describe the transition between the ground state and an excited state which needs to be taken into account in the diabatization procedure. To make the diabatization of these quantities possible we are going to assume that the electronic ground state remains unaffected by molecular vibrations, i.e. |ψFCGS〉 = |ψdistGS〉. This is a reasonable assumption if the ground state has a closed shell configuration and is energetically well separated from the excited states which precludes any mutual mixing. The magnitude of the transition dipole moment (|![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) GS→α|2) cannot be converted directly into the new basis. First, the individual Cartesian components have to be calculated in the new basis. For example, the x-component is calculated as:
GS→α|2) cannot be converted directly into the new basis. First, the individual Cartesian components have to be calculated in the new basis. For example, the x-component is calculated as:
 | (6) |
The magnitude of the transition dipole moment vector is then computed from its components:
|![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) GS→α|2 = μx,GS→α2 + μy,GS→α2 + μz,GS→α2 GS→α|2 = μx,GS→α2 + μy,GS→α2 + μz,GS→α2 | (7) |
The transition dipole moment is converted into oscillator strength, which can be used to compute an absorption spectrum, according to:
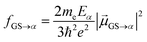 | (8) |
For the charge transfer numbers, the problem is essentially similar to the computation of excited state characters of spin-mixed states, described in ref. 32 One can thus write:
 | (9) |
The absorption spectra, densities of states and charge transfer densities were calculated by collecting the corresponding quantities for each electronic state and distorted geometry along the energy axis into a line spectrum. This spectrum is subsequently broadened via a convolution with a Gaussian. The formula for the absorption spectrum of a single electronic state is:
 | (10) |
3. Computational details
The molecular dynamics simulations of PSII were unchanged from the previous studies.11,13,33 The model of the PSII is based on the crystal structure of T. vulcanus (3WU2.pdb).34 A detailed description is provided in the ESI.†QM/MM geometry optimizations for the reaction center pigments (ChlD1PheoD1, PD1PD2) were performed using the PBE functional,35 def2-TZVP basis set36 and electrostatic embedding in ORCA 5.0.37 Using a GGA functional for optimizations of chlorophylls and related systems is known to provide reasonable structures while maintaining a moderate computational cost.8,10,12 Optimized structures are depicted in Fig. 2a and b. Frequency calculations were performed in vacuo for the optimized pigment pairs on the PBE/def2-TZVP level. Further details are given in the ESI.†
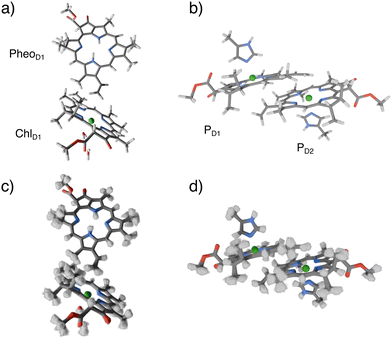 | ||
| Fig. 2 QM/MM optimized structures of the ChlD1PheoD1 and PD1PD2 pairs (a) and (b) and their sampled geometries (c) and (d) at 300 K using a Wigner sampling method. | ||
The sampling of the thermal ensemble was achieved with the Wigner sampling method at 300 K utilizing the frequency calculation described above. The implementation in the SHARC package38 was used. Modes with imaginary frequencies or frequencies lower than 100 cm−1 were discarded from the sampling procedure. An ensemble of 700 distorted geometries was generated for further single-point calculations. The ensembles are shown in Fig. 2c and d. The sampled geometries were then inserted into the frozen protein matrix. We note that additional sampling of the protein environment is conceivable but it would significantly increase the number and complexity of the calculations in practice. For these reasons we will not explore this effect here.
Excited states at each geometry in the ensemble were calculated with the time-dependent density functional theory (TD-DFT) utilizing the TURBOMOLE package.39 The range-separated density functional ωB97X-V40 was employed together with the def2-TZVP basis set.36 The calculations employed the resolution of identity approximation,41 an integration grid of size m3,42 and the convergence criterion of the self-consistent field method was set to 10−8Eh. Seven excited states were calculated for each geometry of the ensemble without the Tamm–Dancoff approximation. The protein environment was modeled as point charges.
Charge transfer numbers were computed using the TheoDORE package.43 The molecule was divided into two fragments corresponding to the two monomers, i.e. ChlD1 and PheoD1, or PD1 and PD2. Since the TD-DFT calculations were performed without the Tamm–Dancoff approximation which employs different normalization of the excitation vector (X), the charge transfer numbers for each state needed to be renormalized to sum up to one.
The overlaps of the wavefunctions between the Franck–Condon and distorted geometries were computed with the WFoverlap program,27 which is a part of the SHARC package.38 The program requires overlaps of atomic orbitals (AOs) between the two geometries, molecular orbitals (MOs), and electronic states as expansions of Slater determinants. Using the MO coefficients of the two wavefunctions, the AO overlaps are transformed to the MO overlaps and subsequently to the overlaps between the determinants.27
The overlap matrix between the AO bases was computed using the ORCA37 orca_fragovl module. The two gbw files for both geometries required as an input can be generated for example with a Hartree–Fock calculation with no SCF iterations and the same basis set as the TD-DFT calculations. The output of orca_fragovl was then reformatted for the WFoverlap program. The 1s orbitals of non-hydrogen atoms were discarded from the overlap calculation.
The TD-DFT states are described as expansions of singly excited determinants. The expansion coefficients are written into the sing_a file generated by TURBOMOLE. They need to be reformatted for the WFoverlap program.
The studied systems contain around 3000 orbitals and have hundreds of thousands of possible single excitations. Calculating a wavefunction overlap would thus require determining roughly 1011 determinant pairs. A calculation of this magnitude would be too demanding regarding both CPU time and memory requirements. To reduce the number of singly excited determinants we employed a commonly used truncation of the wavefunction.27 The squared expansion coefficients were first sorted in descending order. Then, the configurations were taken from the ordered list to the overlap calculation until the sum of the squared expansion coefficient reached a threshold of 0.996 for ChlD1PheoD1 pair and 0.994 for PD1PD2 pair. In this way, the number of determinants was reduced to only several thousands which led to a significant reduction of computational costs while maintaining accuracy.
The analysis scripts can be freely accessed in an open-source format at: https://git.rwth-aachen.de/ak-krewald/nuclear_ensemble_analysis. Details on their usage are provided in the ESI.†
4. Results and discussion
4.1. State mixing and reordering in nuclear ensembles
To calculate the total absorption spectrum for the full ensemble it would be straightforward to sum over the individual spectra of each member of the ensemble. Similarly, the densities of states (DOS) and densities of charge transfer (CT) character can be easily accessed. However, for a more detailed analysis it is of interest to deconvolve the properties of the average spectrum into the contributions of the individual electronic states. Examining the characters and contributions of individual states in each member of an ensemble is not straightforward because the electronic structure at each distorted geometry will differ. This is caused by a reordering of the excited electronic states or by a mixing of their characters. In other words, the electronic states of the distorted geometries are not going to be in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence with the states at the optimized geometry. The physical origins of reordering and mixing of the excited states can be traced to the presence of conical intersections and the Herzberg–Teller effect,44 respectively.
1 correspondence with the states at the optimized geometry. The physical origins of reordering and mixing of the excited states can be traced to the presence of conical intersections and the Herzberg–Teller effect,44 respectively.
For the discussion of charge separation in light harvesting and energy conversion devices, it is of central importance to understand at which energies the charge separation takes place and which electronically excited states are responsible for this process. To facilitate this analysis, we chose a set of well-defined reference states and use these as a basis for the analysis of spectral properties. An intuitive and meaningful choice of reference states are the electronic states at the optimized geometry, i.e. the FC geometry. We analyse their characters via charge transfer numbers43 (see Fig. 3) and natural transition orbitals (see ESI†).
The reference states are characterized in Fig. 3via the charge transfer numbers. For the ChlD1PheoD1 pair (Fig. 3a), we find three charge transfer states at 1.64, 2.15 and 2.80 eV. They correspond to the first, third and seventh state, and have pure ChlD1 → PheoD1 CT character. For the PD1PD2 pair (Fig. 3b), we also find three CT states, here at 2.90, 3.19 and 3.35 eV, which correspond to the fifth, sixth and seventh states at the FC point. These states have either PD1 → PD2 or PD2 → PD1 character mixed with local excitation character.
To assess the state characters at the distorted geometries, we define a transformation between the reference states and the electronic states at a particular distorted geometry via wavefunction (WF) overlaps27,45 of the two sets of states. Each electronic state at a distorted geometry is expressed as a linear combination of the reference states. The properties of the excited states in the distorted geometries are calculated accordingly.
In Fig. 4 we show the CT characters and oscillator strengths for the reference states of the ChlD1PheoD1 pair at the FC geometry. And the effects of the vibrational distortions on the electronic states are illustrated for two representative geometries of the ensemble, geometry #58 and geometry #355.
In geometry #58, the excited states arise from the mixing of state characters at the FC geometry. This means that an electronic state of the distorted geometry has similar WF overlap values with two or more states at the reference geometry, as is illustrated with connecting lines of different weights in Fig. 4. As a result, the excited states of this geometry have intermediate values of CT character, in contrast to the reference states that have CT character of either close to 0% (local excitations) or 100% (CT excitations). In contrast, in geometry #355 the excited states are formed mainly by reordering of the reference states. This means that each excited state at a distorted geometry has significant overlap with only one of the reference states. This reordering is shown in Fig. 4 by one dominant line connecting the states at the distorted geometry with the reference states at the FC geometry. As a result, the excited states are also either CT states or locally excited ones (i.e. CT character close to 0 or 100%); only their order is different than at the FC geometry.
In conclusion, relating the excited states between a distorted geometry in the ensemble and FC geometry or between two distorted geometries of the ensemble simply based on their energetic ordering cannot provide detailed insight into the properties of the ensemble. This is exemplified Fig. 4, where a change in geometry by a vibrational distortion leads to a different set of excited electronic states.
4.2. Analysis with the reference states
Electronic states in a nuclear ensemble need to be characterized in a unified basis to suppress their mixing and reordering upon change in the nuclear configuration. Herein, we propose to use the electronic states at the FC geometry as the reference states and express each electronic state at a distorted geometry of the ensemble as a linear combination of them utilizing the wavefunction overlaps. The workflow is described in the Methodology section. In Fig. 5, we illustrate the proposed method schematically.Fig. 5a shows the conventional calculation of a spectral feature (absorption spectrum, density of states, etc.) where the electronic states are simply ordered by their energies. The resulting composition of the first peak in the spectrum is a mixture of two electronic states with different characters. When the analysis in the basis of the reference states as proposed here is introduced, the excited states become ordered by their character, see Fig. 5b. The spectral features are now comprised only of excited states with the same character. In this way, the true distribution of the density of a single electronic state (or any other property) along the energy axis can be extracted from a nuclear ensemble.
While the results presented in this work are based on TD-DFT calculations, an extension to wavefunction methods is conceivable and not hindered by any fundamental limitations. This will be connected with a higher computational cost when computing the wavefunction overlaps, but the true bottleneck will lie in reformatting the electronic states to expansions of Slater determinants. Efforts in this direction were recently presented in conjunction with different quantum chemistry packages.27,46,47
4.3. Reaction center in photosystem II
Applying the presented methodology to the thermally populated ensembles of the PSII pigments ChlD1PheoD1 and PD1PD2 means that we will be able to correctly discuss the contributions of the individual states to the DOS, to the absorption spectra, and to the densities of CT character.For the ChlD1PheoD1 pair, the distribution of the density of ChlD1 → PheoD1 CT character is almost uniform, see Fig. 6a. The CT character is predominantly due to three excited states, S1, S4 and S7. Importantly, the lowest-energy state has CT character (S1 state). This means that for any type of excitation, either directly by visible light or by energy transfer from the antenna system, the ChlD1PheoD1 pair is expected to relax by internal conversion into this charge separated state. The absorption spectrum of ChlD1PheoD1 pair is plotted in Fig. 6b. It covers almost the entire visible spectrum with the highest absorption at the low energy end. The pair can thus act as a light absorber itself, e.g. via S2, and then relax into the charge separated state S1.
For the PD1PD2 pair, charge transfer states (PD1 → PD2, PD2 → PD1) appear only at the high energy end of the spectrum, see Fig. 6c. Notably, no CT character occurs for the lowest lying excited states. This means that any energy that the PD1PD2 pair receives, radiatively or non-radiatively, would not be funneled into a charge separated state upon internal conversion. This behaviour is in a strong contrast to the ChlD1PheoD1 pair.
The properties of the PD1PD2 pair as a light absorber also differ from ChlD1PheoD1 pair. The highest absorption is observed only at the red and blue ends of the visible spectrum, see Fig. 6d, while in the energy window from 2.1 to 2.7 eV the PD1PD2 pair absorbs only weakly. The pair thus appears to utilise visible light in a not very efficient manner, supporting the argument that the excitation of the PD1PD2 pair happens via an energy transfer.
Looking at the interplay of the two pairs as reflected by our findings, we note that the DOS of ChlD1PheoD1 extends almost to 1 eV at the low energy end, whereas the DOS of the PD1PD2 pair does not go below 1.5 eV. This implies that energy transfer from PD1PD2 to ChlD1PheoD1 might be possible, allowing for charge separation in the S1 state of ChlD1PheoD1 pair at the bottom of the energy funnel.
Pathways for the charge separation often involve both pigment pairs together, which leads to multiple possible charge separated species (radical pairs) within the D1 branch, with the exact identities of electron transfer intermediates remaining under investigation.13,17,18,48–52 Although the requisite calculations at the present level of theory would be computationally very demanding, extending the presented methodology to the whole tetramer is in principle possible and conceptually straightforward.
5. Conclusion
Herein, we present an ensemble-based computational approach that accounts for the influence of zero-point energy and finite temperature on the electronic states of pigments in PSII. Furthermore, by utilizing wavefunction overlaps with a set of reference states, the mixing and reordering of electronic states in the ensemble is resolved, which provides insights into individual state contributions to the spectral properties like the DOS, the density of CT character or the absorption spectrum. Our method is transferable to any biological or artificial system in which charge-separation or charge transfer can occur (i.e. systems with well-defined donor and acceptor sites).Our results suggest that the ability of the ChlD1PheoD1 pair to create a charge separated species is much greater than of the PD1PD2 pair. Intriguingly, the ChlD1PheoD1 pair exhibits a uniform distribution of ChlD1 → PheoD1 CT character over the entire visible spectrum. Moreover, the lowest lying excited state is a CT state, which suggests a possible stabilization of the charge separated species after vibrational cooling and internal conversion. In contrast, CT character is only found at the high energy end of the visible spectrum of the PD1PD2 pair. Internal conversion after an excitation would thus produce only locally excited states. The present results therefore provide independent support to the mechanistic scenario where the ChlD1PheoD1 pair is the actual “special pair” for the primary charge separation in PSII. This conclusion contrasts with interpretations proposed in some experimental studies that favor initial charge separation within the PD1PD2 pair or implicate ChlD1 as acceptor,51,53,54 but is aligned with the intepretations reached by several other studies,19,55,56 as well as with recent multiscale theoretical investigations of the RC.11–13,16,17
In terms of future perspectives, we note that our results can be used to parameterize model exciton Hamiltonians for open quantum system simulations to reconstruct time-resolved or two-dimensional spectra,20,57–59 an approach that would complement other recent efforts in this direction.31 Most importantly, the approach demonstrated here for the charge-separating pigment assembly of oxygenic photosynthesis can be applied directly to synthetic systems, leading to a deeper understanding of the structural factors—and, hence, identification of design principles—that control the initiation of electron transfer cascades in natural and artificial photosynthesis.
Data availability
The data supporting this article have been included as part of the ESI.† The analysis scripts are freely available in an open-source format at: https://git.rwth-aachen.de/ak-krewald/nuclear_ensemble_analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Felix Plasser for insightful discussions. D. A. P. and S. B. gratefully acknowledge support by the Max Planck Society. S. B. thanks the International Max Planck Research School on Reactive Structure Analysis for Chemical Reactions (IMPRS-RECHARGE) for support. A. S. thanks the Merck’sche Gesellschaft für Kunst und Wissenschaft e.V. for financial support. The authors gratefully acknowledge the computing time provided to them on the high-performance computer Lichtenberg at the NHR Center NHR4CES at TU Darmstadt. This is funded by the German Federal Ministry of Education and Research (BMBF) and the Hessian Ministry of Science and Research, Art and Culture (HMWK). Open Access funding provided by the Max Planck Society.Notes and references
- R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley, Chichester, 3rd edn, 2021, pp. 352 Search PubMed.
- M. R. Wasielewski, Chem. Rev., 1992, 92, 435–461 CrossRef CAS.
- H. Dau and I. Zaharieva, Acc. Chem. Res., 2009, 42, 1861–1870 CrossRef CAS PubMed.
- L. Hammarström, Acc. Chem. Res., 2015, 48, 840–850 CrossRef PubMed.
- R. Croce, R. v Grondelle, H. v Amerongen and I. v Stokkum, Light Harvesting in Photosynthesis, Taylor & Francis/CRC Press, Boca Raton, 2018 Search PubMed.
- D. Shevela, J. F. Kern, G. Govindjee and J. Messinger, Photosynth. Res., 2023, 156, 279–307 CrossRef CAS PubMed.
- R. Croce and H. van Amerongen, Nat. Chem. Biol., 2014, 10, 492–501 CrossRef CAS PubMed.
- A. Sirohiwal, R. Berraud-Pache, F. Neese, R. Izsák and D. A. Pantazis, J. Phys. Chem. B, 2020, 124, 8761–8771 CrossRef CAS PubMed.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2021, 17, 1858–1873 CrossRef CAS PubMed.
- A. Sirohiwal and D. A. Pantazis, Phys. Chem. Chem. Phys., 2021, 23, 24677–24684 RSC.
- M. Drosou, S. Bhattacharjee and D. A. Pantazis, J. Chem. Theory Comput., 2024, 20, 7210–7226 CAS.
- A. Sirohiwal, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2020, 142, 18174–18190 CrossRef CAS PubMed.
- A. Sirohiwal and D. A. Pantazis, Acc. Chem. Res., 2023, 56, 2921–2932 CrossRef CAS PubMed.
- D. Narzi, D. Bovi, P. De Gaetano and L. Guidoni, J. Am. Chem. Soc., 2016, 138, 257–264 CrossRef CAS PubMed.
- A. Forde, S. Maity, V. M. Freixas, S. Fernandez-Alberti, A. J. Neukirch, U. Kleinekathöfer and S. Tretiak, J. Phys. Chem. Lett., 2024, 15, 4142–4150 CrossRef CAS PubMed.
- A. Sirohiwal and D. A. Pantazis, Angew. Chem., Int. Ed., 2022, 61, e202200356 CrossRef CAS PubMed.
- M. Capone, A. Sirohiwal, M. Aschi, D. A. Pantazis and I. Daidone, Angew. Chem., Int. Ed., 2023, 62, e202216276 CrossRef CAS PubMed.
- H. H. Nguyen, Y. Song, E. L. Maret, Y. Silori, R. Willow, C. F. Yocum and J. P. Ogilvie, Sci. Adv., 2023, 9, eade7190 CrossRef CAS PubMed.
- Y. Yoneda, E. A. Arsenault, S.-J. Yang, K. Orcutt, M. Iwai and G. R. Fleming, Nat. Commun., 2022, 13, 2275 CrossRef CAS PubMed.
- H.-G. Duan, V. I. Prokhorenko, E. Wientjes, R. Croce, M. Thorwart and R. J. D. Miller, Sci. Rep., 2017, 7, 12347 CrossRef PubMed.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- F. Plasser, S. A. Bäppler, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024107 CrossRef PubMed.
- F. Plasser and H. Lischka, J. Chem. Theory Comput., 2012, 8, 2777–2789 CrossRef CAS PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- H. Tamura, J. Phys. Chem. A, 2016, 120, 9341–9347 CrossRef CAS PubMed.
- Y. Xie, S. Jiang, J. Zheng and Z. Lan, J. Phys. Chem. A, 2017, 121, 9567–9578 CrossRef CAS PubMed.
- F. Plasser, M. Ruckenbauer, S. Mai, M. Oppel, P. Marquetand and L. González, J. Chem. Theory Comput., 2016, 12, 1207–1219 CAS.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615 CAS.
- F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico and H. Lischka, J. Chem. Phys., 2012, 137, 22A514 Search PubMed.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615 CrossRef CAS.
- H. Tamura, K. Saito and H. Ishikita, Chem. Sci., 2021, 12, 8131–8140 CAS.
- S. Mai, F. Plasser, J. Dorn, M. Fumanal, C. Daniel and L. González, Coord. Chem. Rev., 2018, 361, 74–97 CrossRef CAS.
- S. Bhattacharjee, S. Arra, I. Daidone and D. A. Pantazis, Chem. Sci., 2024, 15, 7269–7284 RSC.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, WIREs Comput. Mol. Sci., 2022, 12, 1–15 Search PubMed.
- S. Mai, D. Avagliano, M. Heindl, P. Marquetand, M. F. S. J. Menger, M. Oppel, F. Plasser, S. Polonius, M. Ruckenbauer, Y. Shu, D. G. Truhlar, L. Zhang, P. Zobel and L. González, SHARC3.0: Surface Hopping Including Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics, 2023, https://sharc-md.org/ Search PubMed.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS.
- F. Plasser, J. Chem. Phys., 2020, 152, 084108 CrossRef CAS PubMed.
- W. Domcke, H. Köppel and L. S. Cederbaum, Mol. Phys., 1981, 43, 851–875 CrossRef CAS.
- H.-T. Chen, J. Chen, D. V. Cofer-Shabica, Z. Zhou, V. Athavale, G. Medders, M. F. S. J. Menger, J. E. Subotnik and Z. Jin, J. Chem. Theory Comput., 2022, 18, 3296–3307 CrossRef CAS PubMed.
- G. Cárdenas and J. J. Nogueira, Int. J. Quantum Chem., 2021, 121, 26533 CrossRef.
- A. Loreti, V. M. Freixas, D. Avagliano, F. Segatta, H. Song, S. Tretiak, S. Mukamel, M. Garavelli, N. Govind and A. Nenov, J. Chem. Theory Comput., 2024, 20, 4804–4819 CrossRef CAS PubMed.
- E. Romero, I. H. Van Stokkum, V. I. Novoderezhkin, J. P. Dekker and R. Van Grondelle, Biochemistry, 2010, 49, 4300–4307 CrossRef CAS PubMed.
- V. I. Novoderezhkin, E. Romero, J. P. Dekker and R. van Grondelle, ChemPhysChem, 2011, 12, 681–688 CrossRef CAS PubMed.
- T. Renger and E. Schlodder, J. Photochem. Photobiol., B, 2011, 104, 126–141 CrossRef CAS PubMed.
- I. V. Shelaev, F. E. Gostev, V. A. Nadtochenko, A. Y. Shkuropatov, A. A. Zabelin, M. D. Mamedov, A. Y. Semenov, O. M. Sarkisov and V. A. Shuvalov, Photosynth. Res., 2008, 98, 95–103 CrossRef CAS PubMed.
- Y. Silori, R. Willow, H. H. Nguyen, G. Shen, Y. Song, C. J. Gisriel, G. W. Brudvig, D. A. Bryant and J. P. Ogilvie, J. Phys. Chem. Lett., 2023, 14, 10300–10308 CrossRef CAS PubMed.
- I. V. Shelaev, F. E. Gostev, M. I. Vishnev, A. Y. Shkuropatov, V. V. Ptushenko, M. D. Mamedov, O. M. Sarkisov, V. A. Nadtochenko, A. Y. Semenov and V. A. Shuvalov, J. Photochem. Photobiol., B, 2011, 104, 44–50 CrossRef CAS PubMed.
- E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. van Grondelle, Nat. Phys., 2014, 10, 676–682 Search PubMed.
- A. R. Holzwarth, M. G. Müller, M. Reus, M. Nowaczyk, J. Sander and M. Rögner, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6895–6900 CrossRef CAS PubMed.
- A. Pavlou, J. Jacques, N. Ahmadova, F. Mamedov and S. Styring, Sci. Rep., 2018, 8, 2837 CrossRef PubMed.
- A. Jha, P.-P. Zhang, V. Tiwari, L. Chen, M. Thorwart, R. J. D. Miller and H.-G. Duan, Sci. Adv., 2024, 10, eadk1312 CrossRef CAS PubMed.
- E. Betti, P. Saraceno, E. Cignoni, L. Cupellini and B. Mennucci, J. Phys. Chem. B, 2024, 128, 5188–5200 CrossRef CAS PubMed.
- V. I. Novoderezhkin, J. P. Dekker and R. van Grondelle, Biophys. J., 2007, 93, 1293–1311 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Further details on system setup and QM/MM calculations; analysis scripts; natural transition orbitals; charge transfer numbers; spectral quantities in adiabatic representation. See DOI: https://doi.org/10.1039/d5cp00317b |
| This journal is © the Owner Societies 2025 |





