Open Access Article
Open Access ArticleFluctuating signal and reversibility limit information and entropy in a MAPK signalling cascade
Harshita
Saxena
 a and
Rati
Sharma
a and
Rati
Sharma
 *b
*b
aDepartment of Physics, Indian Institute of Science Education and Research (IISER) Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462066, India
bDepartment of Chemistry, Indian Institute of Science Education and Research (IISER) Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462066, India. E-mail: rati@iiserb.ac.in
First published on 13th May 2025
Abstract
Intracellular signalling pathways act as communication channels that transmit information about the environment and enable cells to respond appropriately. The quantification of this information, along with the energetic cost involved, has therefore been an active area of research. The information transmitted, however, is often limited by the network architecture, noise and parameters or rate constants of the biochemical reactions involved in the pathway. In this work, therefore, we studied the well-known and ubiquitous mitogen-activated protein kinase (MAPK) pathway and showed that information transmission gets limited by introducing reversibility. In particular, we carried out stochastic simulations of two models of the MAPK system with a fluctuating ligand as the input and compared and contrasted the mutual information and energetic cost of the corresponding output, values of which are within the physiological range of MAPK systems studied experimentally. Furthermore, we also explored ways by which the pathway can optimize its functioning by adjusting its parameters, thereby, carrying out trade-offs between energy, fidelity and amplification.
I. Introduction
Signalling pathways form the core of the communication between a cell and its environment. Most signalling pathways consist of layers of feedback loops and complex interactions between biomolecules to achieve the desired kind of information from the surroundings and subsequent cellular actions like growth and movement. Biochemical reactions are inherently noisy, which means that they may take place at random times and positions and the trajectories of participating species or molecules, i.e., the amounts of species at a particular position and time, never look the same even in two identical cells.1–13 This difference in trajectories of (bio)molecules becomes prominent because of low copy numbers of the molecules and the resulting stochasticity causes variability in the responses of individual cells in a population, which also reflects in the inherent energetics of the system.3,5,14 Cells, in fact, constantly require energy for carrying out various biochemical and biomechanical processes and therefore employ energy efficient mechanisms for partitioning the bioenergetic costs for these tasks.15–18 This implies that along with the temporal kinetics and dynamics of signalling pathways, their stochastic thermodynamics is also an essential first step towards understanding the physical nature of such interconnected, stochastic reactions.19 This can then also help in gaining an understanding of why certain pathways might perform better or relay more information than others.Over the past few years, discussion on the thermodynamic description of biological systems with the goal of discovering bounds on their efficiency, similar to those in classical thermodynamics, has led to the emergence of a structured theory called stochastic thermodynamics.20,21 The theory defines fundamental thermodynamic measures, such as work, heat and entropy in a stochastic sense, making it relevant for microscopic systems. In particular, the stochastic entropy of Markovian dynamics, defined on a single trajectory level, is a useful indicator of mesoscopic irreversibility, and, in turn, the non-equilibrium nature of the process.22 Since living cells operate in the non-equilibrium regime, constantly exchanging matter and energy with the surroundings and dissipating heat in the process,15 an understanding of their stochastic thermodynamics is of paramount importance.
A quantity closely related to entropy is mutual information (measured in bits), which can be used to quantify the efficiency with which information is passed on from input to output. Since cellular signalling pathways are essentially communication channels, concepts from information theory can be applied to both quantify the bandwidth of the channel and suggest mechanisms that can increase information transmission. This idea has therefore inspired several experimental and theoretical studies on genetic networks and signalling pathways. Experiments on hyperosmolar glycerol (HOG) mitogen-activated protein (MAP) kinase pathway in S. cerevisiae single cells, for example, showed that response or output faithfully reproduced the signal only when input oscillations had frequencies less than the bandwidth or channel capacity. Therefore, the higher the bandwidth, the higher the changes in signal the resulting response can emulate.23 Another experimental study on G-protein coupled receptors in single cells showed that the receptors can reliably transmit more than 2 bits of information, indicating a high channel capacity.24 These and other theoretical studies also demonstrate that the type of signalling network, specifically, the feedback mechanism, strongly impacts the channel capacity, and, in turn, information flow.25–28 In particular, low concentration input is best optimized by self-activation and high concentration by self-repression, for example.28 However, cells are often limited by the information that they can access due to noise or other constraints and theories have also been developed to assess the maximum information that can be passed on despite this bottleneck.29,30 Studies specifically looking at the noise filter and its role in genetic and biochemical circuits have been able to determine the bounds on signal fidelity or mutual information.31–37 Therefore, apart from channel capacity, input distributions, internal and external noise and input–output curves can also affect the information relayed, all of which have been studied over the years.38–43
Although, as detailed above, cellular reaction networks have been looked at extensively through the lens of information theory, not many studies have explored the effect of reversibility on information transmission through a generally irreversible, non-equilibrium stochastic signalling pathway. Furthermore, quantification of thermodynamic measures such as entropy has also not been the focus of many studies. Therefore, in this work, we take the example of a well-known signalling mechanism, the MAP kinase pathway to better understand the energetic cost and information flow under varying reversibility paramaters. The MAP kinase pathway is a ubiquitous pathway in most eukaryotic cells. It is involved in the identification of gradients of chemical signals in the cell's surroundings.44–46 This pathway is activated when receptors present on the membrane of the cell recognize and bind to signalling molecules, called ligands, to form a receptor–ligand complex. This then starts a complex chain of biochemical phosphorylation reactions, which eventually lead to asymmetry in the cell via creation of an internal gradient of phosphorylated protein kinase. The accumulation of phosphorylated kinases to a certain region in the interior of the cell later translates into a site of cell growth or movement. The reversibility of chemotaxis pathways like the MAPK pathway, in response to a change in stimuli, is important for a cell to adapt to changes in its surroundings.47,48 By calculating entropy production in a part of the MAPK pathway associated with constructing a polarized site, we lay the foundation for future studies where entropy production can be linked to the reversibility of polarization. This will be particularly useful when our current model is supplemented with pathways that deconstruct polarized sites in cells during chemotaxis.
Since the MAP kinase pathway receives and decodes chemical information from its environment, it is an example of a biological information-processing device. The information processing capacity and transmission efficiency are affected by a number of factors. For example, the presence of negative feedback has been shown to be important in reproducing the dynamical output range of the MEK-ERK MAPK system even in the presence of basal activity (leaky system).49 Another experimental and statistical study on the same system showed that the presence of extrinsic noise in a population of genetically identical single cells decreased the mutual information between the signal and response by half, from 0.8 to 0.4 bits.50 A more recent experimental study showed that the presence of a negative feedback loop in this pathway, instead of increasing the channel capacity, maximizes information transmitted per unit of energetic cost.51 Apart from these, information between input and output distributions in these kinds of MAPK systems has also been correlated to the chemical potential of adenosine triphosphate (ATP) molecules in the cell.35 Therefore, relating information transmission to the network architecture as well as chemical potential and entropy is important.
To this end, in our study, we carry out simulations of the MAPK signalling cascade in the presence of fluctuating ligand concentration and determine the mutual information, chemical potential and energetic cost in terms of entropy for the system. We study two models of the MAPK system with increasing levels of positive feedback and find that the presence of fluctuating ligand concentration between two concentration values restricts the mutual information between a signal (ligand) and a response (phosphorylated kinase) to less than 1.0 bit. This is further reduced when reversibility is introduced in the pathway. We also compute the total entropy production rate for the system and find that in line with mutual information, this too decreases with reversibility. This work, therefore, presents a unified view of the pathway that finds regions of optimum reversibility and information exchange. This approach can also further be extended to other kinds of phosphorylation cascades with feedback and be used to develop physical concepts on signalling and its evolution.
The rest of the article is organized as follows. In Section II, we discuss the two MAP kinase models used to carry out this study. In Section III, we provide the theoretical background for the computation of mutual information, chemical potential and entropy production rate. We discuss the results and conclusions of our study in Sections IV and V, respectively.
II. The MAP kinase pathway and its models
A. Kinetic model
We use a previously employed kinetic model of the MAP kinase signalling pathway52,53 for the purposes of this study. This kinetic model has been used in the past to understand the role of phosphorylation and positive feedback in localizing the phosphorylated kinases, eventually leading to cell polarity.53 In this work, we compare and contrast the information transmission and energetic cost for two models of the pathway. Model-1 leads to the production of a singly phosphorylated kinase, which acts as the response, whereas, model-2 has additional positive feedback in the pathway, leading to the production of both singly and doubly phosphorylated kinases. The two kinetic models and the corresponding rate constants for the reaction system are given in Tables 1 and 2, respectively. The models are also represented schematically in Fig. 1. Since we are interested in exploring how information transmission is affected by the reversibility of a generally irreversible pathway, we have modified this model, as detailed in Table 1, by including backward reactions and their corresponding rate constants. Although the participating ATP, ADP and Pi molecules involved are also explicitly shown in each reaction in Table 1, like in previous studies,52,53 it is assumed that the rate constants implicitly include the concentrations of these molecules. This means that the reactions with three participating reactant species are assumed to be pseudo-second-order reactions. As also indicated in the table, the first five reactions are common to both models. Model-2 has additional reactions (6)–(10). The forward and backward rates of reaction no. r are specified by ar and br, respectively. Backward rates are not specified explicitly as they are to be determined through eqn (1) and (2). Furthermore, the initial conditions, i.e., the initial number of molecules of each species present at the start of the simulations, are specified in Table 3.| Reaction no. | Model | Reaction | Rates |
|---|---|---|---|
| 1 | 1,2 | RL ⇌ R + L | a 1,b1 |
| 2 | 1,2 | ATP + K + K ⇌ Kp + K + ADP | a 2,b2 |
| 3 | 1,2 | ATP + K + Kp ⇌ Kp + Kp + ADP | a 3,b3 |
| 4 | 1,2 | Kp + P ⇌ K + P + Pi | a 4,b4 |
| 5 | 1,2 | ATP + K + RL ⇌ Kp + RL + ADP | a 5,b5 |
| 6 | 2 | ATP + Kp + K ⇌ Kpp + K + ADP | a 6,b6 |
| 7 | 2 | ATP + Kp + Kp ⇌ Kpp + Kp + ADP | a 7,b7 |
| 8 | 2 | ATP + K + Kpp ⇌ Kp + Kpp + ADP | a 8,b8 |
| 9 | 2 | ATP + Kp + Kpp ⇌ Kpp + Kpp + ADP | a 9,b9 |
| 10 | 2 | Kpp + P ⇌ Kp + P + Pi | a 10,b10 |
| Rate | Value in model-1 | Value in model-2 |
|---|---|---|
| a 1 | 4 × 10−3 | 8 × 10−3 |
| b 1 | 8 × 10−3 | 8 × 10−3 |
| a 2 | 4 × 10−5 | 8 × 10−5 |
| a 3 | 8 × 10−5 | 2.32 × 10−4 |
| a 4 | 1 × 10−3 | 4 × 10−3 |
| a 5 | 1 × 10−4 | 8 × 10−5 |
| a 6 | — | 4 × 10−5 |
| a 7 | — | 1.16 × 10−4 |
| a 8 | — | 8 × 10−3 |
| a 9 | — | 4 × 10−3 |
| a 10 | — | 8 × 10−3 |
 | ||
| Fig. 1 Schematic of the phosphorylation cascade. The reaction numbers corresponding to both kinetic models are given in red and the ones present in only model-2 are shown in green. | ||
| L | RL | R | K | Kp | Kpp | P | |
|---|---|---|---|---|---|---|---|
| Model-1 | Variable | 0 | 400 | 64 | 0 | 0 | 16 |
| Model-2 | Variable | 0 | 400 | 64 | 0 | 0 | 16 |
The goal of this research is to study the entropy production rate and mutual information of a MAP kinase pathway with respect to the “reversibility” of the involved chemical reactions. This serves as a natural extension of previous works35,54 where the authors studied information flux and sensitivity of simpler phosphorylation cascades. We define two parameters γ and σ as a measure of reversibility of the phosphorylation reactions and phosphatase reaction respectively as
 | (1) |
 | (2) |
B. Stochastic simulations
We use the LatticeMicrobes software55 to simulate the models using the Gillespie Algorithm56 assuming a well-mixed homogenous system. All the reactions are simulated as per the models listed in Table 1 and the rate constants and initial conditions listed in Tables 2 and 3, respectively. The reactions are simulated for 5000 seconds with the state of the system stored every second. The distributions of the entropy production rate are determined from 1000 replicates of the simulations, while the other computations are averaged over 100 replicates.We discuss the theoretical aspects of entropy and information in the next section before moving on to the implications of the parameters on these quantities.
III. Theoretical background and methodology
A. Stochastic entropy
Entropy production is one of the key thermodynamic variables that can be defined for a system of stochastic chemical reactions. The state of such a system at time t is given by the concentration or number of molecules of each of the individual chemical species and is therefore denoted by the vector![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (t). The probability distributions of the states change as per probability fluxes in and out of neighbouring states, with the transition rates defined through the stochastic rates, cr,57 of the reaction, where r labels the reaction among a total of R reactions. This concept is mathematically captured by the chemical master equation (CME):
(t). The probability distributions of the states change as per probability fluxes in and out of neighbouring states, with the transition rates defined through the stochastic rates, cr,57 of the reaction, where r labels the reaction among a total of R reactions. This concept is mathematically captured by the chemical master equation (CME): | (3) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) is the reaction propensity (probability per unit time) for reaction r and is given by fr = hr × cr. Here h is the number of pairs of molecules available for a given reaction and c is the stochastic rate constant. The factor f(r) can be calculated in the following manner:
) is the reaction propensity (probability per unit time) for reaction r and is given by fr = hr × cr. Here h is the number of pairs of molecules available for a given reaction and c is the stochastic rate constant. The factor f(r) can be calculated in the following manner:| For a reaction S1 + S2 → …, f = c[S1][S2] | (4) |
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ] represents the number of molecules of the species present.
] represents the number of molecules of the species present.
For the MAP kinase pathway, as shown in Table 1, the species which are part of ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (t) are the biomolecules involved in the pathway. The concentrations of species ATP, ADP, and Pi are chemostatted via a closed chemical network. This means that the concentrations of these species stay constant during the whole simulation time, as they are assumed to be replenished by the cell continuously.58 Concentrations chemostatted via an open network might experience transient changes as they are used up in the chemical reactions and not replenished immediately.59 A thermodynamic picture of the pathway is shown in Fig. 2.
(t) are the biomolecules involved in the pathway. The concentrations of species ATP, ADP, and Pi are chemostatted via a closed chemical network. This means that the concentrations of these species stay constant during the whole simulation time, as they are assumed to be replenished by the cell continuously.58 Concentrations chemostatted via an open network might experience transient changes as they are used up in the chemical reactions and not replenished immediately.59 A thermodynamic picture of the pathway is shown in Fig. 2.
An arbitrary stochastic trajectory of a chemical system contains a smoothly varying curve x(t) according to a time varying protocol that does work on the system and jumps or transitions due to chemical reactions. For the master equation represented in eqn (3), the entropy production per unit time of the system along a stochastic trajectory is then defined as:22,60
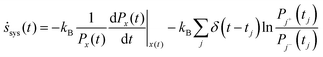 | (6a) |
s = −kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P | (6b) |
The first term on the RHS of eqn (6a) is the entropy production during a continuous change in energy of the system which causes a change in the probabilities of the states. The second term represents the jumps in the trajectory that occur at times tj, where at each jump, the system transitions from state j− to j+. kB is the Boltzmann constant. Although stochastic entropy is defined on a trajectory, the probabilities must be computed from an ensemble of trajectories. Furthermore, the probabilities can also change with time if the initial distribution Px(0) ≠ Psx (the steady state) and the system is approaching the steady state distribution. The instantaneous probabilities, Px(t), are well-defined if we assume that the chemical system evolves according to the chemical master equation (eqn (3)).
The heat dissipated into the medium, which is at equilibrium during the whole process by virtue of the medium acting as the reservoir, is identified with the entropy production per unit time of the medium:61
 | (7) |
Here,  denotes the reaction propensities of all the reactions sj that were responsible for the change in state of the system from j− to j+. Therefore, the total entropy production (system + medium) per unit time is given by
denotes the reaction propensities of all the reactions sj that were responsible for the change in state of the system from j− to j+. Therefore, the total entropy production (system + medium) per unit time is given by
 | (8) |
In order to find the average entropy production over all possible trajectories, we note that the probability that a jump occurs at time t = tj from state j− to j+ is  or the flux. In our study, the probabilities of various states of the system are calculated by simulating many “copies” of the system under fixed initial conditions. The system is observed to attain a steady-state with small fluctuations around the average for all models and initial conditions. The discussion in the context of the studied model is presented in the next section and the associated distributions are shown in Fig. 4. Thus, the probabilities are time-independent and depend only on the initial conditions. Considering this, the average system + medium entropy production per unit time is
or the flux. In our study, the probabilities of various states of the system are calculated by simulating many “copies” of the system under fixed initial conditions. The system is observed to attain a steady-state with small fluctuations around the average for all models and initial conditions. The discussion in the context of the studied model is presented in the next section and the associated distributions are shown in Fig. 4. Thus, the probabilities are time-independent and depend only on the initial conditions. Considering this, the average system + medium entropy production per unit time is
 | (9) |
B. Mutual information
Having discussed the rate of entropy production, we now provide background for a related quantity, i.e., mutual information. In general, there is always an output corresponding to the input that a signalling pathway receives. However, the response of the pathway is not always one-to-one, i.e., in the case of the pathway studied here for example, a single value of ligand amount does not lead to a single, constant value of the amount of phosphorylated kinase. Therefore, looking at a given output distribution, to what accuracy can the corresponding input distribution be back calculated is an intuitive way of understanding the fidelity of the signalling network. There have been multiple studies on the fidelity or the mutual information between input and output distributions of a biological pathway.62,63 The merits and challenges of accepting mutual information as a biological function that correlates to the survival and evolution of an organism have also been discussed in detail.27In this work, we first compute the output distributions of the pathway to a given input distribution set by us through simulations under different initial conditions and varying parameters. In this way, the initial ligand amount (variable X) and the corresponding amount of phosphorylated kinase (variable Y) become random variables. Mutual information can be thought of as a measure of “dependence” between the two random variables, based on the difference between their joint probability distribution P(X,Y) and the product of marginal distributions P(X)P(Y). Mutual information between distributions of two random variables X and Y is defined as63,64
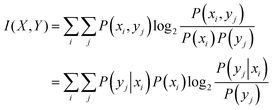 | (10) |
It turns out that I(X,Y) ≥ 0, where the equality holds when X and Y are independent. In that case, P(X,Y) = P(X)P(Y).
In order to calculate mutual information for the models of the MAPK pathway studied here, we use the following formulation. Suppose the environment contains two values of ligand concentration/amount: L1 and L2. Let the ligand amount L ∈ {L1,L2} be a random variable such that probability P(L1) = p and P(L2) = 1 − p. This could happen because, for example, the input to our pathway is itself a response of some other bistable pathway, so that L fluctuates between two values L1 and L2. Then, probability p is proportional to the fraction of time for which the value of L is L1. The mutual information (eqn (10)) for such a binary input distribution answers the simple question of how capable the system distinguishes between two input ligand values (L1 and L2) via its own phosphorylation kinase distribution. However, note that the reasons why L is described by a binary distribution do not affect the results of this study and such a setup is assumed only to simplify calculations and to build intuition to analyse more complex input distributions. Then the following steps are carried out.
• Fix initial conditions and set initial L = L1. Also fix values of parameters that are not variable.
• Run the simulation and store the distribution of phosphorylated kinase as conditional probability P(Kp|L1) for model-1 and as P(Kp + Kpp|L1) for model-2.
• Repeat the above step for initial L = L2. Use all probabilities to calculate 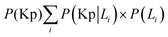 for model-1 and
for model-1 and 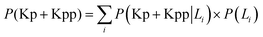 for model-2.
for model-2.
• Calculate mutual information I(Kp,L) or I(Kp + Kpp,L) using eqn (10).
With the theoretical background and simulation setup in place, we now move to a discussion of the results of the simulation studies of the two models.
C. Phosphorylation potential
We now define a quantity called phosphorylation potential, ΔGphosph, for both models. This is defined as the natural logarithm of the ratio of the product of forward and backward rates. For model-1, | (11) |
If one assumes all the biomolecules to be present in low concentrations, then the energy levels of the internal states of proteins and that of the source molecules (ATP, ADP, and Pi) will be approximately independent of the surrounding molecules as there are no other interactions between them except for the prescribed chemical reactions. We assume that the energy levels are negligible compared to the chemical potentials μα where α = ATP, ADP, and Pi. The definition of the chemical potential remains true even under non-equilibrium conditions if the particle reservoirs are assumed to be large. The free energy change at constant pressure and temperature then has contributions only from the chemical potentials.61 This implies
 | (12) |
Similarly, the phosphorylation potential for model-2 is defined as
 | (13) |
As in earlier studies,54 we use ΔGphosph as a measure of the potential maintained by the cell. Note that changing γ and σ changes the phosphorylation potential ΔGphosph and thus we control these two parameters in our simulations instead of actual concentrations or chemical potentials of the source molecules. Eqn (12) tells us that if the cell maintains a higher concentration of ATP than ADP, the forward rates of the phosphorylation reactions (reaction no. 2, 3, and 5) and the phosphatase reaction (reaction number 4) will increase. Hence, it is not immediately obvious what the effect of higher potential is going to be on the amount of phosphorylated kinase. Fig. 3 shows the variation of the phosphorylation potential with the reversibility parameters and, as expected from the formulae given above, the potential decreases with increasing reversibility. Our computed values of phosphorylation potential match well with the physiological potential values of around 10–30kBT15,35,65 for an appreciable range of reversibility parameters. Furthermore, even though the architecture of model-2 leads to higher ΔGphosph in comparison with model-1, the values can be brought down at high enough γ.
IV. Results and discussion
In Fig. 4, we plot the distribution of phosphorylated kinases as per the simulated trajectories from the two kinetic models. For the selected reversibility parameters, the distributions, except those in Fig. 4(b), have a single peak that moves to higher phosphorylation as the initial number of ligand molecules increases. Fig. 5 further shows the variation in the amount of phosphorylated kinases (Kp or Kp + Kpp), averaged over all replicates and simulation time, with the reversibility parameters σ and γ. In model-1, the average Kp increases with σ but decreases with γ. This is because on increasing σ, the phosphatase dephosphorylation reaction approaches reversibility and its effect weakens. Similarly, on increasing γ, all phosphorylation reactions approach reversibility and kinases spend more time in their dephosphorylated states as well. Furthermore, a higher L0 would lead to more phosphorylation as per reaction no. 5 in Table 1. For model-2 (Fig. 5(c) and (d)), however, we see that changes in L0 do not make a noticeable difference in the average number of phosphorylated kinase (Kp + Kpp). In fact, even for model-1 (see Fig. 5(b)), the variation is limited to a few tens of molecules. This implies that introducing reversibility in the phosphatase reactions “freezes” the pathway into a single response irrespective of the input value. The reasons for other observed trends in average Kp + Kpp with the reversibility parameters are the same as discussed for model-1.Fig. 6(a) and (c) show the entropy production rate ΔS(t) with time, i.e., the entropy change in a small time interval Δt = 1 s for both the system and the medium. Here, the entropy production rate is computed in units of the Boltzmann constant kB (e.g. J K−1) per second. One of the main differences between stochastic and macroscopic thermodynamics is that entropy changes of isolated systems defined in the former theory, as shown in the figure, can be negative.20 Although the negative entropy changes are few and far between, they still exist.
The total entropy change ΔStot for a given replicate is the sum of all entropy changes over the whole duration of the simulation. Distributions of the total entropy change over 1000 replicates of both models are shown in Fig. 6(b) and (d). Note that the scales on the x-axes of these two plots are different. The mean of the distribution for model-1 (Fig. 6(b)) is 30372.6kB and the standard deviation is 484.7kB. The coefficient of variation is calculated to be 0.016. The entropy production rate averaged over all replicates and time is 6.1kB s−1. The entropy production rate in model-2 was found to be higher than that in model-1 on average. The average entropy production rate over all replicates for model-2 with the same initial conditions and parameter values as in model-1 is 17kB s−1. A high ΔStot for model-2 in comparison with model-1 also corresponds to a high ΔGphosph and the presence of additional feedback loops in the architecture. The mean of the distribution of ΔStot shown in Fig. 6(d) is 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117kB and the standard deviation is 28
117kB and the standard deviation is 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 604kB for the same L0, time duration and the number of replicates as for model-1. The coefficient of variation in this case is 0.336.
604kB for the same L0, time duration and the number of replicates as for model-1. The coefficient of variation in this case is 0.336.
We now look into the total entropy change, averaged over all replicates, with respect to reversibility parameters. This is shown in Fig. 7. Entropy production due to the evolution of a chemical system is a measure of the irreversibility of the dynamics. A reversible trajectory of a chemical evolution can retrace its chemical reactions in the backward order with the same probability as it can go in the forward order. The trend in average ΔStot is similar for both reversibility parameters in the case of model-1. This suggests that cells that maintain the pathway at a high ΔGphosph (or low reversibility parameter values) generate more entropy and make the chemical evolution more irreversible and farther away from equilibrium. For model-2, just like the average phosphorylated kinase, the average ΔStot shows a similar low sensitivity to L0 in Fig. 7(c) and (d). A noteworthy observation is that the average ΔStot has the minimum value at σ = 0.0001 in Fig. 7(d) and reaches a maximum before monotonously decreasing until σ = 1. However, note that the actual σ value where the maximum occurs could be less or more than the one seen in the figure as only discrete points are plotted here. This highlights the difference between the reversibility of the trajectories as given by their respective entropy production and the reversibility of individual reactions as given by the reversibility parameters. Fig. 7, therefore, shows that an increase in reversibility (through the reversibility parameter here) does not always accompany an increase in overall entropy production. Since there is a visible trend of increasing entropy production with an initial amount of ligand, we plot this for both the models in Fig. 7(c) and (f), respectively.
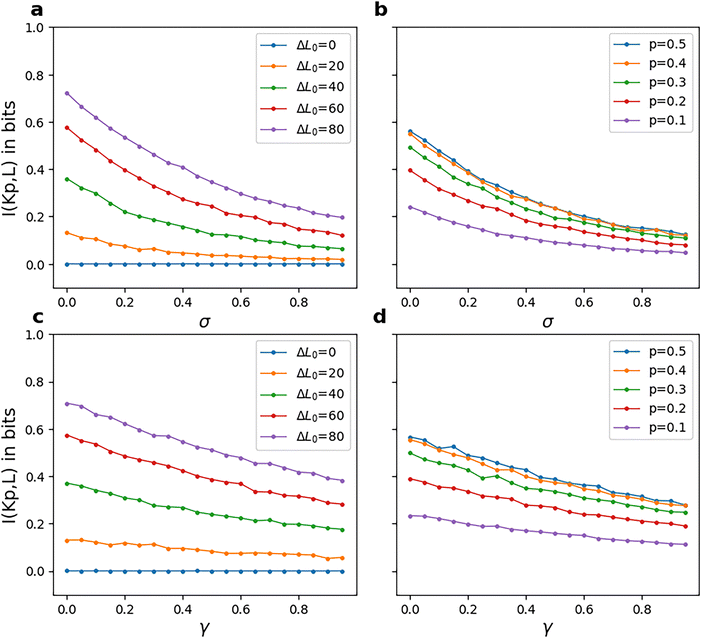
Having compared the amplification or response in terms of the average number of phosphorylated kinases and energetics in terms of phosphorylation potential and entropy for the two models, we can now look into how information processing capacity is affected by reversibility. Fig. 8 shows the variation of mutual information I(Kp|L) with reversibility parameters, σ and γ for a series of constant ΔL0 and probability p. For almost all sets of rate parameters, I(Kp|L) increases as ΔL0 increases or as p becomes closer to 0.5. The higher the difference between the two initial ligand amounts, the lesser the overlap between their corresponding output distributions. This makes the output distributions distinguishable from each other and the fidelity of the response can be said to improve. Markovian (single-layer) signalling pathways have previously been reported to have information of less than 1 bit.32 1 bit is also the mathematical upper bound on mutual information when the system needs to distinguish between two inputs. A mutual information of 1 bit implies zero overlap between the output distributions. In our study too, this upper bound is apparent for the mutual information plots of model-1 (see Fig. 8). A study on the MEK-ERK MAPK pathway showed that mutual information reduces by half in the presence of extrinsic noise, from ∼0.8 to ∼0.4.50 Similar observation can be made in the results of our study (Fig. 8) as well, where this quantity decreases as we go to lower ΔL0 values, implying a higher overlap between the two inputs and consequently equivalent to the presence of external noise in the system. In the case of binary input, a symmetric input distribution (p = 0.5) leads to higher fidelity compared to asymmetric distributions. This also complies well with conclusions from a theoretical study43 that showed mathematically that low stimuli must occur in high frequency in order to maximize mutual information. We further observe a decrease in I(Kp|L) with both σ and γ. The slopes of these plots become noticeably steeper as ΔL0 increases. On comparing these plots with Fig. 3, we conclude that cells must maintain a higher potential in order to achieve greater fidelity, similar to the results for oscillatory inputs in a phosphorylation cascade.35
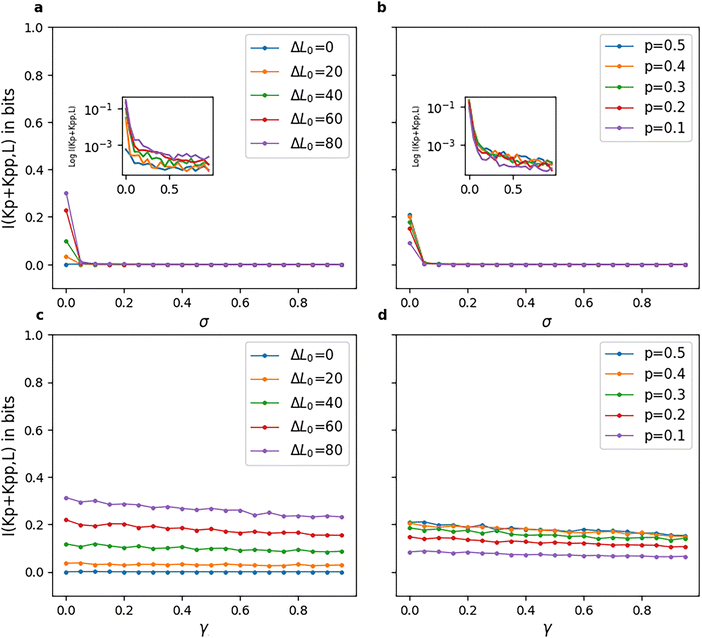
The mutual information for model-2 is shown in Fig. 9. Fig. 9(a) and (b) show very low values (close to zero) as the reversibility of the phosphatase reactions, i.e., their σ value, is increased. Fig. 9(c) and (d) show an almost constant I(Kp + Kpp|L) for all γ values, with a slight negative slope. These figures, along with Fig. 5(c) and (d), imply that high reversibility parameters in a model-2 type pathway have a profound effect on both the amplification and fidelity of the pathway, locking the pathway into a response solely dictated by ΔL0 and the value of the reversibility parameter σ of the chemical reactions. This restricts a phosphorylation cascade of such a model or network to a very small range of forward and backward rates that ensures both appreciable amplification of input and fidelity between outputs. Fig. 5(c) and (d) indicate the absence of a graded response to input. These results that we report here for model-2 also match with phosphorylation cascades with no negative feedback loops which have been found to give almost zero mutual information.49
To summarize the results, we see that high (close to 1) σ values in model-1, which are associated with high amplification of up to 40 phosphorylated kinase molecules but fidelity less than 0.4, lead to low entropy values of ∼1.5 × 104kB. On the other hand, high γ values are associated with low amplification (10–20 molecules), low entropy and low fidelity. This implies that the amplification–information–reversibility correlation strongly depends on the type of reaction in question. A phosphorylation pathway that requires both high amplification and fidelity can do so by having highly irreversible phosphorylation steps and, therefore, an overall trajectory of high entropy production. High entropy production arising due to a highly irreversible phosphatase step (low σ) can achieve high fidelity but not amplification. Highly irreversible reactions require high phosphorylation potentials and the cell must expend energy to maintain the ATP–ADP balance. All of the above is true for pathways resembling a model-1 type architecture. The kinetic model-2 has a very narrow range of optimal fidelity. For such models, a σ value close to zero or almost irreversible phosphatase steps are the only way to achieve non-zero mutual information for a binary input. High γ values are also not favourable in terms of amplification.
V. Conclusions
The results of this study provide biophysical context to the dynamical irreversibility of a signalling pathway by correlating it with amplification (average phosphorylated kinase) and fidelity (mutual information). This can enhance our understanding of whether a cell might benefit from a certain amount of reversibility in a signalling process. Energy expenditure of the cell in the form of the chemical potential of ATP is an important factor to consider while understanding the evolution of the cell and its pathways. Our work puts the intricacies of signalling pathways into a wider perspective by introducing tradeoffs between energy, fidelity and amplification over a wide range of “reversibilities” of the involved chemical reactions in the context of two kinetic models with different levels of phosphorylation. While most studies focus on finding the maximum mutual information, we also attempt to find optimal ranges of operation by pointing out parameter values that lead to minimum or zero mutual information values. This study is therefore an important addition to existing literature on information flow in signalling pathways and can serve as a blueprint for exploring other signal response mechanisms with varying negative and positive feedbacks and autoregulation of increasing complexity.Data availability
All data are included in the manuscript.Conflicts of interest
There are no conflicts of interest to declare.References
- M. Thattai and A. Van Oudenaarden, Intrinsic noise in gene regulatory networks, Proc. Natl. Acad. Sci. U. S. A., 2001, 98(15), 8614–8619 CrossRef PubMed.
- A. Eldar and M. B. Elowitz, Functional roles for noise in genetic circuits, Nature, 2010, 467(7312), 167–173 CrossRef PubMed.
- D. Schultz, E. Ben Jacob, J. N. Onuchic and P. G. Wolynes, Molecular level stochastic model for competence cycles in bacillus subtilis, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(45), 17582–17587 CrossRef.
- H. Qian, P.-Z. Shi and J. Xing, Stochastic bifurcation, slow fluctuations, and bistability as an origin of biochemical complexity, Phys. Chem. Chem. Phys., 2009, 11(24), 4861–4870 RSC.
- G. Balázsi, A. Van Oudenaarden and J. J. Collins, Cellular decision making and biological noise: from microbes to mammals, Cell, 2011, 144(6), 910–925 CrossRef.
- R. Sharma and B. J. Cherayil, Reaction dynamics under confinement: an exact path integral treatment of a two-stage model of stochastic gene expression, J. Stat. Mech.: Theory Exp., 2013, 2013(10), P10029 CrossRef.
- E. Roberts, S. Be’er, C. Bohrer, R. Sharma and M. Assaf, Dynamics of simple gene-network motifs subject to extrinsic fluctuations, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(6), 062717 CrossRef PubMed.
- G. J. Lapeyre and M. Dentz, Reaction-diffusion with stochastic decay rates, Phys. Chem. Chem. Phys., 2017, 19(29), 18863–18879 RSC.
- S. Pal and R. Sharma, Transcription factors and chaperone proteins play a role in launching a faster response to heat stress and aggregation, Comput. Biol. Chem., 2021, 93, 107534 CrossRef PubMed.
- A. Batra and R. Sharma, A near analytic solution of a stochastic immune response model considering variability in virus and t-cell dynamics, J. Chem. Phys., 2021, 154, 195104 CrossRef PubMed.
- R. Sharma, Extrinsic noise effects on ribosomal traffic during the translation process, J. Stat. Mech.: Theory Exp., 2022, 2022(5), 053504 CrossRef.
- A. Batra, S. C. Banerjee and R. Sharma, Persistent correlation in cellular noise determines longevity of viral infections, J. Phys. Chem. Lett., 2022, 13(31), 7252–7260 CrossRef.
- P. Kundu, S. Saha and G. Gangopadhyay, A minimal kinetic model for the interpretation of complex catalysis in single enzyme molecules, Phys. Chem. Chem. Phys., 2024, 26(1), 463–476 RSC.
- M. Esposito, Stochastic thermodynamics under coarse graining, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(4), 041125 CrossRef.
- G. Lan, P. Sartori, S. Neumann, V. Sourjik and Y. Tu, The energy-speed-accuracy trade-off in sensory adaptation, Nat. Phys., 2012, 8(5), 422–428 Search PubMed.
- M. Lynch and G. K. Marinov, The bioenergetic costs of a gene, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(51), 15690–15695 CrossRef CAS PubMed.
- X. Yang, M. Heinemann, J. Howard, G. Huber, S. Iyer-Biswas and G. Le Treut, et al., Physical bioenergetics: Energy fluxes, budgets, and constraints in cells, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(26), e2026786118 CrossRef CAS PubMed.
- S. J. Bryant and B. B. Machta, Physical constraints in intracellular signaling: the cost of sending a bit, Phys. Rev. Lett., 2023, 131(6), 068401 CrossRef CAS PubMed.
- M. Morrison, M. Razo-Mejia and R. Phillips, Reconciling kinetic and thermodynamic models of bacterial transcription, PLoS Comput. Biol., 2021, 17(1), e1008572 CrossRef PubMed.
- U. Seifert, Stochastic thermodynamics, fluctuation theorems and molecular machines, Rep. Prog. Phys., 2012, 75(12), 126001 CrossRef PubMed.
- D. H. Wolpert, J. Korbel, C. W. Lynn, F. Tasnim, J. A. Grochow and G. Kardeş, Is stochastic thermodynamics the key to understanding the energy costs of computation?, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(45), e2321112121 CrossRef.
- L. Peliti and S. Pigolotti, Stochastic thermodynamics: an introduction, Princeton University Press, 2021 Search PubMed.
- P. Hersen, M. N. McClean, L. Mahadevan and S. Ramanathan, Signal processing by the hog map kinase pathway, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(20), 7165–7170 CrossRef PubMed.
- A. Keshelava, G. P. Solis, M. Hersch, A. Koval, M. Kryuchkov and S. Bergmann, et al., High capacity in G protein-coupled receptor signaling, Nat. Commun., 2018, 9(1), 876 CrossRef.
- G. Tkačik, A. M. Walczak and W. Bialek, Optimizing information flow in small genetic networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80(3), 031920 CrossRef PubMed.
- A. M. Walczak, G. Tkačik and W. Bialek, Optimizing information flow in small genetic networks. ii. feed-forward interactions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81(4), 041905 CrossRef.
- G. Tkačik and A. M. Walczak, Information transmission in genetic regulatory networks: a review, J. Phys.: Condens. Matter, 2011, 23(15), 153102 CrossRef.
- G. Tkačik, A. M. Walczak and W. Bialek, Optimizing information flow in small genetic networks. iii. a self-interacting gene, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(4), 041903 CrossRef.
- M. Bauer, M. D. Petkova, T. Gregor, E. F. Wieschaus and W. Bialek, Trading bits in the readout from a genetic network, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(46), e2109011118 CrossRef.
- M. Bauer and W. Bialek, Information bottleneck in molecular sensing, PRX Life, 2023, 1(2), 023005 CrossRef.
- M. Hinczewski and D. Thirumalai, Cellular signaling networks function as generalized Wiener–Kolmogorov filters to suppress noise, Phys. Rev. X, 2014, 4(4), 041017 Search PubMed.
- N. B. Becker, A. Mugler and P. R. Ten Wolde, Optimal prediction by cellular signaling networks, Phys. Rev. Lett., 2015, 115(25), 258103 CrossRef.
- M. Hinczewski and D. Thirumalai, Noise control in gene regulatory networks with negative feedback, J. Phys. Chem. B, 2016, 120(26), 6166–6177 CrossRef PubMed.
- C. Zechner, G. Seelig, M. Rullan and M. Khammash, Molecular circuits for dynamic noise filtering, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(17), 4729–4734 CrossRef.
- T.-L. Wang, B. Kuznets-Speck, J. Broderick and M. Hinczewski, The price of a bit: energetic costs and the evolution of cellular signaling, bioRxiv, 2020, preprint DOI:10.1101/2020.10.06.327700.
- C. Weisenberger, D. Hathcock and M. Hinczewski, Cellular signaling beyond the Wiener–Kolmogorov limit, J. Phys. Chem. B, 2021, 125(46), 12698–12711 CrossRef PubMed.
- E. Ilker and M. Hinczewski, Bioenergetic costs and the evolution of noise regulation by micrornas, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(9), e2308796121 CrossRef.
- P. B. Detwiler, S. Ramanathan, A. Sengupta and B. I. Shraiman, Engineering aspects of enzymatic signal transduction: photoreceptors in the retina, Biophys. J., 2000, 79(6), 2801–2817 CrossRef.
- G. Tkačik, C. G. Callan Jr and W. Bialek, Information flow and optimization in transcriptional regulation, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(34), 12265–12270 CrossRef.
- T. Lenaerts, J. Ferkinghoff-Borg, J. Schymkowitz and F. Rousseau, Information theoretical quantification of cooperativity in signalling complexes, BMC Syst. Biol., 2009, 3, 1–12 CrossRef.
- F. Tostevin and P. R. Ten Wolde, Mutual information between input and output trajectories of biochemical networks, Phys. Rev. Lett., 2009, 102(21), 218101 CrossRef.
- T. R. Sokolowski and G. Tkačik, Optimizing information flow in small genetic networks. iv. spatial coupling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(6), 062710 CrossRef PubMed.
- G. Micali and R. G. Endres, Maximal information transmission is compatible with ultrasensitive biological pathways, Sci. Rep., 2019, 9(1), 16898 CrossRef PubMed.
- S. Paliwal, P. A. Iglesias, K. Campbell, Z. Hilioti, A. Groisman and A. Levchenko, Mapk-mediated bimodal gene expression and adaptive gradient sensing in yeast, Nature, 2007, 446(7131), 46–51 CrossRef.
- M. K. Malleshaiah, V. Shahrezaei, P. S. Swain and S. W. Michnick, The scaffold protein ste5 directly controls a switch-like mating decision in yeast, Nature, 2010, 465(7294), 101–105 CrossRef PubMed.
- K. F. Swaney, C.-H. Huang and P. N. Devreotes, Eukaryotic chemotaxis: a network of signaling pathways controls motility, directional sensing, and polarity, Annu. Rev. Biophys., 2010, 39, 265–289 CrossRef PubMed.
- M. Camps, A. Nichols and S. Arkinstall, Dual specificity phosphatases: a gene family for control of map kinase function, FASEB J., 2000, 14(1), 6–16 CrossRef PubMed.
- S. A. Ramirez, M. Pablo, S. Burk, D. J. Lew and T. C. Elston, A novel stochastic simulation approach enables exploration of mechanisms for regulating polarity site movement, PLoS Comput. Biol., 2021, 17(7), e1008525 CrossRef.
- M. Voliotis, R. M. Perrett, C. McWilliams, C. A. McArdle and C. G. Bowsher, Information transfer by leaky, heterogeneous, protein kinase signaling systems, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(3), E326–E333 CrossRef.
- S. Filippi, C. P. Barnes, P. D. W. Kirk, T. Kudo, K. Kunida and S. S. McMahon, et al., Robustness of mek-erk dynamics and origins of cell-to-cell variability in mapk signaling, Cell Rep., 2016, 15(11), 2524–2535 CrossRef.
- A. Anders, B. Ghosh, T. Glatter and V. Sourjik, Design of a MAPK signalling cascade balances energetic cost versus accuracy of information transmission, Nat. Commun., 2020, 11(1), 3494 CrossRef PubMed.
- M. Kochańczyk, J. Jaruszewicz and T. Lipniacki, Stochastic transitions in a bistable reaction system on the membrane, J. R. Soc., Interface, 2013, 10(84), 20130151 Search PubMed.
- R. Sharma and E. Roberts, Gradient sensing by a bistable regulatory motif enhances signal amplification but decreases accuracy in individual cells, Phys. Biol., 2016, 13(3), 036003 CrossRef PubMed.
- H. Qian, Thermodynamic and kinetic analysis of sensitivity amplification in biological signal transduction, Biophys. Chem., 2003, 105(2–3), 585–593 CrossRef PubMed.
- E. Roberts, J. E. Stone and Z. Luthey-Schulten, Lattice microbes: High-performance stochastic simulation method for the reaction-diffusion master equation, J. Comput. Chem., 2013, 34(3), 245–255 CrossRef PubMed.
- D. T. Gillespie, Exact stochastic simulation of coupled chemical reactions, J. Phys. Chem., 1977, 81(25), 2340–2361 CrossRef.
- J. R. Peterson, M. J. Hallock, J. A. Cole and Z. Luthey-Schulten, A problem solving environment for stochastic biological simulations, Proceedings High Performance Computing Networking, Storage and Analysis Companion (SCC), 2013 Search PubMed.
- E. R. Stadtman and P. B. Chock, Superiority of interconvertible enzyme cascades in metabolic regulation: analysis of monocyclic systems, Proc. Natl. Acad. Sci. U. S. A., 1977, 74(7), 2761–2765 CrossRef PubMed.
- R. Rao and M. Esposito, Nonequilibrium thermodynamics of chemical reaction networks: Wisdom from stochastic thermodynamics, Phys. Rev. X, 2016, 6(4), 041064 Search PubMed.
- U. Seifert, Entropy production along a stochastic trajectory and an integral fluctuation theorem, Phys. Rev. Lett., 2005, 95(4), 040602 CrossRef PubMed.
- T. Schmiedl, T. Speck and U. Seifert, Entropy production for mechanically or chemically driven biomolecules, J. Stat. Phys., 2007, 128, 77–93 CrossRef CAS.
- S. Uda and S. Kuroda, Analysis of cellular signal transduction from an information theoretic approach, Seminars in cell & developmental biology, Elsevier, 2016, vol. 51, pp. 24–31 Search PubMed.
- C. Waltermann and E. Klipp, Information theory based approaches to cellular signaling, Biochim. Biophys. Acta, Gen. Subj., 2011, 1810(10), 924–932 CrossRef CAS.
- T. M. Cover, Elements of information theory, John Wiley & Sons, 1999 Search PubMed.
- R. Milo and R. Phillips, Cell biology by the numbers, Garland Science, 2015 Search PubMed.
| This journal is © the Owner Societies 2025 |