A molecular dynamics study of the effect of annealing temperature on the structure of ASW

Abstract

Amorphous solid water (ASW) is a disordered form of ice created by low-temperature and low-pressure vapour deposition. The ASW deposited under these conditions are usually very porous – allowing for a large amount of other molecular species to be stored within these pores. However, metastable interstellar ASW seems to lose porosity as a function of time or temperature. The chemical physics understanding of ASW pore evolution remains unresolved. This paper utilises molecular dynamics simulations to track the structural evolution of vapour deposited ASW upon annealing, using the TIP4P/2005 water potential. Our results exhibit good quantitative agreement with laboratory experiments, despite the time and size limitations of MD simulations. Upon annealing, our ice structures undergo significant compaction and pore collapse. These changes are found to be governed by a very subtle mechanism in the ice, wherein the water molecules continuously undergo small rearrangements until the highest temperatures above 160 K.

---

1. Introduction

Amorphous solid water (ASW) is a form of disordered ice formed by low-temperature and low-pressure vapour deposition. The physical and chemical properties of ASW are of interest to physical chemists, cryobiologists, astrochemists and planetary scientists.¹ On Earth, ice clouds form at and below the high latitude mesopause which could form ASW due to the <100 K temperatures.² Additionally, ASW is used as a model for super-cooled liquid water and also finds a use in cryogenic electron microscopy, where samples are embedded in an environment of vitreous water (another name for amorphous ice).³ Outside of Earth, it forms naturally in a variety of astrophysical environments, including dense molecular clouds, comets (at heliocentric distances beyond ≈6 AU), icy moons (e.g. Europa and Ganymede) and perhaps Kuiper Belt objects as the temperatures are low enough.^4–8

ASW has so far been identified as a continuous random network of primarily four-coordinated water molecules that lacks long range order (similar to liquids).^5,9–11 Its surface morphology, wherein porous ASW provides large effective surface areas as large as hundreds of m² g⁻¹, greatly influences the diffusivity of reactions, access to reaction partners and the sticking properties of atoms and molecules – making it a crucial component governing the extent to which chemical complexity evolves with time and temperature.^12–24

Both experimental and computational studies have made it clear that the ASW structure obtained is significantly affected by the deposition conditions.^{5,9,10,16,17,25–35} The effects of deposition temperature on the ASW structure are less studied within the literature, but the general consensus is that with increasing deposition temperature, ASW is more compact and has a low surface area and porosity.

The effects of temperature when annealing ASW is the focus of this work. So far, it is known that annealing ASW leads to the loss of porosity and surface area, along with a general compaction of the ice. At low temperatures of <10 K, a high-density amorphous form of ice exists.³⁶ At 38–68 K, an irreversible phase transition occurs gradually creating a low density and less porous amorphous phase. Further warming gradually compacts the ice until it undergoes a ‘glass transition’ in the region of 135 K.³⁷ This forms a super-cooled metastable liquid before eventually crystallizing at 140 K onwards.^{11,15,17,23,25,29,35,36,38–40} The specific temperatures at which these phase transitions occur depend on the deposition parameters, presence of impurities and heating rate.³⁶

Although we know that structural changes occur to ASW when heated, we still do not know how these changes occur, especially at low temperatures where diffusion is limited, or why they have such a drastic impact on the ASW structure and properties.^13,41 One theory of how the process occurs is that of Jenniskens et al. (1994) who state that, in the 38–68 K range, the breaking of a hydrogen bond becomes possible and that is what triggers the phase transition.³⁶ Subsequently, in the temperature range of 60–80 K, He et al. (2019) observe that the diffusion of water becomes efficient enough to play a role in the surface area and porosity loss, and increases at higher temperatures.⁴² Their structures begin to smooth, by first eliminating the smaller pores until eventually all of the pores are removed and the ice reaches a maximum density at 150 K.

To uncover the mechanism of the processes, simulations are very useful, as a complement to experiments, as they can directly probe structural information on an atomistic scale. Computational studies attempting to answer how temperature affects ASW upon annealing are limited to single-run studies of annealing structures that were either created by unrealistic methods (e.g. quenching) or with no variety in the temperatures they were grown at.^28,42–44 As we are studying a metastable material, where its structure is never in equilibrium and is dependent on its pathway, it is important to explore the range of structural outcomes possible, which single-run studies are not capable of achieving.

The aim of this paper is to address that overarching question of “what happens when ASW is heated and annealed?”. We have tackled the problem using molecular dynamics simulations, using vapour deposited ASW ice structures grown at a variety of surface temperatures (from Hashemi et al. (2022)).⁴⁵ We have step-wise heated the ASW ‘samples’ to emulate similar heating profiles in the laboratory. Notwithstanding the time and size limits of MD simulations, there is good quantitative agreement between our simulation results and laboratory experiments in the literature. The quantitative analysis of our simulations drives towards answering two key questions that experiments are unable to address from a molecular level; (a) when, how and why does the pore collapse process in ASW occur on heating (b) what is the link between the structural changes observed in the ices, and molecular level changes in the material.

The remainder of this paper focuses on those aspects, showing conclusively that the global structural changes in ASW on heating are likely to be governed by small rearrangements of the water molecules.

2. Methodology

2.1. Creating ice structures

The starting ASW structures for this study are described previously by Hashemi et al. (2022).⁴⁵ Briefly, hundreds of different ASW structures were simulated, by growing the ice structures through virtual vapour deposition of H₂O molecules onto coarse-grained SiO₂ surface.

Typically, the incoming molecules were extracted from a Maxwell Boltzmann distribution of water vapour at an equivalent kinetic temperature of either 10, 150 and 300 K. These molecules were then ‘dropped’ one-by-one onto the SiO₂ substrate, with random x, y and z velocity components. This is to simulate, in molecular dynamics, a ‘background deposition’ of material akin to experimental conditions (e.g. Mate et al. (2012)).⁴⁰ The simulations were stopped when 500 water molecules were accommodated to the surface.

The process was repeated at surface temperatures ranging from 10 to 120 K, in 10 K steps, with up to 10 different simulations at each temperature step, and 30 simulations at surface temperatures of 30, 60 and 100 K. Full details of the simulations, resultant structures and their properties are detailed in Hashemi et al. (2022).⁴⁵

These structures appear to well reproduce some global properties of ASW observed experimentally, as well as more detailed molecular level properties.⁴⁵ Six of these structures were used as the starting point for the simulations presented in this paper. First, the structures used for this work were selected from those grown with incoming H₂O molecules set at 300 K, to most closely reproduce the conditions in laboratory experiments with ASW. Second, only one structure was randomly selected at each surface temperature growth value between 20 and 120 K, giving 6 distinct ASW structures for the annealing simulations (seen in Fig. 1). This number of structures was chosen as it gave a good compromise between probing each deposition temperature and being able to anneal and analyse them in an appropriate time frame.

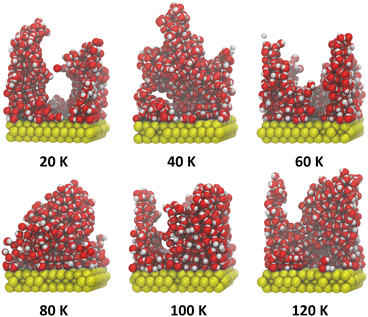Fig. 1 Images of simulation output of the starting structures used for our heating simulations, reproduced from Hashemi et al. (2022) after vapour deposition at 20, 40, 60, 80, 100 and 120 K.⁴⁵

All the pores in these ASW structures are considered to be “microporosity” following the IUPAC definition.⁴⁶ Therefore, the ASW porosity discussed herein is microporosity, noting that the pores are in the nm not μm range.

2.2. Annealing method

From the work of Hashemi et al. (2022), we have some starting structures to use for the annealing simulations (seen in Fig. 1) undertaken in Gromacs, version 2021.4.^45,47Fig. 2 outlines the method used to anneal the ASW structures from their starting temperature (commensurate with the deposition temperature) to the final annealing temperature of 200 K. For the sake of brevity and clarity, the deposition and annealing temperatures will be referred to as T_dep and T_anneal, respectively, for the remainder of this paper.

Fig. 2 Example of the annealing method used herein. Starting structure with T_dep = 20 K (image of structure shown) is annealed to 30 K over 5 ns. The structure output of that simulation is taken as the input for the next simulation that will anneal it to 40 K over 5 ns. This is repeated until the end T_anneal of 200 K.

The starting structures are heated to 200 K in 10 K increments, where the output structure of one 10 K increase is used as the input for the next. For example, the output of heating an ice with T_dep = 20 K to 30 K is used as the input to heat to 40 K, and so on until it reaches 200 K. We do not heat past 200 K as, by that point, we see motion of the water molecules of over a bond length and full compaction without crystallisation occurring. Our chosen water potential TIP4P/2005 is not optimised for modelling this phase change and so if we were to heat further, we would likely start to obtain nonphysical results. Our focus is on the structural changes to the disordered state prior to crystallisation and so it is still preferable to use TIP4P/2005 as it models the disordered state better than models that would be ideal for crystallisation.

The simulation setup for annealing the ASW structures uses the leap-frog algorithm, with a time step of 2 fs, and the Verlet pair list scheme for neighbor searching. The coulomb and van der Waals cutoffs were set to 14 Å, while the long-range electrostatic interactions were handled using the particle mesh ewald (PME) procedure. This cutoff of 14 Å is about half the shortest box length and is much larger than the cutoffs used in other studies. For example, Essmann and Geiger (1995) use a cutoff of 8.5 Å.⁴⁸ The TIP4P/2005 potential was used to describe the interaction between water molecules as it was found to reproduce well the Ih–HDA and LDA–HDA transitions and the general properties of water in liquid and glassy forms.^49–53 Additionally, the water molecules are treated as rigid bodies, meaning that intramolecular degrees of freedom are neglected.

The surface is comprised of 300 silica particles modeled in a coarse-grained manner as ‘beads’ of Lennard-Jones potentials, whereby the equation for this potential is:

Parameters used in this equation for these ‘beads’ are: σ = 0.28 and ε = 5.7632. They are arranged in three layers spanning around 31 Å in the x and y directions. This slab is essentially representative of hydrophobic substrates. However, the surface needs to be able to interact with the water molecules and ‘sump’ energy; therefore, of the three layers, the top two were allowed to freely move, while the bottom layer is fixed to anchor the system.

Periodic boundary conditions (PBC) were only set in the x and y axes to stop water molecules desorbing and depositing on top of a different image. To use these PBCs in conjuction with PME for the electrostatic interactions, we had to add walls on either side of the box in the z axis so that it is not infinite in that direction. These walls were placed several cutoffs away (both above the water structure and below the silica surface) with only a short-range potential to avoid our ASW system interacting with them.

To maintain a given temperature of the whole system in the simulation, we used v-rescale, which is a modified Berendsen thermostat that includes a stochastic term in its scaling to ensure that a proper canonical ensemble is generated.⁵⁴ Although we could use the simplest mechanism of regulating temperature – velocity scaling – this method is unsuitable for long-term timestep-by-timestep operation of the simulation as it dampens down genuinely extant fluctuations in temperature. These extant fluctuations occur in the physical system as it has a finite time of thermal redistribution. To overcome this issue, we need a weak form of temperature scaling, which is the Berendsen thermostat. This thermostat also gives us stable and smooth changes to new values of temperature without the need for intermediate adjustments. The temperature coupling constant used is 0.1 ps for each coupling group.

ASW is a metastable material and therefore the structure is not in equilibrium and cannot reach it unless it changes to a different form through a phase transition.^55,56 As it is never in equilibrium, its thermal history to a certain structure is very important. Compared to laboratory experiments, our simulation heating rates and thus thermal histories are significantly different, meaning that the outcomes would be different at certain temperature points. Therefore our focus is on the general trends found, rather than changes at specific temperatures.

The run time for each 10 K increment (denoted as ‘isothermal step time’ from here on) is consistent across a run as seen in Fig. 2. The isothermal step times used were 5, 10 and 100 ns. Typically, a run from T_dep = 20 to T_anneal = 200 K took on average just over a day when using the 5 ns step time and 27 days for the 100 ns step time. We chose to not to go over 100 ns for the isothermal step times as this was the limit at which simulations ran in a reasonable timescale. At the end of each time step, regardless of the isothermal step time used, the system is not in equilibrium and would not be even if a longer time were used, due again to the metastability of ASW.

Fig. 3 shows, for the isothermal step times used, the average potential energy as a function of the 10 K increment end point (T_anneal). We see herein that the longer timescales allow for the system to reach a lower potential energy and therefore move more towards equilibrium without ever reaching it (as expected). From this, as we can see that the energies differ across the isothermal step times used, it is clear that they will obtain different structural results.

Fig. 3 Average potential energy as a function of annealing temperature for each isothermal step time used: 5, 10 and 100 ns. The potential energy shown is of the end point of each 10 K increment, of annealing the ice with T_dep = 20 K (see Fig. 1) to 200 K. This is averaged across 10 runs with the same isothermal step time and the error bars show the standard deviation across this average.

Within the different isothermal step times, we see that every run has a unique journey and outcome, as will be discussed in Section 3. To test whether this would also be the case for runs that have the same starting and simulation conditions, we did 10 runs of each full annealing simulation. It is more beneficial to conduct many ‘short’ simulations (isothermal step times not exceeding 100 ns) rather than few longer ones as we want to explore the range of outcomes brought on by the metastability of the material.

Overall, this resulted in a total of 60 simulation runs across the different starting temperatures using 5 ns as the time for each 10 K increment, 60 runs for 10 ns and then 60 runs of 100 ns – for a total of 180 annealing simulation (T_dep to 200 K) runs across all the ice systems. This is shown in Table 1 where the structure of the runs conducted are presented.

Table 1 Example of the structure of the runs conducted in this study, which is used for each of the three isothermal step times used. Each starting structure (see Fig. 1), with T_dep written in the first column, is heated in 10 K increments to 200 K. If a structure is heated to a certain temperature, the cell at that temperature (under T_anneal) is coloured green. Every annealing run, from T_dep to 200 K, is repeated 10 times as written in the last column

---

3. Qualitative results

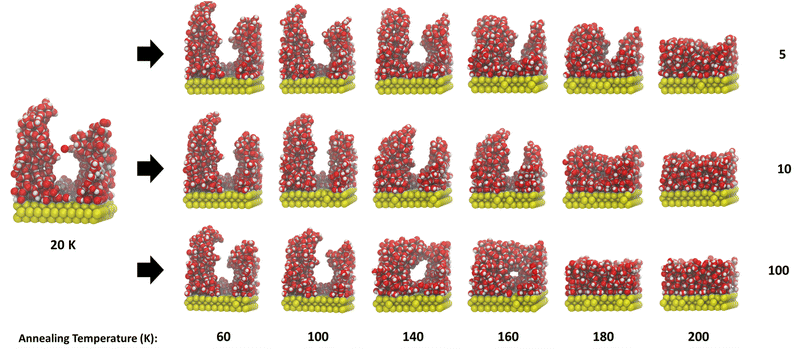
Our starting ice structures, shown in Fig. 1, are clearly amorphous and display irregular arrangements of water molecules, with clear pores and towers at the lower deposition temperatures. Within this section, we will discuss qualitatively the outcome of annealing (i) all the starting structures (ii) the same starting structure with different isothermal step times and (iii) the same starting structure with the same isothermal step time ten times.

Fig. 4 shows one example run of annealing each starting ice structure to 200 K. We see in Fig. 4 that, across every ice system, annealing leads to a decrease in height and compaction into a more slab-like structure once T_anneal reaches 200 K. The ice structure deposited at 20 K starts with two prominent towers that collapse to form a pore at T_anneal beyond 120 K and, by 200 K, the pore is destroyed once the ice compacts across the whole surface. Ice systems deposited at 60, 100 and 120 K also start with similar yet smaller towers; however, these structures do not form a pore like the 20 K structure. The towers seemingly collapse into themselves as temperatures increase. Lastly, the ice structures deposited at 40 and 80 K do not exhibit such tower-like structures; they instead start fairly symmetrical in the middle of the surface until they fully collapse to cover the entire surface.

Fig. 4 Images showing example runs of annealing each starting structure, shown on the left side before the arrows, from their T_dep to 200 K, in 10 K increments, using an isothermal step time of 100 ns. Structures obtained at various temperature stages of the full annealing run are shown with their respective temperatures written at the bottom of the figure.

The point at which all of these starting structures fully compact is not the same. For example, the ice structure with T_dep = 40 K becomes compact already by T_anneal = 160 K, whereas the other structures compact at T_anneal above 180 K.

It is also seen in Fig. 4 that an ice annealed to a certain temperature is not the same structure as one deposited at that temperature. As previously discussed, this is due to the metastable nature of ASW. This means that the annealing path to a structure at a certain temperature is important – the structure is dependent on thermal history.

The observed trend of irregular starting structures compacting and smoothing out upon annealing is similar to the Monte Carlo simulation work of He et al. (2019), who found that their initial column-like ice at 10 K became smoother with increasing temperature, until they get an entirely smooth surface at 140–150 K.⁴² They however do not test other starting structures created at various temperatures as we have. Clements et al. (2018) find the same smoothing of their ice structures by 130 K.²⁶ Although the trends from these simulation studies are the same as ours, our ice structures do not become smooth until T_anneal above 160 K, which may be due to differences in heating rate and/or the starting structures used and how they were formed.

Experimental studies find the same thermally induced pore collapse as that observed in this work. For example, the TPD experiments of Ayotte et al. (2001), Collings et al. (2003) and Collings et al. (2004) all observe the same ice compaction and pore collapse brought on by annealing, with a full loss of porosity by 140–160 K when ASW crystallises.^21,23,57 This was shown by the extrusion of adsorbates as the pores that they are stored in change and are destroyed. Raut et al. (2007) used a combination of QCM, UV-vis interferometry and infrared reflectance spectrometry, in tandem with methane adsorption, and found that there is microporosity and mesoporosity in their vapour-deposited ASW that also decreases with annealing.¹⁷ The amount of methane adsorbed for some samples indicated pore widths below a few molecular diameters. Mitterdorfer et al. (2014) and Hill et al. (2016) found, using neutron scattering, that the nanopores of their ASW remain stable up to 120–140 K and then experience a sudden collapse.^34,37

As discussed in Section 2, we have used three isothermal step times to explore the metastable nature of ASW and the path-dependency of each annealing outcome. Fig. 5 shows the outcome of annealing the same starting ice structure, where T_dep = 20 K, to 200 K using the isothermal step times of 5, 10 and 100 ns. Universally, the ice structures compact by T_anneal = 200 K regardless of the isothermal step time used. Of the three isothermal step times used, it is the 100 ns that features the lowest temperature of full compaction, at 180 K, and is also the only one of the three runs shown in Fig. 5 that forms an enclosed pore. Instead, the 5 and 10 ns runs show the two towers compact into themselves. In each case the journeys are unique – the structures from each run are not the same at the same temperature points.

Fig. 5 Three example runs of annealing the starting structure deposited at 20 K, imaged on the left side before the arrows, to 200 K using the three different isothermal step times: 5 (top), 10 (middle) and 100 ns (bottom). Structures obtained at various temperature points are shown with their respective T_anneal written underneath.

Another way we have explored the path-dependency of this metastable material is to do 10 repeats of every simulation run that has the same input structure and isothermal step time. Fig. 6 shows 10 runs of annealing the same starting structure, with T_dep = 20 K, to 200 K using the isothermal step time of 100 ns. Across all the runs, we see here again that annealing leads to the loss of height and, by 200 K, a smoothing of the structure upon compaction. Of these runs, only run 1 shows the creation of an enclosed pore by the collapse of one tower into another (shown previously in Fig. 4 and 5). The other runs show the two starting towers collapsing into themselves; however, their journeys to compaction are all unique. Runs 2–5 and 7–9 still have small towers present at T_anneal = 160 K, whereas runs 6 and 10 are much more compact and flat at that point. By T_anneal = 200 K, every run obtains a flattened ice structure that seemingly covers the surface.

Fig. 6 Images showing the 10 runs (run no. written on the right hand side) of annealing the starting structure deposited at 20 K, shown on the left side before the arrows, to 200 K, using the isothermal step time of 100 ns. Structures obtained at various temperature points are shown with their respective T_anneal written underneath.

From this qualitative overview of the structural changes in the ice, we conclude that there are many structural changes occurring in our ices as they are annealed that have been observed in other experimental studies of these systems. For example, our data corroborate the known behaviours and properties of ASW observed in experimental studies such as; the tower-like structures that form in the ice depositions (e.g. Laufer et al. 1987, Rosufinsen et al. 2016 and Marchione et al. 2019), pore collapse on annealing (e.g. Ayotte et al. 2001, Collings et al. 2003/2004, Raut et al. 2007, Mitterdorfer et al. 2014 and Hill et al. 2016) and height reduction on annealing (e.g. Bossa et al. 2012 and Isokoski et al. 2014).^{16–18,21,23,34,37,39,57–59} These observations also reflect the picture that ice structures obtained are ‘path’ dependent; i.e. ice structures of ices ‘grown’ at one particular surface (simulation) temperature do not have the exact same structural appearance when heated to higher temperatures as those initially ‘grown’ at higher surface temperatures.

4. Quantitative results

The power in exploiting molecular dynamics methods to study ASW is that, unlike with experiments, it is possible to interrogate the ice properties on molecular scales in absolute detail. This allows us to address the overall motivation of this work – to understand how and why structural changes occur to the ASW on heating, well below the barriers to translational diffusion.

In this next section, we probe porosity changes in the ice structure by quantitatively examining the global changes in ice height, specific surface area (SSA) and surface occlusion. This is to test whether any (or all) of these nanoscale properties are a proxy for porosity. We then investigate the radial distribution functions, nearest neighbour distribution histograms and kinetic displacement of individual molecules, to understand how inter-molecular scale processes might be driving the global structural changes observed as the ice is heated.

As Table 1 clearly demonstrates, and as described previously in Section 3, each annealing simulation ‘run’ generated between 8 and 18 unique ice structures, repeated at 3 different time-step intervals, which were then re-started 10 times per starting deposition temperature, giving 2340 distinct ice structures. This large sample generates many different prospective routes to statistically presenting the data, though in all of the results presented below, we have chosen to compare data between the different isothermal step times (5, 10 and 100 ns), keeping results from simulations on different time-scales separate (i.e. 780 unique structures per isothermal step time). This can be well justified because our systems are always dynamically changing and never really reach an equilibrium. As with experiments, where laboratory data also corroborate this non-equilibrium hypothesis, data show that the structural changes in annealed ASW samples are dependent on both heating rates and the length of time a sample is held isothermally at any one surface temperature. Ultimately, the more energy input to the ice system, the more changes occur; this is also reflected in our data presented here.

Conversely, we do not present data from individual simulation ‘runs’ (except where explicitly stated); rather, all data outputs are averaged over the 10 independent annealing ‘runs’, from the 6 T_dep, at each T_anneal (i.e. averaged at each ‘box’ across the rows in Table 1, never down the columns). Therefore, unless specified otherwise, in all the figures this section, this averaging is reflected as a single data point plotted as the mean value, together with a range bar (indicating the minimum and maximum values obtained across the 10 ‘runs’). This allows for the metastable nature of ASW to be highlighted and explored. Unlike in traditional equilibrium molecular dynamics where reproducibility is key, here we are studying a metastable material, where the outcomes are always irreversible and ‘path-dependent’, so every time we heat an ASW sample the outcome should be different, and generate a different molecular configuration, just as we observe. Furthermore, the simulation annealing process is a ‘one-way’ journey. Once the ice is heated, that structure is retained and determines the starting point for subsequent heating steps. It is impossible to revert to the previous molecular configuration.

4.1. Height

Height is one of the simplest parameters to measure and is very useful to extract from our data, as it is a direct measure of ice compaction that can be compared easily to experimental data. Fig. 7 shows how the mean maximum height of each ice structure varies as a function of T_anneal applied to the system during the simulation. To measure the height, we calculate the z axis distance between the topmost molecule in the silica surface and the furthest oxygen atom from that surface.

Fig. 7 Variation in the mean maximum height (in Å) of the ice (across 10 ‘runs’) as a function of the T_anneal, for time-steps of 5 ns (left panel), 10 ns (middle panel) and 100 ns (right panel). Trace colours, indicated by the colour bar on the right hand side, reflect the initial T_dep and the range bars reflect the minimum and maximum values in the distribution of heights in the individual ‘runs’.

Universally, the maximum height of the ice structures decreases non-linearly as the material is heated from T_dep. Regardless of the initial ice surface temperature, on annealing all the ice systems converge to the same maximum height, within the ranges bars of each system. The percentage change in heights are very similar across all simulations, as shown in Table 2

Table 2 Percentage decrease of maximum height (third column) in the ice upon heating from the respective T_dep (second column) to 200 K, for the different isothermal step times (first column)

Isothermal step time (ns)	T dep (K)	Height decrease (%)
5	20	50.02
	40	55.56
	60	44.67
	80	41.79
	100	39.29
	120	46.59
10	20	52.21
	40	56.70
	60	44.32
	80	43.95
	100	40.02
	120	49.21
100	20	51.63
	40	57.37
	60	45.79
	80	43.37
	100	39.51
	120	47.05

---

The average height loss for the 100 ns runs, across each system, is 47%. This is a much larger percentage change than what is seen in, for example, the experimental studies of Bossa et al. (2012) and Isokoski et al. (2013) who both quote a thickness decrease of 12% for an ice deposited at 15 and 20 K respectively. Isokoski et al. (2013) monitor the thickness change for ice structures deposited at various deposition temperatures and this thickness change decreases from 12% down to around 1% as the deposition temperature increases from 20 to 110 K. Our percentage change across our ice structures also decreases with increasing T_anneal, but with still much larger percentage changes. We believe this is due to the (necessary) small sizes used in simulation studies. Both Bossa et al. (2012) and Isokoski et al. (2013) have ice thicknesses of between 800 and 900 nm, whereas our ‘virtual; ices are two orders of magnitude smaller, where the likely highly porous vacuum-ice interface is proportionally a larger part of the ice.

Although the ices deposited at different temperatures have different initial maximum heights, qualitatively the rate of change of the height (i.e. the gradient of the slope) is comparable between all the data until T_anneal reaches beyond ≈140 K.

Across the entire dataset there is significant variance in the magnitude of the range bars. However, in general the range bars are smaller at T_anneal close to T_dep, then get larger as the ice is heated, and converge again at the highest temperatures where the ice structures are more compact (see e.g.Fig. 4). These observations are entirely consistent with the behaviour of a metastable material on heating, and the potential distribution of unique structures that could arise. Close to T_dep, it is expected that in short timescales the molecular structures from different annealing simulation ‘runs’ will not significantly vary from each other, and the range bars will therefore be small. However with more time (and more energy input) there is a greater chance of the ice restructuring and wider range of maximum heights will be observed. This is evident in Fig. 7 where the range bars for the ices heated with an isothermal step time of 100 ns are already larger than those for the ices heated with 5 ns time-steps, at the equivalent T_anneale.g. 40 to 120 K. At the highest temperatures, the range bars are much smaller and that is because the ices are compact, as seen in Section 3, and cannot change much more in terms of height.

In every instance, for the different isothermal step times used, we see again the same trend that the maximum height of the ice structures decreases non-linearly as they are annealed. Additionally, this quantitative data supports what is seen qualitatively that the simulations starting from the same ice structure deposited at a certain temperature, but with different isothermal step times, have differing journeys to this compaction.

At the highest T_anneal beyond ≈160 K, the convergence and flattening of the curves are different across the isothermal step times. For the 100 ns runs, shown in the right panel of Fig. 7, the flattening is far more prominent and occurs at an earlier T_anneal than for the 5 and 10 ns runs, which are shown in the left and middle panels respectively. This is due to the 100 ns runs having more time to approach (not reach) equilibrium.

4.2. Specific surface area

We also measured porosity through surface area, which gives a more complete picture of ice compaction. Laboratory and simulation studies have shown that a porous ice has significantly higher surface area than a compact ice, as there is the internal added surface area from the pores themselves.^17,42,44 High surface areas are very beneficial for trapping large numbers of atoms and molecules that adsorb onto/within the ice, which can then eventually react together.

To calculate the surface area of our ice structures, we utilised the program dms.^60,61 In essence this ‘rolls’ a probe sphere over the entire surface of our ice structures at the end of each 10 K increment. The area that is traced by the probe sphere is therefore the ‘sphere accessible surface area’ (SASA). We chose a radius of 1 Å for the probe sphere to represent small adsorbates, such as H₂, which are commonly found in the interstellar regions of interest to our work.

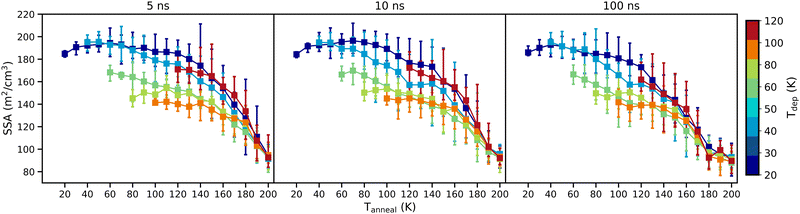
Fig. 8 shows how the surface area available to an adsorbate (represented by the probe sphere) in each ice structure varies as a function of T_anneal. Experimental values for surface area are usually specific surface areas (SSA) and so to be able to compare our work to such studies, we normalised our available surface area results to give their respective SSAs. Our absolute values of SSA, as shown in Fig. 8, are comparable to experimental values such as, for example, the work of Mitterdorfer et al. (2014) who quote initial SSAs of up to 230 m² g⁻¹ for ASW formed at 77 K.

Fig. 8 Variation in the mean SSA (in m² cm⁻³) of the ice structures (across 10 ‘runs’) as a function of the T_anneal, for time-steps of 5 ns (left panel), 10 ns (middle panel) and 100 ns (right panel). Trace colours, indicated by the colour bar on the right hand side, reflect T_dep and the range bars reflect the minimum and maximum values in the distribution of SSAs in the individual ‘runs’.

For all of the ice structures and simulations, as with height (see Fig. 7), the SSAs decrease non-linearly as the structures are heated from their respective T_dep. This trend of SSA loss with increasing temperature is commensurate with the experimental side of the study by He et al. (2019).⁴² They found that their accessible pore surface area stays fairly constant until temperatures above 80 K where there is then a steep decline through to 150 K.

Our ice structures all converge, on annealing, to the same SSA, within the range bars of each system, by 200 K. Larger changes in SSA are therefore found for the ice structures deposited at lower temperatures as they start with higher SSAs than those deposited at higher temperatures, which is likely due to them starting with taller structures (see Fig. 7). This is shown in Table 3, where the percentage change in SSA upon annealing to 200 K is presented for each starting ice structure.

Table 3 Percentage decrease of SSA (third column) in the ice upon heating from the respective T_dep (second column) to 200 K, for the different isothermal step times (first column)

Isothermal step time (ns)	T dep (K)	SSA decrease (%)
5	20	48.87
	40	53.11
	60	44.87
	80	35.54
	100	32.99
	120	45.80
10	20	48.30
	40	50.90
	60	44.66
	80	39.24
	100	35.73
	120	46.56
100	20	50.05
	40	52.39
	60	47.15
	80	39.21
	100	36.80
	120	44.65

---

The average SSA loss for the ice samples annealed with an isothermal step time of 100 ns is 45%, averaged from the values shown in Table 3. Laboratory studies mainly observe much larger losses in SSA, such as for example Bar-Nun et al. (1985) who quote a 90% loss of SSA when their ice is annealed from 10/20 to 122 K.⁶² As surface area is dependent on thickness, whereby thicker films such as that of BarNun et al. (1985) (1–2 μm) can have large networks of pores throughout them – creating much larger initial surface areas if they are accessible to the adsorbates.⁴² The Monte Carlo simulation work of Cazaux et al. (2015) exhibit networks of pores that become disconnected and eventually destroyed upon annealing – leading to a loss in SSA. When annealing up to 120 K, pore clustering may also occur in these larger-scale systems that can lead to a plateau or even an increase in SSA before more is lost upon further heating.^37,38,44 Our ice systems do not have networks of pores due to our system size and so our SSA is likely mostly from the external surface. Upon compaction, a lot of this external surface area would still remain and so we would not have as large of a percentage loss in SSA as these other larger-scale studies.

Trends seen with SSA in Fig. 8 are similar to that of height (see Fig. 7). Ices deposited at different temperatures have different initial SSAs, with those deposited at the lowest temperatures featuring the highest SSA. Qualitatively, the rate of change of the SSA is comparable between all the data until T_anneal reaches beyond ≈140 K where there is then a steep decline.

Across the isothermal step times, the same trend is evident that annealing all of the starting ice structures leads to a loss of SSA. The rate at which this occurs is the same, however, the journeys and points of convergence differ.

4.3. Density maps

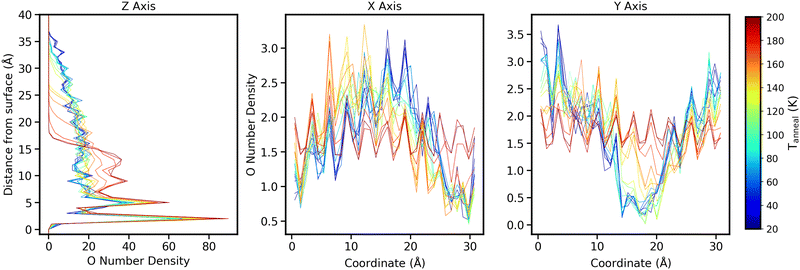
To get a more detailed picture of how the macroscopic ice structure evolves, we have calculated the distribution of the oxygen number density across each axis for all the ice structures obtained. To do this, we used the inbuilt gmx density utility.⁴⁷

Fig. 9 shows how the oxygen density varies for each ice structures at different distances from the silica surface as a function of T_anneal. In all cases, at low temperatures, there are two sharp peaks positioned at 2 and 5 Å away from the silica surface-indicative of a partial, semi-amorphous water bilayer. These peaks are more intense for ices deposited at higher temperatures. This is commensurate with the work of Essmann and Geiger (1985) who obtain two sharp peaks at low z, however, they are positioned at 6 and 8 Å.⁴⁸ This difference may be due to differences in what is used as z = 0 and/or the type of surface atoms. At distances above 7 Å, there is little further structure found and the overall density decreases due to rough and sometimes tower-like surfaces.

Fig. 9 Oxygen number density variations of the ice structures as a function of distance (in Å) from the silica surface in the z direction (averaged across 10 runs with an isothermal step time of 100 ns). Trace colours of each line denotes the temperature the system is at, as shown by the colour bar on the right hand side. The temperature at which the respective starting ice structure was deposited is written in the grey boxes on the top right hand corner of each plot.

In addition to density in the z axis, the x and y density distributions give us more information on how towers may collapse. Fig. 10 shows how the oxygen density varies as a function of T_anneal across all 3 axes for an ice deposited at 20 K and annealed to 200 K (run 1 of the 10 runs shown in Fig. 6). This run features the two towers in the starting structure collapsing to form a pore that eventually disappears, as discussed in Section 3.

Fig. 10 Oxygen number density as a function of T_anneal across all 3 axes (left panel Z, middle panel X and right panel Y axes). The left panel shows the densities as a function of height from the surface, whereas the middle and left panels show it as a function of coordinate on the surface. Trace colours represent the temperature the system is at, indicated by the colour bar on right hand side.

In the rightmost panel of Fig. 10, the highest oxygen densities at low temperatures are on the sides of the surface, representing the two towers we see in Fig. 4–6. In the middle panel, the highest densities are in the middle of the surface, representing the side profile of one of the towers.

As the ice is annealed, the oxygen densities across both the x and y axes begin to level out as the ice starts covering the entire surface. At T_anneal beyond ≈160 K, the densities are almost level across the surface which is consistent with the ice becoming compact as discussed in previous sections.

4.4. Surface occlusion

We see in Fig. 1 that the starting ice structures do not cover the entire silica surface – there is only a partial wetting layer. Exposed surface would have implications for the adsorption of atoms/molecules and their diffusion to meet for reactions as there are differences in the interaction with water or surface.

Fig. 11 shows how surface coverage changes as a function of T_anneal, as viewed from the side (panel a) and from above (panel b). In Fig. 11, we can see in panel a that a tower collapses into the other, creating a pore by 140 K, which is then gone by 200 K as the ice is compact. From above, as seen in Fig. 11 panel b, this creation of a pore at 140 K looks as though the surface is covered on the left hand side. However, as we know from panel a, this is not the case, there is the empty space of the pore present created by the overhanging structure. One way to account for this is to quantify the surface coverage layer-by-layer in the ice structure.

Fig. 11 Images of an ice deposited at 20 K that is annealed to 200 K, from the side (panel a) and from above (panel b). Temperatures of each structure shown is written underneath the images.

To quantify this surface coverage change, we calculated the percentage of the surface that is occluded by water molecules as a function of T_anneal, at various distances from the surface by running a ‘probe’ of diameter 2.75 Å (steric size of a water molecule) across the accessible surface, including pores open to the surface but excluding the sides and internal (non surface accessible) pores. This allows us to obtain a local description of the structures and to account for instances where a pore may be 'covered' over from above. The distances chosen were those which are equivalent to where the first 50 water molecules are, then where there is a total of 100, 150, 200 and so on until the full 500. This is based on the z axis oxygen number density results for each 10 K step, shown and discussed earlier in Section 4.3.

Fig. 12 shows examples of these layers for the starting structure deposited at 20 K, where you can see the layers from the side (panel a) and from above (panel b). Within this example, we can see that there is exposed surface in the bottom right corner at 50 water molecules that is covered up at 200 water molecules onwards. At no point across the structure, even at the base, is there full surface coverage.

Fig. 12 Images of the starting ice structure deposited at 20 K with various layers, based on number of water molecules. Panel a shows the structure layers from the side and panel b shows the layers from above. The respective number of water molecules present in the structure shown is written underneath.

The distances used for the layers change as an ice structure is heated, as the ice restructuring inevitably changes where the first 50, 100, 150 and so on water molecules are. Calculating the surface occlusion at these various distances gives us the distribution of how the surface is covered and also see where the water molecules are in all axes as a function of height.

Fig. 13 shows, in the left panel, how the surface occlusion varies for each layer as a function of T_anneal. This is for the simulation run presented in Fig. 4 as run 1 of the 10 runs shown, which was used earlier in Section 4.3 as well. As mentioned previously, the distances used for the layers change as the ice restructures upon annealing, which is shown by the middle and left panels that show the oxygen densities of the ice structure deposited at 20 K (middle panel) and that ice at 200 K after annealing (right panel). On both of these plots, the horizontal dashed lines show the position of where the first 50, 100, 150 and so on water molecules are positioned from the surface.

Fig. 13 Variation of the surface occlusion, shown in the left panel, as a function of T_anneal for each layer (comprised of the number of water molecules indicated by the colour bar on the left hand side). The middle and right panels show the oxygen number density as a function of distance from the surface for the structure at 20 K (middle panel) and 200 K (right panel). Horizontal dashed lines on these plots show the distance at which 50, 100, 150 and so on water molecules are present for the layers.

Universally for all layers, as seen in Fig. 12, the surface is not fully occluded even at the base (first 50 and 100 water molecules), until T_anneal beyond ≈170 K when the ice starts compacting (seen in Fig. 4–6). Until ≈110 K, there is little change in the proportion of the surface that is occluded for layers of more than 50 water molecules and then there is a steady increase until a plateau at 100% surface occlusion, at the highest temperatures. For the layer of 50 water molecules at the base of the ice, the surface occlusion increases at the same rate throughout the annealing, and does not reach 100% surface occlusion even at 200 K, meaning there are likely gaps between the water molecules that were not ‘filled’ in as the ice compacted.

Surface occlusion allows us to understand how the surface and structure is spread out. This is important when related to adsorbates interacting with the ice. These results, along with those discussed in Sections 4.1, 4.2 and 4.3, give us a good overall measure of the structure and porosity of ASW and how it evolves as it is annealed.

4.5. Radial distribution function

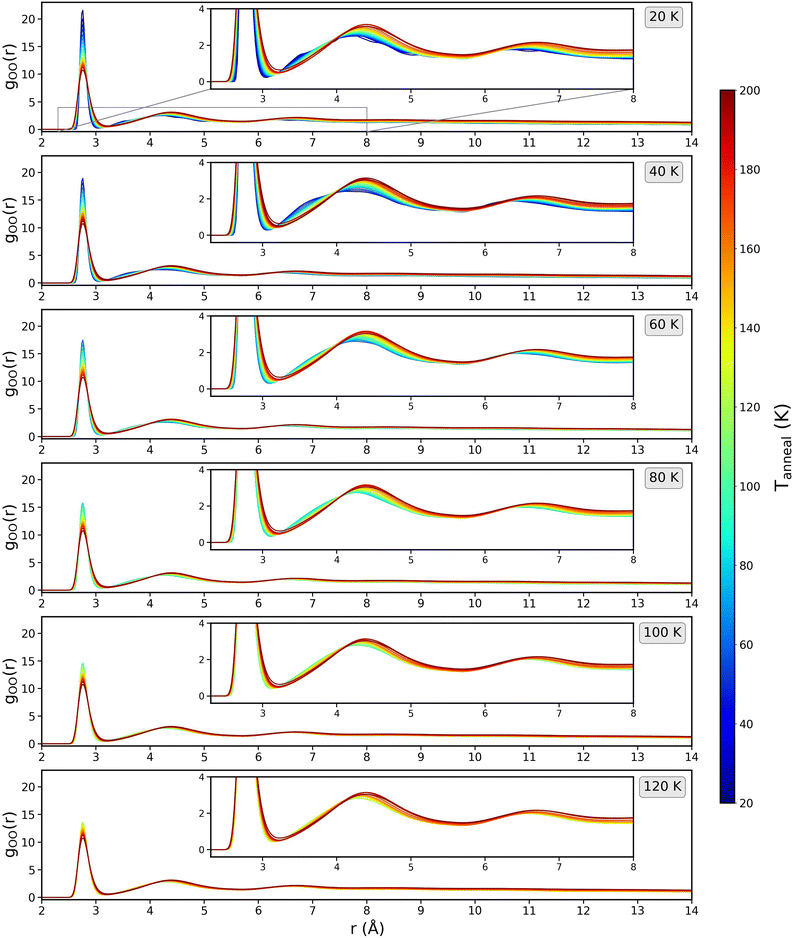
Radial distribution functions (RDF) are a key metric for quantifying local structure in non-crystalline systems. The RDF is the ratio of the local density of atom A, at a distance r from atom B, to the bulk density. RDFs can be readily obtained from simulations and by careful analysis of neutron/X-ray total scattering experiments.^{28,33,43,48,63–68} Amorphous ice is known to display order at short range and disorder at longer range.⁴³

Fig. 14 shows the g_OO(r) (averaged over 10 runs) as a function of T_anneal for each starting structure used (shown in Fig. 1), calculated using the in-built analysis routine gmx rdf.⁴⁷ At both low T_dep and T_anneal, every ice system displays a sharp peak at 2.76 Å, a second peak at 4.16 Å and third at 6.32 Å, representing the first, second and third solvation shells respectively.

Fig. 14 Variations of g_OO(r) as a function of T_anneal for each starting structure, deposited at the temperature indicated in the top right corners of each plot in the grey box. Trace colours represent the temperature the system is at and is indicated by the colorbar on the right side. These RDF plots are averages across 10 runs with the same isothermal step time of 100 ns.

The first peak position is within ±0.01 of the positions reported experimentally (e.g. Finney et al. 2002, Guillot and Guissani 2004 and Bowron et al. 2006) and in other simulation work (e.g. Esmann & Geiger 1995, Martonak et al. 2005 and Guesquiere et al. 2015).^{28,43,48,63,66,68} However, our peak intensity is much larger than what is reported in the experimental literature, which is due to our model not taking into account quantum effects that would usually smooth the experimentally measured structure of amorphous water, especially at low temperature, as was observed in the simulation work of Essmann and Geiger (1995).⁴⁸ In experimental data, changes arise from the presence of intramolecular vibrations. However, in the simulation, any intramolecular degree of freedom is neglected as the water molecule is treated as a rigid body.

As the temperature increases, we see in Fig. 14 that the first peak at 2.76 Å broadens and lowers in intensity but does not change position. This lower intensity is due to a decrease of the structural nearest-neighbour organization, meaning the short range structure is becoming more disordered. Guesquiere et al. (2015) observe the same phenomenon.⁴³ The second and third peaks in Fig. 14 increase in intensity and increase in distance from 4.1 and 6.4 to 4.4 Å and 6.7 Å, respectively, as T_anneal is increased to 200 K. Broadening of the peaks at short range is indicative of disordering occurring at short-range, while there is ordering at longer range shown by the second and third peaks shifting to longer range.⁴⁸ Local disorder (decreased first peak) allows some small movement so that positions in the 2/3rd shells are more energetically favourable and therefore less disordered.

The second peak moving to 4.4 Å at higher temperatures brings it to the same peak position as found in other studies. Bowron et al. (2006) report a second peak position of 4.4 Å in their neutron scattering work which, when related to the first peak position of 2.7 Å, is attributed to a mean O–O–O angle in the LDA network of around 111° – close to the ideal tetrahedral angle of 109 degrees – meaning that the short range structure relates closely to a hydrogen bonded tetrahedral network of water molecules.⁶³ Guillot and Guissani (2004) also attribute their 4.5 Å peak as the well-known signature for the 3D hydrogen bond network of water.²⁸

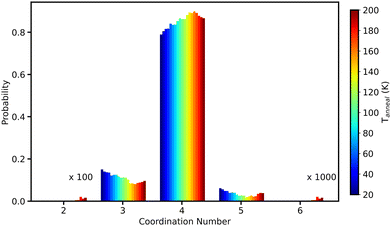
This first peak in Fig. 14 in every ice system is composed of the four first neighbors.⁶³Fig. 15 shows the variation of number of nearest neighbours (O–O coordination number) as a function of T_anneal for run 1 of the 10 runs shown in Fig. 6. The cutoff for this calculation was based on the minimum of the first g_OO(r) peak in Fig. 14; as the peak broadens with increasing temperature, the cutoff used changes from 3 to 3.2 Å.

Fig. 15 O–O coordination number as a function of T_anneal, with the bar colours indicating the temperature, shown by the colourbar on the right hand side. This is calculated for one run of annealing the starting ice structure, deposited at 20 K (see Fig. 1), to 200 K.

Without exception, at all temperatures, a water oxygen is most likely to have four nearest neighbours, as seen in Fig. 15. The water molecules being predominantly four-coordinated is in line with the optimal hydrogen bonding coordination number of two hydrogen atoms that are hydrogen bonded to each water oxygen atom.

As the temperature increases, the probability of being four- and five-coordinated increases, while the probability of being two- and three-coordinated decreases. This is commensurate with the experimental literature such as Hornekaer et al. (2005) wherein their IR bands assigned to two- and three-coordinated molecules in their ASW diminish with increasing temperature, until eventually only four-coordinated water molecules are observed at temperatures above 120 K – corresponding to a fully hydrogen bonded H₂O.⁶⁹ Even at our highest temperatures however, we do still observe water molecules that are three-coordinated. Finney et al. (2002) and Bowron et al. (2006) both also report more four- and five-coordinated water molecules when the ice is more dense.^63,66 The simulation work of Cazaux et al. (2015) attributes the increase in coordination number to the ability for water molecules to diffuse more easily at higher temperatures (something we also observe – see Section 4.6).⁴⁴

Fig. 16 shows the g_OH(r) (averaged over 10 runs) as a function of annealing temperature for each starting structure used. The first peak is positioned at 1.8 Å and the second peak at 3.12 Å; when annealed to 200 K, they shift to 1.82 and 3.16 Å, respectively. These peak positions are commensurate with the g_OH(r) of the ASW and LDA samples of Bowron et al. (2006) at 80 K.⁶³

Fig. 16 Variations of g_OH(r) as a function of T_anneal for each starting structure, deposited at the temperature indicated in the top right corners of each plot in the grey box. Trace colours represent the temperature the system is at, indicated by the colorbar on the right side. These RDF plots are averages across 10 runs with the same isothermal step time of 100 ns.

Using a cutoff of 2.4 Å, based on the minimum of the first peak of g_OH(r), the O–H coordination number was calculated. Fig. 17 shows the variation of this O–H coordination number as a function of T_anneal for the same run used for the O–O coordination number (shown in Fig. 15). As seen for the O–O coordination number, an oxygen is most likely to be four-coordinated to hydrogens (this includes intra-molecular H). With increasing temperature, the probability of being four-coordinated increases, while the probability of being three- and five-coordinated decreases. After T_anneal = 160 K, the probability of being four-coordinated decreases and being two-, three-, five- and six-coordinated increases. At the highest temperatures, we start to enter an nonphysical regime as shown by the ice not obeying the ice rules- there are more over- and under-coordinated water oxygens (for both O–O and O–H).⁷⁰ This is because our MD is not optimized for crystallisation and so the results at these high temperatures are not accurate. We are however only interested in the structural changes occurring prior to this nonphysical regime.

Fig. 17 O–H coordination number as a function of T_anneal, with the bar colours indicating the temperature, shown by the colourbar on the right hand side. This is calculated for one run of annealing the starting ice structure, deposited at 20 K (see Fig. 1), to 200 K.

We conclude from this section that the short-range structure of our ices is disordered and on average tetrahedral coordinated. This is based on the relation between the first and second peak positions in g_OO(r) (see Fig. 14) and the first peak position in g_OH(r) (see Fig. 16). As our ice structures are annealed, they all exhibit increased disordering with the first shell while simultaneously ordering with the 2/3rd shells. We saw in the preceding sections that annealing our ices leads to their compaction and so as this compaction occurs, the water molecules shift from being two- and three-coordinated (with four being the most probable) to higher numbers.

4.6. Diffusion

We have seen in the preceding sections that there are large structural changes occurring to the ice as it is annealed, regardless of the starting ice structure. However, the mechanisms responsible for these changes are poorly understood, especially at low temperatures where diffusion of molecules should be limited.⁴¹

Fundamentally, to understand what governs the pore collapse process, the movement of the water molecules need to be ascertained. Fig. 18 shows the average mean square displacement (MSD) as a function of time interval τ (also called lag time) for the 10 runs of annealing the starting ice with T_dep = 20 K to T_anneal = 200 K, using an isothermal step time of 100 ns. The MSD is a measure of the deviation of the position of a molecule with respect to a certain reference position over a time interval and was calculated using the inbuilt msd utility.⁴⁷ Although there are few simulation studies that calculate the MSD of this type of ice, our values for MSD are similar to what is found in the work of Essmann and Geiger (1985), who quote a range of around 0.45 to 5 Ų when annealing their simulated ice from 292 to 310 K.⁴⁸ However, not only do they use higher temperatures, they also use much shorter simulation times – increasing the temperature by 2 K every 6 ps.

Fig. 18 Average mean square displacement of the water molecules as a function of Δτ. This is calculated for and averaged over 10 runs of annealing the starting ice structure deposited at 20 K (see Fig. 1) to T_anneal = 200 K with an isothermal step time of 100 ns. Trace colours represent the temperature the system is at and is indicated by the colourbar on the right side.

Fig. 18 shows that with increasing T_anneal, the MSD increases. At low temperatures, below 80 K, there is very little movement of the water molecules (less than a bond length), meaning that they are likely not moving far from their positions (near zero MSD). As T_anneal increases past 80 K, we start to see movement across distances that are larger than a bond length, and eventually more than the diameter of a water molecule, which is unsurprising considering that we know that large scale structural changes start occurring at these higher temperatures, such as, for example, towers collapsing to form pores. At the highest temperatures, the water molecules are, on average, moving distances of around 15 Å. Although this may seem like a large distance, Section 4.1 outlines that the ice structure loses about half of its height which, for an ice deposited at 20 K, would be a decrease of about 20 Å. Additionally, as discussed in the previous section, we are likely in a nonphysical regime at the highest temperatures.

The observed diffusion in our MD studies is commensurate with what little there is in the literature. Cazaux et al. (2015) find that, in their Monte Carlo simulation, their water molecules travel much larger distances as temperatures increase, allowing them to rearrange into a more stable configuration.⁴⁴ We see this move towards higher stability by how there are more four- and five-coordinated water molecules at higher temperatures, seen in Fig. 15. Kimmel et al. (2001) suggest that the diffusion likely occurs for molecules with higher average coordination, i.e., more bulk diffusion.

Fig. 19 shows the average diffusion coefficient as a function of T_anneal for the water molecules in the ice systems. The diffusion coefficient is determined by simple linear regression of the MSD between Δτ of 5 and 60 000 ps. It was calculated and averaged over the 10 runs of annealing the starting structure deposited at 20 K. Overall, the diffusion coefficient increases linearly with increasing temperature.

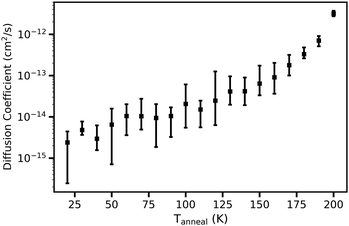Fig. 19 Average diffusion coefficient for the water molecules as a function of T_anneal. This is calculated for and averaged over 10 runs of annealing the starting ice structure deposited at 20 K (see Fig. 1) to T_anneal = 200 K, with an isothermal step time of 100 ns.

This trend of increasing diffusion coefficient with increasing temperature aligns with the LDA simulation work of Guesquiere et al. (2015) who obtained diffusion coefficients that fall into three different regimes: ‘low temperature’ regime below 90 K; ‘medium’ between 90 and 170 K, and ‘high’ between 200 and 270 K. In the low temperature regime, they found that the MSDs are too small to determine the diffusion coefficients with good precision. Their LDA ‘self-diffusion’ coefficients are in the same range as ours for the T_anneal range of 90–170 K, on the order of 10⁻¹⁵ to 10⁻¹¹ cm² s⁻¹. For temperatures between 200 and 270 K, they obtained self-diffusion coefficients ranging from 10⁻⁷ cm² s⁻¹ to 10⁻⁵ cm² s⁻¹, which are higher than what we obtain. We however do not heat past 200 K as they do.

Several studies of diffusion of/in ice have done so at higher temperatures and are therefore looking at crystalline ice. For example, the experimental work of Scott Smith et al. (2000) calculate self-diffusion coefficients that range from 10⁻¹⁵ to 10⁻¹² cm² s⁻¹ for temperatures between 150 and 160 K.⁷¹ Other examples at higher temperatures include the MD simulation work of Ikeda-Fukazawa et al. (2004) who obtain water diffusion coefficients in I_h of 10⁻⁶ to 10⁻⁵ cm² s⁻¹ at temperatures of 200 to 270 K and the experimental work of Oka et al. (2024) with a self-diffusion coefficient of 10⁻⁶ cm² s⁻¹ for supercooled water at 238 K.^72,73 Where they exist, we align with studies of similar ices; whereas for crystalline ices, different diffusion coefficients are observed.

We conclude in this section that, at low temperatures below 80 K, there is little movement of the water molecules until higher temperatures when drastic bulk structure changes occur – like a tower collapsing. Previous sections have shown that drastic pore collapse starts occurring past around 130 K. Even at this point, the water molecules only have an average MSD of up to 5 Ų, meaning that there must be some moving more than this while others only exhibit small rearrangements.

5. Conclusions

We have used molecular dynamics simulations to answer whether annealing temperature impacts the ASW structure. Throughout both our qualitative and quantitative results, it is clear that annealing ASW does impact its structure by inducing global changes. The global changes we observe are commensurate with experimental studies. This match up is impressive considering the simplicity of our model and its underlying physics and therefore gives us confidence to use the model to interrogate on a molecular level how these processes are happening, in a way that you cannot do in a laboratory measurement.

On the nanoscale, our ice structures start as irregular surfaces with towers in some instances. Upon annealing, we witness the following:

1. Every run, regardless of whether the starting parameters are identical, has different results in the key ‘translational’ region (i.e. between deposition and complete collapse). Therefore, it is clearly important to study several replicas in both simulation and laboratory work to study the range.

2. If towers are present, they either compact into themselves or collapse into each other to form a pore that disappears upon further heating.

3. Presence of a water bilayer at the solid interface at the lowest temperatures that increases in prominence with increasing temperature.

4. At lowest temperatures, surface is not entirely covered (partial wetting layer) – only becomes covered at T_anneal beyond ≈160 K. This has implications for how adsorbates would interact with a surface.

5. Both ordering of structure at short-ranges (≤2.8 Å) and disordering at longer ranges (≥2.8 Å) as temperatures increase – getting closer to a less-strained structure.

6. Water molecules more likely to have higher coordination numbers at higher temperatures. Most probable is always to be four-coordinated.

Our MSD calculations tell us that these changes are governed by a very subtle mechanism in the ice. Until the highest temperatures of over 160 K, the water molecules only have an average MSD of up to around 5 Ų, over 100 ns. Therefore, it seems that the process of pore collapse is underpinned by the water molecules undergoing small rearrangements and they do not move far from their positions.

We conclude with this that molecular dynamics simulations are a good tool for probing the structural and dynamical effects of annealing ASW. However, it is important to understand the results in terms of the time scales used. We have very different heating rates to that of experimental studies and, as ASW is metastable, that difference in thermal history does affect the structural outcomes. Within our own study, we see these differences between the time scales used and even in just doing 10 runs with the same parameters – they all have a unique pathway and outcome.

Author contributions

Z. Amato: formal analysis, investigation, methodology, software, visualization, writing – original draft and writing – review & editing. P. Ghesquière: methodology and software. T. F. Headen and H. J. Fraser: conceptualization, funding acquisition, methodology, project administration, resources, supervision, validation and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

All relevant data are within the paper.

Acknowledgements

Astrochemistry at the Open University is currently supported by STFC under grant agreement numbers ST/X001164/1, ST/T005424/1 and ST/Z510087/1 and Z. Amato also thanks The Open University and the ISIS Neutron and Muon Source for funding his PhD studentship. Earlier research leading to the original theoretical MD work presented in this paper was undertaken at the OU and was previously supported by EU FP7 FP7-PEOPLE-ITN-2008-238258 LASSIE Research Training Network, EU COST Action CM1401 and UKRI - STFC under grant agreement numbers ST/M003051/1 and ST/P000584/1, as well as the Open University HPC, start-up funds for HJF, and previously the University of Strathclyde. We gratefully acknowledge the earlier inputs of James Miller, Pavel Elkind, Gunnar Nyman, James McCann and Martin Sweatman to the development of the methodology and calculations of the water ice structures.

References

1. S. Malyk, G. Kumi, H. Reisler and C. Wittig, J. Phys. Chem. A, 2007, 111, 13365–13370.
2. B. J. Murray and E. J. Jensen, J. Atmos. Sol.-Terr. Phys., 2010, 72, 51–61.
3. P. Schultz, Q. Rev. Biophys., 1988, 21, 129–228.
4. K. J. Meech, J. Pittichova, A. Bar-Nun, G. Notesco, D. Laufer, O. R. Hainaut, S. C. Lowry, D. K. Yeomans and M. Pitts, Icarus, 2009, 201, 719–739.
5. D. E. Brown, S. M. George, C. Huang, E. K. L. Wong, K. B. Rider, R. S. Smith and B. D. Kay, J. Phys. Chem., 1996, 100, 4988–4995.
6. E. L. Gibb, D. C. B. Whittet, W. A. Schutte, A. C. A. Boogert, J. E. Chiar, P. Ehrenfreund, P. A. Gerakines, J. V. Keane, A. G. G. M. Tielens, E. F. van Dishoeck and O. Kerkhof, Astrophys. J., 2000, 536, 347.
7. G. B. Hansen and T. B. McCord, J. Geophys. Res.: Planets, 2004, 109, E01012.
8. E. Mayer and R. Pletzer, Nature, 1986, 319, 298–301.
9. J. P. Devlin, J. Geophys. Res.: Planets, 2001, 106, 33333–33349.
10. A. Al-Halabi, H. J. Fraser, G. J. Kroes and E. F. V. Dishoeck, Astron. Astrophys., 2004, 422, 777–791.
11. P. Ehrenfreund, H. J. Fraser, J. Blum, J. H. Cartwright, J. M. Garcia-Ruiz, E. Hadamcik, A. C. Levasseur-Regourd, S. Price, F. Prodi and A. Sarkissian, Planet. Space Sci., 2003, 51, 473–494.
12. A. C. A. Boogert, P. A. Gerakines and D. C. B. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541–581.
13. R. T. Garrod, Astrophys. J., 2013, 778, 158.
14. T. Hama, K. Kuwahata, N. Watanabe, A. Kouchi, Y. Kimura, T. Chigai and V. Pirronello, Astrophys. J., 2012, 757, 185.
15. R. A. Baragiola, Planet. Space Sci., 2003, 51, 953–961.
16. J. B. Bossa, K. Isokoski, M. S. D. Valois and H. Linnartz, Astron. Astrophys., 2012, 545, A82.
17. U. Raut, M. Fama, B. D. Teolis and R. A. Baragiola, J. Chem. Phys., 2007, 127(20), 204713.
18. D. Laufer, E. Kochavi and A. Bar-Nun, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 9219–9227.
19. J. B. Bossa, K. Isokoski, D. M. Paardekooper, M. Bonnin, E. P. V. D. Linden, T. Triemstra, S. Cazaux, A. Tielens and H. Linnartz, Astron. Astrophys., 2014, 561, A136.
20. G. Molpeceres and J. Kastner, Phys. Chem. Chem. Phys., 2020, 22, 7552–7563.
21. P. Ayotte, R. S. Smith, K. P. Stevenson, Z. Dohnalek, G. A. Kimmel and B. D. Kay, J. Geophys. Res.: Planets, 2001, 106, 33387–33392.
22. A. Kouchi, K. Furuya, T. Hama, T. Chigai, T. Kozasa and N. Watanabe, Astrophys. J., Lett., 2020, 891, L22.
23. M. P. Collings, J. W. Dever, H. J. Fraser and M. R. S. McCoustra, Astrophys. Space Sci., 2003, 285, 633–659.
24. M. Upadhyay, M. Pezzella and M. Meuwly, J. Phys. Chem. Lett., 2021, 12, 6781–6787.
25. D. J. Burke and W. A. Brown, Phys. Chem. Chem. Phys., 2010, 12, 5947–5969.
26. A. R. Clements, B. Berk, I. R. Cooke and R. T. Garrod, Phys. Chem. Chem. Phys., 2018, 20, 5553–5568.
27. H. M. Cuppen and E. Herbst, Astrophys. J., 2007, 668, 294.
28. B. Guillot and Y. Guissani, J. Chem. Phys., 2004, 120, 4366–4382.
29. K. P. Stevenson, G. A. Kimmel, Z. Dohnalek, R. S. Smith and B. D. Kay, Science, 1999, 283, 1505–1507.
30. N. Watanabe and A. Kouchi, Prog. Surf. Sci., 2008, 83, 439–489.
31. N. Horimoto, H. S. Kato and M. Kawai, J. Chem. Phys., 2002, 116, 4375–4378.
32. E. Vichnevetski, P. Cloutier and L. Sanche, J. Chem. Phys., 1999, 110, 8112–8118.
33. H. Li, A. Karina, M. Ladd-Parada, A. Spah, F. Perakis, C. Benmore and K. Amann-Winkel, J. Phys. Chem. B, 2021, 125, 13320–13328.
34. C. Mitterdorfer, M. Bauer, T. G. Youngs, D. T. Bowron, C. R. Hill, H. J. Fraser, J. L. Finney and T. Loerting, Phys. Chem. Chem. Phys., 2014, 16, 16013–16020.
35. O. Galvez, B. Mate, V. J. Herrero and R. Escribano, Icarus, 2008, 197, 599–605.
36. P. Jenniskens and D. F. Blake, Science, 1994, 265, 753–756.
37. C. R. Hill, C. Mitterdorfer, T. G. Youngs, D. T. Bowron, H. J. Fraser and T. Loerting, Phys. Rev. Lett., 2016, 116, 215501.
38. Y. C. Wu, J. Jiang, S. J. Wang, A. Kallis and P. G. Coleman, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 064123.
39. K. Isokoski, J. B. Bossa, T. Triemstra and H. Linnartz, Phys. Chem. Chem. Phys., 2014, 16, 3456–3465.
40. B. Mate, Y. Rodriguez-Lazcano and V. J. Herrero, Phys. Chem. Chem. Phys., 2012, 14, 10595–10602.
41. R. T. Garrod, S. L. W. Weaver and E. Herbst, Astrophys. J., 2008, 682, 283.
42. J. He, A. R. Clements, S. M. Emtiaz, F. Toriello, R. T. Garrod and G. Vidali, Astrophys. J., 2019, 878, 94.
43. P. Ghesquiere, T. Mineva, D. Talbi, P. Theule, J. A. Noble and T. Chiavassa, Phys. Chem. Chem. Phys., 2015, 17, 11455–11468.
44. S. Cazaux, J. B. Bossa, H. Linnartz and A. G. G. M. Tielens, Astron. Astrophys., 2015, 573, A16.
45. S. R. Hashemi, M. R. S. McCoustra, H. J. Fraser and G. Nyman, Phys. Chem. Chem. Phys., 2022, 24, 12922–12925.
46. I. U. of Pure and A. C. (IUPAC), Micropore, 2025, https://goldbook.iupac.org/terms/view/M03906, Accessed: 05-06-2025.
47. M. Abraham, A. Alekseenko, V. Basov, C. Bergh, E. Briand, A. Brown, M. Doijade, G. Fiorin, S. Fleischmann, S. Gorelov, G. Gouaillardet, A. Grey, M. E. Irrgang, F. Jalalypour, J. Jordan, C. Kutzner, J. A. Lemkul, M. Lundborg, P. Merz, V. Miletic, D. Morozov, J. Nabet, S. Pall, A. Pasquadibisceglie, M. Pellegrino, H. Santuz, R. Schulz, T. Shugaeva, A. Shvetsov, A. Villa, S. Wingbermuehle, B. Hess and E. Lindahl, GROMACS 2024.2 Manual, 2024 DOI:10.5281/zenodo.11148638.
48. U. Essmann and A. Geiger, J. Chem. Phys., 1995, 103, 4678–4692.
49. J. S. Tse and M. L. Klein, Phys. Rev. Lett., 1987, 58, 1672–1675.
50. I. Okabe, H. Tanaka and K. Nakanishi, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 2638–2647.
51. E. Sanz, C. Vega, J. L. Abascal and L. G. MacDowell, Phys. Rev. Lett., 2004, 92, 255701.
52. J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
53. J. Wong, D. A. Jahn and N. Giovambattista, J. Chem. Phys., 2015, 143, 074501.
54. H. J. C. Berendsen, J. P. Postma, W. F. V. Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
55. P. H. Handle, T. Loerting and F. Sciortino, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13336–13344.
56. R. S. Smith, C. Huang, E. K. L. Wong and B. D. Kay, Surf. Sci., 1996, 367, L13–L18.
57. M. P. Collings, M. A. Anderson, R. Chen, J. W. Dever, S. Viti, D. A. Williams and M. R. McCoustra, Mon. Not. R. Astron. Soc., 2004, 354, 1133–1140.
58. D. Marchione, A. Rosu-Finsen, S. Taj, J. Lasne, A. G. M. Abdulgalil, J. D. Thrower, V. L. Frankland, M. P. Collings and M. R. McCoustra, ACS Earth Space Chem., 2019, 3, 1915–1931.
59. A. Rosu-Finsen, D. Marchione, T. L. Salter, J. W. Stubbing, W. A. Brown and M. R. S. McCoustra, Phys. Chem. Chem. Phys., 2016, 18, 31930–31935.
60. C. Huang, dms Software, 2024, https://www.cgl.ucsf.edu/chimera/docs/UsersGuide/midas/dms1.html, Accessed: 2024-06-25.
61. F. M. Richards, Annu. Rev. Biophys., 1977, 6, 151–176.
62. A. Bar-nun, G. Herman, D. Laufer and M. L. Rappaport, Icarus, 1985, 63, 317–332.
63. D. T. Bowron, J. L. Finney, A. Hallbrucker, I. Kohl, T. Loerting, E. Mayer and A. K. Soper, J. Chem. Phys., 2006, 125, 194502.
64. D. T. Bowron, A. K. Soper, K. Jones, S. Ansell, S. Birch, J. Norris, L. Perrott, D. Riedel, N. J. Rhodes, S. R. Wakefield, A. Botti, M. A. Ricci, F. Grazzi and M. Zoppi, Rev. Sci. Instrum., 2010, 81, 033905.
65. K. Winkel, D. T. Bowron, T. Loerting, E. Mayer and J. L. Finney, J. Chem. Phys., 2009, 130, 204502.
66. J. L. Finney, A. Hallbrucker, I. Kohl, A. K. Soper, A. K. Soper, D. T. Bowron and D. T. Bowron, Phys. Rev. Lett., 2002, 88, 225503/1.
67. L. Bosio, G. P. Johari and J. Teixeira, Phys. Rev. Lett., 1986, 56, 460–463.
68. R. Martonak, D. Donadio and M. Parrinello, J. Chem. Phys., 2005, 122, 134501.
69. L. Hornekaer, A. Baurichter, V. V. Petrunin, A. C. Luntz, B. D. Kay and A. Al-Halabi, J. Chem. Phys., 2005, 122, 124701.
70. J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548.
71. R. S. Smith, Z. Dohnalek, G. A. Kimmel, K. P. Stevenson and B. D. Kay, Chem. Phys., 2000, 258, 291–305.
72. T. Ikeda-Fukazawa, K. Kawamura and T. Hondoh, Mol. Simul., 2004, 30, 973–979.
73. K. Oka, H. Akiba, N. Tohnai, T. Shibue and O. Yamamuro, J. Phys. Chem. Lett., 2024, 15, 267–271.

---