Photoswitching dynamics of a guanidine anion receptor

Abstract

Photoswitchable molecules involving large-scale structural changes such as E/Z photoisomerization offer remarkable opportunities for light-stimulated catch-and-release chemical separations. While the feasibility of this photochemically driven mechanism has been demonstrated in pioneering studies, the electronic excited-state relaxation processes and concomitant structural changes of such a functional photoswitcher remain largely unexplored. Here, we investigate an exceptional photoswitchable molecule, 2-pyridyl-diiminoguanidinium (2PyDIG), which exhibits strong and selective anion binding, along with an extraordinary capability for light-induced release of a guest ion. Through time-resolved fluorescence measurements and multireference and time-dependent density functional theory calculations, we reveal the dynamics underlying electronic excited state relaxation and photoisomerization central to photoswitching. A very rapid and dominant decay component was found that is consistent with radiationless de-excitation from S₁ to S₀ through conical intersections. This process competes effectively with the slower photoisomerization process taking place in 94 ps. We further identified the underlying causes through theoretical calculations and potential routes towards improved photoisomerization efficiencies.

---

Introduction

Photoswitchable molecules, especially those involving large-scale structural changes such as E/Z photoisomerization, offer remarkable flexibility for designing and creating new chemical functionalities.^1–3 Through light driven chemical processes, one gains access to a contact-free, noninvasive and environmentally friendly approach to manipulate chemical binding, thereby opening the door for light-stimulated catch-and-release chemical separations. This novel mechanism has inspired several pioneering studies on chemical separations by leveraging the structural changes arising from azobenzene photoisomerization first pioneered by Shinkai.^4–7 Flood and coworkers have approached anion recognition using photofoldamers inspired from biomolecules such as halorhodopsins.^1,8,9 Here, conformational stability is facilitated by the number of π–π stacking interactions in the cis and trans forms, which in turn affect the preorganization of the receptor to accommodate a wide variety of anions (Cl⁻, Br⁻, I⁻, NO₃⁻, SCN⁻, BF₄⁻, ClO₄⁻, ReO₄⁻, PF₆⁻, and SbF₆⁻). Feringa and coworkers incorporated a stiff-stilbene group to enable a conformation switch with light for photocontrolled anion recognition, while appended urea groups act as anion recognition sites that are brought together to chelate the anion in the Z conformation of stilbene.^10–12 These classes of compounds have been used for the recognition of a wide variety of anions in solution including Cl⁻, Br⁻, NO₃⁻, CH₃CO₂⁻, H₂PO₄⁻, and HSO₄⁻. These examples highlight the potential in using light as a driving force in chemical separations; however, the mechanisms and the factors governing the efficacy of such catch and release approaches for a range of complex separations remain largely unexplored.

To address these complexities and provide a new means for photocontrolled separations, we build on our synthesis and characterization of a photoswitchable molecule, 2-pyridyl-diiminoguanidine (2PyDIG) (Scheme 1), that acts as a remarkable anion-binding receptor in the cationic diiminoguanidinium form.¹³ The photoswitching between the open E,E and closed Z,Z isomers provides a binding–release mechanism for efficient oxyanion separations. Upon photoisomerization with UV-visible light, the binding of sulfate is essentially shut off in the Z,Z form, resulting in a five orders of magnitude light-induced reduction in sulfate ion binding. The near quantitative photoisomerization coupled with the remarkable on–off binding makes this receptor, to the best of our knowledge, one of the leading anion receptors for photocontrolled sulfate recognition. To further improve its performance, an understanding of the dynamics of its electronic excited-state relaxation and concomitant photoisomerization that ultimately dictates its quantum efficiency is critically needed.

Scheme 1 The E,E → Z,Z photoisomerization reaction of 2PyDIG.

Here, we report a combined experimental and theoretical study on 2PyDIG in DMSO using time-resolved fluorescence spectroscopy, along with multireference, ground-state density functional theory (DFT) and time-dependent DFT (TDDFT) calculations. Upon selective optical excitation of either the E,E isomer alone or simultaneous excitation of both the E,E and Z,Z isomers, we found that the time-resolved fluorescence decay is dominated by a very rapid decay component with an instrument response limited decay lifetime on the order of 8 ps, consistent with radiationless de-excitation from S₁ to S₀ through conical intersections, as established recently through multi-configurational electronic structure calculations for a mono-substituted 2-pyridyl-iminoguanidinium (2PyMIG) salt.¹⁴ In comparison, the E,E → Z,Z photoisomerization on the S₁ surface takes place in an approximately one order of magnitude slower timescale of 94 ps. The presence of this instrument response limited fast decay component effectively competes with the experimentally resolved slower photoisomerization process, limiting the quantum efficiency for the E,E → Z,Z photoisomerization of this molecule. We further identified the underlying causes based on theoretical calculations and potential routes towards improved photoisomerization efficiencies. The reaction pathway leading to conical intersections was previously¹⁴ investigated for the smaller 2PyMIG molecule to enable direct comparison with multireference calculations, which are limited by the active space size required to describe geometries near these intersections. The presence of very rapid decay components in both systems suggests a similar mechanism, further supported by the shorter timescale observed for 2PyDIG, which contains two isomerizable C–N bonds. Therefore, this decay pathway is not further investigated computationally. Instead, our electronic structure calculations for 2PyDIG are focused exclusively on characterizing the photoisomerization process along the S₁ potential energy surface, which was not previously examined. The insight gained from this combined spectroscopic and theoretical study not only offers useful guidance for improving the photophysical properties of this photoswitchable molecule, but also underscores the importance of probing the ultrafast electronic excited-state and associated structural changes in real time using time-resolved optical spectroscopy.

Materials and methods

Sample preparation

Freshly synthesized 2PyDIG-HOTf (triflate salt) was dissolved in dry DMSO purged for ∼2 hours with N₂ gas before each experiment. Here, a 126 μM solution was prepared to avoid reabsorption of fluorescence photons, a concentration significantly lower than the previously used ca. 1 mM solution in DMSO.¹³ A Cary 4E UV-VIS-NIR absorption spectrometer was used to record the absorption spectra before and after time-resolved fluorescence measurements. The corrected fluorescence emission spectra were recorded using a Fluorolog-3 spectrofluorometer upon excitation at 315 nm. Typical bandwidths for both the excitation and emission monochromators were 5 nm.

Time-resolved fluorescence experiments

Picosecond time-resolved fluorescence measurements were performed using a time-correlated single-photon-counting (TCSPC) apparatus based on an actively quenched single photon avalanche photodiode (PDM 50CT module, Micro Photon Devices) in combination with a PicoQuant TCSPC system (PicoHarp 300, PicoQuant).¹⁵ The excitation light source was generated using an optical parametric amplifier (OPA) pumped using a 250 kHz Ti:Sapphire femtosecond regenerative amplifier, and the OPA output was further frequency doubled using a 2 mm thick BBO crystal to obtain excitation pulses centered at either 336 or 356 nm with a typical pulse energy of <2 nJ. Fluorescence emission at different wavelengths was selected using 10 nm (FWHM) bandpass filters. The shortest instrument response function (IRF) showed a FWHM of ∼40 ps as recorded at several wavelengths within the spectral range of our fluorescence emission detection using dilute suspensions of coffee creamer in water. To account for the wavelength dependence of our avalanche photodiode, additional measurements of IRFs were further performed using excitation light scattering from aqueous solutions of Ludox TMA colloidal silica at different concentrations, water Raman signal, and fluorescence emission from selected fluorophores with ultra-short fluorescence lifetimes including malachite green¹⁶ and pyridinium styryl dyes.¹⁷ A 4.0-ps channel time was chosen and data acquisition at each wavelength took 1 hour to accumulate as many counts as possible. The relative polarization between the fluorescence emission and the linearly polarized laser excitation was set to the magic angle (54.7°) using an emission polarizer. This enabled us to eliminate potential contribution from molecular rotation dynamics to the measured time-resolved data.

Computational methods

Electronic structures and density functional theory (DFT) calculations were carried out using the Gaussian 16¹⁸ Revision A.03 and ORCA 4.2.1^19,20 software packages. The structures of the ligands in the ground state for absorption spectrum calculations were optimized using B3LYP^21,22 and M06-2ײ³ density functionals in conjunction with the def2TZVPP basis set. To predict the absorption spectra, we employed the similarity transformed equation of motion CCSD method with the domain-based local pair natural orbital (DLPNO) approximation (STEM-DLPNO-CCSD)²⁴ by using the TightPNO settings in conjunction with the def2TZVP basis set. The reliability of the STEM-DLPNO-CCSD excitation energies was confirmed by including a sufficiently large number of roots (NRootsCISNAT = 100) and orbitals (OTHRESH/VTHRESH = 0.0005) in the active space. The absorption spectra of the E,E and Z,Z forms were obtained as Boltzmann-weighted sums of two dominant conformations, which is shown in Fig. S1 in the ESI.‡ Relative free energies from DFT calculations were corrected by single point energies at the CCSD(T)/cc-pVTZ level using the DLPNO²⁵ approximation with tightPNO settings. The TDDFT at the CAM-B3LYP/def2TZVP²⁶ level was employed to investigate the nature of the excited states at the Franck–Condon geometry and to obtain the equilibrium geometries of the E,E and Z,Z forms in the lowest excited singlet S₁(ππ*) state. Zero-point energies and thermal corrections were obtained based on the gas-phase optimized geometries at the M06-2X/def2TZVPP level using the rigid rotor-harmonic oscillator approximation, except for the low-frequency vibrational modes that were treated as described elsewhere.²⁷ Solvent effects on the relative free energy state at the M06-2X/def2TZVPP level were described by including implicit solvent corrections for DMSO using the SMD solvation model²⁸ in Gaussian 16. The PCM solvation model²⁹ in Gaussian 16 was employed for geometry optimization at the CAM-B3LYP/def2TZVP level and the CPCM solvation model³⁰ in ORCA was used for absorption spectrum calculations.

Multi-configurational calculations were performed with the complete active space self-consistent field (CASSCF) method and the 6-31G** basis set using the Molpro 2012 software package.³¹ The choice of active space (13 orbitals and 12 electrons, see Fig. S2, ESI‡) in the CASSCF calculations is motivated by the inclusion of all π orbitals that are essential to describe the C=N stretch and dihedral rotation motions along the E,E to E,Z isomerization pathway. According to STEM-DLPNO-CCSD calculations (see below), the n–π* excited states lie much higher in energy than the π–π* excited states and, thus, do not contribute to S₁.

Results

Fig. 1a shows the absorption spectra of the E,E and Z,Z isomers recorded using the same sample solution before and after photoisomerization. The two spectra are strongly overlapped except in the long wavelength region, where a weak band peaking at 376 nm is found exclusively for the E,E isomer. Through selective optical excitation of this E,E isomer with fine-tuned laser pulses, we can follow the E,E → Z,Z photoisomerization process in real time using time-resolved optical spectroscopy. In addition, the long tail seen in both spectra originates from the neutral form according to our absorption titration experiments. Although the E,E → Z,Z transformation highlights the initial and final states, the following discussion assumes a stepwise mechanism: first converting E,E to E,Z and then E,Z to Z,Z, through sequential rotations around the two C–N bonds. While this appears a straightforward spectroscopic experiment provided that the spectral and temporal resolutions are sufficient, a practical complication must be taken into account for this specific photoswitchable molecule. Because the reverse Z,Z → E,E conversion is extremely slow, which takes place several hours or longer at room temperature, the absorbance of this weak band will gradually decrease for each successive pulse of optical excitation. Consequently, care must be taken to ensure that a substantial portion of the E,E isomer remains in the sample during an experiment. By recording absorption spectra at various times during a time-resolved fluorescence experiment, we found that a fresh sample can be used for measurements for at least two hours, leading to a maximum decrease of the sample absorbance on the order of <20%. Based on this observation, we replaced the sample solution every two hours during the measurements described in this work.

Fig. 1 (a) Absorption spectra before and after photoisomerization, and (b) steady-state fluorescence emission spectra before and after light illumination to induce the E,E → Z,Z photoisomerization using a xenon lamp for 30 and 60 minutes, respectively. The excitation wavelength was 315 nm. The arrow indicates the second peak at 291 nm seen only for the Z,Z form.

The assignment of the E,E and Z,Z absorption spectra above is consistent with the theoretical prediction based on the STEOM-CCSD methodology in the DLPNO framework as an efficient way to calculate vertical excitation energies with an accuracy approaching the equation-of-motion coupled cluster model. Except for a systematic shift to higher energies by ∼0.3 eV, which is typical for excited state calculations, our simulations reproduce the absorption spectra quite well (Fig. 2), including a slight bathochromic shift and a drop in the intensity of the main band going from the E,E isomer to the Z,Z isomer. The E,Z isomer shows a main peak of intermediate intensity that is positioned closer to the Z,Z isomer peak at a slightly shorter wavelength. Furthermore, the second peak at the higher energy observed experimentally only for the Z,Z form, which is located at 291 nm as indicated by the blue arrow in Fig. 1a, is also presented in the simulated spectrum at the expected frequency marked by the asterisk. A broad band in the experimental spectrum at 376 nm is assigned to the π–π* transitions of the neutral form, as this peak is suppressed upon decreasing pH or increasing ligand concentration. Analysis of the canonical orbitals involved in the transitions reveals that all visible bands in Fig. 2 are due to the π–π* transitions involving molecular orbitals, which are delocalized over the conjugated planar π system involving both the iminoguanidinium moiety and the pyridyl rings. This is fully consistent with a more compact representation of the molecular orbitals through natural transition orbitals (NTO) computed at the TDDFT level using the CAM-B3LYP functional. The S₁(π–π*) state, as shown in Fig. 3, can be described in terms of two main NTO transitions, namely, HOMO to LUMO and HOMO−1 to LUMO+1. It is the conjugation over the whole molecule that lowers the energy of the π–π* transitions with respect to the isolated fragments. As a result, the π–π* transitions at 316–320 nm observed for 2PyDIG appear at ∼255 nm for pyridine.³² In contrast, weakly allowed n–π* transitions involving pyridine and imine C=N lone pairs are more localized and less affected by the extension of the π system. STEOM-CCSD calculations for 2PyDIG indicate that the lowest energy n–π* states involving the lone pair on pyridine nitrogen atoms are blue shifted by 0.29–039 eV with respect to the S₁(ππ*) state. The n–π* states involving the lone pairs on C=N fragments show up at much higher energies, at least 1.2 eV above the S₁(ππ*) state.

Fig. 2 The predicted absorption spectra for the E,E, E,Z, and Z,Z isomers in DMSO computed using the STEOM-DLPNO-CCSD theory. The oscillator strengths of 0–0 transitions of the dominant conformers are shown as vertical bars. The spectra are broadened using Gaussian functions with a linewidth of 2500 cm⁻¹. The asterisk marks the peak corresponding to the experimentally observed peak indicated by the arrow in Fig. 1a.

Fig. 3 Natural transition orbitals (NTO) for S₀ to S₁ excitations and the compositions of the excited states of the most stable conformers of the E,E and Z,Z isomers from CAM-B3LYP calculations. Orbital isosurface values are ±0.0194.

The absorption spectra shown in Fig. 1a allows us to choose the wavelengths for selective optical excitation of one or both isomers. The feasibility for this selective excitation is further supported by the pronounced differences between the steady-state fluorescence excitation spectra acquired before and after light illumination to induce the E,E → Z,Z photoisomerization using a xenon lamp for 90 minutes, which are shown in Fig. S3 in the ESI.‡ In order to choose the spectral range for our time-resolved fluorescence experiment, we further acquired the steady-state fluorescence emission spectra before and after light illumination to induce the E,E → Z,Z photoisomerization using a xenon lamp for 30 and 60 minutes, respectively. Similar to the absorption spectra, the fluorescence emission spectra are again strongly overlapped as shown in Fig. 1b. Specifically, the fluorescence emission from the E,E isomer has a higher intensity than the corresponding emission from the Z,Z isomer at a wavelength of >475 nm, whereas at shorter wavelengths, the emission from the Z,Z isomer becomes dominant. Upon the selective excitation of the E,E isomer, the associated time-resolved fluorescence kinetics should initiate with a decay component owing to the E,E → Z,Z photoisomerization, whereas the corresponding kinetics of the Z,Z isomer should exhibit an initial rise component accordingly. The superposition of these distinct kinetics will lead to an overall decay or rise behavior in the early times at a longer or shorter wavelength region, respectively.

The anticipated initial decay and rise behavior are indeed observed in the time-resolved fluorescence data measured at different wavelengths. As shown in Fig. 4, all the data acquired at longer wavelengths of 480, 500, 520, 540, and 560 nm exhibit an initial fast decay component, albeit its relative amplitude is clearly different with respect to the long-lived portion of the decays. While the data measured at shorter wavelengths of 420 and 440 nm initiates with a noticeable initial decay component as well, they are both followed by a dominant rise component along with a subsequent slower decay. The data measured at 460 nm appear distinct from those obtained at both shorter and longer wavelengths, as neither a clear rise nor a decay component is observed on a similar timescale as those seen at the shorter and longer wavelengths, respectively.

Fig. 4 Time-resolved fluorescence data measured at different emission wavelengths upon excitation with laser pulses centered at 356 nm. The peak intensities are scaled to 1.0 for all data except the one measured at 420 nm, where the scaling was made for the initial shoulder close to time zero. The data are vertically offset for clarity and the solid black lines are the corresponding fits obtained through global lifetime analysis.

Quantitative analysis of the time-resolved data was performed either individually or through a global lifetime analysis^33,34 in which the entire data set acquired at different emission wavelengths is fitted simultaneously. In both cases, a least-squares deconvolution fitting algorithm with explicit consideration of the finite IRF in combination with a model function consisting of a sum of exponential components was employed. In the global lifetime analysis, the lifetimes were treated as global parameters and a single set of their values that could best describe all the data was sought during the fitting, whereas all the amplitudes were taken as independent, local variables. However, because of the complicated temporal behavior of the data, we found that a satisfactory description over the entire time window of interest (up to ∼18 ns) is simply unattainable. We therefore employed a piecemeal approach to analyze the time-resolved fluorescence data described here. Specifically, we began by treating the initial IRF limited decay component as an instantaneous response and fitting the data over the entire time window of interest (∼18 ns) using global lifetime analysis. For the data shown in Fig. 4, we found that a model function consisting of four exponential components is needed for satisfactory fitting, and the resulting lifetimes are 94 ± 19 ps, 355 ± 37 ps, 1.52 ± 0.07 ns, and 6.04 ± 0.17 ns, respectively. Note that the error ranges given in this report refer to the upper and lower bounds of a fitted parameter returned by the deconvolution data analysis. The global lifetime analysis further enables us to obtain the decay-associated spectra (DAS), a plot of the resulting amplitudes weighted by the corresponding steady-state emission intensities as a function of the emission wavelength. As shown in Fig. 5, the amplitudes associated with the shortest lifetime component (94 ps) are negative at wavelengths <460 nm, whereas they become positive at longer wavelengths. The negative- and positive-signed components correspond to, respectively, the initial rise and decay components as shown in Fig. 4. Such a DAS is a typical characteristic for the presence of electronic excitation energy and photoinduced electron transfer processes from a donor to an acceptor.^33,35–39 Here, we can confidently assign this initial rise and decay component to E,E → Z,Z photoisomerization based on the following two reasons. First, we selectively excited the E,E isomer in our time-resolved fluorescence measurements, and the resulting photoisomerization will lead to a time-resolved fluorescence decay in the spectral region with dominant emission from the E,E isomer, along with a corresponding rise in the dominant emission region of the Z,Z isomer. This initial rise/decay behavior can be clearly seen from the reconstructed time-resolved fluorescence spectra shown in Fig. S4a (ESI‡), which were made following the procedure detailed in the ESI‡ using TCSPC data acquired at different emission wavelengths as shown in Fig. 4. Second, this expected correspondence between the observed initial rise/decay component at different wavelengths and the spectrally distinct contributions from the E,E and Z,Z isomers in the steady-state fluorescence emission spectra shown in Fig. 1b is fully consistent with this assignment. Specifically, the fluorescence wavelength for the Z,Z isomer is shifted to higher energies, which is fully consistent with previous equation-of-motion coupled-cluster calculations for the E- and Z-isomers of a closely related 2PyMIG system.¹⁴ Following the photoisomerization process, the subsequent electronic excited-state relaxation can be described by three DAS with positive amplitudes at all detection wavelengths. Upon closer visualization of these three different DAS, we further found that the relaxation timescales exhibit noticeable wavelength dependence, indicating either spectral heterogeneity or/and possibly complex electronic structure of the Z,Z isomer.

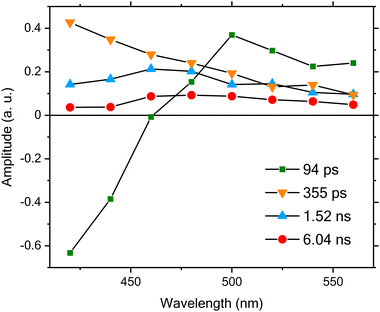Fig. 5 DAS obtained for the time-resolved fluorescence data measured at different emission wavelengths upon an excitation using laser pulses centered at 356 nm. The solid lines are guides to the eye.

The early time portions of the time-resolved fluorescence data are essential to understand the overall dynamics of electronic excited-state relaxation and its associated photoisomerization. The existence of such a fast initial decay component can be clearly seen by comparing the early time decay with the IRF as shown in Fig. 6. As the global lifetime analysis described above failed to capture this very rapid decay component, we instead perform the deconvolution fitting individually for each time-resolved fluorescence decay that exhibits no clear rise behavior. Our analysis for the data acquired at 500, 520, 540, and 560 nm shows that their satisfactory description is only possible with inclusion of a fast initial decay component with a lifetime of 5 ± 0.2, 9 ± 0.4, 8 ± 0.5, and 7 ± 0.3 ps, respectively. Note that these timescales are only a fraction of the IRF, and based on early studies by Holzwarth and coworkers extraction of such an ultrashort timescale would be possible for such a TCSPC experiment with comparable IRF and channel time only when the experimental data possess a sufficiently high signal-to-noise ratio corresponding to about 30 000 counts in the peak channel and the ultrashort decay component of interest has its relative amplitude greater than 65%.^40,41 However, our data have a lower signal-to-noise ratio owing to lower counts on the order of 2000–3000 in the peak channel. This means that the extracted lifetimes will have significantly larger errors than the upper and lower bounds returned from the fitting. Nevertheless, the presence of this fast decay component with a relative amplitude greater than 97% immediately explains why the fluorescence emission signal is so weak: non-radiative relaxation pathways are readily accessible.

Fig. 6 Early time portions of the time-resolved fluorescence decays acquired at 520 (a) and 560 nm (b), their corresponding deconvolution fits (solid lines) and the IRF (dash lines). The peak intensities of these data are scaled to 1.0 for ease of comparison.

To further verify our assignment of the observed initial rise and decay component to the E,E → Z,Z photoisomerization, we performed time-resolved fluorescence measurements using an optical excitation centered at 336 nm as shown in Fig. 7. At this wavelength, both the E,E isomer and the subsequently formed Z,Z isomer will be excited, making the contribution from the Z,Z isomer even more pronounced. As a result, fluorescence emissions at 440 and 420 nm became too weak to be acquired with a reasonable signal-to-noise ratio. As the rise component observed under 336 nm excitation is no longer pronounced in this case, we found that the data measured at all seven emission wavelengths can be satisfactorily described by global lifetime analysis with a model of function consisting of four exponential components, and the resulting lifetimes are (8 ± 0.5) ps, (298 ± 28) ps, (1.85 ± 0.07) ns, and (9.47 ± 0.25) ns, respectively. Again, the fastest decay component has the largest relative amplitude by far, which ranges from 84% at 460 nm to 98% at 580 nm. As both E,E and Z,Z isomers are simultaneously excited at 336 nm, identification of this predominant rapid decay component indicates that the electronic excited-state relaxation of the Z,Z isomer is very fast upon either direct optical excitation or via E,E → Z,Z photoisomerization. This observation explains once again why the fluorescence photon counts in our time-resolved measurements are so low upon optical excitation with short pulses centered at either 336 or 356 nm. Furthermore, from the fits shown in Fig. 7, one can clearly see that this global lifetime analysis is capable of capturing all the details in the experimental data except the weak rise seen around 200 ps in the data measured at 460 nm.

Fig. 7 Time-resolved fluorescence kinetics measured at different emission wavelengths upon excitation with laser pulses centered at 336 nm. The peak intensities are scaled to 1.0 for all data, and the kinetics are vertically offset for clarity. The solid black lines are the corresponding fits obtained through global lifetime analysis.

The absence of a pronounced rise component in the data shown in Fig. 7 leads to the DAS with all positive amplitudes as shown in Fig. 8, meaning that the time-resolved fluorescence data measured at all wavelengths are dominated by a decay behavior. This behavior can be further seen from the reconstructed time-resolved fluorescence spectra shown in Fig. S4b (ESI‡), where no rise behavior is seen at all emission wavelengths. However, this does not mean that an optical excitation at this wavelength would be unfavorable for the E,E → Z,Z photoisomerization. Instead, it simply reflects a superposition between a rise component expected for such an isomerization process and a more dominant decay component arising from the electronic excited-state relaxation of the E,E isomer itself and the Z,Z isomer. This superposition makes the dynamical process associated with the photoisomerization unresolvable. As observed for the 356 nm excitation shown in Fig. 5, we further found a noticeable wavelength dependence of all four decay components, indicating again either wavelength-dependent relative contributions from E,E and Z,Z isomers or/and possibly the complex electronic structure of the Z,Z isomer.

Fig. 8 DAS obtained for the time-resolved fluorescence kinetics measured at various emission wavelengths upon an excitation using laser pulses centered at 336 nm. The DAS associated with the 8 ps component are scaled by multiplying 0.1 and the solid lines are guides to the eye.

Our assignment of the long-lived timescales shown in Fig. 5 and 8 to the Z,Z isomer is fully consistent with the pronounced fluorescence intensity of the slow decay portion of the time-resolved fluorescence data observed upon excitation at 336 nm. As an example, Fig. 9 shows the normalized fluorescence data acquired at 480 and 560 nm, where those measured with the 336 nm excitation exhibit clearly greater intensity than the corresponding one acquired with the 356 nm excitation. Such a difference was observed at all emission wavelengths except at 460 nm, where a more pronounced contribution from the Z,Z isomer is expected for both excitation wavelengths.

Fig. 9 Comparison of the time-resolved fluorescence decays measured at 480 nm (a) and 560 nm (b) upon optical excitation at 336 nm (blue lines) and 356 nm (red lines). The peak intensities of all these data are scaled to 1.0 for ease of comparison.

We have previously¹⁴ established a weakly activated pathway from the E isomer of the structurally similar 2PyMIG to the minimum energy conical intersection (MECI) between the S₀ and S₁ states. The initial path to overcome a small barrier (4.3 to 6.5 kcal mol⁻¹) started with a rotation around the CN–NC bond, followed by a sharply downhill rearrangement (>35 kcal mol⁻¹) involving changes in the CNNC and NNCC dihedral angles. Expecting a qualitatively similar pathway to reach MECI for 2PyDIG via a coupled rotation of the CN–NC and NN–CC bonds, this work explores an adiabatic E,E to E,Z reaction pathway on the S₁ state. The focus is on a single rotation around the NN–CC bond to prevent trapping in the twisted geometry near MECI, which lies far below the E,E and E,Z states on the S₁ surface. First, the optimized geometries of an E,E isomer and an E,Z isomer were calculated at both S₀ and S₁ electronic states. Next, four types of constrained geometry optimizations were carried out to calculate the potential energies along the S₁ state minimum potential energy path (MEP) at the SA2-CAS(13,12)SCF/6-31G** level of theory. In the first type, the C=N distance, denoted as r_CN, was restrained. Next, in the second type, the C=N dihedral angle, denoted as θ_NNCC, was restrained at angles between 0 (E,Z) and 180 (E,E) degrees, while the C=N retains elongated. We observed that scanning the NNCC dihedral angle without initially elongating the C=N bond led to an increased energy barrier (Fig. S8, ESI‡). In the third type, in the E,Z-2PyDIG configuration (at θ_NNCC = 0), the C=N distance was restrained again. Finally, in the fourth type, the N–H distance was varied between the two states in which the proton resides on the guanidinium and pyridine nitrogen atoms. All orthogonal degrees of freedom are relaxed in these optimizations. The resulting free energy profile depicted in Fig. 10 indicates that the adiabatic photoisomerization on the S₁ surface is a weekly activated process.

Fig. 10 The potential energy surface diagram for interconversion between the E,E- and E,Z-2PyDIG isomers in the S₁ state and the positions of the minima in the S₀ state. The reaction coordinates computed at the SA2-CAS(13,12)SCF/6-31G** level of theory describe the four-step isomerization mechanism denoted by blue squares, orange triangles, green dots, and red crosses, respectively. Gray dots and dotted lines correspond to their single-point energies in the S₀ electronic state. During the four steps, the primary reaction coordinates are the r_CN, θ_NNCC, r_CN, and r_NH, respectively. “FC” denotes the CASSCF energy at the E,E Franck–Condon point.

Discussion

Although our time-resolved fluorescence data exhibit a complex decay/rise behavior depending on both the excitation and detection wavelengths, the key findings of this work include the observation of a very rapid fluorescence decay with an IRF limited lifetime and a predominant relative amplitude in combination with a subsequent photoisomerization process taking place in a timescale roughly one order of magnitude slower. To understand the physical mechanisms underlying these key dynamical processes, we will first begin with the initial rapid fluorescence decay component. As this photoswitcher is a pyridine-functionalized iminoguanidinium molecule, it is helpful to first discuss the spectral properties of each fragment, pyridine, imine, and guanidinium, separately. Spectroscopic data for guanidine, to the best of our knowledge, remain very limited so far. The only available experimental UV spectrum of guanidine hydrochloride in water shows appreciable absorption only between 220 and 250 nm.⁴² Theoretical calculations based on ab initio and DFT approaches further revealed that guanidine is a weakly absorbing species with the excitation spectrum consisting mostly of transitions to Rydberg excited states and one valence n–π₄ state in the far UV range. The lowest energy band had maximum at ca. 6.9 eV (∼180 nm), and its potential fluorescence emission was calculated to be at 4.39 eV (∼280 nm).⁴³ The presence of the conjugate C=N groups is characterized by a π–π transition between 225 and 235 nm.⁴⁴ Pyridine has been shown to exhibit strong absorption at about 255 nm.^45–47 Although the absorption spectra of all these fragments are essentially out of the spectral range of the 2PyDIG absorption spectra shown in Fig. 1a, our calculations described above show that the conjugation over the whole molecule lowers the energy of the ππ* transitions with respect to the isolated fragments, resulting in the ππ* transitions of 2PyDIG at 316–320 nm instead of at ∼255 nm for pyridine.

Despite the decreased ππ* transition energies of the whole 2PyDIG molecule with respect to those of its fragments, the observation of a fast initial decay component appears to bear some resemblance to the pyridine fragment. Specifically, rapid nonradiative decay processes from both the first and second singlet excited-states, i.e., the S₁ and S₂ states, along with its extremely low fluorescence quantum yields of ∼5.9 × 10⁻⁵ and ∼2.7 × 10⁻⁶ upon S₁ and S₂ excitation in the gas phase, respectively, were reported.^48,49 Application of femtosecond transient absorption spectroscopy to various pyridine solutions (H₂O, ethylene glycol, acetonitrile, and 3-methylpentane) further revealed nonradiative deactivation of the S₁ state in 9–23 ps due to, to a large extent, intersystem crossing (ISC).³² However, the absence of the detectable long-lived signal in our nanosecond transient absorption measurements as shown in Fig. S5 and S6 (ESI‡) does suggest some alterations of its electronic structure upon functionalization, leading to a significantly reduced ISC or its complete absence. In fact, an efficient S₁(nπ*) to T₁(ππ*) ISC is fully expected for pyridine based on El-Sayed's rules.⁵⁰ In the case of 2PyDIG, our DFT calculations show that the S₁ state has ππ* character (Fig. 3) and the ISC for S₁(ππ*) → T₁(ππ*) is forbidden to a first order. While there are some examples of a relatively efficient ISC for S₁(ππ*) → T₁(ππ*), which is typically observed when the singlet lifetimes are relatively long (>1 ns),⁵¹ this is not the case for 2PyDIG. Phenyl and pyridine-functionalized acylhydrazones are the closest analogues of 2PyDIG that have been shown to exhibit strong absorption in the same spectral range.⁵² Furthermore, compounds with C=N double bonds, such as imines and hydrazones, are not fluorescent and generally expected to undergo the cis–trans isomerization with a mechanism similar to alkenes,⁵³ including a possibility of a nonadiabatic transitions between the S₁ and S₀ states through conical intersections.

We further note that the observed spectra and dynamics, namely, the strongly overlapped absorption and fluorescence emission spectra of different isomers (see Fig. 1 and 2), the extremely low fluorescence emission signal, and the competing electronic excited-state dynamics, exhibit certain similarities to the photoisomerization dynamics of dehydrocholesterol and analogs, which have been a subject of extensive studies over past 30 years.^54–57 Based on the number of exponential components needed to satisfactorily describe the time-resolved data, we can reasonably conclude that the electronic excited-state relaxation and photoisomerization processes of this 2PyDIG appear more complex than those reported for dehydrocholesterol and its related analogs.^55,57

The fast initial excited-state relaxation process for 2PyDIG with an IRF limited lifetime on the order of 8 ps is significantly faster than the rate of jump from the S₁ to the S₀ surface though an avoided crossing, as the latter is not expected to be faster than a few ns.⁵¹ Such a fast decay to S₀ thus suggests that the 2PyDIG molecule enters the S₀ surface through a conical intersection. This hypothesis is strongly supported by recent multireference calculations^13,14 for the monosubstituted 2-pyridylaminoguanidinium ligand (2PyMIG), which shows a small barrier on the reaction path from the Franck–Condon geometry of the E isomer to the minimum energy conical intersection. We note that the molecule at this geometry has a twisted C=N bond with a dihedral angle close to 90° and can move in both directions, either returning to its original E isomer or proceeding to the Z photoisomer at the S₀ surface. However, the absence of a rise component upon excitation at 336 nm with a lifetime comparable to that resolved for the fast decay component upon excitation at 356 nm (Fig. 5) indicates that the pathway to Z,Z isomers in the 2PyDIG molecule is insignificant. This consideration further suggests a low quantum efficiency of this photoswitcher. Taking the average of these lifetimes as 7.3 ps for the fast decay component resolved from the data acquired at 500, 520, 540, and 560 nm upon excitation at 356 nm and 94 ps for the photoisomerization process, we can approximately estimate the quantum efficiency of this photoswitcher being only 7.3/94 ≈ 8%!

Our time-resolved fluorescence data suggest an adiabatic photochemical conversion occurring on the S₁ surface with a timescale of 94 ps. For this process to be viable, the energy of the E,E isomer in the excited state must be higher than that of the Z,Z isomer, so that the system moves downhill, and the barrier to form the Z,Z photoproduct must not be very large. As expected, the TDDFT theory was not suitable for describing the twisted geometry, where the S₀–S₁ energy gap is small. However, we were able to obtain the TDDFT equilibrium geometries of the E,E and Z,Z isomers in the excited states starting from the Franck–Condon points on S₁. A comparison of the ground and excited state geometries in Fig. S7 (ESI‡) reveals that exciting one electron to the antibonding π* orbital results in the elongation of the C=N bond and a slight twisting along this bond. At the same time, the N–N bond shortens and becomes less basic, leading to the spontaneous proton transfer from the guanidinium to the pyridine nitrogen atom in the Z,Z isomer. The reduced C=N bond order together with an increased relative stability of the Z,Z form with respect to the E,E form in S₁ suggests that a one-way adiabatic photoisomerization from the higher E,E isomer to the lower energy Z,Z isomer is a viable pathway for 2PyDIG.

A more precise picture of the photochemical isomerization process can be obtained from the multi-configurational electronic structure calculations. Fig. 10 shows the adiabatic transformation of one of the E,E* isomers to the intermediate E,Z* isomer on the S₁ potential energy surface computed at the CASSCF level. Microscopically, the E,E* → E,Z* isomerization process at the S₁ state can be divided into 3 steps: (1) C=N bond elongation from 1.30 to 1.42 Å in a planar E,E configuration (θ_NNCC = 180 degree); (2) rotation about the N–N–C–C dihedral angle from 180 to 0 degree, where r_CN remains elongated; and (3) the C=N bond shortened from 1.42 to 1.30 Å in a planar E,Z-2PyDIG isomer configuration (θ_NNCC = 0). As discussed in the SI sections, these three steps are uncorrelated (Fig. S8, ESI‡), justifying scanning the potential energy surface along a single reaction coordinate. The E,Z* isomer is 9.1 kcal mol⁻¹ more stable than E,E*, and adiabatically forming the Z,Z* isomer is expected to be more exothermic. Three transition state (TS) structures are found along the minimum potential energy path (MEP), where the first TS is 1.6 kcal mol⁻¹ higher than the optimized E,E* isomer, and the other two TS are submerged barriers. In addition, an intramolecular proton transfer can take place from the guanidinium nitrogen atom to the pyridine nitrogen atom in the E,Z* isomer, although with a more substantial free energy barrier. As shown in Fig. 10, after the proton transfer, the E,Z* isomer gains an additional stability in the first excited state, but this tautomer is relatively unstable in the ground state. We note that the barrier for the rotation around the NN–CC bond is likely underestimated in our calculations that do not include solvation effects. Experimentally, it is often found that the rotation dynamics around a double bond is strongly influenced by the polarity of the solvent,⁵⁸ slowing down the rotation with the increase in the solvent dielectric constant. With these considerations, a timescale of 94 ps determined from the time-resolved fluorescence data can be reasonably associated with the adiabatic E-to-Z photoisomerization on the S₁ surface.

From the calculations shown in Fig. 10, we observe that the E,Z* form is more stable than the E,E* form by 9.1 kcal mol⁻¹. Given that the first transition state lies ∼1.6 kcal mol⁻¹ above the E,E reactant state (likely underestimated), the overall barrier for the reverse process from E,Z* to E,E* is at least 10.7 kcal mol⁻¹. This implies that, once the E,Z* isomer is formed on the S₁ surface, it is unlikely to revert to the E,E* form within the timescale of several hundred picoseconds. Therefore, the adiabatic E,Z* to E,E* pathway is expected to contribute minimally to the overall reaction mechanism. While we have not explicitly performed reaction path calculations for the E,Z* to Z,Z* transformation, this step involves a rotation around the same C–C–N–N dihedral angle as the E,E* → E,Z* transition and therefore it is reasonable to expect a barrier with a similar magnitude. This is consistent with an 80–100 ps timescale, as observed experimentally, for the formation of the Z,Z* isomer on the S₁ surface. Under these conditions, a single photon would be sufficient to drive the complete transformation from E,E* to Z,Z* via the adiabatic pathway. While the occurrence of such two single-bond rotations on an adiabatic surface upon a single photon excitation is extremely unlikely and has not been observed previously, an unambiguous test of its feasibility would be a very interesting topic for follow-up studies. Nevertheless, experimental data and literature suggest that nonadiabatic decay through conical intersections is significantly more efficient—by roughly an order of magnitude.^14,32 This would lead to populating both E,E and E,Z isomers in the ground state, but the exact branching ratio remains uncertain in the absence of nonadiabatic dynamics calculations.

Notably, we have not directly observed the E,Z isomer by NMR or UV-Vis,¹³ which may be due to its relatively low steady-state concentration under our experimental conditions. This observation suggests two possible scenarios: (1) the branching ratio at the conical intersection favors return to E,E over formation of E,Z, making E,Z a minority product; and (2) the E,Z isomer, once formed, is efficiently re-excited and converted to Z,Z*, thereby preventing significant accumulation. Both cases are consistent with E,Z acting as a short-lived intermediate whose population remains low despite its involvement in the reaction pathway. The second scenario further supports a two-photon nonadiabatic mechanism for the E,E to Z,Z isomerization involving ground-state formation and re-excitation of the E,Z intermediate.

Our experimental and theoretical results further suggest potential routes towards increasing the quantum efficiency of this photoswitcher. Because this efficiency is defined primarily by the ratio of the lifetimes of the initial fast decay component and the photoisomerization process, its increase can be achieved by either slowing down the former or accelerating the latter. A straightforward solution might be to use of a different solvent other than DMSO. As reported in ref. 32, the timescale of this rapid decay increases from ∼9 ps in water to ∼23 ps in acetonitrile for pyridine. Since acetonitrile has a lower viscosity of 0.369 mPa·s at 25 °C than DMSO with a viscosity of 1.987 mPa s at the same temperature,⁵⁹ an accelerated photoisomerization should take place owing to the involvement of a large amplitude motion of two separate fragments of the same photoswitchable molecule in combination with the essential role of solute–solvent interactions in photoisomerization processes in the condensed phase.^60–64 However, an alternative and more effective route to increase the quantum efficiency of this photoswitcher is no doubt to replace the pyridine fragment with a less bulky species free of fast excited-state relaxation. Nevertheless, the feasibility of any chosen routes relies critically on whether its exceptional chemical functionality can be maintained. Thus, the first step of our quest for optimizing this photoswitcher would be to assess the chemical functionalities under different experimental conditions (solvent and/or temperature) in combination with modification of its molecular structure. Once any desired experimental condition or/and structural modification is identified, detailed time-resolved optical spectroscopic studies will be subsequently applied to quantify its quantum efficiency.

Summary

We performed time-resolved fluorescence spectroscopic measurements and excited-state calculations on a photoswitchable molecule based on pyridine-functionalized iminoguanidinium that possesses an exceptional chemical functionality of photocontrolled anion binding. Detailed analysis of the experimental data acquired at different excitation and emission wavelengths enabled us to reveal the complex dynamics of the electronic excited-state relaxation and concomitant photoisomerization. Notably, we identified a predominant excited-state relaxation process upon optical excitation of either the E,E isomer or the Z,Z isomer, which is characterized by an ultrashort, IRF limited lifetime on the order of 8 ps. In comparison, the E,E → Z,Z photoisomerization was significantly slower with a characteristic timescale of 94 ps. These competing processes were found to result in not only an overall low quantum efficiency for this photoswitcher but also an extremely low fluorescence emission signal. The physical mechanisms underlying these key observations were further identified to reflect a fast radiationless deactivation from the S₁(ππ*) state via conical intersections on the strongly downhill path with a small barrier and a slower process involving an adiabatic photoisomerization on the S₁(ππ*) surface. We further outlined several potential routes towards optimizing the quantum efficiency of such a photoswitcher. We believe that the insight gained through this study underscores the importance of probing the ultrafast electronic excited-state and associated structural changes involved in functional photoswitchable molecules for chemical applications in real time.

Data availability

The data supporting this article have been included as part of the ESI.‡

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, Separation Sciences. The computational work used resources of the National Energy Research Scientific Computing Center (NERSC) and the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory, both of which are supported by the Office of Science of the U.S. Department of Energy under contracts DE-AC02-05CH11231 and DE-AC05-00OR22725, respectively. The manuscript was produced by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The publisher acknowledges the U.S. Government license to provide public access under the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan).

References

1. S. Lee and A. H. Flood, Photoresponsive receptors for binding and releasing anions, J. Phys. Org. Chem., 2013, 26, 79–86.
2. A. Goulet-Hanssens, F. Eisenreich and S. Hecht, Enlightening Materials with Photoswitches, Adv. Mater., 2020, 32, 1905966.
3. J. Volarić, W. Szymanski, N. A. Simeth and B. L. Feringa, Molecular photoswitches in aqueous environments, Chem. Soc. Rev., 2021, 50, 12377–12449.
4. S. Shinkai, T. Ogawa, T. Nakaji, Y. Kusano and O. Nanabe, Photocontrolled extraction ability of azobenzene-bridged azacrown ether, Tetrahedron Lett., 1979, 20, 4569–4572.
5. Z. Li, C. Zhang, Y. Ren, J. Yin and S. H. Liu, Amide- and Urea-Functionalized Dithienylethene: Synthesis, Photochromism, and Binding with Halide Anions, Org. Lett., 2011, 13, 6022–6025.
6. S. Xiong and Q. He, Photoresponsive Macrocycles for Selective Binding and Release of Sulfate, Chem. Commun., 2021, 57, 13514–13517.
7. K. Dąbrowa and J. Jurczak, Tetra-(Meta-Butylcarbamoyl)Azobenzene: A Rationally Designed Photoswitch with Binding Affinity for Oxoanions in a Long-Lived Z-State, Org. Lett., 2017, 19, 1378–1381.
8. Y. Hua and A. H. Flood, Flipping the Switch on Chloride Concentrations with a Light-Active Foldamer, J. Am. Chem. Soc., 2010, 132, 12838–12840.
9. F. C. Parks, Y. Liu, S. Debnath, S. R. Stutsman, K. Raghavachari and A. H. Flood, Allosteric Control of Photofoldamers for Selecting between Anion Regulation and Double-to-Single Helix Switching, J. Am. Chem. Soc., 2018, 140, 17711–17723.
10. J. de Jong, B. L. Feringa and S. J. Wezenberg, Light-Modulated Self-Blockage of a Urea Binding Site in a Stiff-Stilbene Based Anion Receptor, ChemPhysChem, 2019, 20, 3306–3310.
11. S. J. Wezenberg and B. L. Feringa, Photocontrol of Anion Binding Affinity to a Bis-urea Receptor Derived from Stiff-Stilbene, Org. Lett., 2017, 19, 324–327.
12. S. J. Wezenberg, M. Vlatković, J. C. M. Kistemaker and B. L. Feringa, Multi-State Regulation of the Dihydrogen Phosphate Binding Affinity to a Light- and Heat-Responsive Bis-Urea Receptor, J. Am. Chem. Soc., 2014, 136, 16784–16787.
13. J. D. Einkauf, V. S. Bryantsev, B. A. Moyer and R. Custelcean, A Photoresponsive Receptor with a 105 Magnitude of Reversible Anion-Binding Switching, Chem. – Eur. J., 2022, 28, e202200719.
14. D.-K. Dang, J. D. Einkauf, X. Ma, R. Custelcean, Y.-Z. Ma, P. M. Zimmerman and V. S. Bryantsev, Photoisomerization mechanism of iminoguanidinium receptors from spectroscopic methods and quantum chemical calculations, Phys. Chem. Chem. Phys., 2024, 26, 24008–24020.
15. Y.-Z. Ma, H. Lin, M.-H. Du, B. Doughty and B. Ma, Direct Evidence of Exciton–Exciton Annihilation in Single-Crystalline Organic Metal Halide Nanotube Assemblies, J. Phys. Chem. Lett., 2018, 9, 2164–2169.
16. Y. Zhou, G. G. Gurzadyan, W. Ni, M. F. Gelin and L. Sun, Upper Excited State Photophysics of Malachite Green in Solution and Films, J. Phys. Chem. B, 2020, 124, 4293–4302.
17. L. Li, M. Chang, H. Yi, M. Jia, X. Cao, Z. Zhou, S. Zhang, H. Pan, C.-W. Shih, R. Jimenez and J. Xu, Using Pyridinium Styryl Dyes as the Standards of Time-Resolved Instrument Response, Appl. Spectroscopy, 2016, 70, 1195–1201.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, 2016.
19. F. Neese, The ORCA program system, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 73–78.
20. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, e1327.
21. A. D. Becke, Density-functional thermochemistry, III, The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
22. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
23. Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120, 215–241.
24. A. K. Dutta, M. Saitow, B. Demoulin, F. Neese and R. Izsák, A domain-based local pair natural orbital implementation of the equation of motion coupled cluster method for electron attached states, J. Chem. Phys., 2019, 150, 164123.
25. W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework, J. Chem. Theory Comput., 2016, 12, 4778–4792.
26. T. Yanai, D. Tew and N. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
27. A. S. Ivanov and V. S. Bryantsev, A Computational Approach to Predicting Ligand Selectivity for the Size-Based Separation of Trivalent Lanthanides, Eur. J. Inorg. Chem., 2016, 3474–3479.
28. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.
29. R. Improta, V. Barone, G. Scalmani and M. J. Frisch, A state-specific polarizable continuum model time dependent density functional method for excited state calculations in solution, J. Chem. Phys., 2006, 125, 054103.
30. V. Barone and M. Cossi, Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model, J. Phys. Chem. A, 1998, 102, 1995–2001.
31. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 242–253.
32. M. Chachisvilis and A. H. Zewail, Femtosecond Dynamics of Pyridine in the Condensed Phase:  Valence Isomerization by Conical Intersections, J. Phys. Chem. A, 1999, 103, 7408–7418.
33. A. R. Holzwarth, in Biophysical Techniques in Photosynthesis, ed. J. Amesz and A. J. Hoff, Kluwer Academic Publishers, The Netherlands, 1996, pp. 75–92.
34. I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Global and target analysis of time-resolved spectra, Biochim. Biophys. Acta, Bioenerg., 1657, 2004, 82–104.
35. J. Pšenčík, Y.-Z. Ma, J. B. Arellano, J. Hála and T. Gillbro, Excitation energy transfer dynamics and excited-state structure in chlorosomes of chlorobium phaeobacteroides, Biophys. J., 2003, 84, 1161–1179.
36. Y.-Z. Ma, R. P. Cox, T. Gillbro and M. Miller, Bacteriochlorophyll organization and energy transfer kinetics in chlorosomes from Chloroflexus aurantiacus depend on the light regime during growth, Photosynth. Res., 1996, 47, 157–165.
37. Y.-Z. Ma, R. A. Miller, G. R. Fleming and M. B. Francis, Energy Transfer Dynamics in Light-Harvesting Assemblies Templated by the Tobacco Mosaic Virus Coat Protein, J. Phys. Chem. B, 2008, 112, 6887–6892.
38. Y.-Z. Ma, C. Zhou, B. Doughty, D. C. Easley, J. Deterding and B. Ma, Solvent Effect on the Photoinduced Structural Change of a Phosphorescent Molecular Butterfly, Chem. – Eur. J., 2017, 23, 17734–17739.
39. A. R. Holzwarth, M. Katterle, M. G. Müller, Y.-Z. Ma and V. Prokhorenko, Electron-transfer dyads suitable for novel self-assembled light-harvesting antenna/electron-transfer devices, Pure Appl. Chem., 2001, 73, 469–474.
40. T. A. Roelofs, S. L. S. Kwa, R. van Grondelle, J. P. Dekker and A. R. Holzwarth, Primary processes and structure of the Photosystem II reaction center: II. Low-temperature picosecond fluorescence kinetics of a D1-D2-cyt-b-559 reaction center complex isolated by short Triton exposure, Biochim. Biophys. Acta, Bioenerg., 1993, 1143, 147–157.
41. T. A. Roelofs, M. Gilbert, V. A. Shuvalov and A. R. Holzwarth, Picosecond fluorescence kinetics of the D1-D2-cyt-b-559 photosystem II reaction center complex. Energy transfer and primary charge separation processes, Biochim. Biophys. Acta, Bioenerg., 1991, 1060, 237–244.
42. I. M. Klotz and T. Askounis, Absorption Spectra and Tautomerism of Cyanuric Acid, Melamine and Some Related Compounds, J. Am. Chem. Soc., 1947, 69, 801–803.
43. I. Antol, Z. Glasovac, R. Crespo-Otero and M. Barbatti, Guanidine and guanidinium cation in the excited state—theoretical investigation, J. Chem. Phys., 2014, 141, 074307.
44. J.-L. Schmitt, A.-M. Stadler, N. Kyritsakas and J.-M. Lehn, Helicity-Encoded Molecular Strands: Efficient Access by the Hydrazone Route and Structural Features, Helv. Chim. Acta, 2003, 86, 1598–1624.
45. J. Otsuki and K. Narutaki, Photochromism of Phenylazopyridines and Its Application to the Fluorescence Modulation of Zinc–Porphyrins, Bull. Chem. Soc. Jpn., 2004, 77, 1537–1544.
46. B. Mravec, J. Filo, K. Csicsai, V. Garaj, M. Kemka, A. Marini, M. Mantero, A. Bianco and M. Cigáň, Photoswitching Hydrazones Based on Benzoylpyridine, Phys. Chem. Chem. Phys., 2019, 21, 24749–24757.
47. H. Ren, P. Yang and F. M. Winnik, Azopyridine: a smart photo- and chemo-responsive substituent for polymers and supramolecular assemblies, Polym. Chem., 2020, 11, 5955–5961.
48. I. Yamazaki and H. Baba, Observation of fluorescence of pyridine in the vapor phase, J. Chem. Phys., 1977, 66, 5826–5827.
49. I. Yamazaki, K. Sushida and H. Baba, Vapor-phase fluorescence emissions of pyridine and its methyl derivatives: Excitation-energy dependence of nonradiative electronic relaxation, J. Chem. Phys., 1979, 71, 381–387.
50. M. A. El-Sayed, Spin—Orbit Coupling and the Radiationless Processes in Nitrogen Heterocyclics, J. Chem. Phys., 1963, 38, 2834–2838.
51. N. J. Turro, V. Ramamurthy and J. C. Scaiano, Modern molecular photochemistry of organic molecules, Viva Books, University Science Books, Sausalito, CA, 2017.
52. D. J. van Dijken, P. Kovaříček, S. P. Ihrig and S. Hecht, Acylhydrazones as Widely Tunable Photoswitches, J. Am. Chem. Soc., 2015, 137, 14982–14991.
53. M. Persico and G. Granucci, Photochemistry: A modern theoretical perspective, Springer, Cham, Switzerland, 2018.
54. W. Fuss, T. Höfer, P. Hering, K. L. Kompa, S. Lochbrunner, T. Schikarski and W. E. Schmid, Ring Opening in the Dehydrocholesterol−Previtamin D System Studied by Ultrafast Spectroscopy, J. Phys. Chem., 1996, 100, 921–927.
55. K.-C. Tang, A. Rury, M. B. Orozco, J. Egendorf, K. G. Spears and R. J. Sension, Ultrafast electrocyclic ring opening of 7-dehydrocholesterol in solution: The influence of solvent on excited state dynamics, J. Chem. Phys., 2011, 134, 104503.
56. B. C. Arruda, B. Smith, K. G. Spears and R. J. Sension, Ultrafast ring-opening reactions: a comparison of α-terpinene, α-phellandrene, and 7-dehydrocholesterol with 1,3-cyclohexadiene, Faraday Discuss., 2013, 163, 159–171.
57. D. L. Sofferman, A. Konar, K. G. Spears and R. J. Sension, Ultrafast excited state dynamics of provitamin D3 and analogs in solution and in lipid bilayers, J. Chem. Phys., 2021, 154, 094309.
58. Y.-Z. Ma, U. I. Premadasa, V. S. Bryantsev, A. R. Miles, I. N. Ivanov, A. Elgattar, Y. Liao and B. Doughty, Unravelling photoisomerization dynamics in a metastable-state photoacid, Phys. Chem. Chem. Phys., 2024, 26, 4062–4070.
59. CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC, Taylor & Francis, Boca Raton, FL, 102nd edn, 2021, (Internet Version 2021).
60. A. Rosspeintner, B. Lang and E. Vauthey, Ultrafast phtochemistry in liquids, Ann. Rev. Phys. Chem., 2013, 64, 247–271.
61. G. R. Fleming, Subpicosecond spectroscopy, Ann. Rev. Phys. Chem., 1986, 37, 81–104.
62. S. K. Kim and G. R. Fleming, Reorientation and isomerization of trans-stilbene in alkane solutions, J. Phys. Chem., 1988, 92, 2168–2172.
63. V. Sundström and T. Gillbro, A discussion of the problem of determining multiple lifetimes from picosecond absorption recovery data as encountered in two carbocyanine dyes, Appl. Phys. B, 1983, 31, 235–247.
64. D. Gegiou, K. A. Muszkat and E. Fischer, Temperature dependence of photoisomerization. VI. Viscosity effect, J. Am. Chem. Soc., 1968, 90, 12–18.

---

Footnotes

† This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://energy.gov/downloads/doe-public-access-plan)

‡ Electronic supplementary information (ESI) available. see DOI: https://doi.org/10.1039/d5cp00233h

---