 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Discrepant lithium transference numbers due to heterogeneous speciation†
Frederik
Philippi‡
 *a,
Yuna
Matsuyama
a,
Simon
Buyting
bc,
Taku
Sudoh
a,
Keisuke
Shigenobu
d,
Wataru
Shinoda
*a,
Yuna
Matsuyama
a,
Simon
Buyting
bc,
Taku
Sudoh
a,
Keisuke
Shigenobu
d,
Wataru
Shinoda
 d,
Monika
Schönhoff
d,
Monika
Schönhoff
 b,
Masayoshi
Watanabe
b,
Masayoshi
Watanabe
 e and
Kazuhide
Ueno
e and
Kazuhide
Ueno
 ae
ae
aDepartment of Chemistry and Life Science, Yokohama National University, 79-5 Tokiwadai, Hodogaya-ku, Yokohama, Kanagawa 240-8501, Japan. E-mail: publications@ionic-liquids.com
bUniversity of Münster, Institute of Physical Chemistry, Corrensstr. 28/30, Münster, D-48149, Germany
cInternational Graduate School for Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA), University of Münster, Münster, 48149, Germany
dResearch Institute for Interdisciplinary Science, Okayama University, 3-1-1 Tsushimanaka, Kita-ku, Okayama, Okayama 700-8530, Japan
eInstitute of Advanced Sciences, Yokohama National University, 79-5 Tokiwadai, Hodogaya-ku, Yokohama, 240-8501, Japan
First published on 27th June 2025
Abstract
Understanding lithium secondary battery electrolytes to the point where they can be designed and tailored is of extraordinary importance. This is especially true for lithium transference and lithium mobility, both of which are to be maximized in the design of a high-performance battery. However, how these properties relate to the species present in the bulk electrolyte remains poorly understood. Here we show how different species in [Li(G1)3][PO2F2] contribute to experimentally observable properties. We find unprecedented heterogeneity in the form of well-separated, negatively charged oligomeric aggregates co-existing with free solvent molecules. Our approach also allows us to estimate the electrophoretic mobilities of different species such as [Li(G1)2]+, aggregates formed by communal solvation, or free glyme. Importantly, the widely used Bruce–Vincent method fails in this case, giving unreasonably high lithium transference numbers. Thus, we present a framework to rationalise the discrepancy in lithium transference and mobility obtained from different methods, which provides a new level of detail in the understanding of battery electrolytes.
Introduction
Highly concentrated electrolytes (HCEs) are increasingly attracting attention for their potential application in lithium secondary batteries. Importantly, when the salt concentration exceeds ≈3 to 5 mol L−1, the properties change drastically compared to dilute electrolytes.1–3 Some of the beneficial key properties of a HCE are increased stability and safety.4–8 HCEs can be considered intermediary between dilute electrolytes and ionic liquids due to the high density of charge carriers. In the extreme case of a solvate ionic liquid, the solvent and the lithium cation form a well-defined, persistent complex.9–11 Similar to ionic liquids, HCEs often exhibit high viscosities as dynamics slow down near charged domains,12,13 while ion correlations further complicate their theoretical description.14–17The motions of ions within a HCE are profoundly different from what is known for dilute electrolytes, and ion correlations are ubiquitous. Ion correlations are usually rationalised with two different, but not mutually exclusive, concepts. The first and intuitive concept is that of strongly interacting ions moving together, i.e. two or more ions moving together as an ion pair or a larger cluster, representing a positive correlation. The second concept is that of conserved quantities. Ion correlations, especially anticorrelations, can arise due to conservation of momentum or volume.16,17 At present, such correlations are usually described in the community using Onsager coefficients, the interested reader is referred to a recent review article.14
In this paper, we will make extensive use of various concepts to describe structural and dynamic phenomena. The meaning and interpretation of these concepts varies across different disciplines, groups, and communities. Some concepts, such as that of an ‘aggregate’, are often used but without providing a clear definition. Hence, for the sake of clarity, we will follow these definitions:
– Constituent: chemically independent entities connected by covalent bonds, here lithium, glyme, and the molecular anion.
– Coordination environment: only refers to the local surroundings, i.e. the nearest neighbours which form the first solvation shell. For example, [Li(anion)4]3−, even if this coordination environment is never found in isolation but only engaged in communal solvation.
– Communal solvation: a situation where a molecule is part of two or more first solvation shells. For example, an anion which coordinates two different cations; each of the cations can have a different coordination environment with many nearest neighbours shared with other cations.
– Cluster: only used in context of the structural cluster analysis, i.e. with a running cutoff as described in the literature and as implemented in the TRAVIS software package.18
– Aggregate: an extended network arising from repeated communal solvation. In other words, it is possible to trace a path between every constituent that is part of the aggregate by only going through nearest neighbours in the coordination environment.
– Species: a collection of ions/molecules that can be treated as one unit in terms of diffusion and migration. This can be the persistent cationic complex in a solvate ionic liquid, an independent ion pair, free solvent, an aggregate including communal solvation, etc.
We note that the species is the only term relating to transport, while all other entities describe mere structural properties. In HCEs, speciation has a very important effect on ion correlations and macroscopic properties. First, speciation directly affects the drift direction of lithium within the electrolyte in an electric field. If the lithium is contained in species with a net negative charge, then the drift direction might even oppose the desired lithium transport from anode to cathode.19,20 Second, speciation affects the activity of lithium ions in the bulk electrolyte, and thus changes the electrode potential of lithium metal.9,21 Third, as a rule of thumb, a balance between anion and solvent coordination to lithium is required to achieve fast lithium transport.3,22 The last aspect is further complicated by the fact that the same constituents can have very different mobilities when contained in different species.2
In a perfect lithium secondary battery electrolyte, only the lithium ions would contribute to its macroscopic ionic conductivity. Any net movement of the anion, the solvent, or other constituents leads to the formation of an undesirable concentration gradient, which reduces the efficiency of the battery. The relative contribution of lithium ions to the ionic conductivity, commonly referred to as transference number, can be quantified in several ways which usually give different results.23,24 The very popular Bruce–Vincent method uses a symmetric Li‖Li cell to which a small potential is applied under anion blocking conditions, following the current over time. At the beginning of the experiment, the constituents migrate in the electric field according to their electrophoretic mobility. However, under anion blocking conditions, only lithium can react at the electrodes. Thus, a concentration gradient is built up until a steady state is reached where diffusion and migration cancel each other out. This experiment yields the lithium transference number under anion blocking conditions,  . Alternatively, the lithium transference number can be calculated from electrophoretic mobilities μi of the ions, as
. Alternatively, the lithium transference number can be calculated from electrophoretic mobilities μi of the ions, as 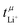 . The electrophoretic mobilities are accessible through electrophoretic NMR (eNMR), a method of growing popularity in the community due to technical improvements, which made it accessible to concentrated electrolytes.19 Here, a pulsed field gradient experiment is employed to measure the drift velocity of the constituents during a short electric field pulse. It is a measurement in bulk, not affected by interfacial resistances. Hence,
. The electrophoretic mobilities are accessible through electrophoretic NMR (eNMR), a method of growing popularity in the community due to technical improvements, which made it accessible to concentrated electrolytes.19 Here, a pulsed field gradient experiment is employed to measure the drift velocity of the constituents during a short electric field pulse. It is a measurement in bulk, not affected by interfacial resistances. Hence,  essentially corresponds to the situation at the beginning of a Bruce–Vincent type experiment, before the concentration gradient is built up.
essentially corresponds to the situation at the beginning of a Bruce–Vincent type experiment, before the concentration gradient is built up.
One of the key physical properties that define the performance of a lithium battery electrolyte is the Li+ ionic conductivity, i.e. the product between the transference number and the total ionic conductivity.23,24 In general, a trade-off between conductivity and transference number is observed, making the design of an optimal electrolyte difficult.3,25 To the best of our knowledge, there is no physical principle which forbids a liquid single ion conductor with both a high conductivity and a high lithium transference number. However, in order to reach this goal, lithium mobility would need to be large compared to the mobilities of the other charged constituents. This situation is difficult to achieve since the highly charged Li+ usually acquires a pronounced solvation shell. Similarly, unfavourable ion–ion correlations can compromise the performance of the electrolyte even if the lithium mobility is high. Naturally, there is no room for molecular design in Li+ itself, and its behaviour can only be indirectly affected through the choice of anions, solvents, and additives.
Ether solvents are commonly used in electrolyte formulations for lithium secondary batteries due to their ability to solvate Li+via the ether oxygen atoms. In the case of larger glycol ethers such as tetraethylene glycol dimethyl ether (tetraglyme, G4), the chelate effect favours Li+ coordination to a degree where solvate ionic liquids can be formed with weakly coordinating anions.10,26,27 For example, in [Li(G4)][NTf2], a long lived complex cation [Li(G4)]+ is formed.10,28,29 Such systems share desirable properties with ionic liquids, specifically thermal stability, low vapour pressure, and high electrochemical stability.
A major drawback of many glyme-based solvate electrolytes/solvate ionic liquids is their low transference number. For the prototypical [LiG4][NTf2] at 30 °C,  , although the ionic conductivity is relatively high with σ = 1.31 mS cm−1.30,31 Replacing [NTf2]− with anions of higher coordination tendency such as [TFA]− or [NO3]− leads to a much higher fraction of free glyme, i.e. such systems behave less than a solvate ionic liquid and more like a concentrated solution.9,32,33 The (expected) low ionic conductivity in such systems is accompanied by very high lithium transference numbers, although relatively few systems have been investigated exhaustively. For example, for [LiG3][TFA],
, although the ionic conductivity is relatively high with σ = 1.31 mS cm−1.30,31 Replacing [NTf2]− with anions of higher coordination tendency such as [TFA]− or [NO3]− leads to a much higher fraction of free glyme, i.e. such systems behave less than a solvate ionic liquid and more like a concentrated solution.9,32,33 The (expected) low ionic conductivity in such systems is accompanied by very high lithium transference numbers, although relatively few systems have been investigated exhaustively. For example, for [LiG3][TFA], 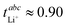 and σ = 0.10 mS cm−1 have been reported.25
and σ = 0.10 mS cm−1 have been reported.25
In the literature, an exceptionally high  has been reported for [Li(G1)1.69][PO2F2], together with a moderate conductivity of σ = 0.45 mS cm−1.34 Ethylene glycol dimethyl ether (monoglyme, G1) is also known as dimethoxyethane (DME). In this work, we use the Gn nomenclature, where n is the number of ethylene glycol units. We focus on glyme based electrolytes with the difluorophosphate [PO2F2]− anion, in combination with glymes of varying length. We use eNMR to obtain
has been reported for [Li(G1)1.69][PO2F2], together with a moderate conductivity of σ = 0.45 mS cm−1.34 Ethylene glycol dimethyl ether (monoglyme, G1) is also known as dimethoxyethane (DME). In this work, we use the Gn nomenclature, where n is the number of ethylene glycol units. We focus on glyme based electrolytes with the difluorophosphate [PO2F2]− anion, in combination with glymes of varying length. We use eNMR to obtain 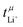 as an alternative to
as an alternative to  from the Bruce–Vincent method. Molecular dynamics simulations of [Li(G1)3][PO2F2] allow us to rationalise our findings. Specifically, we employ a new software tool for the automatic structural and dynamic analysis of the coordination environments of all constituents. The structural analysis also takes into account communal solvation, thus we are able to deduce the global distribution of species in the bulk liquid. Finally, the combination of theoretical and experimental results yields explicit electrophoretic mobilities for different species.
from the Bruce–Vincent method. Molecular dynamics simulations of [Li(G1)3][PO2F2] allow us to rationalise our findings. Specifically, we employ a new software tool for the automatic structural and dynamic analysis of the coordination environments of all constituents. The structural analysis also takes into account communal solvation, thus we are able to deduce the global distribution of species in the bulk liquid. Finally, the combination of theoretical and experimental results yields explicit electrophoretic mobilities for different species.
Results and discussion
The physical properties of the samples in this work are summarised in Table 1, further details can be found in the ESI† (Tables S1–S3). For [Li(G4)][PO2F2], a relatively high viscosity of 217 mPa s was obtained, which is typical for ionic liquids and solvate electrolytes.35 This has the expected effect on other transport properties in the sense that diffusion was slow and the ionic conductivity was low. In contrast, an exceptionally low viscosity of 3.56 mPa s was observed for [Li(G1)3][PO2F2]. This low viscosity is likely the main driver for the relatively high ionic conductivity compared to the other samples with larger glymes.The potentiostatic polarisation experiment yielded very high lithium transference numbers exceeding 0.9, in line with the literature value of  for [Li(G1)1.69][PO2F2]. However, for [Li(G1)3][PO2F2], no stable steady state could be obtained, likely due to instability of this specific electrolyte composition towards lithium metal. Regardless, the initial current did not drop significantly, which suggests a
for [Li(G1)1.69][PO2F2]. However, for [Li(G1)3][PO2F2], no stable steady state could be obtained, likely due to instability of this specific electrolyte composition towards lithium metal. Regardless, the initial current did not drop significantly, which suggests a  formally approaching unity under these conditions.
formally approaching unity under these conditions.
Due to the aforementioned instability towards lithium metal, it was not possible to determine the electrode potentials of lithium metal and thus dΔφ/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c with the necessary accuracy required to deduce Onsager coefficients. However, the observed Δφ were consistently extremely low. Specifically, the lithium metal electrode potentials were negative compared to those in the reference electrolyte, 1 M Li[NTf2] in triglyme. For example, for [Li(G4)0.9][PO2F2] at a salt concentration of ≈4 M, we observed Δφ = −89 mV, despite the much lower concentration of the reference electrolyte. In contrast, HCEs reported in the literature usually exhibit Δφ > 100 mV at such high concentrations due to the drop in activity of free solvent molecules.9,21 This implies the presence of a substantial fraction of free glyme in Li[PO2F2]:Gn mixtures.
c with the necessary accuracy required to deduce Onsager coefficients. However, the observed Δφ were consistently extremely low. Specifically, the lithium metal electrode potentials were negative compared to those in the reference electrolyte, 1 M Li[NTf2] in triglyme. For example, for [Li(G4)0.9][PO2F2] at a salt concentration of ≈4 M, we observed Δφ = −89 mV, despite the much lower concentration of the reference electrolyte. In contrast, HCEs reported in the literature usually exhibit Δφ > 100 mV at such high concentrations due to the drop in activity of free solvent molecules.9,21 This implies the presence of a substantial fraction of free glyme in Li[PO2F2]:Gn mixtures.
For all three electrolytes in Table 1, the diffusion coefficients of Li+ and [PO2F2]− are virtually identical, while the respective glyme molecules diffuse faster by an order of magnitude. This is consistent with significant ion association and the presence of free glyme. For comparison, the self-diffusion coefficient of neat G1 is reported to be ≈2.7 × 10−9 m2 s−1, which is ≈3.4 times higher than in our electrolyte.36 This would correspond to approximately one third of free glyme molecules in a hypothetical scenario where the remaining glyme is completely immobilised. Given that the viscosity of the electrolyte is higher than that of neat G1, which slows down diffusion, the actual amount of free glyme is expected to be also higher than this estimate which thus sets a lower boundary.
From the diffusion coefficients, the ideal ionic conductivity according to the Nernst–Einstein relation can be calculated. The Nernst–Einstein relation neglects ion correlation and ion association, and thus usually yields higher values than the actual, experimental ionic conductivity. In line with this, the ratio between the experimental conductivity and the Nernst–Einstein conductivity, often called ionicity, is very low for the samples in this work, Table 1 (Haven ratio = 1/ionicity). Thus, the ionic conductivity is decreased due to the substantial impact of correlated ion motion. Correlated ion motion, in turn, is a consequence of ion association and the formation of long-lived species, and to some degree affected by constraints such as volume/momentum/charge conservation.
The curious combination of properties in these electrolytes prompted us to perform eNMR experiments (Fig. S2, ESI†) to determine the electrophoretic mobility of the three constituents (Li+, glyme, [PO2F2]−). We chose to investigate the two limiting cases [Li(G1)3][PO2F2] and [Li(G4)][PO2F2], representative raw data are presented in Fig. S3 and S4 (ESI†) and the resulting mobilities in Fig. 1. In both cases, the anion shows the highest mobility and migrates against the direction of the electric field towards the positively charged electrode as expected. Interestingly, the lithium migration occurs in the same direction for [Li(G1)3][PO2F2], which most likely is due to the presence of cation–anion aggregates of overall negative charge (Fig. S3, ESI†). The lithium migration direction could not be determined for [Li(G4)][PO2F2] due to the extremely low value of the mobility, which is zero within error (Fig. S4, ESI†). It is worth noting the different scale used for the two systems, showing the much higher mobilities in [Li(G1)3][PO2F2] compared to [Li(G4)][PO2F2].
 | ||
| Fig. 1 Electrophoretic mobilities measured via eNMR for (a) [Li(G4)][PO2F2] and (b) [Li(G1)3][PO2F2]. | ||
The values for the ionic conductivity measured via eNMR and impedance spectroscopy must agree within experimental uncertainty (cf.Table 1). In contrast, 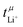 and
and  measure different properties, thus their values can be different.
measure different properties, thus their values can be different.  is nearly 1 for Li[PO2F2]:Gn mixtures, suggesting that the concentration polarisation is negligible under the experimental conditions. In turn,
is nearly 1 for Li[PO2F2]:Gn mixtures, suggesting that the concentration polarisation is negligible under the experimental conditions. In turn, 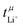 is calculated from the mobilities, eqn (1) and (2).24 Here, zi denotes charge, F is Faraday's constant, ci the concentration, and μi the mobility of the entity with index i. Importantly,
is calculated from the mobilities, eqn (1) and (2).24 Here, zi denotes charge, F is Faraday's constant, ci the concentration, and μi the mobility of the entity with index i. Importantly,  can be negative, which is the case for [Li(G1)3][PO2F2]. Thus, the eNMR experiment provides clear evidence for undesired parasitic currents of both cations and anions. However, these currents are too small compared to the diffusive ion transport in a concentration gradient, hence they are not detected with the Bruce–Vincent method in such a low viscosity environment.
can be negative, which is the case for [Li(G1)3][PO2F2]. Thus, the eNMR experiment provides clear evidence for undesired parasitic currents of both cations and anions. However, these currents are too small compared to the diffusive ion transport in a concentration gradient, hence they are not detected with the Bruce–Vincent method in such a low viscosity environment.
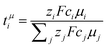 | (1) |
 | (2) |
Critically, the glyme molecules in [Li(G1)3][PO2F2] and [Li(G4)][PO2F2] exhibit significant mobility in the electric field despite being charge neutral. This behaviour is in line with previous eNMR studies of solvate ionic liquids,30,37 and can be rationalised in two ways. First, some glyme molecules might be coordinated to lithium and migrate with it in the direction of the electric field. Second, the motion of glyme might be due to the volume conservation requirement,16 since the large volume flux of the bulky anions requires compensation in form of a volume flux in the opposite direction, which is apparently not provided by Li. The opposite migration directions of glyme and lithium suggest that volume conservation is the dominating factor driving the glyme mobility in [Li(G1)3][PO2F2]. Regardless, the presence of positively charged species like [Li(G1)2]+ cannot be excluded at this stage, since the eNMR experiment results in a weighted average over all Li-containing species.
To gain more insight into the coordination environments in [Li(G1)3][PO2F2], we performed polarisable all-atom molecular dynamics (MD) simulations followed by a structural and dynamic analysis using a cutoff-based algorithm. It is important to note that the purpose of our MD simulations was not to predict transport properties or even transference numbers. Instead, we primarily use the simulation to gain insight into structural phenomena such as coordination and aggregation. Polarisable all-atom simulations are considered the gold standard for the prediction of structural properties in dense ionic fluids, and are necessary to accurately model both short- and long-range structuring.38–42 In general, such models give good dynamic properties as well, although with lower accuracy. Hence, we limit ourselves to a more qualitative discussion of the obtained lifetimes and use only structural data quantitatively. Importantly, both equilibration and production runs were significantly longer than the longest coordination environment lifetime as well as the typical timescale of dynamical heterogeneities (see Section S9, ESI†). This check is important to ensure that the system has sufficient time to reach ergodicity on both the local and collective scale.
Li+, the phosphorus atom of [PO2F2]−, and the oxygen atoms of G1 were used as the reference atoms, the first minima in their respective radial pair distribution functions were chosen as cutoff. Close contacts were observed between Li+ and both O and F of [PO2F2]−, rendering the phosphorus atom the simplest and most meaningful choice, Fig. 2. The coordination environments were numbered #1, #2, … in order of decreasing occurrence. A total of 37 lithium-centred unique coordination environments were identified by our algorithm, the detailed results can be found in the ESI† (Section S7 and accompanying files).
The local coordination environments of lithium are summarised in Table 2 and Fig. 3. Here, the stochiometric coefficients ν([PO2F2]−) and ν(G1) are ensemble averages which take into account communal solvation. If for example an anion is shared by two lithium centres, it only contributes ½ to the respective average ν([PO2F2]−) of those two lithium centres.
| 〈hLi〉 (%) | ν([PO2F2]−) | ν(G1) | Formal composition | |
|---|---|---|---|---|
| #1 | 36 | 1.337 | 0.997 | [Li(PO2F2)2(G1)1]−1 |
| #2 | 28 | — | 2.000 | [Li(G1)2]+1 |
| #3 | 12 | 0.702 | 1.977 | Li(PO2F2)1(G1)2 |
| #4 | 6 | 2.425 | — | [Li(PO2F2)4]−3 |
| #5 | 5 | 0.631 | 1.997 | Li(PO2F2)1(G1)2 |
| #6 | 4 | 2.077 | — | [Li(PO2F2)3]−2 |
 | ||
| Fig. 3 Representative structures for the six most common coordination environments of lithium in the MD simulation, randomly selected from the trajectory. Figure prepared with the prealpha software package and VMD.51 | ||
The most common coordination environment (#1) has the formal composition [Li(PO2F2)2(G1)1]−1, consistent with the experimentally observed migration direction of lithium. This is the case even if communal solvation of the anion is taken into account (overall charge −0.34). In contrast, the second most common coordination environment (#2, [Li(G1)2]+) is cationic and typical of a solvate electrolyte. The G1 molecules in coordination environment #2 do not take part in communal solvation. Hence, #2 is also considered a unique species. In fact, this is the only relevant lithium species which would be expected to migrate towards the negative electrode. Its occurrence in combination with the fast exchange averaging of the 7Li mobility over all Li-containing species explains why the magnitude of the electrophoretic mobility of 7Li is much smaller than that of 19F. In contrast, the other coordination environments will always be found as part of a larger aggregate, since many of the [PO2F2]− ligands are shared (i.e. ν([PO2F2]−) is smaller than the formal composition).
At every point in the trajectory, every lithium atom is assigned to a certain coordination environment. Thus, the lifetimes of all coordination environments can be assessed based on their respective intermittent time autocorrelation functions, Fig. 4. The most long-lived coordination environment is #4, which corresponds to a lithium cation coordinated by four anions, similar to the situation in crystalline Li[PO2F2].43 Such a long lifetime is consistent with research on ionic liquids showing that dynamics are in general slower in charged regions.44–47 Similarly, coordination environment #6 corresponds to a lithium coordinated by three anions (and no glyme) and has a relatively long lifetime. The [PO2F2]− is capable of coordinating the lithium with one (η1) or two (η2) of its electronegative atoms, cf.Fig. 2, which explains the stability of coordination environment #6.
 | ||
| Fig. 4 Time autocorrelation functions for the six most common lithium coordination environments, obtained with the prealpha software package. | ||
The coordination environments which are the most common (#1 and #2) are also among the most long-lived. Some common coordination environments appear as short-lived intermediates, such as #3 and #5, which can be seen as intermediates in the associative/dissociative pathways connecting coordination environments #1 and #2. Coordination environments become decorrelated on a ≈10 ns timescale, which shows the highly dynamic nature of this system.
In all cases, ν([PO2F2]−) is significantly smaller than the anion equivalents from the formal composition. This shows the large extent of communal solvation in the lithium-centred coordination environments. Vice versa, ν(Li+) also deviate significantly from the expected integer values for the G1-centred and the [PO2F2]−-centred coordination environments, Table 3.
| Coordination environment | 〈hG1〉 (%) | ν(Li+) | |
|---|---|---|---|
| G1 | Free G1 | 54 | — |
| G1–Li+ η2 | 40 | 0.678 | |
| G1–Li+ η1 | 6 | 0.435 | |
| 〈h[PO2F2]−〉 (%) | ν(Li+) | ||
|---|---|---|---|
| [PO2F2]− | Free [PO2F2]− | 8 | — |
| [PO2F2]−(Li+)1 | 49 | 0.539 | |
| [PO2F2]−(Li+)2 | 39 | 0.984 | |
| [PO2F2]−(Li+)3 | 4 | 1.370 |
The presence of communal solvation raises the question how large the formed aggregates are. To this end, we performed a cluster analysis using the Li and P atoms as members, Fig. 5(a).18,48,49 Briefly, the cluster analysis used here works by attempting to connect all Li and P atoms by jumping from one atom to the next, only allowing jumps up to a maximum distance. The cluster distance distribution function CDDF shows at which distances new connections are formed, i.e. where it is possible to jump between clusters that were previously unconnected at shorter maximum jump distances. Here, the CDDF between 2 Å and 4 Å resembles the RDF due to the two dominant coordination geometries, cf.Fig. 2. Critically, there is a gap between 4 Å and 5 Å at which almost no new clusters are formed. This indicates the presence of well-segregated aggregates. The cluster count function CCF gives the average number of clusters formed at a given distance. At short distances, all ions (70 cations and 70 anions) are considered as separate; at large distances, all ions are considered as connected in one large cluster. The CCF plateaus at intermediate distances and reaches a value of 50 at the cutoff value chosen in this work. If the clustering occurred homogeneously, then this value for the CCF would correspond to 2.8 ions per cluster.
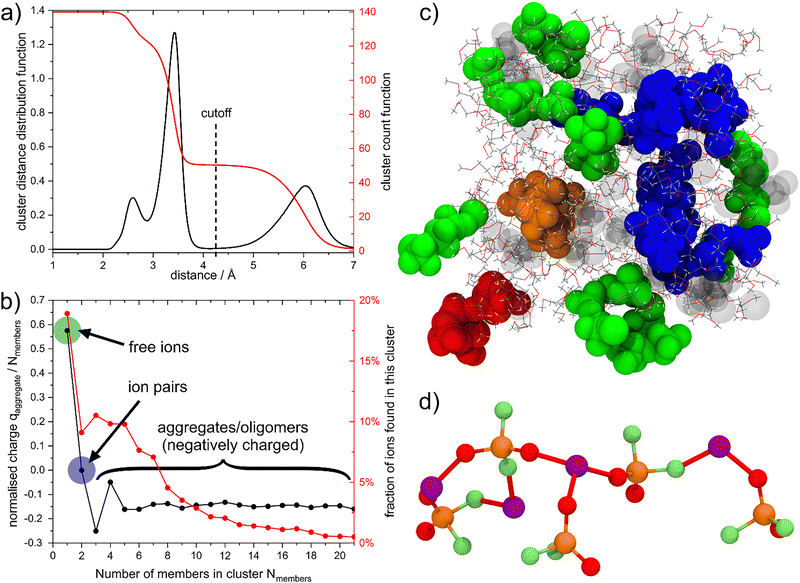 | ||
| Fig. 5 (a) CDDF and CCF obtained using the cluster analysis in the TRAVIS software package. (b) The average charge and the fraction of ions broken down by the number of ions in a given cluster. (c) Snapshot of the simulation box in the last third of the production run. Glyme molecules are shown as thin lines, ions are shown as VdW spheres. Monomers, dimers, and trimers are greyed out; 4-mers and 5-mers are blue; 6-mers and 7-mers are green; the 8-mer is shown in orange, and the 9-mer is shown in red. (d) detailed view of the structure of the 9-mer. Subfigures (b)–(d) have been prepared with the prealpha software package and visualised with VMD.51 | ||
We performed a detailed statistical analysis of the clusters present at the cutoff distance used for the speciation analysis (4.25 Å), Fig. 5(b). To construct this figure, each separate cluster was identified by the number of ions it was composed of, and its charge (divided by the number of ions in the cluster) calculated. Similarly, the percentage of ions belonging to a certain sized cluster is shown in Fig. 5(b). Here, isolated ions encompass Li+ only coordinated by glymes (cf.Table 2) and free [PO2F2]− (cf.Table 3), thus the total fraction of “free ions” is (28% · 70 + 8% · 70)/140 ≈ 18%.
Importantly, more than 50% of the ions are found in oligomers with more than 4 members, which are on average negatively charged (−0.15 e/ion). These relatively large oligomeric aggregates percolate the bulk liquid, Fig. 5(c) and Fig. 5(d). The oligomeric aggregates are decorated by glyme molecules. On average, 27% of glyme molecules are part of an oligomeric structure by coordinating to peripheral lithium. These glyme molecules need to follow the (slow) dynamics of the largely ionic aggregate.
In contrast, there are 54% free glyme molecules which can diffuse much more freely. This explains the dynamical heterogeneity (deviation from normal diffusion) observed for G1, see Fig. S9 (ESI†). 54% of free glyme molecules corresponds to 39% of the total mass. This large fraction of free glyme is in excellent agreement with the thermal gravimetric analysis (cf. Fig. S1, ESI†). In the TGA experiment, a pronounced step is observed with onset near the boiling point of G1. The mass loss in this step was approximately 45% (compared to 39% from the simulation).
Our premise in this work is that, at any point in time, the dynamic behaviour (migration and diffusion) of a constituent depends on the species it belongs to. This premise allows us to separate the experimental mobilities of constituents (μ7Li, μ19F, and μ1H) into their contributions from different species. Specifically, we assume that the observed lithium mobility is an average over [Li(G1)2]+ and the aggregates, eqn (3). Ion pairs are considered as part of the aggregates here. Similarly, the proton and fluorine mobilities are assumed to be an average over the various species, eqn (4) and (5).
| μ7Li = 28%·μ[Li(G1)2]+ + 72%·μAgg | (3) |
| μ1H = 54%·μG1,free + 27%·μAgg + 19%·μ[Li(G1)2]+ | (4) |
| μ19F = 92%·μAgg + 8%·μ[PO2F2]−,free | (5) |
The system of equations is underdetermined. The key approximation allowing us to proceed further is to assume a relative mobility μrel of fluorine in the free anion and the aggregates, eqn (6). Free [PO2F2]− is by far the smallest species, hence its mobility is expected to be high and might become relevant despite the low concentration. However, the dynamical heterogeneity observed in the diffusion of this anion is comparable to Li+ and smaller than that of G1, see Fig. S9 (ESI†). In addition, the experimental diffusion of 7Li and 19F was virtually identical and much slower than that of 1H. Hence, μrel for this electrolyte is not expected to reach extreme values.
| μ[PO2F2]−,free = μrel·μAgg | (6) |
As a further approximation, we neglected the contribution of ion pairs by treating them together with the aggregates. The ion pairs are naturally charge neutral but might nevertheless migrate in the electric field due to local volume conservation. The addition of such constraints to obtain the mobilities of additional species adds significant complexity and is beyond the scope of this work.
For future work, it would be beneficial to include additional data points, ideally until the problem is overdetermined. A recent example of such an approach is the work of Pothmann et al., albeit with a different focus.50 We suggest recording sets of numerical/experimental data points at different compositions, so that the variation in speciation is sufficiently large in both theory and experiment to allow for a robust determination of species mobility. Of particular interest in this regard would be systems which allow for a transition from aggregates to solvate cations, for example by increasingly replacing G1 with 12-crown-4.
Using the experimental electrophoretic mobilities of the constituents, (3)–(6) can be rearranged to yield absolute species specific mobilities. The resulting species mobilities for three different choices of μrel are shown in Fig. 6. μrel = 1 corresponds to the assumption that the electrophoretic mobility of the free anion is the same as that of the anion in the aggregates. On the other hand, μrel = 10 represents the case of the mobility of the free anion being an order of magnitude higher than in the aggregates. The reported uncertainty is an estimate obtained from propagation of the experimental uncertainties.
 | ||
| Fig. 6 (a) Species-averaged electrophoretic mobilities measured via eNMR [Li(G1)3][PO2F2], cf.Fig. 1(b), shown again here to facilitate comparison. The electrophoretic mobilities decomposed into contributions of each species are given in (b) for μrel = 1, (c) for μrel = 2, and (d) for μrel = 10. | ||
This analysis shows that the isolated solvate cation [Li(G1)2]+ is indeed expected to have a very high mobility in such a low viscosity medium, especially at moderate values of μrel.
The electrophoretic mobility of free G1 is even higher than that inferred from the species-averaged μ1H. This shows the importance of volume conservation constraints in this case, since free G1 by itself does not migrate in an electric field. On top of this, migration of some of the G1 together with the aggregates leads to the species averaged electrophoretic mobility being smaller than that of free G1.
The detailed analysis of the MD simulation allows us to rationalise every behaviour observed in our experiments. To this end, Fig. 7 gives an overview of the bulk composition in terms of species and their volume fraction. The detailed steps of how we calculated these fractions from the simulation data are given in the ESI† in Section S8. Speciation in the bulk liquid is highly dynamic as evidenced by the fast decorrelation of local coordination environments.
 | ||
| Fig. 7 Schematic overview of species in bulk [Li(G1)3][PO2F2], their volume fractions, and electrophoretic mobilities. | ||
Free solvent, in this case G1, makes up 44% of the bulk liquid. This explains the low viscosity and, consequently, the relatively fast diffusion and high conductivity in [Li(G1)3][PO2F2]. A species of equal importance are the negatively charged oligomeric aggregates, which make up 37% of the volume of the electrolyte. These aggregates drift in the electric field and lead to the net negative mobility for both constituents Li+ and [PO2F2]− as well as their similar diffusion coefficients. The movement of these aggregates needs to be compensated to ensure volume conservation, which is accomplished by the mobile free solvent. Furthermore, the aggregates help explain the extremely low ionicity observed in these samples.
In the case of G4, it is possible that glyme molecules act as cross-linking points between aggregates. Thus, the slow dynamics of the aggregates is transferred to the bulk liquid. This explains why the viscosity increases sharply for larger glymes without affecting ionicity. In a nutshell, the different viscosities of [Li(G4)][PO2F2] (high) and [Li(G1)3][PO2F2] (low) do not indicate that one behaves as a solvate electrolyte and one as a concentrated solution.
The ‘typical’ solvate cation [Li(G1)2]+ contributes 16% to the bulk volume and is thus important for the macroscopic properties, but does not dominate them. Its high mobility contributes to the migration of G1 and leads to the (species-averaged) electrophoretic mobility of lithium being lower than that of the anion. However, the high mobility of [Li(G1)2]+ is overcompensated by the involvement of Li+ in the oligomeric aggregates.
Conclusions
In this work we introduced a general framework to decompose a macroscopically averaged property – the electrophoretic mobility – into contributions from microscopic species. This framework explains two experimental observations which are counterintuitive at first. First, the migration of 7Li towards the positive electrode. A small fraction of lithium cations does exist in form of the solvate cation, i.e. [Li(G1)2]+, for which we find indeed high electrophoretic mobility in the expected direction towards the negative electrode. However, the macroscopically observed electrophoretic mobility of 7Li is a species average dominated by the excess of lithium cations that are part of negatively charged aggregates. Second, the migration of neutral glyme molecules in an electric field. This is a combination of glyme molecules migrating together with the aggregates or in form of the solvate cation, and the indirect transport of free glyme to fulfil constraints such as volume conservation.The problem at hand is underdetermined, hence Eqn (6) as additional approximation was necessary. However, the results were relatively insensitive to this approximation, and our qualitative conclusions remain unaffected even at μrel = 10 which we consider an upper limit based on the limited evidence for such an extremely high mobility of [PO2F2]−.
Finally, in the bigger picture, these results allow us to rationalise the discrepancy between  and
and  . The high degree of ion association leads to aggregates which are overall negatively charged. However, the average charge on each ion in aggregates is small, around −0.15 e (−0.13 e if ion pairs are included in the definition). Hence, the migration of these aggregates in the electric field is relatively slow, and the diffusion of neutral species as well as the aggregates themselves becomes dominant in the potentiostatic polarisation experiment used to measure
. The high degree of ion association leads to aggregates which are overall negatively charged. However, the average charge on each ion in aggregates is small, around −0.15 e (−0.13 e if ion pairs are included in the definition). Hence, the migration of these aggregates in the electric field is relatively slow, and the diffusion of neutral species as well as the aggregates themselves becomes dominant in the potentiostatic polarisation experiment used to measure  . In other words, the fact that the oligomeric aggregates are embedded in a low viscosity environment means that no concentration gradient can be built up, leading to
. In other words, the fact that the oligomeric aggregates are embedded in a low viscosity environment means that no concentration gradient can be built up, leading to  . Thus, for this class of electrolytes, the Bruce–Vincent method can be misleading as the undesired parasitic currents cannot be detected. In contrast, the eNMR approach directly measures the migration in the electric field from the equilibrium state, revealing that on average, Li+ migrates towards the positively charged electrode.
. Thus, for this class of electrolytes, the Bruce–Vincent method can be misleading as the undesired parasitic currents cannot be detected. In contrast, the eNMR approach directly measures the migration in the electric field from the equilibrium state, revealing that on average, Li+ migrates towards the positively charged electrode.
Author contributions
Frederik Philippi: conceptualization, methodology, software (prealpha software package), validation, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization, supervision, project administration, funding acquisition. Yuna Matsuyama: investigation, writing – original draft. Simon Buyting: validation, formal analysis (eNMR), investigation (eNMR). Taku Sudoh: writing – review & editing, supervision. Keisuke Shigenobu: investigation (running MD simulations), writing – original draft, writing – review & editing, visualization. Wataru Shinoda: software (MPDynPFF software package), resources, supervision, funding acquisition. Monika Schönhoff: resources, writing – review & editing, supervision, funding acquisition. Masayoshi Watanabe: resources, writing – review & editing, funding acquisition. Kazuhide Ueno: resources, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
We would like to acknowledge funding by the Japan Society for the Promotion of Science (JSPS) in form of a JSPS International Research Fellowship and JSPS KAKENHI grants (Grant No. 22KF0149 and 22K19082). We are grateful to Imperial College London and The Royal Society in supporting the application to the JSPS.The computation in this work was performed using the facilities of Research Centre for Computational Science, Okazaki, Japan (Project: 23-IMS-C095) and Supercomputer Centre, the Institute for Solid State Physics, the University of Tokyo.
Simon Buyting is supported by the Ministry of Culture and Science of the State North Rhine Westphalia in course of the International Graduate School for Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA). We acknowledge funding of the NMR spectrometer by the DFG (German Science Foundation) via proposal INST 211/999-1 FUGG, project ID 452849940.
References
- C. Fang, D. M. Halat, N. P. Balsara and R. Wang, J. Phys. Chem. B, 2023, 127, 1803–1810 CrossRef CAS.
- A. Hockmann, F. Ackermann, D. Diddens, I. Cekic-Laskovic and M. Schönhoff, Faraday Discuss., 2024, 253, 343–364 RSC.
- F. Philippi, M. Middendorf, K. Shigenobu, Y. Matsuyama, O. Palumbo, D. Pugh, T. Sudoh, K. Dokko, M. Watanabe, M. Schönhoff, W. Shinoda and K. Ueno, Chem. Sci., 2024, 15, 7342–7358 RSC.
- D. W. McOwen, D. M. Seo, O. Borodin, J. Vatamanu, P. D. Boyle and W. A. Henderson, Energy Environ. Sci., 2014, 7, 416–426 RSC.
- Y. Yamada and A. Yamada, J. Electrochem. Soc., 2015, 162, A2406–A2423 CrossRef CAS.
- G. A. Giffin, Nat. Commun., 2022, 13, 5250 CrossRef CAS.
- Y. Ugata, K. Shigenobu, R. Tatara, K. Ueno, M. Watanabe and K. Dokko, Phys. Chem. Chem. Phys., 2021, 23, 21419–21436 RSC.
- J. Qian, W. A. Henderson, W. Xu, P. Bhattacharya, M. Engelhard, O. Borodin and J.-G. Zhang, Nat. Commun., 2015, 6, 6362 CrossRef CAS.
- K. Ueno, R. Tatara, S. Tsuzuki, S. Saito, H. Doi, K. Yoshida, T. Mandai, M. Matsugami, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 8248–8257 RSC.
- S. Saito, H. Watanabe, Y. Hayashi, M. Matsugami, S. Tsuzuki, S. Seki, J. N. Canongia Lopes, R. Atkin, K. Ueno, K. Dokko, M. Watanabe, Y. Kameda and Y. Umebayashi, J. Phys. Chem. Lett., 2016, 7, 2832–2837 CrossRef CAS.
- M. Watanabe, K. Dokko, K. Ueno and M. L. Thomas, Bull. Chem. Soc. Jpn., 2018, 91, 1660–1682 CrossRef CAS.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Phys. Chem. B, 2021, 125, 6264–6271 CrossRef CAS.
- J. C. Araque and C. J. Margulis, J. Chem. Phys., 2018, 149, 144503 CrossRef.
- N. M. Vargas-Barbosa and B. Roling, ChemElectroChem, 2020, 7, 367–385 CrossRef CAS.
- H. K. Kashyap, H. V. R. Annapureddy, F. O. Raineri and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 13212–13221 CrossRef CAS.
- M. Lorenz, F. Kilchert, P. Nürnberg, M. Schammer, A. Latz, B. Horstmann and M. Schönhoff, J. Phys. Chem. Lett., 2022, 13, 8761–8767 CrossRef CAS.
- F. Kilchert, M. Lorenz, M. Schammer, P. Nürnberg, M. Schönhoff, A. Latz and B. Horstmann, Phys. Chem. Chem. Phys., 2023, 25, 25965–25978 RSC.
- T. Frömbgen, J. Blasius, V. Alizadeh, A. Chaumont, M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2022, 62, 5634–5644 CrossRef.
- M. Gouverneur, F. Schmidt and M. Schönhoff, Phys. Chem. Chem. Phys., 2018, 20, 7470–7478 RSC.
- M. Brinkkötter, G. A. Giffin, A. Moretti, S. Jeong, S. Passerini and M. Schönhoff, Chem. Commun., 2018, 54, 4278–4281 RSC.
- H. Moon, R. Tatara, T. Mandai, K. Ueno, K. Yoshida, N. Tachikawa, T. Yasuda, K. Dokko and M. Watanabe, J. Phys. Chem. C, 2014, 118, 20246–20256 CrossRef CAS.
- P. Zhou, W. Hou, Y. Xia, Y. Ou, H.-Y. Zhou, W. Zhang, Y. Lu, X. Song, F. Liu, Q. Cao, H. Liu, S. Yan and K. Liu, ACS Nano, 2023, 17, 17169–17179 Search PubMed.
- K. Xu, Commun. Mater., 2022, 3, 31 CrossRef.
- K. Xu, Electrolytes, Interfaces and Interphases, The Royal Society of Chemistry, 2023 Search PubMed.
- K. Shigenobu, M. Shibata, K. Dokko, M. Watanabe, K. Fujii and K. Ueno, Phys. Chem. Chem. Phys., 2021, 23, 2622–2629 RSC.
- S. Tsuzuki, W. Shinoda, M. Matsugami, Y. Umebayashi, K. Ueno, T. Mandai, S. Seki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 126–129 Search PubMed.
- P. Johansson, J. Tegenfeldt and J. Lindgren, Polymer, 1999, 40, 4399–4406 CrossRef CAS.
- D. Dong, F. Sälzer, B. Roling and D. Bedrov, Phys. Chem. Chem. Phys., 2018, 20, 29174–29183 RSC.
- T. Tamura, T. Hachida, K. Yoshida, N. Tachikawa, K. Dokko and M. Watanabe, J. Power Sources, 2010, 195, 6095–6100 CrossRef CAS.
- S. Pfeifer, F. Ackermann, F. Sälzer, M. Schönhoff and B. Roling, Phys. Chem. Chem. Phys., 2021, 23, 628–640 RSC.
- F. Wohde, M. Balabajew and B. Roling, J. Electrochem. Soc., 2016, 163, A714–A721 CrossRef CAS.
- T. Murphy, S. K. Callear, N. Yepuri, K. Shimizu, M. Watanabe, J. N. Canongia Lopes, T. Darwish, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2016, 18, 17224–17236 RSC.
- K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2012, 116, 11323–11331 CrossRef CAS.
- T. D. Pham, A. Bin Faheem, S. Y. Chun, J. Rho, K. Kwak and K. Lee, Adv. Energy Mater., 2021, 11, 1–17 Search PubMed.
- K. Matsumoto and R. Hagiwara, Inorg. Chem., 2009, 48, 7350–7358 CrossRef CAS.
- K. Hayamizu and Y. Aihara, Electrochim. Acta, 2004, 49, 3397–3402 CrossRef CAS.
- F. Schmidt and M. Schönhoff, J. Phys. Chem. B, 2020, 124, 1245–1252 CrossRef CAS.
- D. Bedrov, J. P. Piquemal, O. Borodin, A. D. MacKerell, B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS.
- C. Schröder, Phys. Chem. Chem. Phys., 2012, 14, 3089 RSC.
- J. G. McDaniel, J. Phys. Chem. B, 2018, 122, 4345–4355 CrossRef CAS.
- J. G. McDaniel and A. Yethiraj, J. Phys. Chem. Lett., 2018, 9, 4765–4770 CrossRef CAS.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 11463–11478 CrossRef CAS.
- G. Han, Y. Wang, H. Li, Z. Yang and S. Pan, Chem. Commun., 2019, 55, 1817–1820 RSC.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Phys. Chem. Lett., 2020, 11, 2062–2066 CrossRef CAS.
- R. Shi and Y. Wang, Sci. Rep., 2016, 6, 1–12 CrossRef.
- J. C. Araque, S. K. Yadav, M. Shadeck, M. Maroncelli and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 7015–7029 CrossRef CAS.
- R. P. Daly, J. C. Araque and C. J. Margulis, J. Chem. Phys., 2017, 147, 061102 CrossRef.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS.
- M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105 CrossRef CAS.
- T. Pothmann, M. Middendorf, C. Gerken, P. Nürnberg, M. Schönhoff and B. Roling, Faraday Discuss., 2024, 253, 100–117 RSC.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of the experimental and computational methods (PDF). Input files for and raw output data of the prealpha software package (ZIP). See DOI: https://doi.org/10.1039/d5cp00222b |
| ‡ Present address: Laboratoire de Chimie ENS de Lyon, Campus Monod Room M6.056, 46 Allée d’Italie, 69364 Lyon Cedex 07, France. |
| This journal is © the Owner Societies 2025 |



