Impact of mass transport on meniscus electrochemistry determined by time-resolved operando X-ray photoelectron spectroscopy

Abstract

Ambient pressure X-ray photoelectron spectroscopy (APXPS) combined with the dip-and-pull method can be used for operando studies of electrochemical systems. A complete coupling between the spectroscopic and the electrochemical measurements is generally challenging due to an inherent difference between the meniscus and the bulk electrolyte – the mass transport. This work investigates meniscus mass transport and its effect on the meniscus electrochemical processes by simultaneously conducting time-resolved APXPS and chronoamperometry for two types of electrochemical processes: capacitive and faradaic. Additionally, experiments are complemented with simulations based on a purposefully constructed transmission line model. In the investigated system, based on a gold electrode and carbonate electrolyte, the meniscus resistance is shown to be over 1000 times larger than the bulk electrolyte resistance. Consequently, during faradaic processes, considerable iR drop in the meniscus results in two to three orders of magnitude slower rate of charge transfer in the meniscus than in the bulk electrolyte. Using the acquired understanding of the meniscus mass transport, we suggest an experimental practice to quantify the iR drop and propose possible remedies for experiments where any impact of the iR drop must be avoided.

---

Introduction

Electrode/electrolyte interfaces constitute the most important segment of electrochemical systems. It is at these interfaces that the key electrochemical process – heterogeneous charge transfer – occurs.^1–3 A thorough understanding of electrochemical interfaces is therefore crucial and operando measurements, which are conducted under realistic conditions, are the preferred manner of investigating these interfaces.^2,4–6 Until now, operando measurements have remained limited due to the challenges inherent to experimental investigation of electrode/electrolyte interfaces and further complicated by the prerequisite to simultaneously exert electrochemical control.^2,7,8 Ambient pressure X-ray photoelectron spectroscopy (APXPS) is a method that has been touted as particularly suitable for the operando investigation of electrified interfaces due to its excellent surface and chemical sensitivity. Additionally, APXPS is capable of probing changes in the electronic electrochemical potential drops across the interface.^7–10 To access the electrode/electrolyte interface, APXPS typically relies on either of two experimental approaches: the liquid cell or the dip-and-pull method.^2,7,8,11 The dip-and-pull method probes the interface from the liquid side and relies on the formation of a thin electrolyte meniscus at the electrode surface. The meniscus is formed by first dipping and afterwards partially retracting the electrode.^2,7,10,12,13 During operando measurements, electric stimulus is applied to the electrochemical cell, while APXPS probes the electrode/electrolyte interface through the meniscus. The meniscus must be very thin (a few tens of nm at most) to enable simultaneous measurements of the electrolyte and the electrode.^10,13–16 The dip-and-pull method is easy to implement for a wide variety of samples and does not require a complex experimental setup, which has resulted in the method installment on several APXPS synchrotron beamlines.^12,17–20 The method has been employed in investigations of electrocatalyst surface evolution during electrocatalysis,^5,12,13,21 electric double layer structure,⁶ electronic band energies at semiconductor/liquid junctions^4,22 and solid–electrolyte interphase formation in model Li-ion battery systems.^14,23,24

Although the dip-and-pull method has many advantages, the experimental setup involving thin electrolyte meniscus can face large challenges in its implementation. Mass transport limitations involving reactant and electrolyte species can, if severe enough, lead to a significant iR drop along the meniscus and/or finite diffusion, limited by the meniscus geometry – a contrast to the much smaller iR drop and convection-limited finite diffusion in the bulk electrolyte.^{2,10,13,25,26} Differences between the meniscus mass transport and the bulk electrolyte mass transport can lead to significant variations in the meniscus electrochemical processes as compared to the electrochemical processes in the bulk electrolyte. Specifically, electrochemical processes in the meniscus and in the bulk electrolyte can differ in their nature as well as their rates. It is therefore crucial to understand the extent of mass transport limitations and with that avoid data misinterpretations.² Sluggish mass transport in electrochemical systems is accompanied by electrostatic potential gradients.¹ Until now, indications of mass transport limitations have been reported by several experimental^{13,15,20,22,27} and theoretical²⁸ studies. Notably, Velasco-Velez et al.²⁰ reported that equilibration of the meniscus following an electrochemically initiated adsorption of H⁺ on RuO_x electrode took over 15 min – a time period much longer than the intrinsic kinetics of this adsorption process. In spite of a number of reports pointing to serious mass transport limitations, systematic experimental studies of meniscus mass transport have not yet been conducted. In the absence of quantification of mass transport, it is difficult to adequately apply this knowledge and the appropriate remedies to dip-and-pull APXPS methodology.

In this study, we employ electrochemical and dip-and-pull time-resolved operando APXPS experiments with subsecond time resolution. We combine experiments with simulations to achieve a comprehensive understanding of meniscus mass transport and its effects on meniscus electrochemistry. By developing a transmission line model of the experimental system, we quantify the effects of mass transport during capacitive and faradaic processes at the working electrode. We show that, in the investigated system based on a carbonate electrolyte and a flat Au electrode, the ohmic drop along the meniscus causes a significant deviation from the applied potential at the APXPS measurement point in the presence of a faradaic process. We observe a substantial (two to three orders of magnitude) decrease of the faradaic process rate in the meniscus as compared to the bulk electrolyte. In view of this substantial mass transport impact, we use the developed system model to identify the general experimental approaches to minimize the ohmic drop in the meniscus. Importantly, we point to an easy-to-implement experimental practice for estimating the magnitude of the meniscus ohmic drop in dip-and-pull operando APXPS.

Experimental

Sample preparation

Gold working electrodes were prepared by sputtering gold for 4 min at 70 mA on copper plates (11 mm × 2 mm × 50 mm), which corresponds to roughly 200 nm thick gold layer as measured with a profilometer. Working electrodes (WEs) were then gently washed with ethanol and acetone, dried at 80 °C for 2 h and introduced into the customized glovebox attached to HIPPIE endstation. LTO reference electrodes (REs) were prepared by casting LTO water based slurry constituting lithium titanate (Posco GS Materials), sodium carboxylate cellulose (Sigma-Aldrich) and carbon black (Imerys graphite & carbon, C.NERGY SUPER C65) in 8 : 1 : 1 mass ratio onto aluminium wire. The same procedure was used to prepare LTO counter electrodes (CEs), the only difference being that the slurry was cast onto aluminium plates (11 mm × 2 mm × 50 mm) instead of aluminium wires used for REs. The coated plates and wires were dried in ambient conditions for 24 h then transferred to an argon filled glovebox and dried at 120 °C for 12 h under vacuum. 1 M LiClO₄ electrolyte was prepared by adding lithium perchlorate (Sigma-Aldrich, battery grade 99.99%) to propylene carbonate (Gotion, 99%) in an argon filled glovebox (H₂O < 1 ppm, O₂ < 1 ppm). The electrolyte used in Experiments 2 and 3 was obtained by adding ferrocene (98% purity, Sigma Aldrich) to 1 M LiClO₄ in PC until saturated in Fc (≈0.2 M Fc in PC²⁹).

Prior to being used in (spectro)electrochemical experiments, LTO electrodes were precycled to reach a stable electrode potential. Precycling was done in pouch cells with LTO working electrode, 1 M LiClO₄ in PC (the same electrolyte was used for the dip-and-pull synchrotron experiments), glassy fiber separator (Whatman, GF/A) and Li metal (FMC Lithium, 400 µm thick) counter electrode. Each cell underwent one discharge–charge cycle, followed by the discharge until halfway through the LTO (de)lithiation plateau (1.56 V vs. Li⁺/Li). LTO wires (REs) were cycled with a constant current of 50 µA and LTO plates (CEs) were cycled with a constant current rate of C/10. Only electrodes with a potential stable over more than 24 h were employed in the (spectro)electrochemical experiments described in this work. LTO REs and CEs employed in experiments were in partially lithiated (approximately 50% lithiated) state.

Ambient pressure X-ray photoelectron spectroscopy

Ambient pressure X-ray photoelectron spectroscopy (APXPS) was performed at the HIPPIE B branch end station at MAX IV synchrotron in Lund, Sweden. Samples were introduced into analysis chamber via a customized glovebox. Prior to introducing the samples into the glovebox, a fresh Li foil piece was exposed to the glovebox atmosphere. As no change in Li foil surface appearance (e.g. loss of Li metallic shine or surface colouring) could be observed throughout the measurement duration, water and oxygen contamination of the samples that had been exposed to the glovebox atmosphere for a much shorter time than the Li foil was deemed negligible. Pressure inside the analysis chamber was kept constant at 0.25 mbar, which is slightly higher than the vapor pressure of PC at 25 °C.³⁰ As visible in the gas phase XP spectra, the higher pressure was due to the leftover Ar gas (remains of the glovebox atmosphere). A sacrificial beaker containing PC was placed in the analysis chamber. This effectively decreased evaporation of the PC in the electrolyte on the time scales of our experiments. Electrolyte was degassed prior to performing any measurements. APXPS measurements of the electrolyte were enabled by the dip-and-pull method, which is based on the formation of an electrolyte meniscus on the WE surface. Electrodes were partially immersed in the electrolyte (i.e. not all of the electrode surface was wetted by the electrolyte) both in the “dipped” and in the “pulled” position. Positions of the electrode holder and of the electrolyte holder were precisely controlled by two independent manipulators. WE was grounded to the spectrometer analyzer; all reported kinetic energies are referenced to the spectrometer Fermi level. Beam damage effects (formation of beam damage products) were minimized by continuously scanning horizontally along the sample surface during the measurements. Surface scanning speed was carefully chosen and represented a trade-off between minimizing the intensity of the beam damage peaks (minimized for higher speed) and maintaining tolerable noise levels, which increase with higher speed.

HIPPIE end station is equipped with SPECS Phoibos 150 NAP (10 kV) analyser and a 2D DLD detector. The X-ray incidence angle is 54.7° (magic angle) with respect to the spectrometer. The nominal beam size is 80 µm (horizontal) × 40 µm (vertical). All XP spectra were recorded with the photon energy of 1800 eV. Scanning mode spectra were collected with a step size of 0.1 eV, dwell time of 0.05 s and pass energy 100 eV. When recording in the snapshot mode, a dwell time of 0.25 s and pass energy of 100 eV were used. Time-resolved APXPS experiments were conducted using the snapshot mode, whereas the regular APXPS measurements were performed using the scanning detector mode.

Electrochemical measurements

Electrochemical measurements at the HIPPIE end station were performed using a Biologic SP-200 potentiostat. The potentiostat was used in the floating mode to avoid any leakage currents. Two types of electrochemical experiments were carried out: chronoamperometry (CA) and cyclic voltammetry. Working electrode potential in CA alternated between two potentials, E_i and E_f. The rate of the potential change was 100 V s⁻¹. Such rate was chosen as the WE potential overshoot observed shortly after applying the potential step remained relatively small (less than 10 mV) while the potential rising time was kept sufficiently short (2.5 ms for a potential step of 0.5 V vs. Li⁺/Li and 4.25 ms for a potential step of 0.85 V vs. Li⁺/Li). After stepping in the WE potential, the potential value was kept constant until the current magnitude stabilized (an equilibrium or a steady state were typically reached sometime in between 5 s and 10 min). Cyclic voltammograms (CVs) were recorded by sweeping the WE potential with a rate of 1.0 V s⁻¹ over varied potential intervals.

Time resolved APXPS spectroelectrochemistry

Time-resolved APXPS spectroelectrochemistry combined APXPS measurements of the electrolyte meniscus with CA. CA measurement parameters were the same as outlined in the text above, whereas time-resolved APXPS (tr-APXPS) measurements were performed by recording C 1s spectra in the snapshot mode. A single C 1s spectrum was acquired each 0.293 s (a sum of the dwell time and the accompanying dead time, i.e. the total time elapsed between each subsequent C 1s scan). Each double potential step was conducted as follows. Electrolyte meniscus was first renewed by immersing electrodes dipper in the electrolyte. Electrodes were afterwards retracted back to their initial position and the acquisition of the snapshot C 1s spectra began. After acquiring approximately 50 spectra, a potential step from E_i to E_f was initiated. C 1s acquisition was continued until the kinetic energy of C 1s spectra had been stable for a while (between 200 s and 300 s after the potential step). The same procedure was repeated for the second potential step, going from E_f to E_i. Following each double potential step, the electrodes were again redipped to replenish the electrolyte meniscus. The total time elapsed between the electrode redipping was kept below 30 min to prevent meniscus dryout. Time resolution of the tr-APXPS spectroelectrochemical experiments was limited by the time resolution of the C 1s acquisition which amounted to 0.293 s.

While acquiring C 1s snapshots, beam damage accumulation was prevented by continuously scanning the electrolyte meniscus surface. PES measurements were conducted at the same meniscus height, i.e. 4 mm above the bulk electrolyte level and 2 mm beneath the top of the meniscus. Throughout the measurement duration, the electrodes were in contact with the electrolyte and the depth of the WE immersion in the bulk electrolyte was equal to 4 mm. The meniscus was stable for all WE potentials and formed a continuous electrolyte film. Continuity of the meniscus was frequently examined by scanning along the meniscus surface (in height and width) and checking whether the C 1s spectra show the PC spectral shape. The height of the meniscus varied by ±0.1 mm throughout the experiments.

In tr-APXPS spectroelectrochemical experiments, the WE potential alternated between two pairs of potentials, namely, between 2.75 V and 3.25 V vs. Li⁺/Li (Experiments 1 and 2) and between 2.75 V and 3.6 V vs. Li⁺/Li (Experiment 3). Table 1 underlines the differences between the three Experiments. Double potential step was repeated at least five times for each of the three Experiments.

Table 1 Experimental differences between the spectroelectrochemical Experiments 1, 2 and 3. Potentials are referenced against Li⁺/Li redox couples

	E i [V]	E f [V]	Electrolyte	Process
Experiment 1	2.75	3.25	1 M LiClO4 in PC	Capacitive
Experiment 2	2.75	3.25	1 M LiClO4 and 0.2 M Fc in PC	Faradaic, slower rate (lower overpotential)
Experiment 3	2.75	3.60	1 M LiClO4 and 0.2 M Fc in PC	Faradaic, faster rate (higher overpotential)

---

Data treatment

C 1s spectra acquired during spectroelectrochemical experiments were fitted using a purposefully written Python script, which is available upon a written request to the first author and on Github, DOI: https://doi.org/10.5281/zenodo.12760622. In short, the script did the following: each experimentally obtained C 1s spectrum was compared to the reference C 1s spectrum of PC. The reference C 1s spectrum was found by manually fitting a few C 1s spectra acquired with APXPS. After subtracting a linear background, each spectrum was fitted using symmetric pseudo-Voigt functions with Gaussian full-width at half-maximum (FWHM) of 1.0 eV and Lorentzian FWHM of 0.15 eV. Three peaks were fitted to each C 1s spectrum (Table 2). During automatic fitting, the reference spectrum was moved along x-axis (kinetic energy) and y-axis (photoelectron signal intensity) until the best overlap between the experimental and the reference C 1s spectrum could be found. C 1s fitting was necessary to determine the PC peak position on the kinetic energy scale with sufficient accuracy. Simply tracking the KE at which the highest count of photoelectrons was recorded and using that KE to determine the PC peak positions resulted in too large errors (signal-to-noise ratio in C 1s spectra was too low). The position of the fitted PC spectra is reported as the kinetic energy of the C=O peak, KE. The reader should note that the C–O and the C–C/C–H peaks exhibit the same KE time dependence as the C=O peak (relative positions of the C–O and the C–C/C–H peaks with respect to the C=O position are fixed).

Table 2 Parameters used to construct the PC spectral shape. C=O and C–C/C–H peak positions and intensities are given relative to the position x and the intensity y of the C–O peak. All peaks had a pseudo-Voigt shape with a Lorentzian FWHM of 0.15 eV and a Gaussian FWHM of 1.0 eV

Peak	C=O	C–O	C–C/C–H
Rel. peak position [eV]	x − 3.55	x	x + 2
Rel. peak intensity [counts]	0.625y	y	0.5y

---

In theory, the intensity of the C=O peak, I_C=O, in a randomly oriented PC molecule is supposed to be half of the intensity of the C–O peak, I_C–O. The ratio of I_C=O: I_C–O was observed to be 0.5 when recording C 1s spectra in the scanning mode, but deviated from the expected ratio when the detector operated in the fixed mode. In this case, the C=O peak intensity was observed to be approximately 0.625 I_C–O. Deviation from the expected ratio of I_C=O: I_C–O = 0.5 is most likely a result of the different sensitivity of distinct detector channels. Accuracy of Python-based fitting of PC spectra is discussed in note S1 in ESI.†

Results and discussion

In Fig. 1a, we first present the experimental setup used to investigate the electrostatic potential distribution in the bulk electrolyte and the meniscus during the electrochemical processes at the working electrode. The studied three electrode system consisted of Au working electrode, LTO reference electrode and LTO counter electrode immersed in the supporting electrolyte consisting of 1 M LiClO₄ in propylene carbonate (PC). This supporting electrolyte was chosen because it is one of the systems most frequently studied with APXPS and serves as a model system for the electrolytes most commonly used in Li-ion batteries.^14,23,24 In experiments investigating faradaic processes, ferrocene (Fc) was added to the supporting electrolyte. Changes of the electrostatic potential distribution as a function of time were inferred from two parallel experiments. Electrochemistry was used to exert control over the electrostatic potential difference between the working electrode (WE) and the reference electrode (RE), E_WE.^1,3,31 Using chronoamperometry (CA), a potential step ΔE_WE, was applied between the WE and the RE, and the corresponding current transient recorded. Simultaneously with CA, the kinetic energy (KE) of the C 1s core level photoelectrons originating from the surface of the electrolyte meniscus was monitored with time-resolved APXPS with a time resolution of 0.3 s. The C 1s core level was chosen because it originates from a neutral electrolyte species (PC solvent) present at high concentrations (high signal). Electrolyte meniscus covered 60% of the wetted WE surface area. The remaining 40% of the wetted electrode area was immersed and thus in contact with the bulk electrolyte. APXPS measurements of the meniscus were performed 4 mm above the bulk electrolyte level and 2 mm below the meniscus top edge (see scheme in note S3 in ESI†). At the measuring position, the meniscus was thick enough to prevent the detection of any signals coming from the Au working electrode. Additionally, C 1s peaks were symmetric and narrow, which indicated that the PC molecules located within the APXPS probing depth experienced a similar electrostatic potential.¹² Because of this, we concluded that the C 1s photoelectrons originated from outside of the electric double layer. The meniscus is estimated to be thicker than 20 nm based on the probing depth (i.e. 3-times the photoelectron inelastic mean free path).

Fig. 1 (a) Schematic drawing of the experimental setup. (b) Electrostatic potential ϕ as a function of charge carrier path r. Specifically, charge carrier path r corresponds to the path between the WE and the RE that leads through APXPS probing position on the meniscus (green circles); the location of the APXPS probing position is indicated approximately and is not to scale. At the working electrode potential E_WE, the electrostatic potential difference across the electrochemical interface (i.e. WE/electrolyte interface including the electric double layer) is δϕ. Applying a potential step of ΔE_WE results in a change of δϕ, Δ(δϕ). The change in KE of C 1s, ΔKE, recorded with APXPS, is proportional to the change in the electrostatic potential difference between the WE and the APXPS probing position Δ(δϕ_m). To relate ΔKE to Δ(δϕ_m), Δ(δϕ_m) is multiplied by q = −1 and with that converted from volts to electron volts (see magnified scheme segment). Examples of the electrostatic potential profile between the working and the reference electrode are shown for three points in time: in thermodynamic equilibrium before the potential step (black curve), during relaxation following a potential step of ΔE_WE (red dashed curve) and in thermodynamic equilibrium after the potential step (blue curve). Red curve is an example of ϕ(r) during relaxation at some time t; the curve is drawn for the example where the meniscus has a higher resistivity than the bulk electrolyte, thus resulting in a steeper gradient of ϕ(r) in the meniscus as opposed to the bulk electrolyte. As indicated in this scheme, electrostatic potential drop across the electrochemical interface at the RE is assumed to be constant throughout the experiment duration.

The WE was grounded to the spectrometer analyzer, which meant that any change in the KE of the electrolyte C 1s stemmed from a shift in the electrochemical potential of C 1s core level electrons in the electrolyte relative to the WE.¹⁴ In this work, the chemical potential of C 1s core level electrons in the electrolyte was assumed to be constant based on the experimental findings (see note S4 in ESI†). Constant chemical potential of C 1s and grounded, electronically conducting WE meant that the change in KE of C 1s, ΔKE, was equal to the change in the electrostatic potential difference between the WE and the electrolyte at the meniscus measuring position Δ(δϕ_m) (see note S5 in ESI†).^4,14,22 Since the APXPS measuring point is very close to the WE, the entirety of Δ(δϕ_m) was assumed to be due to a change of the electrostatic potential drop at the electrochemical interface Δ(δϕ) (i.e. across the WE/electrolyte interface including the electric double layer), that is Δ(δϕ_m) ≈ Δ(δϕ). Definitions of distinct types of electronic potentials are provided in note S6 in ESI.† We note that using APXPS, Δ(δϕ_m) is measured locally; hence, the recorded Δ(δϕ_m) is specific for the APXPS measuring position height on the meniscus. Due to this, the local meniscus Δ(δϕ) can be determined with much better accuracy using APXPS than by using the RE.

Assuming a stable RE, the ratio between ΔKE recorded on the electrolyte meniscus and ΔE_WE informs of the change in the electrostatic potential distribution between WE, the meniscus measuring position and RE following a potential step ΔE_WE. A ratio of 1 eV V⁻¹ means that the entire change of the electrostatic potential due to ΔE_WE occurs between the metal working electrode and the measuring position.^4,14 Contrastingly, a ratio of less than 1 eV V⁻¹ indicates that only a fraction of the electrostatic potential change caused by ΔE_WE occurs between the working electrode and the measuring position, since some of the electrostatic potential change is distributed between the measuring point and RE. Fig. 1b illustrates two examples of electrostatic potential distribution leading to different ΔKE-to-ΔE_WE ratios. Assuming the system is initially in thermodynamic equilibrium (black curve), the blue curve corresponds to the case of 1 eV V⁻¹ ratio and the red dashed curve corresponds to a possible electrostatic potential profile with the ratio of less than 1 eV V⁻¹.

By combining CA with time-resolved APXPS, three important bits of information can be attained: (i) using ΔKE, the change in electrostatic potential drop across the electrochemical interface (at the APXPS measuring height) caused by a potential step can be determined with much better accuracy than by relying solely on an estimation based on ΔE_WE. This electrostatic potential drop is essential for understanding the nature and the rate of the electrochemical processes occurring in the meniscus; (ii) similarly, by subtracting ΔKE from ΔE_WE, the electrostatic potential difference between the RE and the APXPS measuring point (which includes the bulk electrolyte and the meniscus) can be determined; and (iii) by comparing the time dependence of i(t) and KE(t) transients, we infer if there is a difference between the current and potential transients in the bulk electrolyte and the meniscus, respectively.

In order to obtain a general understanding of the functionality of the meniscus, we performed our experiments in the presence and absence of ferrocene in 1 M LiClO₄/PC supporting electrolyte. This allowed us to obtain a quantitative insight into the behavior of faradaic processes as well as capacitive processes in our system. The cyclic voltammogram obtained for 0.2 M Fc is shown in Fig. 2a (red curve). The voltammetric peaks centered at 3.3 V towards Li⁺/Li are consistent with the oxidation/reduction of the redox couple Fc⁺/Fc in PC.³² As expected, when Fc was not present in the electrolyte, only capacitive features were observed in a cyclic voltammetry experiment (blue curve in Fig. 2a and b).

Fig. 2 (a) Cyclic voltammogram obtained with 1 V s⁻¹ in the absence of Fc (blue) and with 0.2 M Fc (red). E₀ (2.75 V vs. Li⁺/Li) is the lower (initial) working electrode potential used in CA experiments, while E₁ (3.25 V vs. Li⁺/Li) and E₂ (3.6 V vs. Li⁺/Li) correspond to the upper (final) potentials used in CA experiments. Potential E_io indicates current onset in the forwards scan for the electrolyte containing Fc. (b) Zoom in to the cyclic voltammogram recorded in the absence of ferrocene with a scan rate of 1 V s⁻¹. (c) Chronoamperometric response for a potential step from E₀ to E₁ in the absence of ferrocene (black dots). Potential step was initiated at time 0. Experimental data is overlaid with the fit obtained from the bulk model 1 (blue line) and the meniscus model 1 (red line). Inset shows an enlarged view of the time interval with the largest discrepancy between the experimental data and the bulk model 1. (d) Meniscus models 1 and 2 and bulk model 1 of the investigated system. Meniscus model 1 and 2 comprise of the bulk electrolyte region (blue shading) and the meniscus region (orange shading). As indicated in the legend, in meniscus model 1, the interfacial impedances Z are double layer capacitors (C_dl). In meniscus model 2, each interfacial impedance Z corresponds to a charge transfer resistor R_ct and a double layer capacitor C_dl connected in parallel. Bulk model 1 comprises of only the electric circuit section shaded with blue. For full view of meniscus models 1 and 2, see Fig. 4a in the main text, note S10 in ESI,† respectively. Bulk model 1 is individually shown in note S7 in ESI.† (e) Chronoamperometric response for a potential step from E₀ to E₂ (black dots) with 0.2 M Fc in the electrolyte. Green curve represents best fit of the experimental data using meniscus model 2. Orange curve corresponds to the best fit obtained with the bulk (model 2).

In the absence of Fc, the potential step from E₀ to E₁ (see Fig. 2a) leads to a fast capacitive relaxation of the system (i.e. 1 M LiClO₄). However, fitting the current–time response with a simple “bulk model 1” (Fig. 2c, blue curve), which consists of a resistor due to the bulk electrolyte and a double layer capacitor (Fig. 2d, blue elements), leads to a considerable deviation on the time scale from about 0 to 0.2 s (inset in Fig. 2c). We have assumed that this is mainly due to the fact that the double layer charging of a large part of the electrode surface area (60%) can only proceed via ion transport through the thin meniscus. If the model is upgraded based on this assumption to a transmission line model (“meniscus model 1” in Fig. 2c and d), a near perfect fit of the experimental points is obtained (fitting details in ESI,† S5). Resistances of the bulk electrolyte R_b and the 10 meniscus resistors R_m,n extracted from the fit are shown next to the corresponding circuit elements in Fig. 4a. Most importantly, according to the meniscus model 1, the total meniscus resistance R_m,tot (the sum of all R_m,n) amounts to 140 kΩ – a value more than three orders of magnitude larger than the bulk electrolyte resistance of 100 Ω. This shows that the meniscus plays a very important role in ion transport to a large part of the electrode surface. Further details about both models can be found in notes S7 and S8 in ESI.†

When Fc is added, the current response to oxidative potential steps changes considerably due to the large contribution of the redox reaction to the total current magnitude (black dots in Fig. 2e). In an effort to simulate faradaic current response, we employed several models, each of them describing the system geometry and mass transport to a varying level of detail (notes S9–S12 in ESI†). Following the analysis described in note S9 (ESI†), a satisfactory representation of the system could be achieved with a model containing a detailed description of charge carrier mass transport in the electrolyte (coupled migration and diffusion) and, importantly, with a simplified description of the system geometry (meniscus geometry was neglected). Fig. 2e displays a comparison between the current transients simulated by two distinct models; one with a detailed description of geometry and a basic description of mass transport (“meniscus model 2”, green curve) and one with a basic description of geometry and a detailed description of mass transport (“bulk model 2”, orange curve). Meniscus model 2 and bulk model 2 are shown in notes S11 and S12 in ESI,† respectively. The key conclusion that emerged from the analysis is that the current generated in the meniscus in the presence of the Fc⁺/Fc redox species is negligible compared to the current flowing in the bulk part of the system. This is in agreement with the work of Favaro et al.,²⁷ where a substantially smaller current density was recorded after masking the portion of the WE surface that was immersed in the bulk electrolyte.

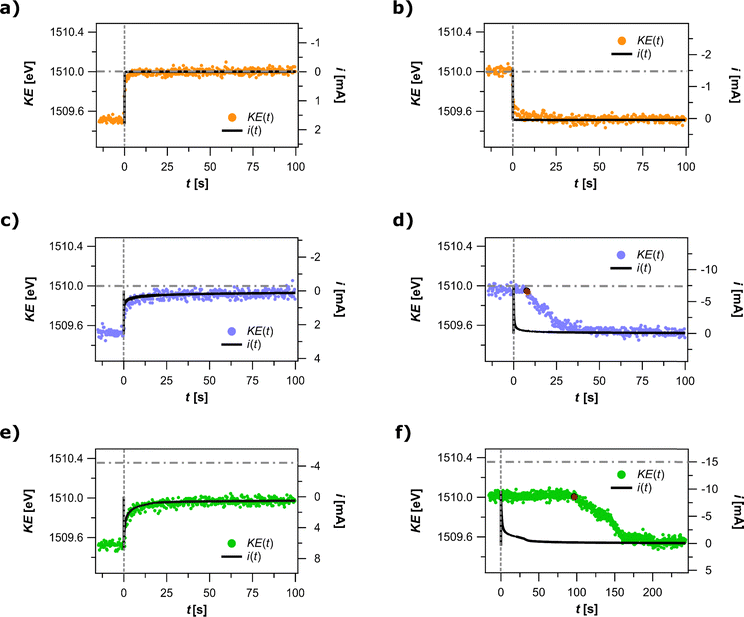
To further test the effect of the meniscus mass transport on the processes taking place in the meniscus, we wanted to experimentally probe the impact of the meniscus resistance on the potential distribution in our system. As mentioned above, the proximity of the APXPS position to the electrochemical interface is such, that ΔKE is assumed to be equal to the change in electrostatic potential drop across the electrochemical interface Δ(δϕ). Hence, by acquiring the APXPS spectra simultaneously with the current response in CA, we were able to determine, what portion of the applied potential the electrochemical interface is experiencing at the meniscus height of the APXPS measuring point. The plots in Fig. 3a and b correspond to the experiments performed in the absence of Fc, where only capacitive processes accompanied a 0.5 V potential step from E₀ to E₁. Transients i(t) and KE(t) are seen to exhibit a similar time-dependent behavior, however, i(t) is seen to reach the steady state about 5 s faster than the KE(t) transient. Considering that i(t) signal predominantly originates in the bulk electrolyte, whereas KE(t) reflects the response of the meniscus, the two transients indicate that the bulk electrolyte and the electrolyte in the meniscus reached the steady state roughly 5 s apart. The total shift in KE amounted to 0.5 eV, thus resulting in ΔKE-to-ΔE_WE ratio of 1 eV V⁻¹. Such ratio meant that once the current stabilized, the bulk electrolyte and the meniscus experienced the same electrostatic potential.

Fig. 3 Electric current i (black line) and kinetic energy KE of the C=O peak of C 1s core level (colored dots) as a function of time. Current transient is smoothened for the purpose of clarity. Potential step was initiated at t = 0 s (vertical dashed line). KE expected for 1 eV V⁻¹ ratio is indicated with a horizontal dash-dotted grey line. (a) Oxidative potential step (from E₀ to E₁) and (b) reductive potential step (from E₁ to E₀) in the absence of ferrocene (capacitive processes). (c) Oxidative potential step (from E₀ to E₁) and (d) reductive potential step (f from E₁ to E₀) with 0.2 M ferrocene in the electrolyte (slower faradaic process). (e) Oxidative potential step (from E₀ to E₂) and (f) reductive potential step (from E₂ to E₀) with 0.2 M ferrocene in the electrolyte (faster faradaic process). Red dots in graphs in (d) and (f) indicate the time until which KE remained constant.

The second pair of plots (Fig. 3c and d) shows the data obtained after the same potential step as above, but now in the presence of Fc, producing a faradaic current transient. Two observations are noteworthy here. In contrast with the response of the capacitive process, the ratio of ΔKE-to-ΔE_WE after the oxidative step is seen to deviate from 1 eV V⁻¹; a potential step of 0.5 V results in ΔKE of 0.42 ± 0.01 eV. We note that the presence of Fc in the electrolyte is the only difference between the first and the second pair of plots as the working electrode potentials employed in the two sets of experiments were the same. This result suggests that at the APXPS measuring point, the electrochemical interface is experiencing 80 mV lower potential than the one applied. Furthermore, both current and KE transients follow a similar time dependence upon an oxidative potential step. This is contrasted by a pronounced difference in their time dependence during a reductive potential step, where a 10 s time difference is observed between the reductive potential step and the initial change in the meniscus electrostatic potential as reported by KE(t).

The two phenomena observed above are even more pronounced when the potential was stepped to E₂ (ΔE_WE of 0.85 eV), where the rate of Fc oxidation is expected to be several times faster on the immersed portion of the electrode (Fig. 3e and f). A major deviation from 1 eV V⁻¹ ratio is observed since applying a potential step of 0.85 V resulted in a total ΔKE of 0.47 ± 0.01 eV, a 0.38 V loss in applied potential. As observed for the experiments with slower Fc oxidation rate, i(t) and KE(t) transients exhibit a similar time dependence during an oxidative potential step and a very different time dependence during a reductive potential step. Following the reductive potential step, the value of KE remains constant at ≈1509.97 eV for as long as 100 s before returning to its initial value of 1509.5 eV (i.e. KE value at E₀ prior to stepping to E₂).

The above spectroelectrochemical results point to phenomena consistent with significant ohmic drop in the meniscus as demonstrated in the electrochemical experiments in Fig. 2. As predicted by the meniscus model 1 in Fig. 2d, any current running across the electrochemical interface in the meniscus will be accompanied by the current along the meniscus and will subsequently cause an ohmic overpotential and hence a deviation from the applied potential. Since the equilibrium current for a capacitive process drops to very small values in a few milliseconds after the oxidative potential step from E₀ to E₁, the measured ΔKE is very close to the applied ΔE_WE, i.e. almost no potential loss is observed. This is very different in the presence of a redox-active molecule such as Fc, where non-zero faradaic current flows in quasi-equilibrium. For the Fc systems, faradaic currents are first observed at the current onset potential E_io, which is roughly 0.40 V higher than E₀ (see voltammogram in Fig. 2a). When stepping from E₀ to E₁ (ΔE_WE = 0.5 V) in the Fc-containing system resulted in a measured ΔKE of 0.42 eV. Notably, the magnitude of ΔKE, when converted from eV to V, surpassed the difference between E₀ and E_io merely by 0.02 eV. This meant that, during steady state oxidation when the electrode potential was set to E₁, the electrochemical interface at the APXPS measuring position experienced the electrostatic potential almost equal to the electrostatic potential characteristic of the current onset potential E_io. The remaining fraction of the electrostatic potential difference, i.e. ΔE_WE − ΔKE, was dissipated elsewhere between the WE and RE. Even when the potential was stepped to E₂ (ΔE_WE = 0.85 V), ΔKE amounted to 0.47 eV, which meant that the electrostatic potential at this position on the electrochemical interface only surpassed E_io by 0.07 V.

To explain the observed ΔKE-to-ΔE_WE ratios of less than 1, we estimated ohmic overpotential in the bulk electrolyte by multiplying the known bulk electrolyte resistance of ≈100 Ω with the steady state current (0.005 mA at E₁ and 0.03 mA at E₂) to obtain 0.005 V and 0.03 V for E₁ and E₂, respectively. This meant that the remaining decrease of the overpotential (0.075 V and 0.35 V for E₁ and E₂, respectively, calculated as E_WE − E_io = iR_b) occurred between the bulk electrolyte and the APXPS measuring point due to the iR drop in the meniscus. The reason why ΔKE moved past the current onset potential E_io by only a fraction of the applied overpotential is easily inferred from the meniscus geometry and the current distribution in the meniscus (see current flow lines in Fig. 4b). According to the model, the higher we are up on the meniscus, the larger is the iR drop and the bigger is the deviation from the set potential at the electrochemical interface. Consequently, only a minor portion of the applied overpotential should be felt at the APXPS measuring point, which is in agreement with what is experimentally observed when applying E₂ instead of E₁ (E₂ − E₁ = 0.35 V), namely, ΔKE increased only by 0.05 eV. Using the meniscus model 2 to further quantify the observed effects on the electrode potential into reaction rates, the rate of the faradaic reaction under kinetic regime conditions is estimated to be between 100- and 1000-fold slower in the meniscus than in the bulk electrolyte. The disparity in the rates of Fc oxidation between the bulk electrolyte and the meniscus is illustrated in Fig. 4b.

Fig. 4 (a) Meniscus model 1 of the investigated system; the capacitance and the resistance values displayed next to their corresponding circuit elements were obtained by fitting meniscus model 1 to the current transient shown in Fig. 2a. (b) Scheme of electrochemical processes in the meniscus and in the bulk. The rate of Fc redox is significantly slower in the meniscus, which is indicated by a thinner reaction arrow (blue). Encircled + and – illustrate ionic migration. Smaller size of migration arrows (black) in the meniscus indicates a larger resistance to ionic migration in the meniscus as opposed to the bulk electrolyte. Red shading of the meniscus indicates the slow-down of the target electrochemical reaction (Fc redox) as we move upwards along the meniscus. Grey curved arrows directed from the meniscus to the WE are current flow lines visualizing the current density and direction described in meniscus model 2 (flow lines are not to scale). (c) Approximate electrostatic potential profiles ϕ(r) along charge carrier path r at the end of the oxidative potential step for the three spectroelectrochemical experiments presented in this work (Fig. 2a, c and e): in thermodynamic equilibrium at E₁ (black), during steady state oxidation at E₁ (red) and during steady state oxidation at E₂ (blue). Green dashed profile represents electrostatic potential profile prior to the oxidative potential step, i.e. in thermodynamic equilibrium at E₀. Profiles were drawn in accordance with a combination of the measured ΔKE, calculated bulk electrolyte ohmic overpotential and the measured WE-RE potential difference. The profile in the meniscus (between the bulk electrolyte and the APXPS measuring point) is for the red and the blue profile approximated based on Butler–Volmer current-overpotential relation.

We can make similar arguments to explain our observations for the behavior of KE signal after subsequent reductive potential step in all three cases. During a purely capacitive response (Fig. 3b), the KE value returned to its initial value of 1509.5 eV when the system reached its steady state (within less than 5 s). The measured ΔKE equaled the applied ΔE_WE, thus matching the 1 eV V⁻¹ ratio that had already been observed for the capacitive response to an oxidative potential step. As alluded to above, in the presence of Fc, fundamental difference was observed between an oxidative and a reductive potential step. Namely, the KE value remained almost unchanged at 1509.92 eV and 1509.97 eV for 10 s and 100 s for the reductive potential jump to E₀ from E₁ and E₂, respectively, before dropping off to the expected 1509.5 eV. To explain such KE time dependence, it is important to realize that prior to a reductive potential step, the system was in an oxidation steady state for 5 min during which we have built some inventory of Fc⁺ in the meniscus. As we apply a reductive potential step to a system in steady state oxidation, the current direction reverses and the large iR drop along the meniscus causes the potential at the APXPS measuring point to retain almost the same value, thus resulting in no change of KE immediately after the potential step. The same potential (and with that the KE value of 1509.92 or 1509.97 eV) is maintained until no faradaic current flows across the electrochemical interface at the APXPS measuring point, i.e. until almost all Fc⁺ in the meniscus is consumed. The time when that happens, which corresponds to the drop-off of KE to 1509.5 eV, depends on the amount of Fc⁺ formed during the preceding oxidative step (note S17 in the ESI†), which is also reflected in the difference between KE(t) transients in Fig. 3d and f. Since a larger amount of Fc⁺ formed in the oxidative step to E₂ than to E₁, the time where KE maintained a constant value (1509.92 eV for E₁ and 1509.97 eV for E₂) was longer for the reductive potential step from E₂ as opposed to a step from E₁.

The qualitative insights into meniscus mass transport gained in this study are generally applicable to any electrolyte where the magnitude of the iR drop depends on the conductivity of the electrolyte, the length of the meniscus and its thickness. Importantly, mass transport limitations are specific for each dip-and-pull system and depend on the meniscus shape, probing position, etc.^{13,15,16,20,22,28} However, it is generally expected that mass transport limitations and the related issues highlighted in this study (most notably, a decrease in the rate of faradaic processes in the meniscus) will be substantially exacerbated in operando APXPS experiments probing the solid/liquid interface.

For practical purposes, electrochemical processes can be divided into two groups based on their current transient or, in other words, based on how significantly the iR drop affects meniscus electrochemistry during APXPS measurements. When only capacitive or pseudocapacitive processes occur at the electrode surface, iR drop is less likely to be problematic since the resulting current transients typically decay to 0 on short time scales; much shorter than the time required for a single APXPS measurement. Contrastingly, faradaic processes have much longer time scales, which means that the iR drop can have a profound impact on the meniscus electrochemistry. Hence, it is crucial to monitor the iR drop magnitude in order to accurately interpret experimental data. As explained and demonstrated above, this can be done through a comparison of ΔKE at the APXPS measuring point and the change in the electrode potential ΔE_WE. With an electronically conducting WE and by assuming that RE is stable, a ΔKE-to-ΔE_WE ratio of less than 1 can indicate an iR drop along the meniscus. When this is the case, it is important to carefully consider the effect of the iR drop on the meniscus electrochemistry. Importantly, in experiments when measurement artefacts due to the iR drop should be entirely avoided, the method should be used as in situ rather than operando method, i.e. electrodes should be kept in the dipped position while the electrochemical processes are on-going and should only be pulled up to the measurement position when the reaction has stopped.

Conclusions

This work investigated mass transport in a carbonate electrolyte meniscus formed on a gold electrode by the dip-and-pull method. By combining chronoamperometry and operando APXPS with a purposefully constructed transmission line model, the resistance within the meniscus was found to be about 1000 times larger than that of the bulk electrolyte. The study revealed that a severe iR drop occurs in the meniscus. The effect of the iR drop on the meniscus electrochemistry was quantified using the developed transmission line model: the rate of the model faradaic process (Fc redox) was estimated to be as much as two to three orders of magnitude slower in the meniscus than in the bulk electrolyte. Importantly, increasing the applied overpotential enhances the rate of the faradaic process in the bulk, while the faradaic process rate in the meniscus increases to a much lesser extent due to an increase in the meniscus iR drop. Based on the findings, we discuss the impact of an iR drop for different classes of electrochemical processes (capacitive, faradaic) and propose in situ experiments with electrodes immersed throughout the duration of an electrochemical process when the experimental artifacts due to the iR-drop must be avoided at all costs. Finally, we strongly advise monitoring of ΔKE-to-ΔE_WE ratio in operando dip-and-pull APXPS experiments with a grounded and electronically conducting WE and a stable RE, since a deviation from 1 : 1 ratio could be indicative of an iR drop in the meniscus. Estimating the iR drop and correcting for its impact on the meniscus electrochemistry is key for accurate interpretation of such operando experiments.

Author contributions

A. K., D. S. and M. H. conceptualized the project. A. K., L. K., Q. L., T. E., R. T. and M. H. conducted experiments, A. K., D. S., O. V., M. G., T. E. and M. H. interpreted data. A. K. wrote the manuscript and all authors reviewed it.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge MAX IV Laboratory for time on HIPPIE Beamline under Proposal 20230767. Research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496. A. K., O. V., D. S., R. D. and M. G. gratefully acknowledge financial support by the Slovenian Research and Innovation Agency ARIS (core program funding P2-0423 and P2-0393 and project funding J7-50227). T. E., L. K., Q. L. and M. H. gratefully acknowledge financial support from the Swedish Research Council (project number 2020-04512 and 2022-06076).

References

1. A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical methods: fundamentals and applications, John Wiley & Sons, 3rd edn, 2022.
2. C. H. Wu, R. S. Weatherup and M. B. Salmeron, Probing electrode/electrolyte interfaces in situ by X-ray spectroscopies: old methods, new tricks, Phys. Chem. Chem. Phys., 2015, 17, 30229–30239.
3. W. Schmickler and E. Santos, Interfacial electrochemistry, Springer Science & Business Media, 2010.
4. M. F. Lichterman, S. Hu, M. H. Richter, E. J. Crumlin, S. Axnanda, M. Favaro, W. Drisdell, Z. Hussain, T. Mayer, B. S. Brunschwig, N. S. Lewis, Z. Liu and H. J. Lewerenz, Direct observation of the energetics at a semiconductor/liquid junction by operando X-ray photoelectron spectroscopy, Energy Environ. Sci., 2015, 8, 2409–2416.
5. M. Favaro, C. Valero-Vidal, J. Eichhorn, F. M. Toma, P. N. Ross, J. Yano, Z. Liu and E. J. Crumlin, Elucidating the alkaline oxygen evolution reaction mechanism on platinum, J. Mater. Chem. A, 2017, 5, 11634–11643.
6. M. Favaro, B. Jeong, P. N. Ross, J. Yano, Z. Hussain, Z. Liu and E. J. Crumlin, Unravelling the electrochemical double layer by direct probing of the solid/liquid interface, Nat. Commun., 2016, 7, 12695.
7. L. Trotochaud, A. R. Head, O. Karslioǧlu, L. Kyhl and H. Bluhm, Ambient pressure photoelectron spectroscopy: practical considerations and experimental frontiers, J. Phys.: Condens. Matter, 2017, 29, 053002.
8. M. Salmeron, From Surfaces to Interfaces: Ambient Pressure XPS and Beyond, Top. Catal., 2018, 61, 2044–2051.
9. T. S. Wesley, M. J. Hülsey, K. S. Westendorff, N. B. Lewis, E. J. Crumlin, Y. Román-Leshkov and Y. Surendranath, Metal nanoparticles supported on a nonconductive oxide undergo pH-dependent spontaneous polarization, Chem. Sci., 2023, 14, 7154–7160.
10. S. Louisia, M. T. M. Koper and R. V. Mom, Prospects for electrochemical X-ray photoelectron spectroscopy as a powerful electrochemical interface characterization technique, Curr. Opin. Electrochem., 2024, 45, 101462.
11. D. E. Starr, M. Favaro, F. F. Abdi, H. Bluhm, E. J. Crumlin and R. van de Krol, Combined soft and hard X-ray ambient pressure photoelectron spectroscopy studies of semiconductor/electrolyte interfaces, J. Electron Spectrosc. Relat. Phenom., 2017, 221, 106–115.
12. S. Axnanda, E. J. Crumlin, B. Mao, S. Rani, R. Chang, P. G. Karlsson, M. O. M. Edwards, M. Lundqvist, R. Moberg, P. Ross, Z. Hussain and Z. Liu, Using ‘tender’ X-ray Ambient Pressure X-Ray Photoelectron Spectroscopy as A Direct Probe of Solid-Liquid Interface, Sci. Rep., 2015, 5, 9788.
13. H. Ali-Löytty, M. W. Louie, M. R. Singh, L. Li, H. G. Sanchez Casalongue, H. Ogasawara, E. J. Crumlin, Z. Liu, A. T. Bell, A. Nilsson and D. Friebel, Ambient-Pressure XPS Study of a Ni-Fe Electrocatalyst for the Oxygen Evolution Reaction, J. Phys. Chem. C, 2016, 120, 2247–2253.
14. I. Källquist, F. Lindgren, M. T. Lee, A. Shavorskiy, K. Edström, H. Rensmo, L. Nyholm, J. Maibach and M. Hahlin, Probing Electrochemical Potential Differences over the Solid/Liquid Interface in Li-Ion Battery Model Systems, ACS Appl. Mater. Interfaces, 2021, 13, 32989–32996.
15. K. A. Stoerzinger, M. Favaro, P. N. Ross, Z. Hussain, Z. Liu, J. Yano and E. J. Crumlin, Stabilizing the Meniscus for Operando Characterization of Platinum During the Electrolyte-Consuming Alkaline Oxygen Evolution Reaction, Top. Catal., 2018, 61, 2152–2160.
16. R. H. Temperton, A. Kawde, A. Eriksson, W. Wang, E. Kokkonen, R. Jones, S. M. Gericke, S. Zhu, W. Quevedo, R. Seidel, J. Schnadt, A. Shavorskiy, P. Persson and J. Uhlig, Dip-and-pull ambient pressure photoelectron spectroscopy as a spectroelectrochemistry tool for probing molecular redox processes, J. Chem. Phys., 2022, 157(24).
17. M. Favaro, P. C. J. Clark, M. J. Sear, M. Johansson, S. Maehl, R. van de Krol and D. E. Starr, Spectroscopic analysis with tender X-rays: SpAnTeX, a new AP-HAXPES end-station at BESSY II, Surf. Sci., 2021, 713, 121903.
18. Z. Novotny, D. Aegerter, N. Comini, B. Tobler, L. Artiglia, U. Maier, T. Moehl, E. Fabbri, T. Huthwelker, T. J. Schmidt, M. Ammann, J. A. Van Bokhoven, J. Raabe and J. Osterwalder, Probing the solid-liquid interface with tender X rays: a new ambient-pressure X-ray photoelectron spectroscopy endstation at the Swiss Light Source, Rev. Sci. Instrum., 2020, 91, 023103.
19. S. Zhu, M. Scardamaglia, J. Knudsen, R. Sankari, H. Tarawneh, R. Temperton, L. Pickworth, F. Cavalca, C. Wang, H. Tissot, J. Weissenrieder, B. Hagman, J. Gustafson, S. Kaya, F. Lindgren, I. Källquist, J. Maibach, M. Hahlin, V. Boix, T. Gallo, F. Rehman, G. D’Acunto, J. Schnadt and A. Shavorskiy, HIPPIE: a new platform for ambient-pressure X-ray photoelectron spectroscopy at the MAX IV Laboratory, J. Synchrotron Radiat., 2021, 28, 624–636.
20. J. J. Velasco-Velez, L. J. Falling, D. Bernsmeier, M. J. Sear, P. C. J. Clark, T. S. Chan, E. Stotz, M. Hävecker, R. Kraehnert, A. Knop-Gericke, C. H. Chuang, D. E. Starr, M. Favaro and R. V. Mom, A comparative study of electrochemical cells for in situ X-ray spectroscopies in the soft and tender X-ray range, J. Phys. D: Appl. Phys., 2021, 54, 124003.
21. Y. Han, S. Axnanda, E. J. Crumlin, R. Chang, B. Mao, Z. Hussain, P. N. Ross, Y. Li and Z. Liu, Observing the Electrochemical Oxidation of Co Metal at the Solid/Liquid Interface Using Ambient Pressure X-ray Photoelectron Spectroscopy, J. Phys. Chem. B, 2018, 122, 666–671.
22. A. Shavorskiy, X. Ye, O. Karslloǧlu, A. D. Poletayev, M. Hartl, I. Zegkinoglou, L. Trotochaud, S. Nemšák, C. M. Schneider, E. J. Crumlin, S. Axnanda, Z. Liu, P. N. Ross, W. Chueh and H. Bluhm, Direct Mapping of Band Positions in Doped and Undoped Hematite during Photoelectrochemical Water Splitting, J. Phys. Chem. Lett., 2017, 8, 5579–5586.
23. I. Källquist, T. Ericson, F. Lindgren, H. Chen, A. Shavorskiy, J. Maibach and M. Hahlin, Potentials in Li-Ion Batteries Probed by Operando Ambient Pressure Photoelectron Spectroscopy, ACS Appl. Mater. Interfaces, 2022, 14, 6465–6475.
24. F. Capone, J. Sottmann, V. Meunier, L. Pérez Ramírez, A. Grimaud, A. Iadecola, M. Scardamaglia, J.-P. Rueff and R. Dedryvère, Operando observation of the dynamic SEI formation on a carbonaceous electrode by near-ambient pressure XPS, Energy Environ. Sci., 2024, 17, 11509–11519.
25. A. Shavorskiy, X. Ye, O. Karslloǧlu, A. D. Poletayev, M. Hartl, I. Zegkinoglou, L. Trotochaud, S. Nemšák, C. M. Schneider, E. J. Crumlin, S. Axnanda, Z. Liu, P. N. Ross, W. Chueh and H. Bluhm, Direct Mapping of Band Positions in Doped and Undoped Hematite during Photoelectrochemical Water Splitting, J. Phys. Chem. Lett., 2017, 8, 5579–5586.
26. D. Teschner, J. Plescher, S. Piccinin, T. E. Jones, A. Hammud, F. Schmidt, A. Knop-Gericke, H. Bluhm and A. Shavorskiy, Understanding Anomalous Gas-Phase Peak Shifts in Dip-and-Pull Ambient Pressure XPS Experiments, J. Phys. Chem. C, 2024, 128, 7096–7105.
27. M. Favaro, F. F. Abdi, E. J. Crumlin, Z. Liu, R. van de Krol and D. E. Starr, Interface Science Using Ambient Pressure Hard X-ray Photoelectron Spectroscopy, Surfaces, 2019, 2, 78–99.
28. M. Favaro, Stochastic Analysis of Electron Transfer and Mass Transport in Confined Solid/Liquid Interfaces, Surfaces, 2020, 3, 392–407.
29. H. S. Kim, T. Yoon, Y. Kim, S. Hwang, J. H. Ryu and S. M. Oh, Increase of both solubility and working voltage by acetyl substitution on ferrocene for non-aqueous flow battery, Electrochem. Commun., 2016, 69, 72–75.
30. K. Nasirzadeh, R. Neueder and W. Kunz, Vapor pressures of propylene carbonate and N,N-dimethylacetamide, J. Chem. Eng. Data, 2005, 50, 26–28.
31. S. W. Boettcher, S. Z. Oener, M. C. Lonergan, Y. Surendranath, S. Ardo, C. Brozek and P. A. Kempler, Potentially Confusing: Potentials in Electrochemistry, ACS Energy Lett., 2021, 6, 261–266.
32. N. Mozhzhukhina and E. J. Calvo, Perspective—The Correct Assessment of Standard Potentials of Reference Electrodes in Non-Aqueous Solution, J. Electrochem. Soc., 2017, 164, A2295–A2297.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00168d

---