Revealing the role of ripples in phonon modes for MoS2 and MoSe2: insights from molecular dynamics and machine learning

Abstract

Interatomic potentials for single-layer MoS₂ and MoSe₂ were developed by training an artificial neural network with a reference data set generated using density functional theory. High accuracy was obtained for the phonon dispersion as well as a direct correspondence of the predicted Raman and infrared (IR) active modes (between 100 cm⁻¹ and 600 cm⁻¹) with molecular dynamics results. The ability to perform simulations with thousands of atoms allowed our system to accommodate spontaneous fluctuations in height and ripples propagating in the material. As a result of these ripples, our simulations suggest the existence of IR activity in the E′ and 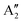modes with inverted polarization, as well as the presence of IR activity at frequencies close to E′′ and 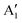, which are generally considered IR-inactive. The rippling of the system is expected to be responsible for breaking the 3-fold rotational symmetry around the z-axis of the material, resulting in non-trivial IR modes.