 Open Access Article
Open Access ArticleEnabling hydrogen chemisorption on charged graphene†
Patrick T.
Shea
,
Andrew J. E.
Rowberg
 and
Brandon C.
Wood
and
Brandon C.
Wood
 *
*
Quantum Simulations Group (QSG) and Laboratory for Energy Applications for the Future (LEAF), Lawrence Livermore National Laboratory, Livermore, California 94550, USA. E-mail: wood37@llnl.gov
First published on 12th June 2025
Abstract
Two-dimensional (2D) materials, including graphitic derivatives, have long been of interest for hydrogen storage applications, due to their high theoretical storage capacity, low weight, and other useful properties. However, poor kinetics for hydrogen adsorption and surface diffusion as part of the proposed spillover process for hydrogenation have limited their technological potential. Here, we use first-principles calculations to study electronic doping as a means to improve hydrogen chemisorption on graphene, which we use here as a proxy for graphitic derivatives more broadly. We find that positively charged graphene sheets have vastly improved kinetics for hydrogen diffusion and adsorption, while they limit unwanted hydrogen desorption. This combination of effects should favor hydrogen chemisorption via spillover. We connect these trends to the C–H bond, which introduces states near the Fermi level. These states are depopulated as electrons are removed, thereby lowering the bond energy and permitting more facile movement of hydrogen. Our results suggest that spillover mechanisms for hydrogen chemisorption should be revisited if strategies to apply a large charge to graphitic systems can be realized. Moreover, switchable application of the charge may lead to the reversible chemisorption of hydrogen. While the large magnitude of charging required suggests that graphene itself may not be suitable for reversible hydrogen chemisorption, the factors we identify and discuss could significantly boost the prospects of graphitic derivatives and other 2D or layered materials for hydrogen storage applications.
1 Introduction
Hydrogen continues to gain attention as a superb energy carrier;1 however, storage and delivery of H2 gas remain costly and inefficient, limiting widespread deployment. Among the proposed storage options, chemisorption or physisorption within a solid matrix has the best overall potential for exceeding current volumetric capacity limitations associated with pressurized gas tanks.2 Solid-state storage can also reduce tank pressures, thereby lowering costs associated with compression and delivery and opening up the possibility of utilizing lower-cost materials for tank designs.3 A wide variety of materials options have been considered for hydrogen storage,4 including interstitial and complex metal hydrides,5–7 metal–organic framework materials,8,9 and porous carbon matrix materials.10–13In principle, porous carbon materials are particularly attractive for gas storage because of their relatively low weight, high surface area, and tunable density.14 Carbon is also inexpensive and can be sourced from multiple earth-abundant feedstocks. Furthermore, many low-dimensional carbon derivatives exhibit excellent thermal conductivity, which can improve heat management during cycling.15 In recent decades, significant advances have been made in high-surface-area carbon synthesis, which offers tunability of chemical and structural properties.16
Nevertheless, despite the adoption of porous carbon materials as viable options for storing natural gas,17 realizing storage of hydrogen in carbon matrices has proved to be far more difficult. In general, physisorption of H2 molecules on two-dimensional (2D) graphitic derivatives is far too weak for practical use, with binding energies under 6 kJ mol−1 H2.18 Proper tuning of pore sizes can provide some benefit, as can the introduction of chemical functionalization,19–22 structural rippling,23,24 point defects,25,26 and Lewis acid complexes27,28 that alter local binding properties. However, the electronic influence of local modifications is typically short ranged, requiring unreasonably high densities of modifiers to alter uptake properties meaningfully. In addition, specific control of functional chemistry can be difficult in high-surface-area materials.
An alternative to hydrogen physisorption on porous carbon materials is to rely on chemisorption, generally via a spillover process using a catalyst that can efficiently dissociate H2 to form C–H bonds.29,30 In this scenario, hydrogen atoms must diffuse across the surface to fill available binding sites. Although this approach promises much larger storage capacity and stronger binding than physisorption, thereby enabling higher-temperature storage and a broader usable pressure range, it is likewise problematic. First of all, hydrogen atoms diffuse rather slowly on graphene-like surfaces at temperatures for which storage can be accessed, with a relatively large diffusion energy barrier between 0.78 and 1.01 eV.31–34 As a result, the H2 dissociation catalyst must be deposited with very high density, which adds weight and complicates synthetic protocols for combatting aggregation. Second, the high diffusion barrier can cause surface hydrogen migration to compete with H2 desorption, which occurs with a comparable energy barrier of 1.1 eV;35 the competing likelihood of desorption further decreases the effective hydrogen surface coverage. Third, the C–H bond is generally too strong, making H2 release under reasonable conditions difficult. For these reasons, the U.S. Department of Energy has determined that materials that rely on spillover processes are unlikely to achieve target storage densities without further modifications.36
In considering possible enhancement strategies that could enable viable physisorption or spillover-based chemisorption in carbon materials, a common factor is the desire to tune the electronic properties throughout the entire matrix. For physisorption, one would wish to strengthen the H2 interaction energy beyond local neighbor effects. For chemisorption, it would be desirable to weaken the C–H interaction and improve surface diffusion kinetics. Recognizing that many graphene derivatives are highly electronically conductive, one possible way to achieve these objectives would be to alter the charge or electrical potential of the material, i.e., via electronic doping. Dopants have been shown to have an appreciable effect on the electronic structure and density of states (DOS) of graphene,37–39 and their incorporation may induce an electric field that could further modify sorption properties. Indeed, several previous first-principles studies have demonstrated that an applied electric field may improve the absorption of hydrogen on graphene40,41 and other 2D materials.42
A number of previous theoretical and experimental studies have explored the possible effects of electronic doping on H2 and H binding on graphene and its derivatives.43 In general, these studies have achieved electronic doping via substitutional chemistry within the lattice (e.g., by BC− or NC+ substitutional species),20,44,45 which shift the Fermi level. However, it is difficult to decouple the local chemical effects of these dopant atoms from wholesale changes to electronic structure. In addition, most experimental studies have generally limited dopant incorporation to relatively dilute concentrations, since elemental substitution in high concentrations without aggregation presents significant synthesis challenges.46–48 Furthermore, significant disagreement remains regarding the magnitude and origin of any observed effects.
In this paper, we systematically explore the effects of electronic doping, using density-functional theory (DFT) calculations to induce electron depletion directly into the simulation cell, mimicking the application of an external bias. Doing so allows us to probe the effects of charge, voltage, and electric field on hydrogen chemisorption and physisorption processes in graphene, decoupled from chemical contributions as would be introduced through doping. We find that if sufficient electron depletion can be introduced, the hydrogen storage properties of graphitic systems can be altered significantly, potentially placing such materials within a window of viability for either physisorption or spillover-based chemisorption. Admittedly, the magnitude of charging required to make hydrogen chemisorption thermodynamically favorable on graphene is very large, likely exceeding what can reasonably be achieved. Thus, any direct application of our results to practical hydrogen storage systems will likely require systems where lower levels of applied charge are needed. Nonetheless, our results suggest that similar materials are worth exploring for hydrogen storage if practical experimental avenues for high levels of external charging can be identified.
2 Computational methods
DFT49 calculations were performed using the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE).50 The plane wave pseudopotential approach was used with ultrasoft pseudopotentials,51 as implemented in the Quantum ESPRESSO software package.52 For atomic relaxations, energies were converged to within 10−4 eV, and atomic forces were considered converged when less than 1 meV Å−1. Transition states for diffusion and desorption and their corresponding energetic barriers were identified using the nudged elastic band (NEB) method with five intermediate images.53 To model isolated chemisorbed hydrogen atoms and dimers, a 6 × 6 supercell of graphene (72 atoms) was constructed with a vacuum spacing of 12 Å to avoid interactions between periodically repeating layers. We used our relaxed lattice constant of 2.470 Å, which is very close to the experimental lattice constant of graphene, 2.461 Å.54 The Brillouin zone was sampled using a 6 × 6 × 1 k-point grid centered on the Γ point.The application of a potential bias and accompanying electric field to the graphene surface was modelled using the effective screening medium (ESM) method.55,56 The ESM method provides a consistent treatment of the electrostatic potential of a charged slab geometry by placing a counter-electrode held at constant potential above the slab. This counter-electrode contains a compensating charge to maintain overall charge neutrality of the simulation cell and to ensure simulation stability. In contrast to the typical method of treating a charged periodic system, where a compensating uniform charge is added, this approach correctly captures the electric field induced between the charged surface and counter-electrode. This electric field is applied only to one side of the graphene sheet; except where otherwise noted, our calculations are conducted on the side of the sheet directly exposed to the field. The electric field introduces a net force distributed uniformly on the charged graphene sheet; geometry optimizations were performed by keeping the center of mass of the graphene sheet fixed in the direction normal to the surface. If the applied charge is less uniformly distributed, as may be the case for chemical doping, the effects we consider may be more localized. We consider applied charges up to +4e per simulation cell, corresponding to a sheet charge density of 7.6 × 1015e cm−2. We restrict our discussion to systems exhibiting electron depletion (i.e., having a positive charge), as electron accumulation is generally more challenging to treat with the ESM method. However, our analysis of graphene sheets with small degrees of electron accumulation (up to −1e per simulation cell) show its effect generally to be less beneficial; these results are briefly discussed in the ESI.†
3 Results
3.1 Energetics of chemisorption
In Fig. 1, we show the structure of adsorbed hydrogen atoms (panel a) and H–H dimers (panels b–d) on the graphene surface. Graphene is characterized by two sublattices (A and B) of carbon atoms (shown in different colors in Fig. 1), such that for a carbon atom on sublattice A, all of its nearest neighbors reside on sublattice B. Previous studies have shown a pronounced energetic benefit for pairs of hydrogen adatoms to bond with carbon atoms belonging to different sublattices, even over a long range.57,58 | ||
| Fig. 1 (a) Geometry of a single chemisorbed hydrogen atom on graphene, with carbon sublattices A and B colored and labeled (as CA and CB, respectively). H–H dimers (b) D1, (c) D2, and (d) D3 are also shown. Structural images were generated with the VESTA3 software.59 | ||
Fig. 1b and d depict two such configurations, D1 and D3, while Fig. 1c depicts configuration D2, in which hydrogen adatoms bond to nearest-neighbor carbon atoms on the same sublattice. In the terminology of organic chemistry, D1 corresponds to the “ortho” configuration, D2 corresponds to the “meta” configuration, and D3 corresponds to the “para” configuration.
Fig. 2 summarizes our findings on the effect of excess surface charge on the energy barriers associated with hydrogen migration on a graphene layer. To begin, Fig. 2a shows energy barriers for the diffusion of single chemisorbed hydrogen atoms (S → S′), along with atoms in the dimer configurations depicted in Fig. 1b–d. It is notable that the diffusion barriers are principally a function of whether H atoms are moving to a configuration where they occupy the same sublattice (D2), or to configurations where they occupy different sublattices (D1 or D3). D1 and D3 differ only in terms of H–H proximity, but they have nearly identical diffusion barriers when moving to the D2 configuration. The reverse barriers are also nearly identical. This result suggests that H–H correlation effects are themselves not particularly strong. As a consequence, for higher surface H concentrations, we expect similar trends to hold, where H migration will favor the occupation of different sublattices as much as possible.
 | ||
| Fig. 2 (a) Migration barriers as a function of system charge for adsorbed atomic hydrogen and dimers D1, D2, and D3, as shown in Fig. 1. (b) Adsorption energies (per H atom) relative to gas phase H2 for the same configurations. (c) Desorption energy barriers for single hydrogen atoms (S is bound to the graphene surface, and H* is desorbed) and H–H dimer D3. | ||
For the single atom, the diffusion barrier decreases as the charge is made more positive (i.e., as graphene is depleted of electrons), dropping from 1.02 eV for the charge-neutral system to 0.52 eV for the system with charge +2e per hydrogen atom. The barriers for diffusion away from the two strongly bound dimer configurations, D1 and D3, also decrease over the same range of charges, from 1.58 eV to approximately 0.7 eV. On the other hand, the barrier for diffusion away from the weakly bound dimer, D2, increases slightly from 0.5 to 0.65 eV. At large positive charges, the diffusion barriers for all three dimer configurations considered here approach similar values, suggesting a flattened potential energy landscape for adsorbed hydrogen and improved diffusion kinetics relative to the neutral graphene surface. We expect that this impact of applied charge will also apply to more heavily H-saturated surfaces, with the caveat that nearly complete H adsorption will mean that there are no migration pathways available for H diffusion.
Next, in Fig. 2b, we plot the adsorption energies for the single atom and dimer configurations relative to gas phase H2. This energy is a purely thermodynamic quantity, defined as the energy difference per H atom between atomic H or molecular H2 above the surface and the adsorbed configuration, i.e.:
| nEads = E(Haboven) − E(nHads). | (1) |
As the surface charge becomes more positive, the adsorption energy decreases, with molecular chemisorption eventually becoming energetically favored over gas phase H2 at charges of +2e per hydrogen atom. The energies of the three dimer configurations also converge at high charge. Thus, while adsorption becomes increasingly favorable in the charged system, the interaction strength between adatoms decreases considerably.
Lastly, Fig. 2c shows the energy barriers for desorption of atomic hydrogen and the D3 H–H dimer. These kinetic barriers are computed using the NEB method, focusing on pathways connecting adsorbed and desorbed H or H2. The kinetic barrier for adsorption is simply the sum of the desorption barrier and nEads; thus, it follows that Eads represents the degree of hysteresis between adsorption and desorption, which in turn is related to the energy difference between breaking H–H bonds and C–H bonds. The energy barriers for desorption increase significantly with increasing positive surface charge. In conjunction with the smaller diffusion barriers, it follows that adsorbed hydrogen will be able to spread out and uniformly coat the graphene surface without desorbing. We also calculated barriers for adsorption of molecular H2 and isolated hydrogen atoms, which we show in Fig. S2 of the ESI.† The adsorption barrier for molecular H2 decreases with increasing positive charge, while that for isolated hydrogen atoms stays relatively constant, further implying improved kinetics for hydrogen uptake.
Taken together, the results of Fig. 2 suggest that applying a positive charge to graphene should significantly improve its performance as a hydrogen storage material. Upon charging, chemisorbed hydrogen is more strongly bound to the surface, such that adsorption from the gas phase is faster, while desorption is suppressed. Surface diffusion, which is critical to the spillover process, proceeds more readily due to the weakened interaction between hydrogen adatoms. The changes in the energetics of chemisorption are related to changes in the electronic structure of graphene as it is electron-depleted or enriched, as well as electrostatic effects from the electric field above the surface. We examine both of these factors in the following sections.
3.2 Electronic structure effects
Fig. 3a shows the projected DOS (PDOS) for chemisorbed hydrogen on graphene [Fig. 1a], with which we can examine the pertinent atoms separately. Two types of hybridized orbitals are formed involving the hydrogen atom: one is hybridized with the in-plane π orbitals of graphene, and the other with the out-of-plane σ orbitals. The hybridized σ orbitals are located about 8 eV below the Fermi level (EF), where a spike in the PDOS can be observed for both atoms involved in the C–H bond. As seen in the inset isosurface, these states are delocalized over the graphene surface. The π orbitals have energies right around EF, where one of the spin channels is filled (“Spin up”) and the other is empty (“Spin down”). In contrast to the σ orbitals, the π orbital charge density is highly concentrated on the hydrogen atom, with smaller peaks on carbon atoms belonging to the opposite sublattice. | ||
| Fig. 3 (a) Projected DOS for neutral graphene with a single chemisorbed hydrogen atom in the stable configuration [shown in Fig. 1a], with isosurfaces of the lowest- and highest-energy occupied states of the C–H bond shown as insets. Projections are shown for hydrogen, carbon bonded to hydrogen [labeled C(H)], and an average over all carbon atoms not bonded to hydrogen. (b) PDOS for the high-energy saddle-point configuration during single-atom hydrogen diffusion across the surface. (c) DOS of the D2 [Fig. 1c] and D3 [Fig. 1d] H–H dimer configurations on graphene. | ||
Because the π orbitals lie at EF, they will be depopulated first as electrons are removed, making the C–H bonds easier to dissociate. Conversely, if electrons are added, the orbitals in the second spin channel will be populated, thereby strengthening the C–H bond. The weakening of the C–H bond with increasing positive charge helps to explain the improved energetics for diffusion and adsorption of hydrogen on graphene, as shown in Fig. 2.
The lowering of the energy barrier for diffusion upon charging [Fig. 2a] can be understood by examining the electronic structure of the high-energy saddle point configuration of the diffusion pathway. To that end, we plot the PDOS for the transition state of single-atom hydrogen diffusion in Fig. 3b. In contrast to Fig. 3a, the localized π states are not present in the saddle point configuration; instead, the higher-lying conduction band states of graphene are partially filled. On account of their high energies, depopulating these states by introducing positive charge will reduce the migration barrier associated with hydrogen diffusion.
To extend our analysis to surface H–H dimers, we plot the DOS for the D2 and D3 configurations in Fig. 3c. For the D2 configuration [Fig. 1c], in which hydrogen atoms are adsorbed on the same graphene sublattice, the DOS near EF resembles that of a single chemisorbed hydrogen atom, i.e. π orbitals at EF with only one spin channel occupied [Fig. 3a]. This similarity suggests that the H–H interaction is very weak, which follows from our examination of the isosurface in Fig. 3a: the π states are localized on the chemisorbed hydrogen, along with carbon atoms of the opposite sublattice; ergo, there should be little or no interaction between hydrogen atoms chemisorbed on the same sublattice.
This analysis is further born out by examining the D3 configuration [Fig. 1d], in which the hydrogen atoms are adsorbed on different sublattices. Here, the π orbitals centered on the two hydrogen atoms combine and are split into broader occupied and unoccupied orbitals centered approximately at energies EF ± 0.6 eV. This shift in energy is on par with the energy difference we calculate between the D2 and D3 configurations (D3 is 0.55 eV lower in energy than D2). The large energy difference between H–H dimers with hydrogen atoms on the same sublattice and those with hydrogen atoms on different sublattices is thus mediated by the interaction between π orbitals. As electrons are removed from the system and these orbitals are depopulated, the energy difference between these different configurations decreases and eventually becomes negligible, as seen in Fig. 2b. Clearly, this effect on the electronic structure of graphene is among the most critical in dictating the impact we observe on hydrogen adsorption and migration.
3.3 Factors influencing the adsorption energy
The C–H bond for chemisorbed hydrogen is polar, with a dipole moment pointing from carbon toward hydrogen. Thus, the system energy should be reduced for a field pointing away from the positively charged surface. As we noted previously, the ESM method creates a counter-electrode on one side of the graphene sheet, where it establishes an electric field. The contribution of the electrostatic effect on hydrogen adsorption can therefore be isolated by placing hydrogen on the opposite side of the surface to the counter-electrode, so that it is mostly shielded from the induced electric field.In Fig. 4, we plot the contributions to adsorption energy for a single atom of hydrogen exclusively from the electric field, and from the overall electrostatic effect, including both charge and the electric field. The energy decreases significantly when both the electric field and charge are included, i.e., when hydrogen is placed on the in-field side of the graphene sheet, as for the data shown in Fig. 2b. Taking the adsorption energy for atomic hydrogen adsorbed to the in-field side [Fig. 2b] and subtracting the adsorption energy for hydrogen adsorbed to the out-of-field side allows us to show quantitatively how much the electric field influences the change in energy, excluding charge effects. This difference is shown in Fig. 4. As can be seen, the field decreases the adsorption energy, and this effect becomes more pronounced as the charge is increased. However, this effect accounts for roughly 25–30% of the overall decrease in energy, suggesting that, on whole, the electrostatic effect from charge effects is more significant than the electric field in tuning the absorption energy.
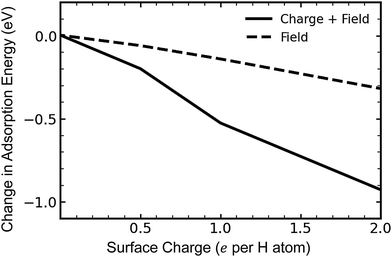 | ||
| Fig. 4 Adsorption energy for a single hydrogen atom on the side of the graphene sheet facing the counter-electrode (“In Field”) and away from the counter-electrode (“Out of Field”). | ||
4 Discussion
It is important to note that the doping levels we implicitly assume in our calculations are rather high. In our supercell, a charge of +e corresponds to a sheet charge density of 1.9 × 1015e cm−2. For comparison, we are aware of experimental sheet charge densities reaching 2 × 1014e cm−2 for twelve layers of graphene,60 which suggests that further engineering advances would be necessary to achieve the doping levels we propose. One possible strategy would be to bond graphene tightly to an oxygen-terminated substrate, such as SiO2. In such a setup, electrons are transferred from graphene to SiO2, resulting in significantly p-type doped graphene.43,61 Chen et al. used first-principles calculations to show that the degree of doping is directly related to the distance between SiO2 and graphene, and for a tight spacing of 1.9 Å, the resultant sheet charge density is approximately 2.1 × 1015e cm−2.43 In our simulation cell, that would correspond to a total charge of +1.1e.As previously discussed, the surface charge in our system correlates directly with an applied electric field perpendicular to the graphene layer. Assuming a uniform distribution of charge q and a flat surface, the electric field E has the familiar expression:
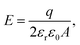 | (2) |
In addition to sustaining a large electric field, the material in a heterostructure with graphene should be permeable to hydrogen. None of the materials listed above are particularly well-known for their high hydrogen mobility; however, all of them are likely permeable to ionic hydrogen, if not molecular H2. Protons (H+) are particularly ubiquitous in oxides, through which they are mobile at relatively low temperatures.67 Protons are also very mobile in diamond.68 Another option lies in the use of negatively charged hydride ions (H−) as the mobile species. Oxyhydrides of the perovskite titanates have shown some potential as hydride ion conductors,69,70 suggesting that SrTiO3, which has a large breakdown field and has been grown in a heterostructure with graphene,64 might an interesting candidate when doped with hydrogen.
Another option could be to integrate graphene with an ionic liquid, which can be chosen to be permeable to ionic and/or molecular hydrogen. Many of these liquids have very high breakdown fields that make them well-suited to high-voltage applications. Indeed, in supercapacitors, electrolytic liquids have been used to increase the achievable operating voltage,71 including in graphene-based devices.72 In our case, confining an appropriate liquid to a small thickness and applying a large voltage would lead to a large electric fields, which will benefit hydrogen storage applications as we have shown.
As a final note, in Fig. 2 and 4, we consider charges up to +4e per simulation cell, which corresponds to a sheet charge density of 7.6 × 1015e cm−2 and a vacuum electric field of 190 MV cm−1. Fig. 2b shows that this level of charge will be necessary to eliminate the barrier to hydrogen chemisorption completely. Such values will be challenging to reach experimentally, not least because there are very few materials known that possess a sufficiently high breakdown field to sustain such a large electric field. However, whether or not such large values can be achieved, our results clearly indicate an improvement in hydrogen storage properties upon electronic doping, even for conditions that should be more experimentally accessible. In addition, it may be lucrative to apply our findings to other 2D materials, following the conclusions of Zhou et al. that more polarizable materials such as monolayer boron nitride require smaller electric fields to stimulate hydrogen storage than do less polarizable materials like graphene.42
5 Conclusions
In summary, we have studied the effect of electronic doping on the chemisorption of hydrogen on graphene, specifically examining the diffusion, adsorption, and desorption of hydrogen. We find that electron depletion of graphene reduces the barriers to adsorption and diffusion of H2 and atomic hydrogen, while it increases the barrier to desorption. For total charges approaching +2e per hydrogen atom, molecular H2 will be energetically favored to adsorb on graphene. In addition, as the charge becomes more positive, the energetic preference for H–H pairs on the graphene surface to occupy different graphene sublattices vanishes, implying that surface diffusion will not be limited by the presence of strongly bound dimers.We connect the improved kinetics of hydrogen to the electronic structure by examining trends in the DOS. For single adsorbed hydrogen atoms or chemisorbed H–H dimers on the same graphene sublattice, there is a sharp peak in the DOS near the Fermi level in the neutral system. Upon removing electrons, this peak is depopulated, which significantly lowers the energy of the C–H bonds. We observe a similar effect for the transition state configuration of hydrogen diffusion, meaning that the energetic migration barrier will be decreased as electrons are removed from the system.
Taking advantage of this charging effect will require careful engineering strategies, seeing as the charges required result in large electric fields. It may be necessary to create graphitic heterostructures with materials having large breakdown fields and dielectric constants, along with high permeability to hydrogen. Other 2D or layered materials may ultimately be more promising due to their ability to adsorb hydrogen tunably with lower degrees of doping or smaller applied electric fields. However, it is clear that the benefits of engineering such a system are immense for hydrogen storage. If a reversible charging approach as we describe here can be realized in practice, graphitic derivatives will demonstrate great promise for hydrogen storage by achieving high levels of chemisorption via spillover.
Author contributions
Patrick T. Shea: investigation, methodology, writing – original draft. Andrew J. E. Rowberg: formal analysis, investigation, visualization, data curation, writing – review & editing. Brandon C. Wood: conceptualization, methodology, supervision, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article, including energies and density of states values used to generate the figures in the main text and ESI,† are available at the Hydrogen Materials Advanced Research Consortium (HyMARC) Data Hub at https://doi.org/10.23722/2497799.Acknowledgements
This work was supported by the Hydrogen Materials Advanced Research Consortium (HyMARC), established as part of the Energy Materials Network by the U.S. Department of Energy (DOE), Office of Energy Efficiency and Renewable Energy (EERE), Hydrogen and Fuel Cell Technologies Office (HFTO). It was performed under the auspices of the DOE by Lawrence Livermore National Laboratory (LLNL) under Contract Number DE-AC52-07NA27344. We acknowledge computational resources from Livermore Computing at LLNL.Notes and references
- L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358 CrossRef CAS PubMed.
- M. D. Allendorf, Z. Hulvey, T. Gennett, A. Ahmed, T. Autrey, J. Camp, E. Seon Cho, H. Furukawa, M. Haranczyk, M. Head-Gordon, S. Jeong, A. Karkamkar, D.-J. Liu, J. R. Long, K. R. Meihaus, I. H. Nayyar, R. Nazarov, D. J. Siegel, V. Stavila, J. J. Urban, S. P. Veccham and B. C. Wood, Energy Environ. Sci., 2018, 11, 2784–2812 RSC.
- P. Jena, J. Phys. Chem. Lett., 2011, 2, 206–211 CrossRef CAS.
- M. Hirscher, V. A. Yartys, M. Baricco, J. B. von Colbe, D. Blanchard, R. C. Bowman Jr, D. P. Broom, C. E. Buckley, F. Chang, P. Chen, Y. W. Cho, J.-C. Crivello, F. Cuevas, W. I. David, P. E. de Jongh, R. V. Denys, M. Dornheim, M. Felderhoff, Y. Filinchuk, G. E. Froudakis, D. M. Grant, E. M. Gray, B. C. Hauback, T. He, T. D. Humphries, T. R. Jensen, S. Kim, Y. Kojima, M. Latroche, H.-W. Li, M. V. Lototskyy, J. W. Makepeace, K. T. Møller, L. Naheed, P. Ngene, D. Noréus, M. M. Nygård, S.-I. Orimo, M. Paskevicius, L. Pasquini, D. B. Ravnsbæk, M. V. Sofianos, T. J. Udovic, T. Vegge, G. S. Walker, C. J. Webb, C. Weidenthaler and C. Zlotea, J. Alloys Compd., 2020, 827, 153548 CrossRef CAS.
- M. B. Ley, L. H. Jepsen, Y.-S. Lee, J. M. Bellosta von Colbe, M. Dornheim, M. Rokni, J. O. Jensen, M. Sloth, Y. Filinchuk, J. E. Jørgensen, F. Besenbacher and T. R. Jensen, Mater. Today, 2014, 17, 122–128 CrossRef CAS.
- S.-i Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed.
- L. Pasquini, K. Sakaki, E. Akiba, M. D. Allendorf, E. Alvares, J. R. Ares, D. Babai, M. Baricco, J. B. von Colbe, M. Bereznitsky, C. E. Buckley, Y. W. Cho, F. Cuevas, P. de Rango, E. M. Dematteis, R. V. Denys, M. Dornheim, J. F. Fernández, A. Hariyadi, B. C. Hauback, T. W. Heo, M. Hirscher, T. D. Humphries, J. Huot, I. Jacob, T. R. Jensen, P. Jerabek, S. Y. Kang, N. Keilbart, H. Kim, M. Latroche, F. Leardini, H. Li, S. Ling, M. V. Lototskyy, R. Mullen, S. Ichi Orimo, M. Paskevicius, C. Pistidda, M. Polanski, J. Puszkiel, E. Rabkin, M. Sahlberg, S. Sartori, A. Santhosh, T. Sato, R. Z. Shneck, M. H. Sørby, Y. Shang, V. Stavila, J.-Y. Suh, S. Suwarno, L. T. Thu, L. F. Wan, C. J. Webb, M. Witman, C. Wan, B. C. Wood and V. A. Yartys, Prog. Energy, 2022, 4, 032007 CrossRef CAS.
- Y. Li and R. T. Yang, J. Am. Chem. Soc., 2006, 128, 726–727 CrossRef CAS PubMed.
- A. Schneemann, L. F. Wan, A. S. Lipton, Y.-S. Liu, J. L. Snider, A. A. Baker, J. D. Sugar, C. D. Spataru, J. Guo, T. S. Autrey, M. Jørgensen, T. R. Jensen, B. C. Wood, M. D. Allendorf and V. Stavila, ACS Nano, 2020, 14, 10294–10304 CrossRef CAS PubMed.
- Y. Zhao, Y.-H. Kim, A. C. Dillon, M. J. Heben and S. B. Zhang, Phys. Rev. Lett., 2005, 94, 155504 CrossRef PubMed.
- Y. Cho, S. Li, J. L. Snider, M. A. T. Marple, N. A. Strange, J. D. Sugar, F. El Gabaly, A. Schneemann, S. Kang, M.-H. Kang, H. Park, J. Park, L. F. Wan, H. E. Mason, M. D. Allendorf, B. C. Wood, E. S. Cho and V. Stavila, ACS Nano, 2021, 15, 10163–10174 CrossRef CAS PubMed.
- D. Kim, J. Koh, S. Kang, T. W. Heo, B. C. Wood, E. S. Cho and S. M. Han, J. Mater. Chem. A, 2021, 9, 11641–11650 RSC.
- A. Schneemann, J. L. White, S. Kang, S. Jeong, L. F. Wan, E. S. Cho, T. W. Heo, D. Prendergast, J. J. Urban, B. C. Wood, M. D. Allendorf and V. Stavila, Chem. Rev., 2018, 118, 10775–10839 CrossRef CAS PubMed.
- Y. Xia, Z. Yang and Y. Zhu, J. Mater. Chem. A, 2013, 1, 9365–9381 RSC.
- A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907 CrossRef CAS PubMed.
- Z.-Y. Yang, L.-J. Jin, G.-Q. Lu, Q.-Q. Xiao, Y.-X. Zhang, L. Jing, X.-X. Zhang, Y.-M. Yan and K.-N. Sun, Adv. Funct. Mater., 2014, 24, 3917–3925 CrossRef CAS.
- J. MacDonald and D. Quinn, Fuel, 1998, 77, 61–64 CrossRef CAS.
- V. Tozzini and V. Pellegrini, Phys. Chem. Chem. Phys., 2013, 15, 80–89 RSC.
- C. Ataca, E. Aktürk, S. Ciraci and H. Ustunel, Appl. Phys. Lett., 2008, 93, 043123 CrossRef.
- Z. Ao and F. Peeters, J. Phys. Chem. C, 2010, 114, 14503–14509 CrossRef CAS.
- Z. Ramezani and H. Dehghani, Int. J. Hydrogen Energy, 2022, 47, 1026–1035 CrossRef CAS.
- J. Navarro-Ruiz, J. Audevard, M. Vidal, C. H. Campos, I. Del Rosal, P. Serp and I. C. Gerber, ACS Catal., 2024, 14, 7111–7126 CrossRef CAS.
- C.-E. Kim, J. Lee, A. Walsh, V. Lordi and D. F. Bahr, J. Chem. Phys., 2022, 156, 054708 CrossRef CAS PubMed.
- F. Ling, R. Liao, C. Yuan, X. Shi, L. Li, X. Zhou, X. Tang, C. Jing, Y. Wang and S. Jiang, J. Chem. Phys., 2023, 158, 084702 CrossRef CAS PubMed.
- S. Yadav, Z. Zhu and C. V. Singh, Int. J. Hydrogen Energy, 2014, 39, 4981–4995 CrossRef CAS.
- D. Kag, N. Luhadiya, N. D. Patil and S. Kundalwal, Int. J. Hydrogen Energy, 2021, 46, 22599–22610 CrossRef CAS.
- X. Sun, B. Li, T. Liu, J. Song and D. S. Su, Phys. Chem. Chem. Phys., 2016, 18, 11120–11124 RSC.
- T. G. Senthamaraikannan, S. Krishnamurty and S. Kaliaperumal, New J. Chem., 2021, 45, 9959–9966 RSC.
- L. Wang and R. T. Yang, Energy Environ. Sci., 2008, 1, 268–279 RSC.
- Y. Lin, F. Ding and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 041402 CrossRef.
- J. C. Meyer, C. O. Girit, M. Crommie and A. Zettl, Nature, 2008, 454, 319–322 CrossRef CAS PubMed.
- T. O. Wehling, M. I. Katsnelson and A. I. Lichtenstein, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085428 CrossRef.
- L. F. Huang, M. Y. Ni, X. H. Zheng, W. H. Zhou, Y. G. Li and Z. Zeng, J. Phys. Chem. C, 2010, 114, 22636–22643 CrossRef CAS.
- H. McKay, D. J. Wales, S. J. Jenkins, J. A. Verges and P. L. de Andres, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075425 CrossRef.
- V. A. Borodin, T. T. Vehviläinen, M. G. Ganchenkova and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075486 CrossRef.
- T. Gennett, Position Paper: Hydrogen Spillover Limitations for Onboard Hydrogen Storage, National Renewable Energy Lab.(NREL), Golden, CO (United States) technical report, 2019.
- M. Calandra and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 161406 CrossRef.
- F. Joucken, Y. Tison, P. Le Fèvre, A. Tejeda, A. Taleb-Ibrahimi, E. Conrad, V. Repain, C. Chacon, A. Bellec, Y. Girard, S. Rousset, J. Ghijsen, R. Sporken, H. Amara, F. Ducastelle and J. Lagoute, Sci. Rep., 2015, 5, 1–10 Search PubMed.
- F. Joucken, L. Henrard and J. Lagoute, Phys. Rev. Mater., 2019, 3, 110301 CrossRef CAS.
- Z. Ao and F. Peeters, Appl. Phys. Lett., 2010, 96, 253106 CrossRef.
- C. Cab, R. Medina-Esquivel, C. Acosta, J. Mendez-Gamboa, F. Peñuñuri and A. Tapia, Adv. Condens. Matter Phys., 2015, 847804 Search PubMed.
- J. Zhou, Q. Wang, Q. Sun, P. Jena and X. Chen, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2801–2806 CrossRef CAS PubMed.
- K. Chen, X. Wang, J.-B. Xu, L. Pan, X. Wang and Y. Shi, J. Phys. Chem. C, 2012, 116, 6259–6267 CrossRef CAS.
- Y. Zhou, X. T. Zu, F. Gao, J. Nie and H. Xiao, J. Appl. Phys., 2009, 105, 014309 CrossRef.
- F. Chen, X. Zhang, X. Guan, S. Gao, J. Hao, L. Li, Y. Yuan, C. Zhang, W. Chen and P. Lu, Appl. Surf. Sci., 2023, 622, 156895 CrossRef CAS.
- P. Wu, Y. Qian, P. Du, H. Zhang and C. Cai, J. Mater. Chem., 2012, 22, 6402–6412 RSC.
- A. Ariharan, B. Viswanathan and V. Nandhakumar, Graphene, 2017, 6, 41–60 CrossRef CAS.
- H. Aghajani, A. T. Tabrizi, R. Ghorbani, S. Behrangi, M. Stupavska and N. Abdian, J. Alloys Compd., 2022, 906, 164284 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical properties of carbon nanotubes, Imperial College Press, 1998 Search PubMed.
- M. Otani and O. Sugino, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115407 CrossRef.
- I. Hamada, O. Sugino, N. Bonnet and M. Otani, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155427 CrossRef.
- W. Zhang, W.-C. Lu, H.-X. Zhang, K.-M. Ho and C.-Z. Wang, Carbon, 2018, 131, 137–141 CrossRef CAS.
- A. V. Shytov, D. A. Abanin and L. S. Levitov, Phys. Rev. Lett., 2009, 103, 016806 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M.-S. Kim, M. Kim, S. Son, S.-Y. Cho, S. Lee, D.-K. Won, J. Ryu, I. Bae, H.-M. Kim and K.-B. Kim, ACS Appl. Mater. Interfaces, 2020, 12, 30932–30940 CrossRef CAS PubMed.
- M. Ishigami, J. Chen, W. Cullen, M. Fuhrer and E. Williams, Nano Lett., 2007, 7, 1643–1648 CrossRef CAS PubMed.
- E. V. Castro, K. S. Novoselov, S. V. Morozov, N. M. R. Peres, J. M. B. L. dos Santos, J. Nilsson, F. Guinea, A. K. Geim and A. H. C. Neto, Phys. Rev. Lett., 2007, 99, 216802 CrossRef PubMed.
- W. Hu, Z. Li and J. Yang, J. Chem. Phys., 2013, 138, 054701 CrossRef PubMed.
- J. Sun, T. Gao, X. Song, Y. Zhao, Y. Lin, H. Wang, D. Ma, Y. Chen, W. Xiang, J. Wang, Y. Zhang and Z. Liu, J. Am. Chem. Soc., 2014, 136, 6574–6577 CrossRef CAS PubMed.
- X. Yan, I. S. Esqueda, J. Ma, J. Tice and H. Wang, Appl. Phys. Lett., 2018, 112, 032101 CrossRef.
- L. Zheng, X. Cheng, D. Cao, G. Wang, Z. Wang, D. Xu, C. Xia, L. Shen, Y. Yu and D. Shen, ACS Appl. Mater. Interfaces, 2014, 6, 7014–7019 CrossRef CAS PubMed.
- T. Norby, M. Widerøe, R. Glöckner and Y. Larring, Dalton Trans., 2004, 3012–3018 RSC.
- J. P. Goss, R. Jones, M. I. Heggie, C. P. Ewels, P. R. Briddon and S. Öberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 115207 CrossRef.
- Y. Kobayashi, O. J. Hernandez, T. Sakaguchi, T. Yajima, T. Roisnel, Y. Tsujimoto, M. Morita, Y. Noda, Y. Mogami, A. Kitada, M. Ohkura, S. Hosokawa, Z. Li, K. Hayashi, Y. Kusano, J. E. Kim, N. Tsuji, A. Fujiwara, Y. Matsushita, K. Yoshimura, K. Takegoshi, M. Inoue, M. Takano and H. Kageyama, Nat. Mater., 2012, 11, 507–511 CrossRef CAS PubMed.
- X. Liu, T. S. Bjørheim and R. Haugsrud, J. Mater. Chem. A, 2017, 5, 1050–1056 RSC.
- A. Brandt, S. Pohlmann, A. Varzi, A. Balducci and S. Passerini, MRS Bull., 2013, 38, 554–559 CrossRef CAS.
- M. D. Stoller, S. Park, Y. Zhu, J. An and R. S. Ruoff, Nano Lett., 2008, 8, 3498–3502 CrossRef CAS PubMed.
Footnote |
| † Electronic Supplementary Information (ESI) available: migration, adsorption and desorption energies of isolated hydrogen atoms and dimers including cases of charge accumulation; and selected energy pathways for hydrogen adsorption. See DOI: https://doi.org/10.1039/d5cp00150a |
| This journal is © the Owner Societies 2025 |
