Effect of microhydration on the aromatic charge resonance interaction: the case of the pyrrole dimer cation

Abstract

Charge resonance (CR) interactions between aromatic molecules are amongst the strongest intermolecular forces and responsible for many phenomena in chemistry and biology. Microhydration of an aromatic radical dimer cation allows investigation of the strong effects of stepwise solvation on the charge distribution and strength of the CR. We characterise herein the microhydration process of the pyrrole dimer cation (Py₂⁺), a prototypical aromatic homodimer with a strong CR. The NH and OH stretch vibrations (ν_NH/OH) of mass-selected bare and colder Ar-tagged hydrated clusters of Py₂⁺, Py₂⁺(H₂O)_nAr_m (n ≤ 3, m ≤ 1), recorded by infrared photodissociation (IRPD) spectroscopy provide detailed insight into the preferred cluster growth and strengths of the various intermolecular interactions by comparison to dispersion-corrected density functional theory calculations. The analysis of systematic frequency shifts, structural parameters, binding energies, and charge distributions allows for a quantitative evaluation of the drastic effects of stepwise hydration on the strength and symmetry of the aromatic CR, the strengths of the various hydrogen bonds (H-bonds), and the competition between slightly noncooperative interior ion hydration and strongly cooperative formation of a H-bonded solvent network. The most stable Py₂⁺H₂O structure exhibits a strong NH⋯O ionic H-bond of H₂O to the antiparallel stacked Py₂⁺(a) core, thereby breaking the symmetry of the CR. Py₂⁺(H₂O)₂ prefers a highly symmetric C_2h structure with two equivalent NH⋯O H-bonds of Py₂⁺(a) and an optimised CR. Starting from n = 3, clusters with a parallel configuration, Py₂⁺(p), are more stable than those with Py₂⁺(a), further highlighting the strong impact of (micro-)solvation on the structural motif of the aromatic CR. The spectral and computational data demonstrate a linear correlation of ν_NH of the free Py unit with its partial charge, illustrating that IR spectroscopy is a powerful tool for probing the charge distribution in aromatic CR cluster cations. Comparison of Py₂⁺(H₂O)_n with neutral Py₂(H₂O)_n and Py⁺(H₂O)_n reveals the impact of the magnitude of positive charge and the number of acidic proton donors on the structure of the microhydration shell and strength of the various competing intermolecular bonds.

---

1. Introduction

Intermolecular interactions involving aromatic π electrons are highly relevant for a large number of chemical and biological phenomena.^1–9 One of the most common interactions between aromatic molecules is π–π stacking, a weak interaction mostly based on London dispersion forces. Such π–π stacking is well-known to stabilise the DNA double-strand and to contribute to protein folding.^10–12 In structural chemistry, π–π stacking often determines the geometry of supramolecules and the properties of solid or liquid crystals.^13–15 In addition, π hydrogen bonds (π H-bonds) such as CH–π bonds are important weak interactions involving aromatic molecules.^16–20 In contrast to these weak interactions, the charge resonance (CR) interaction in charged aromatic dimers is amongst the strongest intermolecular forces, with a strength of around 100 kJ mol⁻¹.^21–23 The CR interaction plays an important role for structure, energetics, and dynamics of intermolecular and intramolecular hole transport in stacked conjugated biological and organic semiconductor materials.^24–31

The CR in aromatic dimer cations (AB⁺) is formed by sharing the positive charge generated by removing a single π electron. This CR gives rise to two electronic states described by

ψ₊ = c₁ϕ(A⁺)ϕ(B) + c₂ϕ(A)ϕ(B⁺)

ψ₋ = c₂ϕ(A⁺)ϕ(B) – c₁ϕ(A)ϕ(B⁺)

whereby ψ₊ is the stabilised ground electronic state and ψ₋ is the repulsive excited electronic state.³² The splitting between the two states ψ_± is typically of the order of ∼1 eV and gives rise to a strongly allowed optical transition in the near-IR range (∼1000 nm). In general, the splitting between these two electronic states depends strongly on the difference in the ionisation energies (ΔIE) of A and B, whereby the CR becomes stronger, the smaller ΔIE and thus is strongest for homodimer cations, A₂⁺ (i.e., A = B and c₁ = c₂).^23,33

CR interactions were first detected in the condensed phase by electron spin resonance^34–36 and optical absorption spectroscopy.^37–40 However, these experiments suffer from environmental perturbations such as solvent and counter ions. In the gas phase, the binding energies of several isolated aromatic homo- and heterodimers were measured by mass spectrometric techniques.^41–43 The spectra of the electronic CR transitions recorded for the aromatic homodimers of benzene,^44–47 naphthalene,^48–50 toluene,⁵¹ pyrene,⁵² and several heterodimers^32,51,53 have proven that the splitting between the two electronic states ψ_± depends on the size and ΔIE of the two monomer units. The strength of the CR interaction is controlled by the charge distribution on the respective monomers.^32,51,53 However, the electronic CR bands observed by optical absorption in the spectral range around 1 eV are too broad even in the gas phase due to their transitions into the repulsive ψ₋ state, preventing a precise estimation of the partial charge distribution on the interacting monomers. To circumvent this problem, we previously demonstrated an efficient spectroscopic method to estimate the charge distribution in isolated aromatic A₂⁺ and AB⁺ dimers by monitoring their vibrational transitions in the ground state (ψ₊) utilising infrared photodissociation spectroscopy (IRPD).²³ This study concentrated on the pyrrole dimer cation (Py₂⁺), its clusters, and related heterodimers because of its strong CR interaction and the high sensitivity of the NH stretch frequency (ν_NH) of Py (C₄H₅N) to its partial charge.²³ Besides being a fundamental building block of many important biomolecules such as porphyrins, amino acids, proteins, and DNA bases, Py has a single isolated, uncoupled, and strongly IR-active NH stretch oscillator, whose frequency is indeed rather sensitive to the charge state of Py^q (e.g., ν_NH = 3531 and 3447 cm⁻¹ for q_Py = 0 and 1e).^54,55 The latter property differs from that of bare aromatic hydrocarbons, such as benzene and related polycyclic aromatic hydrocarbons, whose CH stretch frequencies (ν_CH) are less sensitive to charges and have weaker IR oscillator strengths in the cation ground state. Furthermore, often strong anharmonic or vibronic couplings further complicate the CH stretch range in these hydrocarbons (e.g., Fermi resonances in C₆H₆ and C₆H₄Cl₂⁺ or Jahn–Teller effect in C₆H₆⁺).^{45,53,56–60}

Because Py has an acidic NH group and aromatic π electrons, neutral Py₂ dimer forms a weak NH⋯π H-bond,^61–63 with an interaction energy of 0.07 eV.⁶⁴ Its T-shaped structure has been confirmed by microwave,⁶⁴ IR,^63,65 and Raman spectroscopy,⁶⁵ as well as quantum chemical calculations.^61,66 Py₂⁺ radical cations formed in a supersonic plasma expansion based on electron ionisation (EI) have a stacked sandwich structure stabilised by a strong CR interaction (1.01 eV), which has been characterised by IRPD and quantum chemical calculations.²³ Further analysis of IRPD spectra of cold Py₂⁺ dimers tagged with Ar or N₂ reveals that the antiparallel Py₂⁺(a) isomer with C_2h symmetry is significantly more stable than the parallel Py₂⁺(p) local minimum with C_s symmetry (by around 10 kJ mol⁻¹) and thus dominates the population in the plasma expansion.⁶⁷ A minor population of hot Py₂⁺ ions (<15%) has been attributed to H-bonded clusters produced by intramolecular H-transfer and subsequent ring-opening reactions.⁶⁷ The presence of these high-energy isomers has been inferred from additional transitions observed in the IRPD spectrum of hot Py₂⁺ ions, which are absent in spectra recorded for cold Py₂⁺Ar_n clusters.⁶⁷ These additional transitions have also been observed in the IRPD spectra of Py₂⁺ ions generated by VUV ionisation of neutral Py_n clusters but interpreted by isomers, in which the two heterocyclic units are connected by a chemical C–C or C–N bond.^68,69 However, as the IR spectra computed for these chemically-bonded isomers are not compatible with the measured IRPD spectra of Py₂⁺ for both EI⁶⁷ and VUV⁶⁸ generation, we currently prefer an assignment to H-bonded rather than chemically-bonded isomers.⁶⁷

Py₂⁺(a) is an ideal prototypical model to characterise in detail the aromatic CR interaction by IR spectroscopy of its bound ψ₊(²A_u) ground electronic state.²³ First, its small five-membered ring causes the CR interaction to be very strong, in particular, stronger than any ionic NH⋯N H-bond or NH⋯π cation–π interaction.⁶⁷ Moreover, the frequency of its rather isolated and strongly IR-active ν_NH mode provides a rather sensitive measure of the partial positive charge located on Py, which thus can precisely be measured by high-resolution IR spectroscopy.²³ For example, the symmetric Py₂⁺(a) dimer with a partial charge of q_Py = 0.5e on each Py unit has its ν_NH (3480 cm⁻¹) midway between those of Py (3531 cm⁻¹) and Py⁺ (3447 cm⁻¹).²³ Indeed, we established a linear relation between ν_NH and q_Py expressed as ν_NH(q_Py)/cm⁻¹ = −83.8 q_Py/e + 3527.8.²³ This linear correlation derived from data for Py, Py⁺, and Py₂⁺ (q_Py/e = 0, 1.0, and 0.5) was shown to hold for related clusters, in which the symmetry of Py₂⁺ is reduced either by solvation (e.g., Py₂⁺N₂) or by substitution of functional groups (e.g., by replacing one Py by N-methyl-Py, NMPy).²³ In both heterodimers (Py-PyN₂, Py-NMPy), the IE of the aromatic binding partner is lowered compared to Py, leading to an asymmetric charge distribution in [Py-PyN₂]⁺ and [Py-NMPy]⁺ with q_Py < 0.5e and thus a blueshift in the free ν_NH of the remaining Py unit.²³ In Py₂⁺N₂, N₂ binds via an NH⋯N H-bond to one of the free acidic NH groups of Py₂⁺(a).^23,67 Therefore, stronger bases like H₂O are expected to act as better H-bond acceptors with a larger reduction in symmetry of the geometric structure, the charge distribution, and thus the CR.

Herein, we characterise the microhydration process of Py₂⁺ using IRPD of mass-selected Py₂⁺(H₂O)_nAr_m clusters (n ≤ 3, m ≤ 1) in the CH, NH, and OH stretch ranges (ν_CH/NH/OH). Ar-tagging is applied to generate clusters with lower internal energy and to reduce the effective dissociation energy, leading to higher-resolution spectra and larger photodissociation efficiency.⁷ Complementary dispersion-corrected density functional theory (DFT) calculations at the B3LYP-D3/aug-cc-pVTZ level are employed to assign the measured IRPD spectra and to analyse the observed intermolecular interactions. The present study is motivated by the following main reasons. First, stepwise microhydration of Py₂⁺ enables the investigation of breaking and restoring the symmetry of the CR interaction. Because H₂O has a significantly higher proton affinity than N₂ (PA = 691 vs. 494 kJ mol⁻¹),⁷⁰ it forms a much stronger NH⋯O ionic H-bond and thus causes a larger perturbation of the CR due to the larger difference in the IE of Py and PyH₂O (computed herein as IE = 8.09 and 7.06 eV, respectively, vide infra). In addition, the magnitude of symmetry breaking can also be controlled by the degree of hydration (n). For example, the linear H-bonded (H₂O)₂ is an even stronger H-bond acceptor than a single H₂O ligand, because of its larger PA (808 kJ mol⁻¹),⁷¹ causing a larger perturbation of the CR in Py₂⁺. Hence, we can address for the first time in detail the correlation between the CR in stacked π–π dimers and the strength of its H-bonds to the (dipolar) solvent molecules. In passing, we note that also only a few spectroscopic studies have been reported on the solvation effects of the related σ–σ^72,73 and σ–π⁷⁴ hemibonded dimer cation systems which reveal the dependence of the stability of the σ–σ and σ–π hemibonds upon solvation with various ligands. Second, microhydration of Py₂⁺ is expected to show different hydration motifs than those of the neutral and cationic Py⁽⁺⁾ monomers, because Py₂⁺ offers two acidic NH groups as H-bond donors and an intermediate charge state (0.5e for each Py unit). Hence, we can follow the evolution of the Py_n(H₂O)_m cluster network (structure and interaction strength) as a function of (i) charge and (ii) number of available acidic proton donors in (aromatic solute)-(dipolar solvent) systems. Previous studies reveal that PyH₂O^{20,55,75–79} and Py⁺H₂O⁵⁴ form conventional σ-type NH⋯O H-bonds, whereby the H-bond in the cation is much stronger than in the neutral (65.1 vs. 17.6 kJ mol⁻¹), mainly due to the additional electrostatic and induction forces of the excess charge (charge-dipole and charge-induced dipole).^54,80 Moreover, we have recently reported the hydration motif of Py⁺(H₂O)₂, in which the linear (H₂O)₂ chain is directly H-bonded to the NH group of Py⁺.⁸⁰ Strong cooperativity of the nonadditive induction forces make the NH⋯O and OH⋯O H-bonds in the Py⁺(H₂O)₂ trimer much stronger than those in the respective Py⁺H₂O and (H₂O)₂ dimers. In contrast to Py⁺, Py₂⁺ has the potential to develop at least two principally different and competing H-bonding motifs in Py₂⁺(H₂O)₂, such that either a (H₂O)₂ chain is H-bonded to one NH group (i.e., formation of a H-bonded solvent network) or two single H₂O molecules are H-bonded to each NH group (i.e., interior ion solvation). Third, it is possible that the hydration process may change the preferred orientation of the two NH groups in π-stacked Py₂⁺ from antiparallel (a) to parallel (p) and thus modify the structural motif, symmetry, and strength of the CR interaction. Our previous B3LYP-D3 calculations suggest that the Py₂⁺(p) local minimum is less stable than the Py₂⁺(a) global minimum by only 7.5 kJ mol⁻¹.⁶⁷ As this energy difference is much smaller than typical monohydration energies of aromatic ions with an NH⋯O ionic H-bond (∼50 kJ mol⁻¹),^80–83 stepwise hydration may indeed be able to induce a Py₂⁺(a) → Py₂⁺(p) transition of the CR core ion at a critical size (n_c). Because Py₂⁺(p) offers the possibility of forming cyclic hydration motifs in Py₂⁺(p)(H₂O)_n clusters with one additional H-bond as compared to Py₂⁺(a)(H₂O)_n, such a Py₂⁺(a) → Py₂⁺(p) switch in the preferred structural CR motif may indeed occur upon progressive hydration.

2. Experimental and computational details

IRPD spectra of mass-selected Py₂⁺(H₂O)_nAr_m cluster cations (n = 1–3, m = 0–1) are measured in a tandem quadrupole mass spectrometer coupled to an EI source and an octupole ion guide.^9,84 Cluster cations are produced in a pulsed supersonic plasma expansion of Py (Sigma-Aldrich, >98%, heated to 50 °C) seeded in Ar carrier gas. Hydrated cluster cations are generated by adding distilled H₂O into the gas inlet system. In general, ionic clusters are formed by electron (and/or chemical) ionisation (EI) of Py close to the nozzle orifice and subsequent three-body aggregation reactions. Hydrated clusters may also be produced by EI of neutral Py_p≥2(H₂O)_q≥n clusters and subsequent fragmentation into Py₂⁺(H₂O)_n. The cluster cations of interest are selected by the first quadrupole mass filter and irradiated in the adjacent octupole with a tunable IR laser pulse (ν_IR) generated by an optical parametric oscillator and amplifier (OPO/OPA) pumped by a Q-switched nanosecond Nd:YAG laser. The IR radiation is characterised by a pulse energy of 2–5 mJ, a bandwidth of <2 cm⁻¹, and a repetition rate of 10 Hz. The IR laser frequency is calibrated to better than 1 cm⁻¹ using a wavemeter. Resonant vibrational excitation induces the loss of the most weakly bonded ligand, i.e., either H₂O or Ar. The generated fragment ions are selected by the second quadrupole mass filter and monitored by a Daly detector as a function of ν_IR to obtain the IRPD action spectrum of the parent cluster. The ion source is triggered at twice the laser frequency to subtract the metastable decay background from the total fragment ion signal to extract the laser-induced fragmentation signal. All IRPD spectra are normalised for frequency-dependent variations in the IR photon flux measured by a pyroelectric detector. The peak widths of the vibrational transitions observed in the IRPD spectra are mainly caused by unresolved rotational structure, sequence hot bands involving inter- and intramolecular modes, and possibly contributions of several isomers. In addition to laser-induced dissociation (IRPD and LID), low-energy collision-induced dissociation (CID) experiments are performed in the octupole ion guide to confirm the composition of the mass-selected parent clusters. For the latter mass spectra, the octupole is filled with N₂ gas or air (10⁻⁵ mbar) resulting in collisions with 10 eV energy in the laboratory frame. The respective CID and LID spectra of the mass-selected parent clusters are shown in Fig. S1 in ESI.†

Quantum chemical calculations are carried out at the dispersion-corrected B3LYP-D3/aug-cc-pVTZ level to determine the structural, energetic, vibrational, and electronic properties of the investigated cluster cations.^85–89 This level of calculation has provided reliable results in our previous studies of related pyrrole cluster ions.^23,54,67,80 Harmonic vibrational frequencies are scaled by factors of 0.9619 for NH and CH stretch vibrations and 0.9631 for OH stretch vibrations to optimise the agreement with the measured frequencies of bare Py and H₂O (ν_NH = 3531 cm⁻¹, ν_1/3 = 3657/3756 cm⁻¹), respectively.^63,80,90 Intermolecular interaction energies (D₀) and relative energies (E₀) are corrected for zero-point vibrational energy. Relative free energies (G₀) are calculated at 298 K. The counterpoise procedure for correcting energies for basis set superposition error is not included because such corrections are expected to be 1% or less for the large basis set employed, as has been shown for related microhydrated aromatic cluster cations.^82,91 The natural charge distributions on each molecular component and the donor–acceptor interaction energies (E⁽²⁾) describing the strengths of H-bonds are obtained employing the natural bond orbital (NBO) analysis.⁹² Anharmonic vibrational calculations are carried out at the lower B3LYP-D3/aug-cc-pVDZ level to reduce computational costs and at the PBE0/aug-cc-pVDZ level to evaluate the dependence on the DFT functional.^85,93 The reliability of the results obtained at the reduced basis set and the different DFT functional is evaluated by comparing the harmonic frequencies of each method to the frequencies obtained at the B3LYP-D3/aug-cc-pVTZ level. Harmonic vibrational frequencies calculated at the B3LYP-D3/aug-cc-pVDZ level are scaled by factors of 0.9628 for ν_CH/NH and 0.9621 for ν_OH and at the PBE0/aug-cc-pVDZ level by factors of 0.9522 for ν_CH/NH and 0.9474 for ν_OH. Vertical CR transition energies are obtained from time-dependent DFT (TD-DFT) calculations at the B3LYP-D3⁸⁵ level for the optimised ground state geometry and compared with results from the B3PW91-D3,⁹⁴ CAM-B3LYP-D3,⁹⁵ and M06-2X⁹⁶ functionals using the aug-cc-pVTZ basis set. The evaluation of the strengths of the intermolecular H-bonds is facilitated by the noncovalent interaction (NCI) approach.^97–99 This method is based on the analysis of the electron densities (ρ) and their reduced density gradients (RDG), s(ρ), and therefore highlights the interactions in the low-density region.⁹⁹ The NCI analysis provides an index based on a plot of s(ρ) in the area in which s(ρ) is close to its minima of ρ. The final visualisation is then obtained by plotting RDG against ρ oriented by the sign of the second eigenvalue λ₂ of the Hessian matrix, ρ* = sign (λ₂)ρ.^100,101 The plotted NCI surfaces cover the range −0.05 < ρ* < 0.0 a.u., with an isosurface value of 0.3 a.u. The NCI color code uses blue surfaces for attractive interactions (negative λ₂), green surfaces for weak van der Waals contacts (λ₂ near 0), and red surfaces for repulsive interactions (positive λ₂). Cartesian coordinates of all considered isomers and their corresponding energies are provided in ESI.†

3. Results and discussion

3.1. Overview of IRPD spectra of Py₂⁺(H₂O)_n

Fig. 1 compares the IRPD spectra of Py₂⁺(H₂O)_n with n = 1–3 measured in the H₂O loss channel. For comparison, the previously reported IRPD spectra of Py⁺Ar and Py₂⁺ measured in the Ar and Py loss channels, respectively, are included as well.^54,67 The positions and widths of the bands observed are listed in Table S1 (ESI†) along with the suggested vibrational and isomer assignments. The spectral range investigated (2600–3800 cm⁻¹ for Py₂⁺(H₂O)_n with n = 1–2 and 3000–3800 for n = 3) covers the free and bound OH and NH stretch bands of the H₂O ligands and the Py₂⁺ cation, as well as the aromatic CH stretch modes of Py₂⁺. The IRPD spectra in Fig. 1 exhibit systematic shifts in the OH and NH stretch bands as a function of cluster size and composition, providing detailed information about the stepwise microhydration process around Py₂⁺. The free OH stretch range (3600–3800 cm⁻¹) contains the symmetric and antisymmetric OH stretch bands of H₂O ligands acting as single/double acceptors (ν₁ and ν₃, B and A) and the free OH stretch bands of H₂O ligands acting as single/double acceptor and single donor (ν^f_OH, C). The corresponding H-bonded OH stretch modes of H₂O involved as an H-bond donor occur near 3400 cm⁻¹ (ν^b_OH, D). The free NH stretch of Py₂⁺ occurs near 3500 cm⁻¹ (ν^f_NH, E), while the H-bonded NH stretch shifts strongly to the red down to 3000–3300 cm⁻¹ upon hydration (ν^b_NH, F, F1). Peak G observed at ∼3130 cm⁻¹ in all spectra is assigned to the aromatic CH stretch vibrations (ν_CH) of Py₂⁺. Bands X, Y, and Y′ cannot arise from fundamentals of Py₂⁺(H₂O)_n clusters with π-stacked Py₂⁺(a/p) cores and are attributed at this initial stage to either overtone and/or combination bands or transitions of other minor isomers.^102,103 The pronounced broad peak F* in the IRPD spectrum of Py₂⁺ has been assigned in our previous study to ν^b_NH of a minor population of H-bonded isomers, Py₂(CC/OC)⁺.⁶⁷ Its absence in the IRPD spectra of Py₂⁺(H₂O)_n and their Ar-tagged clusters indicates that these isomers are below the detection limit for the hydrated clusters. In the following sections, the structures of the microhydrated Py₂⁺ clusters are identified by comparing the measured IRPD spectra with linear IR absorption spectra computed for low-energy isomers. The IRPD spectra of their Ar-tagged clusters are also considered because their lower temperature yields narrower bands in the IRPD spectra, which provide more precise vibrational assignments.

Fig. 1 IRPD spectra of Py₂⁺(H₂O)_n with n = 0–3 (and Py⁺Ar for comparison)⁵⁴ recorded in the CH, NH, and OH stretch range. The positions, width, and assignments of the observed transitions are compiled in Table S1 (ESI†).

3.2. Py_1/2⁺ and (H₂O)_1/2

Before considering the Py₂⁺(H₂O)_n clusters, we briefly review the available knowledge on the Py_1/2⁺ and (H₂O)_1/2 subunits relevant to the current study. The structures of Py and Py⁺ in their ¹A₁ and ²A₂ electronic ground states are planar (C_2v), and the N–H bond length increases by 7 mÅ from r_NH = 1.0031 to 1.0102 Å upon ionisation from the π(a₂) HOMO orbital (Fig. 2). This geometry change results in a large calculated redshift from 3531 to 3459 cm⁻¹ (Δν^f_NH = −72 cm⁻¹), which compares favourably with the measured values of 3531 and 3447 cm⁻¹ (Δν^f_NH = −84 cm⁻¹), respectively.^54,63 The IRPD spectrum of Py⁺Ar shown in Fig. 1 exhibits two bands E and F at 3450 and 3423 cm⁻¹ assigned to ν^f_NH of π-bonded Py⁺Ar(π) and ν^b_NH of H-bonded of Py⁺Ar(H), respectively.⁵⁴ Because the π-bonded local minimum with D₀ = 6.6 kJ mol⁻¹ shows a computed ν^f_NH blueshift of only 3 cm⁻¹ from that of bare Py⁺ (3459 vs. 3462 cm⁻¹), an accurate experimental value can be estimated for bare Py⁺ as ν^f_NH = 3447 cm⁻¹.⁵⁴ The formation of the NH⋯Ar H-bond in the planar Py⁺Ar(H) global minimum (C_2v) with D₀ = 9.4 kJ mol⁻¹ and R_e = 2.470 Å causes a larger redshift measured as Δν^b_NH = −50 cm⁻¹.

Fig. 2 Structures of (a) Py⁽⁺⁾, (b) H₂O and (H₂O)₂, (c) Py₂⁺(a), and (d) Py₂⁺(p) obtained at the B3LYP-D3/aug-cc-pVTZ level. Selected intra- and intermolecular bond lengths (in Å) are given in black and red, respectively. Values in dark red indicate NBO charges (in units of e). The dissociation energies (D₀, in parentheses) are given in kJ mol⁻¹.

Because of the CR, the positive charge in Py₂⁺(a) is equally shared between the two equivalent Py units and both N–H bond lengths and NH stretch frequencies of Py₂⁺ are intermediate between those of Py and Py⁺ (Fig. 2).²³ Indeed, for the Py₂⁺(a) global minimum, r_NH = 1.0061 Å is close to the average of Py and Py⁺ (r_NH = 1.0031 and 1.0102 Å). As a result, the calculated frequencies of the antisymmetric IR-active and symmetric IR-forbidden NH stretch modes, ν^f_NH = 3500 and 3501 cm⁻¹, are midway between those of Py and Py⁺ computed as ν^f_NH = 3531 and 3459 cm⁻¹. These computational predictions agree well with band E observed at ν^f_NH = 3479 cm⁻¹ in the IRPD spectrum of Py₂⁺ (Fig. 1), which is also midway between those of Py and Py⁺ observed at ν^f_NH = 3531 and 3447 cm⁻¹.^23,67 The slightly less stable Py₂⁺(p) local minimum structure with a parallel orientation of the two NH groups (Fig. 2) has two IR-active NH stretch modes calculated as ν^f_NH = 3499 and 3510 cm⁻¹ with a splitting of 11 cm⁻¹ (Table S2, ESI†). As these frequencies are similar to those of the Py₂⁺(a) global minimum, one cannot exclude the contribution of Py₂⁺(p) to band E in the IRPD of bare Py₂⁺ because its width (19 cm⁻¹) is much larger than the ν^f_NH shifts and splittings for the Py₂⁺(a/p) rotamers.⁶⁷ However, from the energetic point of view, the Py₂⁺ population will be dominated by Py₂⁺(a) because it is more stable than Py₂⁺(p) by 7.5 kJ mol⁻¹ (B3LYP-D3). Indeed, in our recent study on the internal energy dependence of the formation of Py₂⁺ in our EI source, the higher-resolution IRPD spectra of cold Py₂⁺L_n clusters tagged with L = Ar and N₂ suggest that the population of Py₂⁺(p) is at most 15% of the π-stacked Py₂⁺ dimers.⁶⁷ The high rotational barriers (V_b) for a → p and p → a isomerisation computed at different computational levels suggest that the Py₂⁺(a/p) isomers are kinetically trapped in their potential well rather than isomerising between each other. Therefore, the estimated Py₂⁺(p) abundance using a Boltzmann distribution based on ΔE₀(B3LYP-D3) = 7.5 kJ mol⁻¹ is 17% at 298 K, which is compatible with the experiment (≤15%). In the same study, we assigned the additional bands at 2888 (X) and 3028 (F*) cm⁻¹ observed in the IRPD spectrum of bare Py₂⁺ (but not in Py₂⁺L_n) to a Fermi doublet (2β_NH and ν^b_NH) of a minor population (10%) of H-bonded Py₂(OC)⁺ isomers containing one open-cycle (OC) Py unit. The latter dimers are characterized by an NH⋯N ionic H-bond between Py⁺ and a neutral noncyclic Py isomer formed by H-migration and subsequent ring opening in the EI source.⁶⁷

The calculated O–H bond parameters of H₂O in its ¹A₁ ground state (r_OH = 0.9618 Å, ν₁ = 3657 cm⁻¹, ν₃ = 3756 cm⁻¹) agree well with the experimental data (0.9578 Å, 3657 and 3756 cm⁻¹).⁹⁰ Our computed (H₂O)₂ equilibrium geometry has the known trans-linear H-bonded structure (Fig. 2), with an O⋯O distance (r_OO = 2.909 Å) and an angle of the acceptor H₂O axis with respect to r_OO (59.1°) consistent with corresponding experimental values (2.98 Å, 58°).¹⁰⁴ The four calculated OH stretch frequencies of the H₂O acceptor (ν_1/3 = 3652/3747 cm⁻¹) and donor (ν^b/f_OH = 3540/3728 cm⁻¹) are also close to their experimental data (ν_1/3 = 3654/3746 cm⁻¹, ν^b/f_OH = 3601/3735 cm⁻¹), respectively.^105–107 The H-bond strength computed as D₀ = 13.0 kJ mol⁻¹ compares again favourably with the experimental determination of D₀ = 13.2 ± 0.1 kJ mol⁻¹ (1105 ± 10 cm⁻¹),¹⁰⁸ illustrating that the chosen B3LYP-D3 level reliably describes the H₂O⋯H₂O interaction. The IEs of (H₂O)_n calculated at the B3LYP-D3 level (12.60 and 10.73 eV for n = 1 and 2) are much higher than the IEs of both Py (8.09 eV) and Py₂ (7.22 eV), indicating that the positive charge is mostly located on Py₂ rather than on the H₂O ligands, which justifies the notation of Py₂⁺(H₂O)_n. These calculated IEs are close to available experimental values (IE = 12.615, 11.21, 8.207 for H₂O, (H₂O)₂, Py, respectively).^109–113

3.3. Py₂⁺H₂O

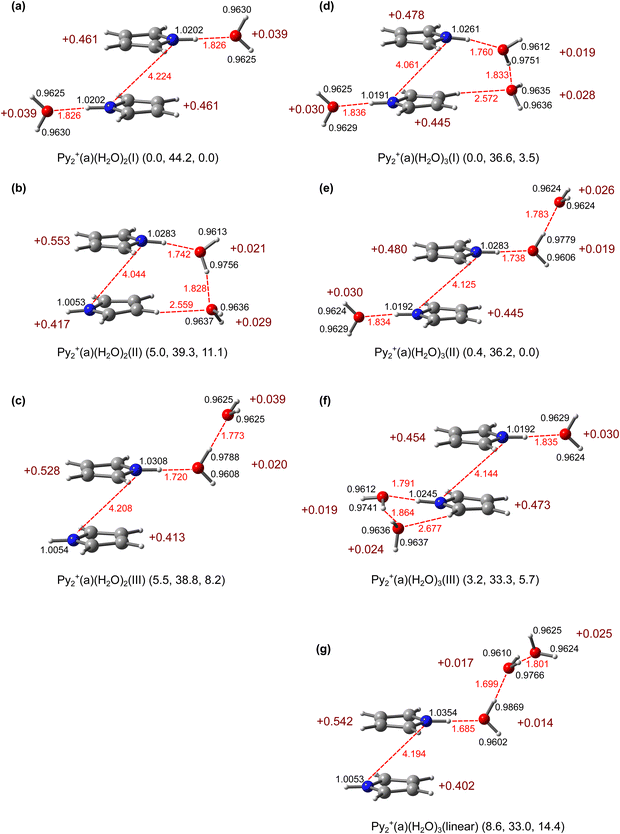
Based on the two stacked Py₂⁺(a/p) minima, several low-energy Py₂⁺H₂O structures are obtained, and the four most stable ones, Py₂⁺(a/p)H₂O(I and II), are shown in Fig. 3 and Fig. S2 (ESI†). Their computed IR spectra are compared in Fig. 4 and Fig. S3 (ESI†) to the IRPD spectra recorded for Py₂⁺H₂O and Py₂⁺H₂OAr. In the most stable structure, Py₂⁺(a)H₂O(I), H₂O is attached to Py₂⁺(a) via a nearly linear NH⋯O H-bond, a binding motif similar to the NH⋯N H-bond reported previously for Py₍₂₎⁺(a)N₂.^54,67 The H-bond in Py₂⁺(a)H₂O(I) is substantially weaker than that in Py⁺H₂O(H)⁵⁴ (R_NH⋯O = 1.809 vs. 1.704 Å, D₀ = 46.3 vs. 65.1 kJ mol⁻¹, E⁽²⁾ = 30.0 vs. 46.4 kJ mol⁻¹), because of the strongly reduced charge on the proton-donor Py molecule upon attachment of the second Py unit (from 1.0 to 0.5e). As a result of the weaker H-bond, the charge transfer to H₂O is smaller (q_H2O = 0.033 vs. 0.051e). The N–H donor bond becomes less elongated (r_NH = 1.0219 vs. 1.0363 Å, Δr_NH = 16 vs. 26 mÅ), leading to a smaller redshift in ν^b_NH (Δν^b_NH = −278 vs. −455 cm⁻¹, ν^b_NH = 3223 vs. 3004 cm⁻¹). The free N–H bond of the second Py unit contracts slightly upon monohydration (1.0057 vs. 1.0061 Å), resulting in an observed blueshift of 6 cm⁻¹ (ν^f_NH = 3506 vs. 3500 cm⁻¹). Monohydration completely decouples the two NH stretch oscillators of Py₂⁺(a), and the free NH stretch is a pure local mode of the free Py unit. Its partial charge is smaller than that on the H-bonded Py molecule (q_Py = 0.441 vs. 0.526e), which may be rationalised by the lower ionisation energy of PyH₂O as compared to Py (calculated as IE = 7.60 vs. 8.09 eV). This asymmetry in the Py₂⁺(a) charge distribution reduces the strength of the CR (vide infra). According to the q_Py–ν^f_NH relation, the lower charge is fully consistent with the blueshift of ν^f_NH. As in Py₂⁺(a)H₂O(I) the H-bond to H₂O is weaker than that in Py⁺H₂O(H), the O–H bonds in H₂O are less elongated (r_OH = 0.9632/0.9627 vs. 0.9636 Å) and the computed OH stretch frequencies are correspondingly higher (ν_1/3 = 3651/3739 vs. 3643/3729 cm⁻¹).

Fig. 3 Structures of (a) and (b) Py₂⁺(a)H₂O(I and II), (c) Py₂⁺(p)H₂O(I), and (d) Py₂⁺(a)H₂O(I)Ar(I) obtained at the B3LYP-D3/aug-cc-pVTZ level. Selected intra- and intermolecular bond lengths (in Å) are given in black and red, respectively. Values in dark red indicate NBO charges (in units of e). Energies in parentheses are the relative energy, the dissociation energy of the most weakly bonded ligand, and the relative Gibbs free energy at 298 K (E₀, D₀, and G₀ in kJ mol⁻¹).

Fig. 4 IRPD spectra of Py₂⁺H₂OAr_n (n = 0–1) recorded in the CH, NH, and OH stretch range are compared to linear IR absorption spectra calculated for Py₂⁺(a)H₂O(I and II) and Py₂⁺(a)H₂O(I)Ar(I and II) at the B3LYP-D3/aug-cc-pVTZ level (Tables S1 and S3, ESI†).

Py₂⁺(a)H₂O(II) is the second most stable isomer with a Py₂⁺(a) core. Its C₂ symmetric structure has a bifurcated CH⋯O H-bond of H₂O to two CH groups of the two Py units, with R_CH⋯O = 2.467 Å and D₀ = 28.5 kJ mol⁻¹. It is substantially less stable than the global minimum by 17.8 kJ mol⁻¹, because the two CH⋯O H-bonds are much weaker than the single NH⋯O H-bond, resulting in a smaller charge transfer to H₂O (q_H2O = 0.010 vs. 0.033e). The remaining charge on Py₂⁺ is shared symmetrically (leading to an optimised and fully developed CR) but somewhat lower than in bare Py₂⁺ (q_Py = 0.495 vs. 0.500e) due to the minor charge transfer to H₂O. In line with the q_Py–ν^f_NH relation, the N–H bonds are slightly shorter (1.0057 vs. 1.0061 Å), leading to a calculated blueshift of 5 cm⁻¹ for the two ν^f_NH frequencies (Table S3, ESI†).

The most stable isomer with a Py₂⁺(p) core, Py₂⁺(p)H₂O(I), shown in Fig. 3 features an asymmetric bifurcated nonlinear H-bond of H₂O (double acceptor) to both available NH donor groups (R_NH⋯O = 1.988 and 2.292 Å) and thus the highest H₂O dissociation energy (D₀ = 50.1 kJ mol⁻¹), although the individual NH⋯O H-bonds are much weaker than in Py₂⁺(a)H₂O(I). Hence, its energy gap to the Py₂⁺(a)H₂O(I) global minimum is reduced to only 3.7 kJ mol⁻¹. The two Py units are not equivalent, and the relatively free Py unit carries less positive charge than the more strongly H-bonded bottom one (q_Py = 0.456 vs. 0.517e). The weaker H-bond is strongly nonlinear and gives rise to an almost free ν_NH (E⁽²⁾ = 4.4 kJ mol⁻¹), while the stronger H-bond is more linear (E⁽²⁾ = 17.6 kJ mol⁻¹). As both NH groups are involved in H-bonding, we cannot readily apply the q_Py–ν^f_NH relation. The weaker H-bonded N–H bond is less elongated than the more strongly H-bonded one (r_NH = 1.0082 and 1.0147 Å), which results in two redshifted and strongly IR-active ν^b_NH modes at 3339 and 3466 cm⁻¹, respectively (Table S4, ESI†). To enable bifurcated H-bonding, the H₂O plane has to rotate by 90° providing direct access to both lone pairs of the O atom. In this way, H₂O attachment strongly reduces the distance between the two Py rings (R_N⋯N = 3.026 vs. 4.217 Å). Due to the charge transfer to H₂O (q_H2O = 0.027e), the O–H bonds become longer (r_OH = 0.9646 Å) and the OH stretch frequencies are redshifted compared to H₂O (ν_1/3 = 3632/3713 vs. 3657/3756 cm⁻¹). In contrast to Py₂⁺(p)H₂O(I), Py₂⁺(p)H₂O(II) has a single NH⋯O H-bond to the top Py unit. The geometric, energetic, and vibrational parameters of this NH⋯O H-bond are quite similar to those in Py₂⁺(a)H₂O(I), indicating that internal rotation of the free Py unit by 180° has only a small impact on the remote monohydration motif and interaction strength. As a result, the IR spectra predicted for Py₂⁺(a)H₂O(I) and Py₂⁺(p)H₂O(II) are very similar, too. The largest difference in both structures refers to the free N–H bond, which is shorter in Py₂⁺(p)H₂O(II) leading to a higher ν^f_NH (r_NH = 1.0048 vs. 1.0057 Å, ν^f_NH = 3517 vs. 3506 cm⁻¹), consistent with the modified CR, which is less asymmetric (0.485/0.483 vs. 0.526/0.441e).

Next, we briefly consider the predicted effects of Ar tagging on the properties of Py₂⁺H₂O by taking the example of the most stable Py₂⁺(a)H₂O(I) isomer (Fig. 3 and Fig. S4, ESI†). All considered Ar-tagged clusters have similar dissociation energies of D₀ = 4.2–6.8 kJ mol⁻¹, which are consistent with the experimentally determined Ar binding energy.⁶⁷ Because the Ar binding energy is very low compared to ∼100 and ∼50 kJ mol⁻¹ for the much stronger Py⁺⋯Py and Py₂⁺⋯H₂O interactions, respectively, the effects of Ar tagging are minor and thus we discuss only the two most stable Ar isomers, Py₂⁺(a)H₂O(I)Ar(I and II). They have slightly different N–H and O–H bond lengths because Ar affects their H-bonds in a different fashion. The NH⋯Ar H-bond of Ar to the free Py unit in Py₂⁺(a)H₂O(I)Ar(I) induces an N–H bond elongation by 0.8 mÅ to 1.0065 Å, resulting in a slight redshift of ν^f_NH from 3506 to 3494 cm⁻¹ (Table S1, ESI†). In Py₂⁺(a)H₂O(I)Ar(II), Ar forms an OH⋯Ar H-bond to the H₂O ligand and interacts weakly with two adjacent CH groups. Its proton donor N–H bond is longer by 0.8 mÅ than in Py₂⁺(a)H₂O(I)Ar(I) (1.0225 vs. 1.0217 Å), as H₂OAr has a larger PA than H₂O, which leads to a slight redshift in ν^b_NH from 3226 to 3212 cm⁻¹ (Table S3, ESI†). For the structures, binding energies, and IR spectra of the Py₂⁺(a)H₂O(I)Ar(III–V) and Py₂⁺(p)H₂O(I)Ar(I) isomers, the reader is referred to Fig. S2–S4 and Tables S3 and S4 (ESI†).

The IRPD spectra of Py₂⁺H₂O and Py₂⁺H₂OAr are compared in Fig. 4 to the IR spectra computed for the Py₂⁺(a)H₂O(I and II) and Py₂⁺(a)H₂O(I)Ar(I and II) isomers. The positions and widths of the transitions observed are listed in Table S1 (ESI†) along with vibrational and isomer assignments. The IRPD spectrum of Py₂⁺H₂O exhibits ten main transitions A, A′, B, B′, E, F, F′, G, Y, and Y′ at 3725, 3705, 3639, 3605, 3492, 3228, 3282, 3134, 3006, and 3175 cm⁻¹ with widths of 13–58 cm⁻¹. The IRPD spectrum of Py₂⁺H₂OAr shows corresponding, but better resolved, transitions at 3727, 3706, 3642, 3607, 3488, 3210, 3274, 3133, 3010, and 3175 cm⁻¹, respectively, with similar intensity ratios but much smaller widths (4–28 cm⁻¹), because the lower binding energy leads to colder clusters. The small shifts of ≤10 cm⁻¹ imply that Ar tagging has indeed little impact on the Py₂⁺H₂O structure and resulting IR spectrum apart from the substantially improved spectral resolution. An even colder IRPD spectrum of Py₂⁺H₂OAr measured in the range of 3100–3800 cm⁻¹ exhibits only six main transitions (A, B, E, F, G, and Y′ at 3727, 3642, 3489, 3213, 3141, and 3178 cm⁻¹) with even narrower widths and the absence of the minor peaks A′, B′, and F′ present in the IRPD spectra of Py₂⁺H₂O and Py₂⁺H₂OAr recorded under warmer conditions. This difference suggests a minor contribution of less stable isomers that are responsible for A′, B′, and F′. The colder IRPD spectrum of Py₂⁺H₂OAr also shows that the most abundant and thus most stable isomer can be probed by tagging under the coldest conditions. The major transitions in the IRPD spectra of Py₂⁺H₂O(Ar) can be explained by the most stable Py₂⁺(a)H₂O(I) isomer. Indeed, good agreement is observed between measured and computed IR spectra concerning both the positions and relative intensities of the vibrational transitions. Bands A and B of Py₂⁺H₂O at 3725 and 3639 cm⁻¹ correspond well with the predicted transitions of ν₃ = 3739 and ν₁ = 3651 cm⁻¹. Band E at 3492 cm⁻¹ can be assigned to ν^f_NH predicted at 3506 cm⁻¹. Its modest blueshift of 13 cm⁻¹ upon monohydration from 3479 to 3492 cm⁻¹ is well reproduced by the calculations (from 3500 to 3506 cm⁻¹). The intense band F at 3228 cm⁻¹ is readily assigned to ν^b_NH predicted at 3223 cm⁻¹. Its blue-shaded band contour confirms the assignment to a proton-donor stretch vibration, consistent with the strong NH⋯O ionic H-bond.^54,80,81,114 This band shows again drastic narrowing and a small redshift (−18 cm⁻¹) as a result of cooling by Ar tagging.^54,80–82 Band G observed at 3134 cm⁻¹ is attributed to the eight unresolved and nearly degenerate ν_CH modes with a predicted spread of only 24 cm⁻¹. The colder IRPD spectrum of Py₂⁺H₂OAr exhibits only the major peaks A, B, E, F, G, and Y′ assigned to Py₂⁺H₂O(I)Ar(I). Therefore, the absent minor peaks A′, B′, and F′ observed in the IRPD spectrum of Py₂⁺H₂O and warmer Py₂⁺H₂OAr must come from a higher-energy isomer. Although the substantially less stable Py₂⁺(a)H₂O(II) can at first glance be excluded as a major carrier of the spectrum because of its high relative energy (E₀ = 17.8 kJ mol⁻¹) and the lack of the intense ν^b_NH transition (band F), it can be still considered as a candidate for the minor contribution from its predicted (scaled) harmonic frequencies (vide infra). Next, Py₂⁺(p)H₂O(I) can be excluded as the predominant carrier (Fig. S3a, ESI†) because of the lack of its intense ν^b_NH band predicted at 3339 cm⁻¹ in the observed IRPD spectrum although its relative energy is higher by only 3.7 kJ mol⁻¹ compared to Py₂⁺(a)H₂O(I). However, the predicted harmonic ν_1/3 of Py₂⁺(p)H₂O(I) are lower than those of Py₂⁺(a)H₂O(I) (3651/3713 vs. 3651/3739) and ν^b_NH is higher (3339 vs. 3223 cm⁻¹), indicating that Py₂⁺(p)H₂O(I) may contribute to the minor peaks A′, B′, and F′. The slightly less stable Py₂⁺(p)H₂O(II) isomer will not be considered any further because of the close similarity of its predicted spectrum to that of the assigned Py₂⁺(a)H₂O(I) global minimum. Although the scaled harmonic spectra of Py₂⁺(a/p)H₂O(I) explain most of the peaks (A–G), none of the structures can explain peaks Y and Y′. Therefore, we consider anharmonic calculations for Py₂⁺(a)(H₂O)(I) conducted at the reduced B3LYP-D3/aug-cc-pVDZ level (Fig. S3b, ESI†). These calculations suggest an assignment of band Y to the NH bend overtone (2β_NH) of the N–H⋯O H-bonded Py unit, which gains intensity via Fermi resonance with the nearby and strongly IR-active ν^b_NH fundamental.^{82,102,103,115} Shoulder Y′ may be assigned to the OH bend overtone (2β_OH) of H₂O.^116–119 Although the B3LYP-D3/aug-cc-pVDZ level explains the anharmonicity of Py₂⁺(a) well, it overestimates the anharmonicity of ν_1/3 of NH⋯O H-bonded H₂O. Therefore, we also consider the PBE0/aug-cc-pVDZ level to support our anharmonic predictions. Fig. S3b (ESI†) shows the reliability of the PBE0/aug-cc-pVDZ level by comparison to the harmonic and anharmonic spectra calculated at the B3LYP-D3/aug-cc-pV(D/T)Z levels. The anharmonic frequencies of Py₂⁺(a/p)H₂O(I) calculated at the PBE0/aug-cc-pVDZ level are again in good agreement with our assignment.

The higher-resolved IRPD spectra of the colder Ar-tagged ions reveal small additional bands under certain experimental conditions, indicating the minor presence of higher-energy isomers. These may arise from different Py₂⁺H₂O isomers or different Ar tagging sites of the major assigned Py₂⁺(a)H₂O(I) core. Band E observed at 3489 cm⁻¹ and assigned to ν^f_NH of Py₂⁺H₂OAr in the cold spectrum is redshifted by 3 cm⁻¹ from that of Py₂⁺H₂O (3492 cm⁻¹), suggesting that Ar is attached to the free NH group of Py₂⁺(a)H₂O(I) in the major Py₂⁺H₂OAr isomer, with a computed redshift of 13 cm⁻¹. The other four Py₂⁺(a)H₂O(I)Ar(II–V) isomers, in which Ar does not bind to the NH group, do not reproduce this ν^f_NH redshift (Fig. S4 and Table S3, ESI†). The somewhat warmer Py₂⁺H₂OAr spectrum in Fig. 4 shows additional small bands A′, B′, and F′ at 3706, 3607, and 3274 cm⁻¹, which are similar to those of the bare Py₂⁺H₂O spectrum at 3705, 3605, and 3282 cm⁻¹, indicating a small contribution of Py₂⁺(p)H₂O(I)Ar. The observed redshift in F′ from 3282 to 3274 cm⁻¹ suggests that the Ar may bind to the NH group of Py₂⁺(p)H₂O(I) as shown in Fig. S2 and S3 (ESI†). The abundance of Py₂⁺(p)H₂O(I)Ar(I) is estimated to be below 25% when considering its computed ν^b_NH intensity (Fig. S3e, ESI†). The IRPD spectrum of colder Py₂⁺H₂OAr exhibits sharp bands with no splitting in the range of ν_1/3, revealing the sole presence of Py₂⁺(a)H₂O(I), while the other high-energy isomers are below the detection limit of 5% by considering the signal-to-noise ratio of peak F (ν^b_NH).

3.4. Py₂⁺(H₂O)₂

Our B3LYP-D3 calculations yield seven dihydrated isomers with a Py₂⁺(a) core, Py₂⁺(a)(H₂O)₂(I–VII) (Fig. 5 and Fig. S5, ESI†). These can be divided into two groups depending on whether two individual H₂O ligands or an H-bonded (H₂O)₂ dimer are attached to Py₂⁺(a). In the highly-symmetric global minimum (C_2h), Py₂⁺(a)(H₂O)₂(I), which belongs to the first group, two individual H₂O ligands form equivalent NH⋯O H-bonds to the two available acidic NH groups of Py₂⁺(a). The next two isomers II and III belong to the second group, in which a (H₂O)₂ dimer chain is attached to one of the NH groups either with or without a second CH⋯O contact, respectively, while the other NH group remains free. The latter structure is similar to that of Py⁺(H₂O)₂ reported previously.⁸⁰ The relative energies calculated for isomers I–III are E₀ = 0.0, 5.0, and 5.5 kJ mol⁻¹, and their relative free energies amount to G₀ = 0.0, 11.1, and 8.2 kJ mol⁻¹, respectively. The energy gap between I and both II and III increases significantly with temperature due to the reduced entropy contribution for the less flexible isomers II and III resulting from the structural constraints of the (H₂O)₂ unit. From the energetics, I–III are expected to dominate the Py₂⁺(H₂O)₂ population in the molecular beam. The other isomers IV–VII, which also feature NH⋯O and CH⋯O H-bonds, are substantially higher in energy (E₀ = 8.5–37.2 and G₀ = 15.4–40.6 kJ mol⁻¹) and thus not considered in detail further.

Fig. 5 Structures of Py₂⁺(a)(H₂O)_n with n = 2 (a)–(c) and n = 3 (d)–(g) obtained at the B3LYP-D3/aug-cc-pVTZ level. Selected intra- and intermolecular bond lengths (in Å) are given in black and red, respectively. Values in dark red indicate NBO charges (in units of e). Energies in parentheses indicate the relative energy, the dissociation energy of the most weakly bonded ligand, and the relative Gibbs free energy at 298 K (E₀, D₀, and G₀ in kJ mol⁻¹).

The NH⋯O H-bonds in the dihydrated Py₂⁺(a)(H₂O)₂(I) global mininum are slightly weaker than that of the related monohydrated Py₂⁺(a)H₂O(I) isomer (R_NH⋯O = 1.826 vs. 1.809 Å, D₀ = 44.2 vs. 46.3 kJ mol⁻¹, E⁽²⁾ = 37.7 vs. 30.0 kJ mol⁻¹), with a smaller perturbation of the N–H proton donor bond (r_NH = 1.0202 vs. 1.0219 Å, ν^b_NH = 3247 vs. 3223 cm⁻¹). This is the result of the slightly noncooperative three-body induction forces for interior ion solvation with individual ligands due to extended delocalisation of the positive charge. The asymmetric CR in Py₂⁺(a)H₂O(I) becomes symmetric again in Py₂⁺(a)(H₂O)₂(I) (q_Py = 0.526/0.441 vs. 0.461/0.461e). Although the individual H-bonds are weaker, the charge transfer to the H₂O ligands is increased in Py₂⁺(a)(H₂O)₂(I) (q_H2O = 0.039 vs. 0.033e) because of the restored symmetry and optimised CR interaction.

Both Py₂⁺(a)(H₂O)₂(II and III) local minima have a similar solvent configuration with one free NH group and one NH group solvated by (H₂O)₂, resulting in a similar charge distribution. Their major difference is that the terminal H₂O in II has an additional weak CH⋯O contact with Py₂⁺(a), forming a four-membered cyclic ring. This additional H-bond causes, however, strain on the other H-bonds which become weaker in II compared to III, so that the net energy gain by increasing the size of the H-bonded network is only 0.5 kJ mol⁻¹. The intermolecular Py⋯H₂O and H₂O⋯H₂O distances in isomer II are longer than in III, and the N–H proton donor bond elongates less (r_NH = 1.0283 vs. 1.0308 Å, ν^b_NH = 3107 vs. 3068 cm⁻¹) due to the weakened NH⋯O H-bond. As (H₂O)₂ is attached to Py₂⁺ in II and III, the resulting NH⋯O H-bond is much stronger than in I (R = 1.742 and 1.720 vs. 1.826 Å), because of the higher PA of (H₂O)₂ compared to H₂O and the enhanced charge transfer to the solvent (q_H2O = 0.050 and 0.059 vs. 0.039e). As a result, the elongation of the N–H proton donor bond is larger (r_NH = 1.0283 and 1.308 vs. 1.0202 Å), causing larger NH stretch redshifts (ν^b_NH = 3107 and 3068 vs. 3247 cm⁻¹). The same PA argument explains the stronger NH⋯O H-bond in dihydrated Py₂⁺(a)(H₂O)₂(III) compared to that in monohydrated Py₂⁺(a)H₂O(I). The high cooperativity of three-body induction forces typical for H-bonded solvent networks also strongly strengthens the H-bond of (H₂O)₂ (Fig. 2) by the presence of the positive charge of the nearby Py₂⁺ ion (R = 1.773 vs. 1.946 Å, D₀ = 38.8 vs. 13.0 kJ mol⁻¹). Nonetheless, these H-bonds are in Py₂⁺(a)(H₂O)₂(III) with a Py₂⁺(a) core substantially weaker than those in Py⁺(H₂O)₂(I) with a Py⁺ core (R_NH⋯O = 1.720 vs. 1.609 Å, R_OH⋯O = 1.773 vs. 1.732 Å) due to the increased charge delocalisation arising from the CR (q_Py = 0.528 vs. 0.926e). The free NH group of Py₂⁺(a) becomes progressively less acidic with mono- and dihydration (r_NH = 1.0061, 1.0057, 1.0054 Å for n = 0–2), resulting in small incremental blueshifts of ν^f_NH as n increases from 0 to 2 (3500, 3506, and 3510 cm⁻¹).

Before comparing the computed IR spectra to the IRPD spectra, we briefly discuss the effects of Ar tagging on the structure and energy of Py₂⁺(a)(H₂O)₂ (Fig. S6, ESI†), with particular focus on the Py₂⁺(a)(H₂O)₂(I) global minimum with C_2h symmetry. The three most stable Py₂⁺(a)(H₂O)₂(I)Ar(I–III) isomers have Ar binding energies of D₀ = 6.7, 4.3, and 3.2 kJ mol⁻¹. In the most stable Ar(I) isomer, Ar binds to the OH group of H₂O and one CH group of Py. In the Ar(II) isomer, Ar interacts with the π electron ring of Py and thus has the least perturbation on the structure and IR spectrum of Py₂⁺(a)(H₂O)₂. In Ar(III), Ar forms a linear OH⋯Ar H-bond to one of the H₂O ligands, which causes redshifts of 7 and 5 cm⁻¹ in ν₃ and ν₁ of Py₂⁺(a)(H₂O)₂(I), respectively. In Ar complexes of the higher-energy isomer Py₂⁺(a)(H₂O)₂(II), Ar preferentially binds to the free NH group, resulting in its slight elongation of 0.2 mÅ. Nevertheless, ν^f_NH redshifts by only 2 cm⁻¹ (3508 vs. 3510 cm⁻¹). In Py₂⁺(a)(H₂O)₂(III)Ar(I), Ar is part of a four-membered ring with OH⋯Ar⋯HC bonds, whereas in isoenergetic Py₂⁺(a)(H₂O)₂(III)Ar(II), Ar binds to the free NH group of Py and elongates its N–H bond by 0.7 mÅ, resulting in a slight redshift of ν^f_NH by 8 cm⁻¹ (from 3508 to 3500 cm⁻¹). At higher temperature, Py₂⁺(a)(H₂O)₂(III)Ar(II) is more favourable than Py₂⁺(a)(H₂O)₂(III)Ar(I) due to entropy (G₀ = 2.4 vs. 10.3 kJ mol⁻¹). For the structures, binding energies, and IR spectra of the less stable Py₂⁺(a)(H₂O)₂(IV-VI)Ar isomers, the reader is referred to Fig. S6 and Table S5 (ESI†). As expected from the weak Ar interaction energies (D₀ ≤ 7 kJ mol⁻¹), the overall impact of Ar tagging on the computed IR spectra (<10 cm⁻¹) and energetic order is very minor for all considered Py₂⁺(a)(H₂O)₂ isomers and thus not considered in detail further.

The IRPD spectra of Py₂⁺(H₂O)₂ and Py₂⁺(H₂O)₂Ar are compared in Fig. 6 to the IR spectra computed for the three most stable isomers Py₂⁺(a)(H₂O)₂(I–III) with a Py₂⁺(a) core. The positions and widths of the transitions observed are listed in Table S1 (ESI†), along with vibrational and isomer assignments. The IRPD spectrum of Py₂⁺(H₂O)₂ exhibits 13 major transitions at 3726 (A), 3639 (B), 3703 (C′), 3684 (C′′), 3430 (D′), 3388 (D′′), 3493 (E), 3260 (F), 3093 (F′), 3014 (F′′), 3136 (G), 2852 (X), and 2967 (Y) cm⁻¹, with widths of 12–64 cm⁻¹. The IRPD spectrum of Py₂⁺(H₂O)₂Ar recorded in a smaller spectral range has corresponding transitions at 3730 (A), 3643 (B), 3706 (C′), 3700 (C′′), 3424 (D′), 3376 (D′′), 3493 (E), 3242 (F), and 3135 (G) cm⁻¹, respectively, with similar intensity ratios but much smaller widths (3–19 cm⁻¹). Ar tagging shifts of those peaks are less than 18 cm⁻¹ and on average only 7 cm⁻¹. Thus, Ar tagging has essentially no impact on the intermolecular structure and vibrational signatures of the observed Py₂⁺(H₂O)₂ isomers. As Py₂⁺(a)(H₂O)₂ has only six NH/OH stretch oscillators (2ν_NH, 4ν_OH), a single isomer cannot explain all observed features detected in this spectral range. Therefore, several isomers need to be considered. The major three bands A, B, and F observed for Py₂⁺(H₂O)₂ and Py₂⁺(H₂O)₂Ar are fully reproduced by the most stable isomer of Py₂⁺(a)(H₂O)₂(I) concerning both band positions and relative intensities. The most intense and strongly blueshaded band F is readily assigned to ν^b_NH, while the weak bands A and B are assigned to ν₃ and ν₁, respectively. Because of C_2h symmetry of Py₂⁺(a)(H₂O)₂(I), only three out of the six OH/NH stretch fundamentals are IR-active, namely the out-of-phase linear combinations of ν^b_NH, ν₁, and ν₃. Band G at 3136 cm⁻¹ assigned to ν_CH is not sensitive to isomeric structure. Band E at 3493 cm⁻¹ is close to ν^f_NH of Py₂⁺ and well reproduced by Py₂⁺(a)(H₂O)₂(II and III), both of which exhibit a free NH group. In addition, the (H₂O)₂ unit of isomers II and III give rise to ν^b_OH and ν^f_OH bands of the H₂O donor, which are predicted to be close to the D′/D′′ and C′/C′′ pairs. Their corresponding ν^b_NH bands may be attributed to bands F′/F′′. The interpretation of the weak bands Y and X is less certain, as no fundamentals are predicted in this range for any of the considered isomers. Similar to the n = 1 cluster, they may arise from Fermi resonance of 2β_NH/ν^b_NH.^54,67 In summary, Py₂⁺(a)(H₂O)₂(I) is concluded as the major carrier of the IRPD spectrum of Py₂⁺(H₂O)₂, while Py₂⁺(a)(H₂O)₂(II and III) account for all remaining weaker transitions. When comparing the computed and measured intensities of the assigned ν^b_NH bands (Fig. 6a), the relative abundances of isomers I–III can roughly be estimated as 65, 10, and 25%, consistent with their relative free energies of G₀ = 0.0, 11.1, and 8.2 kJ mol⁻¹, respectively.

Fig. 6 IRPD spectra of (a) Py₂⁺(H₂O)₂Ar_n (n = 0–1) and (b) Py₂⁺(H₂O)₃ recorded in the CH, NH, and OH stretch range are compared to the linear IR absorption spectra calculated for Py₂⁺(a)(H₂O)_n(I–III) (n = 2–3) at the B3LYP-D3/aug-cc-pVTZ level (Tables S1, S5, and S7, ESI†).

Interestingly, microhydration reduces the energy gap ΔE₀(a–p) between Py₂⁺(a) and Py₂⁺(p) due to the more favourable formation of H-bonded solvent networks with two NH⋯O ionic H-bonds. For example, ΔE₀(a–p) = 7.5 and 3.7 kJ mol⁻¹ for n = 0 and 1, respectively. Indeed, for n = 2 the most stable Py₂⁺(p)(H₂O)₂(I) isomer with a Py₂⁺(p) core is computed to be even more stable than Py₂⁺(a)(H₂O)₂(I) by ΔE₀(a–p) = −1.0 kJ mol⁻¹ (Fig. S7, ESI†). However, from an entropic point of view, ΔG₀(a–p) = +6.0 kJ mol⁻¹ for n = 2 due to the strain imposed by the H-bonded network. The two most stable Py₂⁺(p)(H₂O)₂(I and II) isomers form tetra- and tricyclic rings involving Py₂⁺(p) and (H₂O)₂, with ΔE₀ = −1.0 and +3.4 kJ mol⁻¹, respectively. In Py₂⁺(p)(H₂O)₂(I), (H₂O)₂ acts as a dual H-bond acceptor with two individual NH⋯O H-bonds, while in Py₂⁺(p)(H₂O)₂(II) both NH groups attack the donor of (H₂O)₂via a bifurcated O⋯(HN)₂ configuration, similar to monohydrated Py₂⁺(p)H₂O(I). The larger PA of (H₂O)₂ results in a larger cooperative effect, thereby reducing ΔE₀(a–p). Although Py₂⁺(p)(H₂O)₂(I) is predicted as the most stable Py₂⁺(H₂O)₂ structure at T = 0 K and the OH stretches (ν₃, ν^f_OH, ν₁, ν^b_OH) seem to be consistent with the observed bands A, B, and E, the predicted ν^b_NH bands disagree with the IRPD spectrum (Fig. S8 and Table S6, ESI†). The same conclusion applies also to the next stable Py₂⁺(p)H₂O(II) isomer with a Py₂⁺(p) core. Therefore, the population of Py₂⁺(p)(H₂O)₂ isomers is concluded to be below the detection limit of 15%, considering the achieved signal-to-noise ratio of band F and the computed IR oscillator strengths of ν^b_NH bands of Py₂⁺(a/p)(H₂O)₂(I).

3.5. Py₂⁺(H₂O)₃

The optimised geometries of Py₂⁺(a)(H₂O)₃(I–III) based on the most abundant structure of Py₂⁺(a)(H₂O)₂(I) are shown in Fig. 5d–f. All isomers are constructed through two NH⋯O H-bonds, in which one NH group is solvated by (H₂O)₂ and the other one by a single H₂O. They differ only by the orientation of the linear (H₂O)₂, which is close to that in isomers II–IV of Py₂⁺(a)(H₂O)₂, and their energies increase as E₀ = 0.0, 0.4, and 3.2 kJ mol⁻¹, respectively. Similar to Py₂⁺(a)(H₂O)₂(II and III), Py₂⁺(a)(H₂O)₃(II) with the free dangling (H₂O)₂ is more stable than Py₂⁺(a)(H₂O)₃(I) at higher temperature (G₀ = 0.0 vs. 3.5 kJ mol⁻¹). In general, the intermolecular distances in Py₂⁺(a)(H₂O)₃(I–III) are longer compared to those of Py₂⁺(H₂O)₂(II–IV) due to the weaker H-bonds, resulting in slight blueshifts of ν^b_NH/OH. The weaker H-bonds in n = 3 are due to increased delocalisation of the excess positive charges on the Py units compared to n = 2, resulting again from an increased perturbation of the CR by the third H₂O ligand.

The IRPD spectrum of Py₂⁺(H₂O)₃ is compared in Fig. 6 to the linear IR spectra computed for Py₂⁺(a)(H₂O)₃(I–III). The positions and widths of the transitions observed are listed in Tables S1 and Fig. S7 (ESI†) along with vibrational and isomer assignments. The isomers based on the Py₂⁺(p) core are shown in Fig. S9 (ESI†) and their IR spectra are compared in Fig. S10 (ESI†). Compared to the n = 1–2 clusters, the IRPD spectrum of n = 3 is significantly more congested with broader bands (9–85 cm⁻¹), thus complicating the assignment. It exhibits nine transitions at 3732 (A), 3642 (B), 3702 (C′), 3683 (C), 3293 (F), 3139 (F′), 3459 (D), 3388 (D′), and 3139 (G) cm⁻¹. The trend in the IRPD spectra of mono- and dihydrated Py₂⁺(a) in Fig. 1 provides hints about potential Py₂⁺(H₂O)₃ structures. First, the absence of a sharp peak E (ν^f_NH) indicates that both NH groups of Py₂⁺ are hydrated. Second, bands C/C′ and D/D′, which are typical for ν^f_OH and ν^b_OH modes of single-donor H₂O ligands are enhanced compared to those in the IRPD spectrum of Py₂⁺(H₂O)₂. This observation suggests an increased abundance of structures with an NH⋯O H-bond of the NH groups to a (H₂O)₂ chain. Band F (ν^b_NH) at 3293 cm⁻¹ appears similarly to ν^b_NH of n = 1–2, indicating the presence of a NH group which is H-bonded to a single H₂O ligand. The intense and broad feature attributed to F1/G at 3139 cm⁻¹ covers ν_CH and has a comparable intensity to band F assigned to the more strongly H-bonded ν^b_NH of an NH group binding to (H₂O)₂. Band F of the n = 3 cluster is blueshifted compared to those of n = 1–2, indicating that the H-bond strength weakens with increasing number of H₂O ligands around Py₂⁺. This observation is typical for noncooperative effects of progressive interior ion solvation and indicates that the partial positive charge on the Py units of Py₂⁺ decreases with increasing n, thereby weakening the charge-dipole interaction of the NH⋯O H-bonds. Overall, the IRPD spectrum of Py₂⁺(H₂O)₃ is consistent with the computed Py₂⁺(a)(H₂O)₃(I–III) isomers, although only I and II are required to explain all observed transitions, in particular in the ν^b_OH range.

Because I and II are nearly isoenergetic, both isomers should be considered. Py₂⁺(a)(H₂O)₃(I) has three intense bands (ν^b_NH, ν^b_OH) predicted below 3500 cm⁻¹ and five weak bands (ν₁, ν^f_OH, ν₃) above 3600 cm⁻¹. The lowest ν^b_NH band arising from the H-bond to (H₂O)₂ is strongly coupled with the aromatic ν_CH modes (local mode mixing). This coupled ν^b_NH and the second ν^b_NH at 3268 cm⁻¹, which comes from the H-bond to H₂O, are consistent with the observed bands at 3139 and 3293 cm⁻¹ (F1 and F), respectively. The ν^b_OH mode of the OH⋯O H-bond of (H₂O)₂ reproduces the observed band at 3459 cm⁻¹ (D). The free OH stretches ν₃, ν^f_OH, and ν₁ correspond to the observed bands A and B. However, the bands C and C′ at 3683 and 3702 cm⁻¹, which are more intense and sharper than A and B and correspond to ν^f_OH of a single-donor H₂O, are not predicted well by isomer I. On the other hand, isomer II offers the same assignment as Py₂⁺(a)(H₂O)₃(I), except that ν^b_OH corresponds to the observed band D′. However, again bands C and C′ cannot be fully explained by II in terms of both their intensities and positions.

In an effort to assign bands C and C′, isomers based on Py₂⁺(p) are considered because the most stable structure found for n = 3, Py₂⁺(p)(H₂O)₃(I), is indeed more stable than Py₂⁺(a)(H₂O)₃(I), D₀ = 43.3 vs. 36.6 kJ mol⁻¹ (Fig. S9, ESI†). In this structure, the third H₂O expands the H-bonded solvent network of the four-membered Py₂⁺(p)(H₂O)₂(I) ring at its surface, resulting in two ionic NH⋯O and two neutral OH⋯O H-bonds. Compared to Py₂⁺(a)(H₂O)₂(I), all H-bonds become stronger because of cooperativity. Due to the same cooperative effect, Py₂⁺(p)(H₂O)₃(I) is more stable than Py₂⁺(a)(H₂O)₃(I) by ΔE₀ = 7.7 kJ mol⁻¹. However, due to the strain of its cyclic H-bond network, ΔG₀ is still in favour of Py₂⁺(a)(H₂O)₃(I) by 1.4 kJ mol⁻¹. Its predicted IR spectrum differs slightly in the ν_OH range, exhibiting two ν^f_OH and two ν^b_OH at 3720/3706 and 3458/3363 cm⁻¹, and ν_3/1 = 3727/3641 cm⁻¹, respectively. Comparing this predicted IR spectrum with the measured IRPD spectrum, peaks A and B may also be assigned to ν₃ and ν₁, C/C′ to ν^f_OH, and D/D′ to ν^b_OH, while F/F′ match with ν^b_NH (Fig. S10 and Table S8, ESI†). A further local minimum, Py₂⁺(p)(H₂O)₃(II), in which the third H₂O is attached at another binding site in the (H₂O)₃ network is also predicted to be more stable than Py₂⁺(a)(H₂O)₃(I) by ΔE₀ = 5.0 kJ mol⁻¹ (Fig. S9, ESI†). Its predicted IR spectrum is, however, not compatible with the IRPD spectrum in the ν^b_NH range. Hence, the two most stable antiparallel Py₂⁺(a)(H₂O)₃(I and II) isomers and the most stable parallel Py₂⁺(p)(H₂O)₃(I) isomer can fully account for the measured IRPD spectrum. Due to the broad widths of the bands observed in the IRPD spectrum, a more definitive determination of their individual contributions is not feasible at the current spectral resolution. Unfortunately, the achieved Py₂⁺(H₂O)₃Ar ion yield has been insufficient to record a cold spectrum with better resolution for the n = 3 cluster.

3.6. Impact of stepwise hydration on the CR

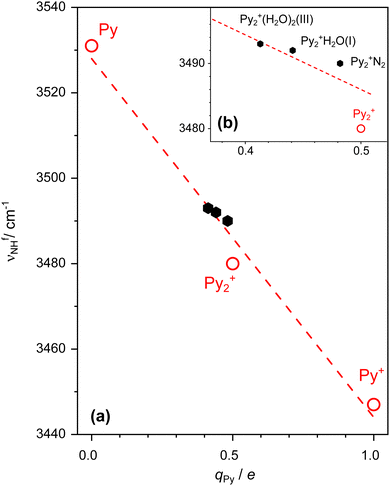
Inspection of Fig. 1 reveals that the free NH stretch band ν^f_NH (band E) of the free Py units shows small but systematic shifts as a function of solvation. Our previous study demonstrates a linear correlation between ν^f_NH of the free Py unit in Py_n⁺ with n = 0–2 and its partial charge q_Py, ν^f_NH(q_Py)/cm⁻¹ = −83.8 q_Py/e + 3527.8 as indicated by the dashed line in Fig. 7.²³ Using this correlation, ν^f_NH measured for Py₂⁺N₂ has been successfully used to determine small changes in the charge distribution of Py₂⁺(a) upon N₂ complexation due to symmetry breaking and charge delocalisation.²³ H₂O solvation induces a stronger perturbation of Py₂⁺(a) because of its large dipole moment,^54,102 leading to a stronger H-bond and larger charge delocalisation. As a result, ν^f_NH measured for Py₂⁺H₂O is slightly more blueshifted than ν^f_NH of Py₂⁺N₂ (3492 vs. 3490 cm⁻¹), corresponding to a lower partial charge on free Py (q_Py = 0.427 vs. 0.451e). This experimentally determined charge, q_Py = 0.427e, agrees reasonably well with the NBO charge computed for Py₂⁺(a)H₂O(I), q_Py = 0.441e. For Py₂⁺(H₂O)₂, ν^f_NH observed at 3493 cm⁻¹ is assigned to the minor Py₂⁺(a)(H₂O)₂(III) isomer. The partial charge of its free Py unit estimated as q_Py = 0.415e from the correlation is well reproduced by its NBO charge of 0.413e. Its NH⋯O H-bond is stronger than in Py₂⁺(a)H₂O(I) because the PA of (H₂O)₂ is higher than the PA of H₂O (808 vs. 691 kJ mol⁻¹).^70,71,80 Because the IE of the Py(H₂O)₂ unit in Py₂⁺(a)(H₂O)₂(III) is lower than the IE of PyH₂O in Py₂⁺(a)H₂O(I), the partial charge on free Py is lowered in Py₂⁺(a)(H₂O)₂(III) compared to Py₂⁺(a)H₂O(I). Interestingly, a comparison between the higher-energy isomers III and IV of Py₂⁺(a)(H₂O)₂, which differ by the way the (H₂O)₂ dimer binds to Py₂⁺(a) (linear or cyclic) reveals that subtle differences in the solvation network also have an impact on the charge of the free Py unit (q_Py = 0.413 vs. 0.425e, Fig. S5, ESI†). The smaller charge transfer to (H₂O)₂ in IV compared to III (q_H2O = 0.046 vs. 0.059e) may be an indication of the weaker H-bonds in the solvent network. Therefore, the charge distribution and CR in Py₂⁺(a) can be affected by the H-bond strength even for similar hydration motifs. As can be seen from Fig. 7, the two available experimental ν^f_NH data points for isomer I of n = 1 and isomer III of n = 2 are compatible with the initially derived linear q_Py–ν^f_NH dependence.

Fig. 7 (a) Observed ν^f_NH values for Py, Py⁺, and Py₂⁺ (open circles) and Py₂⁺N₂ and Py₂⁺(H₂O)_1,2 (filled circles) as a function of the calculated NBO charge on the free Py unit (q_Py). The dashed line is a linear fit obtained by using ν^f_NH of Py, Py⁺, and Py₂⁺. (b) Expanded view in the vicinity of Py₂⁺ and its solvated clusters.

To systematically analyse the impact of stepwise hydration on the CR, we consider the related Py₂⁺(a)(H₂O)_n isomers for n = 1–3, in which a linear (H₂O)_n chain is attached to one Py unit via a linear NH⋯O ionic H-bond. These are isomers I (n = 1), III (n = 2), and linear (n = 3) shown in Fig. 3 and 5, respectively. As the PA of (H₂O)_n clusters increases with n (691 < 808 < 862 kJ mol⁻¹ for n = 1–3)^{70,71,120,121} the NH⋯O H-bond becomes stronger and shorter (1.809 > 1.720 > 1.685 Å). The gradually increasing negative ρ* values with increasing n (−0.034, −0.043, −0.047 a.u.) from the NCI analysis (Fig. S11, ESI†) and E⁽²⁾ donor–acceptor interaction energies (30.0 < 54.6 ≈ 50.5 kJ mol⁻¹) support the increased H-bond strengths, which are well reproduced by the strongly redshifted ν^b_NH available from the experiment (3228 > 3014 cm⁻¹ for n = 1–2) and the calculation (3223 > 3068 > 2937 cm⁻¹ for n = 1–3, Table S9, ESI†). The increased H-bond strengths of the NH⋯O and OH⋯O H-bonds as a function of n are also visible in the increased cooperativity calculated from the difference between the total interaction energy and the sum of the individual interactions (13% for n = 2 and 20% for n = 3, Table S10, ESI†). This result is in line with the increasing charge transfer to the solvent (0.033, 0.059, 0.056e). As a result of the stronger H-bond, the N–H bond of the free Py units contracts slightly (1.0057 > 1.0054 > 1.0053 Å), leading to increasing computed ν^f_NH (3506 < 3510 < 3512 cm⁻¹ for n = 1–3), which are in good agreement with available experimental values (3492 < 3493 for n = 1–2). As ν^f_NH increases with n, the computed NBO charges on the free Py unit decrease accordingly (0.441 > 0.413 > 0.402e). These values agree well with those derived from the q_Py–ν^f_NH relation using the experimental ν^f_NH values (0.427 > 0.415 > 0.403e). Interestingly, the total charge transfer to (H₂O)₃ of 0.056e is close to that of (H₂O)₂, 0.059e, due to the similar IEs of Py(H₂O)₂ and Py(H₂O)₃ computed as 7.46 and 7.47 eV, which relates to the similar IEs of (H₂O)₂ and (H₂O)₃ reported as 10.73 and 10.06 eV.¹²² Therefore, the critical hydration number for the partial charge transfer from Py₂⁺(a) to the H₂O solvent cluster may be determined as n = 2.

Next, we discuss the impact of the CR interaction on the H-bond motifs. Due to its C_2h symmetry, the two N–H bonds in Py₂⁺(a) have the same acidity and strength (r_NH = 1.0061 Å). In Py₂⁺(a)H₂O(I), H₂O forms an NH⋯O H-bond (R_NH⋯O = 1.809 Å, D₀ = 46.3 kJ mol⁻¹) to one of the two NH groups and elongates it to r_NH = 1.0219 Å. Symmetry reduction upon monohydration causes an unequal charge distribution on the two Py units, q_Py = 0.526 and 0.441e. Due to the decreased positive partial charge on the free Py unit, its N–H bond contracts to r_NH = 1.0057 Å. In Py₂⁺(a)(H₂O)₂(I), the second H₂O ligand prefers to solvate the remaining free NH group and restores C_2h symmetry and consequently the maximal CR in Py₂⁺(a) (q_Py = 0.461e), rather than forming a (H₂O)₂ solvent network. This preference for interior ion solvation over the formation of the H-bonded network is observed because the additional strong charge-dipole interaction, although slightly noncooperative, is still more favourable than the significantly cooperative dipole–dipole interaction in the (H₂O)₂ chain. As a result of restored C_2h symmetry, the two H-bonds in Py₂⁺(a)(H₂O)₂(I) have equal strength with R_NH⋯O = 1.826 Å, r_NH = 1.0202 Å, and D₀ = 44.2 kJ mol⁻¹, although slightly weaker than the single one in monohydrated Py₂⁺(a)H₂O(I). These relative H-bond strengths are also obtained from the NCI analysis (ρ* = −0.034 > −0.033 a.u. for n = 1 and 2, Fig. S11, ESI†). The weaker H-bond in dihydrated Py₂⁺(a)(H₂O)₂(I) is rationalised by the reduced charge on the H-bond donor Py units (0.461 vs. 0.526e, Fig. 3 and 5), resulting in weaker local charge-dipole interactions between Py and H₂O.

As a next step, we analyse the impact of hydration on the CR of Py₂⁺(a), Py₂⁺(a)H₂O(I), and Py₂⁺(a)(H₂O)₂(I) by comparing the vertical excitation energies for the CR transition (ΔE) using the TD-DFT approach. First, the reliability of the considered dispersion-corrected DFT functionals for predicting the CR transition, namely B3LYP, CAM-B3LYP, B3PW91, and M06-2X with the aug-cc-pVTZ basis set is evaluated by comparing the TD-DFT transition energies of the cations of benzene dimer (Bz₂⁺), benzene-naphthalene (BzNp⁺), and benzene-toluene (BzTol⁺) in their optimised ground state geometries to their experimentally reported values (Table S11, ESI†).^{32,44,45,51,53} The CAM-B3LYP-D3 and M06-2X functionals yield results closest to the experimental values. Therefore, the ΔE values, obtained for the optimised ground state geometries of Py₂⁺(a), Py₂⁺(a)H₂O(I), and Py₂⁺(a)(H₂O)₂(I) at the B3LYP-D3 level, are supported by those obtained with the CAM-B3LYP-D3 and M06-2X functionals (Fig. S12 and Table S12, ESI†). To this end, ΔE values increase slightly with n (1.7917 < 1.7982 < 1.8015 eV, Fig. S12, ESI†). The CR transition energy of the dimer cation is roughly given by the difference in the ionisation energies of the two units and its binding energy, ΔE ≈ ΔIE + 2D₀.⁵¹ Within this approximation, D₀ corresponds to the orbital coupling term (2D₀ = 2V). For the Py₂⁺(a) homodimer (i.e., ΔIE = 0), the coupling is maximised and given by D₀ (107.4 kJ mol⁻¹ or 1.11 eV), in line with roughly half of the computed excitation energy (ΔE = 1.79 eV). For monohydrated Py₂⁺(a), the nonvanishing ΔIE value of 0.49 eV for PyH₂O and Py (7.60 and 8.09 eV) reduces the orbital overlap and lowers D₀ of Py₂⁺H₂O → Py⁺H₂O + Py compared to that of Py₂⁺(a) from 107.4 to 88.2 kJ mol⁻¹ (1.11 < 0.91 eV). However, the contribution of ΔIE to ΔE roughly compensates for the reduced D₀ value caused by poorer coupling arising from symmetry reduction, leading to an ΔE value comparable to that of Py₂⁺(a). Because ΔIE = 0 for the symmetrically dihydrated Py₂⁺(a)(H₂O)₂(I) cluster, the CR interaction becomes stronger again due to optimised overlap of the two HOMOs. The ΔE of Py₂⁺(a)(H₂O)₂(I) and D₀ for dissociating the core according to Py₂⁺(a)(H₂O)₂ → Py⁺H₂O + PyH₂O are predicted to be slightly higher than that of Py₂⁺(a) (1.8015 vs. 1.7917 eV and 114.4 vs. 107.4 kJ mol⁻¹, 1.19 vs. 1.11 eV, respectively), suggesting that charge delocalisation into the H₂O molecules (0.922 vs. 1.0e) might strengthen the CR interaction in the core.

Interestingly, the energy gap ΔE₀(a–p) of Py₂⁺(H₂O)_n with n = 0–3 decreases with increasing degree of hydration as 7.5 > 3.7 > −1.0 > −7.7 kJ mol⁻¹ for the most stable isomers (Fig. 8). Hence, stepwise hydration is predicted to reverse the energetic order of the Py₂⁺(a) and Py₂⁺(p) cores between n = 2 and 3, suggesting a hydration-induced switch in the structural CR motif. A similar result has been reported for the formation of the most stable Py₃⁺ trimer cation, in which Py solvates a Py₂⁺(p) core whereas Py₂⁺(a) is most stable for Py₂⁺.⁶⁸ For Py₂⁺(H₂O)_n with n = 2, the Py₂⁺(p) core isomer becomes more stable because of cooperative NH⋯O and OH⋯O H-bonds and increased H-bond strengths as compared to n = 1 while at the same time the Py₂⁺(a) core isomer suffers from slight noncooperativity arising from internal ion solvation and slightly reduced H-bond strengths (Fig. S13, ESI†). Both effects are further enhanced for n = 3 (Table S10, ESI†), thereby changing the ΔE₀(a–p) gap even more in favour of the Py₂⁺(p) core. While the measured IRPD spectra are consistent with this computational prediction, better-resolved IRPD spectra are required to provide definitive experimental proof for this drastic impact of solvation on the structure motif of the aromatic CR.

Fig. 8 Relative energy differences (ΔE₀ in kJ mol⁻¹) of the most stable structures of Py₂⁺(a)(H₂O)_n and Py₂⁺(p)(H₂O)_n (n = 0–3) depending on the hydration number (n) calculated at the B3LYP-D3/aug-cc-pVTZ level.

3.7. Impact of partial charge of Py on strength of H-bonds

The current study offers the unique opportunity to evaluate the strengths of the NH⋯O H-bonds between H₂O and Py as a function of the Py charge in PyH₂O, Py₂⁺(a)H₂O(I), and Py⁺H₂O because in all three charge states (q_Py = 0.0, 0.5, 1.0e) a similar linear H-bond motif is observed.^54,55,80 Indeed, with increasing charge, the experimental ν^b_NH values shift progressively to the red (3448 > 3228 > 2945 cm⁻¹)^54,55 due to the increasing strength of the NH⋯O H-bond. This trend is well supported by the computations, according to which the H-bonds become shorter and stronger with increasing charge (R_NH⋯O = 1.991 > 1.809 > 1.704 Å, D₀ = 17.6 < 46.3 < 65.1 kJ mol⁻¹, ρ* = −0.023 > −0.034 > −0.045 a.u., Fig. S14, ESI†), mostly due to the additional charge-dipole forces. The H-bond in Py₂⁺(a)H₂O is quite a bit stronger than the average of PyH₂O and Py⁺H₂O (by 5.0 kJ mol⁻¹) mainly due to the reorganisation of the charge resonance in Py₂⁺(a) upon monohydration, causing the charge of the proton donor Py (0.526e) to be slightly higher than 0.5e.

Next, we consider the preferred dihydration motifs of Py, Py⁺, and Py₂⁺ to discuss the evolution of the H-bonded solvent network as a function of charge and the number of available NH proton donor groups. Neutral Py(H₂O)₂ has a cyclic (σ–π bridge) structure, in which a linear OH⋯O H-bonded (H₂O)₂ dimer binds to Py by NH⋯O and OH⋯π H-bonds.⁵⁵ In contrast, Py⁺(H₂O)₂ has a linear chain structure with adjacent NH⋯O and OH⋯O H-bonds because of the strongly anisotropic charge-dipole interaction and the repulsive interaction between Py⁺ and the π-bonded OH hydrogen.⁸⁰ On the other hand, Py₂⁺(a) with its two NH groups offers two strongly acidic H-bond attractors for individual H₂O ligands so that in the Py₂⁺(a)(H₂O)₂(I) global minimum both positive partial charges are solvated, thereby restoring the CR. Nonetheless, the Py₂⁺(a)(H₂O)₂(II and III) local minima with an NH⋯O H-bond of one NH group to a linear (H₂O)₂ are energetically competitive with Py₂⁺(a)(H₂O)₂(I). Isomer III is more stable than II at higher temperatures due to entropy and exhibits a similar binding motif as Py⁺(H₂O)₂. Because of the CR interaction and the strongly reduced positive charge, the NH⋯O and OH⋯O H-bonds in Py₂⁺(a)(H₂O)₂(III) are weaker than those in Py⁺(H₂O)₂ (R_NH⋯O = 1.720 vs. 1.609 Å, R_OH⋯O = 1.773 vs. 1.732 Å, D₀ = 38.8 vs. 46.1 kJ mol⁻¹ for loss of H₂O, ρ*_NH⋯O = −0.043 vs. −0.050 a.u., ρ*_OH⋯O = −0.037 vs. −0.041 a.u., Fig. S14, ESI†) which is well supported by the measured ν^b_OH values (3306 vs. 3388 cm⁻¹ for q_Py = 1.0 and 0.5e).⁸⁰ The H-bond cooperativity is drastically reduced from 30% to 13% (Table S10, ESI†), which is nearly the same as that of the neutral cluster (12%),⁸⁰ although the H-bonds are much stronger in Py₂⁺(H₂O)₂(III) (Fig. S14, ESI†). Therefore, although the excess charge of 0.5e substantially increases the H-bond strength due to the additional charge-dipole interaction, it does not increase the degree of cooperativity in the H-bonded network.

In the following, we compare the mono- and dihydration motifs of neutral and cationic Py₂⁽⁺⁾ by considering Py₂(H₂O)_n and Py₂⁺(H₂O)_n with n = 1–2. Neutral Py₂ has a T-shaped structure with an NH⋯π H-bond.^61,63,66 In Py₂H₂O(I), H₂O forms a cyclic structure with T-shaped Py₂via NH⋯OH⋯π bonds (Fig. S15, ESI†).^55,123 Upon ionisation, the cyclic Py₂H₂O structure opens toward linear Py₂⁺(a)H₂O(I) due to the repulsive interaction between Py₂⁺ and the π-bonded H₂O ligand arising from the excess positive charge.⁸⁰ Interestingly, due to the stable cyclic structure with two neutral H-bonds, D₀ of Py₂H₂O is almost comparable to that of Py₂⁺H₂O featuring a single ionic H-bond (38.3 vs. 46.3 kJ mol⁻¹). All minima calculated for neutral Py₂(H₂O)₂ have cyclic structures and differ depending on whether one or two H₂O molecules are present in the cycle (Fig. S15, ESI†). The global minimum, Py₂(H₂O)₂(I), has a similar structure as Py₂H₂O(I) with a (H₂O)₂ dimer replacing H₂O. In Py₂(H₂O)₂(II), higher in energy by only 3.3 kJ mol⁻¹, both H₂O molecules form individual NH⋯O and OH⋯π H-bonds to the two Py units. Upon π electron emission, Py₂(H₂O)₂(I) likely converts to Py₂⁺(a)(H₂O)₂(II and III), while Py₂(H₂O)₂(II) probably generates Py₂⁺(a)(H₂O)₂(I) due to the repulsive interactions between the positive excess charge and the π-bonded OH hydrogens, thus breaking the OH⋯π H-bonds. In the cationic clusters, Py₂⁺(a)(H₂O)₂(I) becomes more stable because it forms a stronger CR than Py₂⁺(a)(H₂O)₂(II and III). Hence, ionisation changes the order of the isomeric structures of dihydrated Py₂.

Py₂⁺(a) offers two spatially separated acidic functional NH groups. Their hydration motifs, interior ion solvation or formation of a single H-bonded solvent network, become competitive starting from two H₂O molecules, as demonstrated for Py₂⁺(a)(H₂O)₂(I) and Py₂⁺(a)(H₂O)₂(II and III). Similar competing hydration motifs are observed for the previously studied microsolvation of the 5-hydroxyindole cation (5HI⁺), a bicyclic aromatic ion offering an NH group in the pyrrole ring and an OH group at the phenyl ring.⁸³ 5HI⁺(H₂O)₂(OH/NH), in which both acidic functional groups are solvated by a single H₂O ligand, corresponding to interior ion solvation, is found as the dominant isomer, whereas 5HI⁺(H₂O)₂(OH/H₂O or NH/H₂O) isomers with the (H₂O)₂ dimer chain attached to either the NH or OH group provide only a minor contribution to the population. The high abundance of 5HI⁺(H₂O)₂(OH/NH) with slightly noncooperative H-bonds originates from two strongly acidic functional groups.⁸³ Similarly, the presence of two acidic NH groups is mainly responsible for the high abundance of Py₂⁺(a)(H₂O)₂(I) with interior ion solvation, in addition to its favourable CR interaction.

4. Concluding remarks

Herein, we investigate the effects of stepwise microhydration on the CR-stabilised Py₂⁺ homodimer cation by IRPD spectroscopy of mass-selected bare and Ar-tagged Py₂⁺(H₂O)_n clusters and complementary quantum chemical calculations at the B3LYP-D3/aug-cc-pVTZ level including NCI, NBO, and TD-DFT analysis. Systematic shifts observed for the ν_NH and ν_OH stretch bands provide detailed information about the structure and bonding of the observed cluster isomers and the preferred cluster growth, including charge distributions, cooperativity, and the strengths of the CR and H-bonds as a function of the degree and site of hydration. Significantly, the results provide for the first time information about the solvation effects on the fundamental aromatic CR interaction in isolated clusters. The salient results may be summarised as follows.

(1) The preferred cluster growth of Py₂⁺(a) begins with hydrating the two available acidic NH protons (n = 1–2) followed by the formation of a H-bonded solvent network (n ≥ 3). In general, interior ion hydration is slightly noncooperative, leading to slightly weaker NH⋯O H-bonds for n = 2 compared to n = 1. On the other hand, formation of the H-bonded solvent network via OH⋯O H-bonds is strongly cooperative due to nonadditive induction forces. To this end, for n = 2 the local minina with a (H₂O)₂ attached to a single NH group become energetically competitive with the most stable symmetrically hydrated global minimum, with an observed population ratio of around 1 : 2 in our plasma expansion. When considering the n = 1–3 isomers in which one of the Py units of Py₂⁺(a) is solvated by a linear (H₂O)_n chain, the NH⋯O ionic H-bond to the solvent cluster becomes progressively stronger due to increasing proton affinity of (H₂O)_n, resulting in larger charge transfer to solvent and stronger ν^b_NH redshifts, an effect that seems to converge around n = 2–3.

(2) The new experimental and computational data for the various Py₂⁺(H₂O)_n clusters allow us to further confirm the roughly linear q_Py–ν^f_NH correlation between the free NH stretch frequency of the Py unit and its partial positive charge developed earlier from data of Py⁽⁺⁾ and Py₂⁺.²³ The experimental q_Py values obtained for Py₂⁺(H₂O)_n with n = 1–3 from this q_Py–ν^f_NH correlation are in good agreement with the computed NBO charges, once again validating our approach of characterising the CR interaction in aromatic dimers utilising the IRPD technique in the ground electronic state (ψ₊).

(3) Our characterisation of the Py₂⁺(H₂O)_n clusters offers the unique opportunity to determine the effects of sequential hydration on the CR interaction as a function of isomeric structure and cluster size n. According to a rough approximation, two competing factors have to be considered, namely the difference in the ionisation energies (ΔIE) and the coupling constant (V) approximated by the binding energy D₀. Monohydration of Py₂⁺(a) reduces the symmetry of the cluster and thus the CR interaction for n = 1. Symmetric dihydration for n = 2 restores the symmetry and increases the CR again. However, when taking ΔIE into account, the splitting between ψ₊ and ψ₋ (ΔE) giving rise to the CR transition is only weakly affected upon mono- and dihydration, as confirmed by TD-DFT calculations.

(4) Moreover, our experimental IRPD spectra, along with the computational results, provide the first evidence that stepwise hydration induces a change in the preferred CR core ion from the symmetric Py₂⁺(a) structure (n ≤ 2) to the parallel Py₂⁺(p) core (n ≥ 3) due to the strong cooperativity favouring the formation of single-sided H-bonded hydration networks. However, IR spectra at higher resolution are required for a definitive proof of this scenario. To this end, IR spectra for clusters with n > 3 may shed further light on this preliminary conclusion, while at the same time further expanding the correlation between the CR interaction and the H-bond motifs.

(5) Comparison of microhydration of Py, Py⁺, and Py₂⁺ offers the valuable opportunity to quantitatively characterise the H-bond strength of the aromatic solute to the (dipolar) solvent network as a function of its positive partial charge. Due to the increasing charge-dipole interaction, the NH⋯O H-bond becomes progressively stronger the larger the charge on the Py unit.

As an outlook, we are currently expanding these studies on the CR interaction in several directions using the same combined experimental and computational approach, including (i) Py₂⁺ dimers solvated by molecules with different proton affinities (e.g., CH₃OH), (ii) larger Py_n⁺ clusters, and (iii) clusters of [PyA]⁺ heterodimers with aromatic molecules A with different IEs.

Data availability

The data supporting this article has been included as part of the ESI.† ESI† includes LID and CID mass spectra, additional isomeric structures and energies, measured and computed harmonic and anharmonic IR spectra of Py₂⁽⁺⁾(H₂O)_n and Py₂⁺(H₂O)_nAr, NCI analysis of Py^q(H₂O)_n, and frontier MOs and computed CR transition energies of Py₂⁺(H₂O)_n.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by Deutsche Forschungsgemeinschaft (DFG, project DO 729/10) and the Japan Society for the Promotion of Science (JSPS) Core-to-Core Program (Grant JPJSCCA20210004, JPJSCCA20240002). YM is grateful for travel support from the Open Partnership Joint Research Project of JSPS (JPJSBP120229917). YM also appreciates the financial support from the Cooperative Research Program of “Network Joint Research Centre for Material and Devices” (No. 20221199). OD acknowledges support from the World Research Hub Initiative (WRHI) of the Institute of Science Tokyo. DA was also partly supported by the International Max Planck Research School for Elementary Processes in Physical Chemistry.

Notes and references

1. C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2001, 651.
2. S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029.
3. K. E. Riley and P. Hobza, Acc. Chem. Res., 2013, 46, 927.
4. P. Hobza, H. L. Selzle and E. W. Schlag, Chem. Rev., 1994, 94, 1767.
5. K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143.
6. A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775.
7. O. Dopfer and M. Fujii, Chem. Rev., 2016, 116, 5432.
8. M. Fujii and O. Dopfer, Int. Rev. Phys. Chem., 2012, 31, 131.
9. O. Dopfer, Z. Phys. Chem., 2005, 219, 125.
10. L. M. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808.
11. E. A. Meyer, R. K. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210.
12. E. T. Kool, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 1.
13. R. Bu, Y. Xiong and C. Zhang, Cryst. Growth Des., 2020, 20, 2824.
14. N. Gospodinova and E. Tomšík, Prog. Polym. Sci., 2015, 43, 33.
15. K. Binnemans, Chem. Rev., 2005, 105, 4148.
16. S. Suzuki, P. G. Green, R. E. Bumgarner, S. Dasgupta, W. A. Goddard and G. A. Blake, Science, 1992, 257, 942.
17. D. A. Dougherty, Science, 1996, 271, 163.
18. J. C. Ma and D. A. Dougherty, Chem. Rev., 1997, 97, 1303.
19. K. S. Kim, P. Tarakeshwar and J. Y. Lee, Chem. Rev., 2000, 100, 4145.
20. R. E. Dawson, A. Hennig, D. P. Weimann, D. Emery, V. Ravikumar, J. Montenegro, T. Takeuchi, S. Gabutti, M. Mayor, J. Mareda, C. A. Schalley and S. Matile, Nat. Chem., 2010, 2, 533.
21. B. Badger and B. Brocklehurst, Nature, 1968, 219, 263.
22. A. K. Chandra, K. Bhanuprakash, V. J. Bhasu and D. Srikanthan, Mol. Phys., 1984, 52, 733.
23. K. Chatterjee, Y. Matsumoto and O. Dopfer, Angew. Chem., Int. Ed., 2019, 58, 3351.
24. V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926.
25. A. J. Heeger, J. Phys. Chem. B, 2001, 105, 8475.
26. J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804.
27. M. Kitamura and Y. Arakawa, J. Phys.: Condens. Matter, 2008, 20, 184011.
28. B. Giese, Acc. Chem. Res., 2000, 33, 631.
29. B. Giese, Annu. Rev. Biochem., 2002, 71, 51.
30. B. Giese, J. Amaudrut, A. K. Köhler, M. Spormann and S. Wessely, Nature, 2001, 412, 318.
31. S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 3843.
32. M. Matsumoto, Y. Inokuchi, K. Ohashi and N. Nishi, J. Phys. Chem. A, 1997, 101, 4574.
33. Y. Tsujii, A. Tsuchida, S. Ito and M. Yamamoto, Macromolecules, 1991, 24, 4061.
34. I. C. Lewis and L. S. Singer, J. Chem. Phys., 1965, 43, 2712.
35. H. van Willigen, E. de Boer, J. T. Cooper and W. F. Forbes, J. Chem. Phys., 1968, 49, 1190.
36. O. W. Howarth and G. K. Fraenkel, J. Am. Chem. Soc., 1966, 88, 4514.
37. B. Badger and B. Brocklehurst, Trans. Faraday Soc., 1969, 65, 2582.
38. B. Badger, B. Brocklehurst and R. D. Russell, Chem. Phys. Lett., 1967, 1, 122.
39. J. K. Kochi, R. Rathore and P. L. Magueres, J. Org. Chem., 2000, 65, 6826.
40. B. Badger and B. Brocklehurst, Trans. Faraday Soc., 1970, 66, 2939.
41. M. S. El-Shall and M. Meot-Ner, J. Phys. Chem., 1987, 91, 1088.
42. M. Meot-Ner, P. Hamlet, E. P. Hunter and F. H. Field, J. Am. Chem. Soc., 1978, 100, 5466.
43. M. Rusyniak, Y. Ibrahim, E. Alsharaeh, M. Meot-Ner (Mautner) and M. S. El-Shall, J. Phys. Chem. A, 2003, 107, 7656.
44. K. Ohashi, Y. Nakai, T. Shibata and N. Nishi, Laser Chem., 1994, 14, 3.
45. K. Ohashi and N. Nishi, J. Phys. Chem., 1992, 96, 2931.
46. K. Ohashi, Y. Inokuchi and N. Nishi, Chem. Phys. Lett., 1996, 263, 167.
47. Y. Inokuchi and N. Nishi, J. Chem. Phys., 2001, 114, 7059.
48. Y. Inokuchi, K. Ohashi, M. Matsumoto and N. Nishi, J. Phys. Chem., 1995, 99, 3416.
49. J. Bernard, A. Al-Mogeeth, A.-R. Allouche, L. Chen, G. Montagne and S. Martin, J. Chem. Phys., 2019, 150, 54303.
50. J. Bernard, S. Martin, A. Al-Mogeeth, C. Joblin, M. Ji, H. Zettergren, H. Cederquist, M. H. Stockett, S. Indrajith, L. Dontot, F. Spiegelman, D. Toublanc and M. Rapacioli, Phys. Chem. Chem. Phys., 2024, 26, 18571.
51. K. Ohashi, Y. Nakane, Y. Inokuchi, Y. Nakai and N. Nishi, Chem. Phys., 1998, 239, 429.
52. J. Bernard, A. Al-Mogeeth, S. Martin, G. Montagne, C. Joblin, L. Dontot, F. Spiegelman and M. Rapacioli, Phys. Chem. Chem. Phys., 2021, 23, 6017.
53. Y. Inokuchi, K. Ohashi, H. Sekiya and N. Nishi, J. Chem. Phys., 2002, 117, 10648.
54. M. Schütz, Y. Matsumoto, A. Bouchet, M. Öztürk and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 3970.
55. Y. Matsumoto and K. Honma, J. Chem. Phys., 2009, 130, 54311.
56. S. Chakraborty, A. Patzer, A. Lagutschenkov, J. Langer and O. Dopfer, Int. J. Mass Spectrom., 2010, 297, 85.
57. A. Fujii, E. Fujimaki, T. Ebata and N. Mikami, J. Chem. Phys., 2000, 112, 6275.
58. K. Chatterjee and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 32262.
59. P. A. Pieniazek, S. E. Bradforth and A. I. Krylov, J. Chem. Phys., 2008, 129, 74104.
60. R. Lindner, K. Müller-Dethlefs, E. Wedum, K. Haber and E. R. Grant, Science, 1996, 271, 1698.
61. H. Park and S. Lee, Chem. Phys. Lett., 1999, 301, 487.
62. V. Stefov, L. Pejov and B. Šoptrajanov, J. Mol. Struct., 2003, 649, 231.
63. Y. Matsumoto and K. Honma, J. Chem. Phys., 2007, 127, 184310.
64. G. Columberg and A. Bauder, J. Chem. Phys., 1997, 106, 504.
65. I. Dauster, C. A. Rice, P. Zielke and M. A. Suhm, Phys. Chem. Chem. Phys., 2008, 10, 2827.
66. V. Profant, V. Poterya, M. Fárník, P. Slavícek and U. Buck, J. Phys. Chem. A, 2007, 111, 12477.
67. D. Arildii, Y. Matsumoto and O. Dopfer, J. Phys. Chem. A, 2024, 128, 3993.
68. C. Wei, X. Chen, Y. Wang, Y. Li, J. Gao, M. Xie and Y. Hu, Phys. Chem. Chem. Phys., 2023, 25, 11368.
69. X. Chen, C. Wei, M. Xie and Y. Hu, J. Phys. Chem. A, 2023, 127, 8272.
70. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413.
71. D. J. Goebbert and P. G. Wentold, Eur. J. Mass Spectrom., 2004, 10, 837.
72. K. Hattori, D. Wang and A. Fujii, Phys. Chem. Chem. Phys., 2019, 21, 16064.
73. M. Xie, H.-R. Tsai, A. Fujii and Y.-P. Lee, Phys. Chem. Chem. Phys., 2019, 21, 16055.
74. T. Kato and A. Fujii, J. Phys. Chem. A, 2023, 127, 742.
75. M. J. Tubergen, A. M. Andrews and R. L. Kuczkowski, J. Phys. Chem. Lett., 1993, 97, 7451.
76. J. E. Del Bene and I. Cohen, J. Am. Chem. Soc., 1978, 100, 5285.
77. P. I. Nagy, G. Durant and D. A. Smith, J. Am. Chem. Soc., 1993, 115, 2912.
78. A. Kumar, M. Kołaski and K. S. Kim, J. Chem. Phys., 2008, 128, 34304.
79. A. L. Sobolewski and W. Domcke, Chem. Phys. Lett., 2000, 321, 479.
80. D. Arildii, Y. Matsumoto and O. Dopfer, J. Phys. Chem. A, 2023, 127, 2523.
81. J. Klyne, M. Schmies, M. Fujii and O. Dopfer, J. Phys. Chem. B, 2015, 119, 1388.
82. J. Klyne, M. Schmies, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3148.
83. J. Klyne, M. Miyazaki, M. Fujii and O. Dopfer, Phys. Chem. Chem. Phys., 2018, 20, 3092.
84. O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437.
85. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, GAUSSIAN 16 (Revision C.01), Gaussian Inc., Wallingford, CT, 2016.
86. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
87. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
88. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
89. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
90. A. G. Császár, G. Czakó, T. Furtenbacher, J. Tennyson, V. Szalay, S. V. Shirin, N. F. Zobov and O. L. Polyansky, J. Chem. Phys., 2005, 122, 214305.
91. K. Chatterjee and O. Dopfer, Chem. Sci., 2018, 9, 2301.
92. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429.
93. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982.
94. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
95. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51.
96. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
97. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498.
98. J. Contreras-García, W. Yang and E. R. Johnson, J. Phys. Chem. A, 2011, 115, 12983.
99. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625.
100. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.
101. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
102. J. Klyne, M. Schmies and O. Dopfer, J. Phys. Chem. B, 2014, 118, 3005.
103. C.-K. Lin, R. Shishido, Q.-R. Huang, A. Fujii and J.-L. Kuo, Phys. Chem. Chem. Phys., 2020, 22, 22035.
104. T. R. Dyke, K. M. Mack and J. S. Muenter, J. Chem. Phys., 1977, 66, 498.
105. F. Huisken, M. Kaloudis and A. Kulcke, J. Chem. Phys., 1996, 104, 17.
106. Z. S. Huang and R. E. Miller, J. Chem. Phys., 1989, 91, 6613.
107. K. Kuyanov-Prozument, M. Y. Choi and A. F. Vilesov, J. Chem. Phys., 2010, 132, 14304.
108. B. E. Rocher-Casterline, L. C. Ch'ng, A. K. Mollner and H. Reisler, J. Chem. Phys., 2011, 134, 211101.
109. P. J. Derrick, L. Åsbrink, O. Edqvist and E. Lindholm, Spectrochim. Acta, Part A, 1971, 27, 2525.
110. A. J. van den Brom, M. Kapelios, T. N. Kitsopoulos, N. H. Nahler, B. Cronin and M. N. R. Ashfold, Phys. Chem. Chem. Phys., 2005, 7, 892.
111. S. Tomoda, Y. Achiba and K. Kimura, Chem. Phys. Lett., 1982, 87, 197.
112. C. Y. Ng, D. J. Trevor, P. W. Tiedemann, S. T. Ceyer, P. L. Kronebusch, B. H. Mahan and Y. T. Lee, J. Chem. Phys., 1977, 67, 4235.
113. L. Karlsson, L. Mattsson, R. Jadrny, R. G. Albridge, S. Pinchas, T. Bergmark and K. Siegbahn, J. Chem. Phys., 1975, 62, 4745.
114. K. Sakota, Y. Kouno, S. Harada, M. Miyazaki, M. Fujii and H. Sekiya, J. Chem. Phys., 2012, 137, 224311.
115. Q.-R. Huang, R. Shishido, C.-K. Lin, C.-W. Tsai, J. A. Tan, A. Fujii and J.-L. Kuo, Angew. Chem., Int. Ed., 2021, 60, 1936.
116. T. Seki, K.-Y. Chiang, C.-C. Yu, X. Yu, M. Okuno, J. Hunger, Y. Nagata and M. Bonn, J. Phys. Chem. Lett., 2020, 11, 8459.
117. A. A. Kananenka and J. L. Skinner, J. Chem. Phys., 2018, 148, 244107.
118. K. Chatterjee and O. Dopfer, J. Phys. Chem. A, 2019, 123, 7637.
119. B. M. Auer and J. L. Skinner, J. Chem. Phys., 2008, 128, 224511.
120. R. Knochenmuss and S. Leutwyler, J. Chem. Phys., 1989, 91, 1268.
121. A. Courty, M. Mons, J. Le Calvé, F. Piuzzi and I. Dimicoli, J. Phys. Chem. A, 1997, 101, 1445.
122. R. N. Barnett and U. Landman, J. Phys. Chem. A, 1997, 101, 164.
123. S. Sarkar, N. Ramanathan and K. Sundararajan, J. Phys. Chem. A, 2018, 122, 2445.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00067j

---