Deacetylation mechanism of histone deacetylase 8: insights from QM/MM MP2 calculations

Abstract

Understanding the catalytic mechanism of histone deacetylases can greatly benefit the development of targeted therapies that are safe and effective. Combined quantum mechanical and molecular mechanical (QM/MM) Møller–Plesset second-order perturbation theory (MP2) geometry optimizations are performed to investigate the catalytic mechanism of the deacetylation reaction of a tetrapeptide catalyzed by human Histone Deacetylase 8. A three-step catalytic mechanism is identified: the first step is the formation of a negatively charged tetrahedral intermediate via nucleophilic addition of the activated water to the amide C atom and a proton transfer from the water to His143; the second step is the formation of a neutral tetrahedral intermediate with an elongated amide C–N bond via a proton transfer from His143 to the amide N atom. The third step is the complete cleavage of the amide C–N bond, accompanied by a proton transfer from the newly formed carboxylic group of the neutral tetrahedral intermediate to His142. These three steps have similar computed energy barriers, with the second step having the highest calculated activation free energy of 19.6 kcal mol⁻¹. When there is no potassium ion at site 1, the calculated activation free energy is 17.7 kcal mol⁻¹. Both values are in good agreement with an experimental value of 17.5 kcal mol⁻¹. Their difference implies that there would be a 25-fold increase in the enzyme's activity, in line with experiments. The solvent hydrogen–deuterium kinetic isotope effect was computed to be ∼3.8 for the second step in both cases. It is also found that the energy barriers are significantly and systematically higher on the QM/MM B3LYP and QM/MM B3LYP-D3 potential energy surfaces. In particular, the QM/MM B3LYP and B3LYP-D3 methods fail to predict the neutral tetrahedral intermediate and a meaningful transition state for the third step, leading to a two-step mechanism. With a sufficiently large basis set such as aug-cc-pVDZ, QM/MM M05-2X, M06-2X, M06, and MN15 methods can give results much closer to the QM/MM MP2 method. However, when a smaller basis set such as 6-31G* is used, these methods can lead to errors as large as 10 kcal mol⁻¹ on the reaction pathway. These results highlight the importance of using accurate QM methods in the computational study of enzyme catalysis.

---

I. Introduction

The reversible acetylation of lysine residues in protein is important to many physiological processes, such as gene expression and cancer progression.^1–4 Histone deacetylases (HDACs) are a family of enzymes that catalyze the hydrolysis of acetyl-lysine of histone to yield lysine and acetate. The normal balance of HDAC and histone acetyltransferase (HAT) (responsible for acetylation of the substrate) function is vital for the epigenetic regulation of gene expression and healthy deoxyribonucleic acid (DNA) replication and repair.^5,6 The acetylation status of the ε-amino lysines of N-terminal histone tails controls chromatin structure, essential to transcription and DNA replication machinery.⁷ Unregulated HDAC activity is observed in cancer and neurodegenerative diseases. Only a few anti-histone deacetylase inhibitors have been approved for use in cancer chemotherapy, including Vorinostat,⁸ Romidepsin,⁹ and Belinostat¹⁰ for the treatment of cutaneous T-cell lymphoma, and Panobinostat¹¹ for the treatment of multiple myeloma.² Clinical trials also involve many different inhibitors for solid and hematological malignancies.^6,12–14 It is crucial to fully characterize the mechanism of reaction for the lysine deacetylation by HDACs to develop more targeted therapies that are safer and more effective.

Eukaryotic HDACs are grouped into four classes. Class I, II, and IV HDACs are zinc-dependent enzymes containing a zinc catalytic binding domain with amino acid residues in similar conformations.^15,16 Due to their biomedical relevance, class I HDACs have been widely studied. Many crystal structures have been reported for class I HDACs, especially Human histone deacetylase 8 (HDAC8).¹⁷ Buried at the bottom of a narrow hydrophobic tract (Fig. 1), the active site in the HDAC8 enzyme has a zinc ion coordinating with two aspartates, a histidine, and a catalytic water molecule in the first coordination sphere. The acetamide carbonyl group of the acetylated lysine in the substrate coordinates with the Zn ions and interacts with the hydroxyl group of a tyrosine residue (Tyr306), which can rotate and undergo a conformational transition to accommodate substrate binding. It is worth noting that there are two K⁺ binding sites (site 1 and site 2) in HDAC8, as shown in Fig. 1. Site 1 is about 7 Å away from the catalytic zinc ion, while site 2 is near the periphery of the protein. The functional roles of the K⁺ ions at these two sites in HDAC8 catalysis have been probed experimentally. Vannini et al. found that K⁺ ions can increase the thermal stability of HDAC8 but did not differentiate the contributions from site 1 and site 2.¹⁸ Fierke and co-workers found that the enzyme activity is sensitive to changes in the K⁺ ion concentration in solution.¹⁹

Fig. 1 Structure of histone deacetylases 8 (HDAC8) in complex with a tetrapeptide substrate. The right panel shows the QM region (105 atoms) in our QM/MM calculations, including the zinc ion, the tetrapeptide substrate, His142, His143, Asp176, Asp178, Asp183, His180, Asp267, and Tyr306.

Two possible mechanisms for HDACs have been proposed in the literature (Fig. 2A and B). Based on X-ray crystallographic analysis, Finnin et al. proposed the first mechanism (mechanism 1 in Fig. 2A).²⁰ In this two-step mechanism, the active site involves a singly protonated His142 and a doubly protonated His143, and the His142–Asp176 dyad acts as a general base to accept a proton from the active site water molecule. The water oxygen then attacks the carbonyl carbon of the acetyl-lysine substrate followed by the His143–Asp183 dyad protonating the amine N atom. Zhang and co-workers proposed another two-step mechanism (mechanism 2 in Fig. 2B) based on combined quantum mechanical and molecular mechanical (QM/MM) geometry optimization and molecular dynamics (MD) simulations.^21,22 They found that both His142 and His143 are singly protonated on the δ nitrogen position and the His143–Asp183 dyad of human HDAC8 acts as a general base for accepting a water proton in the initial nucleophilic attack to form the negative tetrahedral intermediate. Chen et al. revisited the two two-step mechanisms with a QM/MM geometry optimization method and found it difficult to energetically distinguish which histidine residue, His143 or His142, should be protonated in the initial step, raising controversy over the catalytic mechanism of HDAC8.²³ Interestingly, Chen et al. suggested that removing the K⁺ ion from site 1 increases the reactivity of HDAC8,²³ while Wu et al. found a decrease.^21,22 Using a QM/MM geometry optimization method, Gleeson et al.²⁴ examined several possible pathways and found that the most favorable catalytic pathway is mechanism 2, where the His143 is protonated in the initial step with a comparable but lower energy barrier than that of His142.

Fig. 2 The two 2-step catalytic mechanisms (mechanisms 1 and 2) proposed for the deacetylation reaction catalyzed by histone deacetylases 8 (HDAC8) in the literature and the 3-step mechanism (mechanism 3) revealed with QM/MM MP2 calculations.

In general, the discrepancies in the catalytic mechanism obtained with different QM/MM methods may result from the use of different starting structures, QM methods, QM region sizes, and the treatment of QM and MM coupling. The choice of QM methods is often the most prominent factor that causes the differences in QM/MM computed energies. It is well known that popular density functional theory (DFT) methods, which have been used in the above QM/MM studies, tend to underestimate weak interactions in chemical systems.²⁵ For example, the B3LYP^26,27 method tends to underestimate the intermolecular dispersion interaction, especially for systems involving ligand coordination of transition metals.²⁸ By directly introducing electron correlation into Hartree–Fock energy, Møller–Plesset second-order perturbation theory (MP2)²⁹ methods are considered more accurate in describing intermolecular interactions than DFT methods for many closed-shell chemical systems.³⁰ A multi-configuration self-consistent-field (MCSCF)³¹ method is another type of post-Hartree–Fock method that is the best choice for describing static electronic correlation but is insufficient for dynamic electronic correlation without going to a very large active space or using a subsequent perturbation treatment. More accurate post-Hartree–Fock methods such as coupled cluster methods³² are prohibitively expensive for the geometry optimization and transition state search of enzyme active sites consisting of ∼100 atoms. The MP2 method is probably the only practical post-Hartree–Fock method that can be routinely used for QM/MM geometry optimization and transition state search of enzymatic systems.

In this work, we performed high-level QM/MM MP2 calculations to explore the HDAC8 catalytic reaction pathway and used the coupled-cluster singles, doubles, and non-iterative triples [i.e., CCSD(T)]^33–35 method on small model systems extracted from the QM/MM MP2 optimized active site structures on the pathway to assess and confirm the accuracy of the MP2 method. A diacetylated tetrapeptide derived from a p53 tumor suppressor protein was used as the substrate. A crystal structure of an HDAC8 mutant containing this tetrapeptide is available (details in the next section). This substrate has been extensively used in experimental studies because it retains sufficient binding and catalytic relevance for histone deacetylases.^36–38 In particular, it preserves the key interactions at the active site, thus is a good model substrate for the study of the hydrolytic mechanism. Computational mechanistic studies in the literature also used the same tetrapeptide substrate.^21–24 Using a common substrate ensures a direct comparison between our results and the experimental and theoretical results in the literature. The hydrolytic mechanism obtained for this substrate can also be compared to those found for other substrates.

For HDAC8 with a K⁺ ion at site 1, we found that an additional intermediate is involved in the catalytic pathway, leading to a three-step catalytic mechanism. When no K⁺ ion is at site 1, it reduces to a two-step mechanism. Due to variations in the settings of QM/MM calculations, it is usually difficult to directly compare different QM/MM results in the literature. Our QuanPol³⁹ program is a seamless and full-spectrum QM/MM program that can work with different QM methods and MM methods within the same framework, providing a great opportunity for comparing the accuracies of different QM methods. We performed QM/MM B3LYP^26,27 (with and without an empirical dispersion correction) calculations and found significant structural and energetic differences from the QM/MM MP2 results. The QM/MM MP2 method appears to offer more accurate descriptions of the structures and energetics, largely due to a better description of the long-range dispersion interaction among the groups at the active site. We also compared the QM/MM results of the M05-2X,⁴⁰ M06,⁴¹ M06-2X,⁴¹ and MN15⁴² density functional methods to QM/MM MP2 results and found that these functionals work reasonably well when a sufficiently large basis set is used.

II. Computational methods

All calculations were performed with our recently developed quantum chemistry polarizable force field (QuanPol³⁹) program, which was integrated into the general atomic and molecular electronic structure system (GAMESS⁴³) package.

The X-ray crystal structure of a Tyr306Phe mutated HDAC8-substrate complex (2V5W.PDB, resolution 2.0 Å)³⁶ was obtained from the Protein Data Bank (PDB⁴⁴). The file was modified by deleting all chains and the corresponding water molecules except for chains A and I.³⁶ Chain A is a monomer of the asymmetric dimer crystal structure containing two structurally essential K⁺ ions and the active site coordinating Zn²⁺; Chain I is a tetrapeptide substrate (a p53 tumor suppressor protein derived diacetylated peptide): (acetyl)-L, Arg-L, His-L, Lys (e-acetyl)-L, Lys(e-acetyl). The Phe306 was changed back to Tyr306 as in the wild type.⁴⁵ The Chimera program⁴⁶ was used to add hydrogen atoms to the protein portion (chain A) and the water molecules, with all histidines in the active site (His142, His143, and His180) singly protonated on the δ nitrogen. The QuanPol program was used to assign the AMBER^47–49 ff12SB⁵⁰ force field to chain A. The QuanPol three-point flexible water model QP301 was used for the water molecules.

Using the QuanPol option LOUT = 1, the tetrapeptide substrate was assigned a universal force field for all 120 atoms with a zero net charge. Then the five H atoms of the Arg residue were manually changed from +0.30e to +0.50e so the total charge of the tetrapeptide was +1e. This universal force field has Lennard-Jones (LJ) potential parameters identical to the AMBER force field used here. The atomic charges and covalent parameters are similar to the MMFF94⁵¹ force field. Using a slightly different force field for the substrate would not cause significant differences in the results as the substrate has much fewer atoms than the enzyme. The differences in the force fields have essentially no direct (but some indirect) impacts on the subsequent QM/MM calculations, in which most of the substrate atoms are in the QM region. For an arbitrary organic molecule such as the diacetylated tetrapeptide substrate studied here, there is no standard AMBER force field, so an ad hoc force field or a universal force field like MMFF94 needs to be generated and mixed with the standard AMBER protein force field.

The QuanPol option ICOMBIN = 1 was used to combine the enzyme (chain A) and substrate (chain I) force field files. After combination, the total number of atoms was 6857, with a net charge of −2e. The enzyme–substrate system was then solvated in an 84 Å × 72 Å × 83 Å rectangular periodic boundary condition (PBC) box and filled with 25 Na⁺ atoms, 23 Cl⁻ ions, and 13 673 water molecules. The QuanPol three-point flexible water model QP301 was used for all water molecules. The whole system had a total of 47 924 atoms and a zero net charge.

The system was equilibrated for 10 ns using MD simulations. To preserve the experimentally measured X-ray structure of the zinc center, seven atoms were fixed in their original Cartesian coordinates in the crystal structure: the Zn²⁺ ion, the O of the catalytic H₂O, the H_Z of Tyr306, the N-term O and C atoms of the tetrapeptide substrate, and the two K²⁺ ions. Temporarily fixing these atoms in a force field calculation was necessary because the zinc ion did not have covalent force field parameters. Our experiences show that merely using charge–charge and LJ potentials to describe the Zn–ligand coordination in force field MD simulation and geometry optimization can lead to unrealistic active site structures (especially the bond angles and dihedral angles) that are far away from the experimental observation or QM/MM calculation. In earlier studies of Zn enzymes, we also found that for non-reactive Zn–ligand coordinate bonds, QM/MM optimized structures are often very close to experimentally measured crystal structures for the corresponding states.^52,53 Therefore, when a covalent force field for the Zn active site is not available, the default practice would be fixing several active site atoms in their original crystal coordinates to prevent unpredictable disruptions of the active site. These atoms were not fixed in the later QM/MM geometry optimization. A shifting function (QuanPol keyword ISHIFT = 4) was used to adjust the long-range charge–charge interactions up to 12 Å. A switching function (QuanPol keyword ISWITCH = 1) was used to adjust the long-range Lennard-Jones (LJ) interactions from 10 to 12 Å. The Berendsen thermostat and barostat were used with a temperature scaling time constant of 200 fs and a pressure scaling time constant of 200 fs, and with a bath temperature T of 298.15 K and bath pressure P of 1.00 bar. The MD simulations were run using the Beeman integration algorithm.⁵⁴ At the end of the 1 ns MD simulation, the volume of the PBC box was 81.91 Å × 70.21 Å × 80.94 Å. At the end of the 10 ns MD simulation, the volume of the PBC box was 81.95 Å × 70.24 Å × 80.98 Å. A superposition of the geometries from the 1 ns and 10 ns MD simulation shows that the two geometries are similar (Fig. S3, ESI†). The last geometries from the 1 ns and 10 ns MD simulation were used for subsequent QM/MM B3LYP,^26,27 B3LYP with Grimme's empirical dispersion corrections (denoted B3LYP-D3⁵⁵) and MP2²⁹ geometry optimizations.

The QM/MM geometry optimizations for the 1 ns snapshot were performed for 1844 atoms within 16 Å of the oxygen atom of the catalytic water molecule in the presence of the rest of the 46 080 atoms. The same 1844 atoms were optimized in all QM/MM calculations for the 1 ns snapshot. For the 10 ns snapshot, 1876 atoms within 16 Å of the oxygen atom of the catalytic water molecule were optimized, and the same 1876 atoms were optimized in all QM/MM calculations for the 10 ns snapshot. A comparison of the QM/MM structures and energies obtained with 1 ns and 10 ns snapshots (Table S6, ESI†) suggests that the thermal fluctuations in the protein matrix have an insignificant effect on the reaction energies and do not alter the catalytic mechanism. The details can be found in the ESI.† Discussions in the rest of the paper will focus on the results obtained with a 1 ns snapshot unless specifically mentioned.

In the QM/MM calculations, 105 atoms were in the QM region (Fig. 1): the Zn²⁺ ion, the catalytic H₂O, His142, His143, His180, Asp176, Asp178, Asp183, Asp267, and the acetyl-lysine side chains of the tetrapeptide substrate. The net charge of the QM region was −2e. The QM/MM boundary was fragmented at the C_α–C_β bonds of each respective side chain and the default capping H atom method implemented in QuanPol was used to treat the covalent bonds between the QM and MM regions.³⁹ The 6-31G* basis set⁵⁶ was used for 82 QM atoms. The aug-cc-pVDZ basis set^57,58 was used for the 23 most relevant atoms, which were the Zn ion, the three atoms of the H₂O molecule, four carboxylate O atoms of Asp178 and Asp267, the two carboxylate O atoms of Asp176 and Asp183, the four N and H atoms of His142 and His143, one N atom of His180, and the four N, H, C, and O atoms of the tetrapeptide substrate. In all the QM/MM calculations, the QM–MM LJ interaction was used (the QM atoms used their original MM LJ parameters). The force field charges of the MM atoms interact directly with the electrons and nuclei of the QM atoms and affect the Hartree–Fock wavefunction and subsequent MP2 energy and gradient.^59–61 A shifting function (QuanPol keyword ISHIFT = 4) was used for MM charge–charge interaction up to 12 Å. A switching function (QuanPol keyword ISWITCH = 1) was used for MM LJ interaction from 10 to 12 Å. A QM–MM switching function (QuanPol keyword ISWITCH = 1) was used for QM–LJ, QM–charge interactions from 22 to 32 Å. The parallel MP2 program implemented by Ishimura, Pulay, and Nagase et al.^62,63 was used together with the QuanPol routines that add MM interactions to the MP2 method.⁶⁰

All QM/MM geometry optimizations and transition state searches were performed with the Hessian guided optimization method we implemented in the QuanPol program. First, all 1844 (for 1 ns snapshot) or 1876 (10 ns snapshot) atoms were optimized using a steepest descent scheme at the MM level. The Hessian for these atoms was then computed at the MM level and used to guide subsequent QM/MM geometry optimization. The QM/MM geometry optimization was started at the Hartree–Fock level (with the 6-31G* basis set and Grimme's dispersion correction) for the ES state, using the MM Hessian as the guide. The Hessian was systematically updated and improved as the QM/MM geometry optimization proceeded to finish. Based on the optimized ES structure and the improved Hessian, other states were constructed (by repositioning a few atoms) and optimized. All transition states were optimized with a saddle point search method by preparing a trial structure and supplying a Hessian matrix containing a leading negative mode. We have implemented a convenient and low-cost method in the QuanPol program to compute and update part of an existing and all-positive-mode Hessian to produce a new Hessian that (if lucky) contains one negative mode for a trial TS structure. The QM/MM optimized structures and the improved Hessian matrices obtained at the Hartree–Fock level of theory can be used as starting points for subsequent B3LYP, B3LYP-D3, and MP2 optimization. All transition states found at the B3LYP-D3 level of theory were confirmed with the partial Hessian vibration analysis method implemented in QuanPol. The results are shown in Table S1 (ESI†). The relative electronic energies of each species are in Table 1. The corresponding QM/MM MP2 and spin component scaled MP2 (SCS-MP2⁶⁴) single point energies (using four different basis sets) were calculated for all QM/MM MP2 optimized structures. The relative single-point energies are given in Table S2 (ESI†). The optimized coordinates of the enzyme and substrate at various reaction stages are available as PDB files in the ESI.†

Table 1 Relative electronic energies (kcal mol⁻¹) of each species involved in the catalytic mechanism for B3LYP/MM, B3LYP-D3/MM, and MP2/MM (with mixed aug-cc-pVDZ and 6-31G* basis set) optimized structures with and without a K⁺ ion, which coordinates with Asp176 near the active site

	ES	TS1a	EI1a	TS1	EI1	TS2	EI2	TS3	EI3	EP
With a K^+ ion at site 1
B3LYP/MM	0.0	18.3	17.1	24.1	21.3	30.6	17.2	18.9	10.8	1.5
B3LYP-D3/MM	0.0	16.9	15.5	22.9	19.0	25.8	16.5	19.4	13.5	6.1
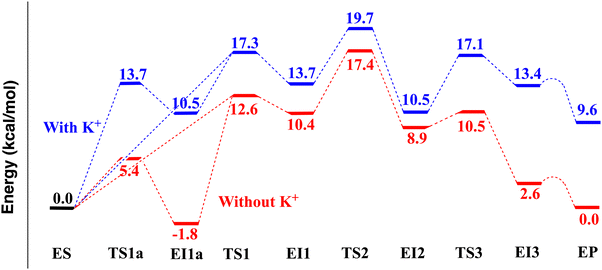
MP2/MM	0.0	13.7	10.5	17.3	13.7	19.7	10.5	17.1	13.4	9.6
No K^+ ion at site 1
B3LYP-D3/MM	0.0	9.5	5.5	19.9	16.5	24.4	15.1	16.7	4.9	−1.7
MP2/MM	0.0	5.4	−1.8	12.6	10.4	17.4	8.9	10.5	2.6	0.0

---

III. Results and discussion

III.A. Zn(II)-HDAC8 with two K⁺ ions

III.A.1. Three-step reaction mechanism. The K⁺ ion at site 1 interacts with the zinc catalytic site by coordinating with Asp176 (Fig. 1). In the QM/MM MP2 optimized ES state, the Zn²⁺ forms five coordinate bonds with the substrate carbonyl C=O, H₂O, Asp178 carboxylate COO⁻, Asp267 carboxylate COO⁻, and His180 neutral imidazole. The MP2/MM computed reaction pathway energetics show a three-step mechanism (Fig. 2C), which is different from mechanisms 1 and 2 (Fig. 2A and B) proposed in the literature. The relative electronic energies of the species are shown in Table 1 and Fig. 3. Compared to mechanism 2 (Fig. 2B), in which the amide C–N bond cleavage, protonation of amide N atom, and the protonation of His142 are concerted, the three-step mechanism found here has an additional intermediate EI2 (as shown in Fig. 2C). Due to this intermediate, the proton transfer from His143 to the amide N atom and the amide C–N bond cleavage are separated into two distinctive steps. In the following, we describe the details of this three-step mechanism.

Fig. 3 The MP2/MM (with mixed aug-cc-pVDZ and 6-31G* basis set) computed electronic energy profiles along the deacetylation reaction pathway of a tetrapeptide catalyzed by HDAC8 with (blue) and without (red) a K⁺ ion at site 1.

The first step is the nucleophilic addition of the Zn-bound water molecule to the acetamide carbonyl carbon atom (C_sub). To activate the water molecule, either His142 or His143 (both with only δ-N protonated) could accept a proton from the water molecule. These two possibilities are examined with the MP2/MM geometry optimization method. Similar to the results of Chen et al. and Gleeson et al.,^23,24 we found that a water proton (H2_wat) can pass a transition state (TS1, Fig. 4B) and bind to His143 (EI1 in Fig. 4C). The electronic energy for the transition state TS1 is 17.3 kcal mol⁻¹. In the ES state (Fig. 4A), the distance between the Zn ion and the O atom of the carbonyl group of the substrate (see Zn–O_sub in Table S4, ESI†) from the MP2/MM geometry optimization is 2.16 Å. In TS1, this distance is shortened to 1.93 Å. The proton transfer from the water to His143 is accompanied by the nucleophilic attack of the partially formed hydroxide to the carbonyl carbon atom (C_sub), leading to a negatively charged tetrahedral intermediate (EI1 in Fig. 4C). The relative electronic energy for EI1 is 13.7 kcal mol⁻¹. The O_wat–C_sub distance is shortened from 2.55 Å in ES (Fig. 4A) to 1.50 Å in TS1 (Fig. 4B). The interaction between the Zn ion and O_wat is significantly weakened in EI1, as shown by the elongation of the distance between the two atoms (from 2.09 Å in ES to 2.51 Å in TS1). The distance between O_wat and the C atom of the carbonyl group of the substrate (O_wat–C_sub in Table S4, ESI†) is 1.48 Å in the negative tetrahedral intermediate EI1, longer than the standard carboxylic C–O distance of 1.34 Å.

Fig. 4 The MP2/MM (with a mixed aug-cc-pVDZ and 6-31G* basis set) optimized structures for representative reaction species involved in the deacetylation reaction pathway of a tetrapeptide catalyzed by the HDAC8 system with a K⁺ ion at site 1.

We also found that a water proton (H1_wat) can transfer to His142. The electronic energy for the transition state (TS1a, Fig. S7B, ESI†) is 13.7 kcal mol⁻¹ (relative to ES). While the proton transfers from the water to His142, the partially formed hydroxide approaches the carbonyl carbon atom (C_sub), leading to a negatively charged tetrahedral intermediate (EI1a in Fig. 5A and Fig. S7C, ESI†). The relative electronic energy for EI1a is 10.5 kcal mol⁻¹. However, because the protonation of His143 (i.e., EI1) is the prerequisite for the subsequent protonation of the amide N atom, EI1a must change into EI1. Chen et al.²³ found a transition state (denoted as 2TS3a′ in their paper) between EI1a and EI1. Here, our transition state search on the MP2/MM potential energy surface (PES) shows that the transition state between EI1a and EI1 is simply TS1 (Fig. 4B), the same transition state bridging ES and EI1. Therefore, on the MP2/MM PES, there are two pathways from ES to EI1: one is ES – TS1a – EI1a – TS1 – EI1; the other is ES – TS1 – EI1.

Fig. 5 Comparison of the MP2/MM (with a mixed aug-cc-pVDZ and 6-31G* basis set) optimized structures that have different protonation states in the deacetylation reaction pathway of a tetrapeptide catalyzed by HDAC8 with and without a K⁺ ion at site 1.

The second step is the protonation of the amide N atom by His143 and the formation of a neutral tetrahedral intermediate (EI2 in Fig. 4E). The distance between O_wat and the C atom of the carbonyl group of the substrate (O_wat–C_sub) is shortened from 1.47 Å in EI1 (Fig. 4C) to 1.45 Å in TS2 (Fig. 4D) and finally to 1.41 Å in EI2 (Fig. 4E). The protonation of N_sub leads to a weakened amide C–N bond (from 1.46 Å in EI1 to 1.49 Å in TS2, and finally to 1.57 Å in EI2). The electronic energy of TS2 is 19.7 kcal mol⁻¹ higher than ES. The electronic energy of the neutral tetrahedral intermediate EI2 is 10.5 kcal mol⁻¹, 3.2 kcal mol⁻¹ lower than the negative tetrahedral intermediate EI1 (13.7 kcal mol⁻¹).

The third step is the complete cleavage of the amide C–N bond in the tetrapeptide substrate, accompanied by a proton transfer from the newly formed carboxylic group to His142. The proton has already transferred to His142 (H1_wat–N_H142 1.10 Å) when the C–N distance is at the transition state (TS3, Fig. 4F) length of 1.99 Å. The electronic energy barrier from EI2 to the transition state TS3 (Fig. 4F) is 6.6 kcal mol⁻¹, and the electronic energy of TS3 is 17.1 kcal mol⁻¹ higher than ES. The amide C–N distance is elongated from 1.57 Å in EI2 to 1.99 Å in TS3, and finally to 2.57 Å in the intermediate EI3 (Fig. 5C). The electronic energy of EI3 is 13.4 kcal mol⁻¹ higher than ES. However, as an immediate local minimum just passing TS3, EI3 is not very stable because Tyr306 forms a probably weak hydrogen bond with the newly formed carboxylic group. Passing a low and flat electronic energy barrier (0.26 kcal mol⁻¹), Tyr306 can rotate and form a (presumably stronger) hydrogen bond to the newly formed amine group (–CNH₂) of the substrate, leading to a more stable structure EP (Fig. 3 and 5E). EP has a relative electronic energy of 9.6 kcal mol⁻¹ (relative to ES), 3.8 kcal mol⁻¹ lower than EI3 (Table 1 and Fig. 3). EP is likely the final enzyme–product complex minimum state. Because the transition state between EI3 and EP has a very low and flat electronic energy barrier, it may not be a meaningful free energy barrier when zero-point energy and thermal free energy are considered. Similarly low and flat electronic energy barriers (0.01 and 0.14 kcal mol⁻¹) were also observed on the QM/MM B3LYP and B3LYP-D3 potential energy surfaces. Therefore, in the rest of the paper, this transition state is not discussed.

The first step in the three-step mechanism identified in this work is identical to the first step in mechanism 2 (Fig. 2B) proposed in the literature for Zn(II)-HDAC8 with two K⁺ ions: a negatively charged tetrahedral intermediate is formed after the initial hydroxide attack. In the two-step mechanism (mechanism 2 in Fig. 2B), the negative tetrahedral intermediate directly decomposes into the final product (via a concerted protonation of amide N by His143, C–N cleavage, and protonation of His142). In the three-step mechanism (Fig. 2C), the negative tetrahedral intermediate evolves into a neutral tetrahedral intermediate (via protonation of amide N by His143), then decomposes into the final product (via C–N cleavage and protonation of His142).

III.A.2. Accuracy of MP2 and SCS-MP2. The electronic correlation energy recovered by MP2 methods is basis set dependent. In addition, it has been shown the SCS-MP2⁶⁴ method can generally improve the accuracy of the regular MP2 method. SCS-MP2/MM (aug-cc-pVDZ for 23 atoms and the 6-31G* basis set for the rest) single point energy calculations (all SCS-MP2 results are presented in Table S2, ESI†) show that the relative electronic energies of TS1, TS2, and TS3 are 20.9, 22.1, and 18.1 kcal mol⁻¹, respectively. The spin-component scaling leads to 2–3 kcal mol⁻¹ changes to the values for TS1 and TS2, but a very small change to TS3. The mixed basis set (aug-cc-pVDZ for 23 atoms and 6-31G* basis set for 82 atoms) used here for the QM region has a balanced accuracy and efficiency. In general, when a mixed basis set is used, caution is needed to avoid unbalanced electronic polarization and correlation, which may potentially lead to significant errors in the computed structures and relative energies. It is often necessary to carry out calibration calculations using a consistent and balanced basis set. Single point energy MP2/MM calculations with a larger basis set (aug-cc-pVTZ^57,58 for 23 atoms and 6-31G* for the rest) show that the relative electronic energies for TS1, TS2 and TS3 are 15.5, 17.2, and 16.6 kcal mol⁻¹, respectively, slightly lower than the aug-cc-pVDZ values; the corresponding SCS-MP2/MM relative electronic energies are 19.2, 19.7, and 17.7 kcal mol⁻¹. Further increment of the basis set to aug-cc-pVDZ for all 105 QM atoms, and to aug-cc-pVTZ for 23 QM atoms and aug-cc-pVDZ for 82 QM atoms does not lead to large changes to the relative electronic energies (Table S2, ESI†). Clearly, none of these relative energies exhibits large deviations from the values optimized with MP2/MM and the mixed aug-cc-pVDZ and 6-31G* basis set. While it remains to be further verified, we did notice that for HDAC8, the aug-cc-pVDZ basis set is sufficient for MP2 computation of the structures and relative energies on the reaction pathway to achieve an accuracy of ∼2 kcal mol⁻¹. Replacing aug-cc-pVDZ with the smaller 6-31G* basis set for the non-reactive atoms in the QM region indeed introduces some errors, mainly due to the reduction of the long-ranged static polarizabilities of the affected QM atoms. This is apparent because these two basis sets differ mainly in the number of diffuse functions and polarizable functions. It also affects the MP2 computed relative electronic correlation energies for the species on the reaction pathway. Single-point energy calculations using the aug-cc-pVDZ basis set would be sufficient for identifying possible large errors obtained with smaller basis sets. In general, for QM/MM MP2 geometry optimization calculations like the ones in this study, using a very large basis set for the QM region would not necessarily improve the overall results because the dynamic fluctuations of the enzyme matrix and solvent molecules, which can typically cause a couple of kcal mol⁻¹ energy differences in the computed relative energies, are not sufficiently sampled. In addition, if the force field for the protein matrix and solvent water molecules is not electronically polarizable, solely improving the description of the polarizabilities of the QM atoms at higher computational costs would only marginally improve the overall accuracy.

To verify the accuracy of the MP2 and SCS-MP2 methods, we performed coupled-cluster singles, doubles with non-iterative triples [i.e., CCSD(T)]^33–35 calculations for a set of 34-atom active site models (Fig. S6, ESI†) extracted from the QM/MM MP2 optimized structures. These models include the core reactive groups: the Zn ion, the water, the substrate acetamide group, and the imidazole groups of His142 and His143. The SPK-ADZP⁶⁵ basis set was used as it was similar to but slightly smaller than the aug-cc-pVDZ basis set and led to a significant reduction of computer resource requirements, as well as good convergence. The relative CCSD(T) corrections across the models are small, 2.1 kcal mol⁻¹ for regular MP2 and 1.3 kcal mol⁻¹ for SCS-MP2, at maximum (Table S7, ESI†). These results suggest that for the reaction pathway studied here, the MP2 and SCS-MP2 methods have an accuracy of about 1–2 kcal mol⁻¹.

III.A.3. Comparison to experiments.
The k_cat value. There is no experimental k_cat value for Zn(II)-HDAC8 with both sites 1 and 2 occupied by K⁺ ions. The experimental rate constant k_cat for Zn(II)-HDAC8 was measured as 0.90 ± 0.03 s⁻¹ in an assay buffer solution containing 137 mM NaCl and 2.7 mM KCl.⁶⁶ Using unimolecular transition state theory, the apparent activation free energy under this condition is 17.5 kcal mol⁻¹ at 298 K. At a low concentration of 2.7 mM, K⁺ can hardly bind to either site 1 (with a K_1/2,inhib = 130 ± 30 mM) or site 2 (with a K_1/2,act = 14 ± 2 mM) of Zn(II)-HDAC8.¹⁹ It is difficult to accurately measure the K_1/2,inhib and K_1/2,act of Na⁺ for Zn(II)-HDAC8. However, for Co(II)-HDAC8, it was experimentally found that the site-1 K_1/2,inhib for Na⁺ and K⁺ are 320 ± 140 mM and 26 ± 3 mM, and the site-2 K_1/2,act for Na⁺ and K⁺ are 90 ± 40 mM and 3.4 ± 0.3 mM.¹⁹ Here we assume the ratios of the affinities for both sites are transferable from Co(II)-HDAC8 to Zn(II)-HDAC8, so the site-1 K_1/2,inhib and site-2 K_1/2,act of Na⁺ for Zn(II)-HDAC8 can be estimated to be 1600 mM and 370 mM, respectively. In a solution containing 137 mM NaCl, the Zn(II)-HDAC8 inhibition site-1 would be 8% occupied, and the activation site-2 would be 27% occupied, by Na⁺. If site 1 was 0% occupied and site 2 was 100% occupied by Na⁺, the k_cat for Zn(II)-HDAC8 would be 3.3 s⁻¹ (0.90 s⁻¹ divided by 0.27). Using unimolecular transition state theory, the activation free energy would be 16.7 kcal mol⁻¹ at 298 K. It has also been experimentally determined that, for Co(II)-HDAC8, when both site 1 and site 2 are 100% occupied by K⁺ ions, the k_cat/K_M value would decrease by 11-fold as compared to the case when site 1 is empty and site 2 is 100% occupied by K⁺ ions.¹⁹ The site-1 K⁺ depletion is a pretty large charge perturbation. When K⁺ ions are replaced by Na⁺ ions (same charge, but slightly different ionic radius, polarizability, and dispersion interaction) at either or both site 1 and site 2, the perturbation is much smaller than depleting the K⁺ ions; thus, the changes in the activity would be in much smaller scales than 11-fold. Accordingly, as a rough approximation for estimating the k_cat value, here we assume that the effects of Na⁺ and K⁺ at both sites are equivalent, so replacing the site-2 Na⁺ by K⁺ would result in roughly the same k_cat of 3.3 s⁻¹ for Zn(II)-HDAC8 with site 1 being 0% occupied and site 2 being 100% occupied by K⁺. In addition, since the K_M value is insensitive to K⁺ binding, it also implies that it is the k_cat value that would have decreased by 11-fold upon site-1 K⁺ binding. These analyses suggest that if site 1 was 100% occupied and site 2 was 100% occupied, both by K⁺, the k_cat for Zn(II)-HDAC8 would be 0.30 s⁻¹, corresponding to an activation free energy of 18.1 kcal mol⁻¹ at 298 K. While being approximate, these analyses are reasonable. For example, based on these analyses, in a solution containing 130 mM K⁺, it is expected that site 1 is roughly 50% occupied (note K_1/2,inhib = 130 ± 30 mM) and site 2 is roughly 100% occupied (note K_1/2,act = 14 ± 2 mM), by K⁺, and the apparent k_cat would be (3.3 + 0.3) × 0.5 = 1.8 s⁻¹. In a recent experimental measurement of the apparent k_cat of HDAC8 in a solution containing 130 mM K⁺ (50 mM K₂HPO₄ and 30 mM KCl), two k_cat values were obtained from two kinetic fitting models, one was 2.0 s⁻¹ and the other was 2.9 s⁻¹.⁶⁷ The fitted value 2.0 s⁻¹ is close to the 1.8 s⁻¹ value estimated here.

According to our MP2/MM calculations (as shown in Fig. 3), the relative electronic energies of TS1, TS2, and TS3 are 17.3, 19.7, and 17.1 kcal mol⁻¹, respectively. Though these values are comparable, the second step (TS2) has the highest electronic energy. Zero-point energy (ZPE) and free energy corrections are estimated with partial Hessian harmonic frequencies. Due to the high computational cost of the MP2 method, the partial Hessian harmonic frequency calculations are performed with the B3LYP-D3/MM method. Twenty-six key reactive and zinc-binding atoms are included in the partial Hessian calculations: the Zn ion, N_His142, H_His142, N_His143, H_His143, O_Asp176, O_Asp178, O_Asp183, N_His180, O_Asp267, O, and H atoms of the catalytic water, as well as the reactive N, H, O, and C atoms in the substrate. The ZPE and thermal free energy corrections are −1.7, −0.1, and −0.5 kcal mol⁻¹, respectively, for TS1, TS2, and TS3 (relative to ES). After correction, the activation free energies for TS1, TS2, and TS3 are 15.6, 19.6, and 16.6 kcal mol⁻¹, respectively. TS2 still has the highest value. Therefore, our best estimation of the free energy barrier is 19.6 kcal mol⁻¹ for 298 K, which is in good agreement with the experimental value of 17.5 kcal mol⁻¹ for Zn(II)-HDAC8 in 137 mM NaCl and 2.7 mM KCl. If the estimated experimental value 18.1 kcal mol⁻¹ for Zn(II)-HDAC8 (with two K⁺ ions) is used for comparison, the agreement is also good.

Thermodynamics and kinetics of HDAC8. We noticed that some researchers have misunderstandings about enzymatic thermodynamics and kinetics. For example, some researchers mistakenly believe that each enzyme–intermediate complex on the catalytic pathway should have a forward reaction energy barrier lower than the backward reaction barrier, so the forward reaction can proceed faster than the backward reaction. However, the rate is determined by two factors: the rate constant (i.e., barrier) and concentration. Driven by concentration differences, a multi-step reaction can always proceed from reactant to product, and vice versa, to reach an equilibrium or steady state, no matter what the reaction pathway energy profile is. Some researchers also mistakenly believe that in enzyme catalysis the EP state must have a lower energy than the ES state, i.e., ES to EP must be exothermic or exergonic, to favor the forward reaction. However, the overall reaction is from free substrate and enzyme (E + S, not the ES complex) to free product and enzyme (E + P, not the EP complex). If the free E + P state has a lower free energy than the ES state, the enzyme catalytic reaction can always proceed no matter how high (but of course, should always be lower than the rate-determining transition state) the energy of the EP state is. The relative energy of the ES and EP is irrelevant to whether the catalytic reaction can proceed or not, it only affects the relative equilibrium or steady state populations of ES and EP (more ES if ES is lower, more EP if EP is lower).

Consider the following general enzyme-catalyzed reaction and the standard (physical chemistry standard state, i.e., activity = 1.0 when solute concentration is near 1.0 M) Gibbs free energy changes on the pathway:

The overall reaction E + S to E + P (i.e., free S to free P) is typically exergonic at standard state, but slightly endergonic is also very common:

ΔG^o₁ + ΔG^o₂ + ΔG^o₃ < 0 (can be slightly > 0) (2)

Slightly endergonic is allowed because in biological systems P may have a lower metabolic concentration than S, thus lower free energy, especially when the P state has two independent molecules and larger translational entropy.

E + S to ES is typically exergonic at the standard state, but endergonic is not a problem:

ΔG^o₁ < 0 (can be >0) (3)

An endergonic E + S to ES process means the formation of ES is not thermochemically favored (but ES can still form, just has a low equilibrium concentration), and most of the enzyme molecules remain in their free state. If the enzymatic rate-determining transition state is energetically lower than the non-catalyzed one, the enzyme is still an effective catalyst, despite its weak binding ability to the substrate. The fact that enzymes exhibit favorable substrate binding (exergonic) is a result of biological evolution rather than thermodynamics because an unfavorable substrate binding would require the production of a greater number of enzyme molecules, a disadvantageous survival burden.

Here we use EI_lowest to denote the state with the lowest standard free energy (global minimum) on the reaction pathway. It can be either ES or EP, or any other state before E + P, including E + S. EI_lowest to E + P is typically exergonic at standard state, but slightly endergonic is also common, because P is always at concentrations orders lower than the standard state concentration 1 M. In case the EI_lowest is ES, we should have:

ΔG^o₂ + ΔG^o₃ < 0 (can be slightly > 0) (4)

In case the EI_lowest is EP, we should have:

ΔG^o₃ <0 (can be slightly > 0) (5)

None of these inequalities in eqn (2)–(5) put any sign restrictions on ΔG^o₂: it can be either positive (endergonic) or negative (exergonic).

For the Zn(II)-HDAC8 (with two K⁺ ions) catalyzed deacetylation reaction studied here, the standard binding free energy change ΔG^o₁ for the R-H-K(Ac)-K(Ac) tetrapeptide and enzyme has been experimentally measured to be −4.0 kcal mol⁻¹ (K_M = 1.1 × 10⁻³ M) at 298.15 K.⁶⁶ It was also experimentally found that the ΔG^o₁ is insensitive to site-1 K⁺ depletion and mutations of some active site residues.³⁸ Literature results on the standard free energy change or equilibrium constant for the hydrolysis of the tetrapeptide substrate are not available. It has been experimentally measured that the standard free energy of hydrolysis of acetamide (CH₃CONH₂) to acetate and ammonium is −2.1 kcal mol⁻¹,⁶⁸ and is −2.4 kcal mol⁻¹ for N,N-dimethyl-acetamide.⁶⁹ The hydrolysis of the acetamide group in the R-H-K(Ac)-K(Ac) tetrapeptide substrate studied here should be close to these two values because all acetamide hydrolyses have similar free energy changes. For convenience of discussion, here we use an estimated value of −2.2 kcal mol⁻¹. The following experimental results for HDAC8 catalysis can be established:

ΔG^o₁ + ΔG^o₂ + ΔG^o₃ = −2.2 kcal mol⁻¹ (6)

ΔG^o₁ = −4.0 kcal mol⁻¹ (7)

Eqn (6) satisfies eqn (2) and eqn (7) satisfies eqn (3). Combining eqn (6) and (7), we have the following experimental relationship:

ΔG^o₂ + ΔG^o₃ = +1.8 kcal mol⁻¹ (8)

No experimental values for ΔG^o₂ or ΔG^o₃ are available.

The experimental relationship in eqn (8) can be used to examine ΔG^o₂ values from theoretical calculations. In this work, ΔG^o₂ is computed to be +8.8 kcal mol⁻¹ (electronic energy 9.6 kcal mol⁻¹ with −0.8 kcal mol⁻¹ ZPE and thermal free energy correction, Table 2 and Table S1, ESI†) for HDAC8 with two K⁺ ions, so ΔG^o₃ must be around −7.0 kcal mol⁻¹. Since here ES is computed to be the global minimum, the slightly positive ΔG^o₂ + ΔG^o₃ is the overall free energy of dissociation and satisfies eqn (4). This ΔG^o₂ + ΔG^o₃ value corresponds to a thermodynamic dissociation equilibrium constant of 0.05 (unit-less, using activity and physical chemistry standard states) for ES = E + P1 + P2 (note the products are acetate and ammonium, denoted as P1 and P2). This equilibrium constant allows for a highly favorable dissociation of ES into E + P at typical biological and experimental concentrations such that [E]_total is 1.2–50 μM and [S] and [P] are 5–2000 μM.³⁸ Therefore, the computed ΔG^o₂ value of +8.8 kcal mol⁻¹ in this work (the direct consequence of this result is that ES is the global minimum) is reasonable and not contradictory to experimental facts. In contrast, in an earlier work by Corminboeuf et al.,²¹ ΔG^o₂ was computed to be around −8.9 kcal mol⁻¹ for HDAC8 with two K⁺ ions, so the EP state was the global minimum (Table 2). Based on the experimental relationship in eqn (8), ΔG^o₃ must be around +10.7 kcal mol⁻¹, which is too large to allow for a favorable dissociation of EP into E + P. Similarly, in an earlier work by Chen et al.,²³ ΔG^o₂ was computed to be around −4.4 kcal mol⁻¹ for HDAC8 with one K⁺ ion (Table 2), also leading to a large ΔG^o₃ and unfavorable dissociation of EP into E + P. To be discussed later, these two problematic ΔG^o₂ values were computed with inaccurate QM methods and/or a small basis set.

Table 2 Comparison of QM/MM relative single point energies (kcal mol⁻¹) of each species involved in the catalytic mechanism calculated with different DFT functionals. The MP2/MM (with a mixed aug-cc-pVDZ and 6-31G* basis set) optimized structures are used in the calculations with two basis sets: the BS1 (a mixed aug-cc-pVDZ and 6-31G* basis set) and 6-31G*. Reaction energies obtained from the literature and relative electronic energies obtained from our B3LYP/MM, B3LYP-D3/MM, MP2/MM, and SCS-MP2/MM calculations are included for comparison

QM method	ES	TS1a	EI1a	TS1	EI1	TS2	EI2	TS3	EI3	EP
With a K^+ ion at site 1
MP2/BS1	0.0	13.7	10.5	17.3	13.7	19.7	10.5	17.1	13.4	9.6
SCS-MP2/BS1//MP2/BS1	0.0	15.5	12.1	20.9	15.6	22.1	12.2	18.1	12.5	7.6
B3LYP/BS1	0.0	18.3	17.1	24.1	21.3	30.6	17.2	18.9	10.8	1.5
B3LYP-D3/BS1	0.0	16.9	15.5	22.9	19.0	25.8	16.5	19.4	13.5	6.1
M05-2X/BS1//MP2/BS1	0.0	15.9	13.4	20.6	16.9	22.4	13.4	19.0	15.0	10.3
M06/BS1//MP2/BS1	0.0	16.9	13.6	20.2	16.8	22.5	13.5	20.0	15.3	11.5
M06-2X/BS1//MP2/BS1	0.0	17.8	15.4	23.0	18.3	25.5	15.9	20.1	13.6	10.2
MN15/BS1//MP2/BS1	0.0	15.0	11.4	20.1	14.7	21.5	13.5	19.0	13.6	10.5
B3LYP/6-31G*//MP2/BS1	0.0	15.4	12.9	22.2	16.7	23.3	13.0	13.2	6.4	−1.2
M05-2X/6-31G*//MP2/BS1	0.0	13.7	9.0	16.9	12.1	18.0	8.6	14.1	10.5	7.1
M06/6-31G*//MP2/BS1	0.0	15.6	9.4	17.0	12.2	18.3	8.9	14.8	10.7	8.3
M06-2X/6-31G*//MP2/BS1	0.0	15.6	10.8	19.2	13.6	21.4	11.0	15.0	8.4	6.4
MN15/6-31G*//MP2/BS1	0.0	12.3	5.8	15.3	8.7	16.2	7.7	12.8	7.0	4.9
Corminboeuf et al.^21	0.0	—	—	15.0	10.6	13.7	—	—	−8.9	—
Wu et al.^22	0.0	—	—	18.3	∼13.0	∼15.3	—	—	−7.1	—
Chen et al.^23	0.0	14.0	9.8	15.2	10.2	9.6	4.4	10.8	8.5	—
Gleeson et al.^24	0.0	17.9	10.8	—	—	12.1	—	—	−2.2	—
No K^+ ion at site 1
MP2/BS1	0.0	5.4	−1.8	12.6	10.4	17.4	8.9	10.5	2.6	0.0
SCS-MP2/BS1//MP2/BS1	0.0	6.5	−0.7	16.3	12.4	19.9	10.6	13.0	1.4	−2.3
B3LYP/BS1	0.0	9.5	5.5	19.9	16.5	24.4	15.0	16.7	4.9	−1.7
M05-2X/BS1//MP2/BS1	0.0	8.5	1.3	16.4	13.7	20.2	11.7	13.6	4.8	1.3
M06/BS1//MP2/BS1	0.0	8.5	0.6	16.4	13.4	20.3	11.7	13.9	4.3	2.1
M06-2X/BS1//MP2/BS1	0.0	7.8	1.4	19.9	14.5	22.1	12.9	15.7	1.1	−0.3
MN15/BS1//MP2/BS1	0.0	6.5	−1.2	15.9	11.4	18.8	11.3	13.7	2.4	0.8
M05-2X/6-31G*//MP2/BS1	0.0	4.6	−5.8	12.4	8.8	15.6	6.8	9.2	−2.2	−4.1
M06/6-31G*//MP2/BS1	0.0	4.7	−6.1	12.4	8.6	15.7	6.9	9.5	−2.6	−3.0
M06-2X/6-31G*//MP2/BS1	0.0	4.2	−5.5	15.7	9.6	17.8	7.9	11.3	−6.4	−6.1
MN15/6-31G*//MP2/BS1	0.0	2.5	−9.2	10.7	5.2	13.5	5.4	8.7	−6.3	−6.6
Wu et al.^22	0.0	—	—	22.6	—	—	—	—	—	—
Chen et al.^23	0.0	8.5	−0.6	11.1	7.4	8.9	2.9	6.2	−4.4	—

---

Solvent kinetic isotope effect. The solvent hydrogen–deuterium kinetic isotope effect (sKIE) on HDAC8 activity has been experimentally measured by Hansen and coworkers.⁶⁷ It was found that in pure D₂O solvent with 137 mM NaCl and 2.7 mM KCl, the activity (i.e., k_cat/K_M ratio) of HDAC8 is about 19% of that in pure H₂O solvent. It was also found that the K_M is insensitive to deuteration, so the sKIE is mainly in the k_cat. We note that the authors reported a sKIE of 6.2, but their plotted data suggest that the value is more likely around 5.3. Here the sKIE is computed with the partial Hessian harmonic vibration method (for T = 298.15 K) and the QM/MM B3LYP-D3 optimized geometries. As described earlier, for H₂O solvent (all H atoms in the QM/MM system had a mass of 1.008 amu), the ZPE and thermal free energy corrections were computed to be −1.684, −0.043, and 0.489 kcal mol⁻¹, respectively, for TS1, TS2, and TS3 (relative to ES, which is the global minimum before E + P). Using the same Hessian force constant matrices but with a mass of 2.014 amu for the two D atoms of the catalytic water molecule and the hydroxyl D atom of Tyr306 (which should be rapidly deuterated in D₂O solvent as its pK_a is about 10.5), the ZPE and thermal free energy corrections were computed to be −0.677, +0.741, and 0.588 kcal mol⁻¹, respectively, for TS1, TS2, and TS3 (relative to ES). These changes suggest that the sKIE on k_cat would be 5.5, 3.8, and 1.2, respectively, for TS1, TS2, and TS3. As already discussed, the free energies of TS1, TS2, and TS3 are within a couple of kcal mol⁻¹, with TS2 being the highest and rate-determining. Therefore, the experimentally measured sKIE (6.2 as reported by the original authors, but we think it is more likely 5.3) should be due to TS2 (computed to be 3.8 here) when both site 1 and site 2 are occupied by K⁺ or Na⁺ ions. The difference between the experimental value 6.2 (or 5.3) and the computed value 3.8 appears to be large, but the underlying free energy (mainly zero-point energy) difference is only 0.30 kcal mol⁻¹, which is small. If the experimental value is 5.3, the underlying energy difference would be only 0.20 kcal mol⁻¹. In general, it is difficult to reproduce experimental sKIE values using approximate computational methods such as the QM/MM B3LYP-D3 and the partial Hessian method used here. As to be discussed later, compared to MP2, the B3LYP-D3 method has significant errors in the relative energies for the species on the HDAC8 catalytic pathway, and the QM/MM B3LYP-D3 optimized bond lengths are also noticeably different from those optimized with QM/MM MP2 (the overall geometries are still similar for the relevant states). Therefore, the harmonic force constants and frequencies computed at the QM/MM B3LYP-D3 level of theory are likely inferior to those from the QM/MM MP2 calculations, which are much more costly to perform. Even when the harmonic force constants can be computed to a satisfactory level of accuracy, other factors such as structural fluctuation and anharmonic corrections, are still missing, so the computed sKIE may still be banded by errors in the order of tenths of kcal mol⁻¹. Using only three D atoms in the sKIE calculation may be another nonnegligible source of error since a comprehensive calculation should consider the deuteration of all relevant H atoms, including solvent H₂O molecules as some of them are near the active site, and may contribute to the sKIE. The partial Hessian calculation performed here for 26 QM atoms did not include any solvent water molecules. In general, it is expected that sKIE is larger when more H atoms are deuterated. For a simple comparison, we performed sKIE calculations with two D atoms for the catalytic water (Tyr306 had a H, not D) and obtained 4.8, 3.2, and 1.1, respectively, for TS1, TS2, and TS3. This is a hypothetical case because Tyr306 should be deuterated in D₂O. This comparison shows that the deuteration of a non-reactive active site group indeed has positive contributions (∼0.1 kcal mol⁻¹ in energy) to the sKIE due to the intrinsic delocalization nature of the vibration modes. While how to improve the sKIE calculation for enzymes is an interesting research topic and worth exploring, it is apparently out of the focus of the current work. Finally, we note that it appears that the experimental value could be better explained if the TS1 is rate-determining and has a larger computed value of 5.5. More discussions on the sKIE and their relationship to the possible rate-determining steps will be presented in the next sub-section for HDAC8 without K⁺ at site 1.

III.B. Effects of K⁺ depletion from site 1

A perturbation scheme was used here to examine the effect of the K⁺ at site 1 on the catalytic pathway. For the 1 ns MD snapshot (with a K⁺ at site 1), two sets of MP2/MM geometry optimization and transition state search calculations were performed. In the first set of MP2/MM calculations, the K⁺ was at site 1 (unperturbed state). The results from the first set have been discussed above. The second set had a perturbation in the MM region: the force field charge of the K⁺ ion at site 1 was set to zero (the LJ potential of the K⁺ was retained to avoid significant structural changes to the protein matrix). If two independent MD simulations were performed, one with K⁺ and one without, the differences between the QM/MM results from the two MD trajectories would contain random thermal fluctuations up to a few kcal mol⁻¹. Unless the QM/MM difference is expected to be large (e.g., more than 10 kcal mol⁻¹), two independent MD trajectories should be avoided.

The results are shown in Table 1 and Fig. 3. In general, the reaction pathways with and without a K⁺ ion at site 1 are very similar and can be characterized by the same set of intermediates and transition states (with the same names).

The first step is the nucleophilic addition of the Zn-bound water molecule to the amide carbonyl carbon atom (C_sub). The ES (Fig. S8A, ESI†) can pass TS1 (Fig. S8D, ESI†) and evolve into EI1 (Fig. S8E, ESI†) by transferring a proton from water to His143. It can also pass TS1a (Fig. S8B, ESI†) and evolve into EI1a (Fig. 5B and Fig. S8C, ESI†) by transferring a proton from water to His142. The EI1a state has an electronic energy −1.8 kcal mol⁻¹ lower than ES. When zero-point energy and thermal free energy (+1.7 kcal mol⁻¹, Table S1, ESI†) are included, the free energy of EI1a is −0.1 kcal mol⁻¹ lower than ES. SCS-MP2 calculation with a larger basis set (Table S2, ESI†) suggests that the free energy of EI1a should be a couple of tenths kcal mol⁻¹ higher than ES. In EI1a the proton on δ-N_H142 is already transferred to Asp176, suggesting that the removal of the K⁺ ion from site 1 leads to an increment in the electronegativity of the oxygen atom of Asp176. Similar to the case with a K⁺ at site 1, our transition state search on the MP2/MM PES shows that the transition state between EI1a and EI1 is again TS1 (Fig. S8D, ESI†), the same transition state bridging ES and EI1.

The second step is the protonation of the amide N atom by His143 and the formation of a neutral tetrahedral intermediate (EI2 in Fig. S8G, ESI†). The electronic energy of TS2 (Fig. S8F, ESI†) is 17.4 kcal mol⁻¹ (relative to ES). The electronic energy of the neutral tetrahedral intermediate EI2 is 8.9 kcal mol⁻¹, 1.5 kcal mol⁻¹ lower than the negative tetrahedral intermediate EI1 (10.4 kcal mol⁻¹).

The third step is the complete cleavage of the amide C–N bond in the tetrapeptide substrate. Different from the one with K⁺ ions at site 1, this step involves a concerted transition state (TS3 in Fig. S8H, ESI†), where C–N bond breaking is associated with a proton transfer from the newly formed carboxylic group to His142. In TS3, the proton is between N of His142 and water (H1_wat–N_H142 1.25 Å and H1_wat–O_wat 1.26 Å). Passing TS3, as H1_wat is completely transferred to His142, the proton on δ-N_H142 would transfer to Asp176, finally leading to the EI3 state (Fig. 5D and Fig. S8I, ESI†). Therefore, the EI3 state for a K⁺-free site 1 is different from that for a K⁺-bound site 1 due to an increased proton binding ability of Asp176 upon K⁺ removal (Fig. 5C and D). The electronic energy barrier from EI2 to the transition state TS3 (Fig. S8H, ESI†) is 1.7 kcal mol⁻¹. The ZPE and thermal free energy correction is −2.9 kcal mol⁻¹ from EI2 to TS3. After the correction, the free energy barrier from EI2 to TS3 is −1.3 kcal mol⁻¹ (not really a barrier). Therefore, after K⁺ depletion from site 1, it is likely a two-step mechanism. The electronic energy of EI3 (Fig. S8I, ESI†) is 2.6 kcal mol⁻¹ higher than ES. Passing a low and flat (0.47 kcal mol⁻¹) electronic energy barrier, Tyr306 can rotate and form a hydrogen bond with the newly formed amine group (–CNH₂) of the substrate, leading to a more stable structure EP (Fig. 3 and 5F). Because the transition state between EI3 and EP is low and flat, it may not be a meaningful free energy barrier. In the rest of the paper, this transition state is not discussed. EP has a relative electronic energy of 0.0 kcal mol⁻¹ (relative to ES, Table 1 and Fig. 3). In both EI3 and EP (Fig. 5D and F) the proton on δ-N_H142 is already transferred to Asp176 due to an increased proton binding ability of Asp176 upon K⁺ removal. As discussed earlier, when a K⁺ ion is at site 1, the relative electronic energy for EP is 9.6 kcal mol⁻¹. Clearly, a K⁺-free site 1 significantly favors the EP state, due to a proton transfer from His142 to Asp176. However, the stability of the EP state is irrelevant to whether the catalytic reaction can proceed or not. HDAC8 can catalyze the reaction in both cases: with and without K⁺ at site 1. The only difference is the catalytic efficiency, as discussed below.

The relative electronic energies of TS1a, EI1a, TS1, and TS2 are 5.4, −1.8, 12.6, and 17.4 kcal mol⁻¹, respectively. TS2 remains to be the rate-determining transition state. Since EI1a (–1.8 kcal mol⁻¹ in relative electronic energy, −0.1 kcal mol⁻¹ in relative free energy) is the lowest energy point in the reaction pathway (Fig. 3), the activation free energy should be derived using EI1a and TS2. The ZPE and thermal free energy correction for EI1a to TS2 is −1.5 kcal mol⁻¹ (Table S1, ESI†). Therefore, our best estimation of the free energy barrier is 17.7 kcal mol⁻¹ for 298 K. The free energy barrier (17.7 kcal mol⁻¹) for K⁺-free site 1 is 1.9 kcal mol⁻¹ lower than that for K⁺-bound site 1, implicating a 25-fold difference in the catalytic activity of Zn(II)-HDAC8. For comparison, experimental kinetic studies found that the Co(II)-HDAC8 exhibited an 11-fold difference in activity between K⁺-free and K⁺-bound site 1.¹⁹ The MP2/MM result obtained here is in good quantitative agreement with the site-1 K⁺ depletion experimental values. The computed free energy barrier of 17.7 kcal mol⁻¹ for Zn(II)-HDAC8 with only a site-2 K⁺ is in good agreement with the experimental value of 17.5 kcal mol⁻¹ for Zn(II)-HDAC8 in 137 mM NaCl and 2.7 mM KCl. If the estimated experimental value of 16.7 kcal mol⁻¹ for Zn(II)-HDAC8 with only a site-2 K⁺ is used for comparison, the agreement is also good.

In summary, the K⁺ depletion from site 1 significantly increases the proton binding ability of Asp176, which then preferentially stabilizes TS1a, EI1a, and TS1 in the first step, and TS3, EI3, and EP in the third step, by providing stronger hydrogen bonding through His142 or even accepting the proton from His142. In contrast, the stabilities of EI1, TS2, and EI2 are much less affected by this K⁺ depletion because the reactive proton is on the His143 side in these states.

Using the QM/MM B3LYP-D3 optimized structures (which are similar to those from QM/MM MP2 optimization), the sKIEs were computed to be 8.9 and 4.0, respectively, for TS1 and TS2 (relative to EI1a). Because the computed free energy (with H atoms, not D) of EI1a is only lower than the ES state by 0.1 kcal mol⁻¹, when computational errors are considered, ES may be lower than EI1a. Using ES as the reference, the computed sKIEs are 8.5 and 3.8, respectively, for TS1 and TS2 (relative to ES). These two sets of sKIEs (relative to EI1a and ES, respectively) are close to each other. Here, the chance of TS1 being the rate-determining step is very low because it is 7 kcal mol⁻¹ lower than TS2 in computed free energy. Therefore, the experimentally measured sKIE should be mainly due to TS2 when site 1 has no K⁺. As described earlier, when there is a K⁺ ion at site 1, the TS2 isotope effect was computed to be 3.8. Therefore, the computed sKIEs are insensitive to K⁺ occupation at site 1, implying that the apparent sKIE would remain at roughly a constant (computed to be ∼3.8 here) when the K⁺ concentration varies (the ratio of mono-K⁺-HDAC8 to bi-K⁺-HDAC8 changes). This prediction can be verified by experiments. If the experimentally measured sKIE remains constant at ∼3.8 (or another value as experimentally measured, such as 6.2 or 5.3), it may suggest that the TS2 is the rate-determining transition state in both cases (site 1 has K⁺ or not). If the sKIE increases at higher K⁺ ion concentrations, it may suggest that the TS1 is rate-determining when both site 1 and site 2 have K⁺ ions (in this case, the TS1 value is 5.5). If the sKIE decreases at higher K⁺ ion concentrations, it may suggest that the TS3 is rate-determining when both site 1 and site 2 have K⁺ ions (in this case, the TS3 value is 1.2).

III.C. Comparison of QM methods

III.C.1. Comparison of B3LYP, B3LYP-D3 and MP2. Here we examine the differences in the geometries and energies optimized with the B3LYP/MM, B3LYP-D3/MM, and MP2/MM methods. All calculations were performed with the same basis set and the same QM/MM settings as described in the Computational methods section.

The Zn–O_wat and Zn–O_sub coordination bond distances optimized with B3LYP/MM are generally longer than those optimized with B3LYP-D3/MM and MP2/MM (Fig. 6). For example, the Zn–O_wat distances in EI1 (Fig. 6A and Table S5, ESI†) optimized with B3LYP/MM (2.51 Å) are 0.08 Å and 0.14 Å longer than that with B3LYP-D3/MM (2.43 Å) and MP2/MM (2.37 Å), respectively. In the ES, the Zn–O_sub distances (Fig. S1, ESI†) optimized with B3LYP/MM (2.40 Å) and B3LYP-D3/MM (2.17 Å) are longer than 2.16 Å optimized with the MP2/MM method. For comparison, the Zn–O_sub distance in the crystal structure (2V5W.PDB) is 2.02 Å. In the crystal structure, Tyr306 is replaced by Phe306, so the hydrogen bond between the O_sub atom and Tyr306 does not exist. This would leave a slightly stronger interaction and a shorter distance between the O_sub atom and the Zn ion. Indeed, the MP2/MM optimized Zn–O_sub distance (2.16 Å, with Tyr306) is slightly longer than the 2.02 Å (with Phe306) in the crystal structure. The B3LYP/MM optimized Zn–O_wat and Zn–O_sub distances in other reaction species (i.e. TS1a, EI1a, TS1, EI1, TS2, EI2, TS3, EI3, and EP) are slightly longer than those optimized with B3LYP-D3/MM and MP2/MM methods. The B3LYP method tends to underestimate the interactions between the Zn ion and its ligands and predict longer coordinate distances.

Fig. 6 Comparison of the optimized distances between zinc ions and the reactive oxygen atoms (O_wat and O_sub) in each reaction species obtained with different QM/MM methods for HDAC8 systems with a K⁺ ion at site 1.

The relative electronic energies obtained with the B3LYP/MM method are 24.1, 30.6, and 18.9 kcal mol⁻¹, respectively, for TS1, TS2, and TS3 (Fig. 7, all compared to ES). TS2 is the highest, thus rate-determining. However, it is ∼13 kcal mol⁻¹ larger than the experimental value of ∼17.5 kcal mol⁻¹. Inclusion of Grimme's empirical dispersion correction to B3LYP (i.e., B3LYP-D3) leads to optimized structures and energies closer to the MP2 results: the B3LYP-D3/MM optimized relative electronic energies are 22.9 kcal mol⁻¹ and 25.8 kcal mol⁻¹ for TS1 and TS2, respectively (Fig. 7). Here, the empirical dispersion correction leads to more than 4 kcal mol⁻¹ energy improvement for the rate-determining step, which is significant. Our previous work on cytochrome P450_cam obtained similar corrections.⁷⁰ Even with the empirical dispersion correction, the B3LYP-D3/MM relative energies of TS1 and TS2 are still 5.6 and 5.9 kcal mol⁻¹ higher than the MP2/MM values 17.3 and 19.7 kcal mol⁻¹.

Fig. 7 The B3LYP/MM (magenta), B3LYP-D3/MM (red), and MP2/MM (blue) computed electronic energy profiles (with a mixed aug-cc-pVDZ and 6-31G* basis set) along the deacetylation reaction pathway of a tetrapeptide catalyzed by HDAC8 with a K⁺ ion at site 1.

For TS3, the B3LYP/MM and B3LYP-D3/MM energies, 18.9 and 19.4 kcal mol⁻¹, respectively, are comparable to the MP2/MM value of 17.1 kcal mol⁻¹. However, the B3LYP/MM and B3LYP-D3/MM computed electronic energy barriers from EI2 to TS3 are only 1.7 and 2.9 kcal mol⁻¹, respectively. For comparison, the MP2/MM computed barrier from EI2 to TS3 is 6.6 kcal mol⁻¹ (SCS-MP2/MM results are similar, see Table S2, ESI†). We note that, in MP2/MM optimized TS3, the proton has already transferred to the N atom of His142, while in B3LYP/MM and B3LYP-D3/MM optimized TS3 structures, the proton is still on the oxygen atom of water. When ZPE and free energy correction (which is −1.7 kcal mol⁻¹ ongoing from EI2 to TS3 as computed with the B3LYP-D3/MM partial Hessian method) is applied, the free energy barrier becomes 0.0 and +1.3 kcal mol⁻¹, respectively, on the B3LYP/MM and B3LYP-D3/MM PESs. Therefore, due to the very low electronic energy barriers, TS3 is not a meaningful transition state on the B3LYP/MM and B3LYP-D3 PESs. Even when only electronic energy is considered, there is a good chance that the TS3 would not appear in a QM/MM B3LYP (or B3LYP-D3) calculation with settings different from those used in this work, especially when different starting structures and basis sets are used. For example, when the small 6-31G* basis set is used, the QM/MM B3LYP relative single-point energies of EI2 and TS3 (based on QM/MM MP2 optimized structures) are 13.0 and 13.2 kcal mol⁻¹, respectively, virtually no difference (Table 2). It is not surprising that the two-step mechanism (mechanism 2 in Fig. 2B) was obtained with B3LYP/MM.^21,22 Other QM/MM DFT methods may also predict the same two-step mechanism.²⁴ Using a QM/MM DFT method, Chen et al. obtained a N-protonated neutral tetrahedral intermediate similar to the neutral tetrahedral intermediate EI2 in this work, but the proton transfer from His143 to the amide N atom is barrier-less, and the subsequent C–N bond cleavage requires a very low activation energy, thus not a meaningful transition state.²³ Their results resemble the B3LYP/MM and B3LYP-D3/MM results in this work.

Some key interatomic distances involved in the reaction are shown in Fig. S2 (ESI†). Most of the distances optimized with B3LYP/MM are longer than those optimized with B3LYP-D3/MM and MP2/MM. For example, the B3LYP/MM optimized C_sub–O_wat distance is 2.73 Å in ES and 1.70 Å in TS1. The B3LYP-D3/MM optimized C_sub–O_wat distances are shorter, 2.67 Å in ES and 1.60 Å in TS1. The MP2/MM optimized C_sub–O_wat distances are the shortest, 2.55 Å in ES and 1.50 Å in TS1. The B3LYP/MM optimized H1_wat–N_H142 and H2_wat–N_H143 distances (Fig. S2C and S2D, ESI†) are longer than B3LYP-D3/MM and MP2/MM values on the reaction pathway. These longer distances are a general reflection of the fact that the B3LYP functional lacks long-range dispersion. Empirical dispersion correction (B3LYP-D3) can only partially remedy this problem.

Interestingly, the relative energies obtained with MP2/MM single-point energy calculation based on B3LYP/MM and B3LYP-D3/MM optimized structures resemble the MP2/MM optimized relative energies (Table S4, ESI†). Using MP2/MM optimized values (with mixed aug-cc-pVDZ and 6-31G* basis set) as references, the largest unsigned differences in relative energies are 2.4 kcal mol⁻¹ and 1.0 kcal mol⁻¹, respectively, for B3LYP/MM and B3LYP-D3/MM optimized structures, with average unsigned differences being 0.8 kcal mol⁻¹ and 0.5 kcal mol⁻¹. Therefore, if the PESs and the optimized structures are similar, MP2 single point energy calculations can be used to obtain a quick estimation of the effects of many-body dispersion energy on the catalytic pathway. However, if some minimum or maximum points are missing, this strategy cannot be used.

For the catalytic pathway without K⁺ at site 1, we examined the differences in the geometries and energies optimized with the B3LYP-D3/MM and MP2/MM methods. The results are shown in Table 1 and Table S5 (ESI†). Again, the relative energies for TS1 and TS2 (19.9 kcal mol⁻¹ and 24.4 kcal mol⁻¹) obtained from B3LYP-D3/MM geometry optimizations are significantly higher than those from MP2/MM (12.6 and 17.4 kcal mol⁻¹). For geometries, most of the distances optimized with B3LYP-D3/MM are slightly longer than those optimized with MP2/MM (Table S5, ESI†).

III.C.2. Comparison of M05-2X, M06, M06-2X, MN15 and MP2. We performed QM/MM single point energy calculations with the M05-2X,⁴⁰ M06,⁴¹ M06-2X,⁴¹ and MN15⁴² density functional methods based on the MP2/MM optimized structures. The results are shown in Table 2 and Fig. S5 (ESI†).
Catalytic pathway with K⁺ at site 1. With the BS1 basis set (aug-cc-pVDZ for 23 atoms and 6-31G* basis set for the rest), all these DFT single point relative energies are slightly higher than the MP2/MM values (Table 2 and Fig. S5A, ESI†). For example, the relative energies for TS2 are 22.4, 22.5, 25.5, and 21.5 kcal mol⁻¹ for M05-2X, M06, M06-2X, and MN15, respectively, higher than the MP2 value of 19.7 kcal mol⁻¹. The more recent MN15 functional gives the best overall matches to MP2. Using M05-2X/MM and M06/MM, but with a much smaller basis set (virtually all 6-31G*), Chen et al.²³ and Gleeson et al.²⁴ obtained reaction energies systematically lower than the M05-2X/MM and M06/MM results obtained here with a larger basis set BS1 (Table 2), signaling a basis set deficiency in their calculations. Indeed, when the smaller 6-31G* basis set is used here, we obtained similarly lower reaction pathway energies (Fig. S5A, ESI†). For example, the TS2 energies are 18.0 and 18.3 kcal mol⁻¹ with M05-2X/6-31G* and M06/6-31G*, respectively, 4.4 and 4.2 kcal mol⁻¹ lower than the M05-2X/BS1 and M06/BS1 values (22.4 and 22.5 kcal mol⁻¹, respectively). Very similar basis set dependence is observed for the MN15 functional. For example, the relative energy of TS2 is lowered by 5.3 kcal mol⁻¹ from BS1 to 6-31G*. In particular, the relative energy of EI3, 10.5 kcal mol⁻¹, obtained here with the M05-2X/6-31G* method on MP2/AMBER optimized structures, is close to 8.5 kcal mol⁻¹ obtained by Chen et al. using the QM/MM M05-2X/6-31G* optimization method, suggesting that the chemical models and molecular structures in the current work and their work have similarity. This is not a surprising result because the active site of HDAC8 is deeply buried and rigid, and can only show small structural variations when different MM and QM/MM methods, settings, and procedures are used. These results confirm that Chen et al.'s and Gleeson et al.'s calculations suffered significant basis set deficiency, which had caused errors as large as 10.1 kcal mol⁻¹ on the reaction pathway (e.g., TS2 in Table 2, our MP2/BS1 value 19.7 kcal mol⁻¹vs. Chen et al.'s value 9.6 kcal mol⁻¹) and led to inaccurate perspectives of the catalytic mechanism.
Catalytic pathway without K⁺ at site 1. Similarly, with the same BS1 basis set, all M05-2X, M06, M06-2X, and MN15 relative energies are slightly higher than the corresponding MP2 values (Fig. S5B, ESI†). The more recent MN15 functional best resembles MP2. When the smaller 6-31G* basis set is used, the reaction pathway energies are significantly lowered (Table 2 and Fig. S5B, ESI†). The basis set deficiency could cause errors as large as 8.5 kcal mol⁻¹ on this reaction pathway (e.g., TS2 in Table 2, our MP2/BS1 value 17.4 kcal mol⁻¹vs. Chen et al.'s value 8.9 kcal mol⁻¹). Again, the relative energy of EI3, −2.2 kcal mol⁻¹, obtained here with the M05-2X/6-31G* method on MP2/AMBER optimized structures, is close to −4.4 kcal mol⁻¹ obtained by Chen et al. using the QM/MM M05-2X/6-31G* optimization method, suggesting that the chemical models and molecular structures in the current work and their work are similar.

III.C.3. Relevance to inhibitor design. The rational design of mechanism-based inhibitors that can differentially modulate the activities of human HDACs is a promising approach to developing potential therapeutics or drugs against diseases related to HDACs. For example, Wu, Zhang, and their co-workers have studied the inhibition of hydroxamate, thiol-based suberoylanilide hydroxamic acid, β-aminomethyl chalcone, and β-hydroxymethyl chalcone toward HDACs.^71–73 The QM/MM MP2 results in this work suggest that His143 in HDAC8 plays an essential role in accepting a proton from the water (TS1), passing the proton to the amide N atom of the acetylated lysine (TS2), and finally causing the amide C–N bond cleavage (TS3), in line with an experimental mutation study, in which His143Ala-Co(II)-HDAC8 exhibited an 80 000-fold decrease in activity.³⁸ The overall hydrolytic pathways and energetics should be similar for other HDACs and their natural substrates. One possible design strategy is to introduce functional groups to an inhibitor that can, through slightly different interactions in different HDACs, raise the barrier heights of TS2 (but could also be TS1 or even TS3 as the energetics may change) in different HDACs by different amounts (e.g., 1–3 kcal mol⁻¹), to achieve selective and differential inhibitions of HDACs to various extents (e.g., 5–100 folds). No matter what design strategies are used, the catalytic pathway and energetics for each designed inhibitor must be examined case by case using experimental and/or theoretical methods. For computational design, the methods should have a consistent accuracy better than 1–3 kcal mol⁻¹ in the relative energies (sometimes including inhibitor–enzyme binding energies) within each and across all reaction pathways under examination. Compared to the QM/MM DFT methods discussed above, the QM/MM MP2 method used here shows an accuracy of 1–2 kcal mol⁻¹ for the hydrolytic pathway of HDAC8. It should have similar accuracies for the reaction pathways of other inhibitor/substrate compounds (if they are closed-shell molecules) and other HDACs, thus a promising method.

IV. Conclusion

In this work, QM/MM MP2 geometry optimizations were performed to understand the catalytic mechanism of the deacetylation reaction catalyzed by human Histone Deacetylase 8 (HDAC8). A three-step catalytic mechanism is identified. The first step is the formation of a negatively charged tetrahedral intermediate via a nucleophilic addition of the water molecule to the amide C atom and a proton transfer from the water to His143. The second step is the formation of a neutral tetrahedral intermediate with an elongated but not completely broken amide C–N bond via a proton transfer from His143 to the amide N atom. The third step is the complete cleavage of the amide C–N bond, accompanied by a proton transfer from the newly formed carboxylic group to His142. The transition states for these three steps have very similar electronic energies: 15.6 kcal mol⁻¹, 19.6 kcal mol⁻¹, and 16.6 kcal mol⁻¹, respectively. After ZPE and thermal free energy correction, the second step is the rate-determining step with an activation free energy of 19.6 kcal mol⁻¹. For HDAC8 with a K⁺-free site 1 (another K⁺ is still at site 2), the catalytic reaction pathway is very similar to the case with a K⁺-bound site 1. The second step remains to be the rate-determining step, with a computed activation free energy of 17.7 kcal mol⁻¹. Both values agree well with an experimental value of 17.5 kcal mol⁻¹. According to the MP2/MM results, there would be a 25-fold increase in the catalytic efficiency upon site-1 K⁺ removal. This result is in good agreement with the experiments on Co(II)-HDAC8.¹⁹ The solvent hydrogen–deuterium kinetic isotope effects were computed to be ∼3.8 in the rate-determining step (the second step, TS2) for Zn(II)-HDAC8 with and without a K⁺ at site 1, in line with experimental measurements.⁶⁷ The catalytic mechanism obtained here suggests that His143 plays an essential and rate-determining role in accepting a proton from the water (TS1), passing the proton to the amide N atom of the acetylated lysine (TS2), and finally causing the amide C–N bond cleavage (TS3), in line with an experimental finding that His143Ala-Co(II)-HDAC8 exhibited an 80 000-fold decrease in activity.³⁸

We also compared the structures and energies obtained with the MP2/MM, B3LYP/MM, and B3LYP-D3/MM methods. It is found that the B3LYP/MM method predicts too high transition state energies. Including Grimme's empirical dispersion correction to the B3LYP can lower the reaction barriers by ∼4 kcal mol⁻¹, highlighting the importance of active site intermolecular dispersion interactions in enzyme catalysis. Even with the empirical dispersion correction (i.e., B3LYP-D3/MM), the computed reaction energy barriers for the first and second steps are still ∼5 kcal mol⁻¹ higher than those obtained with the MP2/MM method. Although both B3LYP/MM and B3LYP-D3/MM predict the same third transition state (TS3) as MP2/MM does, the B3LYP/MM and B3LYP-D3/MM predicted electronic energy barriers from EI2 to TS3 are too low (1.7 kcal mol⁻¹ and 2.9 kcal mol⁻¹, respectively). With ZPE and thermal free energy corrections, the activation free energies are even lower or negative on the B3LYP/MM and B3LYP-D3/MM potential energy surfaces, reducing the three-step mechanism to a two-step mechanism. In contrast, MP2/MM predicts a significant electronic energy barrier of 6.6 kcal mol⁻¹ from EI2 to TS3, solidifying a three-step mechanism for systems with a K⁺ ion at site 1. When a sufficiently large basis set such as aug-cc-pVDZ is used, the M05-2X, M06, M06-2X, and MN15 functionals can generate results closer to MP2. However, when smaller basis sets such as 6-31G* are used, the errors can be as large as 10 kcal mol⁻¹ in the computed relative energies, causing incorrect perspectives of the HDAC8 catalytic mechanism. Caution must be used when choosing the QM method and basis set in QM/MM study of enzyme catalysis.

Author contributions

R. L. and H. L.: conceptualization, methodology, data curation, formal analysis, investigation, writing.

Data availability

The coordinates of the system are included in the ESI.† Additional figures and tables are also included in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The calculations were performed with resources at the University of Nebraska-Lincoln Holland Computing Center, which receives support from the Nebraska Research Initiative. This work was partially supported by a grant to R. L. from the National Natural Science Foundation of China (NSFC 22303102).

References

1. S. K. Bajpai, Nisha, S. Pandita, A. Bahadur and P. C. Verma, Recent advancements in the role of histone acetylation dynamics to improve stress responses in plants, Mol. Biol. Rep., 2024, 51, 413.
2. S.-Y. Park and J.-S. Kim, A short guide to histone deacetylases including recent progress on class II enzymes, Exp. Mol. Med., 2020, 52, 204–212.
3. N. D. Werbeck, V. K. Shukla, M. B. A. Kunze, H. Yalinca, R. B. Pritchard, L. Siemons, S. Mondal, S. O. R. Greenwood, J. Kirkpatrick, C. M. Marson and D. F. Hansen, A distal regulatory region of a class I human histone deacetylase, Nat. Commun., 2020, 11, 3841.
4. M. M. Mihaylova and R. J. Shaw, Metabolic reprogramming by class I and II histone deacetylases, Trends Endocrinol. Metab., 2013, 24, 48–57.
5. K. R. Stengel and S. W. Hiebert, Class I HDACs Affect DNA Replication, Repair, and Chromatin Structure: Implications for Cancer Therapy, Antioxid. Redox Signaling, 2015, 23(1), 51–65.
6. K. Ververis, A. Hiong, T. C. Karagiannis and P. V. Licciardi, Histone deacetylase inhibitors (HDACIs): multitargeted anticancer agents, Biol.: Targets Ther., 2013, 7, 47–60.
7. B. C. Smith and J. M. Denu, Chemical mechanisms of histone lysine and arginine modifications, Biochim. Biophys. Acta, Gene Regul. Mech., 2009, 1789, 45–57.
8. B. S. Mann, J. R. Johnson, M. H. Cohen, R. Justice and R. Pazdur, FDA approval summary: vorinostat for treatment of advanced primary cutaneous T-cell lymphoma, Oncologist, 2007, 12, 1247–1252.
9. H. M. Prince and M. Dickinson, Romidepsin for cutaneous T-cell lymphoma, Clin. Cancer Res., 2012, 18, 3509–3515.
10. J. A. Plumb, P. W. Finn, R. J. Williams, M. J. Bandara, M. R. Romero, C. J. Watkins, N. B. La Thangue and R. Brown, Pharmacodynamic response and inhibition of growth of human tumor xenografts by the novel histone deacetylase inhibitor PXD101, Mol. Cancer Ther., 2003, 2, 721–728.
11. H. M. Prince, M. J. Bishton and S. J. Harrison, Clinical studies of histone deacetylase inhibitors, Clin. Cancer Res., 2009, 15, 3958–3969.
12. L. Hontecillas-Prieto, R. Flores-Campos, A. Silver, E. de Álava, N. Hajji and D. J. García-Domínguez, Synergistic Enhancement of Cancer Therapy Using HDAC Inhibitors: Opportunity for Clinical Trials, Front. Genet., 2020, 11.
13. T. Eckschlager, J. Plch, M. Stiborova and J. Hrabeta, Histone deacetylase inhibitors as anticancer drugs, Int. J. Mol. Sci., 2017, 18, 1414.
14. A. D. Bondarev, M. M. Attwood, J. Jonsson, V. N. Chubarev, V. V. Tarasov and H. B. Schiöth, Recent developments of HDAC inhibitors: Emerging indications and novel molecules, Br. J. Clin. Pharmacol., 2021, 87, 4577–4597.
15. X. J. Yang and E. Seto, The Rpd3/Hda1 family of lysine deacetylases: from bacteria and yeast to mice and men, Nat. Rev. Mol. Cell Biol., 2008, 9, 206–218.
16. I. V. Gregoretti, Y. M. Lee and H. V. Goodson, Molecular evolution of the histone deacetylase family: functional implications of phylogenetic analysis, J. Mol. Biol., 2004, 338, 17–31.
17. N. J. Porter and D. W. Christianson, Structure, mechanism, and inhibition of the zinc-dependent histone deacetylases, Curr. Opin. Struct. Biol., 2019, 59, 9–18.
18. A. Vannini, C. Volpari, G. Filocamo, E. C. Casavola, M. Brunetti, D. Renzoni, P. Chakravarty, C. Paolini, R. De Francesco, P. Gallinari, C. Steinkühler and S. Di Marco, Crystal structure of a eukaryotic zinc-dependent histone deacetylase, human HDAC8, complexed with a hydroxamic acid inhibitor, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15064–15069.
19. S. Gantt, C. Joseph and C. Fierke, Activation and Inhibition of Histone Deacetylase 8 by Monovalent Cations. The, J. Biol. Chem., 2010, 285, 6036–6043.
20. M. S. Finnin, J. R. Doniglas, A. Cohen, V. M. Richon, R. A. Rifkind, P. A. Marks, R. Breslow and N. P. Pavletich, Structures of a histone deacetylase homologue bound to the TSA and SAHA inhibitors, Nature, 1999, 401, 188–193.
21. C. Corminboeuf, P. Hu, M. E. Tuckerman and Y. Zhang, Unexpected deacetylation mechanism suggested by a density functional theory QM/MM study of histone-deacetylase-like protein, J. Am. Chem. Soc., 2006, 128, 4530–4531.
22. R. Wu, S. Wang, N. Zhou, Z. Cao and Y. Zhang, A proton-shuttle reaction mechanism for histone deacetylase 8 and the catalytic role of metal ions, J. Am. Chem. Soc., 2010, 132, 9471–9479.
23. K. Chen, X. Zhang, Y.-D. Wu and O. Wiest, Inhibition and Mechanism of HDAC8 Revisited, J. Am. Chem. Soc., 2014, 136, 11636–11643.
24. D. Gleeson and M. P. Gleeson, Application of QM/MM and QM methods to investigate histone deacetylase 8, MedChemComm, 2015, 6, 477–485.
25. S. N. Steinmann, C. Piemontesi, A. Delachat and C. Corminboeuf, Why are the Interaction Energies of Charge-Transfer Complexes Challenging for DFT?, J. Chem. Theory Comput., 2012, 8, 1629–1640.
26. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
27. R. H. Hertwig and W. Koch, On the parameterization of the local correlation functional. What is Becke-3-LYP?, Chem. Phys. Lett., 1997, 268, 345–351.
28. E. K. Gross, J. Dobson and M. Petersilka, Density functional theory of time-dependent phenomena, in Density functional theory II, Springer, 1996, pp. 81–172.
29. C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618–622.
30. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions, J. Phys. Chem. A, 2013, 117, 12590–12600.
31. P. E. M. Siegbahn, J. Almlof, A. Heiberg and B. O. Roos, The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule, J. Chem. Phys., 1981, 74, 2384–2396.
32. R. J. Bartlett, Perspective on Coupled-cluster Theory. The evolution toward simplicity in quantum chemistry, Phys. Chem. Chem. Phys., 2024, 26, 8013–8037.
33. P. Piecuch, S. A. Kucharski, K. Kowalski and M. Musial, Efficient computer implementation of the renormalized coupled-cluster methods: The R-CCSD[T], R-CCSD(T), CR-CCSD[T], and CR-CCSD(T) approaches, Comput. Phys. Commun., 2002, 149, 71–96.
34. J. L. Bentz, R. M. Olson, M. S. Gordon, M. W. Schmidt and R. A. Kendall, Coupled cluster algorithms for networks of shared memory parallel processors, Comput. Phys. Commun., 2007, 176, 589–600.
35. R. M. Olson, J. L. Bentz, R. A. Kendall, M. W. Schmidt and M. S. Gordon, A novel approach to parallel coupled cluster calculations: Combining distributed and shared memory techniques for modern cluster based systems, J. Chem. Theory Comput., 2007, 3, 1312–1328.
36. A. Vannini, C. Volpari, P. Gallinari, P. Jones, M. Mattu, A. Carfi, R. De Francesco, C. Steinkuhler and S. Di Marco, Substrate binding to histone deacetylases as shown by the crystal structure of the HDAC8-substrate complex, EMBO Rep., 2007, 8, 879–884.
37. C. Decroos, C. M. Bowman, J.-A. S. Moser, K. E. Christianson, M. A. Deardorff and D. W. Christianson, Compromised Structure and Function of HDAC8 Mutants Identified in Cornelia de Lange Syndrome Spectrum Disorders, ACS Chem. Biol., 2014, 9, 2157–2164.
38. S. M. L. F. Gantt, C. Decroos, M. S. Lee, L. E. Gullett, C. M. Bowman, D. W. Christianson and C. A. Fierke, General Base–General Acid Catalysis in Human Histone Deacetylase 8, Biochemistry, 2016, 55, 820–832.
39. N. M. Thellamurege, D. Si, F. Cui, H. Zhu, R. Lai and H. Li, QuanPol: A full spectrum and seamless QM/MM program, J. Comput. Chem., 2013, 34, 2816–2833.
40. Y. Zhao, N. E. Schultz and D. G. Truhlar, Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions, J. Chem. Theory Comput., 2006, 2, 364–382.
41. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241.
42. H. S. Yu, X. He, S. L. Li and D. G. Truhlar, MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7, 5032–5051.
43. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. D. Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. G. Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, Recent developments in the general atomic and molecular electronic structure system, J. Chem. Phys., 2020, 152, 154102.
44. H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, The protein data bank, Nucleic Acids Res., 2000, 28, 235–242.
45. R. L. Dunbrack, Rotamer libraries in the 21st century, Curr. Opin. Struct. Biol., 2002, 12, 431–440.
46. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, UCSF Chimera—A visualization system for exploratory research and analysis, J. Comput. Chem., 2004, 25, 1605–1612.
47. P. Cieplak, J. Caldwell and P. Kollman, Molecular mechanical models for organic and biological systems going beyond the atom centered two body additive approximation: Aqueous solution free energies of methanol and N-methyl acetamide, nucleic acid base, and amide hydrogen bonding and chloroform/water partition coefficients of the nucleic acid bases, J. Comput. Chem., 2001, 22, 1048–1057.
48. D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, The Amber biomolecular simulation programs, J. Comput. Chem., 2005, 26, 1668–1688.
49. Z. X. Wang, W. Zhang, C. Wu, H. X. Lei, P. Cieplak and Y. Duan, Strike a balance: Optimization of backbone torsion parameters of AMBER polarizable force field for simulations of proteins and peptides, J. Comput. Chem., 2006, 27, 781–790.
50. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB, J. Chem. Theory Comput., 2015, 11, 3696–3713.
51. T. A. Halgren, Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94, J. Comput. Chem., 1996, 17, 490–519.
52. R. Lai, W.-J. Tang and H. Li, Catalytic Mechanism of Amyloid-β Peptide Degradation by Insulin Degrading Enzyme: Insights from Quantum Mechanics and Molecular Mechanics Style Møller–Plesset Second Order Perturbation Theory Calculation, J. Chem. Inf. Model., 2018, 58, 1926–1934.
53. R. Lai and H. Li, Mechanism of Ampicillin Hydrolysis by New Delhi Metallo-β-Lactamase 1: Insight From QM/MM MP2 Calculation, J. Comput. Chem., 2025, 46, e27544.
54. D. Beeman, Some multistep methods for use in molecular dynamics calculations, J. Comput. Phys., 1976, 20, 130–139.
55. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
56. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. Defrees and J. A. Pople, Self-Consistent Molecular-Orbital Methods. 23. A Polarization-Type Basis Set for 2nd-Row Elements, J. Chem. Phys., 1982, 77, 3654–3665.
57. T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
58. N. B. Balabanov and K. A. Peterson, Systematically convergent basis sets for transition metals. I. All-electron correlation consistent basis sets for the 3d elements Sc–Zn. The, J. Chem. Phys., 2005, 123, 064107.
59. D. J. Si and H. Li, Analytic energy gradients in combined second order Moller-Plesset perturbation theory and conductorlike polarizable continuum model calculation, J. Chem. Phys., 2011, 135, 144107.
60. H. Li, Analytic Energy Gradient in Combined Second-Order Moller-Plesset Perturbation Theory and Polarizable Force Field Calculation, J. Phys. Chem. A, 2011, 115, 11824–11831.
61. N. M. Thellamurege, D. Si, F. Cui and H. Li, Quantum mechanical/molecular mechanical/continuum style solvation model: Second order Møller-Plesset perturbation theory, J. Chem. Phys., 2014, 140, 174115.
62. K. Ishimura, P. Pulay and S. Nagase, A new parallel algorithm of MP2 energy calculations, J. Comput. Chem., 2006, 27, 407–413.
63. K. Ishimura, P. Pulay and S. Nagase, New parallel algorithm for MP2 energy gradient calculations, J. Comput. Chem., 2007, 28, 2034–2042.
64. S. Grimme, Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies, J. Chem. Phys., 2003, 118, 9095–9102.
65. H. Tatewaki and T. Koga, Contracted Gaussian-type basis functions revisited, J. Chem. Phys., 1996, 104, 8493–8499.
66. S. L. Gantt, S. G. Gattis and C. A. Fierke, Catalytic activity and inhibition of human histone deacetylase 8 is dependent on the identity of the active site metal ion, Biochemistry, 2006, 45, 6170–6178.
67. V. K. Shukla, L. Siemons and D. F. Hansen, Intrinsic structural dynamics dictate enzymatic activity and inhibition, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2310910120.
68. R. Wolfenden, Free energies of hydration and hydrolysis of gaseous acetamide, J. Am. Chem. Soc., 1976, 98, 1987–1988.
69. J. P. Guthrie, Hydration of carboxamides. Evaluation of the free energy change for addition of water to acetamide and formamide derivatives, J. Am. Chem. Soc., 1974, 96, 3608–3615.
70. R. Lai and H. Li, Hydrogen Abstraction of Camphor Catalyzed by Cytochrome P450cam: A QM/MM Study, J. Phys. Chem. B, 2016, 120, 12312–12320.
71. R. Wu, Z. Lu, Z. Cao and Y. Zhang, Zinc Chelation with Hydroxamate in Histone Deacetylases Modulated by Water Access to the Linker Binding Channel, J. Am. Chem. Soc., 2011, 133, 6110–6113.
72. W. Gong, R. Wu and Y. Zhang, Thiol versus hydroxamate as zinc binding group in HDAC inhibition: An Ab initio QM/MM molecular dynamics study, J. Comput. Chem., 2015, 36, 2228–2235.
73. J. Zhou, M. Li, N. Chen, S. Wang, H.-B. Luo, Y. Zhang and R. Wu, Computational Design of a Time-Dependent Histone Deacetylase 2 Selective Inhibitor, ACS Chem. Biol., 2015, 10, 687–692.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00002e

---