Revisiting the intricate photodissociation mechanism of ammonia along the minor NH + H₂ pathway

Abstract

In this manuscript we revisit and extend the analysis of the internal conversion and intersystem crossing dynamics of ammonia originating from excitation to its first excited singlet state S₁ and leading to the major NH₂ + H and minor NH + H₂ pathways as investigated by Wang et al. (Phys. Chem. Chem. Phys. 2022, 24, 15060). To perform extensive simulations, we use the machine-learned interatomic potentials, developed by the same authors (Y. Wang et al., J. Chem. Phys. 2021, 154, 094121) interfaced with the SHARC program package. Based on the analysis of 50 000 coupled trajectories, we fit a kinetic model for the major and minor reaction channels that also provides the minimal amount of time required for the dissociation to occur. The model predicts that the time constant associated with the rare pathway is two orders of magnitude larger than that of the frequent reaction, leading to an extrapolated quantum yield of 0.64% for the NH + H₂ photoproduct. This quantum yield is in agreement with available experimental measurements carried out with an excitation pulse of 193 nm, around which we excite ammonia. A comprehensive analysis of the electronic states and structures involved in the minor channel reveals that dissociation occurs in a concerted manner via three main mechanisms. The majority of the trajectories (98%) undergo nonradiative relaxation to the electronic ground state, from where 29% directly dissociate. Additionally, we observe reverse internal conversion (58%) as well as intersystem crossing (10%), as operative pathways responsible of the rare photodissociation reaction. These findings provide valuable insights into the dynamics of ammonia photodissociation, particularly its less-studied fragmentation pathway.

---

1 Introduction

Ammonia plays an essential role in chemical and biological systems, as well as in industrial processes, as it is one of the most widely produced chemicals globally. Beyond its terrestrial presence, ammonia is also found in the atmosphere of outer planets in our solar system, where it participates in complex reaction networks.¹ These diverse roles make photochemical processes involving ammonia an important subject of investigation.

The photolysis of ammonia is one of the most studied processes, with the primary photodissociation pathway identified as,^2–10

where the NH₂ fragment potentially undergoes subsequent decay

NH₂ + H⁻ → NH + H + H (2)

A secondary, less frequent dissociation pathway is also known,

This rare pathway has been studied experimentally, although less extensively.^2,11–25 Despite these efforts, some ambiguity remains regarding the relative contributions of these channels at different excitation energies.^5,17–19,23 This uncertainty arises mainly due to the challenge of attributing the NH fragments to either the sequential fragmentation of NH₂ in the frequent channel (2) or the direct dissociation of ammonia via the rare pathway (3).¹ Furthermore, the presence of two-photon processes complicates the interpretation of experimental results.⁵ The potential contribution of the spin-forbidden channel producing NH(X³∑⁻) + H₂ also remains unclear.¹⁵

Computational approaches are essential for elucidating molecular dissociation mechanisms. However, prior studies have focused mainly on the energetically favored NH₂ + H fragmentation.^26–34 Recent advancements, such as the accurate potential energy surfaces (PESs) constructed by Wang et al., have provided new opportunities to investigate the rare NH₃ → NH + H₂ dissociation channel.^35,36 These PESs were tailored to describe both the frequent and rare photolysis pathways. Nonadiabatic dynamics simulations were performed on these surfaces³⁷ using the trajectory surface hopping formalism,³⁸ implemented in the SHARC program package.^39,40

Here, we reexamine the excited-state dynamics of ammonia, with a particular focus on the rare fragmentation pathway leading to NH + H₂, extending beyond previous analyses. Using the PESs developed by Yarkony and coworkers,^35,36 along with an adapted interface to our locally developed excited-state molecular dynamics code SHARC,^39–42 we provide fresh insights into the photochemistry of ammonia, with particular emphasis on the less explored photodissociation channel.

The remainder of this paper is organized as follows: Section 2 outlines the computational methodologies. It summarizes the fitted potentials utilized in this work and describes the mixed quantum classical dynamics employed. Section 3.1 discusses the photodissociation branching ratios and kinetics of the dissociation pathways, while Section 3.2 provides a detailed analysis of the rare NH₃ → NH + H₂ pathway regarding the geometric fragmentation characteristics and electronic states. Finally, Section 4 presents our conclusions.

2 Computational details

2.1 NH₃ potential energy surfaces

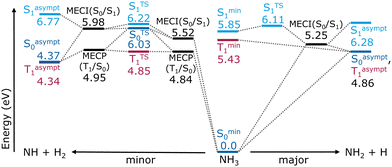
The ammonia molecule was modeled using the machine-learned interatomic potentials and property models reported by Wang et al.⁴³ Permutation invariant polynomial neural networks describe the two lowest-lying singlet states, their coupling, and the lowest-lying triplet. In addition to energies and energy gradients, transition dipoles and spin–orbit couplings are available. The simultaneous fitting and diabatization procedure is based on multi-reference configurational interaction including singles and doubles (MRCISD) computations using the aug-cc-pVTZ basis set with an added Rydberg function on nitrogen. The molecular orbitals originate from state-average multiconfigurational self-consistent-field (SA-MCSCF) calculations obtained with an active space of ten electrons in nine orbitals (10,9), averaged over the S₀, S₁ and T₁, with equal weights. More details on the generation and fitting of these surfaces can be found in ref. 43.

The reaction energy diagram in Fig. 1 provides a schematic overview over critical points of the fitted PESs relevant to the NH + H₂ and NH₂ + H dissociation pathways and also includes asymptotic energies (see Section S1 of the ESI‡ for details on the optimizations). The major channel proceeds through a flat transition state in the S₁ state, and a low lying S₀/S₁ conical intersection, followed by further energy gain (the common product is about 1 eV more favorable in the S₀ than the flat S₁ local minimum). The reaction mainly occurs without involvement of the T₁. In the minor channel, accessible via the same conical intersection leading toward the major products, all three surfaces are relevant. Then, via the ground state, the reaction proceeds through an S₀/S₁ conical intersection, followed by a transition state, and then a second S₀/S₁ conical intersection, ultimately yielding the minor photoproduct. Alternatively, an S₀/T₁ minimum energy crossing point, located 0.7 eV below the corresponding S₀/S₁ intersection, is followed by a second, energetically close, S₀/T₁ crossing point before fragmentation. For both reaction channels, T₁ and S₀ are asymptotically degenerate for the dissociated products. Interestingly, the minor product is the thermodynamic product of this dissociation.

Fig. 1 Energy diagram containing selected critical points of the fitted ammonia PESs, including minima (min), transition state (TS), minimal energy crossing points/conical intersections (MECP/MECI) and asymptotic energies (asympt) for both NH + H₂ and NH₂ + H channels.

2.2 Nonadiabatic dynamics

The nonadiabatic dynamics computations were performed within the surface hopping with arbitrary couplings (SHARC)⁴¹ formalism using Tully's fewest switches surface hopping³⁸ algorithm, as implemented in the SHARC program package.^39,40 Since the ammonia machine-learned potentials⁴³ do not provide second derivatives of the energies, the normal mode frequencies at the ground state minimum were obtained numerically. The S₀ minimum geometry was obtained via gradient descent. The Hessian was computed by displacing each atom by 0.005 Å. The normal modes from the ground state Hessian were used to sample 10⁵ initial coordinates and velocities according to a quantum Wigner distribution^40,44,45 at 297 K, which corresponds to the experimental conditions reported in ref. 16. The total angular momentum is kept zero. A large ensemble of initial conditions is mandatory to have sufficient statistics on the rare photodissociation channel.

Excitation states for the 10⁵ initial conditions were selected based on the excitation energies and oscillator strength,⁴⁶ simulating a vertical excitation over the whole spectral range – in practice from 0 eV to 10 eV. This selection procedure resulted in 85.6% of the initial conditions (85 578 points) being selected as excited to S₁. The obtained excitation energies were used to compute an absorption spectrum employing Gaussian convolution with a full width at half maximum of 0.1 eV (see Section S2 of the ESI‡ for a detailed discussion of the spectrum). From the successfully excited initial conditions, 5 × 10⁴ were taken randomly as starting points for SHARC⁴¹ trajectories, all with S₁ as the initial active state. The trajectories were propagated on the diagonalized potentials for up to 1 ps in 0.2 fs nuclear time steps using 0.008 fs electronic steps. Kinetic energy correction as well as the reflection of frustrated hops was performed parallel to the nonadiabatic couplings.³⁸ The energy-difference based decoherence correction was employed using the standard value of 0.1 Hartree.⁴⁷ An example input file can be found in the Section S3 of the ESI.‡

Given the large number of trajectories required to capture the dynamics of the rare photodissociation channel, evaluations were performed in intervals of 200 fs. The geometries were categorized according to their dissociation pattern into one of the following classes: “NH₃” (i.e. no dissociation), “NH₂ + H”, “NH + H₂”, “NH + H + H”, “N + H + H + H” and “other”. Atoms with an interatomic distance under 6 Bohr (3.15 Å) were considered bonded, while a distance above 8 Bohr (4.23 Å)—roughly four times the equilibrium value—was rated as dissociated. In particular, the three N–H bonds were examined and ordered to obtain the fragment containing the nitrogen atom (NH₃, NH₂, or NH). In cases where more than one hydrogen atom dissociated, the bonds between them were fully characterized. If dissociation occurred, the trajectory was terminated after the current 200 fs interval; otherwise, it was continued for at least another 200 fs, where it was again re-assessed.

After reaching dissociation or a total propagation time of 1 ps, the SHARC trajectories were tested against numerical validity, ensuring a maximum change in total energy of 0.1 eV between consecutive time steps and 0.2 eV over the entire trajectory. Moreover, they were re-categorized following the criteria described above to find not only the dissociation pattern, but also the time at which dissociation takes place. An additional requirement was that the observed fragmentation had to remain as such for at least 10 fs. This condition was introduced to discount transient fluctuations around the bond breaking distance that do not lead to a separation of the fragments.

3 Results

3.1 Ammonia photodissociation ratios

The analysis of the 50 000 trajectories shows that the main photodissociation product, NH₂ + H, is formed in over 94% (47 210) of all trajectories. In total, 4.5% (2231 trajectories) do not dissociate and 0.6% (297 trajectories) follow the rare NH + H₂ channel. A further small portion of 0.5% (241 trajectories) was found to be en route to dissociation, predominantly following the frequent channel. In these cases, at least one N–H distance was between 6 Bohr and 8 Bohr, so neither stable nor fully dissociated within our definition. In addition, 10 and 9 trajectories (0.02%) were found following the N + H + H₂ and N + H + H + H channels, respectively.

It is important to mention that most of the trajectories showing ammonia fragmentation into three or more fragments, as well as a significant number of the NH + H₂ trajectories, exceeded the maximum allowed deviation of 0.1 eV in total energy between consecutive time steps or 0.2 eV over the whole trajectory. However, for further analysis, all the observed rare pathways were included, since the energy conservation issues arise primarily after, or at an advanced stage of dissociation. A more detailed discussion is provided in Section S4 of the ESI.‡ We presume the underlying reason for this to be sudden changes in interstate couplings within one time step near state crossings, which would require slightly smaller nuclear time steps in these regions.

Fig. 2a depicts the time evolution of the relative amount of the three major observed molecular species, i.e. stable ammonia and products of the two main photodissociation channels. A zoom-in on the NH + H₂ curve is shown in the inset. The standard error of the mean is displayed for every curve, but due to the large number of trajectories simulated the error is only visible for the rare dissociation channel in the corresponding inset.

Fig. 2 Photodissociation of ammonia, based on 50 000 surface-hopping trajectories of up to 1 ps. (a) Relative amounts of ammonia (NH₃, blue), the frequent (NH₂ + H, light green) and the rare photodissociation products (NH + H₂, red) over time. The kinetic fit is indicated by dashed lines, and the amounts of each species after 1 ps are noted in percent on the right side of the plot. The inset zooms in on the very small amount of the rare reaction product and includes indications of 1σ and 2σ standard error of the mean as shaded areas around the curve. (b) Kinetic model and fitted time constants τ_i, as well as time delays τ^delay_i for the frequent (freq) channel, rare channel, and a hypothesized nonreactive ammonia species NH₃^nr.

As the relative amount of species are averages over 50 000 simulations, one could think of them as molar fractions. These molar fractions were used to fit the kinetic model sketched in Fig. 2b. The corresponding fitted curves are displayed as dotted lines in Fig. 2a. In addition to reactive ammonia, frequent and rare reaction products, we considered a second ammonia species, termed nonreactive ammonia, NH₃^nr, which can interconvert with reactive NH₃, but not dissociate. The inclusion of this nonreactive species was necessary to fit the observed changes in the relative concentrations. A fit without this hypothetical ammonia species (Fig. S4 in Section S5 of the ESI‡) is unable to capture the kinetics of the three main species correctly. However, this nonreactive species eluded characterization, as we were unable to differentiate it from reactive ammonia based on geometry alone. Kinetic analysis of the trajectory parts when ammonia is still intact by means of time-lagged independent component analysis^48,49 indicates that a slow process is present, but the analysis is also unable to properly separate reactive and non-reactive ammonia conformations. We believe that the nonreactive species cannot be described by a local minimum on a PES, but is rather created by nonadiabatic phenomena, meaning that geometries are in reactive regions of configuration space but on the wrong PES, and therefore able to react.

The kinetic model shown in Fig. 2b contains delay times for the two dissociation channels. They account for the fact that NH₂ and NH are observed only after certain time lags; thus, the delay times can be interpreted as the minimal time required for the particular dissociation to occur. Visually, these time lags are evident at the beginning of the curves of Fig. 2a, indicating that a brief moment is required to reach the regions of the PES where dissociation becomes feasible, followed by overcoming the energy barriers to finally form the fragments. The time delays for the dissociations were fitted to τ^delay_freq = (19.12 ± 0.07) fs and τ^delay_freq = (90.3 ± 0.2) fs. The estimated time constant for the frequent reaction channel (τ_freq = (79.2 ± 0.02) fs or k_freq = (12.622 ± 0.004) ps⁻¹) is two orders of magnitude smaller than that for the rare channel (τ_rare = (5.51 ± 0.01) ps or k_rare = (0.18141 ± 0.0004) ps⁻¹).

The obtained forward and backward reactions between the two ammonia species are, with time constants τ_nr = (609.2 ± 0.5) fs and τ^back_nr = (630.7 ± 0.5) fs respectively, of the same order of magnitude, with the formation of the nonreactive NH₃ being slightly faster. Further details on the kinetic model can be found in Section S5 of the ESI.‡

Extrapolating the dissociations, a final relative amount of (0.6385 ± 0.0007)% NH + H₂ would be reached after all ammonia has dissociated over the course of some picoseconds. This is in excellent agreement with the experimentally determined quantum yield of ≤0.8%.¹⁶ Experimental full widths at half maximum of the rotovibronic absorption bands, Γ_ν,^4,6 estimate the time constant corresponding to the major channel as around 22–23 fs via τ ≈ (2πcΓ_ν)⁻¹. This is around 3.5 times faster than our fitted value of τ_freq ≈ 79 fs and can probably be attributed to tunneling, which is not considered in these simulations.

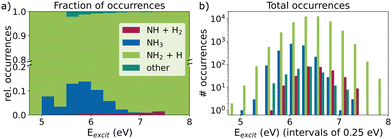
The ratio of rare versus frequent dissociation seems to depend on the excitation energy, as already noted in ref. 37. This is illustrated in Fig. 3, which compares the observed reaction products at 1 ps for different excitation energy windows. Higher excitation energies correspond to a higher fraction of the rare channel, which, however, never significantly exceeds 1% in our trajectories (Fig. 3a). This slight preference for higher excitation energies can also be seen in the total number of occurrences as an asymmetry in the bar heights in Fig. 3b. Although the total number of trajectories and thus the total number of NH + H₂ events decreases with excitation energies higher than the absorption maximum, it is doing so noticeably slower than for energies lower than the maximum.

Fig. 3 Analysis of the reaction products at the end of the simulation time, including non-reacted ammonia, as a function of the excitation energy. (a) Relative amount of observed species in different excitation energy windows of 0.25 eV width, and (b) absolute number of occurrences on logarithmic scale for the same energy windows.

Additionally, we notice that the distribution of non-dissociating trajectories is slightly skewed to the left towards lower energies in Fig. 3b. The same holds for those trajectories, which are currently en route, subsumed under “other” in Fig. 3 together with the few cases of other forms of fragmentation, e.g. N + H + H + H. A similar picture arises when the dependence on the total energy is examined (Section S6 of the ESI‡). With higher total energy, the fraction of the rare process also increases, whereas the non-dissociating trajectories have predominantly below average total energies.

To further analyze the dependency of the relative occurrence of the rare and frequent dissociation event, we fitted the kinetic model to only those trajectories that fall within 0.25 eV excitation energy windows. This way, we obtained excitation-energy-dependent time constants for the two channels and were able to calculate the expected individual fractions of the rare product after full dissociation. The corresponding numerical values for different excitation windows and the final NH + H₂ ratio are compiled in Table 1. While the trend of higher fractions of the rare channel at higher excitation energies is clearly visible here, fewer trajectories with these higher excitation energies exist, such that their absolute numbers do not increase, as shown in Fig. 3. The individual time constants τ for the rare and frequent channels both decrease with excitation energy. The observed relative increase in the rare channel is due to the underlying increase in the ratio of rare to frequent time constant. This ratio is also shown in Table 1. The values vary from 3 × 10² down to 5 with an overall ratio of 70.

Table 1 Number of trajectories, rare photodissociation product fractions after 1 ps with uncertainties, projected outcomes using a kinetic fit and time constant ratios of rare versus frequent reaction for all trajectories together (excitation range 0–1 eV) and grouped by excitation energies E_excit onto 0.25 eV windows

E excit (eV)	# of trajectories	NH + H2 at 1 ps (%)		NH + H2 fit (%)	τ rare/τfreq
Overall	50 000	0.59	±0.03	0.64	70
5.50–5.75	699	0.1	±0.1	0.19	3 × 10^2
5.75–6.00	2999	0.4	±0.1	0.46	156
6.00–5.25	7978	0.40	±0.07	0.48	104
6.25–6.50	13 277	0.62	±0.07	0.69	61
6.50–6.75	13 151	0.59	±0.07	0.59	70
6.75–7.00	7 795	0.71	±0.09	0.72	38
7.00–7.25	3047	0.9	±0.1	0.93	31
7.25–7.50	795	1.1	±0.4	1.21	5

---

The trend is consistent throughout the analyzed energy range, despite a statistical outlier between the 6.25–6.50 eV and 6.50–6.75 eV energy windows. For this, see the resulting fraction after 1 ps in Table 1. The individual fitted constants for each excitation energy window are reported in Table S1 (Section S5) of the ESI.‡

Extrapolating the fitted time constants to higher excitation energies (Fig. S5 in Section S5 of the ESI‡), would suggest that the minor dissociation pathway becomes the dominant channel above approximately 9.5 eV. However, in these high-energy regions we expect other electronic states to be involved, which would drastically alter the photolysis processes.

3.2 NH + H₂ photodissociation channel

Here we analyze the 297 trajectories that undergo the rare photodissociation channel, first in terms of changes in the bonding pattern and then in terms of electronic populations and associated mechanisms.

3.2.1 Nuclear rearrangements involved in the NH + H₂ pathway. The reaction progress is monitored using the second longest N–H bond, while the shortest N–H bond remains below 6 Bohr and the H₂ fragment is stable. A visualization of this second longest N–H bond for all trajectories separately is depicted in Fig. 4a, where the reaction instances displayed as vertical lines are ordered by dissociation time. The term “second longest N–H bond” refers to the particular N–H bond that at the time when the rare dissociation is concluded has the second largest value, i.e. when the second N–H bond stretches beyond 8 Bohr (4.23 Å). In general, the longest and second longest N–H distances do not differ by much. In almost all cases, oscillations of a stable N–H bond—visible as alternations in shades between dark blue and turquoise in Fig. 4a—are followed by the bond cleavage indicated by a transition to yellow.

Fig. 4 (a) Length of N–H bond that is the second longest N–H bond at the end of the dissociation process and (b) H–N–H angle between nitrogen and the dissociating H₂ of the 297 rare photodissociation trajectories sorted according to the dissociation time, from fast to slow.

The bond cleavage takes place rather quickly compared to the time spent oscillating, which is characteristic for rare events and can also be seen in the three example trajectories in Fig. 5a, where all interatomic distances are plotted over time. The bonds of the remaining stable fragments are highlighted in green. Notably, the H–H bond of the leaving H₂ molecule, depicted in light green, is formed at the moment or even before the dissociation process can be detected. While initially all H–H distances oscillate around 2 Å, one shortens to below 1 Å, producing stable H₂. Only once this happens, the NH and H₂ fragments separate, visible through the black and gray lines rapidly advancing to larger distances. In general, the reaction occurs in a concerted manner, just as shown in these examples (all panels in Fig. 5a).

Fig. 5 Example trajectories of the rare photodissociation. (a) Time-resolved ammonia interatomic distances, with the bond between nitrogen and the hydrogen remaining as NH (dark green line), the bond between the hydrogen atoms forming H₂ (light green), dissociating N–H bonds (black) and elongating H–H distances (gray). A color-coded line along the x-axis shows the current active state; (b) potential energies of the active (bold) and inactive (fine) states over time with vertical lines indicating the completed dissociation (dotted) and point with the highest visited potential energy around the dissociation (solid); (c) absolute values of the linear and angular momenta over time for the NH fragment.

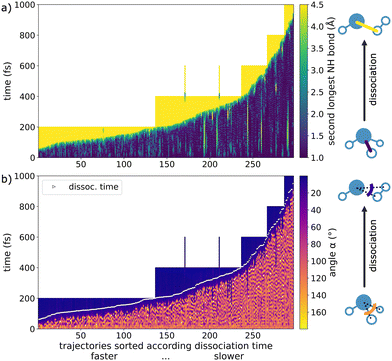
Only in a few instances the dissociation reaction stopped before completion and reverted back to ammonia. This can be seen in Fig. 4a as temporary lighter regions between stable, blue-colored periods. These frustrated dissociations were not classified because they do not lead to a final stable product. Ultimately, since our criterion for dissociation is an N–H distance of 8 Bohr (4.23 Å), the frustrated fragmentations do not count as completed. Only in 2 cases, we actually observed a rare dissociation followed by a brief recombination before finally fully separating (see the two 600 fs long trajectories with dissociation before 400 fs and recombination around 400 fs in Fig. 4a).

For further analysis of the dissociation process itself, we chose a window from 4 Bohr to 8 Bohr (2.12–4.23 Å), which corresponds to the elongation associated with the breaking of the second longest N–H bond. We consider this approach to be more meaningful than defining dissociation at a single point in time, as it allows measuring the duration of the process itself. On average, the rare dissociation takes 39 fs and is thus quick compared to the overall reaction times.

Similarly to the second longest N–H bond, the H–N–H angle, where the hydrogen atoms are those dissociating as H₂, can be used to monitor the reaction progress, since the angle becomes very small upon dissociation (Fig. 4b). We observe sizable oscillations of the angle before fragmentation, followed by a quick, marked decrease upon reaction. White markings indicate the 8 Bohr (4.23 Å) dissociation criterion, at which point the depicted angle is already strongly reduced.

3.2.2 Electronic states involved in the NH + H₂ pathway. The nonadiabatic dynamics provide insights into the mechanism in terms of active electronic states visited throughout the simulation. Fig. 6a shows the overall electronic populations over time for the minor dissociation channel. After excitation, there is a rapid decrease in S₁ population, counterbalanced by an increase of the S₀ one, which peaks around 200 fs and then gradually decreases, stabilizing at around 71%. Meanwhile, the T₁ population slowly increases to around 27% at the final propagation time. While these populations show that all three electronic states, including the triplet, are involved in the rare dissociation channel, they do not clarify the dissociation mechanism. Further insight is obtained by looking at the active state of the individual trajectories around the time of dissociation, see Fig. 6b. The current active state of each trajectory (vertical lines) is color-coded, in shades of blue or red for singlets or the triplet state. The white marking indicates when the dissociation process ends.

Fig. 6 Quantification of the involvement of singlet (S₀ dark blue, S₁ light blue) and triplet (red) states in the NH + H₂ photodissociation channel: (a) electronic populations over time based on the active state, assuming that the system remains in the last active state in cases of simulation end before 1 ps. Shaded areas around the curves indicate 1σ and 2σ standard deviations. (b) Active state over time for each of the 297 rare photodissociation trajectories (vertical lines), sorted according to the dissociation time (same as in Fig. 3). (c) Distribution of pathways undergone by 297 rare photodissociation trajectories, according to the active states before and during dissociation. The pie-chart shows the relative occurrence of electronic states within the dissociation window (gray shaded box, final stretch of second longest N–H bond from 4 Bohr to 8 Bohr (2.12–4.23 Å)). “Other” includes patterns different from the listed ones.

The simulation starts in the S₁ state (light blue) and almost all trajectories (97.8%) eventually relax to the S₀ state (dark blue). While in the S₀ state, there are some cases where temporary intersystem crossings to the triplet state (red) may take place. From there on, different pathways can be observed. Oftentimes, the trajectory stays in S₀, approaches regions near a conical intersection, where it typically (58.2%) transitions briefly back to the S₁ while dissociating, before it returns to the ground state. Another portion of the S₀ trajectories near the conical intersection (28.6%) do not jump back to the excited state, staying in the ground state while dissociating. Alternatively, S₀ → T₁ intersystem crossing takes place, which accounts for 9.4% of all rare dissociations. Some trajectories show a more complex pattern during the dissociation, involving all three states. In few cases, no initial relaxation to the ground state is observed; the trajectories remain in the S₁ until dissociation (1.3%) or intersystem crossing from the S₁ to the T₁ takes place (0.7%). We find that intersystem crossing can also occur after dissociation is completed, which influences the overall triplet population, but is not directly related to the photodissociation process itself.

All the different pathways are summarized in Fig. 6c. Also shown is a pie chart that quantifies the different pathways, based on the populations in the dissociation window discussed above (breaking of the second longest N–H bond from 4 Bohr to 8 Bohr). If a state was visited for only 2 time steps or less, its contribution was discounted. Dissociation on the singlet manifold dominates, with the S₁ being involved in most of the reactions (59.3%). However, there is a significant number of instances in which ammonia dissociates only or mainly on the triplet PES (10.1%). The inclusion of the triplet state is thus essential to understand ammonia photodissociation. The “other” in the pie chart in Fig. 6c collects dissociation patterns different from those explicitly listed. It consists of a variety of more complex behaviors (summarized as “other pattern” in the gray box) and one single pathway fully in the S₁.

Interestingly, the temporal length of the NH + H₂ dissociation windows varies significantly depending on the mechanism. Those trajectories that dissociate in S₀ and those in which T₁ is significantly involved, take each 29 fs on average. When both S₀ and S₁ participate in the dissociation, the average fragmentation takes 41 fs and is thus significantly longer than in the other cases. The five trajectories following more complex dissociation patterns and involving all three states take over 200 fs on average to dissociate. Hence, in general the dissociation sequence is very fast (the fragments mostly separate within a few femtoseconds), yet in some instances the fragmentation process can take much longer. It is possible that the system diffuses along the ridge of the barrier without tipping over.

Fig. 5b depicts the potential energies of the singlet and triplet states over time (with the current active state highlighted in bold) of three trajectories showing the most predominant dissociation patterns. The reaction progress, measured by the second longest N–H distance, is shown as a color bar at the bottom of each plot. All three trajectories display a hop to the S₀. The first sub-panel (example trajectory no. 1 or overall trajectory no. 1327) exemplifies dissociation in the ground state after briefly visiting a region with vanishing singlet–singlet gap. Rare example trajectory no. 2 behaves similarly, but the reverse internal conversion to the S₁ state is visible, before relaxing back to the ground state. The third example (rare trajectory no. 3) depicts a case of dissociation in the triplet state, which is the lowest state in the region of bond breakage. The end of the dissociation (when the second longest N–H bond exceeds 8 Bohr) is indicated by the vertical dotted line. Additionally, the solid vertical line marks the time at which the potential energy reached its maximum around dissociation. Most of the rare trajectories follow one of the three characteristic dissociation patterns. In all these cases, reaching the region of state crossings in S₀ commences the fragmentation.

The time of dissociation for an individual trajectory is governed by the seemingly chaotic oscillations and probabilistic surface hops, mainly leading to S₀→T₁ intersystem crossing or the S₀→S₁ reverse internal conversion, both followed by fragmentation. This stochastic behavior impedes a prediction of the pathway and dissociation time based only on the initial condition of each trajectory. Neither the excitation energy nor other geometrical or energetic descriptors, show meaningful correlations with the bond cleavage mechanism ahead of time. Investigated features include interatomic distances, bond angles, and the out-of-plane angle, kinetic and potential energies, and energy gaps. One notable difference in the mechanism between rare and frequent channels is that the dissociation of a hydrogen radical occurs much more often solely in the S₁ state or right after relaxation from the excited to the ground state (see also ref. 29), whereas the dissociation of H₂ often happens in the ground state and not necessarily right after internal conversion from the S₁ state.

The scatter plot of dissociation time and excitation energy in Fig. 7a underscores stochasticity as the primary driver of the molecular photodissociation channel, as no clear trend is visible between these two plotted quantities. Furthermore, the states during the dissociation window (indicated by different colors in Fig. 7) do not evidence any correlation with excitation energy or reaction time. However, with increasing excitation energy above 6.5 eV, the number of trajectories that take a long time to dissociate decreases strongly. This fits with the observation from Fig. 3 and Table 1, that at higher excitation energies the relative amount of the NH + H₂ photoproducts slightly increases.

Fig. 7 Dissociation time (time for second longest N–H bond to reach 8 Bohr) of the 297 rare photodissociation trajectories versus (a) excitation energy and (b) total energy. Each point is colored according to the electronic states involved in the dissociation window, as indicated.

However, a requirement for the trajectories leading to NH + H₂, is a total energy of at least 6.7 eV. The smallest total energy observed leading to the H₂ elimination is 6.73 eV, whereas trajectories following the frequent channel possess total energies down to 6.08 eV. Fig. 7b indicates that no simulated trajectory with total energy significantly below 7 eV undergoes the rare dissociation, regardless of the electronic states involved. In general, higher total energies lead to shorter times until NH + H₂ formation. This is in accordance with the fact, that higher total energies result in larger NH + H₂ product fractions (Fig. S6 in Section S6 of the ESI‡). However, for total energies below 8 eV the distribution of dissociation times is very broad.

Besides using the second longest N–H bond and an appropriate H–N–H angle (Fig. 4), the momenta of the individual fragments are also suitable to determine the fragmentation and completion of the dissociation, as the linear and angular momenta of the individual fragments become constant once they are sufficiently separated, see Fig. 5c. Note, that the total linear and angular momenta of the entire system are constant. The end of dissociation (dotted vertical line) nicely coincides with the curves plateauing. In many cases, after oscillations in the magnitudes of the momenta, there is a steep increase starting at a maximum in the potential energy, before eventually reaching a plateau where the fragments NH and H₂ can be considered independent. See Section S7 of the ESI‡ for further discussion.

4 Conclusions

The photodissociation of ammonia in the gas phase with a focus on the rare molecular channel NH + H₂ has been revisited using nonadiabatic surface hopping dynamics. A total of 5 × 10⁴ trajectories have been propagated, based on MRCISD machine-learned potentials^37,43 that include the two lowest singlet states and the lowest triplet. In addition to energies and energy gradients, they provide nonadiabatic and spin–orbit couplings for the simulations, which are performed using the SHARC⁴¹ framework.

A kinetic model has been established to fit the major (NH₂ + H) and minor (NH + H₂) photodissociation products. The inclusion of an additional nonreactive ammonia species was necessary to accurately model the reaction dynamics, suggesting that the fragmentation channels are not equally accessible from all regions of the configuration space. Introducing time delay constants that describe the minimum time required for a reaction to occur enables a superior fit. Our large-scale dynamics simulations find that the time constant of the rare reaction channel is two orders of magnitude larger than the corresponding frequent one, for an excitation corresponding to 193 nm. The extrapolated amount of the NH photoproduct is found to be 0.64%, in agreement with experimental measurements,¹⁶ and thus validating our dynamics and resulting kinetic model.

The analysis of the dependence of product ratios on excitation energy shows that the rarer pathway occurs more frequently at higher excitation energies. Likewise, a minimal total energy around 6.7 eV is necessary for the rare dissociation to take place. As criteria for assessing the NH₃ to NH + H₂ dissociation as complete, we defined the elongation of the second longest N–H bond beyond 8 Bohr, a sharp decrease in the H–N–H angle (with the two hydrogen atoms dissociating as H₂) and the stabilization of the linear or angular momentum of either fragment becoming approximately constant. We shed light on the mechanisms of the NH + H₂ fragmentation, which was found to occur mainly concertedly. By analyzing the active state, we identified multiple pathways in which dissociation occurs. In this context, it is crucial to consider the dissociation within a time window rather than at a single point, as this better captures the dynamic nature of the photodissociation process.

In summary, the main mechanism for the hydrogen elimination after excitation to S₁ is preceded by a non-radiative direct deactivation to the ground state by internal conversion. Dissociation then occurs either via reverse internal conversion to S₁, followed by a return to the ground state, or solely in the ground state without involvement of S₁. About 10% dissociates in the triplet T₁ state. The insights presented here offer a better understanding of the reaction network of gas phase ammonia leading to H₂, paving the way for further future studies on the dynamics of its reaction fragments.

Author contributions

BB (conceptualization, methodology, investigation, formal analysis, visualization, writing – review & editing), JCBD (conceptualization, methodology, writing – original draft), LG (conceptualization, supervision, funding acquisition, project administration, writing – review & editing).

Data availability

The employed ML potentials, including gradients and couplings are available at https://github.com/yarkonygrp/surfaces and in ref. 35. The SHARC program package as ref. 40 is available at https://sharc-md.org. Additionally, in order to ensure reproducibility, we provide the ML potentials with interface to SHARC as used in this work, and the initial conditions employed in the dynamical simulations at https://doi.org/10.5281/zenodo.14545219.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the University of Vienna in the framework of the research platform ViRAPID. We are grateful to Yuchen Wang and David R. Yarkony for providing the fitted ammonia PESs employed in this work. The authors also thank all the ViRAPID members, particularly S. Mai and C. Dellago, for continuous fruitful discussions. The Vienna Scientific Cluster is thanked for generous allocation of computer resources.

References

1. R. P. Wayne, J. Geophys. Res.: Planets, 1993, 98, 13119–13136.
2. K. D. Bayes, K. H. Becker, U. K. H. Welge and K. H. Welge, Z. Naturforschg, 1962, 17, 676–680.
3. K. H. Becker, U. K. H. Welge and K. H. Welge, Z. Naturforsch., 1964, 19, 1006–1015.
4. L. D. Ziegler, J. Chem. Phys., 1985, 82, 664–669.
5. A. Hofzumahaus and F. Stuhl, J. Chem. Phys., 1985, 82, 5519–5526.
6. V. Vaida, M. I. McCarthy, P. C. Engelking, P. Rosmus, H.-J. Werner and P. Botschwina, J. Chem. Phys., 1987, 86, 6669–6676.
7. N. L. Evans, H. Yu, G. M. Roberts, V. G. Stavros and S. Ullrich, Phys. Chem. Chem. Phys., 2012, 14, 10401.
8. A. S. Chatterley, G. M. Roberts and V. G. Stavros, J. Chem. Phys., 2013, 139, 034318.
9. H. Yu, N. L. Evans, A. S. Chatterley, G. M. Roberts, V. G. Stavros and S. Ullrich, J. Phys. Chem. A, 2014, 118, 9438–9444.
10. J. D. Rodríguez, M. G. González, L. Rubio-Lago and L. Bañares, Phys. Chem. Chem. Phys., 2014, 16, 406–413.
11. H. Okabe and M. Lenzi, J. Chem. Phys., 1967, 47, 5241–5246.
12. R. Lilly, R. Rebbert and P. Ausloos, J. Photochem., 1973, 2, 49–61.
13. V. Donnelly, A. Baronavski and J. McDonald, Chem. Phys., 1979, 43, 271–281.
14. A. M. Quinton and J. P. Simons, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 1261–1269.
15. C. Y. R. Wu, J. Chem. Phys., 1987, 86, 5584–5586.
16. R. D. Kenner, F. Rohrer and F. Stuhl, J. Chem. Phys., 1987, 86, 2036–2043.
17. R. Kenner, F. Rohrer, R. Browarzik, A. Kaes and F. Stuhl, Chem. Phys., 1987, 118, 141–152.
18. T. G. Slanger and G. Black, J. Chem. Phys., 1982, 77, 2432–2437.
19. M. Suto and L. C. Lee, J. Chem. Phys., 1983, 78, 4515–4522.
20. J. E. Nicholas, A. I. Spiers and N. A. Martin, Plasma Chem. Plasma Process., 1986, 6, 39–51.
21. R. D. Bower, M. T. Jacoby and J. A. Blauer, J. Chem. Phys., 1987, 86, 1954–1956.
22. U. Müller and G. Schulz, J. Chem. Phys., 1992, 96, 5924–5937.
23. S. Leach, H.-W. Jochims and H. Baumgärtel, Phys. Chem. Chem. Phys., 2005, 7, 900–911.
24. M. J. Loeffler and R. A. Baragiola, J. Chem. Phys., 2010, 133, 214506.
25. A. N. Heays, A. D. Bosman and E. F. van Dishoeck, Astron. Astrophys., 2017, 602, A105.
26. U. Mänz, P. Rosmus, H.-J. Werner and P. Botschwina, Chem. Phys., 1988, 122, 387–393.
27. U. Mänz, E.-A. Reinsch, P. Rosmus, H.-J. Werner and S. O. Neil, J. Chem. Soc., Faraday Trans., 1991, 87, 1809–1814.
28. R. Dixon, Mol. Phys., 1989, 68, 263–278.
29. D. Bonhommeau and D. G. Truhlar, J. Chem. Phys., 2008, 129, 014302.
30. D. Bonhommeau, R. Valero, D. G. Truhlar and A. W. Jasper, J. Chem. Phys., 2009, 130, 234303.
31. K. Giri, E. Chapman, C. S. Sanz and G. Worth, J. Chem. Phys., 2011, 135, 044311.
32. C. Xie, X. Zhu, J. Ma, D. R. Yarkony, D. Xie and H. Guo, J. Chem. Phys., 2015, 142, 091101.
33. J. Ma, X. Zhu, H. Guo and D. R. Yarkony, J. Chem. Phys., 2012, 137, 22A541.
34. Y. Guan, H. Guo and D. R. Yarkony, J. Chem. Theory Comput., 2020, 16, 302–313.
35. Y. Wang, Y. Guan, H. Guo and D. R. Yarkony, J. Chem. Phys., 2021, 154, 094121.
36. Y. Wang and D. R. Yarkony, J. Chem. Phys., 2021, 155, 174115.
37. Y. Wang, H. Guo and D. R. Yarkony, Phys. Chem. Chem. Phys., 2022, 24, 15060–15067.
38. J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071.
39. S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
40. S. Mai, D. Avagliano, M. Heindl, P. Marquetand, M. F. S. J. Menger, M. Oppel, F. Plasser, S. Polonius, M. Ruckenbauer, Y. Shu, D. G. Truhlar, L. Zhang, P. Zobel and L. González, SHARC3.0: Surface Hopping Including Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics, https://sharc-md.org/, 2023.
41. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
42. S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231.
43. Y. Wang, Y. Guan, H. Guo and D. R. Yarkony, J. Chem. Phys., 2021, 154, 094121.
44. L. Sun and W. L. Hase, J. Chem. Phys., 2010, 133, 044313.
45. M. Barbatti and K. Sen, Int. J. Quantum Chem., 2016, 116, 762–771.
46. M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, J. Photochem. Photobiol., A, 2007, 190, 228–240.
47. G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111.
48. L. Molgedey and H. G. Schuster, Phys. Rev. Lett., 1994, 72, 3634–3637.
49. Y. Naritomi and S. Fuchigami, J. Chem. Phys., 2011, 134, 065101.

---

Footnotes

† This publication is dedicated to the memory of Prof. David Yarkony (1949–2024), whose sudden death took place before this manuscript was concluded.

‡ Electronic supplementary information (ESI) available: (1) Computational details on the optimization of critical points on the PESs, (2) the computed absorption spectrum of ammonia, (3) the input keywords for the SHARC dynamics simulations, (4) an analysis of those trajectories, which violate the total energy conservation, (5) details regarding the kinetic model and fit, (6) an analysis of the total energy dependence of the reaction outcome, including a comparison to the results of Wang et al.,³⁷ and (7) further information on the linear and angular momenta of the fragments after dissociation via the minor channel. See DOI: https://doi.org/10.1039/d4cp04834b

---