 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Substituted acridones: simple deep blue HIGHrISC emitters in an aprotic environment†
Matthias
Jantz‡
 a,
David
Klaverkamp‡
a,
David
Klaverkamp‡
 a,
Lennart
Bunnemann‡
a,
Lennart
Bunnemann‡
 b,
Martin
Kleinschmidt
b,
Martin
Kleinschmidt
 c,
Constantin
Czekelius
c,
Constantin
Czekelius
 b and
Peter
Gilch
b and
Peter
Gilch
 *a
*a
aInstitut für Physikalische Chemie, Heinrich-Heine-Universität Düsseldorf, Universitätsstr. 1, 40225 Düsseldorf, Germany. E-mail: gilch@hhu.de
bInstitut für Organische Chemie und Makromolekulare Chemie, Heinrich-Heine-Universität Düsseldorf, Universitätsstr. 1, 40225 Düsseldorf, Germany
cInstitut für Theoretische Chemie und Computerchemie, Heinrich-Heine-Universität Düsseldorf, Universitätsstr. 1, 40225 Düsseldorf, Germany
First published on 17th March 2025
Abstract
N-Methylacridones (NMAs) substituted at positions 2 and 7 with +M groups (fluorine and methoxy) were synthesized and characterized by steady-state and time-resolved spectroscopy. Solutions of the NMA derivatives in an aprotic solvent (tetrahydrofuran) emit in the deep blue region of the visible spectrum with radiative rate constants larger than 5.4 × 107 s−1 and fluorescence quantum yields up to 0.84. Sensitization experiments employing 1,4-dichlorobenzene give evidence for HIGHrISC behavior of the NMAs, that is, reverse intersystem crossing (rISC) from a higher triplet state Tn≥2 occurs. The spectroscopic results, which are corroborated by quantum chemical calculations, render these derivatives very promising for applications in organic light emitting diodes (OLEDs).
Introduction
With the HIGHrISC1,2 or hot exciton3,4 approach, triplet excitons can be converted into light. This is of particular interest in organic light-emitting diodes (OLEDs) in which ¾ of the excitons formed by electron–hole recombination adopt triplet spin multiplicity.5 In HIGHrISC emitters, reverse intersystem crossing (rISC) from a higher triplet state Tn≥2 to the emissive singlet state S1 occurs (cf.Fig. 1). For HIGHrISC to be efficient, its respective rate constant krISC ought to be larger than the one for internal conversion (IC) kIC between the Tn and the lowest triplet state T1. Furthermore, the Tn state should be slightly (a few times the thermal energy kBT) higher in energy than the S1 state.1 This ensures that after equilibration of the two states, most of the population resides in the emissive S1 state. El-Sayed-allowed transitions as occurring in carbonyl compounds promise large ISC and thereby also rISC rate constants.6,7 For an emission in the visible range, the carbonyl group ought to be part of a polyaromatic scaffold of the size of anthracene or lager.7 For the closely related aromatic carbonyl compounds xanthones,8 thioxanthones,1 and acridones2 HIGHrISC activity was observed by us. All these compounds emit in the blue region of the visible spectrum. Acridones are particularly promising in this respect as some derivatives dissolved in suitable solvents feature fluorescence quantum yields ϕfl close to one.9 The focus of this study will be on derivatives of N-methylacridone (NMA). Contrary to the parent compound acridone, NMA lacks a an NH group which can act as a hydrogen bond donor. | ||
| Fig. 1 Illustration of the impact of +I/+M substituents at positions 2 and 7 on the NMA excitation energies. The depiction of the molecular orbitals on the bottom (adapted from ref. 10) indicates that only the π-orbital features electron density at positions 2 and 7 (encircled in red). | ||
When inspecting the excited state energies of NMA in the gas phase,10 high fluorescence quantum yields ϕfl in solution seem surprising. In NMA, the emissive singlet state is a 1ππ* one. Three essentially dark states (1nπ*, 3nπ*, and 3ππ*) are lower in energy. Thus, the 1ππ* state may depopulate via a 1ππ* → 1nπ* IC process. Femtosecond spectroscopy of the closely related thioxanthone has shown that such an IC process may occur in a few 100 fs.11 Also, the El-Sayed-allowed 1ππ* → 3nπ* transition can contribute to a fast 1ππ* depopulation.12,13 For NMA to exhibit high fluorescence quantum yields ϕfl and HIGHrISC activity the nπ* states (singlet and triplet) need to be lifted in energy above the 1ππ* one. As the energetic separations (in the gas phase) amount to only 1200 cm−1 (0.15 eV, 1ππ*–1nπ*) and 2300 cm−1 (0.28 eV, 1ππ*–3nπ*),10 respectively, rather small modifications of the molecule or its surroundings can suffice to achieve this goal. Indeed, polar protic solvents can invert the energetic ordering of 1ππ* and 1,3nπ* states.14 However, theoretical14 and experimental studies15 disagree with respect to the polarity which is needed to invert the ordering of states. The 1ππ* excitation in acridones goes along with an increase of the dipole moment14,16 and thus experiences a red-shift with increasing solvent polarity. 1,3nπ*-Excitations commonly,17,18 particularly in acridones,9 experience a blue shift in polar and – most pronounced – protic solvents. These opposite shifts cause both nπ* states of NMA in protic solvents to lie above the 1ππ* one in energy.14 The most visible consequence of this is the strongly increased fluorescence quantum yield ϕfl of NMA in protic solvents (ϕfl ≈ 0.7 in methanol)19 as compared to nonpolar ones (ϕfl ≈ 0.02 in cyclohexane).9 With respect to OLEDs, relying on protic solvents is problematic, however. In OLEDs chromophores are embedded in rather nonpolar and aprotic matrices.20–22
To achieve this inversion in an aprotic environment the 1ππ* energy can be lowered by placing substituents with a positive inductive effect (+I) and/or with a positive mesomeric effect (+M) at suitable positions (Fig. 1).23 The positions can be identified by inspection of the frontier orbitals (cf.Fig. 1). At the positions 2 and 7, the HOMO (π-orbital) features anti-nodes and the LUMO (π*-orbital) nodes. Thus, in a simplified picture, +M substituents placed here are expected to rise the energy of the π-orbital and leave the one of the π*-orbital untouched. This ought to result in the lowering of the 1ππ* energy. Indeed, difluorination (+M effect)24 of NMA at positions 2 and 7 shifts the 1ππ* 0–0 energy by −1130 cm−1 (−0.14 eV, value refers to the compounds dissolved in methanol).19 A quantum chemical investigation on substituent effects on the excitation energy of anthracene – a chromophore of similar size – predicted shifts of the same magnitude.25 The measured red-shift of −1130 cm−1 (−0.14 eV) has the same magnitude as the 1ππ*–1,3nπ* separations mentioned above. Thus, an inversion of the state ordering and a shift into the deep blue region26 of the visible spectrum might be achievable by substitution. By introducing other groups with a +M effect, like methoxy,27 a stronger inversion of the ordering and a greater energetic separation of the states might be attained. Moreover, the emission should be shifted further into the deep blue. Therefore, in addition to the NMA-dF, new derivatives (for structures see Fig. 2) were investigated: one, where one fluorine is exchanged for a methoxy substituent (NMA-OMeF) and one, where both fluorine atoms are exchanged for methoxy substituents (NMA-dOMe). As already mentioned, the inversion of the states should be caused by substituents and not by the formation of hydrogen bonds between the NMA derivatives and the solvent. For this reason, tetrahydrofuran (THF) was chosen as the solvent due to its aprotic nature. Additionally, THF offers a deep UV cutoff28 and its polarity is similar to the one present in an OLED,29 making it an appropriate choice for the study.
In this study, the photophysical properties of NMA, NMA-dF, NMA-OMeF and NMA-dOMe in THF were investigated. For this purpose, stationary absorption and emission spectra were recorded. In addition, time-resolved spectroscopy in the femtosecond and nanosecond regime was performed and a comparison between direct and sensitized excitation was made. For sensitized excitation, 1,4-dichlorobenzene (DCB) was employed as a triplet sensitizer. Triplet-excited DCB serves as a substitute for triplet-correlated electron–hole pairs in an OLED. It is crucial to note, that DCB is not supposed to be utilized in an actual device. Rather, the upper triplet state is directly populated by electron–hole recombination. The results will show that the substituted acridones can convert both singlet and triplet excitons into light even in an aprotic environment. The experimental results are complemented by quantum chemical calculations.
Materials and methods
Steady state spectroscopy
The UV/Vis absorption spectra were measured using a two-beam Lambda 1050+ spectrometer from PerkinElmer GmbH, utilizing standard 1-cm path-length fused silica cells. Fluorescence was recorded in right-angle detection mode with a FluoroMax-4 from Horiba Scientific. To prevent inner filter effects, the absorption at the excitation wavelength was adjusted to ∼0.05 for a 1 cm path length. Coumarin 102 in air-saturated ethanol (ϕfl = 0.764)30 served as the reference for determining the fluorescence quantum yields of the NMAs. All emission spectra were corrected for the spectral sensitivity of the instrument. To determine the 0–0 energies and Stokes shifts, the fluorescence spectra were multiplied by λ2 to convert them from a constant wavelength bandpass to a constant wavenumber bandpass.31 Furthermore, the absorption spectra were multiplied by![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) −1 and the fluorescence spectra by
−1 and the fluorescence spectra by ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) −3 to arrive at the transition dipole representation.32 The 0–0 energies were obtained by the intersection between the absorption and fluorescence spectra in this representation, which were normalized to their respective maxima. Strickler–Berg analysis were conducted according to ref. 33 and 34, wherein only the absorption bands lowest in energy were included. The CIE coordinates were determined using the respective emission spectra and the ARL Spectral Fitting software.35
−3 to arrive at the transition dipole representation.32 The 0–0 energies were obtained by the intersection between the absorption and fluorescence spectra in this representation, which were normalized to their respective maxima. Strickler–Berg analysis were conducted according to ref. 33 and 34, wherein only the absorption bands lowest in energy were included. The CIE coordinates were determined using the respective emission spectra and the ARL Spectral Fitting software.35
Time-resolved absorption spectroscopy
The femtosecond transient absorption (fsTA) setup has been described elsewhere.36 Thus, here only a brief summary is given which focuses on the settings relevant for this study. A 1 kHz Ti:Sa laser amplifier system (Coherent Libra) served as the pulse source, emitting at a wavelength of 800 nm with a pulse duration of 120 fs (full width at half maximum (FWHM)). To produce 400 nm pump pulses, the 800 nm laser output underwent frequency doubling in a β-barium borate crystal. The energy of the pump pulse at the sample was adjusted to approximately 1 μJ, and the beam had a focal diameter of 160 μm on the sample. The absorption change was probed using a white light continuum generated in CaF2, with a diameter of 100 μm at the sample. The relative polarization of the pump and probe beams was set to the magic angle to avoid contributions from rotational diffusion. The time resolution of the measurements was approximately 150 fs (FWHM of the instrument response function (IRF)). Transient spectra were recorded at 139-time delay settings, spanning from −1 to 1 ps on a linear time scale, and from 1 ps to 3.4 ns on a logarithmic one. For each delay setting, 2000 spectra were recorded, and the data were averaged over four successive delay scans. To eliminate solvent signal contributions and correct for time-zero femtosecond artifacts, a solvent measurement was conducted. Its signal was subtracted from the one of the solution after proper scaling.37 The sample solutions were pumped through a silica flow cell (Hellma Analytics) with a path length of 0.5 mm. The absorption of the sample at the excitation wavelength was adjusted to ∼0.7 for a path length of 0.5 mm. Time constants and decay-associated difference spectra (DADS) were obtained using a global fitting procedure with a multi-exponential trial function convoluted with the IRF (see eqn (1)),38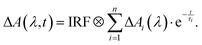 | (1) |
Nanosecond transient absorption (nsTA) data were obtained with a LP980 spectrometer from Edinburgh Instruments. For the excitation, the output of a Nd:YAG laser (Spitlight 600, Innolas) was frequency-quadrupled to arrive at 266 nm. The laser provides pulses with a duration of ∼7 ns at a repetition rate of 10 Hz. The average pulse energy amounted to ∼3 mJ. A pulsed xenon flashlamp (Osram XBO 150 W/CROFR) was used for probing. After passing the sample at a right-angle geometry, the light was dispersed in a grating monochromator and detected by a photomultiplier (Hamamatsu PMT-900). The time resolution was approximately 7 ns (FWHM of the IRF). For NMA-OMeF solutions, the pathlengths of the flow cell were 2 mm in pump and 10 mm in probe direction. For DCB solutions, the pathlengths of the flow cell were 5 mm in pump and 10 mm in probe direction. To obtain the triplet lifetime of NMA-OMeF for each of the four different concentrations twelve time traces were recorded at a probe wavelength of 585 nm. For each time trace 64 shots were averaged. To obtain the self-quenching constant of DCB, the rate constants of the triplet decay were determined for four different concentrations. For each concentration, ten time traces were recorded at 340 nm. For each time trace 80 shots were averaged.
Time-resolved emission spectroscopy
Time-correlated single photon counting (TCSPC) was conducted utilizing a fluorescence lifetime and steady-state spectrometer (FT300 with hybrid PMT detector, Pico Quant, Germany). The excitation process was accomplished using a supercontinuum laser excitation source (EXW-12 with a spectral extension unit EXTEND-UV, NKT Photonics, Denmark) operating at a repetition rate of 4.88 MHz. The output of the supercontinuum laser was frequency-doubled and excitation wavelengths were selected by a monochromator. The wavelengths were chosen to match the different absorption maxima: 375 nm, 416 nm, 424 nm, and 429 nm for NMA, NMA-dF, NMA-OMeF, and NMA-dOMe, respectively. Input and output slit widths of the monochromator were set to 3000 μm, resulting in a detection bandpass of 16.2 nm. The detection wavelengths were set to coincide with the fluorescence maxima for NMA (405 nm), NMA-OMeF (446 nm) and NMA-dOMe (457 nm). The detection wavelength for NMA-dF was set to 450 nm. The emission maximum was not chosen here, as it coincides with the Raman band of the solvent, generating an additional signal. The IRF was determined using a Ludox HS-30 colloidal silica water suspension (Aldrich), featuring a “zero” lifetime. The FWHM of the IRF was approximately 100 ps, and its influence was factored into the fitting process through convolution. Quartz Macro Cell type 111-QS cuvettes (Hellma) were employed for all sample measurements, featuring a light path of 1 cm and a sample volume of 3 mL. Fitting procedures were executed using the ChiSurf software.39 A single exponential including an offset which accounts for detector dark counts and after-pulsing served as a trial function.Time-resolved fluorescence data from the nano- to microsecond regime were acquired with a home-built setup. For the excitation, the pulsed Nd:YAG laser (Spitlight 600, Innolas) mentioned above tuned to 266 nm was used, providing pulses of ∼7 ns FWHM at a repetition rate of 10 Hz. The energy of the laser light was ∼125 μJ per pulse. The excitation beam was focused onto the sample with a cylindrical lens generating a line focus 0.5 mm wide and 2.5 mm long. The emitted fluorescence light was collected under an angle of 54°, then dispersed by a spectrograph (SpectraPro 308, Acton Research) with a grating blazed at 410 nm (121.6 l mm−1) and detected by a gated iCCD camera (PI-MAX, Princeton Instruments). The delay between excitation and detection was controlled electronically (PTG, Princeton Instruments) and enabled delay times from the nanosecond to the millisecond regime. To increase the signal at longer delay times the gain voltage of the microchannel plate was raised. Besides that, the integration time of the detector as well as the number of accumulations were increased for longer delay times. The signals from the CCD chip's pixel rows, where fluorescence light was detected, were summed up (200 rows), and the resulting spectra were spectrally integrated over the emission band of interest. The data were corrected for the baseline by subtracting the integrated signal from rows of the CCD chip where no fluorescence signal was detected. The baseline-corrected data were divided by the number of accumulations and by the integration time applied. To account for the varying gain voltage, a calibration curve was generated using the same instrumental parameters expect for different amplification settings UMCP, ranging from 0 to 255. The spectrally integrated fluorescence signal Sint(UMCP) in dependence of UMCP was fitted to an exponential function according to eqn (2),
| Sint(UMCP) = α·eβ·UMCP. | (2) |
Synthesis of the acridones
2,7-Difluoro-10-methylacridin-9(10H)-one (NMA-dF) was prepared by Ullmann-type coupling from 4-fluoro-aniline and 2-bromo-5-fluoro-benzoic acid, followed by intramolecular Friedel–Crafts acylation to give 2,7-difluoroacridin-9(10H)-one and final N-methylation.2 5-Fluoro-2-((4-methoxyphenyl)amino)benzoic acid was prepared by Ullmann-type coupling from 4-methoxyaniline and 2-bromo-5-fluorobenzoic acid following literature procedure.41 The cyclization to the acridone was done via a modified procedure by Kelly et al.42 using methanesulfonic acid. 2-Fluoro-7-methoxy-10-methylacridin-9(10H)-one (NMA-OMeF) was prepared by final methylation43 (see ESI†). 2,7-Dimethoxy-10-methylacridin-9(10H)-one (NMA-dOMe) was prepared by Ullmann-type coupling from 2-bromo-5-methoxybenzoic acid and 4-methoxyaniline, followed by intramolecular Friedel–Crafts acylation to give 2,7-dimethoxyacridin-9(10H)-one and final N-methylation.42,44–46 The purity of the acridones was verified by 1H-, 13C and 1F-NMR spectroscopy (see ESI,† Fig. S1–S10).Sample preparation
NMA (≥98.0%) and DCB (≥99.0%) were obtained from TCI. THF (≥99.9%) and ethanol (HPLC) were purchased from Sigma Aldrich. Coumarin 102 was purchased from Radiant Dyes Laser & Acc. All measurements were performed at room temperature (∼20 °C). To deoxygenate sample solutions, nitrogen (Air Liquide, 99.999%) or argon (Air Liquide, 99.999%) were bubbled through. Gases were saturated with the solvent to reduce concentration changes. All chemicals obtained commercially were used as received.Quantum chemical calculations
Geometry optimizations were conducted with the Gaussian 16 program47 using density functional theory (DFT) with the PBE0 functional for the ground state and time-dependent DFT (TDDFT) for the excited states, additionally applying the Tamm–Dancoff approximation (TDDFT-TDA) in the triplet manifold. The Ahlrichs def-SVP basis set48 was used throughout. Computed vibrational frequencies confirmed that all geometries obtained correspond to true minima. Vertical excitation energies at fixed geometries were computed with the DFT/MRCI program.49 The redesigned Hamiltonian R201650 was used with standard parameters and a selection threshold of 1.0 Hartree. The core electrons were kept frozen, the initial reference space comprised all single and double excitations of 10 electrons in 10 orbitals and was subsequently optimized to contain the most important configurations of all roots. For the 0–0 energies, vibrational zero-point energies computed at the (TD)DFT level were added to the DFT/MRCI energies. The solvent was considered implicitly employing the polarizable continuum model.47 Spin–orbit coupling matrix elements were computed with the SPOCK program in the atomic mean field approximation.51,52 Nonadiabatic coupling matrix elements (NACMEs) were obtained with the program DELTA.53 ISC and IC rate constants at a temperature of 293.15 K were computed via the generating function approach as implemented in the program VIBES.53–55Results
The absorption band lowest in energy is very similar for all substituted NMAs and NMA dissolved in THF (Fig. 3). All of them feature pronounced vibronic progression with two peaks and a shoulder. Compared to NMA in THF, the absorption of the derivates is bathochromically shifted. The magnitude of this shift increases in the following order: NMA-dF, NMA-OMeF and NMA-dOMe. The absorption of NMA features peaks at 395 nm and 377 nm and a shoulder around 358 nm. NMA-dF features peaks at 415 nm and 394 nm and a shoulder around 374 nm. NMA-OMeF features peaks at 424 nm and 402 nm and a shoulder around 381 nm. NMA-dOMe features peaks at 429 nm and 406 nm and a shoulder around 383 nm. The peak absorption coefficient of NMA at its longest wavelength maximum is around 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1, while the NMA derivatives exhibit a coefficient of around 10
000 M−1 cm−1, while the NMA derivatives exhibit a coefficient of around 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1.
000 M−1 cm−1.
Emission takes place in the range between 380 nm to 600 nm (see Fig. 4, left). Compared to NMA, the emission of NMA-dF, NMA-OMeF and NMA-dOMe is bathochromically shifted. The absorption and fluorescence of NMA and NMA-dF obey the mirror image rule.7 NMA features emission peaks at 405 nm and at 427 nm, resulting in CIE coordinates of (0.16, 0.02). The emission maxima of NMA-dF are located at 425 nm and 449 nm, resulting in CIE coordinates of (0.15, 0.04). For NMA-OMeF and NMA-dOMe the mirror image rule is partially fulfilled. Their emission peak is broadened compared to the absorption, thus obscuring the vibrational progression. Consequently, the emission spectra of NMA-OMeF as well as NMA-dOMe features just one maximum. For NMA-OMeF the maximum appears at 446 nm with CIE coordinates of (0.15, 0.11) and for NMA-dOMe at 457 nm with CIE coordinates of (0.14, 0.12). From the spectra in the transition dipole representation, the 0–0 energy as well as the Stokes shift were obtained. For NMA, a 0–0 energy of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (3.10 eV) and a Stokes shift of 560 cm−1 (69.4 meV), for NMA-dF a 0–0 energy of 23
000 cm−1 (3.10 eV) and a Stokes shift of 560 cm−1 (69.4 meV), for NMA-dF a 0–0 energy of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 (2.95 eV) and a Stokes shift of 570 cm−1 (70.7 meV), for NMA-OMeF of 23
800 cm−1 (2.95 eV) and a Stokes shift of 570 cm−1 (70.7 meV), for NMA-OMeF of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 (2.86 eV) and of 1500 cm−1 (186.0 meV), and for NMA-dOMe of 22
100 cm−1 (2.86 eV) and of 1500 cm−1 (186.0 meV), and for NMA-dOMe of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 (2.83 eV) and of 1530 cm−1 (189.7 meV) were determined. Via Strickler–Berg analysis,33,34 radiative rate constants (krad) for NMA of 7.43 × 107 s−1, for NMA-dF of 6.18 × 107 s−1, for NMA-OMeF of 5.42 × 107 s−1, and for NMA-dOMe of 5.53 × 107 s−1 were determined.
800 cm−1 (2.83 eV) and of 1530 cm−1 (189.7 meV) were determined. Via Strickler–Berg analysis,33,34 radiative rate constants (krad) for NMA of 7.43 × 107 s−1, for NMA-dF of 6.18 × 107 s−1, for NMA-OMeF of 5.42 × 107 s−1, and for NMA-dOMe of 5.53 × 107 s−1 were determined.
The fluorescence quantum yield ϕfl of NMA, NMA-dF, NMA-OMeF and NMA-dOMe in THF were measured with coumarin 102 (ϕfl = 0.764 in air-saturated ethanol30) as a reference. Yields of 0.11 ± 0.02 and 0.09 ± 0.02 (NMA), 0.68 ± 0.02 and 0.53 ± 0.04 (NMA-dF), 0.79 ± 0.02 and 0.54 ± 0.01 (NMA-OMeF), as well as 0.84 ± 0.05 and 0.53 ± 0.02 (NMA-dOMe) in deoxygenized (DO) and air-saturated (air) solutions were obtained. Fluorescence decays of the samples could be modelled single-exponentially. The respective fluorescence lifetimes τfl were determined by TCSPC to be 1.5 and 1.4 ns (NMA), 10.8 and 8.6 ns (NMA-dF), 14.6 and 10.0 ns (NMA-OMeF) as well as 15.4 and 9.7 ns (NMA-dOMe) in deoxygenized (Fig. 4, right) and air-saturated solutions (Fig. S11, ESI†). The error of these lifetimes is <± 1%. The fluorescence lifetimes τfl measured directly can be compared with ones τSBfl derived from the radiative rate constant krad and the fluorescence quantum yield ϕfl according to eqn (3),
 | (3) |
 | (4) |
 | (5) |
ΔEST = −kBT·ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. K. | (6) |
 . The fluorescence quantum yields of air-saturated (ϕairfl) and deoxygenized (ϕDOfl) samples were determined relative to the standard C102 in ethanol.30 Fluorescence lifetimes determined directly by TCPSC (τTCSPC) and from the rate constants krad and yields ϕDOfl (τSB) are included
. The fluorescence quantum yields of air-saturated (ϕairfl) and deoxygenized (ϕDOfl) samples were determined relative to the standard C102 in ethanol.30 Fluorescence lifetimes determined directly by TCPSC (τTCSPC) and from the rate constants krad and yields ϕDOfl (τSB) are included
| Parameters | NMA | NMA-dF | NMA-OMeF | NMA-dOMe |
|---|---|---|---|---|
| λ abs/nm | 396 | 416 | 424 | 429 |
| λ em/nm | 405 | 425 | 446 | 457 |
| Δṽ/cm−1 | 560 | 570 | 1500 | 1530 |
| E 0–0/cm−1 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
| k rad/s−1 | 7.79 × 107 | 6.18 × 107 | 5.42 × 107 | 5.53 × 107 |
| k nr/s−1 | 5.86 × 108 | 2.96 × 107 | 1.43 × 107 | 1.04 × 107 |
| ϕ airfl | 0.09 | 0.53 | 0.54 | 0.53 |
| ϕ DOfl | 0.11 | 0.68 | 0.79 | 0.84 |
| τ SB/ns | 1.36 | 11.00 | 14.58 | 15.19 |
| τ TCSPC/ns | 1.52 | 10.81 | 14.64 | 15.41 |
All of the four compounds have quantum yields ϕfl somewhat smaller than one. This suggests that non-radiative processes are competing with the fluorescence emission. By nanosecond transient absorption spectroscopy, the quantum yield of the lowest triplet state ϕT of NMA-OMeF in THF was estimated to 0.14 ± 0.02 (Fig. S13, ESI†). Like for NMA-dF in MeOH2 it was, thus, shown that the non-radiative decay is mostly due to ISC. Due to the similar structures of NMA, NMA-dF and NMA-dOMe, ISC to the T1 state is expected to be the dominant non-radiative decay channel for these compounds as well.
All three substituted emitters have a high fluorescence quantum yield ϕfl in an aprotic environment and emit with rate constants krad larger than 5.4 × 107 s−1 in the deep blue wavelength range. However, in order to be suitable as OLED emitters, it must first be determined whether the molecules also convert triplet excitations into light in an aprotic environment.
Through sensitized excitation, the Tn state of the emitter can be accessed if the T1 state of the sensitizer is higher in energy than the Tn state of the emitter. However, the energies of the Tn states (3nπ*) are not accessible experimentally. They are presumably close to the energy of the S1 states which are in the order of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–25
800–25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (2.82–3.10 eV, Table 1). In previous studies employing methanol as a solvent,1,2 DCB proved useful in this respect. It features a T1 0–0 energy of 27
000 cm−1 (2.82–3.10 eV, Table 1). In previous studies employing methanol as a solvent,1,2 DCB proved useful in this respect. It features a T1 0–0 energy of 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 cm−1 (3.47 eV) in the solid state61 (higher in energy than the S1 states of all NMAs) and a high triplet quantum yield in methanol solution (ϕMeOHT = 0.96).62 However, the triplet quantum yield of DCB in THF is not known. It is assumed that due to its symmetrical nonpolar nature, the molecule interacts only weakly with its surroundings, resulting in the energy of states remaining nearly unchanged. A comparison of fsTA measurements of DCB in methanol and in THF reveals that the spectral signatures are very similar in the two solvents. DCB in THF, photo-excited at 266 nm, exhibits a time constant of 625 ps (Fig. S14, ESI†) compared to 550 ps reported for DCB in MeOH.1 The time constant is assigned to the S1 decay of DCB and the concomitant population of its T1 state. An estimate of the triplet quantum yield of DCB in THF ϕTHFT is conducted by comparing the transient absorption at time zero due to the S1 (ΔAS1) and the transient absorption of the triplet state (ΔAT1) at ∼3.1 ns, when only the T1 state contributes to the signal. This determination of the yield ϕTHFT rests on the assumption that the difference absorption coefficients of S1 and T1 states are not affected by the solvent. This assumption is supported by the observation that the absorption spectra exhibit only minor changes in the ground state.1 The triplet quantum yield was calculated using eqn (7),
990 cm−1 (3.47 eV) in the solid state61 (higher in energy than the S1 states of all NMAs) and a high triplet quantum yield in methanol solution (ϕMeOHT = 0.96).62 However, the triplet quantum yield of DCB in THF is not known. It is assumed that due to its symmetrical nonpolar nature, the molecule interacts only weakly with its surroundings, resulting in the energy of states remaining nearly unchanged. A comparison of fsTA measurements of DCB in methanol and in THF reveals that the spectral signatures are very similar in the two solvents. DCB in THF, photo-excited at 266 nm, exhibits a time constant of 625 ps (Fig. S14, ESI†) compared to 550 ps reported for DCB in MeOH.1 The time constant is assigned to the S1 decay of DCB and the concomitant population of its T1 state. An estimate of the triplet quantum yield of DCB in THF ϕTHFT is conducted by comparing the transient absorption at time zero due to the S1 (ΔAS1) and the transient absorption of the triplet state (ΔAT1) at ∼3.1 ns, when only the T1 state contributes to the signal. This determination of the yield ϕTHFT rests on the assumption that the difference absorption coefficients of S1 and T1 states are not affected by the solvent. This assumption is supported by the observation that the absorption spectra exhibit only minor changes in the ground state.1 The triplet quantum yield was calculated using eqn (7),
 | (7) |
For the sensitization experiment, deoxygenated solutions containing DCB and the NMAs were excited using 266 nm laser pulses, which corresponds to the lowest energy absorption of DCB. An exclusive excitation of the sensitizer is not possible because the absorption band of DCB overlaps with higher absorption bands of the emitters (cf.Fig. 3). With a gated CCD camera, the emission of the NMAs induced by the laser was monitored. The fluorescence emission of DCB and all NMAs are spectrally well separated (cf.Fig. 3). The time dependence of the NMAs emission was characterized based on spectral integrals. These cover the range of the NMAs steady state emissions. The resulting time traces were plotted using a log–log representation (Fig. 6). For all the NMAs studied, in absence of DCB, a decay on the 1–10 ns time scale as well as one with a characteristic time of ∼1 μs is observed. The latter one, has an amplitude three orders of magnitude smaller than the first one. Spectral signatures of both components match the ones of steady state fluorescence spectroscopy. A single exponential fit of the prompt fluorescence decay accounting for the instrumental response time (∼10 ns) yields time constants of 2.49 ± 0.08 ns for NMA, 11.1 ± 0.02 ns for NMA-dF, 14.5 ± 0.15 ns for NMA-OMeF and 16.1 ± 0.01 ns for NMA-dOMe. These time constants for the substituted NMAs are in very good agreement with the TCSPC results discussed earlier. Minor discrepancies can be explained by the long IRF time (∼10 ns) compared to the observed decay time. Fits of the second decay component afforded lifetimes of 726 ± 26 ns for NMA, 877 ± 13 ns for NMA-dF, 1056 ± 31 ns for NMA-OMeF and 1780 ± 55 ns for NMA-dOMe. Following the reasoning for thioxanthone1 and NMA-dF in methanol,2 this decay component is assigned to triplet–triplet annihilation (TTA). In the weak depletion limit,63 the time constant τTTA determined via time-resolved fluorescence spectroscopy ought to be half of the respective triplet lifetime τT, i.e.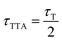 .63 For an exemplary NMA (NMA-OMeF), the triplet lifetime τT was determined by nanosecond transient absorption measurements. The measurement afforded an intrinsic decay of kNMA-OMeF0 = 5.39 × 105 ± 1.38 × 104 s−1 and a self-quenching constant of kNMA-OMeFq = 6.38 × 108 ± 1.09 × 108 M−1 s−1 (cf. Fig. S15, left, ESI†). For the concentration employed in the sensitization experiment (0.29 mM), this translates into a lifetime τT of 1.38 ± 0.1 μs. From the lifetime τTTA one would expect a similar triplet lifetime τT of 2.1 ± 0.06 μs. Presumably, the triplet lifetime τT deduced from the nanosecond transient absorption measurements is more reliable since more data points contribute to its evaluation.
.63 For an exemplary NMA (NMA-OMeF), the triplet lifetime τT was determined by nanosecond transient absorption measurements. The measurement afforded an intrinsic decay of kNMA-OMeF0 = 5.39 × 105 ± 1.38 × 104 s−1 and a self-quenching constant of kNMA-OMeFq = 6.38 × 108 ± 1.09 × 108 M−1 s−1 (cf. Fig. S15, left, ESI†). For the concentration employed in the sensitization experiment (0.29 mM), this translates into a lifetime τT of 1.38 ± 0.1 μs. From the lifetime τTTA one would expect a similar triplet lifetime τT of 2.1 ± 0.06 μs. Presumably, the triplet lifetime τT deduced from the nanosecond transient absorption measurements is more reliable since more data points contribute to its evaluation.
The addition of DCB to the solutions results in a decrease of the initial emission signal. This is expected because less emitter molecules are excited due to the inner filter effect of DCB. For NMA, no significant differences from 10 ns onwards are observed. The observation that the signal levels after ∼10 ns are very similar suggests that triplet energy transfer between DCB and NMA occurs and is followed by TTA. For the NMA derivates, stronger signals from ∼100 ns until ∼1000 ns are observed in presence of DCB compared to emitter only measurements. The emission spectra observed during that period are identical to the ones for prompt fluorescence (Fig. S16, ESI†). This gives clear-cut evidence for an energy transfer (EET) between excited DCB and the NMAs. The time scale of this EET excludes a singlet–singlet mechanism as the DCB S1 lifetime amounts to only 625 ps in THF. Therefore, the triplet states of DCB have to be involved in the EET. Single exponential fits of the additional components afforded time constants (τSens) of 420 ± 8 ns for NMA-dF, 321 ± 2 ns for NMA-OMeF and 407 ± 3 ns for NMA-dOMe. At even longer delay times the decay matches the TTA from the emitter only solutions. There are no signs for an enhanced TTA due to the energy transfer.
The measured time constants τSens ought to relate to rate constants according to eqn (8),
 | (8) |
 via nanosecond transient absorption spectroscopy. Like in methanol,2 DCB in THF exhibits no significant concentration quenching (Fig. S15, right, ESI†). Using the time constants τSens determined from the results in Fig. 6 and eqn (8) the following quenching constants kq result: kNMA-dFq = 3.31 × 109 M−1 s−1, kNMA-OMeFq =5.65 × 109 M−1 s−1, and kNMA-dOMeq = 3.40 × 109 M−1 s−1. The experimentally determined values are close to the diffusion-limited rate constant (1.3 × 1010 M−1 s−1 in THF28). The efficiency η ≤ 1 for the transfer of DCB triplet excitation to emitted NMA photons can be evaluated following a procedure detailed in ref. 2. The procedure requires the fluorescence quantum yields for direct (φEmfl) and sensitized excitation (φSensitizedfl), as well as the fraction of excitation light absorbed by the emitter and the sensitizer. The quantum yields φEmfl and φSensitizedfl are proportional to the areas marked in Fig. 6. The procedure results in an efficiency of ηNMA−dF = 0.070, ηNMA−OMeF = 0.022 and ηNMA−dOMe = 0.037. By considering the triplet quantum yield (ϕTHFT = 0.76), the intrinsic decay constant of the T1 state of DCB kSens0 in THF, and the quenching constant times the corresponding emitter concentration, kq[Emitter], a transfer efficiency η∞ can be calculated. The efficiency η∞ quantifies the fraction of quenching events resulting in an S1 excitation of the emitter for an infinitely high emitter concentration. This efficiency amounts to ηNMA−dF∞ = 0.243, ηNMA−OMeF∞ = 0.055, and ηNMA−dOMe∞ = 0.122.
via nanosecond transient absorption spectroscopy. Like in methanol,2 DCB in THF exhibits no significant concentration quenching (Fig. S15, right, ESI†). Using the time constants τSens determined from the results in Fig. 6 and eqn (8) the following quenching constants kq result: kNMA-dFq = 3.31 × 109 M−1 s−1, kNMA-OMeFq =5.65 × 109 M−1 s−1, and kNMA-dOMeq = 3.40 × 109 M−1 s−1. The experimentally determined values are close to the diffusion-limited rate constant (1.3 × 1010 M−1 s−1 in THF28). The efficiency η ≤ 1 for the transfer of DCB triplet excitation to emitted NMA photons can be evaluated following a procedure detailed in ref. 2. The procedure requires the fluorescence quantum yields for direct (φEmfl) and sensitized excitation (φSensitizedfl), as well as the fraction of excitation light absorbed by the emitter and the sensitizer. The quantum yields φEmfl and φSensitizedfl are proportional to the areas marked in Fig. 6. The procedure results in an efficiency of ηNMA−dF = 0.070, ηNMA−OMeF = 0.022 and ηNMA−dOMe = 0.037. By considering the triplet quantum yield (ϕTHFT = 0.76), the intrinsic decay constant of the T1 state of DCB kSens0 in THF, and the quenching constant times the corresponding emitter concentration, kq[Emitter], a transfer efficiency η∞ can be calculated. The efficiency η∞ quantifies the fraction of quenching events resulting in an S1 excitation of the emitter for an infinitely high emitter concentration. This efficiency amounts to ηNMA−dF∞ = 0.243, ηNMA−OMeF∞ = 0.055, and ηNMA−dOMe∞ = 0.122.
Quantum chemical computations on NMA, NMA-dF, NMA-OMeF, and NMA-dOMe in THF support the experimental results. The computations place the 0–0-energy of the S1 state (1ππ*) for NMA at 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 (3.19 eV), NMA-dF at 24
700 cm−1 (3.19 eV), NMA-dF at 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 (3.05 eV), NMA-OMeF at 24
600 cm−1 (3.05 eV), NMA-OMeF at 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (2.98 eV) and for NMA-dOMe at 22
000 cm−1 (2.98 eV) and for NMA-dOMe at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 (2.83 eV). Radiative rate constants of kNMArad = 6.98 × 107 s−1 (oscillator strength of 0.15816), kNMA−dFrad = 6.90 × 107 s−1 (oscillator strength of 0.17209), kNMA-OMeFrad = 6.24 × 107 s−1 (oscillator strength of 0.16804) and kNMA-dOMerad = 5.56 × 107 s−1 (oscillator strength of 0.16251) were computed. All those computed values are in good agreement with the experimental ones (cf.Tables 1 and 2). The 0–0-energy of the T1 state (3ππ*) are calculated to be 20
800 cm−1 (2.83 eV). Radiative rate constants of kNMArad = 6.98 × 107 s−1 (oscillator strength of 0.15816), kNMA−dFrad = 6.90 × 107 s−1 (oscillator strength of 0.17209), kNMA-OMeFrad = 6.24 × 107 s−1 (oscillator strength of 0.16804) and kNMA-dOMerad = 5.56 × 107 s−1 (oscillator strength of 0.16251) were computed. All those computed values are in good agreement with the experimental ones (cf.Tables 1 and 2). The 0–0-energy of the T1 state (3ππ*) are calculated to be 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 (2.55 eV) for NMA, 19
600 cm−1 (2.55 eV) for NMA, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 (2.37 eV) for NMA-dF, 18
100 cm−1 (2.37 eV) for NMA-dF, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 (2.28 eV) for NMA-OMeF, and 17
400 cm−1 (2.28 eV) for NMA-OMeF, and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 (2.17 eV) for NMA-dOMe. The energy gaps between the bright S1 states and the T1 states are of the order of ∼5300 cm−1 (0.66 eV) excluding a role of the T1 state in thermally activated delayed fluorescence. All the NMAs feature an upper triplet state Tn with 3nπ* character which is close in energy to the S1 state (1ππ*). While the energies of the ππ* states are lowered by up to ∼3000 cm−1 (0.37 eV) by the introduction of the substituents, the energies of the nπ* states remain almost constant. For the vertical excitation energies at different geometries, see Tables S2–S5 (ESI†). The associated molecular orbitals are shown in Fig. S17–S20 (ESI†).
500 cm−1 (2.17 eV) for NMA-dOMe. The energy gaps between the bright S1 states and the T1 states are of the order of ∼5300 cm−1 (0.66 eV) excluding a role of the T1 state in thermally activated delayed fluorescence. All the NMAs feature an upper triplet state Tn with 3nπ* character which is close in energy to the S1 state (1ππ*). While the energies of the ππ* states are lowered by up to ∼3000 cm−1 (0.37 eV) by the introduction of the substituents, the energies of the nπ* states remain almost constant. For the vertical excitation energies at different geometries, see Tables S2–S5 (ESI†). The associated molecular orbitals are shown in Fig. S17–S20 (ESI†).
| Energies/cm−1 | S1 (1ππ*) | S2 (1nπ*) | T1 (3ππ*) | T2 (3nπ*) | T3 (3ππ*) | |
|---|---|---|---|---|---|---|
| NMA | Adiabatic | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
|
| 0–0 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
||
| NMA-dF | Adiabatic | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
|
| 0–0 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
||
| NMA-OMeF | Adiabatic | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
|
| 0–0 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
||
| NMA-dOMe | Adiabatic | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
| 0–0 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
All Tn (n = 2) energies are smaller than 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 cm−1 (3.47 eV, triplet energy of DCB61) indicating that EET from DCB is energetically feasible. Once the Tn (n = 2) state is populated, for HIGHrISC to be relevant, the rate constants of the rISC process (krISC) must be at least of a similar magnitude as the rate constants of the competing T2 → T1 IC process (kIC). Thus, the relevant rate constants were computed using the generating function approach,54,55 the results are compiled in Table 3. The spin–orbit coupling (SOC) matrix elements entering the expression for the (r)ISC rate constants are in the range of ∼10 to 17 cm−1. This is substantially lower than the value of 154 cm−1 for atomic oxygen.28 The oxygen atom of the carbonyl moiety is mostly responsible for the SOC. As other atoms contribute to the relevant MOs (n and π*), its contribution is “diluted”.64 For all compounds, except NMA, rate constants for rISC and IC of the order of 1010–1011 s−1 were calculated. For, e.g., NMA-dOMe, the rate constant of rISC is by a factor of 3.8 higher than the one of IC. So, according to this computation rISC is favored over IC in NMA-dOMe. However, for a proper interpretation of the results, the (small) discrepancies between experimental and computational excited state energies need to be considered (see Discussion).
987 cm−1 (3.47 eV, triplet energy of DCB61) indicating that EET from DCB is energetically feasible. Once the Tn (n = 2) state is populated, for HIGHrISC to be relevant, the rate constants of the rISC process (krISC) must be at least of a similar magnitude as the rate constants of the competing T2 → T1 IC process (kIC). Thus, the relevant rate constants were computed using the generating function approach,54,55 the results are compiled in Table 3. The spin–orbit coupling (SOC) matrix elements entering the expression for the (r)ISC rate constants are in the range of ∼10 to 17 cm−1. This is substantially lower than the value of 154 cm−1 for atomic oxygen.28 The oxygen atom of the carbonyl moiety is mostly responsible for the SOC. As other atoms contribute to the relevant MOs (n and π*), its contribution is “diluted”.64 For all compounds, except NMA, rate constants for rISC and IC of the order of 1010–1011 s−1 were calculated. For, e.g., NMA-dOMe, the rate constant of rISC is by a factor of 3.8 higher than the one of IC. So, according to this computation rISC is favored over IC in NMA-dOMe. However, for a proper interpretation of the results, the (small) discrepancies between experimental and computational excited state energies need to be considered (see Discussion).
| Rate constants/s−1 | NMA | NMA-dF | NMA-OMeF | NMA-dOMe |
|---|---|---|---|---|
| k rISC 3nπ*→ 1ππ* | 1.30 × 109 | 8.80 × 1010 | 4.80 × 1010 | 5.08 × 1010 |
| k ISC 1ππ*→ 3nπ* | 3.18 × 1010 | 7.49 × 1010 | 4.85 × 108 | 1.51 × 106 |
| k IC 3nπ*→ 3ππ* | 2.61 × 1011 | 6.45 × 1010 | 3.67 × 1010 | 1.35 × 1010 |
Discussion
As the orbital diagrams in Fig. 1 suggest, decorating NMA at position 2 and/or 7 with +M substituents lowers the 1ππ* excitation energies. In steady state spectroscopy, red shifts of 0–0 energies of up to ∼2200 cm−1 (0.27 eV) are observed (cf.Table 1 and Fig. 3). The trend in 0–0 energies inferred from spectroscopy is well reproduced by quantum chemistry (cf.Tables 1 and 2). The lowering of the 1ππ* state shifts the emission of the substituted NMAs to the deep blue region. The L’Eclairage (CIE) coordinates of all emitters are located at the bottom left of the CIE chromaticity diagram (cf.Fig. 7). The CIE coordinates of the NMAs are already close to the one of the standard for deep blue emitters (0.14, 0.08) as set by the National Television System Committee (NTSC 1987).26 However, it is important to note that the CIE coordinates of the emitters were determined in solution and not in an OLED.The reduction of the 1ππ* energy goes along with a substantial increase of the fluorescence quantum yield ϕfl. For NMA a value of 0.11 was determined, for NMA-dOMe it is as high as 0.84 (cf.Fig. 4). This indicates that non-radiative decay channels involving nπ* states are suppressed. The quantum chemical computations corroborate this trend. In the computations, +M substitutions at positions 2 and 7 leave nπ*energies essentially untouched (cf.Fig. 8, red circles). This finding is in line with a qualitative consideration based on the molecular orbitals (cf.Fig. 1). The π*-orbital of NMA has nodes at these positions and the n-orbital features no electron density here. As the nπ* states retain their energies upon substitution and ππ* states are lowered, for all substituted derivatives studied, the 1ππ* state is below the 1,3nπ* ones. Accordingly, the fluorescence quantum yields ϕfl increase and the non-radiative rate constants decrease (cf.Table 1 and Fig. 8).
However, according to the quantum chemistry for NMA, the 1nπ* state is seen to be 400 cm−1 above the 1ππ* one and the 3nπ* – 700 cm−1 below this state (see Fig. 8). The experiment suggests that the computation places the nπ* energies slightly too low. The analysis of the early SE decay (cf.Fig. 5) places the 3nπ* state slightly (by 350–380 cm−1) above the 1ππ* one. Due to this discrepancy, the computation predicts a small fluorescence quantum yield  of 0.003 instead of the measured 0.11. Interestingly, measured and calculated time constants τeq for the equilibration between the S1 and the T2 state are very close despite this discrepancy. The value of τeq derived from the computed rate constants via
of 0.003 instead of the measured 0.11. Interestingly, measured and calculated time constants τeq for the equilibration between the S1 and the T2 state are very close despite this discrepancy. The value of τeq derived from the computed rate constants via 65 amounts to 30 ps which compares very favorably with the experimental value of 22 ps. As shown in the ESI† (Fig. S21), for small values of the energy gap ΔES1T2, the time constant τeq is rather insensitive to ΔES1T2. As one shifts the T2 state from small energies towards the S1 state, the rate constant kISC decreases and the rate constant krISC increases leaving kISC + krISC and thereby τeq nearly constant. The calculated rate constants suggest a rapid equilibration between the S1 state and T2 state for all NMAs. For the substituted NMAs, however, no early decay of the SE traces is discernible suggesting that the 3nπ* states are too high in energy for a detectable depletion of the 1ππ* state due to equilibration. The small equilibrium population of the 3nπ* state in the derivatives renders IC from 3nπ* to 3ππ* state inefficient. All this indicates that the substitutions – particularly by methoxy groups – turn NMA also in an aprotic environment into an excellent singlet emitter.
65 amounts to 30 ps which compares very favorably with the experimental value of 22 ps. As shown in the ESI† (Fig. S21), for small values of the energy gap ΔES1T2, the time constant τeq is rather insensitive to ΔES1T2. As one shifts the T2 state from small energies towards the S1 state, the rate constant kISC decreases and the rate constant krISC increases leaving kISC + krISC and thereby τeq nearly constant. The calculated rate constants suggest a rapid equilibration between the S1 state and T2 state for all NMAs. For the substituted NMAs, however, no early decay of the SE traces is discernible suggesting that the 3nπ* states are too high in energy for a detectable depletion of the 1ππ* state due to equilibration. The small equilibrium population of the 3nπ* state in the derivatives renders IC from 3nπ* to 3ππ* state inefficient. All this indicates that the substitutions – particularly by methoxy groups – turn NMA also in an aprotic environment into an excellent singlet emitter.
Of course, for OLED applications an emitter should also “process” triplet excitations. The sensibilization experiments give clear evidence that in all substituted NMA derivatives, HIGHrISC is operative. Triplet excited DCB was shown to transfer excitation energy to the studied acridones. This transfer results in an additional fluorescence emission. Thus, rISC from an NMA triplet to the 1ππ* state has to occur. As the lowest triplet state (3ππ*) of all NMAs is by more than −5000 cm−1 (−0.6 eV) lower in energy than the 1ππ* state (cf.Table 2), the El-Sayed-forbidden rISC from this state can be ruled out safely. This implies that rISC from a higher triplet state (3nπ*) – HIGHrISC is operative. The efficiencies η∞ = 0.24, 0.06, and 0.12 for this process are below one.
Two loss channels are conceivable (see also discussion in ref. 2). (i) During the EET between triplet excited DCB and the NMAs, instead of a selective population of the 3nπ* state, competing transfer to the 3ππ* could be possible. At present, we do not see an experimental approach to quantify the ratio of the EET processes. A computational study by Penfold et al.66 (on thioxanthone and DCB) has shown that the electronic couplings favor an EET to the T1 (3ππ*) state over an EET to the T2 (3nπ*) state. This was attributed to the more delocalized character of the molecular orbitals in the former case. In contrast, the Franck–Condon weighted density of states approximated by a Marcus expression can facilitate the transfer to the T2 state. The substituted NMAs feature lower 3ππ* energies than NMA itself. Therefore, the transfer to the T1 state is expected to lie in the Marcus-inverted region66 which lowers its rate constant. Concomitantly, the efficiency for an EET to the 3nπ* state should rise. Thus, a sizable population of the T2 state or even its preferential population is plausible. (ii) Alternatively, the loss could be due to an IC process between the 3nπ* and the 3ππ* state competing with the rISC transition (see Fig. 1). For NMA the computations suggest that kIC is two orders of magnitude larger than krISC (Fig. 8). This could explain the absence of the component τSens in the experiment on NMA (see Fig. 6). For the substituted NMAs the increase of the energy gap (ΔETT) between the T2 state and T1 state leads to a decrease of kIC (Fig. 8). The behavior is in line with the energy gap law7,67 and/or a Marcus inverted behavior.68 The rate constants krISC and kIC have the same order of magnitude and both processes can compete with each other. Quantum chemical computations on NMA-dF in methanol2 suggest that both loss mechanisms ((i) and (ii)) might be operative. Regardless of the exact nature of the loss channels, the calculations support the assignment of the experimentally observed sensitized emission to HIGHrISC.
Conclusion
This study has shown that the parent compound NMA is not a suitable OLED emitter due to its low fluorescence quantum yield and inability to convert triplet excitons into light in an aprotic environment (such as THF solution). Regarding the use of NMA-dF, NMA-OMeF and NMA-dOMe as deep blue emitters in an OLED, this study has shown that these chromophores can convert both singlet and triplet excitons into light. If the substituted NMA derivative receives energy from a singlet-correlated electron–hole pair, its S1 state efficiently emits photons with a high fluorescence quantum yield (ϕfl = 0.7–0.84) and a short fluorescence lifetime (τ ≈ 11–15 ns). If energy is transferred from a triplet-correlated electron–hole pair, resulting in the population of Tn states, the excitons are converted into photons via rISC from the Tn to the emissive S1 state. However, if the excitation reaches the T1 state, the energy is lost. If the triplet energy is transferred from the host to the emitter by a triplet–triplet energy transfer (as described in ref. 69), the success of the HIGHrISC emitter depends on the choice of a suitable host. The host should be therefore designed in such a way that a predominant transition to the Tn state is achieved.Author contributions
Matthias Jantz, David Klaverkamp conceived, designed, conducted, and analyzed the experiments. Lennart Bunnemann helped design the structural motive of NMA-OMeF and NMA-dOMe. Furthermore, he performed the synthesis and characterization of NMA-OMeF and NMA-dOMe. Martin Kleinschmidt conducted the quantum chemical calculations. Constantin Czekelius synthesized and characterized NMA-dF. Constantin Czekelius and Peter Gilch did the conceptualization, supervision, funding acquisition, composition, and editing of the manuscript together.Data availability
The data that supports the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support by the Deutsche Forschungsgemeinschaft (396890929/GRK2482, “ModISC”) is gratefully acknowledged. Matthias Jantz and David Klaverkamp are grateful for Kekulé scholarships donated by the Fonds der Chemischen Industrie. Thanks to the CeMSA@HHU (Center for Molecular and Structural Analytics @ Heinrich Heine University) for recording the NMR-spectroscopic data. We thank our former bachelor, and master students Lea Hülsmann, Elias Sentob, and Vivienne Laureen Wuttke for their experimental support.References
- C. Torres Ziegenbein, S. Fröbel, M. Glöβ, R. S. Nobuyasu, P. Data, A. Monkman and P. Gilch, ChemPhysChem, 2017, 18, 2314–2317 CrossRef CAS PubMed.
- K. A. Thom, F. Wieser, K. Diestelhorst, A. Reiffers, C. Czekelius, M. Kleinschmidt, M. Bracker, C. M. Marian and P. Gilch, J. Phys. Chem. Lett., 2021, 12, 5703–5709 CrossRef CAS PubMed.
- Y. Pan, W. Li, S. Zhang, L. Yao, C. Gu, H. Xu, B. Yang and Y. Ma, Adv. Opt. Mater., 2014, 2, 510–515 CrossRef CAS.
- Y. Xu, P. Xu, D. Hu and Y. Ma, Chem. Soc. Rev., 2021, 50, 1030–1069 RSC.
- J. Wang, A. Chepelianskii, F. Gao and N. C. Greenham, Nat. Commun., 2012, 3, 1191 CrossRef PubMed.
- M. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- P. Klán and J. Wirz, Photochemistry of organic compounds: from concepts to practice, John Wiley & Sons, 2009 Search PubMed.
- B. Heinz, B. Schmidt, C. Root, H. Satzger, F. Milota, B. Fierz, T. Kiefhaber, W. Zinth and P. Gilch, Phys. Chem. Chem. Phys., 2006, 8, 3432–3439 RSC.
- M. Siegmund and J. Bendig, Berichte der Bunsengesellschaft für physikalische Chemie, 1978, 82, 1061–1068 CrossRef CAS.
- J. Meissner, B. Kosper, C. M. Marian and R. Weinkauf, J. Phys. Chem. A, 2021, 125, 8777–8790 CrossRef CAS PubMed.
- R. Mundt, T. Villnow, C. T. Ziegenbein, P. Gilch, C. Marian and V. Rai-Constapel, Phys. Chem. Chem. Phys., 2016, 18, 6637–6647 RSC.
- M. El-Sayed, J. Chem. Phys., 1964, 41, 2462–2467 CrossRef CAS.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- V. Rai-Constapel and C. M. Marian, RSC Adv., 2016, 6, 18530–18537 RSC.
- M. Lv, X. Wang, H. Pan and J. Chen, J. Phys. Chem. B, 2021, 125, 13291–13297 CrossRef CAS PubMed.
- M. Siegmund and J. Bendig, Z. Naturforsch., A, 1980, 35, 1076–1086 Search PubMed.
- M. Ito, K. Inuzuka and S. Imanishi, J. Am. Chem. Soc., 1960, 82, 1317–1322 CrossRef CAS.
- T. Haldar and S. Bagchi, J. Phys. Chem. Lett., 2016, 7, 2270–2275 CrossRef CAS PubMed.
- K. A. Thom, PhD thesis, Heinrich-Heine-Universität Düsseldorf, 2021 Search PubMed.
- M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444 CrossRef PubMed.
- T. Chatterjee and K. T. Wong, Adv. Opt. Mater., 2019, 7, 1800565 CrossRef.
- F. Rodella, R. Saxena, S. Bagnich, D. Banevičius, G. Kreiza, S. Athanasopoulos, S. Juršėnas, K. Kazlauskas, A. Köhler and P. Strohriegl, J. Mater. Chem. C, 2021, 9, 17471–17482 RSC.
- D. Streets and G. P. Ceasar, Mol. Phys., 1973, 26, 1037–1052 CrossRef CAS.
- B. Milián Medina, D. Beljonne, H.-J. Egelhaaf and J. Gierschner, J. Chem. Phys., 2007, 126, 111101 CrossRef PubMed.
- S. Abou-Hatab, V. A. Spata and S. Matsika, J. Phys. Chem. A, 2017, 121, 1213–1222 CrossRef CAS PubMed.
- D. R. W. G. Hunt, The N.T.S.C. and Similar Systems of Colour Television, 2004 Search PubMed.
- M. B. Smith, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, John Wiley & Sons, 2020 Search PubMed.
- M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, CRC Press, Boca Raton, 2006 Search PubMed.
- E. Skuodis, O. Bezvikonnyi, A. Tomkeviciene, D. Volyniuk, V. Mimaite, A. Lazauskas, A. Bucinskas, R. Keruckiene, G. Sini and J. V. Grazulevicius, Org. Electron., 2018, 63, 29–40 Search PubMed.
- K. Rurack and M. Spieles, Anal. Chem., 2011, 83, 1232–1242 CrossRef CAS PubMed.
- J. Lakowicz, Principles of fluorescence spectroscopy, Springer, New York, 2006 Search PubMed.
- G. Angulo, G. Grampp and A. Rosspeintner, Spectrochim. Acta, Part A, 2006, 65, 727–731 CrossRef PubMed.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- W. W. Parson, Modern optical spectroscopy, Springer, Berlin, 2007 Search PubMed.
- W. R. Roberts, T. N. Rohrabaugh and R. M. O'Donnell, J. Visualized Exp., 2021, e62425 Search PubMed.
- S. Fröbel, L. Buschhaus, T. Villnow, O. Weingart and P. Gilch, Phys. Chem. Chem. Phys., 2015, 17, 376–386 RSC.
- M. Lorenc, M. Ziolek, R. Naskrecki, J. Karolczak, J. Kubicki and A. Maciejewski, Appl. Phys. B, 2002, 74, 19–27 CrossRef CAS.
- H. Satzger and W. Zinth, Chem. Phys., 2003, 295, 287–295 CrossRef CAS.
- T.-O. Peulen, O. Opanasyuk and C. A. Seidel, J. Phys. Chem. B, 2017, 121, 8211–8241 CrossRef CAS PubMed.
- T. Villnow, PhD thesis, Heinrich-Heine-Universität Düsseldorf, 2015 Search PubMed.
- T. Jones, N. Monakhova, F. Guivel-Benhassine, A. Lepioshkin, T. Bruel, T. R. Lane, O. Schwartz, A. C. Puhl, V. Makarov and S. Ekins, ACS Omega, 2023, 8, 40817–40822 Search PubMed.
- P. Kancharla, R. A. Dodean, Y. Li, S. Pou, B. Pybus, V. Melendez, L. Read, C. E. Bane, B. Vesely, M. Kreishman-Deitrick, C. Black, Q. Li, R. Sciotti, R. Olmeda, T.-L. Luong, H. Gaona, B. Potter, J. Sousa, S. Marcsisin and J. Kelly, J. Med. Chem., 2020, 63, 6179–6202 Search PubMed.
- Y. Maegawa, N. Mizoshita, T. Tani and S. Inagaki, J. Mater. Chem., 2010, 20, 4399–4403 RSC.
- A. Joshi-Pangu, F. Lévesque, H. G. Roth, S. F. Oliver, L.-C. Campeau, D. Nicewicz and D. A. DiRocco, J. Org. Chem., 2016, 81, 7244–7249 Search PubMed.
- E. Hamzehpoor, C. Ruchlin, Y. Tao, J. E. Ramos-Sanchez, H. M. Titi, G. Cosa and D. F. Perepichka, J. Phys. Chem. Lett., 2021, 12, 6431–6438 Search PubMed.
- A. Vichet, A.-M. Patellis, J.-P. Galy, A.-M. Galy, J. Barbe and J. Elguero, J. Org. Chem., 1994, 59, 5156–5161 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- I. Lyskov, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2016, 144, 034104 CrossRef PubMed.
- M. Kleinschmidt, J. Tatchen and C. M. Marian, J. Comput. Chem., 2002, 23, 824–833 CrossRef CAS PubMed.
- M. Kleinschmidt and C. M. Marian, Chem. Phys., 2005, 311, 71–79 CrossRef CAS.
- M. Bracker, C. M. Marian and M. Kleinschmidt, J. Chem. Phys., 2021, 155, 014102 CrossRef CAS PubMed.
- M. Etinski, V. Rai-Constapel and C. M. Marian, J. Chem. Phys., 2014, 140, 114104 CrossRef PubMed.
- M. Etinski, J. Tatchen and C. M. Marian, J. Chem. Phys., 2011, 134, 154105 CrossRef PubMed.
- T. Villnow, G. Ryseck, V. Rai-Constapel, C. Marian and P. Gilch, J. Phys. Chem. A, 2014, 118, 11696–11707 CrossRef CAS PubMed.
- B. Bagchi and B. Jana, Chem. Soc. Rev., 2010, 39, 1936–1954 RSC.
- A. Deshpande, A. Beidoun, A. Penzkofer and G. Wagenblast, Chem. Phys., 1990, 142, 123–131 CrossRef CAS.
- O. Peterson, J. Webb, W. McColgin and J. Eberly, J. Appl. Phys., 1971, 42, 1917–1928 CrossRef CAS.
- V. Rai-Constapel, S. Salzmann and C. M. Marian, J. Phys. Chem. A, 2011, 115, 8589–8596 CrossRef CAS PubMed.
- A. P. Marchetti and D. R. Kearns, J. Am. Chem. Soc., 1967, 89, 768–777 CrossRef CAS.
- Z. Alfassi and C. Previtali, J. Photochem., 1985, 30, 127–132 CrossRef CAS.
- S. M. Bachilo and R. B. Weisman, J. Phys. Chem. A, 2000, 104, 7711–7714 CrossRef CAS.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An Introduction, University Science Books, 2009 Search PubMed.
- V. Rai-Constapel, T. Villnow, G. Ryseck, P. Gilch and C. M. Marian, J. Phys. Chem. A, 2014, 118, 11708–11717 CrossRef CAS PubMed.
- T. Northey, T. Keane, J. Eng and T. Penfold, Faraday Discuss., 2019, 216, 395–413 RSC.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- Z. Murtaza, A. P. Zipp, L. A. Worl, D. Graff, W. E. Jones Jr, W. D. Bates and T. J. Meyer, J. Am. Chem. Soc., 1991, 113, 5113–5114 CrossRef CAS.
- T. Zhu and T. Van Voorhis, J. Phys. Chem. C, 2019, 123, 10311–10318 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04781h |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2025 |







