Exploring the origin of electron spin polarization in metal-containing chromophore–radical systems via multireference calculations

Abstract

The electron spin polarization (ESP) phenomenon in photoexcited chromophore–radical connected systems was analyzed by multireference electronic structure calculations. We focused on bpy-M-CAT-mPh-NN (bpy = 4,4′-di-tert-butyl-2,2′-bipyridine, M = Pt or Pd, CAT = 3-tert-butylcatecholate, mPh = meta-phenylene, and NN = nitronyl nitroxide) reported by Kirk et al., which is a connected system consisting of a donor–acceptor complex and a radical, and elucidated the mechanism behind the reversal of the sign of photoinduced ESP depending on the metal species. The low-lying electronic states of these molecules were revealed through the multireference theory, suggesting that the ligand-to-ligand charge-transfer states play a significant role. Additionally, several structural factors that influence the energies of the excited states were identified. To enhance our understanding of the ESP, we incorporated spin–orbit coupling as a direct transition term between excited states and explicitly considered its effects on the ESP. The results of evaluating transition rates through a transition simulation indicate that when the influence of spin–orbit coupling is significant, the sign of the ESP in the ground state can reverse. This novel ESP mechanism mediated by spin–orbit coupling may offer fundamental insights for designing molecules to precisely control electron distribution across multiple spin states.

---

1 Introduction

The electronic spin of molecules is an essential degree of freedom that can be chemically manipulated, and research in spintronics has attracted growing attention in recent years.¹ Electron spin polarization (ESP), a non-Boltzmann distribution of electrons among spin sublevels of a molecule, is a crucial phenomenon involving electronic spins, with significant applications in molecular magnetism, materials science, and quantum information science.^2–4 ESP has been extensively investigated in triplet molecules^5,6 and free radicals.^7,8 A prominent example is the ground triplet state of nitrogen-vacancy (NV) centers in diamonds.⁹ However, synthesizing functional molecules that utilize ESP is still challenging, as achieving the desired functionalities requires precise tuning of molecular structures.

Recently, a novel class of molecules have emerged as a potential source of ESP.¹⁰ These molecules are generally composed of an organic chromophore and a stable radical, covalently bonded through a linker^11–13 (Fig. 1(a)). Upon irradiation with light, the chromophore is excited, leading to the generation of an excited triplet chromophore. At this stage, the molecule contains three spins: an open-shell chromophore and a tethered radical. Excited states with multiple energy levels can emerge in a narrow energy range due to magnetic interactions, such as exchange interaction and zero-field splitting (ZFS), among three spins. As shown in Fig. 1(b), the molecule can exist in states such as “Trip-Quartet” and “Trip-Doublet”, where the chromophore triplet and the radical combine to form an overall quartet and doublet, respectively, as well as the “Sing-Doublet” state, which is an overall doublet formed by the chromophore singlet and the radical spin.

Fig. 1 (a) A simplified picture of the chromophore–radical connected system. (b) A schematic representation of multiple excited states and processes. EISC: enhanced intersystem crossing.

In 2021, Kirk et al. reported the synthesis and properties of an interesting connected system, bpy-M-CAT-mPh-NN (bpy = 4,4′-di-tert-butyl-2,2′-bipyridine, M = Pt or Pd, CAT = 3-tert-butylcatecholate, mPh = meta-phenylene, and NN = nitronyl nitroxide), which contains a metal atom in the chromophore¹⁴ (Fig. 2). These compounds consist of a donor (CAT)–acceptor (bpy) type complex¹⁵ and a stable NN radical¹⁶ connected by a m-phenylene linker. The authors assigned the absorption band of the molecules to the ligand-to-ligand charge transfer (LL′CT) excited state, which is characteristic of a donor–acceptor complex. In this process, a three-spin configuration of bpy˙ CAT˙ NN˙ is formed through the transfer of one electron from CAT to bpy. In this three-spin configuration, due to the exchange interaction between the chromophore and the radical, two doublet states (²T₁, ²S₁) and one quartet state (⁴T₁) are formed. This notation indicates that ²T₁ and ²S₁ represent the “Trip-Doublet” and the “Sing-Doublet” state, respectively, while ⁴T₁ corresponds to the “Trip-Quartet” state. Previous research¹⁷ has established that the exchange coupling between the chromophore and the radical is antiferromagnetic due to the cross-conjugated m-phenylene linker, thereby suggesting that the ²T₁ state is more stable than the ⁴T₁ state. It has also been proposed that the local excited (LE) states of the NN radical may exist in a region close to the LL′CT states.¹⁴ Measurements of low-temperature continuous wave-EPR (cw-EPR) and time-resolved EPR (TR-EPR) after photo-irradiation were performed, and ESP from the radical in the doublet ground state was observed in both bpy-Pt-CAT-mPh-NN and bpy-Pd-CAT-mPh-NN. Notably, the difference in the central metal changes the ground state ESP sign: it becomes absorptive for M = Pt and emissive for M = Pd. Furthermore, subsequent studies have shown that modifying the linker unit with methyl groups in Pt compounds (Fig. 2, right) affects both the sign and magnitude of photo-induced ESP.^18,19 These findings indicate that ESP can be controlled solely through methyl group modification, thereby providing valuable insights into the relationship between the chemical structure and ESP properties.

Fig. 2 Chemical structures of bpy-Pt-CAT-mPh-NN, bpy-Pd-CAT-mPh-NN and linker derivatives.

For such connected systems, the reversed quartet mechanism (RQM) has been proposed as a potential mechanism for ESP^20–22 (Fig. 3(a)). In the RQM, the generation of ESP begins with photo excitation of the molecule to the sing-doublet (²S₁) state and it efficiently transits to the trip-doublet (²T₁) state via radical-enhanced intersystem crossing (EISC).^23,24 Subsequently, spin-selective intersystem crossing induced by zero-field splitting (ZFS) occurs between the energetically proximate ²T₁ and ⁴T₁ states, resulting in the generation of ESP in the ²T₁ and ⁴T₁ states because the ISC rates are different for each spin sublevel.²⁵ This ESP is then transferred to the ground state, allowing the ground-state ESP to be observed by EPR measurements. One of the characteristics of the RQM is that the sign of the exchange interaction J between the chromophore and the radical influences the predicted sign of the ESP in the ground state. In the case of bpy-M-CAT-Linker-NN, the exchange interaction is expected to be antiferromagnetic for all complexes, leading to a prediction that the ground state ESP is emissive. However, experimentally, bpy-Pt-CAT-mPh-NN and many derivatives have been observed to exhibit ESP with the opposite sign, which cannot be explained by the RQM.

Fig. 3 Schematic diagrams of (a) reversed quartet mechanism (RQM) and (b) modified reversed quartet mechanism (mRQM).

Previous research has proposed the modified-reversed quartet mechanism (mRQM) as an extension of the RQM to explain the mechanism of ESP by focusing on the local excited states of the radical (Fig. 3(b)),¹⁹ in which intersystem crossing (ISC) between the low-energy quartet local excited (⁴LE) state and the ²T₁ state competes with the ⁴T₁–²T₁ ISC, thereby generating ESP with a dominant sign. Previous calculations with coupled cluster theory with single and double, and perturbative triple excitations (CCSD(T))¹⁴ indicate that local excited states of doublet and quartet character occur in an energy range close to that of the charge-transfer (CT) states (²T₁, ⁴T₁, ²S₁). However, T₁-diagnostic values²⁶ near 0.02 suggest that the systems exhibit moderate multireference character. Although CCSD(T) generally yields reliable results, given these T₁-diagnostic values, these results should be cross-checked. Furthermore, to the best of our knowledge, no reports on excited-state energy landscapes of connected molecules have been presented to date.

Motivated by these backgrounds, in this study, we performed detailed excited state calculations with multireference perturbation theory on a series of bpy-M-CAT-Linker-NN molecules. It was demonstrated that employing XMS-CASPT2²⁷ calculations enables the accurate computation of multiple excited states. Additionally, we investigated the influence of the molecular structures on the excitation energies. Through calculations and simulations of various spin properties, such as spin–spin coupling (SSC) and spin–orbit coupling (SOC), factors that could affect the sign and the magnitude of ESP were identified.

2 Computational details

In all calculations, model structures were employed with tertiary-butyl groups replaced by methyl groups to reduce computational cost. All geometry optimizations were performed with density functional theory (DFT) for the ground state using the ORCA 5.0 package.²⁸ The BP86 functional²⁹ and def2-TZVP basis set^30–32 were adopted with Stuttgart effective core potential (ECP) for the Pt (60 core electrons) and Pd (28 core electrons) atoms.³³ In addition, the resolution-of-the-identity approximation for the Coulomb integral (RI-J)³⁴ was utilized to enhance computational efficiency.

Several formalisms of the second order perturbation theory with the CASSCF reference wavefunctions (CASPT2) were considered for the excited state calculations, and it was found that only the extended multi-state CASPT2 (XMS-CASPT2) theory²⁷ can reproduce the experimental spectra (vide infra).

For the XMS-CASPT2 calculations, the second order Douglas–Kroll–Hess (DKH2) Hamiltonian^35–37 was used to consider relativistic effects. The ANO-RCC-TZP basis set^38,39 was applied to Pt and Pd, while DKH-def2-TZVPP⁴⁰ was used for nitrogen and oxygen, and DKH-def2-SVP⁴⁰ for carbon and hydrogen. Excited state calculations were accelerated by the RI-JK approximation⁴¹ for the Coulomb and exchange integrals. For the CASSCF calculations, active spaces with 13 electrons and 13 orbitals were employed (see Fig. S8–S13, ESI†). The active orbitals were chosen to include as many valence π orbitals as possible. The state-averaging (SA) method was used to calculate multiple excited states simultaneously, with eight doublet states and three quartet states computed with equal weighting. All excited state calculations were performed using the quantum chemistry program package ORZ.⁴²

For the spin–orbit coupling matrix elements (SOCME) calculations, a perturbative treatment was adopted. While scalar relativistic effects were handled with DKH2, the SOC contributions were evaluated using a first-order Douglas-Kroll (DK1) approximation, and the two-electron SOC terms were approximated using the flexible nuclear screening spin–orbit (FNSSO) method.⁴³ The SA-CASSCF reference wavefunctions were rotated by the unitary transformation that diagonalizes the effective Hamiltonian of XMS-CASPT2. The ZFS D-tensor was calculated by the method developed in our group,⁴⁴ in which we assume that the elements of the spin–spin coupling term in the effective Breit–Pauli Hamiltonian,

where g_e is the electron g-factor, μ_B is the Bohr magneton, α is the fine structure constant, Ŝ(i) is the spin operator of an electron i and r_ij is the distance between electrons i and j, equal to those of the ZFS Hamiltonian,

〈SM|Ĥ_ZFS|SM′〉 (4)

and the elements of the D-tensor are expressed aswhere k, l belong to the set {x, y, z} and d^kl_pqrs is the spin–spin coupling integralsand q_pqrs is the two-particle reduced density matrix,where the subscripts p, q, r, and s represent molecular orbitals.

The reference wave functions for the D-tensor calculations were obtained by the density matrix renormalization group (DMRG)-CASSCF theory,^45–47 which were performed using PySCF and BLOCK2 program packages.^48–51 In the DMRG-CASSCF calculations, the full π valence active spaces, including 22 electrons in 20 orbitals, were selected. We extracted initial active orbitals for each molecule using natural orbitals obtained from the diagonalization of an MP2 density matrix. As usual in DMRG-CASSCF calculations, all valence π orbitals were localized and manually ordered (Fig. S27, ESI†). In DMRG-CASSCF calculations, spin adaptation for the Ŝ² operator, as implemented in BLOCK2,⁵² was used. We applied the ANO-RCC-TZP basis set to Pt and Pd, the def2-TZVPP basis set to N and O, and the def2-SVP basis set to C and H to match the basis functions with those in the CASPT2 calculations as closely as possible. We tested various bond dimension values, ranging from 128 to 1024, and the convergence behavior of the DMRG wavefunction with respect to the bond dimension and its impact on the D tensor are discussed in the main text and the ESI.†

3 Results and discussion

3.1 Assessment of the accuracy of the multireference theories

In order to evaluate the accuracy of quantum chemical calculation methods for the low-lying excited states of the connected system, we performed CASSCF and CASPT2 calculations for the vertical excited (²S₁) state with various formulations and then compared the results with the previously reported experimental UV-Vis absorption spectra.¹⁴ To achieve an accurate description of multiple states of three-spin systems (²S₁, ²T₁, and ⁴T₁), we decided to employ multireference theories, such as CASSCF and CASPT2. This approach was necessary to avoid severe spin contamination and adequately account for the electron correlation.

Table 1 shows the comparison of the vertical excitation energies calculated by CASSCF and various CASPT2 methods with the experimental values (∼17 000 cm⁻¹). First, we found that CASSCF significantly underestimated the vertical excitation energy of ²S₁, likely because dynamical correlation plays an important role in this system. We also observed that the calculated excitation energy from CASSCF varied depending on the number of states considered in the state-averaging, although it was consistently underestimated. The results of the XMS-CASPT2 energies obtained by varying the number of states in the state-averaging are presented in Section 4 of the ESI.† The second-order correction by CASPT2 led to better predictions for the excitation energy. Although a significant error of 5000 cm⁻¹ remained with state-specific CASPT2 (SS-CASPT2),^53,54 the introduction of quasi-degenerate perturbation theory by multi-state CASPT2 (MS-CASPT2)⁵⁵ resulted in a marked improvement in calculation accuracy. Extended multi-state CASPT2 (XMS-CASPT2)²⁷ provided the closest value to the experimental one. The ²S₁ state is energetically close to the ²T₁ state, resulting in significant mixing between these states, which indicates that the elements of state mixing were accurately captured by (X)MS-CASPT2. In light of this result, we adopted the XMS-CASPT2 method as a reliable approach and conducted further calculations.

Table 1 Comparison of vertical excited (²S₁) energies calculated by several multireference methods

	CASSCF/cm^−1	SS-CASPT2/cm^−1	MS-CASPT2/cm^−1
bpy-Pt-CAT-mPh-NN	7480	11 961	14 934

---

	XMS-CASPT2/cm^−1	Experiment/cm^−1
bpy-Pt-CAT-mPh-NN	16 849	∼17 000

---

3.2 Low-lying excited states of bpy-M-CAT-Ph-NN with XMS-CASPT2 theory

To understand the nature of low-lying excited states, we performed the XMS-CASPT2 calculations for a series of bpy-M-CAT-mPh-NN (M = Pt, Pd), and Pt derivatives. As shown in Table 2, the XMS-CASPT2 calculations revealed that there are four characteristic excited states in the low-energy region (Fig. 4); three of which (²T₁, ⁴T₁, ²S₁) are dominated by charge-transfer between the donor (CAT) and the acceptor (bpy), and the other one (²LE) is primarily characterized by local excitation within the PhNN radical (Table 3). Additionally, we have provided their spin densities in the ESI,† to enhance the understanding of these excited states. Since the ²T₁ state appeared lower than the ⁴T₁ state in all compounds, it can be concluded that the exchange interaction between the triplet of those metal complexes and the radical is antiferromagnetic, which is consistent with the previous research.¹⁷ The ²LE state exists in a region close to the CT states, and in some species, Pt-2Me and Pt-6Me, it was predicted to be comparable to the ²S₁ state. The CT states of bpy-Pd appear approximately 2000 cm⁻¹ lower than the experimental value of 17 000 cm⁻¹. We could not resolve the discrepancy, which appears to be an error specific to the Pd species, because calculations for structures without a radical moiety also indicate that the excitation energy of the Pd species is lower than those of Pt molecules (see Section 7 of the ESI†).

Table 2 Excitation energies of the low-lying states calculated by XMS-CASPT2 theory. All structures were optimized for their ground states

	^2T1/cm^−1	^4T1/cm^−1	^2S1/cm^−1	^2LE/cm^−1
bpy-Pt	17 299	17 431	17 899	19 736
Pt-2Me	17 361	17 481	18 033	17 809
Pt-4Me	15 942	16 059	16 614	18 900
Pt-6Me	17 882	18 027	18 523	17 520
Pt-2,4,6Me	16 783	16 910	17 386	20 984
bpy-Pd	14 525	14 755	14 982	18 046

---

Fig. 4 Illustration of each low-lying excited state. The natural orbitals of the bpy-Pt-CAT-mPh molecule are shown. For each state, only the representative configurations of the wavefunctions that satisfy spin symmetry are depicted.

Table 3 CI Vector weights for the low-lying states calculated by XMS-CASPT2 theory. The CI vectors obtained from the preceding CASSCF calculations were rotated to diagnalize the effective Hamiltonian in the XMS-CASPT2 framework to correspond with the XMS-CASPT2 wavefunctions. The major Slater determinants contributing to each state are listed. The Slater determinants for the ground state (²S₀) and LL′CT states represent, from left to right, the LUMO, SOMO, and HOMO of the entire molecule. In contrast, only the Slater determinant for the ²LE state represents the LUMO, SOMO, and HOMO localized on the radical (see Fig. 4)

	^2S0	^2T1			^4T1	^2S1		^2LE
	|02α〉	|αβα〉	|ααβ〉	|βαα〉	|ααα〉	|ααβ〉	|βαα〉	|02α〉	|α02〉
bpy-Pt	0.75590	0.50456	0.09584	0.16060	0.76118	0.40642	0.34147	0.36109	0.29917
Pt-2Me	0.75049	0.48034	0.04825	0.22410	0.75481	0.44114	0.26487	0.33733	0.33206
Pt-4Me	0.77010	0.52227	0.10282	0.16163	0.78697	0.41448	0.35536	0.38297	0.31177
Pt-6Me	0.75843	0.46823	0.04095	0.23223	0.74437	0.44371	0.25029	0.28027	0.34131
Pt-2,4,6Me	0.79884	0.52660	0.13711	0.12630	0.79008	0.38326	0.39408	0.33919	0.27817
bpy-Pd	0.77450	0.51843	0.09324	0.17195	0.78390	0.42602	0.34700	0.39504	0.32349

---

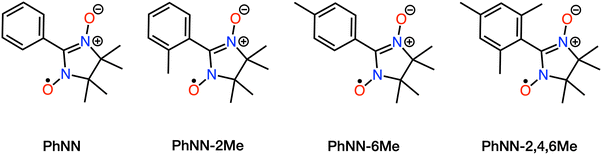
The ⁴LE state, which is the key state of mRQM and assumed to lie below the CT states in the previous study,¹⁴ did not appear in the low energy region in the multireference calculations for the series of bpy-M-CAT-Linker-NN molecules. To estimate the excitation energy of the ⁴LE state, we performed additional CASPT2 calculations on the phenyl nitronyl nitroxide (PhNN) radical¹⁶ and its derivatives (Fig. 5), with the structures extracted from the bpy-M-CAT-Linker-NN system (Tables 4 and 5). While CCSD(T) calculations for the PhNN molecule have been previously reported,¹⁴ it has also been reported that the T₁-diagnostic²⁶ value is high and almost 0.02, which suggests the applicability of the single-reference theory is unclear and the multireference correlation theory, such as CASPT2, should be more appropriate. We also carried out recalculations using CCSD(T) and CCSD for the excited states of PhNN, and as a result, our findings support the possibility that the CCSD level of theory underestimates the excitation energy of PhNN (see section 13 of the ESI†). Additionally, by quantifying the multireference character using mutual information—a measure of the degree of electron correlation between orbitals—we obtained a maximum values of 0.3, indicating that the inclusion of static electron correlation is essential.^56–58 Although the ⁴LE state is expected to be single-configurational in terms of its electron configuration, these results indicate that CASPT2 calculations are valuable to characterize the excited states accurately. The results and theoretical details of mutual information are provided in Section 12 of the ESI.† In the CASPT2 calculations, the basic settings were identical to those described in the section of computational details. However, state averaging was performed over two doublet states and one quartet state, and an active space of 7 electrons in 7 orbitals was selected (Section 8 of the ESI†). Owing to the limited number of states averaged, the excitation energies were calculated using SS-CASPT2 rather than XMS-CASPT2.

Fig. 5 Chemical structures of PhNN and its derivatives.

Table 4 Local excitation (LE) energies of PhNN and its derivatives calculated by SS-CASPT2 theory. The dihedral angle was measured as the angle between the Ph ring and the NN ring. All structures were optimized for their ground states

	^2LE/cm^−1	^4LE/cm^−1	Dihedral angle/degree
PhNN	16 926	25 700	15.7
PhNN-2Me	18 021	28 646	47.5
PhNN-6Me	16 560	24 816	14.6
PhNN-2,4,6Me	18 788	30 515	60.9

---

Table 5 CI vector weights for the low-lying states calculated by CASSCF theory. The major Slater determinants contributing to each state are listed. The Slater determinants for the ²LE and ⁴LE states represent the LUMO, SOMO, and HOMO localized on the radical

	^2LE				^4LE
	|02α〉	|α02〉	|α20〉	|20α〉	|ααα〉
PhNN	0.37163	0.39726	0.07180	0.06835	0.86721
PhNN-2Me	0.39065	0.39302	0.07061	0.07021	0.90186
PhNN-6Me	0.37211	0.38622	0.07265	0.07014	0.85598
PhNN-2,4,6Me	0.40147	0.38996	0.06943	0.07099	0.92260

---

In Table 4, it was found that the ⁴LE of PhNN exists in a much higher region (∼25 000 cm⁻¹) compared to the ²LE and CT states of the connected system. It is reasonable because the ⁴LE state is described by the electron configurations that have at least three singly occupied orbitals whereas the ²LE state is dominated by the electron configurations that have only one singly occupied orbitals. Since the nature of the local excitation states should not be so much different between bpy-M-CAT-m-Linker-NN and PhNN, it can be concluded from these calculations that the ⁴LE state has much higher energy than the ²LE and ²T₁ states in bpy-M-CAT-Linker-NN as well as PhNN. Interestingly, a positive correlation is observed between the dihedral angle between the phenyl ring and the NN ring and the excitation energy in the PhNN species. As the dihedral angle increases, the delocalization of π orbitals between the phenyl ring and the NN ring becomes less efficient, resulting in reduced stabilization of the LUMO of the NN and an accompanying increase in the excitation energy.

3.3 Calculations of SOC matrix elements and ZFS parameters

According to the RQM mechanism,²⁰ which accounts for the ESP of chromophore-radical connected molecules caused by transitions between ²T₁ and ⁴T₁ states, the upper sublevel of the doublet state is more populated, i.e., emissive ESP is observed, if the quartet state is higher than the doublet state. It is therefore contradictory to the fact that absorptive ESP was observed for bpy-Pt, Pt-2Me, Pt-4Me, and Pt-2,4,6Me, though the energy level of their quartet states is higher than that of the doublet states. A modified RQM (mRQM) was proposed in ref. 19 to address this contradiction. In this model, the ⁴LE state is assumed to lie below the ²T₁ state and to participate in the ISC process. However, as shown in Section 3.2, the energy level of ⁴LE of bpy-M-CAT-Linker-NN molecules is too high to be involved in this mechanism.

One important clue is the fact that the sign change in the polarization was observed between bpy-Pt-CAT-mPh-NN and bpy-Pd-CAT-mPh-NN, of which the ESP is absorptive and emissive, respectively. Because they only differ in the central metal ion of the chromophore linked to the NN radical, it should be more reasonable to explain the differences by the heavy-atom effect, which enhances spin–orbit coupling (SOC), rather than attributing it to differences in the energy level of the local excitation of the NN radical. The fact that the absorption peaks corresponding to ²S₁ are not altered between bpy-Pt-CAT-mPh-NN and bpy-Pd-CAT-mPh-NN should also support this assumption. The effects of the SOC on the ESP are neglected in RQM and mRQM, in which the transition between the doublet and the quartet states is assumed to be caused solely by the electron spin dipole–dipole interaction governed by the D-tensor. In addition, it has been reported that the anisotropy of SOC causes the spin polarization of the excited triplet state of pentacene and its derivatives via a spin-selective intersystem crossing.⁵⁹ Motivated by these findings, we hypothesized that the observed sign change in ESP might be influenced by the effects of SOC.

To test this hypothesis, we calculated the spin–orbit coupling matrix elements (SOCMEs) between the excited states. In these calculations, the SA-CASSCF reference wavefunctions were rotated using the unitary transformation that diagonalizes the effective Hamiltonian of XMS-CASPT2. The calculated SOCME values are presented in Table 6. First, comparing the terms between ²T₁ and ⁴T₁, i.e., 〈²T₁|Ĥ_SOC|⁴T₁〉, it is observed that the compounds in the bpy-Pt system generally exhibit larger SOCME values than those of bpy-Pd. This trend aligns with the expectation based on the fact that the Pt atom is heavier than the Pd atom. The magnitudes of the terms 〈²T₁|Ĥ_SOC|⁴T₁〉 are one order smaller compared to the terms 〈²S₁|Ĥ_SOC|⁴T₁〉. This can be attributed to the small change in angular momentum, as there are minimal changes in the MO occupations between the ²T₁ and ⁴T₁ states. It was also revealed that almost all of the calculated SOC values were contributed by Pt or Pd atoms according to the atomic partitioning analysis of SOCMEs. It should be noted that the higher excited CT states (HOMO−1 → LUMO, HOMO → LUMO+1) exhibited significant SOCME (greater than 10 cm⁻¹) with the ²T₁ and ⁴T₁ states. However, since the energies of these states exceeded that of the ²T₁ state by more than 10 000 cm⁻¹, it is unlikely that they are involved in the ESP process.

Table 6 Calculated terms of spin–orbit coupling matrix elements (SOCMEs) for each molecule

	〈^2T1|ĤSOC|^4T1〉/cm^−1	〈^2T1|ĤSOC|^2S1〉/cm^−1	〈^2S1|ĤSOC|^4T1〉/cm^−1
bpy-Pt	0.130	1.020	1.825
Pt-2Me	0.281	0.685	1.189
Pt-4Me	0.187	1.610	2.817
Pt-6Me	0.139	0.360	0.670
Pt-2,4,6Me	0.020	1.669	2.902
bpy-Pd	0.019	0.149	0.273

---

	〈^2T1|ĤSOC|^2LE〉/cm^−1	〈^4T1|ĤSOC|^2LE〉/cm^−1	〈^2S1|ĤSOC|^2LE〉/cm^−1
bpy-Pt	0.037	0.070	0.032
Pt-2Me	0.024	0.044	0.009
Pt-4Me	0.081	0.137	0.078
Pt-6Me	0.016	0.029	0.014
Pt-2,4,6Me	0.005	0.005	0.126
bpy-Pd	0.004	0.009	0.021

---

To further investigate the contribution of the electron spin dipole–dipole interaction to the transition matrix elements between ²T₁ and ⁴T₁, we also calculated the D-tensor of the T₁ state of the bpy-M-CAT moiety (bpy-M-NoRadical, Fig. 6) using the complete active space self-consistent field method combined with the density matrix renormalization group theory (DMRG-CASSCF). This approach, developed in our previous study,⁴⁴ has proven effective in predicting highly accurate zero-field splitting parameters for triplet states of aromatic molecules (see also the section of computational details).

Fig. 6 Chemical structures of bpy-Pt-CAT (bpy-Pt-NoRadical) and bpy-Pd-CAT (bpy-Pd-NoRadical).

Table 7 presents the triplet D- and E-values of the D-tensor for bpy-Pt-NoRadical and bpy-Pd-NoRadical using DMRG-CASSCF theory. The values gradually increased with the bond dimension, but the qualitative trend remained unchanged, revealing that bpy-Pt-CAT exhibited ZFS parameters several times larger than those of bpy-Pd-NoRadical. The convergence of the DMRG wavefunction with respect to bond dimension is discussed in Section 10 of the ESI.†

Table 7 Calculated D- and E-values for the lowest triplet state of bpy-Pt-NoRadical and bpy-Pd-NoRadical. The bond-dimension (M) was set to several values. Note that DMRG-CASSCF calculations did not meet convergence criteria within 150 cycles for M = 128 and 256

	M = 128		M = 256		M = 512		M = 1024
	|D|/cm^−1	|E|/cm^−1	|D|/cm^−1	|E|/cm^−1	|D|/cm^−1	|E|/cm^−1	|D|/cm^−1	|E|/cm^−1
bpy-Pt-NoRadical	0.0870	0.00543	0.0947	0.00712	0.0991	0.00912	0.103	0.00953
bpy-Pd-NoRadical	0.0160	0.00161	0.0160	0.00197	0.0156	0.00154	0.0159	0.00133

---

3.4 Simulation of ESP considering both SOC and ZFS

The rate of intersystem crossing (ISC) between the doublet state Dⁿ and the quartet state Q^m, where n, m indicate the spin sublevels, is often expressed in the form of eqn (8),^20,22where k⁰_DQ is the product of the zero-point motion rate constant and the Frank–Condon factor, V is the perturbation Hamiltonian that couples the initial and final states, and ΔE[Q^m, Dⁿ] is the energy difference between Q^m and Dⁿ. Table 8 shows calculated transition matrix elements when treating ZFS and SOC Hamiltonians as the perturber V. The matrix elements for ZFS Hamiltonian can be found in ref. 60 and the derivation for SOC Hamiltonian can be found in Section 11 of the ESI.† We note that an approximation neglecting the E-values has been employed. D_T and Y_QD denote the D value of the T₁ state of the chromophore moiety and the reduced spin–orbit coupling matrix element between ⁴T₁(Q) and ²T₁(D). When comparing the transition matrix elements for each sublevel, the trend of magnitude reverses between ZFS and SOC (Fig. 7). Using these transition matrix elements and energy differences, we calculated the transition rates between the sublevels of the Dⁿ and Q^m, i.e., ²T₁ and ⁴T₁, with eqn (8), and obtained spin polarization ratio in ²T₁ for both the SOC and ZFS pathways using eqn (9), in which the initial population of the quartet was assumed to be in thermal equilibrium. The temperature and magnetic field conditions were set to the same values as in the experiment, and the magnitude of the exchange interaction was estimated from the energy difference of the bpy-Pt-CAT-mPh-NN system, which we calculated (vide supra).

Table 8 Transition matrix elements of ²T₁–⁴T₁ intersystem crossing via SOC and ZFS perturbation Hamiltonians. Q^m and Dⁿ are the wavefunctions of quartet and doublet three-spin states considering spin sublevels. D means the D value of the D-tensor and Y_QD is the reduced matrix element of SOC

V
ZFS	D ^2/45	2D^2/45	3D^2/45	4D^2/45
SOC	3|YQD|^2/12	2|YQD|^2/12	|YQD|^2/12	0

---

Fig. 7 Schematic diagram of the magnitude of transition matrix elements from (a) ZFS (b) SOC Hamiltonian.

Fig. 8 shows the spin polarization ratio obtained with eqn (9) as a heatmap. Under negligible SOC conditions, i.e., |Y_QD| ∼ 0, emissive polarization, i.e., is predicted, which corresponds to the results of RQM for E(D) < E(Q) systems. In contrast, when the SOC is significant and its magnitude is comparable to the ZFS D-value, an absorptive polarization in the doublet state, i.e., 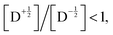is predicted. This result suggests that the sign inversion of ESP observed in bpy-M-CAT-mPh-NN species could be explained by considering the effects of the SOC, which is usually very small between ²T₁ and ⁴T₁ when there is not any heavy atom. As shown in Tables 6 and 7, the values of the SOC matrix elements were predicted to be comparable to the ZFS parameters in the bpy-M-CAT-mPh-NN system. At least, it is consistent with the fact that replacing the central metal ion with a heavier atom, i.e., Pd to Pt, results in the sign inversion of the polarization from emissive to absorptive, although the trend of ESP is not perfectly correlated with the values of the calculated SOC matrix elements for a series of bpy-M-CAT-Linker-NN molecules. To obtain a quantitative prediction for the spin polarization ratio, a more sophisticated simulation could be required than eqn (9), which has many assumptions. Another possible factor is that the ²LE state plays a role in some way, of which the energy is much lower than that of the ⁴LE state and close to that of the ²T₁ state. For example, it is energetically plausible that the ²LE state is involved in the relaxation pathway to the ground state. Further investigation will be required to verify the role of ²LE.

Fig. 8 Simulated electron spin distribution in doublet sublevels.

4 Summary

In this study, we performed detailed quantum chemical calculations for the Pt and Pd complex–radical connected systems reported by Kirk et al., in which the sign of electron spin polarization observed in time-resolved EPR after photo-irradiation was found to reverse depending on the metal atom. A modified reversed quartet mechanism (mRQM) involving a quartet local excited (LE) state, in addition to ligand-to-ligand charge transfer (LL′CT) states, originating from the donor–acceptor–radical three-spin system, has been proposed as a possible mechanism in previous studies.

To clarify the influence of these multiple excited states on ESP, we investigated energetics using multireference perturbation theory. The results of our CASPT2 calculations revealed that both Pt and Pd species have three LL′CT states and a doublet LE state in the low-energy region, while the quartet LE state has a significantly higher energy compared to those, which have been assumed to lie lower than LL′CT states in the mRQM.

To resolve the contradiction between the mRQM and the computational results, we focused on the effects of spin–orbit coupling (SOC), which are neglected in the RQM. We found that the effects of SOC are more pronounced in the Pt complexes than in the Pd complex. The order of SOC matrix elements is one order higher than that of the calculated ZFS (SSC) values, which was assumed to be the source of the transition between doublet and quartet states in the RQM. To investigate the importance of SOC further, we conducted kinetic simulations incorporating the SOC term based on the Hamiltonian previously used in the RQM. The sign of ESP is reversed when the magnitude of the SOC matrix element becomes comparable to the D-value, explaining the experimental inversion of the sign. It should be noted that the simulations did not fully reproduce the experimental ESP when the effects of the methyl substituents were taken into account. This could be attributed to the assumptions made in the simulations or the lack of quantitative accuracy for calculating SOC and ZFS parameters.

Our theoretical study has provided a detailed picture of the excited states of the complex–radical connected systems and revealed the influence of SOC effects on ESP. Controlling the ESP phenomenon in connected systems using SOC could become an important technique for the application of multi-spin sublevels.

Data availability

The data supporting this study's findings are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts of interest to declare in this study.

Acknowledgements

This work was supported by JSPS KAKENHI (JP23H01921), JST-FOREST Program (JPMJFR221R), JST-CREST Program (JPMJCR23I6), and MEXT Q-LEAP Program (JPMXS0120319794). The computation was partly performed at the Research Center for Computational Science, Okazaki, Japan (Project: 24-IMS-C028).

References

1. A. Cornia and P. Seneor, The Molecular Way, Nat. Mater., 2017, 16, 505–506.
2. J. Eills, D. Budker, S. Cavagnero, E. Y. Chekmenev, S. J. Elliott, S. Jannin, A. Lesage, J. Matysik, T. Meersmann, T. Prisner, J. A. Reimer, H. Yang and I. V. Koptyug, Spin Hyperpolarization in Modern Magnetic Resonance, Chem. Rev., 2023, 123, 1417–1551.
3. T. Hamachi and N. Yanai, Recent Developments in Materials and Applications of Triplet Dynamic Nuclear Polarization, Prog. Nucl. Magn. Reson. Spectrosc., 2024, 142–143, 55–68.
4. M. R. Wasielewski, et al., Exploiting Chemistry and Molecular Systems for Quantum Information Science, Nat. Rev. Chem., 2020, 4, 490–504.
5. D. J. Sloop, H.-L. Yu, T.-S. Lin and S. I. Weissman, Electron Spin Echoes of a Photoexcited Triplet: Pentacene in p-Terphenyl Crystals, J. Chem. Phys., 1981, 75, 3746–3757.
6. H. Levanon, Spin Polarized Triplets Oriented in Liquid Crystals, Rev. Chem. Intermed., 1987, 8, 287–320.
7. C. Blättler, F. Jent and H. Paul, A Novel Radical-Triplet Pair Mechanism for Chemically Induced Electron Polarization (CIDEP) of Free Radicals in Solution, Chem. Phys. Lett., 1990, 166, 375–380.
8. A. Kawai, T. Okutsu and K. Obi, Spin Polarization Generated in the Triplet-Doublet Interaction:Hyperfine-Dependent Chemically Induced Dynamic Electron Polarization, J. Phys. Chem., 1991, 95, 9130–9134.
9. P. Delaney, J. C. Greer and J. A. Larsson, Spin-Polarization Mechanisms of the Nitrogen-Vacancy Center in Diamond, Nano Lett., 2010, 10, 610–614.
10. T. Quintes, M. Mayländer and S. Richert, Properties and Applications of Photoexcited Chromophore–Radical Systems, Nat. Rev. Chem., 2023, 7, 75–90.
11. C. Corvaja, M. Maggini, M. Ruzzi, G. Scorrano and A. Toffoletti, Spin Polarization in Fullerene Derivatives Containing a Nitroxide Group. Observation of the Intermediate Photoexcited Quartet State in Radical Triplet Pair Interaction, Appl. Magn. Reson., 1997, 12, 477–493.
12. M. T. Colvin, A. L. Smeigh, E. M. Giacobbe, S. M. M. Conron, A. B. Ricks and M. R. Wasielewski, Ultrafast Intersystem Crossing and Spin Dynamics of Zinc Meso-Tetraphenylporphyrin Covalently Bound to Stable Radicals, J. Phys. Chem. A, 2011, 115, 7538–7549.
13. M. Mayländer, S. Chen, E. R. Lorenzo, M. R. Wasielewski and S. Richert, Exploring Photogenerated Molecular Quartet States as Spin Qubits and Qudits, J. Am. Chem. Soc., 2021, 143, 7050–7058.
14. M. L. Kirk, D. A. Shultz, J. Chen, P. Hewitt, D. Daley, S. Paudel and A. van der Est, Metal Ion Control of Photoinduced Electron Spin Polarization in Electronic Ground States, J. Am. Chem. Soc., 2021, 143, 10519–10523.
15. J. Yang, D. K. Kersi, L. J. Giles, B. W. Stein, C. Feng, C. R. Tichnell, D. A. Shultz and M. L. Kirk, Ligand Control of Donor–Acceptor Excited-State Lifetimes, Inorg. Chem., 2014, 53, 4791–4793.
16. E. F. Ullman, J. H. Osiecki, D. G. B. Boocock and R. Darcy, Stable Free Radicals. X. Nitronyl Nitroxide Monoradicals and Biradicals as Possible Small Molecule Spin Labels, J. Am. Chem. Soc., 1972, 94, 7049–7059.
17. M. L. Kirk, D. A. Shultz, D. E. Stasiw, D. Habel-Rodriguez, B. Stein and P. D. Boyle, Electronic and Exchange Coupling in a Cross-Conjugated D–B–A Biradical: Mechanistic Implications for Quantum Interference Effects, J. Am. Chem. Soc., 2013, 135, 14713–14725.
18. M. L. Kirk, D. A. Shultz, P. Hewitt, D. E. Stasiw, J. Chen and A. van der Est, Chromophore-Radical Excited State Antiferromagnetic Exchange Controls the Sign of Photoinduced Ground State Spin Polarization, Chem. Sci., 2021, 12, 13704–13710.
19. M. L. Kirk, D. A. Shultz, P. Hewitt, A. R. Marri and A. Van Der Est, Competitive Reversed Quartet Mechanisms for Photogenerated Ground State Electron Spin Polarization, Chem. Sci., 2023, 14, 9689–9695.
20. V. Rozenshtein, A. Berg, E. Stavitski, H. Levanon, L. Franco and C. Corvaja, Electron Spin Polarization of Functionalized Fullerenes. Reversed Quartet Mechanism, J. Phys. Chem. A, 2005, 109, 11144–11154.
21. A. K. Tripathi, V. Rane, S. Kundu and R. Das, A Phenomenological Scheme for Reversed Quartet Mechanism of Electron Spin Polarization in Covalently Linked Systems of Chromophore and Free Radical: Determination of Magnitude of Polarization and Application to Pyrene–TEMPO Linked Molecules, J. Chem. Phys., 2019, 151, 154305.
22. K. Kundu, T. Dubroca, V. Rane and F. Mentink-Vigier, Spinning-Driven Dynamic Nuclear Polarization with Optical Pumping, J. Phys. Chem. A, 2022, 126, 2600–2608.
23. A. Kawai and K. Obi, First Observation of a Radical-Triplet Pair Mechanism (RTPM) with Doublet Precursor, J. Phys. Chem., 1992, 96, 52–56.
24. Z. Wang, J. Zhao, A. Barbon, A. Toffoletti, Y. Liu, Y. An, L. Xu, A. Karatay, H. G. Yaglioglu, E. A. Yildiz and M. Hayvali, Radical-Enhanced Intersystem Crossing in New Bodipy Derivatives and Application for Efficient Triplet–Triplet Annihilation Upconversion, J. Am. Chem. Soc., 2017, 139, 7831–7842.
25. A. I. Shushin, CIDEP in Triplet-Doublet Quenching. Quartet-Doublet Nonadiabatic Transitions, Z. Physiol. Chem., 1993, 182, 9–18.
26. T. J. Lee and P. R. Taylor, A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods, Int. J. Quantum Chem., 1989, 36, 199–207.
27. T. Shiozaki, W. Gyorffy, P. Celani and H.-J. Werner, Communication: Extended Multi-State Complete Active Space Second-Order Perturbation Theory: Energy and Nuclear Gradients, J. Chem. Phys., 2011, 135, 081106.
28. F. Neese, Software Update: The ORCA Program System—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
29. J. P. Perdew and W. Yue, Accurate and Simple Density Functional for the Electronic Exchange Energy: Generalized Gradient Approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802.
30. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
31. F. Weigend, Accurate Coulomb-fitting Basis Sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057.
32. A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Optimized Accurate Auxiliary Basis Sets for RI-MP2 and RI-CC2 Calculations for the Atoms Rb to Rn, Theor. Chem. Acc., 2007, 117, 587–597.
33. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Energy-Adjustedab Initio Pseudopotentials for the Second and Third Row Transition Elements, Theor. Chim. Acta, 1990, 77, 123–141.
34. F. Neese, An Improvement of the Resolution of the Identity Approximation for the Formation of the Coulomb Matrix, J. Comput. Chem., 2003, 24, 1740–1747.
35. B. A. Hess, Relativistic Electronic-Structure Calculations Employing a Two-Component No-Pair Formalism with External-Field Projection Operators, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748.
36. A. Wolf, M. Reiher and B. A. Hess, The Generalized Douglas–Kroll Transformation, J. Chem. Phys., 2002, 117, 9215–9226.
37. T. Nakajima and K. Hirao, The Douglas–Kroll–Hess Approach, Chem. Rev., 2012, 112, 385–402.
38. P.-O. Widmark, P.-Å. Malmqvist and B. O. Roos, Density Matrix Averaged Atomic Natural Orbital (ANO) Basis Sets for Correlated MolecularWave Functions, Theor. Chim. Acta, 1990, 77, 291–306.
39. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, New Relativistic ANO Basis Sets for Transition Metal Atoms, J. Phys. Chem. A, 2005, 109, 6575–6579.
40. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297.
41. F. Weigend, A Fully Direct RI-HF Algorithm: Implementation, Optimised Auxiliary Basis Sets, Demonstration of Accuracy and Efficiency, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291.
42. T. Yanai, Y. Kurashige, W. Mizukami, J. Chalupský, T. N. Lan and M. Saitow, Density Matrix Renormalization Group for Ab Initio Calculations and Associated Dynamic Correlation Methods: A Review of Theory and Applications, Int. J. Quantum Chem., 2015, 115, 283–299.
43. J. Chalupský and T. Yanai, Flexible Nuclear Screening Approximation to the Two-Electron Spin–Orbit Coupling Based on Ab Initio Parameterization, J. Chem. Phys., 2013, 139, 204106.
44. K. Miyokawa and Y. Kurashige, Zero-Field Splitting Tensor of the Triplet Excited States of Aromatic Molecules: A Valence Full-π Complete Active Space Self-Consistent Field Study, J. Phys. Chem. A, 2024, 128, 2349–2356.
45. D. Zgid and M. Nooijen, The Density Matrix Renormalization Group Self-Consistent Field Method: Orbital Optimization with the Density Matrix Renormalization Group Method in the Active Space, J. Chem. Phys., 2008, 128, 144116.
46. D. Ghosh, J. Hachmann, T. Yanai and G. K.-L. Chan, Orbital Optimization in the Density Matrix Renormalization Group, with Applications to Polyenes and β-Carotene, J. Chem. Phys., 2008, 128, 144117.
47. T. Yanai, Y. Kurashige, D. Ghosh and G. K.-L. Chan, Accelerating Convergence in Iterative Solution for Large-Scale Complete Active Space Self-Consistent-Field Calculations, Int. J. Quantum Chem., 2009, 109, 2178–2190.
48. Q. Sun, Libcint: An Efficient General Integral Library for Gaussian Basis Functions, J. Comput. Chem., 2015, 36, 1664–1671.
49. Q. Sun, T. C. Berkelbach, N. S. Blunt, G. H. Booth, S. Guo, Z. Li, J. Liu, J. D. McClain, E. R. Sayfutyarova, S. Sharma, S. Wouters and G. K.-L. Chan, PySCF: The Python-based Simulations of Chemistry Framework, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1340.
50. Q. Sun, et al., Recent Developments in the PySCF Program Package, J. Chem. Phys., 2020, 153, 024109.
51. H. Zhai and G. K.-L. Chan, Low Communication High Performance Ab Initio Density Matrix Renormalization Group Algorithms, J. Chem. Phys., 2021, 154, 224116.
52. S. Sharma and G. K.-L. Chan, Spin-Adapted Density Matrix Renormalization Group Algorithms for Quantum Chemistry, J. Chem. Phys., 2012, 136, 124121.
53. K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, Krzysztof. Second-Order Perturbation Theory with a CASSCF Reference Function, J. Phys. Chem., 1990, 94, 5483–5488.
54. K. Andersson, P.-Å. Malmqvist and B. O. Roos, Second-Order Perturbation Theory with a Complete Active Space Self-Consistent Field Reference Function, J. Chem. Phys., 1992, 96, 1218–1226.
55. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The Multi-State CASPT2 Method, Chem. Phys. Lett., 1998, 288, 299–306.
56. J. Rissler, R. M. Noack and S. R. White, Measuring Orbital Interaction Using Quantum Information Theory, Chem. Phys., 2006, 323, 519–531.
57. K. Boguslawski, P. Tecmer, Ö. Legeza and M. Reiher, Entanglement Measures for Single- and Multireference Correlation Effects, J. Phys. Chem. Lett., 2012, 3, 3129–3135.
58. K. Boguslawski, F. Réal, P. Tecmer, C. Duperrouzel, A. S. P. Gomes, Ö. Legeza, P. W. Ayers and V. Vallet, On the Multi-Reference Nature of Plutonium Oxides: PuO₂²⁺, PuO₂, PuO₃ and PuO₂(OH)², Phys. Chem. Chem. Phys., 2017, 19, 4317–4329.
59. K. Sakamoto, T. Hamachi, K. Miyokawa, K. Tateishi, T. Uesaka, Y. Kurashige and N. Yanai, Polarizing Agents beyond Pentacene for Efficient Triplet Dynamic Nuclear Polarization in Glass Matrices, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2307926120.
60. J. M. Hudson and E. W. Evans, Radical Spin Polarization and Magnetosensitivity from Reversible Energy Transfer, J. Phys. Chem. Lett., 2024, 15, 4130–4135.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04695a

---