Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
When carbon monoxide goes “upside down”: vibrational signatures of CO at NaCl(100) from ab initio molecular dynamics†
Shreya
Sinha
 *a,
Alec M.
Wodtke
*a,
Alec M.
Wodtke
 bc and
Peter
Saalfrank
bc and
Peter
Saalfrank
 *a
*a
aTheoretical Chemistry, Institute of Chemistry, University of Potsdam, Karl-Liebknecht-Str. 24-25, 14476 Potsdam, Germany. E-mail: sinha@uni-potsdam.de; peter.saalfrank@uni-potsdam.de; Tel: +49 (0)331-977-6138 Tel: +49 (0)331-977-5232
bDepartment of Dynamics at Surfaces, Max-Planck-Institute for Multidisciplinary Sciences, Am Fassberg 11, 37077 Göttingen, Germany
cInstitute for Physical Chemistry, University of Göttingen, Tammannstr. 6, 37077 Göttingen, Germany
First published on 26th March 2025
Abstract
CO adsorbed on NaCl(100) is a model system for surface science showing a rich variety of interesting phenomena. It features several adsorption phases like tilted/antiparallel or perpendicular/upright, very long vibrational lifetimes of the CO internal stretch (IS) mode, anharmonicity-driven vibrational energy pooling, “C-bound” vs. “O-bound” adsorption, and heavy-atom gateway tunneling during CO inversion at low temperatures. Typically, these features and phenomena are experimentally probed by stationary and time-resolved vibrational spectra, exhibiting characteristic differences between the various adsorption modes and phases. To gain atom- and time-resolved insight into vibrational response of CO molecules on NaCl(100), vibrational density of states (VDOS), infrared (IR) and vibrational sum frequency (VSF) spectra are computed from velocity velocity correlation functions (VVCFs) by ab initio molecular dynamics (AIMD) for various coverages, temperatures and phases. In agreement with experiments, we find that increasing CO (“C-bound”) coverages as well as CO inversion lead to redshifts of the CO IS mode. We predict more diffuse spectra at T = 300 K compared to 30 K, reflecting the disorder of adsorbates and monolayer instability at room temperature. Analyzing molecularly decomposed and internal VDOS curves as well as computed non-linear correlation matrices give further insight into the complex molecular dynamics underlying the vibrational spectra, notably for the low-frequency regime where frustrated rotations, translations and intermolecular motions come into play. On a methodological side, we also test and discuss some intricate details of how to compute IR and VSF response using a modified formulation of the VVCF methods [Ohto et al., J. Chem. Phys., 2015, 143, 124702], by including time and angle-dependent dipole and polarizability derivatives as well as intermolecular couplings by cross correlations. Their effect on computed vibrational spectra is studied. These findings provide a detailed, microscopic insight into the picosecond vibrational spectra and dynamics of CO on NaCl(100), highlighting the effects of temperature, coverage, and changes in adsorbate orientation.
1 Introduction
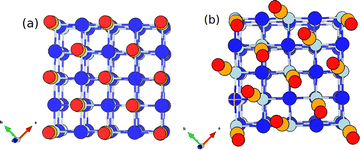
CO on a NaCl(100) surface is a well-known and long-studied model system for adsorption. However, recent new findings demonstrate that this system is still good for surprises, with new structures and phenomena emerging. Many of these phenomena are due to the fact that CO interacts only weakly with NaCl(100), making it an ideal microlab to study intermolecular interactions.Experimentally it is known that, at a coverage of 1 ML (θ = 1, one CO per surface Na+), a (1 × 1) “parallel/upright” (P/U) phase with C atoms pointing downward (to Na+) is the most stable phase above 35 K. Below this temperature a p(1 × 1) P/U → p(2 × 1) T/A phase transition occurs, with T/A denoting a “tilted/antiparallel” orientation.1 Both phases are shown in Fig. 1. Density functional theory (DFT) confirmed that indeed, the most stable monolayer phase of CO/NaCl(100) at low temperatures is T/A.2–4 P/U is favoured at higher T for θ = 1, but also found at low, sub-monolayer coverages, even at low T according to theory. For example, at θ = 1/8, P/U is most stable according to density functional calculations and beyond.4
Such structural details and their changes are typically explored experimentally by various forms of vibrational spectroscopy, in particular the CO stretching mode being a sensitive reporter mode.1,5,6 Specifically, at a coverage θ = 1 (1 ML) and T = 40 K, where the P/U phase dominates, experimentally a single CO peak at 2155 cm−1 was found. At temperatures below the p(1 × 1) P/U → p(2 × 1) T/A transition, a minor peak appears at around 2149 cm−1, and the original peak slightly shifts (by <1 cm−1) to the red.1 This second peak has been interpreted as being due to exciton (Davydov) splitting by ΔD ∼ 6 cm−1, arising from interacting vibrational transition dipole moments of the CO molecules in the T/A phase.7
In another more recent work, Lau et al.8 reported polarized Fourier transformed infrared (FTIR) absorption spectra as a function of coverage between 0.02 and 1.0 ML. They found that even at temperatures as low as 30 K, non-equilibrium structures exist, which broaden the monolayer spectra, indicative of diffusion and island formation. Tilt angles of adsorbed CO as a function of coverage were also extracted, which show an abrupt change between 0.2 and 0.3 ML from 0° (upright) to ∼30° (tilted) for higher coverages, this way supporting the mentioned preference of P/U at low coverage.
In further work, Wodtke and coworkers found by IR fluorescence spectroscopy that, for a CO overlayer buried under a CO adsorbate layer at 7 K, it is possible to flip C-bound CO molecules in the CO monolayer by highly exciting the C–O bond, to an “O-bound” form, i.e., (some of the) CO molecules underwent an isomerization to an “upside-down” configuration.9 The highly vibrationally excited CO molecules (with v = 20–30 vibrational quanta) had been created by IR excitation of adsorbed CO from v = 0 to v = 1 and subsequent vibrational energy pooling (VEP), i.e., vibrational-energy transfer events of the type CO(v) + CO(v) → CO(v − 1) + CO(v + 1). VEP is driven by dipole–dipole coupling between CO molecules and the anharmonicity of the CO vibrational potential,10,11 in combination with extraordinary long vibrational lifetimes (on the order of ms) of CO adsorbed on NaCl(100). The latter is due to the mentioned, weak interaction of CO with the surface. It was also found that the C–O vibration of O-bound species, once formed, was red-shifted by about Δ = 15 cm−1 compared to C-bound.9 In even more recent work,12,13 they further observed, again by vibrational spectroscopy, that even at low temperatures (around 20 K) the backreaction of “O-bound” to “C-bound” occurs, which could be explained qualitatively via a phonon-assisted resonant heavy-atom tunneling mechanism involving “gateway states”.
From the theory side, vibrational properties and spectra of CO molecules at NaCl(100) were mostly studied so far by stationary normal mode analysis, NMA, which neglects anharmonicity and inter-mode couplings and finite temperature.4,14–16 This necessitates dynamical calculations which allow for real-time, atom-resolved insight and additionally include anharmonicity, intramolecular and intermolecular mode couplings and finite temperature effects in simulated vibrational spectra. Below we report an in-depth analysis of vibrational spectra for different phases of CO, both “C-bound” and “O-bound”, on NaCl(100) at different coverages (0.25, 0.5, and 1 ML), and at two different temperatures (T = 30 K, 300 K), i.e., below and above the T/A → P/U phase transition at higher coverages. To do so, we use an ab initio molecular dynamics–velocity velocity correlation function (AIMD–VVCF) approach.
Our paper is organized as follows. Section 2 outlines models and methods used for computing the vibrational spectra and deriving dynamic properties. Section 3 presents results in different subsections dealing with the different kinds of vibrational signatures (vibrational density of states (VDOS), InfraRed (IR) and vibrational sum frequency (VSF) spectra), for some selected initial configurations and their dependence on coverage and temperature. A final section summarizes this work. Many numerical details and additional results can be found in the ESI.†
2 Methods and models
2.1 Electronic structure method and adopted models
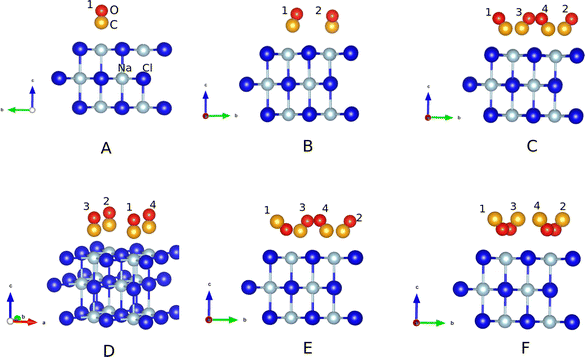
In what follows, periodic supercell calculations using periodic DFT, employing the PBE exchange correlation functional17 and standard pseudopotentials with a projector augmented wave (PAW) basis,18 as implemented in the Vienna ab initio Simulation (VASP) Package,19–22 were carried out. Grimme's D2 correction23 was applied to account for van der Waals interactions. For all calculations, we used a 2 × 2 × 1 Γ-centered k-point mesh and a kinetic energy cutoff of 700 eV.The specific surface models, some of them analogous to ref. 16, are all based on  supercells, with dimensions 8.017 × 8.017 × 30 Å (∼20 Å vacuum along z, the direction perpendicular to the surface), if not stated otherwise. Different models were chosen and geometry-optimized, serving for normal mode analysis (NMA) and ab initio molecular dynamics (AIMD) – see below. For geometry optimizations, the upper surface layer and the CO molecules were relaxed. Fig. 2 shows six different, geometry-optimized models A–F:
supercells, with dimensions 8.017 × 8.017 × 30 Å (∼20 Å vacuum along z, the direction perpendicular to the surface), if not stated otherwise. Different models were chosen and geometry-optimized, serving for normal mode analysis (NMA) and ab initio molecular dynamics (AIMD) – see below. For geometry optimizations, the upper surface layer and the CO molecules were relaxed. Fig. 2 shows six different, geometry-optimized models A–F:
• Model A corresponds to coverage θ = 1/4 (one of four Na+ ions in the upper layer occupied by CO, with “C-down”); note that CO is ideally “upright”.
• Model B corresponds to coverage θ = 1/2 with both CO molecules “C-bound”, and being tilted.
• Model C corresponds to θ = 1, in the most stable T/A phase with all CO molecules “C-bound” and tilted.
• Model D is a metastable form for θ = 1 at low T, the P/U structure with all CO molecules parallel and upright. P/U is found to be 0.02 eV per CO molecule (0.08 eV in total) higher in energy than the T/A phase C, on the PBE+D2 level of theory.
• Model E corresponds also to θ = 1, however, with one of the four CO molecules (denoted 1CO) inverted to “O-bound”. This form is 0.084 eV higher in energy than the T/A model C.
• Model F corresponds again to θ = 1, now, however, all four CO molecules are “O-bound”. On the PBE+D2 level, the corresponding energy is 0.085 eV per CO molecule higher in energy than form C, showing that the inversion energy per CO depends only marginally on the number of molecules which are inverted.
• In addition, (not shown in Fig. 2) a model G was considered, derived from model E by adding two CO overlayers on top of the adsorbate layer. Model G is a candidate structure for the mentioned experiments9,13 with “buried” adsorbate layers (see below, Fig. 4).
The motivation for selecting these models comes from simulating experimentally realistic minimum configurations at both low and higher temperatures, including metastable geometries with one or more “O-down” CO molecules, which were observed experimentally post IR laser excitation of CO IS mode.9
2.2 Ab initio molecular dynamics
Starting from these models, AIMD simulations are performed within the canonical ensemble (NVT) using a Nosé–Hoover thermostat,24 with the goal to arrive at vibrational spectra (see below). Initial velocities for AIMD are generated from Boltzmann distributions at T = 30 K and T = 300 K, respectively. We use the same supercells as for geometry optimization in AIMD for T = 30 K, while for T = 300 K the![[c with combining low line]](https://www.rsc.org/images/entities/i_char_0063_0332.gif) -vector of the tetragonal unit cell was extended from 30 Å to 50 Å. Nuclear degrees of freedom are propagated with a time step of Δt = 0.5 fs. The total simulation time for the low temperature (30 K) is 60–100 ps, that for the higher temperature (300 K) is 100 ps. This was done by running several trajectories for each system, with equilibration and production phases, see the ESI,† Section S1.1 for details. There it is mentioned that for T = 300 K, the protocol was slightly different compared to T = 30 K: trajectories were first propagated in the NVT ensemble (as for T = 30 K), but then propagated within the microcanonical ensemble (NVE) for another 5 ps to remove spurious effects caused by the thermostat coupling. For both temperatures, only the last segment of each trajectory was utilized to sample the correlation functions in an interval [0, tsample]. tsample determines the spectral resolution of vibrational spectra. If not stated otherwise, we choose tsample = 3 ps, leading to a resolution of ∼11 cm−1. This is larger than found in low-temperature experiments, which are typically less than 2 cm−1 (ref. 8)-see also Section 3.4.2 below regarding this.
-vector of the tetragonal unit cell was extended from 30 Å to 50 Å. Nuclear degrees of freedom are propagated with a time step of Δt = 0.5 fs. The total simulation time for the low temperature (30 K) is 60–100 ps, that for the higher temperature (300 K) is 100 ps. This was done by running several trajectories for each system, with equilibration and production phases, see the ESI,† Section S1.1 for details. There it is mentioned that for T = 300 K, the protocol was slightly different compared to T = 30 K: trajectories were first propagated in the NVT ensemble (as for T = 30 K), but then propagated within the microcanonical ensemble (NVE) for another 5 ps to remove spurious effects caused by the thermostat coupling. For both temperatures, only the last segment of each trajectory was utilized to sample the correlation functions in an interval [0, tsample]. tsample determines the spectral resolution of vibrational spectra. If not stated otherwise, we choose tsample = 3 ps, leading to a resolution of ∼11 cm−1. This is larger than found in low-temperature experiments, which are typically less than 2 cm−1 (ref. 8)-see also Section 3.4.2 below regarding this.
2.3 Methods for computing vibrational spectra
 | (1) |
![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) i(t) the velocity of moving atom i at time t and N is the total number of moving atoms. CO molecules and the top NaCl layer atoms were allowed to move. 〈
i(t) the velocity of moving atom i at time t and N is the total number of moving atoms. CO molecules and the top NaCl layer atoms were allowed to move. 〈![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) i(0)·
i(0)·![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) i(t)〉 is the VVAF, averaged over different AIMD trajectories. To evaluate VVAFs, we use the so called “initial position method”26 (see ESI,† Section S1). In practice, the time integral in eqn (1) is evaluated from 0 to tsample, and the integrand is multiplied by a Hann window function w(t) = cos2(πt/(2tsample)) to avoid negative VDOS values.
i(t)〉 is the VVAF, averaged over different AIMD trajectories. To evaluate VVAFs, we use the so called “initial position method”26 (see ESI,† Section S1). In practice, the time integral in eqn (1) is evaluated from 0 to tsample, and the integrand is multiplied by a Hann window function w(t) = cos2(πt/(2tsample)) to avoid negative VDOS values.
Normally, the VDOS is evaluated based on velocities in Cartesian coordinates. To better identify the exact vibrational motion associated with a specific frequency, we report also the “internal VDOS”, wherein the internal motions (frustrated rotations, translations, etc.) are deconvoluted, providing a better assignment of the low-frequency modes.27 In particular, we shall derive VDOS curves resolved w.r.t. to the six coordinates of a CO molecule relative to the surface, namely r (the C–O distance), the surface–molecule distance (Z), the lateral center-of-mass positions (X, Y), and two angular coordinates, the polar (θ) and azimuthal (ϕ) angles. This is done numerically for each trajectory, by using “instantaneous” internal coordinates for each molecule, as outlined in the ESI,† Section S1.3. Also, molecule-wise decomposition of the simulated VDOS spectra will be shown and discussed below.
 | (2) |
 the dipole derivative of the CO chromophore along the C–O coordinate, at its equilibrium position, r = req, assumed independent of ω (Condon approximation). The parametrization of
the dipole derivative of the CO chromophore along the C–O coordinate, at its equilibrium position, r = req, assumed independent of ω (Condon approximation). The parametrization of  is based on quantum chemistry calculations on the CAM-B3LYP+D3 level,28,29 using the Gaussian program30 and a cluster model with a CO upright on-top of NaCl(100), as outlined in the ESI,† Section S1.5, eqn (S6). These give a value of
is based on quantum chemistry calculations on the CAM-B3LYP+D3 level,28,29 using the Gaussian program30 and a cluster model with a CO upright on-top of NaCl(100), as outlined in the ESI,† Section S1.5, eqn (S6). These give a value of 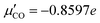 .
.
IR absorption spectra (for modes involving C–O stretches) are calculated from the imaginary part of χab(1). In particular, we will be interested in z-polarized IR spectra, for which the signal intensity is given as IIRz(ω) ∼ Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χzz(1)(ω).26 In practice, the integral in eqn (2) is done again up to a finite time tsample, and complemented by a Hann window function.
χzz(1)(ω).26 In practice, the integral in eqn (2) is done again up to a finite time tsample, and complemented by a Hann window function.
Another simplification of eqn (2), used also in ref. 25 and 26 is that, it assumes dipole moment derivatives being isotropic w.r.t. the surface. For CO/NaCl(100), this is not the case. Rather than re-deriving eqn (2) to include this dependence, we take the anisotropy effect into account by a simplified procedure, leading, for the z-polarized case, to
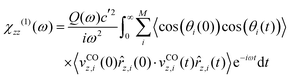 | (3) |
 along z on the polar angle θ (cf. ESI,† Section S1.5 and Fig. S3). Details concerning eqn (3) are described in the ESI,† Section S1.4, where also an expression (eqn (S3), ESI†) valid for x- and y-polarized spectra can be found, utilizing θ-dependent
along z on the polar angle θ (cf. ESI,† Section S1.5 and Fig. S3). Details concerning eqn (3) are described in the ESI,† Section S1.4, where also an expression (eqn (S3), ESI†) valid for x- and y-polarized spectra can be found, utilizing θ-dependent  along x and y, respectively. In eqn (3), c′ (= −0.899e) is a parameter derived from fitting DFT results for a CO/NaCl cluster model of the dipole derivative to
along x and y, respectively. In eqn (3), c′ (= −0.899e) is a parameter derived from fitting DFT results for a CO/NaCl cluster model of the dipole derivative to  , cf. ESI,† Section S1.5. Further
, cf. ESI,† Section S1.5. Further ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) z,i(t) is the z-component of the instantaneous unit CO bond vector for the ith CO molecule at time t. The form (3) is particularly relevant when computing integrated absorbance ratios of the IR response, especially at T = 300 K (see below). We note that before taking the Fourier transform, one should normalize the molecularly decomposed VVAFs w.r.t. the absolute value of the total response, otherwise, the sign induced by so called “orientational” VVAFs would be washed away (see below).
z,i(t) is the z-component of the instantaneous unit CO bond vector for the ith CO molecule at time t. The form (3) is particularly relevant when computing integrated absorbance ratios of the IR response, especially at T = 300 K (see below). We note that before taking the Fourier transform, one should normalize the molecularly decomposed VVAFs w.r.t. the absolute value of the total response, otherwise, the sign induced by so called “orientational” VVAFs would be washed away (see below).
 | (4) |
 is the derivative of the ab component of polarizability of the C–O molecule along the C–O coordinate, r, and assumed independent of ω again. They were either treated as constants or derived from linear fits of dipole derivatives of upright CO on NaCl along the molecular axis, and derivatives of αxx, respectively, using cluster models again (cf. ESI,† Section S1.5), giving
is the derivative of the ab component of polarizability of the C–O molecule along the C–O coordinate, r, and assumed independent of ω again. They were either treated as constants or derived from linear fits of dipole derivatives of upright CO on NaCl along the molecular axis, and derivatives of αxx, respectively, using cluster models again (cf. ESI,† Section S1.5), giving  . Total VSF intensities are computed as IVSFssp ∝ |χxxz(2)(ω)|2 in this work, while real and imaginary parts of χxxz(2)(ω) serve to be useful for understanding orientational effects.
. Total VSF intensities are computed as IVSFssp ∝ |χxxz(2)(ω)|2 in this work, while real and imaginary parts of χxxz(2)(ω) serve to be useful for understanding orientational effects.
Again, the above formulation does not account for anisotropies of the polarizability derivatives, and also not of the dipole derivatives. Following a similar approach as done for the 1st order susceptibility, we modify the original VSF response25 by including the angular dependence of the dipole and polarizability derivatives as, for the “ssp” (or “xxz”) case:
 | (5) |
 in eqn (4) we take specifically for the “ssp” polarized response the αxx derivative, which then leads to eqn (5). The a′, b′, e′ and d′ are parameters, again based on cluster models (see ESI,† Section S1.5), and a fit dαxx/dr = a′
in eqn (4) we take specifically for the “ssp” polarized response the αxx derivative, which then leads to eqn (5). The a′, b′, e′ and d′ are parameters, again based on cluster models (see ESI,† Section S1.5), and a fit dαxx/dr = a′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(b′θ + e′) + d′, with a′ = 2.99, b′ = 1.55, e′ = −2.146 and d′ = 5.62 (all in atomic units, except b′, which is a constant and e′ which is in rad.) The parameter c′ is the same as before.
cos(b′θ + e′) + d′, with a′ = 2.99, b′ = 1.55, e′ = −2.146 and d′ = 5.62 (all in atomic units, except b′, which is a constant and e′ which is in rad.) The parameter c′ is the same as before.
 | (6) |
 | (7) |
2.4 Analysis of internal mode correlations
We quantify internal mode correlations not only from spectra but also from AIMD trajectories. First, angular and CO–surface distance distribution probabilities are calculated as | (8) |
In a more generalized approach, correlation between all internal DoFs can be measured via correlation coefficients. Below we shall occasionally study so-called distance correlation matrices (as defined by Székely et al.31), where covariances of the quantities themselves are evaluated not from their respective means, but from distances of all other points. We evaluate intra- and inter-correlation distance matrices with elements R(a,b), which indicate the correlation of internal DoF a ∈ {r,θ,ϕ,X,Y,Z} of a CO molecule with internal DoF b of the same or another molecule. The mathematical definition of the distance correlation matrices used in this work is given in the ESI,† Section S4.3.
3 Results and discussion
3.1 Energetics of different phases
On the PBE+D2 level of theory, for monolayer structures (C, D, E and F in Fig. 2), the “all C-bound” P/U 1 ML structure D is 20 meV (∼161 cm−1) higher in energy per CO compared to the “all C-bound” 1 ML T/A configuration, D. The latter is the most stable structure found (cf.Table 1). The T/A configurations with one “O-bound” CO per cell (structure E), is 84 meV (∼678 cm−1) higher in energy than D, which is the energy needed to flip one CO from “C-bound” to “O-bound” while keeping the neighbouring COs “C-bound”. Flipping all (four) “C-bound” COs to “O-bound” (structure F), costs 85 meV (∼686 cm−1) per CO molecule, showing that the C-bound → O-bound flipping energy is largely independent of the orientation of CO neighbours. For completeness, we note that the classical isomerization barrier for the back-flipping reaction (O-bound → C-bound) is ∼500 cm−1 in a 1/8 ML coverage compared to ∼570 cm−1 for a 1/4 ML coverage.16 For monolayer and buried monolayer cases, computed minimum energy pathways indicate isomerization barriers near 565 and 600 cm−1 respectively,13 reflecting a dependence of CO coverage on the isomerization barrier.| Configuration | Energy/CO (meV) | C–O stretch frequencies (cm−1) | |||
|---|---|---|---|---|---|
| A (1/4 ML, “C-bound”) | — | 2141.2 | — | — | — |
| B (1/2 ML, “C-bound”) | — | 2128.2 (1.0000) | 2122.7 (0.0763) | — | — |
| C (T/A, “all C-bound”) | 0 | 2128.5 (1.0000) | 2124.2 (0.1738) | 2121.6 (0.0193) | 2119.5 (0.0296) |
| D (P/U, “all C-bound”) | 20 | 2138.6 (1.0000) | 2131.1 (0.0729) | 2127.4 (0.0402) | 2119.3 (0.0041) |
| E (T/A, “one O-bound”) | 84 | 2127.6 (1.0000) | 2122.6 (0.0011) | 2120.9 (0.0432) | 2116.2 (0.0146) |
| F (T/A, “all O-bound”) | 85 | 2121.3 (0.0596) | 2120.9 (0.2314) | 2118.2 (1.0000) | 2109.0 (0.0174) |
We also computed Gibbs free energies, G = H − TS = ESCF + Gvib (with H being the enthalpy and S the entropy), taking vibrations in harmonic approximation from normal mode analysis into account,32cf. Section 3.2. The free energy contains, in addition to SCF energies ESCF, zero-point energy, finite-T vibrational enthalpy contributions and also vibrational entropies (summarized in Gvib). Within the harmonic approximation, we find that the T/A all “C-bound” phase remains the most stable phase for temperatures up to 150 K, i.e., in particular no T/A → P/U phase transition (expected around 35 K) is found, cf. ESI,† Section S2.2. The harmonic approximation and the utilized DFT functional (owing to the presence of small imaginary frequencies for the P/U phase) is found to be insufficient to show such an effect.
3.2 “Vibrational spectra” from normal mode analysis
NMA gives a first idea on vibrational spectra. The harmonic C–O stretch frequencies for the 1 ML phases C–F are also listed in Table 1, as well as the CO frequency of the low-coverage model A for comparison. Further, in the ESI,† Section S2.1 and Fig. S5 we show normal mode “spectra”, obtained from Gaussian broadening of stick spectra for optimized configurations A–F of CO/NaCl(100). (Also, some technical details of NMAs are described in the ESI.†)For the tilted/antiparallel (T/A) phase of the CO monolayer on NaCl(100), the fundamental C–O stretch mode yields vibrational frequencies in the range 2120–2130 cm−1, for different combinations of in-phase and out-of-phase vibrations for the four adsorbed CO molecules. For the lowest coverage studied, i.e., 0.25 ML (model A), the C–O stretch mode is blue-shifted peaking at ∼2141 cm−1. The 1 ML P/U phase (model D) of CO/NaCl(100) shows frequencies between 2138–2119 cm−1 in the C–O stretch region, a broader frequency range compared to the T/A phase (model C). For the remaining metastable 1 ML T/A configurations with one (model E) or more “O-down” CO molecules (model F), we see frequencies in the range 2109–2128 cm−1. Comparing to experimental results in ref. 9, we see a systematic red-shift of the PBE+D2 NMA frequencies by ∼20 cm−1.
In summary, for the 1 ML T/A phases, flipping one or all CO molecules to “O-down” leads (i) to a broader frequency range, and (ii) to an overall red-shift of (some parts of) the spectrum. We further see that (iii) the frequency of low-coverage CO/NaCl(100) (model A) is blue-shifted w.r.t. the highest-energy peak of all T/A ML phases, by at least 10 cm−1.
In addition to the high-frequency modes, CO frustrated bending and CO–surface modes for the “C-bound” configurations are found, with frequencies around 100–160 cm−1 and 70–100 cm−1, respectively. Below 60 cm−1, we mainly find CO librational modes. The substrate phonons span over the frequency region between 0–220 cm−1.
3.3 Vibrational density of states and AIMD analysis
To go beyond harmonic and zero-temperature approximations, VDOS curves were calculated from AIMD at two temperatures, T = 30 and 300 K. The latter corresponding to room temperature was chosen to study (plausible) thermally-induced CO flipping in the system and its influence on the different vibrational spectra simulated below. The AIMD simulations also serve to provide insight into the ongoing dynamics.Before considering low-frequency modes which are also shown in Fig. 3 (left), we discuss the effects of flipping one or several CO molecules “upside down” and of additional CO layers on CO stretch frequencies in Fig. 4. There we report the VDOS curves for 1 ML T/A models with one “O-bound” CO (model E), and all “O-bound” CO configurations (model F). In addition, the already mentioned, new (PBE+D2 optimized) model G is shown, with a CO-buried monolayer with one “O-bound” CO (see also ref. 13).
The VDOS curve for model E shows a broader peak in the CO-stretch region, with the “O-bound” signal around 2116 cm−1, red-shifted from the “C-bound” CO signals around 2125 cm−1 (see also model C, and dashed vertical line). The red-shift of about 9 cm−1 is somewhat lower than the shift of ∼15 cm−1 found experimentally in ref. 9, albeit for a 1 ML 13C18O/NaCl(100) system. The VDOS of the buried model G has a higher VDOS intensity in the C–O stretch region compared to model E, due to the contributions of the CO overlayers. (The same VDOS scale has been used in the three panels F, E, G.) When finally going to model F (no overlayers, all four CO molecules “O-down”), all C–O stretch vibrations are red-shifted w.r.t. “C-down”, in agreement with experiments9 and the NMA (see Table 1).
For the T/A monolayer phases, at T = 30 K, AIMD predict for “C-down” configurations narrow θ distributions with a mean around 30° over the sampling time of the canonical trajectories (cf. ESI,† Section S4.1 and Fig. S11(a)), along with a moderate lateral displacement of COs away from Na+, by <1 Å (not shown). “O-bound” CO have a mean, averaged angular probability distribution P(θ) of 130° (50° w.r.t. the axis perpendicular to the surface), cf. Fig. S11(b) and (c) (ESI†), and show more lateral translation compared to the “C-bound” CO molecules, by up to ∼1.7 Å away from Na+ (not shown). In all cases, the long-range T/A order is largely maintained in the monolayer configurations. We further note that during the timescale of our simulations (∼3 × 30 ps), none of the “O-bound” CO molecules flipped to “C-down” in the monolayer case. In contrast, for a low-coverage case (0.25 ML) in an “O-bound” configuration, we found, in a single test trajectory, CO flipping to the more stable “C-bound” at 22 K within 10 ps (not shown here). This indicates that the presence of neighbouring COs provides new channels for energy transfer and therefore may decrease the flipping rate relative to low coverages. Note that in experiment,12 at around T = 20 K, “O-down” 12C16O molecules in buried monolayers on NaCl, flip with a rate of ∼10−4 s−1, indicating a flipping time of several hours.
Turning now our focus to the low-frequency region of the VDOS curves in Fig. 3 and 4, we find it to be dominated by CO–surface vibrations and CO frustrated translations (tangential motion along the surface) and rotations, as well as phonon modes from the NaCl surface, up to 200 cm−1. We can more unambiguously assign internal motions responsible for respective peaks by inspecting the internally resolved VDOS as defined in the ESI,† Section S1.3. For instance, in Fig. 5(a), we observe that the frustrated θ rotation contributes to peaks observed at ∼150, 180 cm−1 and a minor peak around 40 cm−1. Peaks associated with frustrated translations appear at frequencies below 45 cm−1. The predominant peak at 160 cm−1 arises from the frustrated azimuthal angle (ϕ) rotation, with additional contributions around 90 and 30 cm−1. Motion perpendicular to the CO–surface (Z) results in peaks at around 75, 165, and 205 cm−1. Comparing the Cartesian and internal VDOSs, we note that in the low-frequency region (0–140 cm−1), the latter is smaller than the former, compensated by the larger peak at 160 cm−1 from the frustrated ϕ motion. The enhanced low-frequency normal modes are speculated to stem from coupling between the internal ϕ motion and other librational modes. Note that the total integrated area under the Cartesian and internal VDOS is the same. Interestingly, for “O-bound” CO adsorbates (Fig. 5(b)), all the low frequency modes are also largely red-shifted compared to the vibrations coming from the “C-bound” adsorbates. Note here that the PBE+D2 values for the low-frequency region may lack accuracy due to the dominance of dispersion effects and the incomplete cancellation of self-interaction errors in the applied DFT method. As such, the reported values should be regarded as approximate.
In Fig. 6 we show Cartesian and internal VDOS curves for both studied systems, in low- and high-frequency (C–O stretch) regimes. Also shown are trajectory snapshots for both systems, indicating large-amplitude motions away from the surface and even desorption. In general, the VDOS profile is broader compared to the T = 30 K spectra. (As expected, also angular distributions P(θ) and P(ϕ) are much broader at T = 300 K compared to T = 30 K, cf. Fig. S12 in the ESI,† Section S4.1.) One can discern from Fig. 6(II), that the Cartesian VDOS (orange curve) obtained for the 1 ML P/U phase starting configuration shows a doublet peak around 2110 cm−1 and 2138 cm−1 resulting from rovibrational coupling typically observed for gas-phase CO spectra: the two peaks correspond to two rotational transition branches, R (J → J + 1; blue-shifted) and P (J → J − 1; red-shifted), the dip in the middle signifying the vibrational transition from v → 0 to v → 1. For the internal VDOS (blue), the ro-vibrational structure disappears due to the elimination of the velocity component responsible for the CO bond rotation, and only a single peak appears at ∼2125 cm−1. Upon closer examination, one can also observe oscillations in the total internal VDOS spectra in the CO stretch regime. These stem from the azimuthal DoFs of the pseudo gas-phase CO molecules present above the NaCl surface which undergo rapid azimuthal motion, flipping, “roaming” and desorption of the CO molecules. Insight into large-amplitude motions along Z, for example, at high T, can be gained from CO–surface distance probabilty distributions P(Z) in the ESI,† Section S4.2 and Fig. S13, highlighting also that desorption is negligible at T = 30 K. For the case where initial configuration at equilibrium was one “O-bound” CO surrounded by “C-bound” COs, similar flipping and desorption events are observed. In some trajectories the CO adsorbates are far above the surface and undergo periodic flipping, with a time period of ∼0.7 ps. In the Cartesian VDOS reported in Fig. 6(IV), we find quartet peaks spanning the CO-stretch stretch region, while only one peak with a shoulder appears in the internal VDOS. This showcases more complex dynamics due to the initial presence of differently oriented CO molecules. Note here, a recent study by Nandi et al.,33 which reported roaming-facilitated isomerization dynamics in the same system, albeit at low temperatures, using quasi-classical trajectories and cluster models.
The low-frequency VDOS curves at T = 300 K (panels I, III) are qualitatively similar to those found at T = 30 K, the main difference being larger relative weights in lowest-energy regions at and below ∼50 cm−1. Again, this is a consequence of internal rotation diffusion,27i.e., less hindered translational and rotational motions of some molecules at the higher temperature.
A clear difference can be seen between them in Fig. 7(a), where the joint probability distribution curve manifests a double-stranded structure in contrast to the product probability curve which displays a lack of structure and a wide distribution over {θ,ϕ}. The fact that P(θ,ϕ) ≠ P(θ)P(ϕ) signifies a correlation between the angular degrees of freedom, near room temperature where enough thermal energy for vibrational excitation of the angular modes is available. Also, flipping events manifest as “S-type” curves in the joint probability functions, signifying correlated (θ, ϕ) motion.
In order to go beyond angular correlations, we evaluated distance correlation matrices for all internal DoFs as described in Section 2.4 and ESI,† Section S4.3. Selected intra- and inter-molecular correlation matrices with elements R(a,b) are reported in the ESI,† Section S4.3 (Fig. S14–S16), for various coverages and models. As only one finding we mention here that the internal C–O stretch mode (r), largely independent of model, is typically decoupled from all other modes, both within a molecule and between two CO molecules. In contrast, angular and translational DoFs are more stongly coupled among each other. Further details, also regarding “O-down” vs. “C-down” configurations, are provided in the ESI.†
We also studied diffusion and orientational dynamics of the disordered CO adsorbates at 300 K, more details can be found in ESI,† Section S4.4.
3.4 Infrared spectra
 | (9) |
The parametrized formulation (3) for χab(1)(ω) with ACFs (with orientation factors) has been utilized to simulate the IR responses if not stated otherwise. A comparison with the original formulation (2) without angle-dependent dipole derivatives, can be found in the ESI,† Section S3.1 and Fig. S7, for the T = 300 K case. As argued there, in particular at these higher temperatures when CO molecules undergo large-amplitude motions, eqn (3) (and eqn (S3), ESI†) is expected to be the more accurate approach – more evidence will be given shortly.
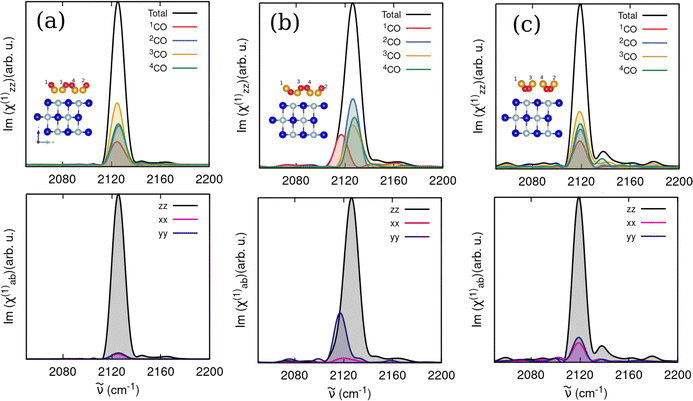
Fig. 8 shows IR spectral responses at T = 30 K, for two low-coverage models of 0.25 ML and 0.5 ML (model A and B in Fig. 2). For 0.25 ML (Fig. 8(a)), the peak maximum is found around 2134 cm−1, blue-shifted compared to the 0.5 ML case (Fig. 8(b)), where the CO-stretch peak occurs at 2128 cm−1. The overall red-shift with increasing coverage is consistent with the VDOS curves reported earlier. Experimentally, FTIR absorption peaks for CO/NaCl at 0.57 ML, for example, at 10 K, are at around 2155 cm−1,8 reflecting a systematic red-shift of the PBE+D2 AIMD frequencies by ∼30 cm−1. Note that the width of the IR spectra reported here arises not only from thermal effects but also from the limited propagation time of the AIMD simulations yielding a resolution of 11 cm−1, as mentioned before.
From the simulated polarization-dependent spectra at both coverages, we observe much weaker x- and y-polarized responses compared to the z-polarized response. The IAR is 0.01 and 0.07 for 0.25 and 0.5 ML coverages, respectively. The IARs are 0.06 and 0.1 when evaluated using the original formulation for the χab(1) in eqn (2), showing that the anisotropy of the dipole moment derivative causes smaller IARs, even at the low temperature of 30 K. Experiments8 give IARs for a 0.25 and 0.5 ML CO/NaCl(100) sample at 10 K of <0.05 and <0.15, respectively. Thus we obtain the same trend, however, due to different temperatures (T = 10 K in experiment, 30 K in simulation), a quantitative agreement cannot be expected.
We then computed analogous spectra in the CO-stretch region for 1 ML T/A CO/NaCl(100) equilibrated at 30 K for different CO orientations, namely all “C-bound” (model C), one “O-bound” (model E) and all “O-bound” (model F) in Fig. 9. For the all “C-bound” configuration (Fig. 9(a)), a Lorentz-like band profile is observed with a single broad peak at ∼2125 cm−1. The one “O-bound” configuration (Fig. 9(b)), results in a broader peak, due to the presence of the red-shifted peak around 2117 cm−1 originating from the “O-bound” CO, similar to the VDOS curves. The all “O-bound” configuration (Fig. 9(c)), yields a peak maximum around 2118 cm−1. The computed IARs are 0.08, 0.33 and 0.38 for the all “C-bound”, one “O-bound” and all “O-bound” configurations, respectively, showing that the CO orientation (“C-down” vs. “O-down”) has a substantial effect on IARs.
We also investigated the effect of intermolecular couplings by including velocity cross-correlation functions among the different CO adsorbates in the first-order susceptibility expressions (eqn (6)). As shown in the ESI,† Section S3.2, for the 1 ML system with one “O down” (model E) at 30 K, the inclusion of cross-correlation influences spectra of all molecules by blue-shifting the C–O peaks by a few wavenumbers (∼4 cm−1), and changing their relative intensities. In this case, IAR values are only moderately increased, from 0.33 without cross-terms to 0.38 with cross-terms. Further discussions on the role of cross-correlations on the IR spectral response can be found in the ESI,† Section S3.2.
 | ||
| Fig. 10 Computed IR spectral response of the CO/NaCl(100) system from trajectories starting from a 1 ML (a) P/U phase (model D), (b) one “O-bound” T/A phase configuration (model E), equilibrated at 300 K. The VVAFs leading to the spectra are averaged over five trajectories. Left panels show molecule-resolved and total spectra, right panels polarization-resolved total spectra with insets giving the same snapshots of AIMD trajectories as in Fig. 6. | ||
In summary, our calculations follow the observed experimental trends at low T for “C-down” species, i.e., increasing IARs with increasing coverage (albeit not quantitatively), and they predict in addition, greatly enhanced IARs due to (i) CO inversion to “O-down” and/or (ii) high temperatures.
We close this section by addressing the issue of Davydov splittings observed for CO/NaCl at low temperatures. All spectra so far were calculated with a resolution of 11 cm−1, which is larger than the Davydov splitting of C–O stretch peaks of ΔD ∼ 6 cm−1, observed for example for the 1 ML T/A phase at temperatures below 30 K.7 In recent work, some of us have developed a machine-learned, neural network (NN) potential constructed from AIMD calculations similar to those here,12 which allowed for tsample = 16 ps and a spectral resolution of ca. 2 cm−1 – enough to resolve the mentioned Davydov splittings. In ref. 12, at T = 5 K trajectories were run on the trained NN potentials, showing indeed a Davydov splitting of the IR C–O stretch signal. More specifically, with the “Generation 6” NN potential, for the 1 ML T/A phases all “C-bound” (model C), one “O-bound” (model E), and all “O-bound” (model F), Davydov splittings of the peaks of 4.5, 3, and 8 cm−1 were found. These are in the correct order of magnitude for model C, and in addition predict a dependence of Davydov splittings if some or all CO molecules are inverted (models E and F).
3.5 Vibrational sum frequency (VSF) spectra
We also simulated VSF responses in the CO-stretch region for CO/NaCl, again, for different coverages, adsorbate orientations and temperatures, which so far have not been reported experimentally or theoretically for this system. Note that similar to the IR response, VSF spectra reported below were computed by the parametrized VVCF formulations that include angle-dependent dipole and polarizability derivatives, eqn (5) (without cross-correlations) or (7) (with cross-correlation). A comparison with the original formulation of Ohto et al.,25eqn (4) can be found in the ESI,† Section S3.3. As mentioned earlier, we also did not consider Fresnel factors and averaging, and rather show as a measure for an ssp-polarized VSF signal |χxxz(2)|2, as well as Im{χxxz(2)} as the absorption response corresponding to the dissipative part as well as Re{χxxz(2)}, the dispersion response.In Fig. 11, we show |χxxz(2)|2, Im{χxxz(2)}, and Re{χxxz(2)} for two 1 ML CO/NaCl(100) models at T = 30 K, namely T/A all “C-bound” (model C), Fig. 11(a), and T/A one “O-bound” (model E), Fig. 11(b) respectively. Solid curves give total (black) and molecule-resolved (coloured) signals, and both the results without cross-correlations (eqn (5), dashed curves) and with cross-correlations (eqn (7) solid curves) are shown.
 | ||
| Fig. 11 VSF spectra (intensity, imaginary and real responses) of (a) 1 ML T/A all “C-bound” CO/NaCl(100) (model C), and (b) T/A one “O-bound” CO/NaCl(100) (model E), at T = 30 K. Spectra are calculated with angular-dependent, parametrized forms, either without cross-correlation terms (eqn (5), dashed) or with cross-correlations included (eqn (7), solid). Besides total (black), also molecule-resolved spectra (coloured) are shown. | ||
The 1 ML CO/NaCl(100) with all “C-bound” CO configuration without cross-correlations gives a total VSF signal for the CO stretch at 2128 cm−1 (Fig. 11(a), upper panel, dashed), similar to IR and VDOS responses. The corresponding Im(χxxz(2)) signal (Fig. 11(a), middle panel) shows a negative signal. For the one “O-bound” configuration, the VSF response in Fig. 11(b), upper panel, yields a CO stretch signal coming from “C-bound” molecules around 2127 cm−1, and a red-shifted peak at 2117 cm−1, giving an overall non-Lorentzian shape. In the imaginary response, the “C-bound” CO(s) yield a negative peak, while the “O-bound” CO yields a positive peak, resulting in a total signal with sign change (Fig. 11(b), middle). As argued in the ESI,† Section S3.3, this sign change for “O-down” is due to a sign change of the dipole derivative. When all adsorbed molecules are “O-bound”, we obtain a CO-stretch peak centered around 2119 cm−1 and a corresponding positive peak in the imaginary response (not shown). Both the non-Lorentzian shape in (b), upper panel, and, even more so, the sign-change in the imaginary part in (b), middle panel, are characteristic signatures of a flipped CO molecule with “O-down”; they should be useful identifiers in VSF spectra. Differences between the one “O-down” and all “C-down” systems for real parts of χxxz(2) in the lower panels of Fig. 11 are less pronounced, and probably not well suited to identify flipped CO.
We note further from Fig. 11, solid curves, that the inclusion of cross-correlations in the correlation functions, eqn (7), has, for the present examples, the consequences that signals are blue-shifted (by typically ∼10 cm−1), and that the asymmetry of the total VSF signal (upper panel of (b)) becomes more pronounced. We find also that introduction of cross-correlation terms, results in two peaks in the molecularly decomposed imaginary responses of all “C-down” ((a), middle panel, solid), making it harder to detect differences to the one “O-down” case ((b), middle panel, solid).
In summary, cross-correlations lead to blue-shifted VSF spectra (similar to IR), and to slightly different lineshapes at high (1 ML) coverages. In the ESI,† Section S3.3, we also report the VSF response at lower coverage (0.5 ML, model B) at T = 30 K, using eqn (5) (angle-dependent dipole and polarizability derivatives, Fig. S9, ESI†). When comparing this against spectra computed viaeqn (4) (no angle-dependence), the differences between the two spectra are found to be negligible. Further, in Fig. S10 in the ESI,† Section S3.3, 1 ML P/U (model D) and 1 ML T/A one “O-bound” starting configurations (model E) were considered, at T = 300 K. In this case, strongly reduced VSF intensities are found compared to T = 30 K due to orientational disorder (and partial desorption) of CO at higher temperatures.
4 Conclusions and outlook
The primary emphasis of this study was in the simulation and analysis of vibrational spectra of CO at NaCl(100), for varying coverages, temperatures, and CO orientations. We aimed to provide insights into the structural and dynamic characteristics, using an AIMD-VVCF methodology. As a methodological aspect, we further attempted to explore effects of inclusion or non-inclusion, of orientational and cross-correlation in the correlation functions used for spectra evaluation. Some of our main findings are:• We find strong dependence of vibrational signals on coverage and CO orientation (“C-down” vs. “O-down”), with higher coverages and “C-down” to “O-down” inversion causing red-shifts, notably of C–O stretch modes, in agreement with experiments.
• At low temperature (30 K), CO molecules undergo only small-amplitude motions while at T = 300 K, large-amplitude motions including roaming and desorption occur, with pronounced effects on spectra beyond simple line broadening. For example, a decrease in the coverage of CO molecules reduces dipole and multipole couplings between them; as a result coherence is lost, resulting in asymmetric tails and diffuse peaks in spectra.
• We have tested a modified formulation of the VVCF methodology with angle-dependent dipole and polarizability derivatives, and how it impacts the overall IR (integrated absorbance ratios) and the VSF response for situations where anisotropy of the dipole moment prevails. The inclusion of non-anistropic terms in the VVCFs is particular important at higher temperatures. Then, also cross-correlations come into play, notably at high coverages.
• VSF spectra have been predicted for CO/NaCl which have the potential to give more direct insight into orientational dynamics campared to IR spectra, notably from imaginary parts of the VSF response.
• Insight into vibrational dynamics and mode couplings was also provided by distribution functions P(a), and intra- as well as inter-molecular correlation distance matrices R(a,b).
One possible extension of this work is to evaluate time-dependent transient spectra for non-equilibrium situations, for instance, pumping additional energy into the CO-stretch mode and follow how the energy redistributes into the neighbouring adsorbates and the NaCl surface. This has implications for various interesting phenomena the CO/NaCl(100) system is famous for, e.g. vibrational energy pooling and CO inversion and will appear soon in a follow-up publication.
Data availability
The optimized geometries used as starting structures for the AIMD simulations are available in Zenodo under https://doi.org/10.5281/zenodo.14356595. Other AIMD data for vibrational spectra and analysis can be obtained upon reasonable request from the author.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Giacomo Melani (Milano) for fruitful discussions on simulations of vibrational spectra, and Christopher Penschke (Potsdam) for help with computation of IR intensities of normal modes. We also thank David Picconi (Düsseldorf) for a useful suggestion about checking angular correlations. We thank the Deutsche Forschungsgemeinschaft (DFG) for support through project Sa 547/18-1 and the North-German Supercomputing Alliance (HLRN) under the Nationales Hochleistungsrechnen (NHR) initiative for providing HPC resources. SS also thanks the International Max Planck Research School for Elementary Processes in Physical Chemistry for support.Notes and references
- J. Heidberg, E. Kampshoff and M. Suhren, J. Chem. Phys., 1991, 95, 9408 CrossRef CAS.
- J. Vogt and B. Vogt, J. Chem. Phys., 2014, 141, 214708 CrossRef PubMed.
- S. Picaud, P. N. M. Hoang, C. Girardet, A. W. Meredith and A. J. Stone, Surf. Sci., 1993, 294, 149–160 CrossRef CAS.
- A. D. Boese and P. Saalfrank, J. Phys. Chem. C, 2016, 120, 12637–12653 CrossRef CAS.
- C. Noda and G. E. Ewing, Surf. Sci., 1990, 240, 181–192 CrossRef CAS.
- C. Noda, H. H. Richardson and G. E. Ewing, J. Chem. Phys., 1990, 92, 2099–2105 Search PubMed.
- D. Dai and G. Ewing, Surf. Sci., 1994, 312, 239–249 Search PubMed.
- J. A. Lau, A.-M. Schönemann, D. Schwarzer and A. M. Wodtke, J. Chem. Phys., 2020, 153, 154703 Search PubMed.
- J. A. Lau, A. Choudhury, C. Li, D. Schwarzer, V. B. Verma and A. M. Wodtke, Science, 2020, 367, 175–178 Search PubMed.
- L. Chen, D. Schwarzer, V. B. Verma, M. J. Stevens, F. Marsili, R. P. Mirin, S. W. Nam and A. M. Wodtke, Acc. Chem. Res., 2017, 50, 1400–1409 Search PubMed.
- S. Corcelli and J. Tully, J. Chem. Phys., 2002, 116, 8079–8092 CrossRef CAS.
- S. Sinha, B. Mladineo, I. Lončarić and P. Saalfrank, J. Phys. Chem. C, 2024, 128, 21117–21131 CrossRef CAS.
- A. Choudhury, S. Sinha, D. Harlander, J. DeVine, A. Kandratsenka, P. Saalfrank, D. Schwarzer and A. M. Wodtke, Nat. Sci., 2023, 3, e20230006 Search PubMed.
- L. Chen, J. A. Lau, D. Schwarzer, J. Meyer, V. B. Verma and A. M. Wodtke, Science, 2019, 363, 158–161 Search PubMed.
- J. Chen, S. Hariharan, J. Meyer and H. Guo, J. Phys. Chem. C, 2020, 124, 19146–19156 Search PubMed.
- S. Sinha and P. Saalfrank, Phys. Chem. Chem. Phys., 2020, 23, 7860–7874 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 Search PubMed.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- T. Ohto, K. Usui, T. Hasegawa, M. Bonn and Y. Nagata, J. Chem. Phys., 2015, 143, 124702 Search PubMed.
- G. Melani, Y. Nagata, R. K. Campen and P. Saalfrank, J. Chem. Phys., 2019, 150, 244701 Search PubMed.
- P.-K. Lai and S.-T. Lin, J. Comput. Chem., 2015, 36, 507–517 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- G. J. Székely, M. L. Rizzo and N. K. Bakirov, Ann. Stat., 2007, 35, 2769–2794 Search PubMed.
- S. Heiden, D. Usvyat and P. Saalfrank, J. Phys. Chem. C, 2019, 123, 6675–6684 Search PubMed.
- A. Nandi, P. Zhang, J. Chen, H. Guo and J. M. Bowman, Nat. Chem., 2021, 13, 249–254 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Technical details on AIMD calculations, computation of VVAFs, VDOS in internal coordinates, anisotropy inclusions in dipole and polarizability derivatives to compute IR and VSF spectra; normal modes and vibrational free energies; testing methodological variants and inclusion of cross-correlations for computing IR and VSF spectra; analysis of trajectories (mode correlations, diffusion and orientation dynamics). See DOI: https://doi.org/10.1039/d4cp04671d |
| This journal is © the Owner Societies 2025 |