Open Access Article
Open Access ArticleUniversal kinetic description for the thermal dehydration of sodium carbonate monohydrate powder across different temperatures and water vapor pressures†
Shunsuke
Fukunaga
,
Yuto
Zushi
,
Mito
Hotta
 and
Nobuyoshi
Koga
and
Nobuyoshi
Koga
 *
*
Department of Science Education, Graduate School of Humanities and Social Sciences, Hiroshima University, 1-1-1 Kagamiyama, Higashi-Hiroshima 739-8524, Japan. E-mail: nkoga@hiroshima-u.ac.jp; Fax: +81-82-424-7092; Tel: +81-82-424-7092
First published on 15th January 2025
Abstract
The thermal dehydration of sodium carbonate monohydrate (SC-MH) exhibits kinetic characteristics that are typical of the thermal decomposition of solids with a reversible nature. One of the characteristics is the physico-geometrical constraints of the reaction due to the heterogeneous reaction feature. Another factor is the considerable impact of the atmospheric and self-generated water vapor on the kinetics. The objective of this study is to develop a universal kinetic description of the dehydration kinetics as a function of temperature, degree of reaction, and partial pressure of water vapor (p(H2O)), deriving kinetic parameters with physico-chemical significance based on the physico-geometrical kinetic model. The kinetic curves for the thermal dehydration of SC-MH were meticulously documented under isothermal and linear nonisothermal conditions at varying p(H2O) values using humidity-controlled thermogravimetry. The mass loss curves at a constant temperature exhibited a sigmoidal shape following an induction period, irrespective of the p(H2O) value. As the p(H2O) value increased, a systematic decrease in the reaction rate was observed. The challenge of providing a kinetic description for the complex reaction process was addressed by a step-by-step approach, which included the following four steps: (1) the development of a universal kinetic description that could be applied across varying temperatures and p(H2O) values, (2) the incorporation of the effect of self-generated water vapor into the universal kinetic description, (3) the interpretation of the physico-chemical meanings of the apparent kinetic parameters within the universal kinetic description, and (4) the extension of the universal kinetic description to encompass the physico-geometrical kinetic modeling.
1. Introduction
The thermal decomposition of solids with a reversible nature has a range of potential applications in practical processes. These applications include numerous technologies that address energy and environmental issues, including chemical heat storage,1–6 hydrogen storage,7–11 capture of various environmentally toxic gases,12–16 and others. In order to develop and refine these future technologies, it is essential to have a fundamental understanding of both the forward reaction of the thermal decomposition of the candidate compound and its reverse reaction of the solid–gas reaction. In particular, an understanding of the reaction thermodynamics and kinetics is crucial for the design of an effective reaction system for the practical applications. The kinetics of both the thermal decomposition of solids and the solid–gas reaction have been the subject of study for over a century. Consequently, the fundamental kinetic theories and analytical procedures for these reaction processes have been established.17–21 However, both the reaction processes exhibit intrinsic physico-chemical and physico-geometrical characteristics due to the geometric constraints inherent to the reaction.22,23 In addition, for reversible reactions occurring in a solid–gas system, both the forward and reverse reactions are significantly affected by the partial pressure of the gaseous species in the system. Therefore, an extension of the fundamental kinetic theories of both forward and reverse reactions is required to describe the kinetics universally as a function of temperature, degree of reaction, and partial pressure of the gaseous species. If possible, the establishment of a unified kinetic theory that is applicable to both the thermal decomposition of solids and the solid–gas reaction in a solid–gas system is desired to provide the necessary insight into the kinetics of both the reactions in a reversible system and to have a kinetic tool to evaluate the system for possible application.A universal kinetic description for the thermal decomposition of solids with a reversible nature has recently been achieved by introducing an accommodation function (AF) into the fundamental kinetic equation.24–38 The AF describes the variation of the reaction rate as a function of the partial pressure of the gaseous species in the reaction system. The practical applicability of the extended kinetic approach has been demonstrated by means of the thermal decomposition of inorganic hydrates,27,28,33,34,37 carbonates,29–32,36 and hydroxides24–26,31,35 over a range of temperatures and partial pressures of the gaseous species. Moreover, the impact of both the external gases in the reaction atmosphere, which serves as the measuring condition for the process, and the self-generated gas from the reaction were taken into account in the universal kinetic approach.32,36–38 Furthermore, it was demonstrated that the apparent kinetic parameters obtained through the universal kinetic approach can be correlated with the intrinsic kinetic parameters for the reaction by considering the contribution of the thermodynamic parameters of the reaction.37,38 Moreover, we have achieved the universal description of the kinetics of solid–gas reactions across different temperatures and partial pressures of gaseous species based on the counterpart theory for the thermal decomposition of solids.39 The practical kinetic analysis was demonstrated for the hydration of lithium sulfate anhydride to form its monohydrate. Consequently, the current objective is to establish a unified theory of the universal kinetic description that is applicable to the thermal decomposition of solids and the solid–gas reaction in a solid–gas system, as well as to develop the practical kinetic procedures for the universal kinetic approach.
The reactions occurring in the sodium carbonate–water vapor system, which include the thermal dehydration of sodium carbonate monohydrate (SC-MH) to form its anhydride (SC-AH) and the hydration reaction of SC-AH with water vapor to form SC-MH, were selected as a model system. The objective was to investigate the parallel applicability of a unified kinetic theory for the universal description of the thermal decomposition of solids and the solid–gas reaction in a specific solid–gas system at different temperatures and partial pressures of the gas involved in the system, as well as to evaluate the merit of the parallel application of a unified theory to the forward and reverse reactions. It was reported that the thermal dehydration of commercially available SC-MH compacted composite grains, consisting of columnar crystals and a matrix produced by the efflorescence of the decahydrate, was found to occur as the partially overlapping two-step process in a stream of dry N2.40 The first mass loss step of the thermal dehydration of the SC-MH matrix occurred as a physico-geometrical consecutive process that was composed of the surface reaction (SR) and three-dimensional (3D) phase boundary-controlled reaction (PBR), occurring after the induction period (IP). The second mass loss step was also regulated by the 3D PBR along with the cubic shape of the original SC-MH grain; however, an initial acceleration of the reaction was observed in the reaction stage characterized by overlapping with the previous mass loss step due to the gradual decrease of the self-generated water vapor. Besides, Baglie and DeVore reported a smooth single-step mass loss process for the thermal dehydration of SC-MH powders obtained by efflorescence of the decahydrate in a stream of dry N2.41 They suggested a significant dependence of the experimental thermoanalytical curves and the kinetic results on the sample mass (m0) due to the effect of the self-generated water vapor during the reaction. We have reported the effect of atmospheric water vapor on the thermal dehydration of the SC-MH compacted composite grain.34 The presence of the atmospheric water vapor resulted in a retardation of both reaction steps in the two-step thermal dehydration process. The kinetics of the individual reaction steps were universally described over different temperatures and the partial pressures of the atmospheric water vapor (p(H2O)ATM). It was proposed that both p(H2O)ATM and the partial pressure of the self-generated water vapor (p(H2O)SG) be considered for the interpretation of the kinetic behavior of the component reaction steps in the scheme of the universal kinetic description. The reversible nature of the thermal dehydration of SC-MH and the subsequent hydration of SC-AH at a lower temperature in the presence of water vapor has been reported by Ball et al.42 The preliminary experiments conducted for this study using a humidity-controlled thermogravimetry (TG) system yielded evidence confirming a smooth single-step mass gain process following an IP at a constant temperature for the SC-AH produced by the thermal dehydration when exposed to a stream of wet N2 with a controlled p(H2O)ATM value. Furthermore, a trend of the promotion of the hydration reaction rate was observed with decreasing temperature and increasing p(H2O)ATM. Therefore, both the thermal dehydration of SC-MH powder and the hydration of SC-AH were found to exhibit specific physico-geometrical reaction behaviors and are significantly influenced by the water vapor present in the reaction system, while the overall reactions are characterized by smooth single-step mass change processes with a reversible nature. The observed behaviors of the reactions in the sodium carbonate–water vapor system indicate its suitability as a model system for the study of the parallel kinetic approaches to both the forward and reverse reactions using a unified theory for the universal kinetic description.
This article presents the initial findings of a series of kinetic studies on the reversible reactions in the sodium carbonate–water vapor system. It reports the universal kinetic description of the forward reaction of the thermal dehydration of SC-MH powders over a range of temperatures and p(H2O) values, including p(H2O)SG and p(H2O)ATM. The theory and analytical procedures of the universal kinetic description for the thermal decomposition of solids, which were previously established, were refined in stages towards further extension and the establishment of a unified theory applicable to both the forward and reverse reactions. Following an examination of the results of the conventional kinetic analysis applied to the thermal dehydration of SC-MH powders at varying p(H2O)ATM values, the universal kinetic description of the IP and mass loss processes across diverse temperatures and p(H2O)ATM values was attained through the implementation of a formal kinetic analysis, which encompassed the assessment of the isoconversional and isothermal kinetic relationships. Subsequently, the effect of p(H2O)SG was incorporated into the extended kinetic equation for extending the universal kinetic approach to include the reactions in a stream of dry N2, i.e., p(H2O)ATM ≈ 0. In addition, the physico-chemical significance of the apparent kinetic parameters determined through the universal kinetic approach was examined in order to obtain a correlation with the intrinsic kinetic parameters. Finally, the universal kinetic approach, founded upon the formal kinetic analysis scheme, was translated into physico-geometrical kinetic modeling for describing the physico-geometrical consecutive IP–SR–PBR process, which is characteristic of the thermal dehydration of SC-MH powders. The results obtained at each analytical stage are expected to provide further insight into the kinetics of the thermal dehydration of SC-MH and the thermal decomposition of solids in general. Furthermore, the strategy proposed for the universal kinetic approach to the thermal dehydration of SC-MH will be extended to the reverse reaction of the hydration of SC-AH, which will be reported separately as the counterpart of this article.
2. Experimental
2.1 Sample and its characterization
The SC-MH powders were prepared by the efflorescence of the chemical reagent of its decahydrate (Na2CO3·10H2O; special grade, FUJIFILM Wako Chem.) by exposure at an ambient temperature of 298 K and flowing dry N2 at a flow rate (qv) of 100 cm3 min−1 in a tube furnace overnight. The solid product obtained by the efflorescence of Na2CO3·10H2O was characterized by powder X-ray diffractometry (XRD), Fourier transform infrared spectrometry (FTIR), and simultaneous TG–differential thermal analysis (DTA) measurements. The XRD pattern of the efflorescence product pressed onto a sample holder plate was recorded using a diffractometer (RINT 2200V, Rigaku). While irradiating the sample with Cu-Kα (40 kV, 20 mA), the 2θ value was scanned from 5° to 60° in 0.02° steps at a scanning speed of 4° min−1 to record the XRD pattern. The FTIR spectrum was recorded using a spectrometer (FT-IR 8400S, Shimadzu) with the diffuse reflection method. After the sample was diluted with KBr, the FTIR measurement was performed in the wavenumber range of 4600–400 cm−1 with a resolution of 4 cm−1, and the spectra were accumulated 40 times. The sample was subjected to TG–DTA measurements to determine the mass loss value during thermal dehydration and to investigate the changes in reaction behavior as a function of m0 and qv of purge gas (i.e., dry N2). For the sample weighed in a Pt pan (diameter: 6 mm; depth: 2.5 mm), TG–DTA measurements were performed using a top-loading type instrument (DTG-60, Shimadzu) under isothermal conditions at a temperature of 315 K and under linear nonisothermal conditions at a heating rate (β) of 3 K min−1 in a stream of dry N2, for which m0 and qv were varied in the ranges of 2–13 mg and 10–100 cm3 min−1, respectively.The morphology of the efflorescence product was characterized by microscopic observations using a scanning electron microscope (SEM) and measurement of the Brunauer–Emmett–Teller (BET) specific surface area (SBET). The SEM observations were performed using an instrument (JSM-6510, JEOL) in the reflection mode after the sample particles were thinly coated with a Pt layer by sputtering (JEC-1600, JEOL; 30 mA, 30 s). The SBET value was determined by the BET single point method using an instrument (FlowSorb II, Micromeritics).
2.2 Tracking of the thermal dehydration in a stream of dry N2
The thermal dehydration of SC-MH in an inert gas atmosphere of a stream of dry N2 (qv = 300 cm3 min−1) was systematically tracked using a horizontal TG–DTA instrument (TG-8121, Thermoplus Evo2 system, Rigaku), for which the m0 weighed into a Pt pan (diameter: 5 mm; depth: 2.5 mm) was controlled to be 5.00 ± 0.05 mg. TG–derivative TG (DTG) curves were recorded in both isothermal and linear nonisothermal modes. In the isothermal mode, the TG–DTG measurements were conducted by initially heating the sample from 303 K to a preset temperature (312 ≤ T/K ≤ 332) at a β of 5 K min−1, and subsequently maintaining the temperature until the mass loss process was completed. In the linear nonisothermal mode, the sample was heated linearly from 303 to 423 K at various β values of 0.5–10 K min−1 to record TG–DTG curves. In particular, it was confirmed prior to the TG–DTG measurements that the N2 flow rate above 300 cm3 min−1 does not cause any significant change in the results compared to those at 300 cm3 min−1.Changes in the sample particle morphologies in the course of the thermal dehydration were investigated using SEM. The samples (m0 = 5.00 ± 0.05 mg) were partially dehydrated to varying degrees of reaction (α) using a TG–DTA instrument (DTG-60) by heating them in isothermal mode at T = 313 K for different times in a stream of dry N2 (qv = 100 cm3 min−1). The samples retained from the TG–DTA instrument were coated with a thin Pt layer via sputtering and subsequently examined under a SEM (JSM-6510).
2.3 Tracking of the thermal dehydration in a stream of wet N2
TG–DTA measurements were systematically conducted for the thermal dehydration of SC-MH in the presence of water vapor using a TG–DTA system (TG-8120, Thermoplus 2, Rigaku) equipped with a humidity controller (HUM-1, Rigaku) in a stream of wet N2 (qv = 400 cm3 min−1) with various p(H2O)ATM values, for which the identical sampling procedures, including the sample pan and m0 values, were employed as in the measurements in a stream of dry N2.A series of TG–DTG curves were recorded by heating the sample to 393 K under linear nonisothermal conditions at a fixed β of 5 K min−1 in a stream of wet N2 characterized by different p(H2O)ATM values (0.2 ≤ p(H2O)ATM/kPa ≤ 12.8). Moreover, by selecting three p(H2O)ATM values of 0.4, 3.7, and 9.2 kPa, the TG–DTG curves were systematically recorded in both isothermal and linear nonisothermal modes, in a manner analogous to the measurements conducted in a stream of dry N2. In the isothermal modes, the preset isothermal temperature ranges were in the range of 324–336 K, 337–348 K, and 352–362 K for the measurements conducted in a stream of wet N2 with p(H2O)ATM values of 0.4, 3.6, and 8.9 kPa, respectively. The measurements in the linear nonisothermal mode were conducted at varying β values, ranging from 0.5 to 10 K min−1.
The calibrations of the TG–DTA instruments (DTG-60, TG-8121, and TG-8120; Table S1, ESI†) and the instrumental controls for the TG–DTG measurements in a stream of wet N2 (Fig. S1, ESI†) are described in the ESI† (Section S1).
3. Results and discussion
3.1 Sample characterization
The sample exhibited an XRD pattern identical to that previously reported for SC-MH (orthorhombic, S.G. = P21ab(29), a = 6.4720, b = 10.7240, c = 5.2590, α = β = γ = 90.000, ICDD-PDF 01-070-0845, Fig. S2, ESI†).43 The FTIR spectrum of the sample exhibited absorption peaks attributed to H2O and CO32− (Fig. S3, ESI†).44 The assignment of individual absorption peaks is listed in Table S2 (ESI†). The sample was identified as an agglomerate of rounded particles with a diameter of several μm (Fig. S4, ESI†), exhibiting a SBET value of 1.23 ± 0.06 m2 g−1.3.2 Thermal behavior in a stream of dry N2
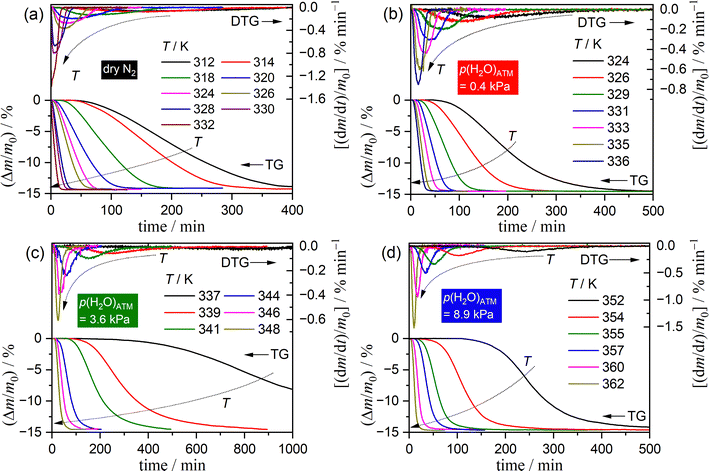
Fig. S5 (ESI†) illustrates the impact of m0 on the TG–DTG–DTA curves for the thermal dehydration of SC-MH under isothermal and linear nonisothermal conditions in a stream of dry N2. Similarly, the influence of qv on the TG–DTG–DTA curves is shown in Fig. S6 (ESI†). The thermoanalytical (TA) curves exhibited a consistent pattern of mass loss, accompanied by an endothermic effect, regardless of the measurement conditions. The mass loss value was determined to be 14.83 ± 0.59%, which corresponds to the calculated value for the thermal dehydration of SC-MH to form its anhydride (SC-AH) (Δm = 14.53%) as follows. | (1) |
Fig. S7 and S8 (ESI†) illustrate the alterations in the XRD pattern of the sample throughout the heating process under stepwise isothermal and isothermal conditions, respectively. The transformation of the crystalline phase was observed under stepwise isothermal conditions in a temperature range between 333 and 353 K (Fig. S7(a), ESI†), which corresponds to the temperature range of mass loss observed in TG. The solid product was identified as SC-AH (monoclinic, C2/m(12), a = 8.9040, b = 5.2390, c = 6.0420, α = 90.000, β = 101.350, γ = 90.000, ICDD PDF 05-001-0022; Fig. S7(b), ESI†).51 Under isothermal conditions at 333 K, no discernible alteration in the XRD pattern was observed during the initial 60 min, indicating that there was no change in the crystal phase during IP. Subsequently, the XRD peaks attributed to SC-MH exhibited gradual attenuation, whereas those of SC-AH demonstrated gradual growth between 60 and 180 min. Notably, no additional XRD peaks were observed during the thermal dehydration of SC-MH, which resulted in the formation of SC-AH.
3.3 Conventional kinetic analysis
Fig. 1 depicts the TG–DTG curves for the thermal dehydration of SC-MH under isothermal conditions at varying temperatures, recorded under distinct atmospheric conditions in a stream of dry or wet N2 with three different p(H2O)ATM values: 0.4, 3.6, and 8.9 kPa. Irrespective of the prevailing atmospheric conditions, an identifiable IP was observed under isothermal conditions. The tIP value was found to increase systematically with a decrease in reaction temperature at each p(H2O)ATM value. The subsequent mass loss process exhibited a sigmoidal curve, irrespective of the reaction temperature and the atmospheric conditions. Notably, the optimal reaction temperature for TA measurements under isothermal conditions should be increased as the p(H2O)ATM value is elevated.From the TG–DTG curves under isothermal conditions, the tIP value was determined based on an empirical definition as the time elapsed between the attainment of the preset isothermal holding temperature (time zero) and the observation of a mass loss of 2.0 μg. When the IP process is not significantly affected by atmospheric water vapor, the kinetics can be analyzed based on the fundamental kinetic equation:52–58
 | (2) |
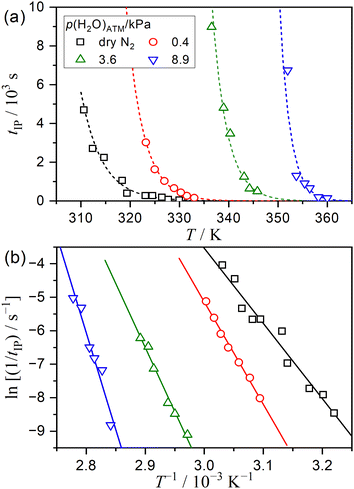 | ||
| Fig. 2 Results of the conventional kinetic analysis for the IP process of the thermal dehydration of SC-MH under isothermal conditions in a stream of dry or wet N2 with different p(H2O)ATM values, conducted using the fundamental kinetic equation (eqn (2)): (a) tIP values at varying temperatures and p(H2O)ATM values and (b) Arrhenius-type plots for the IP process at individual p(H2O)ATM values. The dashed lines in (a) represent the replication curve, which was calculated using the results of the Arrhenius-type plots shown in (b). | ||
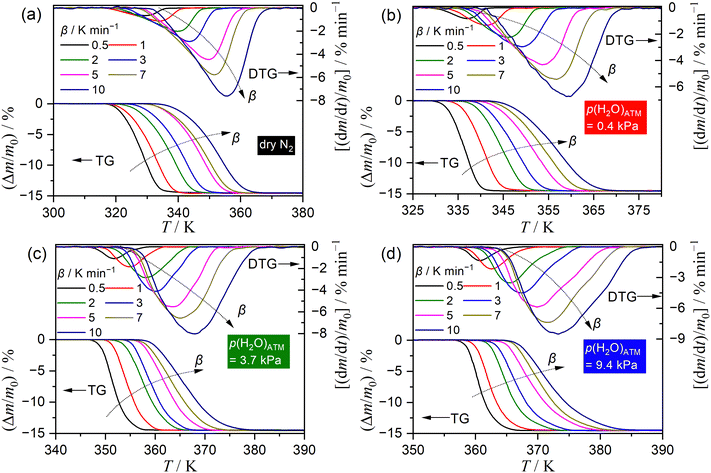
Fig. 3 illustrates the TG–DTG curves recorded under linear nonisothermal conditions at varying β values for the thermal dehydration of SC-MH in a stream of dry or wet N2 with distinct p(H2O)ATM values. At a given p(H2O)ATM value, the TG–DTG curves shifted towards higher temperatures with increasing β. Furthermore, at a selected β, the TG–DTG curves shifted towards higher temperatures with increasing p(H2O)ATM (Fig. S9, ESI†).
For the kinetic analysis of the mass loss process of the thermal dehydration, individual TG–DTG curves recorded under isothermal (Fig. 1) and linear nonisothermal (Fig. 3) conditions were transformed into kinetic curves by calculating the α value with reference to the total mass loss value. This approach yielded a series of data points (time, T, α, dα/dt) representing the kinetic data of individual reactions at varying temperatures and p(H2O)ATM values. At each p(H2O)ATM value, the kinetic curves form a specific coordinate surface in the 3D kinetic coordinate of T−1, α, and ln(dα/dt) (Fig. S10, ESI†). It is notable that distinct coordinate surfaces were obtained for the reactions at varying p(H2O)ATM values. As a preliminary kinetic approach, the kinetic data at individual p(H2O)ATM values, including those recorded in a stream of dry N2, were analyzed separately based on the fundamental kinetic equation, which does not consider the effect of p(H2O)ATM.59,60
 | (3) |
The formal kinetic analysis based on eqn (3) was conducted using its logarithmic form.
 | (4) |
The isothermal kinetic relationship of the reactions under individual atmospheric conditions was analyzed by constructing an experimental master plot. The hypothetical reaction rate (dα/dθ) at the infinite temperature was calculated at varying α values according to the following equation,62–67 utilizing the average Ea value listed in Table S4 (ESI†).
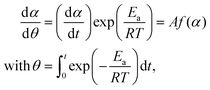 | (5) |
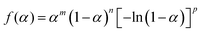 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A: ln
A: ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = a + bEa.38,71–80 Furthermore, assuming a contracting geometry-type reaction, the deceleration stage of the second half of the reaction was fitted by the PBR model: R(n).81
A = a + bEa.38,71–80 Furthermore, assuming a contracting geometry-type reaction, the deceleration stage of the second half of the reaction was fitted by the PBR model: R(n).81 | (7) |
In conclusion, the conventional kinetic analysis, which ignores the effect of atmospheric water vapor, provides an empirical characterization of the kinetic behavior of the reaction under specific atmospheric conditions. However, it does not offer a universal kinetic description that can be applied across different temperatures and p(H2O)ATM values. Notably, the kinetic parameters determined by the conventional kinetic analysis are only empirically significant. For example, they can be used to replicate the experimentally recorded kinetic curves at each p(H2O)ATM value. However, they cannot be directly correlated with the intrinsic kinetics of the reaction from a physico-chemical perspective. It is therefore essential to consider the effect of water vapor in the kinetic equation in order to achieve a universal description of the kinetic behavior as a function of temperature, α, and p(H2O), and to obtain the kinetic parameters that are physico-chemically relevant.
3.4 Extended kinetic analysis considering the effect of water vapor
Incorporation of an AF of p(H2O) and the equilibrium pressure of the reaction (Peq(T)), i.e., h(p(H2O), Peq(T)), into the fundamental kinetic equation is one way to account for the effect of p(H2O) on the kinetics. The temperature dependence of Peq(T) is expressed as follows: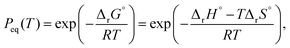 | (8) |
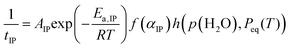 | (9) |
Recently, Koga et al. proposed an analytical form of the AF based on the classical nucleation and interfacial reaction theory, which includes various elementary steps.24–38
 | (10) |
 | (11) |
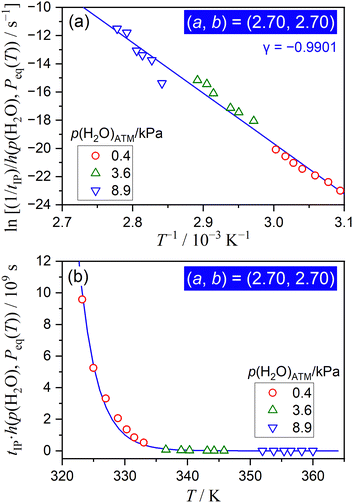 | ||
| Fig. 5 Results of the extended Arrhenius plot for the IP process of the thermal dehydration of SC-MH under isothermal conditions in a stream of wet N2 with different p(H2O)ATM values, examined according to eqn (11) with a = b = 2.70: (a) extended Arrhenius plot and (b) the comparison between the experimental data point and the replicated curve using the apparent kinetic parameters determined by the extended Arrhenius plot. | ||
The mass loss process of the thermal dehydration of SC-MH under various temperatures and p(H2O)ATM values can also be analyzed using an extended kinetic equation with the AF of h(p(H2O), Peq(T)).24–38
 | (12) |
 | (13) |
 | ||
| Fig. 6 Extended Friedman plots at α = 0.50 for the mass loss process of the thermal dehydration of SC-MH under isothermal and linear nonisothermal conditions in a stream of wet N2 with various p(H2O)ATM values, examined according to eqn (13) with different pairs of (a, b) in the AF: (a) (0, 1), (b) (1, 1), and (c) a = b = 1.20. | ||
In order to refine the extended Friedman plot applied over a range of temperatures and p(H2O)ATM values, it is necessary to take into account the potential contribution of the p(H2O)SG. Indeed, the considerable impact of p(H2O)SG on the mass loss process has been anticipated based on the variations in the kinetic data with respect to the m0 and qv of inert gas for the thermal dehydration of SC-MH in a stream of dry N2 gas (Fig. S5 and S6, ESI†). Although the actual value of p(H2O)SG at the reaction interface cannot be measured during the thermal dehydration process, it is anticipated that the value is proportional to the rate of water vapor evolution at the reaction interface. Consequently, the effective p(H2O) (p(H2O)EF), which considers the contributions of both p(H2O)SG and p(H2O)ATM, can be introduced in the extended kinetic equation as an empirical procedure for accounting for the p(H2O)SG.32,36–38
 | (14) |
The extended isoconversional kinetic approach, which considers both the effect of p(H2O)SG and p(H2O)ATM, can be used to incorporate the kinetic data recorded in a stream of dry N2, as the p(H2O)EF value is equivalent to p(H2O)SG. This procedure broadens the temperature and p(H2O) ranges encompassed by the universal kinetic description. Notably, this procedure is not applicable to the IP process due to the absence of the self-generated water vapor. Fig. 8 depicts the results of the kinetic analysis based on the extended kinetic equation (eqn (12)), which considers the effect of p(H2O)EF (eqn (14)), reexamined by incorporating the kinetic data recorded in a stream of dry and wet N2. The preceding results of (a, b, c, d) were used as the initial values, and the coefficient c was optimized to achieve the most optimal linear correlation of the extended Friedman plot at individual α values, encompassing all data points recorded under disparate atmospheric conditions. By optimizing the c value, a statistically significant linear correlation was achieved for the extended Friedman plot, including the data point for the reactions in a stream of dry N2 (Fig. 8(a)), which was observed at various α values during the reaction (Fig. 8(b)). The optimized c values at different α values were larger than those previously optimized for the reactions in a stream of wet N2 (Fig. 8(c)), although the variation trend as the reaction proceeded was similar. The apparent Ea values were also slightly larger than those determined for the reactions in a stream of wet N2 and exhibited a gradual decrease as the reaction proceeded (Fig. 8(c)). However, the average Ea value within the major stage of the reaction (0.10 ≤ α ≤ 0.90) indicated an acceptable standard deviation: Ea = 203.4 ± 4.2 kJ mol−1. It is important to acknowledge that enhancing the extended Friedman plot can be achieved through the optimization of a = b values at each α value, followed by the repetition of the optimization of a = b and c values. However, this approach led to variations in a = b values as the reaction progressed and increases in a = b and c values as the optimization calculation was repeated. In the interest of maintaining the simplicity of the kinetic modeling in the context of a universal kinetic approach, the initial optimization results assuming a constant a = b value during the reaction are reported herein.
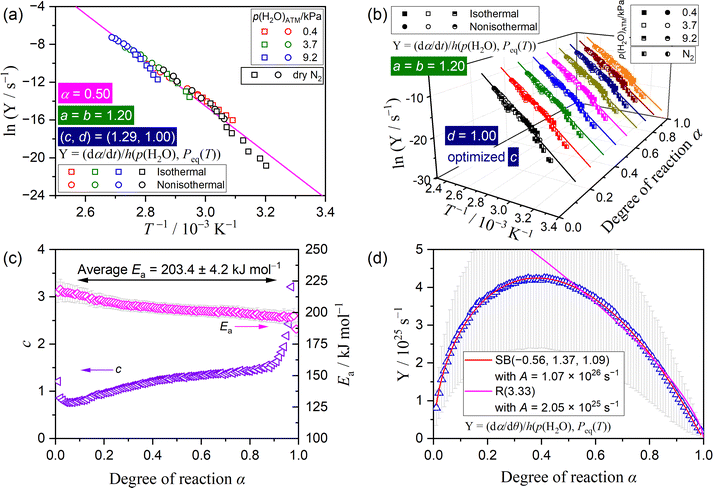 | ||
| Fig. 8 Results of the kinetic analysis based on the extended kinetic equation (eqn (12)) considering p(H2O)EF (eqn (14)) for the mass loss process of the thermal dehydration of SC-MH over different atmospheric conditions in a stream of dry and wet N2 with different p(H2O)ATM values: (a) the extended Friedman plot at α = 0.50, (b) the extended Friedman plots at various α values, (c) the optimized c and apparent Ea values at various α values, and (d) the extended experimental master plot. | ||
Assuming that the overall reaction is characterized by the average Ea value, the experimental master plots based on the extended kinetic equation (eqn (12)) can be obtained by calculating (dα/dθ)/h(p(H2O), Peq(T)) at each α.29,32,36–38
 | (15) |
In interpreting the results of the extended kinetic approach, two points require particular attention. It is important to note that the exponents (a, b) in AF (eqn (10)) and the coefficients (c, d) in p(H2O)EF (eqn (14)) can be varied according to the sample, sampling, and reaction conditions. Such factors include, for instance, the sample particle size, the m0 used to collect kinetic data, and the qv of the purge gas during the reaction. These factors modify the physico-geometrical constraints of the reaction, both within each sample particle and within the reaction system. This alters the effect of p(H2O)SG and p(H2O)ATM on the reaction kinetics. However, if we consider this from the opposite perspective, it may be feasible to parameterize the influence of these empirical factors on the kinetics using the exponents (a, b) and coefficients (c, d).
Secondly, the significance of the apparent Arrhenius parameters (Ea, A) determined by the extended kinetic approach warrants further consideration. The apparent (Ea, A) values determined by the extended kinetic approach over different temperatures and p(H2O) values are typically larger than those determined by the conventional kinetic approach to the reaction in a stream of dry N2. This is due to the fact that the extended Arrhenius-type plots, including the extended Friedman plot, simultaneously examine the temperature dependence of both the rate constant based on the Arrhenius equation and of the equilibrium constant based on the van't Hoff equation. Notably, the contribution of the temperature dependence of the equilibrium constant is multiplied by the exponent b in AF. Consequently, the temperature dependence of the rate constant in the extended kinetic equation can be obtained by subtracting the contribution of the temperature dependence of the equilibrium constant. To illustrate, the extended Friedman plot yields the following equation by subtracting the van’t Hoff plot (logarithmic form of eqn (8)) multiplied by the b value.36–38
 | (16) |
 | (17) |
 | (18) |
 of (58.6, 155.4).45 Similarly, the intrinsic Arrhenius parameters (Ea,int/kJ mol−1, Aint/s−1) were calculated, yielding the values of (133.1 ± 4.2, (1.95 ± 0.01) × 1016).
of (58.6, 155.4).45 Similarly, the intrinsic Arrhenius parameters (Ea,int/kJ mol−1, Aint/s−1) were calculated, yielding the values of (133.1 ± 4.2, (1.95 ± 0.01) × 1016).
3.5 Effect of water vapor on the individual physico-geometrical reaction steps
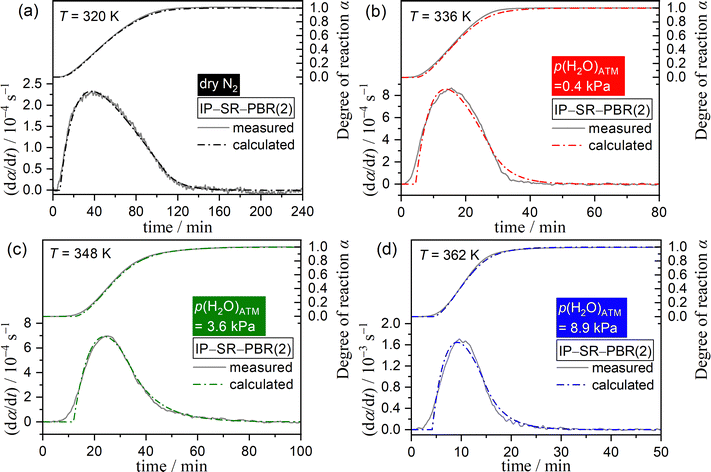
The results of the extended kinetic approach, which considered the effect of water vapor on the IP and mass loss processes, indicated that the physico-geometrical consecutive process, comprising the IP, SR, and PBR, may be suitable for describing the thermal dehydration of SC-MH in a stream of dry and wet N2. Fig. 9 depicts SEM images of partially dehydrated sample particles under isothermal conditions at 313 K in a stream of dry N2. During the IP (Fig. 9(a)), the surface morphology remained unchanged from that of the original sample particles (Fig. S4, ESI†). Immediately following the onset of mass loss, the particle surfaces exhibited a roughened texture, with the emergence of small protruding crystals radiating from the particle surfaces (Fig. 9(b)). This observation indicated that the mass loss process had initiated via the SR. As the reaction proceeded, the surface became increasingly rough (Fig. 9(c) and (d)). At this stage, the particle surface exhibited the emergence of several pores, which may serve as a diffusion path for the water vapor generated at the internal reaction interface of the PBR. Upon completion of the mass loss process, the product particles displayed rough surfaces while maintaining the protruding crystals on the surfaces (Fig. 9(e)). The changes in the surface morphology throughout the thermal dehydration of SC-MH support the physico-geometrical consecutive process of IP–SR–PBR.Based on the Mampel's model,56,82,83 differential kinetic equations of the IP–SR–PBR(n) models with distinct shrinkage dimension n of the reaction interface for the PBR have been derived by Ogasawara and Koga (Table S7, ESI†).56 The individual kinetic data recorded under isothermal conditions at different temperatures in a stream of dry or wet N2 with varying p(H2O)ATM values (Fig. 1) were fitted using these kinetic equations. This was achieved through the optimization of tIP and rate constants for the SR and PBR(n) processes (kSR and kPBR(n)) via nonlinear least-squares analysis with the Levenberg–Marquardt algorithm. The model fitting indicated that the IP–SR–PBR(n) model with the two-dimensional interface shrinkage for the PBR (i.e., IP–SR–PBR(2)) was the most suitable model. Fig. 10 illustrates the typical model fitting results obtained with the IP–SR–PBR(2) model for the reactions under isothermal conditions at different p(H2O)ATM values. Table S8 (ESI†) lists the optimized tIP, kSR, and kPBR values based on the IP–SR–PBR(2) model at different temperatures and p(H2O)ATM values.
The temperature dependence of 1/tIP, kSR, and kPBR(2) was initially examined using the conventional Arrhenius plot.
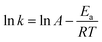 | (19) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A values exhibited a consistent trend of increase with increasing p(H2O)ATM value.
A values exhibited a consistent trend of increase with increasing p(H2O)ATM value.
A universal kinetic description for individual physico-geometrical reaction steps was examined for the reactions in a stream of wet N2 with different p(H2O)ATM values by introducing AF in eqn (10) into eqn (19).24–29,32,34–38
 | (20) |
In all physico-geometrical reaction steps, the extended Arrhenius plot demonstrated a statistically significant linear correlation, including all data points at varying p(H2O)ATM values, as illustrated in Fig. S15 (ESI†). Table 1 lists the apparent kinetic parameters of a = b, Ea, and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, as determined for the individual physico-geometrical reaction steps. The apparent kinetic parameters for IP were found to be significantly reduced in comparison with those determined using the tIP values, which were defined empirically as the duration until the mass loss reached 2 μg (Fig. 5). In contrast, the Ea and ln
A, as determined for the individual physico-geometrical reaction steps. The apparent kinetic parameters for IP were found to be significantly reduced in comparison with those determined using the tIP values, which were defined empirically as the duration until the mass loss reached 2 μg (Fig. 5). In contrast, the Ea and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A values for the SR and PBR(2) processes exhibited larger values in comparison with those determined by the extended Friedman plot (Fig. 7 and 8). It is noteworthy that all kinetic parameters, including a = b, Ea, and ln
A values for the SR and PBR(2) processes exhibited larger values in comparison with those determined by the extended Friedman plot (Fig. 7 and 8). It is noteworthy that all kinetic parameters, including a = b, Ea, and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A, exhibited a systematic decrease as the reaction steps progressed from IP to PBR(2) via SR.
A, exhibited a systematic decrease as the reaction steps progressed from IP to PBR(2) via SR.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A and the intrinsic kinetic parameters of Ea,int and ln
A and the intrinsic kinetic parameters of Ea,int and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aint for the IP, SR, and PBR(2) processes of the thermal dehydration of SC-MH in a stream of wet N2 with different p(H2O)ATM values, determined according to eqn (20) with the AF in eqn (10)
Aint for the IP, SR, and PBR(2) processes of the thermal dehydration of SC-MH in a stream of wet N2 with different p(H2O)ATM values, determined according to eqn (20) with the AF in eqn (10)
| Process | a = b | Apparent kinetic parameter | Intrinsic kinetic parameterb | |||
|---|---|---|---|---|---|---|
| E a/kJ mol−1 | ln(A/s−1) | −γa | E a,int/kJ mol−1 | ln(Aint/s−1) | ||
a Correlation coefficient of the linear regression analysis.
b Calculated according to eqn (17) and (18) using 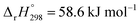 and and  . .
|
||||||
| IP | 2.17 | 237.4 ± 8.8 | 67.9 ± 3.1 | 0.9893 | 110.1 ± 8.8 | 27.3 ± 3.1 |
| SR | 1.91 | 230.9 ± 6.4 | 66.6 ± 2.3 | 0.9939 | 119.0 ± 6.4 | 30.9 ± 2.3 |
| PBR(2) | 1.63 | 211.2 ± 7.7 | 59.8 ± 2.7 | 0.9897 | 115.9 ± 7.7 | 29.3 ± 2.7 |
To further extend the universal kinetic approach, SR and PBR(2) processes were reanalyzed by considering p(H2O)EF in eqn (14) and by optimizing the coefficients (c, d), where the kinetic data recorded in a stream of dry N2 were additionally included for the analysis. It should be noted that the IP process was excluded from the reanalysis since water vapor is not produced during IP. Fig. 11 illustrates the extended Arrhenius plots, with the consideration of p(H2O)EF for the SR and PBR(2) processes. In both the SR and PBR(2) processes, the extended Arrhenius plot, which considered p(H2O)EF, yielded a statistically significant linear correlation that include all data points originating from the reactions in a stream of dry and wet N2 with different p(H2O)ATM values. Table 2 lists the apparent kinetic parameters obtained by the extended Arrhenius plots for the SR and PBR(2) processes. Notably, the coefficient c in the p(H2O)EF increased significantly as the reaction step progressed from SR to PBR(2), indicating that the self-generated water vapor plays a more prominent role in the PBR(2) process. This finding can be explained by the distinct physico-geometrical constraints of the SR and PBR(2) processes with regard to the removal of the self-generated water vapor. The reaction sites during SR are directly exposed to the reaction atmosphere, allowing for the straightforward removal of the evolved water vapor from the reaction sites. In contrast, the diffusion of water vapor through the surface product layer is necessary for the removal of self-generated water vapor at the internal reaction interface during the PBR(2) process. Although the apparent Ea and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A values determined by incorporating p(H2O)EF and including the data points in a stream of dry N2 were larger than those determined by the extended Arrhenius plot with p(H2O)ATM and without data points in a stream of dry N2, the observed trend of decreasing the Arrhenius parameters with reaction step advancement from SR to PBR(2) remained consistent. Notably, the Arrhenius parameters listed in Table 2 cover the universal kinetic description of the reactions in wider p(H2O) and temperature ranges.
A values determined by incorporating p(H2O)EF and including the data points in a stream of dry N2 were larger than those determined by the extended Arrhenius plot with p(H2O)ATM and without data points in a stream of dry N2, the observed trend of decreasing the Arrhenius parameters with reaction step advancement from SR to PBR(2) remained consistent. Notably, the Arrhenius parameters listed in Table 2 cover the universal kinetic description of the reactions in wider p(H2O) and temperature ranges.
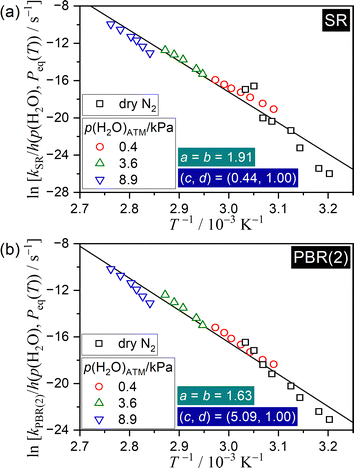 | ||
| Fig. 11 Extended Arrhenius plots for SR and PBR(2) processes of the thermal dehydration of SC-MH in a stream of dry or wet N2 with different p(H2O)ATM values, examined according to eqn (20) with the AF in eqn (10) and considering p(H2O)EF in eqn (14): (a) SR and (b) PBR(2). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A and the intrinsic kinetic parameters of Ea,int and ln
A and the intrinsic kinetic parameters of Ea,int and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aint for the SR and PBR(2) processes of the thermal dehydration of SC-MH in a stream of dry and wet N2 with different p(H2O)ATM values, determined according to eqn (20) with the AF in eqn (10) and by considering p(H2O)EF in eqn (14)
Aint for the SR and PBR(2) processes of the thermal dehydration of SC-MH in a stream of dry and wet N2 with different p(H2O)ATM values, determined according to eqn (20) with the AF in eqn (10) and by considering p(H2O)EF in eqn (14)
| Process | a = b | c | d | Apparent kinetic parameter | Intrinsic kinetic parameterb | |||
|---|---|---|---|---|---|---|---|---|
| E a/kJ mol−1 | ln(A/s−1) | −γa | E a,int/kJ mol−1 | ln(Aint/s−1) | ||||
a Correlation coefficient of the linear regression analysis.
b Calculated according to eqn (17) and (18) using  and and 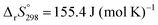 . .
|
||||||||
| SR | 1.91 | 0.44 | 1.00 | 275.6 ± 13.7 | 82.2 ± 5.0 | 0.9716 | 163.6 ± 13.7 | 46.5 ± 5.0 |
| PBR(2) | 1.63 | 5.09 | 1.00 | 228.6 ± 8.0 | 66.0 ± 2.9 | 0.9858 | 133.2 ± 8.0 | 35.6 ± 2.9 |
The apparent Arrhenius parameters determined for the individual reaction step in the IP–SR–PBR scheme by the extended Arrhenius plot can also be correlated to the individual intrinsic values. The intrinsic Arrhenius parameters calculated based on eqn (17) and (18) are listed in Tables 1 and 2. The intrinsic Arrhenius parameters calculated from the apparent kinetic parameters obtained by the extended Arrhenius plot with p(H2O)ATM without data points in a stream of dry N2 were practically identical among distinct reaction steps with reference to the standard error of each value (Table 1). The intrinsic Arrhenius parameters determined by considering p(H2O)EF and including the data points in a stream of dry N2 were found to be larger than those determined without considering p(H2O)SG and without data points in a stream of dry N2 (Table 2). Furthermore, the intrinsic Arrhenius parameters for the SR process were found to be markedly larger than those for the PBR(2) process. The discrepancy between the results of the extended Arrhenius plots with different calculation conditions may suggest that the reactions occurring at lower p(H2O)ATM values are more sensitive to p(H2O)SG. Moreover, this phenomenon is particularly pronounced in the context of the SR process. These were anticipated based on the shift trend of the TA curves to higher temperatures with increasing p(H2O)ATM (Fig. S9, ESI†), where the shift width with increasing p(H2O)ATM was larger at a lower p(H2O)ATM region. Additionally, the shift wide of the onset temperature with p(H2O)ATM was larger than that of the peak top temperature. Furthermore, a distinctive shape was observed in the conventional experimental master plot for the reactions in a stream of dry N2 in comparison with those in the presence of atmospheric water vapor (Fig. 4(c)), indicating that the maximum reaction rate is attained at a smaller α value. The observed phenomenon of the effect of p(H2O)SG and p(H2O)ATM indicates that p(H2O)SG plays an important role in regulating the kinetic behavior of the thermal dehydration of SC-MH, particularly for reactions in a stream of dry N2 and at a lower p(H2O)ATM. This also describes the changes in the kinetic behaviors with m0 and qv in a stream of dry N2.
4. Conclusions
The thermal dehydration kinetics of SC-MH were significantly affected by m0 and qv in a stream of dry N2 due to the influence of the self-generated water vapor. An increase in m0 and a decrease in qv resulted in a deceleration of the overall reaction rate. In addition, a systematic variation in the kinetics was observed when the p(H2O)ATM value of the purge gas was varied, exhibiting a deceleration as the p(H2O)ATM value increased. Therefore, both p(H2O)SG and p(H2O)ATM are the parameters that determine the apparent kinetics of the reaction. The application of the conventional kinetic approach as a function of temperature and α to such a reaction process yielded apparent kinetic results that were only useful for reproducing the kinetic behaviors of the reaction under specific reaction conditions of m0, qv, and p(H2O)ATM. Additionally, a particular physico-geometrical reaction characteristic was anticipated for the reaction, as evidenced by the appearance of IP and the subsequent sigmoidal mass loss curves recorded under isothermal conditions. This can be described by consecutive physico-geometrical steps of IP, SR and PBR. In order to elucidate the kinetics of thermal dehydration of SC-MH across diverse temperatures and p(H2O) values, a comprehensive kinetic approach was conducted in a stepwise manner. This approach comprised four steps: (1) development of a universal kinetic description across varying temperatures and p(H2O)ATM values, (2) incorporation of the effect of self-generated water vapor into the universal kinetic description, (3) interpretation of the physico-chemical meanings of the apparent kinetic parameters within the universal kinetic description, and (4) extension of the universal kinetic description to encompass the physico-geometrical kinetic modeling.Introduction of AF, which describes the variation of the reaction rate as a function of p(H2O) with reference to Peq(T), into the conventional kinetic equation can be a potential approach to describe the kinetics universally as a function of temperature, α, and p(H2O). Such an AF was derived based on the rate-determining step and steady-state approximations of the elementary steps of the surface nucleation and interfacial reaction processes of the thermal dehydration. An analytical form of AF with the variable exponents (a, b) (eqn (10)) was effectively used to realize the universal kinetic description across different temperatures and p(H2O)ATM values during the extended Arrhenius-type plot for the IP process (eqn (11)) and the extended Friedman plot for the mass loss process (eqn (13)), where a = b values of 2.70 and 1.20 were optimized for the IP and mass loss processes of the thermal dehydration of SC-MH, respectively. The kinetics of the IP process could be universally described using the extended Arrhenius plot with the AF. Besides, a universal kinetic description for the mass loss process was achieved by successive isoconversional (eqn (13)) and isothermal (eqn (15)) kinetic analyses based on the extended kinetic equation (eqn (12)) with the AF (eqn (10)). For the mass loss process, the universal kinetic description was further refined by considering p(H2O)EF (eqn (14)), comprising p(H2O)SG and p(H2O)ATM with the coefficients (c, d) describing the respective contributions. This approach enabled us to estimate the variation of the contribution of p(H2O)SG from the changes in the c value as the mass loss process progressed, which indicated the negligible effect at the early stage of the mass loss process, corresponding to the SR process, and the increasing effect at the subsequent stage of the PBR process. On the other hand, the d value remained constant as unity during the reaction. The Arrhenius parameters determined by the extended kinetic approach yielded apparent values due to the simultaneous evaluations of the temperature dependences of the rate constant and Peq(T). Therefore, the intrinsic Arrhenius parameters (Ea,int, Aint) can be estimated by subtracting the contributions of ΔrH° and ΔrS° from the respective apparent values (eqn (17) and (18)). All the context of the universal kinetic description via the formal kinetic analyses of the extended isoconversional and isothermal kinetic analyses for the mass loss process, as well as the extended Arrhenius-type plot for the IP process, can be applied to the physico-geometrical kinetic modeling based on the IP–SR–PBR model. Consequently, the exponents (a, b), coefficients (c, d), and intrinsic Arrhenius parameters (Ea,int, Aint) were determined for the individual physico-geometrical reaction steps of IP, SR, and PBR, as listed in Tables 1 and 2. The results fulfill the universal kinetic description across different temperatures and p(H2O) values with physico-chemically meaningful kinetic parameters based on the physico-geometrical kinetic modeling, which were subjected to this study.
The theory and practical procedures of the universal kinetic analysis demonstrated in this study for the thermal dehydration of SC-MH are applicable to the thermal decomposition of other solids that exhibit a reversible nature. The results of each step of the universal kinetic analysis provide specific insights into the kinetics of thermal decomposition across different temperatures and partial pressures of the gaseous product. Furthermore, the kinetic behavior of thermal decomposition at various temperatures and partial pressures of the gaseous product can be simulated using the kinetic parameters determined by the universal kinetic approach, which has the potential to inform the design of the thermal decomposition process for practical applications.
Data availability
Data will be made available on request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The present work was supported by JSPS KAKENHI Grant Numbers 22K02946, 23K22282, 24K05970, and 24K21457.References
- H. U. Rammelberg, T. Schmidt and W. Ruck, Energy Proc., 2012, 30, 362–369 CrossRef CAS.
- K. E. N’Tsoukpoe, T. Schmidt, H. U. Rammelberg, B. A. Watts and W. K. L. Ruck, Appl. Energy, 2014, 124, 1–16 CrossRef.
- F. Trausel, A.-J. de Jong and R. Cuypers, Energy Proc., 2014, 48, 447–452 CrossRef CAS.
- P. A. J. Donkers, L. C. Sögütoglu, H. P. Huinink, H. R. Fischer and O. C. G. Adan, Appl. Energy, 2017, 199, 45–68 CrossRef CAS.
- H. U. Rammelberg, T. Osterland, B. Priehs, O. Opel and W. K. L. Ruck, Sol. Energy, 2016, 136, 571–589 CrossRef CAS.
- Z. Ge, B. Dou, L. Wang, Y. Ding, H. Chen and Y. Xuan, Carbon Neutrality, 2022, 1, 35 CrossRef.
- X. Yu, Z. Tang, D. Sun, L. Ouyang and M. Zhu, Prog. Mater. Sci., 2017, 88, 1–48 CrossRef.
- L. Ouyang, K. Chen, J. Jiang, X.-S. Yang and M. Zhu, J. Alloys Compd., 2020, 829, 154597 CrossRef CAS.
- M. R. Usman, Renewable Sustainable Energy Rev., 2022, 167, 112743 CrossRef CAS.
- Y. Sun, C. Shen, Q. Lai, W. Liu, D.-W. Wang and K.-F. Aguey-Zinsou, Energy Storage Mater., 2018, 10, 168–198 CrossRef.
- Y. Huang, Y. Cheng and J. Zhang, Ind. Eng. Chem. Res., 2021, 60, 2737–2771 CrossRef CAS.
- V. Prigiobbe, A. Polettini and R. Baciocchi, Chem. Eng. J., 2009, 148, 270–278 CrossRef CAS.
- A. Perejón, L. M. Romeo, Y. Lara, P. Lisbona, A. Martínez and J. M. Valverde, Appl. Energy, 2016, 162, 787–807 CrossRef.
- F. Raganati and P. Ammendola, Energy Fuels, 2023, 37, 1777–1808 CrossRef CAS.
- R. Han, Y. Wang, S. Xing, C. Pang, Y. Hao, C. Song and Q. Liu, Chem. Eng. J., 2022, 450, 137952 CrossRef CAS.
- F. J. Duran-Olivencia, R. Gannoun, A. T. Perez and J. M. Valverde, Ind. Eng. Chem. Res., 2023, 62, 1373–1389 Search PubMed.
- D. A. Young, Decomposition of Solids, Pergamon, Oxford, 1966 Search PubMed.
- B. Delmon, Introduction a la Cinetique Heterogene, Editions Technip, Paris, 1969 Search PubMed.
- A. K. Galwey and M. E. Brown, Thermal Decomposition of Ionic Solids, Elsevier, Amsterdam, 1999 Search PubMed.
- C. H. Bamford, C. F. H. Tipper and R. G. Compton, Reactions of Solids with Gases, Elsevier, Amsterdam, 1984 Search PubMed.
- J. Szekely, J. W. Evans and H. Y. Sohn, Gas-Solid Reactions, Academic Press, New York, 1976 Search PubMed.
- A. K. Galwey, Thermochim. Acta, 2000, 355, 181–238 Search PubMed.
- N. Koga and H. Tanaka, Thermochim. Acta, 2002, 388, 41–61 Search PubMed.
- N. Koga, L. Favergeon and S. Kodani, Phys. Chem. Chem. Phys., 2019, 21, 11615–11632 RSC.
- M. Fukuda, L. Favergeon and N. Koga, J. Phys. Chem. C, 2019, 123, 20903–20915 CrossRef CAS.
- S. Kodani, S. Iwasaki, L. Favergeon and N. Koga, Phys. Chem. Chem. Phys., 2020, 22, 13637–13649 Search PubMed.
- Y. Yamamoto, L. Favergeon and N. Koga, J. Phys. Chem. C, 2020, 124, 11960–11976 Search PubMed.
- J. G. D. Preturlan, L. Vieille, S. Quiligotti and L. Favergeon, J. Phys. Chem. C, 2020, 124, 26352–26367 CrossRef CAS.
- N. Koga, Y. Sakai, M. Fukuda, D. Hara, Y. Tanaka and L. Favergeon, J. Phys. Chem. C, 2021, 125, 1384–1402 CrossRef CAS.
- Y. Sakai, S. Iwasaki, S. Kikuchi and N. Koga, J. Therm. Anal. Calorim., 2021, 147, 5801–5813 CrossRef.
- Y. Sakai and N. Koga, Chem. Eng. J., 2022, 428, 131197 CrossRef CAS.
- M. Hotta, T. Tone, L. Favergeon and N. Koga, J. Phys. Chem. C, 2022, 126, 7880–7895 CrossRef CAS.
- S. Iwasaki, Y. Zushi and N. Koga, Phys. Chem. Chem. Phys., 2022, 24, 9492–9508 RSC.
- Y. Zushi, S. Iwasaki and N. Koga, Phys. Chem. Chem. Phys., 2022, 24, 29827–29840 RSC.
- S. Iwasaki, Y. Sakai, S. Kikuchi and N. Koga, J. Therm. Anal. Calorim., 2022, 147, 6309–6322 CrossRef CAS.
- M. Hotta, L. Favergeon and N. Koga, J. Phys. Chem. C, 2023, 127, 13065–13080 Search PubMed.
- M. Hotta, Y. Zushi, S. Iwasaki, S. Fukunaga and N. Koga, Phys. Chem. Chem. Phys., 2023, 25, 27114–27130 RSC.
- M. Hotta and N. Koga, Thermochim. Acta, 2024, 733, 179699 CrossRef CAS.
- N. Koga, M. Hotta and L. Favergeon, J. Phys. Chem. C, 2024, 128, 15487–15504 Search PubMed.
- Y. Zushi, S. Iwasaki and N. Koga, Phys. Chem. Chem. Phys., 2022, 24, 15736–15748 Search PubMed.
- A. C. Baglie and T. C. DeVore, Thermochim. Acta, 2022, 717, 179364 CrossRef CAS.
- M. C. Ball, C. M. Snelling and A. N. Strachan, J. Chem. Soc., Faraday Trans. 1, 1985, 81, 1761–1766 RSC.
- K. K. Wu and I. D. Brown, Acta Crystallogr., 1975, 31, 890–892 Search PubMed.
- K. Buijs and C. J. H. Schutte, Spectrochim. Acta, 1961, 17, 917–920 CrossRef CAS.
- D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, The NBS Tables of Chemical Thermodynamic Properties. Selected Values for Inorganic and C1 and C2 Organic Substances in SI Units, American Chemical Society, Washington, DC, 1982 Search PubMed.
- S. Iwasaki, Y. Zushi and N. Koga, Phys. Chem. Chem. Phys., 2021, 23, 22972–22983 Search PubMed.
- N. Koga and H. Tanaka, Thermochim. Acta, 1994, 240, 141–151 Search PubMed.
- N. Koga and H. Tanaka, J. Therm. Anal., 1993, 40, 1173–1179 CrossRef CAS.
- N. Koga and H. Tanaka, Thermochim. Acta, 1992, 209, 127–134 CrossRef CAS.
- S. Vyazovkin, K. Chrissafis, M. L. Di Lorenzo, N. Koga, M. Pijolat, B. Roduit, N. Sbirrazzuoli and J. J. Suñol, Thermochim. Acta, 2014, 590, 1–23 Search PubMed.
- W. van Aalst, J. den Holander, W. J. A. M. Peterse and P. M. de Wolff, Acta Crystallogr., 1976, 32, 47–58 CrossRef.
- L. D. Hansen, D. J. Eatough, E. A. Lewis, R. G. Bergstrom, D. Degraft-Johnson and K. Cassidy-Thompson, Can. J. Chem., 1990, 68, 2111–2114 CrossRef CAS.
- P. Šimon, J. Therm. Anal. Calorim., 2006, 84, 263–270 CrossRef.
- N. Koga and T. Kimizu, J. Am. Ceram. Soc., 2008, 91, 4052–4058 CrossRef CAS.
- T. Kimura and N. Koga, J. Phys. Chem. A, 2011, 115, 10491–10501 CrossRef CAS PubMed.
- H. Ogasawara and N. Koga, J. Phys. Chem. A, 2014, 118, 2401–2412 CrossRef CAS PubMed.
- M. Fukuda and N. Koga, J. Phys. Chem. C, 2018, 122, 12869–12879 CrossRef CAS.
- M. Hotta, T. Tone and N. Koga, J. Phys. Chem. C, 2021, 125, 22023–22035 CrossRef CAS.
- N. Koga, J. Šesták and P. Simon, in Thermal analysis of Micro, Nano- and Non-Crystalline Materials, ed. J. Šesták and P. Simon, Springer, Dordrecht, 2013, ch. 1, pp. 1–28 DOI:10.1007/978-90-481-3150-1_1.
- S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19 CrossRef CAS.
- H. L. Friedman, J. Polym. Sci., Part C, 1964, 6, 183–195 CrossRef.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38, 1881–1886 CrossRef CAS.
- T. Ozawa, Thermochim. Acta, 1986, 100, 109–118 CrossRef CAS.
- J. Málek, Thermochim. Acta, 1992, 200, 257–269 CrossRef.
- N. Koga, Thermochim. Acta, 1995, 258, 145–159 CrossRef CAS.
- F. J. Gotor, J. M. Criado, J. Málek and N. Koga, J. Phys. Chem. A, 2000, 104, 10777–10782 Search PubMed.
- J. M. Criado, L. A. Perez-Maqueda, F. J. Gotor, J. Málek and N. Koga, J. Therm. Anal. Calorim., 2003, 72, 901–906 CrossRef CAS.
- J. Šesták and G. Berggren, Thermochim. Acta, 1971, 3, 1–12 Search PubMed.
- J. Šesták, J. Therm. Anal. Calorim., 2011, 110, 5–16 Search PubMed.
- J. Šesták, J. Therm. Anal., 1990, 36, 1997–2007 CrossRef.
- N. Koga and H. Tanaka, J. Therm. Anal., 1991, 37, 347–363 CrossRef CAS.
- N. Koga and J. Šesták, Thermochim. Acta, 1991, 182, 201–208 CrossRef CAS.
- N. Koga and J. Šesták, J. Therm. Anal., 1991, 37, 1103–1108 CrossRef.
- N. Koga, Thermochim. Acta, 1994, 244, 1–20 CrossRef CAS.
- A. K. Galwey and M. Mortimer, Int. J. Chem. Kinet., 2006, 38, 464–473 CrossRef CAS.
- P. J. Barrie, Phys. Chem. Chem. Phys., 2012, 14, 318–326 RSC.
- P. J. Barrie, Phys. Chem. Chem. Phys., 2012, 14, 327–336 RSC.
- D. Xu, M. Chai, Z. Dong, M. M. Rahman, X. Yu and J. Cai, Bioresour. Technol., 2018, 265, 139–145 CrossRef CAS PubMed.
- A. Mianowski, T. Radko and T. Siudyga, React. Kinet., Mech. Catal., 2020, 132, 37–58 CrossRef.
- R. E. Lyon, J. Phys. Chem. A, 2023, 127, 2399–2406 CrossRef CAS PubMed.
- W. D. Spencer and B. Topley, J. Chem. Soc., 1929, 2633–2650, 10.1039/jr9290002633.
- K. L. Mampel, Z. Phys. Chem., Abt. A, 1940, 187, 43–57 Search PubMed.
- L. Favergeon, M. Pijolat and M. Soustelle, Thermochim. Acta, 2017, 654, 18–27 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: (S1) Instrumental setup (Fig. S1 and Table S1); (S2) sample characterization (Fig. S2–S4 and Table S2); (S3) thermal behavior in a stream of dry N2 (Fig. S5–S8); (S4) conventional kinetic analysis (Tables S3, S4 and Fig. S9–S11); (S5) formulation of accommodation function (Fig. S12 and Tables S5, S6); (S6) extended kinetic analysis considering the effect of water vapor (Fig. S13); (S7) effect of water vapor on the individual physico-geometrical reaction steps (Fig. S14, S15 and Tables S7–S9). See DOI: https://doi.org/10.1039/d4cp04624b |
| This journal is © the Owner Societies 2025 |