Open Access Article
Open Access ArticleSteric effects in the adsorption of O2 on a Cu(111) surface†
Lok Yiu
Wu‡
ab,
Maksymilian J.
Roman
 *a,
Brianna R.
Heazlewood
*a,
Brianna R.
Heazlewood
 a and
Mitsunori
Kurahashi
a and
Mitsunori
Kurahashi
 *c
*c
aDepartment of Physics, University of Liverpool, Oxford Street, Liverpool, L69 7ZE, UK. E-mail: m.j.roman@liverpool.ac.uk
bPhysical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford, OX1 3QZ, UK
cNational Institute for Materials Science, 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan. E-mail: kurahashi.mitsunori@nims.go.jp
First published on 12th February 2025
Abstract
Probing the stereodynamics of a gas–surface interaction is a useful tool to investigate the mechanisms responsible for adsorption. Experimental results are provided on the adsorption of alignment-controlled O2 interacting with a Cu(111) surface for the first time, across a range of incident energies (65–550 meV) and angles of incidence (0–60°). Molecules of O2 in a supersonic beam are prepared in a single spin-rotational state, and aligned with a Cu(111) surface so that the rotational angular momentum of O2 is either parallel or perpendicular to the surface. A strong steric effect is observed, where the initial sticking probability is higher in the case of a 'side-on' collision, with measurable adsorption appearing at normal incident energies of 100 meV. The onset of sticking occurs at incident energies of approximately 200 meV in the case of an 'end-on' collision. The results also indicate that the adsorption of O2 on Cu(111) is predominantly due to an activated process in the energy range probed, corroborating previous experimental and theoretical results.
Introduction
As an abundant and reactive component of our atmosphere, molecular oxygen is responsible for many important reactions that occur on exposed surfaces. The corrosion of metal surfaces has been a long-standing issue, and many strategies have been developed in a bid to minimise corrosion—indeed, copper utensils were plated with tin as long ago as Roman times.1 More recently, there has been significant and sustained interest in copper due to its widespread use in modern electronic components and as an inexpensive active metal catalyst. In order to efficiently and effectively protect copper surfaces from corrosion, and to improve the design of Cu-based catalysts more broadly, reactions between O2 and copper must be better understood.The adsorption of oxygen on a Cu(111) surface has been extensively studied using a variety of spectroscopic techniques that can probe gas–surface interactions. Dissociative adsorption can proceed through two pathways, known as ‘direct’ and ‘indirect’ processes. In the direct process, the O2 molecule in the gas phase dissociates on impact and each O atom forms a bond with the surface. As bond-breaking of the molecule occurs, this is often an activated process, with the translational or internal energy of the molecule providing the energy needed to overcome the dissociation activation barrier. In the indirect case, the O2 molecule is first physisorbed onto the surface, and two competing mechanisms can then occur: desorption of the O2 molecule back into the gas phase, or dissociation into two adsorbed O atoms on the surface. The indirect process is also known as a trapping-mediated process, as the molecule is trapped onto the surface for a period of time.
Ultraviolet photoelectron spectroscopy (UPS) studies have shown that adsorption of oxygen is dissociative at 300 K—the O(1s) spectrum of oxygen adsorbed on a Cu(111) surface shows a single peak at 300 K due to the atomic species, while at 100 K, the spectrum shows an additional higher binding energy peak due to the molecular species.2 In high resolution electron energy loss (HREEL) spectra recorded at 100 K, it was found that molecular oxygen could bind to Cu(111) surfaces in two ways (the bridged and bound on top peroxo species), with atomic oxygen also present.3 The presence of molecular oxygen is in agreement with a theoretical study by Ramos et al. conducted using density functional theory (DFT) with a semi-local exchange–correlation functional and quasi-classical trajectory (QCT) calculations, where oxygen adsorption was found to be non-dissociative at low surface temperatures (110 K) as the O2 molecule can be trapped in a stable adsorption well after overcoming an initial energy barrier.4 A late barrier then emerges for the dissociation of O2 into O atoms. The heights of the early and late barriers were found to depend on the impact site of O2 on the Cu(111) surface—with the lowest energy entrance channel being the top-bridge-top (t-b-t) configuration, and the lowest energy exit channel involving the bridge-fcc-bridge (b-fcc-b) configuration. As such, the minimum energy pathway for the combined process is for the molecule to approach and adsorb in a t-b-t configuration, then to rearrange and adopt a b-fcc-b geometry prior to dissociation. Another approach has been taken recently by van Bree and Kroes, using a screened hybrid density functional and QCT calculations to investigate the dissociation dynamics of O2 on Cu(111).5 Similar to Ramos et al., the potential energy surfaces (PESs) show that the exit barrier is high for the lowest energy entrance barrier, and so the minimum energy pathway requires a rearrangement of the O2 molecule on the surface.
Experimentally measured sticking probabilities are one way to probe the dynamics occurring in gas–surface interactions. As the quantum state (including orientation), angle of incidence, and velocity of the incoming beam all influence how O2 molecules interact with Cu(111) surfaces, molecular beams are a useful tool for gaining insight into this process—providing a mechanism for exerting control over the distribution of incident energies and the rovibrational states initially populated in the oxygen beam. Previous studies have used the King and Wells method6 (described in further detail in the Experimental section) to measure the sticking coefficient of O2 on Cu(111). A 2012 study by Minniti et al. involving molecular beams found that the sticking coefficient increases exponentially with incident energy, up to 400 meV.7 This is in qualitative agreement with a more recent molecular beam study conducted by Zhang et al., which showed the same trend, but reported higher sticking coefficients.8 The study by Zhang et al. measured the sticking coefficients as a function of incident energy (100 to 400 meV), angle of incidence, surface temperature (90 K to 670 K), and coverage.8 They identified an activated adsorption process with an activation barrier of approximately 100 meV at higher surface temperatures, in agreement with entrance via the t-b-t channel in the previous theoretical study by Ramos et al.4 However, at the lowest surface temperature probed in the study (90 K), although no signs of trapping were detected, the possibility of a molecular precursor state could not be excluded.
While the cumulative knowledge arising from these studies has enhanced our understanding of the sticking of O2 on a Cu(111) surface, several questions still remain. For instance, the sticking probabilities obtained from theory and experiment, and indeed between the two experiments reported thus far, while qualitatively consistent, lack quantitative agreement. There has been a call for more experimental measurements to be undertaken to resolve these points of difference.5 In addition, the effect of the molecular alignment of O2 with respect to a Cu(111) surface has not been studied experimentally with molecular beams. The PES is predicted to have a strong anisotropy9—the activation barrier for dissociation is higher for an end-on collision, where the molecular axis is perpendicular to the surface, compared to a side-on collision. In addition to the activated processes that appear in the high energy regime, questions also remain regarding the contribution of processes that occur in the low energy regime, such as trapping-mediated adsorption or steering.10,11
Here, experimental measurements are presented that allow us to begin answering these questions. In its ground (3Σg−) electronic state, molecular oxygen is paramagnetic and hence possesses a magnetic dipole moment due to the presence of the unpaired electrons. As it is best described by Hund's case (b), the total angular momentum J is due to the spin-rotation coupling of the molecule. By selecting a single spin-rotational state of O2 and controlling its quantisation axis direction using external magnetic fields, measurements of steric effects in the adsorption of O2 on a Cu(111) surface are experimentally probed and reported here for the first time.
Experimental
The experimental setup has been previously described in detail,12 with the key features set out briefly here. A schematic diagram of the apparatus is shown in Fig. 1. A continuous beam of O2 molecules seeded in He is generated via a supersonic expansion, with the ratio of O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He varied (and in some cases, with the nozzle heated) to create beams with mean translational energies of 65–548 meV. A series of hexapolar magnets focus target O2 molecules in the (J,MJ) = (2,2) state around a centre stop and into the reaction chamber. Here J is the total angular momentum quantum number and MJ is the projection of the total angular momentum J onto the quantisation axis. Previous characterisation studies have established that transmitted O2 molecules are nearly 100% quantum state-selected.13 Linear motion feedthroughs are connected to the seven selection hexapoles, allowing each of these hexapoles to be independently retracted or positioned on the beam axis, depending on the beam velocity. The centre stop removes non-target particles that are travelling along the central beam propagation axis, such as the He carrier gas. After traversing the hexapoles and centre stop, O2 molecules enter the spin flipper region. In this instance, the spin-flipper is operated in a non-flip mode, and simply maintains a quantisation axis through to the main reaction chamber, where the O2 molecules impinge on the Cu(111) surface. Gas composition analysis conducted in the main chamber confirms that close to 100% of the species that successfully traverse the hexapoles are O2 molecules.
He varied (and in some cases, with the nozzle heated) to create beams with mean translational energies of 65–548 meV. A series of hexapolar magnets focus target O2 molecules in the (J,MJ) = (2,2) state around a centre stop and into the reaction chamber. Here J is the total angular momentum quantum number and MJ is the projection of the total angular momentum J onto the quantisation axis. Previous characterisation studies have established that transmitted O2 molecules are nearly 100% quantum state-selected.13 Linear motion feedthroughs are connected to the seven selection hexapoles, allowing each of these hexapoles to be independently retracted or positioned on the beam axis, depending on the beam velocity. The centre stop removes non-target particles that are travelling along the central beam propagation axis, such as the He carrier gas. After traversing the hexapoles and centre stop, O2 molecules enter the spin flipper region. In this instance, the spin-flipper is operated in a non-flip mode, and simply maintains a quantisation axis through to the main reaction chamber, where the O2 molecules impinge on the Cu(111) surface. Gas composition analysis conducted in the main chamber confirms that close to 100% of the species that successfully traverse the hexapoles are O2 molecules.
The Cu(111) surface is first prepared in the sample preparation chamber, where it undergoes argon ion sputter cleaning and annealing at 773 K, with the crystal structure confirmed by low energy electron diffraction (LEED) measurements. Once cleaned, the sample is transferred to the main reaction chamber, where it is mounted on a three-dimensional (x,y,z) linear and angular (θ) translation stage with stepper motors. The sample has a temperature of 305–313 K following annealing and transfer.
The main reaction chamber is encapsulated by three sets of Helmholtz coils, allowing a magnetic field to be applied to the chamber. By defining the quantisation axis of the magnetic field, the alignment of the O2 molecules with respect to the Cu(111) surface can be controlled, as shown in Fig. 2. The axis of the end-over-end rotation of the O2 molecule aligns with the direction of the external magnetic field. By altering the magnetic field direction, three different interaction configurations can be achieved: a helicopter alignment (H), where the rotation axis is along the x-axis; and two cartwheel orientations (Cy, Cz), where the O2 molecule rotates around the y- and z-axes, respectively. Here, the x-axis is defined as the direction parallel to the surface normal. In the helicopter alignment, the O2 internuclear axis is predominantly parallel to the surface. For the cartwheel geometries, the O2 internuclear axis rotates parallel and perpendicular to the surface, through a continuous range of mixed intermediate orientations.
The sticking probability of O2 on the Cu(111) surface is established using the King and Wells method,6 with beam flags regulating the exposure of the molecular beam to the surface and an ion gauge serving as the detector. A gate valve between the beam preparation chamber and the main reaction chamber is first opened, with an inert beam flag present in front of the surface, allowing the background for the case where no O2 sticking occurs to be determined. The beam flag in front of the sample is then retracted, allowing O2 molecules to impinge on the surface. For each measurement, an alternating control signal is used to switch the molecules between two alignments, allowing the sticking probability of two geometries ([H vs. Cz] or [Cyvs. Cz]) to be obtained in the same measurement. Each measurement is repeated seven times, with a fresh part of the surface exposed to the beam each time (achieved using the translation stage). The ion gauge signal is recorded throughout the repeat measurements. Species with residence time shorter than the timescale of the experiment do not contribute to the decrease in the ion gauge signal. Sticking coefficients are measured for a range of incident beam energies and angles, by varying the O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He ratio and rotating the surface relative to the molecular beam axis.
He ratio and rotating the surface relative to the molecular beam axis.
When sticking probability measurements are completed, the surface is removed from the reaction chamber and a beam composition analysis is performed using a residual gas analyser (RGA). Following the RGA measurements, a second gate valve is opened (see Fig. 1), allowing the O2 molecular beam to pass through the main reaction chamber and into the analysis chamber. There, the O2 molecules pass through a series of analyser hexapoles and into a quadrupole mass spectrometer (QMS) where time-of-flight (ToF) profiles are obtained by monitoring the time-resolved O2 QMS signal while switching the spin flipper mode as described in previous studies.14
Results
The translational energy distributions of the different O2 beams have been recorded as ToF profiles and are provided in the ESI† (see Fig. S1). From these distributions, we can define the most probable incident energy for each set of conditions, denoted as Ei. In configurations where the copper surface is rotated by an angle of incidence (θi), the normal component of the incident energy, En, is calculated. The range of incident beam energies used in this study, alongside the corresponding experimental conditions, are set out in Table S1.†An example of a King and Wells measurement is provided in Fig. 3, recorded with the O2 beam travelling at Ei = 150 meV and at θi = 0°. The change in the ion gauge current (reflecting the change of pressure inside the experimental chamber) is recorded during the King and Wells measurement. When the gate valve is opened, the molecular beam is admitted into the main reaction chamber and the pressure gauge signal rapidly increases. After the signal has been given time to equilibrate, the flag is retracted, exposing the Cu(111) surface to the molecular beam and resulting in a short, sharp spike in the signal due to outgassing caused by the motion of the flag. The peak of the signal spike can be seen to occur at t0 = 7.3 s, corresponding to when the surface is first fully exposed to the molecular beam. After the initial spike, the ion gauge signal falls again, as oxygen adsorbs on the surface—thereby removing it from the gas phase. The magnitude of this decrease in signal is dependent on the initial sticking probability, S0, for a given set of experimental conditions (Ei, θi, oxygen alignment). Further measurements are provided in the ESI† showing the signal recorded under different experimental conditions.
The control signal with which the magnetic field is switched is indicated in Fig. 3 in blue, where the resulting alternation between the helicopter and cartwheel geometries is shown. The coverage of oxygen on the surface increases steadily over the time taken to record a complete measurement, decreasing the number of available adsorption sites. This is reflected in the average signal recorded after the surface is exposed increasing with time, and reducing the differences in the interactions of the different O2 geometries. After approximately 10 seconds of exposure, the flag is raised and the Cu(111) surface is blocked from the molecular beam, accompanied by a second spike in the ion gauge signal. Following the spike, the signal can be seen to return to approximately the same equilibrium level as it was after the gate valve was opened and before the surface was exposed.
For experimental conditions that yield large S0 values—corresponding to high initial sticking probabilities, as typically seen for high Ei and low θi—the presence of steric effects in the adsorption of O2 on Cu(111) is immediately evident in the King and Wells data. For example, as can be seen in Fig. 3, alternating between the helicopter and cartwheel geometries results in distinctly different measured ion gauge signals; the adsorption is lower for the cartwheel alignment, resulting in a higher ion gauge signal (as more O2 remains in the gas phase). These initial observations can be confirmed quantitatively by measuring the initial sticking probability, S0, values for each alignment and configuration. The data from a single King and Wells measurement can be separated into two sets, one for each O2 geometry. A masking function (corresponding to the times at which the external magnetic fields are switched, cf. the block function in Fig. 3) can then be used to parse the data. While the magnetic field direction can be switched effectively instantaneously, the system takes a non-trivial amount of time to respond to this change due to the time constant of the vacuum system. As set out in the ESI,† care is taken to ensure that this delay is considered in the data analysis by excluding the first few data points following the magnetic field switch. Once parsed, the selected data points are fitted (using non-linear least squares) to an exponential function, from which the value of the ion gauge signal at t0, corresponding to the time when the surface is exposed, is extracted. The S0 value for each trace is established from the ratio of the ion gauge signal at t0 to the baseline (i.e., the signal before the Cu(111) surface is exposed to the beam). The baseline value is obtained from the mean of 180 data points between ca. 2.5 and 7 s in Fig. 3. The offset value of the ion gauge signal (i.e., the signal before the gate valve is opened to the molecular beam) must also be taken into account. The offset value is obtained from the mean of 95 data points before ca. 2.4 s in Fig. 3.
In cases of low adsorption probability (particularly at large θi, low Ei, or both), the exponential function does not provide a reliable fit to the data and a linear fit is used instead. In the few instances where there were very low adsorption probabilities, neither (exponential nor linear) fitting approach provided a good representation of the data. In such cases, the S0 value was taken as the average of the data points included in that particular measurement. Using the same procedure for measurements where the O2 geometry is switched between Cy and Cz (see Fig. S7 for an example, ESI†), no measurable differences are found in the behaviour of the two alignments; the same values of S0 are obtained for the same beam conditions. We note here that the S0(Cz) values measured from these experiments are on average higher by approximately 12% compared to the S0(Cz) values measured in the experiments alternating between the H and the Cz alignments. Therefore, the S0(Cz) values presented in the text may be slightly undervalued.
The quantified steric effect can be seen in Fig. 4, where the initial sticking probability for the parallel alignment [S0(‖)] and the perpendicular alignment [S0(⊥)] are shown as a function of the normal component of the incident energy, En. As the horizontally aligned O2 keeps the molecular axis mostly parallel to the plane of the surface, S0(H) can be used to quantify S0(‖). Although the perpendicular alignment is not directly probed, adsorption of a distribution of alignments around the perpendicular one (here simply referred to as S0(⊥)) for close-packed (111) surfaces can be obtained from the relationship set out in eqn (1):
| S0(⊥) = 2S0(C) − S0(H) | (1) |
 | ||
| Fig. 4 The S0 values for perpendicular (red) and parallel (blue) geometries of O2 molecules encountering a Cu(111) surface are shown plotted against the normal component of the incident energy, En. The contributions of different experimental θi values can be seen from the use of different symbols. Error bars indicate the standard deviation obtained from the repeated King and Wells measurements. The dashed lines represent fits to the experimental data, using the equation from Harris et al.15 | ||
For both parallel and perpendicular configurations, the value of S0 increases with increasing En, following an S-shaped curve (see Fig. 4). Focusing first on the parallel alignment, a measurable adsorption appears at around En = 100 meV. The S0(‖) values start to plateau above 400 meV, reaching a maximum value of 0.89 at the highest experimental incident energy considered in this work (En = 548 meV). The steric effect can be seen in the apparent translation of the S0 curve from parallel to perpendicular, where the shape of the distribution is consistent but the onset energy is approximately 100 meV higher for the S0(⊥) dataset. Measurable adsorption for the perpendicular alignment appears at roughly 200 meV, with the maximum measured S0(⊥) value of 0.83 obtained at the onset of the high energy plateau (which is not fully observed for this alignment, as it extends beyond the highest achievable incident energy). For both alignments, normal energy scaling (NES) applies as the data for all θi can be seen to lie on the same curve when plotted against En. The simulations by van Bree and Kroes5 have predicted that the NES holds well at high En where S0 > 0.1 while deviation from it occurs at low En where S0 < 0.1. Our results are thought to be consistent with the simulation since the measured S0 values are mostly > 0.1.
The S0 plots are typically fitted using a sigmoidal function, such as the function set out in eqn (2).
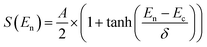 | (2) |
| O2 alignment | A | E c (meV) | δ (meV) |
|---|---|---|---|
| Parallel | 0.86 ± 0.02 | 245 ± 5 | 108 ± 7 |
| Perpendicular | 0.85 ± 0.04 | 347 ± 8 | 105 ± 10 |
The presence of a high energy plateau, and the values obtained for the A parameter, indicate that saturation in O2 adsorption on Cu(111) occurs at S0 < 1. This is qualitatively consistent with the results of a previous theoretical study by Ramos et al.,4 where a similar saturation trend was predicted—although they expected the plateau to occur at a lower S0 value of approximately 0.65. Recent theoretical work by van Bree and Kroes also reported a plateau region, again occurring at a lower S0 value than is observed experimentally.5 Interestingly, Ramos et al. also predicted a decrease in S0 to occur at higher energies, En > 400 meV. This predicted fall in S0 was not observed in the study by Zhang et al.,8 who instead observed an onset of saturation around that En (similar to what is seen in this study). However, the experimental beam energies in the Zhang et al. study only reached 396 meV, and that may have prevented them from seeing a high energy S0 decrease. Importantly, we can confirm that no such decrease in S0 is observed in the results reported here, where we extend the En range well beyond 400 meV (up to 548 meV).
Discussion
The steric effect
The increased reactivity of the parallel alignment compared to the perpendicular alignment, as shown in Fig. 4, has been previously predicted by density functional calculations performed by Moritani et al.9 Previous theoretical studies found the minimum entrance barrier for parallel O2 impacting with the t-b-t geometry to be 97 meV (Ramos et al.)4 and 280 meV (van Bree et al.).5 Although they are not directly equivalent, these values correlate well with the onset of measurable S0(H) at En ∼ 100 meV measured in this work. A preference for the parallel alignment has also been seen experimentally in previous studies of O2 adsorption on Al(111)10; Si(100);16 Pt(111);17,18 Ag(110);19 Cu(110);20 and Fe(110)/W(110), Ni(111)/W(110), Co(0001)/W(110).21 Among these prior studies, a comparison between the findings reported in this work and those reported for the O2 adsorption on an Al(111) surface may be appropriate, given the common surface structure. Trends in the sticking probabilities with respect to the incident beam energy are very similar, following an S-shaped curve for both surfaces. This implies that a direct activated adsorption mechanism is occurring in both systems, for beam energies > 100 meV. The energy gap between the two O2 geometries (parallel and perpendicular) is around 80 meV for Al(111), which is similar to the results reported here for Cu(111).The mechanism(s) responsible for O2 adsorption on Cu(111)
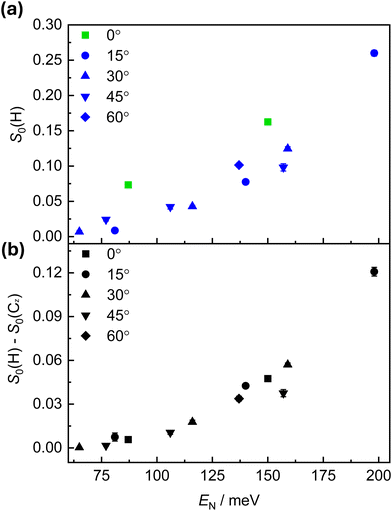
Recently, experiments conducted using a supersonic beam of randomly aligned O2 molecules provided insights into the mechanism of O2 dissociative adsorption on a Cu(111) surface.8 At room temperature, it was established that the adsorption proceeds via a direct, activated mechanism, where only molecules with energies above the height of the barrier to adsorption (as established for the most favourable geometry of approach) will stick to the surface. The experimental reality is more complicated than can be expressed in a simplified single-barrier model, and there will be a distribution of energy barriers that depend on factors such as the surface structure, impact site, angle of incidence, and the orientation of the impinging molecule. Geometric factors can be treated by the 'hole model' developed by Karikorpi et al.22 Dynamical effects that steer an incident molecule into a more favourable alignment are also known to affect the sticking probability, as has been seen theoretically.23,24 This distribution of adsorption barriers, and the presence of an activated mechanism, is reflected in the slope of the S-curve of the sticking probability measurements presented in Fig. 4.Fig. 5(a) shows the low-energy O2 adsorption as a plot of S0(H) against En (equivalent to a low energy fragment of the blue data in Fig. 4). In this low incident energy regime, contributions of a process mediated by a physisorbed precursor and/or by a steering effect which reorients an impinging molecule to a more favourable geometry need to be considered. Fig. 5(b) shows the difference between the sticking of helicoptering and cartwheeling O2 molecules. The quantity is proportional to the difference in the ion gauge signal observed while alternating the O2 geometry (see Fig. 3), and tends to be less affected by the experimental conditions.
An interesting finding, presented in Fig. 5(a), is that the S0 values recorded at θi = 0° are consistently higher than those obtained at other angles of incidence. This trend can be seen for both experimental alignments. While quantitatively accounting for the increased adsorption is beyond the scope of this study, and would likely require comprehensive theoretical investigation alongside more in-depth experimental studies, some possible explanations can be proposed.
Excitation of the internal states of the adsorbate have been found to affect the sticking probabilities—vibrational excitation has been shown to increase sticking probability in the direct adsorption of O2 on Cu(100), Cu(110), Cu(111),9 and Al(111).25 However, at room temperature, the population of excited vibrational levels of O2 is negligibly small.9 As only the O2 beams with high incident energy are produced with a heated nozzle, no vibrational excitation is expected for O2 at low En. While rotational excitation is also thought to influence sticking probability (with an inverse relationship between the two), it is not expected to play a role here. There may be some variation in the O2 internal state distribution following supersonic expansion, from the use of different gas mixtures and nozzle temperatures, but the O2 beam is then state-selected by the hexapoles prior to reaching the surface. The focusing of the target (J,MJ) = (2,2) state around the centre stop, and the findings from previous characterisation studies,13 suggest there is likely to be very little variation in the internal state distribution of O2 molecules that reach the Cu(111) surface. As such, internal excitation cannot account for the angular dependence that is observed.
An uptake process mediated via a trapped physisorbed state has been observed previously in the adsorption of low-energy O2 on hexagonally close-packed transition metal surfaces such as Ni(111),26 Pt(111),27 and Ru(0001).28 The probability of trapping-mediated O2 adsorption on Ru(0001) and Pt(111) exhibits a weak θi dependence—if S0 is plotted against En, it shows higher values at smaller θi.27,28 Additionally, the trapping-mediated adsorption of O2 is known to exhibit little alignment effect12 and Fig. 5(b) shows that the difference in the S0(θi = 0°) values between the helicopter and cartwheel alignments at En = 87 meV is very small. Thus, the combination of enhanced sticking probability and minimal alignment dependence at En = 87 meV and θi = 0° could indicate the presence of a trapping-mediated mechanism at low energy conditions. It may also be possible that steering contributes to the low alignment dependence of S0 under these conditions. A previous study by Zhang et al.8 had a minimum Ei value of 216 meV, requiring their lowest En measurements to be performed at high angles of incidence (as denoted by the symbols in Fig. 6). Their approach makes it challenging to observe subtle low-energy effects, and as such it has not been possible to compare our experimental findings quantitatively in the low-energy regime. In a recent theoretical study, van Bree and Kroes' QCT simulations determined negligible trapping of O2 molecules, with a trapping probability of approximately 0.002 following trajectory calculations propagated for 1 ns.5 Trapping occurred only for oxygen molecules impacting the surface at En < 50 meV, lower than the minimum En values studied experimentally. The authors did, however, note that their model did not include provisions for energy dissipation into the surface upon adsorbate collision, and as such may not simulate trapping processes accurately.
 | ||
| Fig. 6 The values of S0(R) established from eqn (3) are plotted as purple solid symbols as a function of En, at several different angles of incidence. Experimental data reported by Zhang et al.8 (yellow hollow symbols) and Minniti et al.7 (green solid circles) are also provided to facilitate a comparison between the experiments. The contributions of different experimental θi values can be seen from the use of differently shaped symbols. The dashed lines indicate the fits from eqn (2) to data from this work and from Zhang et al. | ||
To explore whether a trapping-mediated mechanism may be present, additional S0 measurements have been conducted at Tsurf = 107 K, for both helicopter and cartwheel O2 alignments and at θi = 0, 30, and 45°. The temperature dependence of the probability of trapping-mediated adsorption is determined by the dynamic competition between thermal desorption and dissociation of the trapped molecule. Lower desorption rates correspond to a higher probability of trapping-mediated adsorption at lower temperatures.27 Measurements recorded at Tsurf = 107 K yield S0 values that are only marginally larger than (and falling within the uncertainty range of) the equivalent room temperature measurements. Further details are provided in the ESI.† As such, we conclude that the presence of a low-energy trapping-mediated adsorption channel is consistent with the experimental data, but cannot be confirmed at this stage.
Comparison with prior work
In two prior experimental studies, S0 measurements were carried out for randomly aligned O2 interacting with Cu(111).7,8 Some differences were reported in the adsorption probability for En > 200 meV in the two studies, and this was attributed to differences in surface cleanliness and preparation. This discrepancy poses an issue for theoreticians trying to compare their simulated energy-dependent sticking probabilities to experimental results, as highlighted in the recent work by van Bree and Kroes.5 To provide independent verification of S0 recorded without any control over the molecular geometry [S0(R)], the helicopter [S0(H)] and cartwheel [S0(C)] alignment results presented in this work can be combined to give a ‘random’ distribution using the relationship set out in eqn (3).10,12 | (3) |
The resulting S0(R) values are presented in Fig. 6, alongside the measurements reported by Zhang et al.8 and Minniti et al.7 A fit of eqn (2) to the data of Zhang et al. is also included. The fitting parameters are provided in Table 2, where they can be compared to the values established by Zhang et al.8 It should be noted that Zhang's data were initially plotted as a function of average energy, measured from their O2 beam ToF profiles. To facilitate a direct comparison to the work presented here, Zhang's data are presented as a function of the most probable beam energies, established from the same ToF profiles. As such, the fitting parameters differ slightly from those quoted by Zhang et al. in their article. The agreement between our results and those of Zhang et al. is very good. While there are minor discrepancies at the highest En values considered by Zhang et al., where the maximum beam energy was 396 meV, and in the low-energy range (close to the detection limit of the King and Wells method), the agreement in these regions is still qualitatively strong. Notably, Zhang et al. reported measurable adsorption appearing around 100 meV,8 which matches the onset of adsorption of parallel-aligned O2 in this work.
| Label | A | E c (meV) | δ (meV) |
|---|---|---|---|
| This study | 0.87 ± 0.03 | 280 ± 7 | 126 ± 9 |
| Zhang et al. | Not reported | 290 ± 9 | 103 ± 11 |
When comparing the parameters extracted from fits to the data presented in this work, and those reported by Zhang et al., the Ec values are consistent for both studies (see Table 2). The value of the δ parameter is higher in the data reported here, suggesting a broader distribution of adsorption barriers for our experimental conditions. Comparing the widths of the measured velocity distributions, derived from ToF measurements, is non-trivial due to differences in the two experimental setups. For example, in this work, ToF traces are recorded after the beam traversed a second set of hexapoles, which can affect the shape of the derived velocity distribution. While the ToF measurements permit comparison of the beam conditions within each setup, they do not allow for straightforward absolute comparisons between the two different experimental setups. Surface temperature and sample cleanliness could also impact the value of the δ parameter, and again these conditions are hard to assess and compare between two different experiments.
Overall, the quantitative agreement in the Ec value, and the similarity in the shape of the S0(R) distribution as a function of energy, confirms that the findings reported here are in good agreement with those measured by Zhang et al.8 and hence also inconsistent with those of Minniti et al.7
Conclusions
The sticking probability of an alignment-controlled O2 beam interacting with a Cu(111) surface has been studied across a range of incident energies and angles of incidence. A strong steric effect is observed, with the sticking of O2 with its molecular axis parallel to the Cu(111) surface occurring at a normal incident energy of approximately 100 meV, with the onset occurring ∼ 100 meV later for O2 molecules aligned with their molecular axis perpendicular to the surface. In the energy regime probed, O2 adsorption on Cu(111) is predominantly an activated direct dissociative process—consistent with previous molecular beam and theoretical studies. The measurements reported here provide the first experimental confirmation that molecular alignment plays an important role in O2 interactions with Cu(111) surfaces. The findings both deepen our understanding of the adsorption process and provide key benchmarking data for future theoretical studies.Author contributions
Conceptualization and methodology: M. K.; performing experimental measurements: M. K., M. J. R., L. Y. W.; formal analysis and investigation: all authors; writing – original draft preparation: M. J. R., L. Y. W.; writing – review and editing: all authors; funding acquisition: B. R. H., M. K.; supervision: B. R. H., M. K.Data availability
Data for this article, including the tabulated results underpinning the figures in the main text and the ESI† are available at https://doi.org/10.17638/datacat.liverpool.ac.uk/2948.Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. R. H. is grateful to the European Commission (ERC Starting Grant project 948373) and the Leverhulme Trust (RPG-2022-264, PLP-2022-215) for funding. M. K. thanks JSPS KAKENHI (Grant Numbers 20H02623 and 24K01349) and Iketani Science and Technology Foundation for support. M. J. R. is grateful to the School of Physical Sciences at the University of Liverpool for a Postdoctoral Development Award.References
- R. M. Burns and W. W. Bradley, Protective coatings for metals, Reinhold Publishing Corporation, New York, 1967 Search PubMed.
- M. Rajumon, K. Prabhakaran and C. Rao, Surf. Sci., 1990, 233, L237–L242 CrossRef CAS.
- T. Sueyoshi, T. Sasaki and Y. Iwasawa, Surf. Sci., 1996, 365, 310–318 CrossRef CAS.
- M. Ramos, C. Díaz, A. E. Martínez, H. F. Busnengo and F. Martín, Phys. Chem. Chem. Phys., 2017, 19, 10217–10221 RSC.
- R. van Bree and G. J. Kroes, J. Phys. Chem. C, 2024, 128, 19182–19196 CrossRef CAS.
- D. A. King and M. G. Wells, Surf. Sci., 1972, 29, 454–482 CrossRef CAS.
- M. Minniti, D. Farías, P. Perna and R. Miranda, J. Chem. Phys., 2012, 137, 074706 CrossRef CAS PubMed.
- D. Zhang, C. Jansen, A. W. Kleyn and L. B. F. Juurlink, Phys. Chem. Chem. Phys., 2023, 25, 14862–14868 RSC.
- K. Moritani, M. Tsuda, Y. Teraoka, M. Okada, A. Yoshigoe, T. Fukuyama, T. Kasai and H. Kasai, J. Phys. Chem. C, 2007, 111, 9961–9967 CrossRef CAS.
- M. Kurahashi and Y. Yamauchi, Phys. Rev. Lett., 2013, 110, 246102 CrossRef PubMed.
- A. J. Komrowski, H. Ternow, B. Razaznejad, B. Berenbak, J. Z. Sexton, I. Zoric, B. Kasemo, B. I. Lundqvist, S. Stolte, A. W. Kleyn and A. C. Kummel, J. Chem. Phys., 2002, 117, 8185–8189 CrossRef CAS.
- M. Kurahashi, Prog. Surf. Sci., 2016, 91, 29–55 CrossRef CAS.
- M. Kurahashi and Y. Yamauchi, Rev. Sci. Instrum., 2009, 80, 083103 CrossRef PubMed.
- M. Kurahashi, Rev. Sci. Instrum., 2021, 92, 013201 CrossRef CAS PubMed.
- J. Harris, Surf. Sci., 1989, 221, 335–345 CrossRef CAS.
- M. Kurahashi and Y. Yamauchi, J. Chem. Phys., 2014, 140, 031102 CrossRef PubMed.
- H. Ueta and M. Kurahashi, Angew. Chem., Int. Ed., 2017, 56, 4174–4177 CrossRef CAS PubMed.
- M. J. E. de Willigen, M. Kurahashi and L. B. F. Juurlink, Phys. Chem. Chem. Phys., 2022, 24, 18227–18235 RSC.
- M. Kurahashi, J. Chem. Phys., 2019, 151, 084702 CrossRef PubMed.
- Y. Tsuda, J. S. Gueriba, H. Ueta, W. A. Diño, M. Kurahashi and M. Okada, JACS Au, 2022, 2, 1839–1847 CrossRef CAS PubMed.
- M. Kurahashi, J. Chem. Phys., 2022, 157, 124703 CrossRef CAS PubMed.
- M. Karikorpi, S. Holloway, N. Henriksen and J. Nørskov, Surf. Sci., 1987, 179, L41–L48 CrossRef CAS.
- R. A. B. V. Bree, N. Gerrits and G.-J. Kroes, Faraday Discuss., 2024, 361, 251 Search PubMed.
- A. Gross, S. Wilke and M. Scheffler, Phys. Rev. Lett., 1995, 75, 2718 CrossRef CAS PubMed.
- L. Österlund, I. Zorić and B. Kasemo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15452–15455 CrossRef.
- M. Beutl, K. Rendulic and G. Castro, Surf. Sci., 1997, 385, 97–106 CrossRef CAS.
- A. C. Luntz, M. D. Williams and D. S. Bethune, J. Chem. Phys., 1988, 89, 4381–4395 CrossRef CAS.
- M. C. Wheeler, D. C. Seets and C. B. Mullins, J. Chem. Phys., 1996, 105, 1572–1583 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Further details on the molecular beam properties, data analysis procedure, and additional experimental results. See DOI: https://doi.org/10.1039/d4cp04595e |
| ‡ Current address: School of Chemistry, University of Birmingham, Edgbaston B15 2TT, UK. |
| This journal is © the Owner Societies 2025 |