 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic quenching of sulfur induced by argon collisions
David M. G.
Williams
 *a,
Nicole
Weike
*a,
Nicole
Weike
 b,
Manuel
Lara
b,
Manuel
Lara
 c,
Kevin M.
Dunseath
c,
Kevin M.
Dunseath
 a and
Alexandra
Viel
a and
Alexandra
Viel
 a
a
aUniv Rennes, CNRS, IPR (Institut de Physique de Rennes) – UMR 6251, F-35000 Rennes, France. E-mail: david.williams@univ-rennes.fr
bTheoretische Chemie, Universität Bielefeld, Postfach 100131, D-33501 Bielefeld, Germany
cDepartamento de Química Física Aplicada, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Madrid, Spain
First published on 24th January 2025
Abstract
An accurate potential energy model, explicitly designed for studying scattering and treating the spin–orbit and nonadiabatic couplings on an equal footing, is proposed for the S + Ar system. The model is based on the Effective Relativistic Coupling by Asymptotic Representation (ERCAR) approach, building the geometry dependence of the spin–orbit interaction via a diabatisation scheme. The resulting full diabatic model is used in close-coupling calculations to compute inelastic scattering cross sections for de-excitation from the S(1D2) fine structure level into the 3P multiplet. The energy grid is tuned to resolve the many resonances present and to guarantee converged thermal rates from 1 to 300 K. At temperatures above 100 K, the computed thermal rate coefficients for quenching of S(1D2) are in good agreement with results from an earlier experimental and theoretical study. The branching ratio at 296 K for de-excitation into the S(3P0) level agrees well with the value obtained by a different experiment. A discrepancy however remains between theory and experiment at lower temperatures. This is discussed in light of the interference mechanisms at play during this quenching process.
I. Introduction
The de-excitation (quenching), or removal of electronically excited atoms and molecules plays a key role in the chemical evolution of gaseous environments such as planetary atmospheres, combustion engines, and the interstellar medium. It can also have a sometimes undesirable effect in more controlled environments such as atomic and molecular beam experiments. Due to their low reactivity, noble gases such as helium and argon are often used as carriers of other atomic and molecular species that are the actual subjects of the study. In spite of this, they can significantly quench the population of excited states before the process of interest can occur. In particular, sulfur in its S(1D) excited state has received much attention in beam experiments since the 1970's.1,2 The rate coefficient for the removal of S(1D) by Ar, determined by Black and Jusinski,3 was 1.4 × 10−11 cm3 molecule−1 s−1, of the same order of magnitude as the net removal by reaction and quenching combined in collisions with H2 (2.1 × 10−11 cm3 molecule−1 s−1). However, the removal rate corresponding to helium is 3 orders of magnitude smaller than that for argon. For this reason, helium rather than argon was chosen as the carrier gas in a subsequent experiment analyzing the reactive collision S(1D) + H2 → SH + H using the CRESU (Cinétique de Réaction en Ecoulement Supersonique Uniforme or Reaction Kinetics in a Uniform Supersonic Flow) technique.4 A later experiment by the same group investigated specifically the quenching of S(1D) by collisions with argon for a wider range of temperatures.5 They found in particular a rate coefficient of 1.78 × 10−11 cm3 molecule−1 s−1 at 300 K, slightly larger than the value proposed by Black and Jusinski.3 While all these studies provided total rate coefficients, Stout et al.6 were able to deduce the fine-structure distribution of the quenched sulfur atoms by argon using time-resolved coherent anti-Stokes Raman spectroscopy (CARS), concluding that approximately 80% of the total S(3P) yield is produced in the 3P0 level.The experimental work on quenching of S(1D) by argon reported by Lara et al.5 was accompanied by a theoretical study based on close-coupling calculations with the aim of understanding further the dynamics involved. The theoretical rate coefficients obtained are in good agreement with the experimental results at higher temperatures, but overestimate them at lower temperatures. At 5.8 K for example, the theoretical rate is a factor two larger than the experimental one. It is interesting to note that similar discrepancies between theory and experiment are seen in recent studies on the electronic quenching of O(1D) in collisions with noble gases.7–9 In particular, for the case of O + Ar, the differences are also of the order of a factor of two, not just at low temperatures but throughout the range from 50 to 350 K. Implementation details of the scattering simulations notwithstanding, we infer that the differences between theory and experiment for these chemically very similar systems are likely caused by results being extremely sensitive to the underlying potential energy curves. Indeed, for S + Ar, Lara et al.5 attributed this discrepancy to the interference mechanism underlying the process. In simple terms, the quenching process can be understood as probability transfers (jumps) localized around crossing points of the various potential curves and in particular those correlating with S(1D) and S(3P). The system traverses the crossings twice, once when the atoms are approaching and once when they are receding (having been reflected by the repulsive barrier). This creates two portions of flux which have travelled along different paths and hence have different phases. The resulting interference produces oscillations in the quenching probability as a function of the energy, known as Stückelberg oscillations.10 In the S + Ar system, there are crucial avoided crossings whose intrinsic interference mechanism makes the theoretical results extremely sensitive to any small change in the position of these crossings. This poses a stringent test for any theoretical simulation of this kind of process: any small inaccuracy in the potential energy curves will have a radical effect in the interference pattern and hence in the scattering simulation. Determining the curve crossings with an accuracy of a few cm−1, particularly challenging at crossings in the repulsive walls, was therefore deemed necessary in order to better reproduce this quantum interference process. This stringent dependence on the quality of the ab initio computation motivates us to use the Effective Relativistic Coupling by Asymptotic Representation (ERCAR) approach to reinvestigate the electronic quenching of S by Ar. Indeed the ERCAR scheme is one of the rare approaches for building accurate potential energy surface (PES) models that treat vibronic and spin–orbit coupling on an equal footing. Furthermore, the PES is furnished in a form suitable for scattering studies, as demonstrated in a recent application to the collisions of H with I.11,12
This paper is organized as follows. In Section II, the theoretical background is given while Section III provides the computational details. The coupled potential curves thus obtained are presented in Section IV A, and the results of the scattering computations are discussed in Section IV B. Finally, this work is summarized in Section V.
II. Theory
A. Theory for the potential energy surface
The potential energy surfaces (PESs) are developed within the Effective Relativistic Coupling by Asymptotic Representation (ERCAR) approach13–18 to accurately account for the spin–orbit (SO) effect of a relativistically-treated atom within a molecule. The approach utilizes the idea that SO coupling is an atom-based effect. The full molecular Hamiltonian is thus represented in a diabatic asymptotic direct product basis composed of states of the relativistic atom and the remaining molecular fragment. In the following, the key ideas of the approach are given briefly.The molecular electronic Hamiltonian Ĥe can be separated into the Coulomb Hamiltonian Ĥc, which also contains all scalar relativistic effects, and the SO Hamiltonian ĤSO as
| Ĥe = Ĥc + ĤSO. | (1) |
 of the relativistic atom and fragment states
of the relativistic atom and fragment states 
 | (2) |
 describes the sulfur atom while the molecular fragment is just the argon atom, so that the fragment states
describes the sulfur atom while the molecular fragment is just the argon atom, so that the fragment states  here do not depend on Q.
here do not depend on Q.
The molecular electronic Hamiltonian Ĥe is represented in the basis (2) and the matrix elements Wdjk(Q, R) of the resulting diabatic model read
 | (3) |
In the determination of the SO model, the following effective n-electron SO operator is applied to the diabatic basis states,
 | (4) |
![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) k is the orbital angular momentum operator, ŝk is the spin operator, and both act on each electron k. There are two atomic state projectors (
k is the orbital angular momentum operator, ŝk is the spin operator, and both act on each electron k. There are two atomic state projectors (![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) i2 and
i2 and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) j2) to account for both intra-state SO coupling for couplings within a single atomic multiplet and for inter-state SO coupling for couplings between different atomic terms of the same electron configuration. Both projectors act on the basis function to ensure that the operators
j2) to account for both intra-state SO coupling for couplings within a single atomic multiplet and for inter-state SO coupling for couplings between different atomic terms of the same electron configuration. Both projectors act on the basis function to ensure that the operators ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) k·ŝk act on the intended atomic states of the relativistic atom. The λi2j2 are the respective coupling constants for the intra-state and the inter-state SO coupling.
k·ŝk act on the intended atomic states of the relativistic atom. The λi2j2 are the respective coupling constants for the intra-state and the inter-state SO coupling.
More details on the ERCAR approach can be found for example in ref. 16. The particular expressions for the geometry dependent Coulomb and the (geometry independent) SO model are system dependent. The details for the S + Ar system, where R is the sole internal coordinate, are given in Section III.
B. Theory of scattering
We use the close-coupling formalism for an atomic collision of the type A + B given by Launay,19 as summarized in ref. 12. The total Hamiltonian for the system may be written as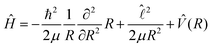 | (5) |
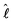 is the orbital angular momentum operator for the relative motion of the two atoms and
is the orbital angular momentum operator for the relative motion of the two atoms and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (R) denotes the electronic Hamiltonian. The solution of the corresponding Schrödinger equation is expanded in terms of partial waves |ψJMJ〉, which are eigenstates of the operators Ĵ2 and Ĵz for the total angular momentum J. These partial waves are further expanded in terms of space-fixed basis functions, eigenstates of ĵAB2,
(R) denotes the electronic Hamiltonian. The solution of the corresponding Schrödinger equation is expanded in terms of partial waves |ψJMJ〉, which are eigenstates of the operators Ĵ2 and Ĵz for the total angular momentum J. These partial waves are further expanded in terms of space-fixed basis functions, eigenstates of ĵAB2, 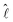 2 as well as Ĵ2 and Ĵz, where jAB denotes the angular momentum obtained by coupling the individual angular momenta jA and jB of atoms A and B:
2 as well as Ĵ2 and Ĵz, where jAB denotes the angular momentum obtained by coupling the individual angular momenta jA and jB of atoms A and B: | (6) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), and γ labels the different asymptotic energy levels. The total angular momentum is then
), and γ labels the different asymptotic energy levels. The total angular momentum is then  . Substituting this expansion into the Schrödinger equation and projecting onto a particular basis function yields a set of coupled second-order differential equations for the radial basis functions in matrix form,
. Substituting this expansion into the Schrödinger equation and projecting onto a particular basis function yields a set of coupled second-order differential equations for the radial basis functions in matrix form, | (7) |
The partial integral cross section for a transition from level γ to level γ′ for a given J, averaged over initial states and summed over final states, is given by
 | (8) |
| TJ = −2iKJ(1 − iKJ)−1. |
The total integral cross section  is then obtained by summing the partial cross sections over all values of the total angular momentum J. Energy-dependent rate coefficients may also be defined as
is then obtained by summing the partial cross sections over all values of the total angular momentum J. Energy-dependent rate coefficients may also be defined as
 | (9) |
To compare with the experimental results, it is necessary to introduce thermal rates. Collisional rate coefficients kγγ′(T) at temperature T for a transition from level γ to level γ′ are given by averaging the integral cross section 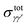 over a Maxwellian distribution:
over a Maxwellian distribution:
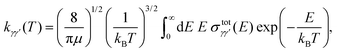 | (10) |
III. Computational details
A. Ab initio computations
The ERCAR approach requires an ensemble of adiabatic electronic energies against which the model is fitted. These SO-free Coulombic energies were obtained in a two-step procedure combining complete active-space self-consistent field (CASSCF) calculations with multi-reference configuration interaction (MRCI) calculations with Davidson corrections (MRCI+Q) to properly capture the multi-configurational character of the states of interest. All calculations were performed in C2v symmetry using the MOLPRO software package.20 After testing both larger and smaller basis sets, the aug-cc-pV5Z orbital basis was found to be optimal in terms of accuracy versus CPU time and was used for ab initio data generation. Calculations were performed along the S–Ar distance comprising 520 data points lying between 3.9 and 1890 bohr (1000 Å). A fine grid is used for distances below 15 bohr, with a higher density of points in the interaction region and repulsive walls, so that 75% of the points lie below 7.6 bohr. Nine adiabatic energies were computed per point, which converge asymptotically to 3 distinct energy levels. From the components of the 3P (3Σ−,3Π), 1D (11Σ+, 1Π, 1Δ) and 1S (21Σ+) states of sulfur, a total of 15 fine structure states of the composite system can be formed. Note that although the 1S (21Σ+) state lies much higher in energy, it is necessary to include it in order to have all states corresponding to the [Ne]3s23p4 ground configuration of sulfur.Molecular orbitals and reference wave functions were first computed by state-averaged CASSCF calculations for each data point. The active space includes the 3p orbitals of sulfur. The orbitals were diabatized for each data point with respect to a reference calculation performed at a large S–Ar separation (1890 bohr). These diabatic orbitals then form the one-electron basis in the MRCI calculations in which the 3s and 3p orbitals of both sulfur and argon were used in the active space. Correlation and Davidson correction energies were rescaled by a factor of 1.123 for the lowest-lying triplet and singlet curves to maximally resemble a CCSD(T) reference coupled cluster calculation.
B. Diabatic Coulomb Hamiltonian model
In the following we describe the Coulomb part of the diabatic model Hamiltonian. Without spin–orbit coupling, the model is most easily expressed in terms of a basis of a 9 × 9 diabatic model reproducing the SO-free adiabatic energies. The diabatic state basis order is taken to be 3Σ−, 3Π, 11Σ+, 1Π, 1Δ, 21Σ+ throughout this section, and also specified in Table 1. All distances are given in bohr. As in ref. 11, the nuclear configuration space is split into three overlapping domains, henceforth called the repulsion domain (R ≤ 10.8), the dispersion domain
(R ≤ 10.8), the dispersion domain  (R ≥ 15.1) and the interaction domain
(R ≥ 15.1) and the interaction domain  (7.4 ≤ R ≤ 19). Each diabatic matrix element is modelled by a sum of twice differentiable domain-specific functions, constructed such that their contributions vanish exactly outside of their respective domain. In other words, each diabatic matrix element Wjk(R) (where j,k range from 1 to 9) can be expressed as
(7.4 ≤ R ≤ 19). Each diabatic matrix element is modelled by a sum of twice differentiable domain-specific functions, constructed such that their contributions vanish exactly outside of their respective domain. In other words, each diabatic matrix element Wjk(R) (where j,k range from 1 to 9) can be expressed as| Wjk(R) = WRjk(R) + WIjk(R) + WDjk(R) | (11) |
 | (12) |
| S | Symmetry | j | R R 0j | R R 1j |
|---|---|---|---|---|
| 3P | 3Σ− | 1 | 9.26 | 10.77 |
| 3Π | 2–3 | 8.88 | 10.02 | |
| 1D | 11Σ+ | 4 | 7.37 | 8.13 |
| 1Π | 5–6 | 9.35 | 10.02 | |
| 1Δ | 7–8 | 9.35 | 10.02 | |
| 1S | 21Σ+ | 9 | 7.37 | 8.13 |
To ensure eqn (12) holds, we employ a switching function defined by
 | (13) |
In the present case, the matrix W(R) has only one symmetry-allowed diabatic coupling element between 11Σ+ and 21Σ+ (states 4 and 9). This coupling term is of course vanishing at infinite separation of the two atoms, resulting in a diagonal W(R) matrix for large enough values of R. The diagonal matrix elements are modelled as
 | (14) |
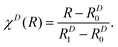 | (15) |
This ansatz is exact in the asymptotic limit of R → ∞ because both Ar and S are neutral atoms. Since the adiabatic and diabatic representations coincide for R > 19 bohr, cD6j was obtained via a linear fit against ab initio data on a double logarithmic scale, confirming the asymptotic behavior. We verified that no additional orders are needed in this dispersion domain to properly reproduce the ab initio data. χD(R) serves to shift and scale the distance coordinate R such that the contribution of the dispersion term vanishes for R ≤ RD0 = 15 bohr whereas WRjj(R) and WIjj(R) vanish for R ≥ RD1 = 9 bohr. The functions used for the diagonal matrix elements in the repulsion domain are similar but less constrained in their functional form. They are given by
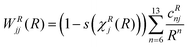 | (16) |
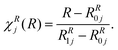 | (17) |
By construction WRjj(R) vanishes for all R ≥ RR1j, where RR1j depends on the particular state j, as given in Table 1. The diagonal functions in the interaction domain are defined such that they vanish at each domain boundary and are given by
 | (18) |
Finally, the lone diabatic coupling element (j ≠ k) is modelled similarly, but adding an exponential term for both interaction and repulsion domains:
 | (19) |
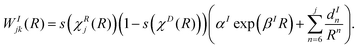 | (20) |
As stated above, WDjk(R) = 0.
All parameters for the repulsion and interaction domains have been obtained using a Levenberg–Marquardt fitting algorithm. Since only two states are coupled, most could be directly fitted against ab initio data. The coupled 2 × 2 sub-block describing the 1Σ+ states had to be diagonalized before fitting.
C. Spin–orbit model
The model contains 15 basis states corresponding asymptotically to the atomic states 3P, 1D and 1S of sulfur and 1S of argon. The SO matrix is easily expressed in the basis of the four-electron Slater determinant spinors corresponding to each of the 3 states of sulfur considered here. The basis definition is given in Table 2. In this basis, the SO matrix can be written in block matrix form as | (21) |
| Basis number | L S | S S | L Ar | S Ar | j S | j Ar | j SAr | M j SAr |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 2 | 0 | 2 | −2 |
| 2 | 1 | 1 | 0 | 0 | 2 | 0 | 2 | −1 |
| 3 | 1 | 1 | 0 | 0 | 2 | 0 | 2 | 0 |
| 4 | 1 | 1 | 0 | 0 | 2 | 0 | 2 | 1 |
| 5 | 1 | 1 | 0 | 0 | 2 | 0 | 2 | 2 |
| 6 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | −1 |
| 7 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 8 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 9 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | −2 |
| 11 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | −1 |
| 12 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 0 |
| 13 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 1 |
| 14 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 2 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The strategy followed to fit the three λi parameters aims at reproducing the experimental levels of the sulfur atom.21 In our model, the 5 asymptotic energies are obtained by diagonalization of the sum of the SO matrix and the three asymptotic energies of the Coulomb part. These three SO-free ab initio energies differ from the weighted average of the observed values21 by at most 70 cm−1 due to inaccuracies in the ab initio computations. As a consequence, the optimization of the λi parameters was combined with the modification of the asymptotic energies of the Coulomb model in order to match with the experimental values. Experimental transition energies are 396.055 cm−1, 573.64 cm−1, 9238.609 cm−1 and 22179.954 cm−1, respectively.21 These numbers are (by construction) perfectly reproduced by our model.
It should be noted that the inter-state SO couplings expressed in the basis given in Table 2 do not vanish at large distances. These couplings mix different terms arising from the same electron configuration and having the same total angular momentum jSAr. As a result, the physical states, characterized by the quantum number jSAr, are described by linear combinations of the basis states of Table 2. To facilitate the matching process and to compute collision cross sections, a basis transformation must be performed to diagonalize the potential matrix at large distances.
IV. Results
A. Potential energy curves
The parameters of the Coulomb model of the potential energy surface (PES) are obtained by fitting the ansatz described in Section III B against the ab initio data (see Section III A). The exceptions are the dispersion parameters cD6j in eqn (14), which could be obtained more directly through a linear fit against the ab initio data on a double logarithmic scale. Since the dispersion term describes the shape of the long-range interaction to an accuracy beyond that of the underlying electronic structure (≤1 cm−1), no higher order terms are considered in this domain.Table 3 compares the long-range interaction coefficients thus obtained with those of ref. 5. In this earlier work, ab initio electronic energies were obtained using MOLPRO from MRCI+Q calculations in C2v symmetry, with the aug-cc-pV5Z orbital basis. The energies were corrected for the basis set superposition error (BSSE) using the counterpoise procedure of Boys and Bernardi.22 Once the MRCI wavefunctions for the nine electronic states had been determined, the matrix elements of the SO part of the Breit-Pauli Hamiltonian were calculated at each internuclear distance. The long-range interactions corresponding to the 11Σ+ state were independently calculated using a multipolar expansion of the electrostatic interaction operator, treated at the second order of perturbation theory. The resulting energies were matched at large distances with their MRCI counterpart.
The values obtained in the current calculation are about 10% larger than those reported in ref. 5. We infer that this comes from the different electronic structure, as well as from the different methodology employed to obtain these coefficients. Our values for the well depths and equilibrium distances also subtly deviate from those reported in ref. 5. The largest difference in equilibrium distance is found to be 0.12 bohr for the two states of Σ+ symmetry. The well depths obtained in the current work agree with those given in ref. 5 to within 30 cm−1. The largest differences are obtained for the ground 3Π (27 cm−1 shallower) and for the 11Σ+ (25 cm−1 deeper) curves. The total root mean square error (RMSE) achieved by the fit across all ab initio data points is 28 cm−1 including all adiabatic energies up to 1 eV above their respective dissociation energy. The RMSE is dominated by the error in the repulsive walls, with differences between model and ab initio data consistently ≤1 cm−1 for large ranges of R, for all considered states. Fig. 1 shows the energies of the Coulomb model corresponding to the 3P and 1D channels. The 1S is about 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the 3P state (and thus not shown). On the scale of the figure, the ab initio energies are indistinguishable from the presented curves. The 11Σ+ state exhibits a characteristically “dented” shape between the minimum and the repulsive wall with a moderate slope. Due to this particular shape, the intersections of this curve with the two triplet states are extremely sensitive to minor changes in the electronic structure. These singlet–triplet intersections become avoided crossings when the SO coupling is taken into account. The dented shape of the 11Σ+ state is caused by subtle nonadiabatic coupling effects with the 21Σ+ state. Indeed our model shows a strong coupling between these two electronic states especially for distances less than 6.5 bohr, where the coupling strength approaches the size of the energy gap between the adiabatic energies (on the eV scale). We thus infer that the exact shape of the 11Σ+ potential curve is extremely sensitive to the electronic structure calculation and especially to the convergence of the nonadiabatic coupling. This is a key limitation, as it is far more difficult to converge electronic wave function properties rather than the adiabatic energies.
000 cm−1 above the 3P state (and thus not shown). On the scale of the figure, the ab initio energies are indistinguishable from the presented curves. The 11Σ+ state exhibits a characteristically “dented” shape between the minimum and the repulsive wall with a moderate slope. Due to this particular shape, the intersections of this curve with the two triplet states are extremely sensitive to minor changes in the electronic structure. These singlet–triplet intersections become avoided crossings when the SO coupling is taken into account. The dented shape of the 11Σ+ state is caused by subtle nonadiabatic coupling effects with the 21Σ+ state. Indeed our model shows a strong coupling between these two electronic states especially for distances less than 6.5 bohr, where the coupling strength approaches the size of the energy gap between the adiabatic energies (on the eV scale). We thus infer that the exact shape of the 11Σ+ potential curve is extremely sensitive to the electronic structure calculation and especially to the convergence of the nonadiabatic coupling. This is a key limitation, as it is far more difficult to converge electronic wave function properties rather than the adiabatic energies.
Fig. 2 shows the adiabatic energies obtained from the full ERCAR potential model, including SO coupling. The asymptotic energies are split into 5 levels corresponding to Ar(1S0) and S(3P2,1,0, 1D2, 1S0). As outlined in Section III C, experimental transition energies for atomic sulfur are reproduced by construction. Note that the S–Ar adiabatic curves are labelled by their Ω = |MjSAr| quantum number as is common in spectroscopy. For Ω = 0±, the upper index denotes whether the state is odd or even with respect to reflections in a plane which contains the atoms.
 | ||
| Fig. 2 Adiabatic potential curves over the full energy range. The S–Ar distance is given in bohr and the energies in cm−1. Zero is defined as the asymptotic limit of the lowest curve. | ||
At shorter inter-atomic distances, the 3P2 level splits into Ω = 2, 1 and 0+ components with Ω = 2 being the lowest curve (see Fig. 3). The 3P1 level is composed of Ω = 1 and Ω = 0− curves while 3P0 corresponds to the second Ω = 0+. Finally, the 1D2 channel splits into another set of Ω = 2, 1, 0+ curves as shown in Fig. 4, while 1S0 forms the fourth Ω = 0+. The curves of identical Ω form avoided crossings where the former 11Σ+ intersects with the 3Π and 3Σ−. In particular the Ω = 0+ curves present two avoided crossings at distances between 4 and 5 bohr. Fig. 4 shows the aforementioned avoided crossings in greater detail. It is of particular note that the lower-lying crossing nearly coincides with the dissociation energy of the 1D2 channel, making it a dynamically accessible and extremely relevant feature of the surface. The horizontal line in Fig. 4 corresponding to the energy of the 1D2 channel is drawn to emphasize this particularity. The second crossing, at a distance about half a bohr shorter and only 400 cm−1 higher in energy, is also expected to be dynamically reachable.
 | ||
| Fig. 3 Zoom on the low energy part of the adiabatic potential curves. The S–Ar distance is given in bohr and the energies in cm−1. | ||
B. Scattering
In all the scattering calculations, the reduced mass of the S + Ar system is taken to be μ = 32377.6463 a.u. Partial waves up to J = 120 were included. The basis transformation matrix that diagonalizes the inter-state SO couplings was obtained by diagonalizing the potential matrix at 5 × 107 bohr. For each partial wave and collision energy, the logarithmic derivative matrix was propagated from 3.6 bohr out to 60 bohr in steps of 0.003 bohr, where it was matched to the corresponding logarithmic derivative for the asymptotic solutions to give the scattering matrix K. Cross sections were calculated for collision energies up to 3000 cm−1, and then used to compute energy-dependent rates as well as thermal rates up to 300 K. We have verified that the results obtained are converged with respect to the number of partial waves, the step length and the matching radius.In Fig. 5 we present the total energy-dependent rate coefficient, eqn (9), for the quenching process from the S(1D2) level down to the 3P multiplet. We also show the individual rates for quenching into the 3P0,1,2 fine structure levels. Transitions into the 3P0 level provide the largest contribution to the total quenching rate, although its relative importance compared to the contribution from the 3P2 level diminishes as the collision energy (relative to the initial S(1D2) level) increases. Quenching into the 3P1 level is very small throughout the energy range considered. This can be attributed to the absence of any coupling between the Ω = 0+ component of the asymptotic S(1D2) potential curve and the Ω = 0− component of the S(3P1) curve in the neighborhood of the relevant crossings, see Fig. 2–4. Populating the 3P1 level hence requires changing Ω through Coriolis couplings (i.e. off-diagonal elements of the centrifugal potential in the BF basis), whose action has been shown to be very small for S + Ar.5
 | ||
| Fig. 5 Total and partial energy-dependent rate coefficients as a function of the collision energy relative to the initial S(1D2) level. | ||
Resonances are discernable at collision energies below 60 cm−1, as can be seen in Fig. 6 which provides a zoom on this energy region. Most are associated with the 1D2 → 3P0 transition simply because this is the dominant contribution at these energies. Occurring in different partial waves (J values), resonances are signatures of quasi-bound states supported by the effective potential in each channel resulting from the combination of the attractive well and the repulsive centrifugal barrier. The resulting potential landscape can then be quite tortuous due to the various avoided crossings in the adiabatic potential curves shown in Fig. 4. While the individual resonance structures themselves are quite narrow, they nevertheless have an important effect on the thermally averaged rates at low temperatures. It is therefore important to adequately resolve these resonances.
 | ||
| Fig. 6 Total and partial energy-dependent rate coefficients as a function of the collision energy in the resonance region close to threshold. | ||
Comparing with the corresponding energy-dependent rates given in Fig. 6 of ref. 5 reveals a number of important differences. For collision energies above 500 cm−1, the current total energy-dependent rate is consistently larger than that of ref. 5, the percentage differences reaching as much as 30%. In the resonance region shown in Fig. 6, however, the results of ref. 5 tend to be larger, for example by approximately 30% between 20 and 30 cm−1 where our total energy-dependent rate has a minimum. While it may appear that there are more resonances in the current results than in those of ref. 5, this is almost certainly due to the much finer energy grid used here to adequately resolve the resonance structure. The most striking differences occur in the partial energy-dependent rates into the 3P0 and 3P2 levels. In the earlier work, these partial rates as a function of collision energy cross near 110 cm−1, so that at higher energies the main contribution comes from transitions into the 3P2 level. The authors attributed this to a crossing of potential energy curves at 6.86 bohr (labelled as C3 in their work). In the current work, however, no such crossing occurs, so that the major contribution to the quenching process is always from transitions into the 3P0 level. Indeed, at collision energies corresponding to temperatures in the vicinity of 296 K (∼206 cm−1), transitions into the 3P0 and 3P2 levels contribute roughly 82% and 17% respectively to the total energy-dependent rate.
In Fig. 7 we present the total and partial thermal rate coefficients, eqn (10), for temperatures from 5 to 300 K. The experimental and theoretical results from ref. 5 are also shown. The two experimental data points above 100 K are well reproduced by both calculations. Below 50 K, neither of the two theoretical thermal rates agree with the experimental data. While the earlier results overestimate the experimental values, with a maximum near 10 K, the current results underestimate them, displaying a minimum between 20 and 30 K. The sensitivity of the theoretical thermal rates is directly related to the fine details of the coupled potential curves used, as shown in Fig. 11 of ref. 5. We further infer that the position of the avoided crossing at the energy of the entrance channel is responsible for this. We also remark that the partial thermal rate at 296 K for transitions into the 3P0 level accounts for approximately 77% of the total rate, close to the experimental estimation6 of around 80%, while transitions into the 3P2 level contribute roughly 23%. Comparing with the branching ratios for the energy-dependent rates, we see that the thermal averaging has slightly reduced the relative contributions from transitions into S(3P0), enhancing those into S(3P2).
 | ||
| Fig. 7 Total and partial thermal rate coefficients for quenching. The experimental data and the green curve labelled Lara et al. are from ref. 5. | ||
Our branching ratios thus indicate a strong propensity for quenching into the 3P0 fine structure level throughout the temperature range considered. A similar propensity was seen for quenching of O(1D) by Ar,9 which should not be surprising since oxygen lies just above sulfur in the periodic table. It is interesting to note that while the calculations in ref. 5 give similar values to ours for the total rate coefficient, their branching ratios are very different with a propensity for populating the 3P2 level at 296 K. Despite the continuing discrepancy in the rate coefficients at low temperature, our results would thus appear to be a step in the right direction.
V. Conclusion
We have developed an accurate spin–orbit coupled diabatic potential model for the scattering of sulfur in its ground configuration with argon, and applied it to the study of electronic quenching of the S(1D2) fine structure level. The states of interest are all fine structure states corresponding to the asymptotic limits S(1D2) + Ar(1S0) and S(3P2,1,0) + Ar(1S0). To account for nonadiabatic coupling effects the S(1S0) + Ar(1S0) asymptotic limit is also included in the model. Using the ERCAR approach, the coupled diabatic potential model relies on accurate SO-free ab initio data for the nine adiabatic energies of S + Ar, namely 3Σ−, 3Π, 11Σ+, 1Π, 1Δ and 21Σ+. These correlate to three asymptotic energies corresponding to the 3P, 1D and 1S states of sulfur. When the spin–orbit (SO) interaction is included, 15 fine structure states are obtained. The ERCAR approach allows us to use the experimental SO energies of atomic sulfur as well as an asymptotic diabatic basis to build a fully coupled 15 × 15 diabatic representation of the interaction potential for S + Ar at all inter-atomic distances. The advantages of ERCAR are its high accuracy and low computational demand, recovering geometry-dependent spin–orbit information while being able to keep ab initio calculations at the SO-free level for all distances except for at most one point at infinite separation. Alternatively atomic spin–orbit data can be taken from experiment instead, forgoing the need of SO calculations entirely. In the resulting model, the spin–orbit interaction is intrinsically a function of the inter-atomic distance.The coupled surfaces thus obtained have been used to compute the energy-dependent and thermal rates for the quenching of S(1D2) by Ar. Since the underlying basis is constructed using eigenstates of the electronic angular momentum, the close coupling equations follow directly. Partial waves up to total angular momentum J = 120 have been used to compute quenching cross sections at collision energies up to 3000 cm−1 and hence thermal rates from 1 to 300 K. The results above 100 K are in good agreement with those of a previous theoretical and experimental study.5 At low temperatures however the discrepancy between the theoretical and the experimental data remains. In contrast to the earlier work, the computed branching ratio at 296 K for transitions into the 3P0 fine structure level is in good agreement with the experiment of Stout et al.6
The S + Ar system has a delicate electronic structure with multiple avoided crossings. We infer that at least the position of one of these is responsible for the high sensitivity of the scattering results to fine details of the potential model. Since our diabatic PES reproduces ab initio data well, we conclude that inaccuracies in the underlying data are a dominant source of error, rather than the surface itself. Further work is clearly necessary in order to reconcile theory and experiment, particularly in view of the different trends shown by the two calculations and the experiment as the temperature approaches 0 K. On the theory side, ab initio calculations going beyond those used here are clearly necessary, while additional experimental work would help confirm and extend the existing measurements.
Data availability
All essential data is already provided within the manuscript. Further data is available from the author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project (COFUND Bienvenüe-2023 NADIA) has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 899546. The authors also acknowledge the financial support of CNRS and of the University of Rennes via the IRN MCTDH grant project. NW is grateful for financial support by the Deutsche Forschungsgemeinschaft (DFG). M. L. G. acknowledges funding by the Spanish Ministry of Science and Innovation (Grant No. PID2021-122839NB-I00).References
- W. H. Breckenridge and H. Taube, Some Reactions of Ground State (3P) and Electronically Excited (1D) Sulfur Atoms, J. Chem. Phys., 1970, 53(5), 1750–1767 CrossRef CAS.
- K. Schofield, Critically Evaluated Rate Constants for Gaseous Reactions of Several Electronically Excited Species, J. Phys. Chem. Ref. Data, 1979, 8(3), 723–798 CrossRef CAS.
- G. Black and L. E. Jusinski, Rate coefficients for S(1D) removal at 300 K, J. Chem. Phys., 1985, 82, 789–793 CrossRef CAS.
- C. Berteloite, M. Lara, A. Bergeat, S. D. Le Picard, F. Dayou and K. M. Hickson, et al., Kinetics and Dynamics of the S(1D2) + H2 → SH + H Reaction at Very Low Temperatures and Collision Energies, Phys. Rev. Lett., 2010, 105, 203201 CrossRef PubMed.
- M. Lara, C. Berteloite, M. Paniagua, F. Dayou, S. D. Le Picard and J. M. Launay, Experimental and theoretical study of the collisional quenching of S(1D) by Ar, Phys. Chem. Chem. Phys., 2017, 19, 28555–28571 RSC.
- J. E. Stout, B. K. Andrews, T. J. Bevilacqua and R. B. Weisman, Cars observation of the fine structure population inversion from atomic quenching: S(1D) + Ar → S(3P0) + Ar, Chem. Phys. Lett., 1988, 151, 156–160 CrossRef CAS.
- P. J. Dagdigian, M. H. Alexander and J. Kłos, Theoretical investigation of the dynamics of O (1D → 3P) electronic quenching by collision with Xe, J. Chem. Phys., 2015, 143, 054306 CrossRef PubMed.
- L. A. Garofalo, M. C. Smith, P. J. Dagdigian, J. Kłos, M. H. Alexander and K. A. Boering, et al., Electronic quenching of O (1D) by Xe: Oscillations in the product angular distribution and their dependence on collision energy, J. Chem. Phys., 2015, 143, 054307 CrossRef PubMed.
- D. Nuñez-Reyes, J. Kłos, M. H. Alexander, P. J. Dagdigian and K. M. Hickson, Experimental and theoretical investigation of the temperature dependent electronic quenching of O (1D) atoms in collisions with Kr, J. Chem. Phys., 2018, 148, 124311 CrossRef PubMed.
- E. C. G. Stückelberg, Theorie der unelastischen Stösse zwischen Atomen, Helv. Phys. Acta, 1932, 5, 369 Search PubMed.
- N. Weike, A. Viel and W. Eisfeld, Hydrogen – iodine scattering: I. Development of an accurate spin–orbit coupled diabatic potential energy model, J. Chem. Phys., 2023, 159, 244119 CrossRef CAS PubMed.
- N. Weike, W. Eisfeld, K. M. Dunseath and A. Viel, Hydrogen – iodine scattering: II. Rovibronic analysis and collisional dynamic, J. Chem. Phys., 2024, 161, 014302-118 CrossRef PubMed.
- H. Ndome, R. Welsch and W. Eisfeld, A New Method to Generate Spin-Orbit Coupled Potential Energy Surfaces: Effective Relativistic Coupling by Asymptotic Representation, J. Chem. Phys., 2012, 136, 034103 CrossRef PubMed.
- H. Ndome and W. Eisfeld, Spin-Orbit Coupled Potential Energy Surfaces and Properties Using Effective Relativistic Coupling by Asymptotic Representation, J. Chem. Phys., 2012, 137, 064101 CrossRef PubMed.
- N. Wittenbrink, H. Ndome and W. Eisfeld, Toward Spin-Orbit Coupled Diabatic Potential Energy Surfaces for Methyl Iodide Using Effective Relativistic Coupling by Asymptotic Representation, J. Phys. Chem. A, 2013, 117(32), 7408–7420 CrossRef CAS PubMed.
- N. Wittenbrink and W. Eisfeld, An improved spin-orbit coupling model for use within the effective relativistic coupling by asymptotic representation (ERCAR) method, J. Chem. Phys., 2017, 146(14), 144110 CrossRef PubMed.
- N. Wittenbrink and W. Eisfeld, Extension of the Effective Relativistic Coupling by Asymptotic Representation (ERCAR) approach to multi-dimensional potential energy surfaces: 3D model for CH3I, J. Chem. Phys., 2018, 148, 094102 CrossRef.
- N. Weike, E. Chanut, H. Hoppe and W. Eisfeld, Development of a Fully Coupled Diabatic Spin-Orbit Model for the Photodissociation of Phenyl Iodide, J. Chem. Phys., 2022, 156, 224109 CrossRef CAS PubMed.
- J. M. Launay, Molecular collision processes. I. Body-fixed theory of collisions between two systems with arbitrary angular momenta, J. Phys. B:At., Mol. Phys., 1977, 10(18), 3665 CrossRef.
- H. J. Werner, P. J. Knowles, et al. MOLPRO 2009.1 is a package of ab initio programs. Stuttgart, Germany: see https://www.molpro.net.
- Y. Ralchenko, A. E. Kramida, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (version 3.1.5). Available: https://physics.nist.gov/asd3; 2008.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
| This journal is © the Owner Societies 2025 |


