Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical tuning of magnons in NiO(001) by Fe-phthalocyanine adsorption†
Marco
Marino
 *a,
Gonzalo
Rivero-Carracedo
*a,
Gonzalo
Rivero-Carracedo
 b,
Andrey
Rybakov
b,
Andrey
Rybakov
 b,
José J.
Baldoví
b,
José J.
Baldoví
 *b and
Guido
Fratesi
*b and
Guido
Fratesi
 a
a
aETSF and Physics Department “Aldo Pontremoli”, University of Milan, Via Celoria 16, 20133, Milan, Italy. E-mail: marco.marino1@unimi.it
bInstituto de Ciencia Molecular, Universitat de València, Catedrático José Beltrán 2, 46980, Paterna, Spain. E-mail: j.jaime.baldovi@uv.es
First published on 3rd March 2025
Abstract
Magnonics is a rapidly growing field that is nowadays broadly recognized as a paradigm shift for information and communication technologies. In this context, antiferromagnetic materials are particularly relevant due to the lack of stray fields and their faster dynamics, with frequencies in the THz range and longer spin relaxation times. Herein, we investigate the chemical tuning of magnons in a prototypical antiferromagnetic transition metal oxide through the creation of a hybrid heterostructure formed by an Fe-phthalocyanine layer over a NiO(001) substrate. Our first-principles calculations for the hybrid material allow us to evaluate the effect of the adsorbed molecules on the electronic structure, charge transfer and magnetic exchange couplings of NiO. In particular, we observe an electron density flow from the O towards the Ni atoms in the substrate, and from the O atoms towards the molecule at the interface. As a result, the magnetic couplings are enhanced by 7.7% at the surface, accompanied by a decrease by 19.1% in the layer below the surface. Interestingly, our results predict a shift of the magnon frequencies by ∼10 meV in the optical branch. This work provides a new step towards the design of molecular controlled magnetic materials for magnonic applications.
1. Introduction
Antiferromagnetic materials are emerging as key components for next-generation spintronic devices due to their robustness against external perturbations and ultrafast dynamics, even in the presence of uncontrolled size effects and sample-to-sample variability.1,2 Moreover, they represent ideal candidates for magnonics, which is an emerging technology that uses spin waves as information carriers as an alternative to electric charges in electronics, thus offering more efficient devices.3,4 A promising direction in this field lies in combining antiferromagnets with organic materials to form hybrid organic-antiferromagnetic interfaces, the so-called spinterfaces.5,6 These hybrid systems utilize the tunability and manipulability of organic compounds to modify and read the local magnetic ordering in antiferromagnets,7 motivating further exploration of organic-antiferromagnetic spinterfaces.8–10Among this family of materials, insulating transition metal oxides (TMO) are particularly attractive, as they can retain the intrinsic properties of organic compounds at the interface while simultaneously allowing moderate hybridization. Previous theoretical studies have already investigated interfaces involving organic compounds and oxides such as In2O3,11 SrTiO3,12 TiOx and MoOx,13 CoO,14 MnO,15 NiO,8 and Cr2O3.16 These works mainly focus on structural deformations, charge-transfer mechanisms, and electronic properties.
However, a full understanding of the magnetic properties within these systems remains an open challenge. This is especially relevant given the molecule-induced effects observed in other magnetic materials such as YIG,17 CrSBr,18,19 Cr2Ge2Te6,20 or Fe3GeTe2.21 Among transition-metal oxides, NiO stands out as an antiferromagnetic insulator22 with a high Néel temperature (TN = 525 K),23 with dominant super-exchange couplings.24,25 Its low spin–orbit coupling makes it a good candidate to sustain spin waves over long distances.26 Moreover, it exhibits superluminal-like magnon propagation,27 and can be integrated with YIG to create magnon valves.28 On the molecular side, metal-phthalocyanines, such as Fe-phthalocyanine (FePc),29 offer the possibility to facilitate the light-activation30 of the substrate and chemical tunability through functionalization.31–34 Moreover, Fe-phthalocyanine has been already deposited on different surfaces preserving its structural integrity.35,36
In this work, we explore the hybrid spinterface formed by FePc molecules deposited on NiO(001) through first-principles calculations. Our efficient methodology starts with Hubbard-corrected density functional theory (DFT+U), projected onto a tight-binding Hamiltonian in the basis of maximally-localized Wannier functions, and leads to the construction of a Heisenberg model within a perturbative approach. This allows us to determine the electronic structure, estimate the charge transfer and calculate magnetic exchange interactions in the hybrid heterostructure. Finally, we analyze how molecular adsorption influences magnon dispersion in the NiO slab. Our results provide a new step on the design and development of chemically-tuned hybrid magnonic devices based on molecular adsorption on magnetic substrates.
2. Computational methods
The ground state and its properties are evaluated using DFT in a plane-waves basis set as implemented in Quantum ESPRESSO.37,38 Hubbard corrections are included using Dudarev's formulation (i.e., Ueff = U − J), to describe on-site correlation effects of the transition-metal atoms. We considered UFe = 5.0 eV, which describes well the electronic properties (density of states) of the localized orbitals for the isolated system as demonstrated by some of us recently.8 For the Ni atoms, instead, we selected UNi = 5.8 eV in order to properly reproduce the experimentally measured magnon dispersion of bulk NiO.26,39 We have verified that choosing a different U for the Fe atom changes only the local super-exchange coupling Fe–O–Ni, with no significant effect on the average values of the exchange in the substrate. We include van der Waals interactions between the molecule and the substrate by using the vdW-DF-C09 exchange and correlation (xc) functional.40,41 Vanderbilt ultrasoft pseudopotentials (GBRV)42 with semi-core corrections are used, selecting a plane wave cutoff of 70 Ry for the wavefunctions and of 270 Ry for the charge density.The substrate is modelled by a slab that includes 3 NiO layers. Given the large size of the supercell that we adopt for molecule adsorption on NiO, the surface Brillouin zone (BZ) is sampled by the Γ point only, whereas for the BZ of bulk NiO we use a 8 × 8 × 8 grid of k-points. The minimal adsorption energy configuration is taken from our previous work,8 and reoptimized with the computational parameters described above.
Subsequently, we apply a Wannierisation procedure as implemented in Wannier90 code,43 where p orbitals of O, C and N atoms, and the d orbitals of Ni and Fe were considered with the selected energy window was (−9, 1) eV with respect to the Fermi energy. Note that no localization iteration has been applied in order to avoid spurious hybridisation between the different orbitals in the building of the tight-binding Hamiltonian. More details on the Wannierisation and the quality of the fitted electronic structure are given in the ESI.† The derived tight-binding model is used to calculate the magnetic exchange couplings in a perturbative approach, based on the magnetic force theorem (MFT) as implemented in the TB2J code:.44 As a result we obtain a Heisenberg model of the form
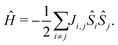 | (1) |
3. Results
Bulk NiO is a prototypical antiferromagnet (AFII) that crystallizes in a cubic structure within the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. According to our DFT optimization the lattice parameter is 4.168 Å, which is in good agreement with previous works.47–52 Ni atoms are octahedrally coordinated by O atoms, leading to a crystal field splitting of the 3d orbitals into lower-energy t2g (dxy, dxz, dyz) and higher-energy eg (dz2 and dx2−y2) electronic states. The antiferromagnetic order stems from super-exchange interactions53 between neighboring Ni spins mediated by O atoms. In this regard, the obtained magnetic moment for Ni atoms of 1.63μB is similar to previous theoretical findings.54
m space group. According to our DFT optimization the lattice parameter is 4.168 Å, which is in good agreement with previous works.47–52 Ni atoms are octahedrally coordinated by O atoms, leading to a crystal field splitting of the 3d orbitals into lower-energy t2g (dxy, dxz, dyz) and higher-energy eg (dz2 and dx2−y2) electronic states. The antiferromagnetic order stems from super-exchange interactions53 between neighboring Ni spins mediated by O atoms. In this regard, the obtained magnetic moment for Ni atoms of 1.63μB is similar to previous theoretical findings.54
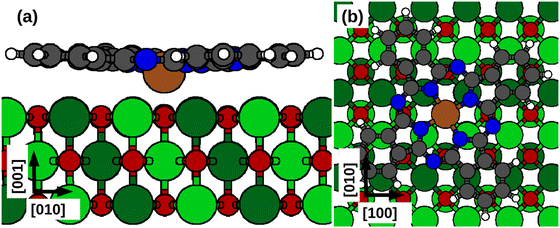
First, we study the deposition of FePc molecules by creating a supercell with 36 Ni atoms per layer and 3 layers, considering an epitaxy matrix ((6,0), (3,3)) with respect to the magnetic unit cell.8 As we shall see below, the effects of the molecule on the magnetic properties are mainly short-range, which supports the choice of a relatively thin NiO slab for modelling the substrate. After an initial relaxation of the atomic coordinates in the surface, we positioned the molecule in the most stable adsorption configuration (see Fig. 1). For the detailed discussion on the adsorption configurations, energies, and electronic properties we refer to our previous work.8
In the stable configuration, the Fe center of the molecule is located on top of an O atom at a distance of 2.05 Å, with the O atom 0.10 Å above the average surface height. In addition, we observe the change in the occupancy of the 3d orbital of the Fe atom due to a spin crossover transition from  to
to 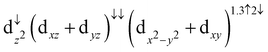 . This transition leads to the switch of the magnetic moment of the Fe atom from 2.17μB to 3.76μB.
. This transition leads to the switch of the magnetic moment of the Fe atom from 2.17μB to 3.76μB.
Next, we investigate the effect of molecular deposition of FePc on the magnetic exchange interactions in the substrate. Herein, we considered the first-nearest-neighbor couplings J1 and J2 between both types—parallelly and antiparallelly magnetized—of Ni atoms and also J3, that describe the O-mediated super-exchange interaction. All couplings are schematically indicated in Fig. 2. The averaged values of exchange couplings (inter- and intra-layer couplings of top, middle and bottom layers) of the substrate and the heterostructure are shown in Table 1. The most noticeable effect is the increase in modulus of J3 in the top layer, which enhances the antiferromagnetic coupling, and the reduction in modulus of the J3 coupling between the top and bottom layers. Analogue variations in the exchange couplings due to molecular adsorption have been already computed, for example a change of 31% in the case of TTF-CH3 deposited on CrSBr.19 Note that variations of J1 and J2 will not be analyzed given that their small values significantly depend on the numerical setup.
 | ||
| Fig. 2 Side view (a) and top view (b) of the NiO(001) substrate. The exchange couplings are underlined with colored lines. Yellow indicates J2 in the top layer; pink – J3 between top-bottom layers; blue – J1 between top-middle layers; purple – J3 in the top layer; orange – J1 in the top layer. Symmetrically equivalent exchange couplings are easily identified. Atomic colors as in Fig. 1. | ||
| Substrate | Substrate + molecule [meV] | ||
|---|---|---|---|
| Intra-layers | |||
| Top | J 1 | 1.03 | −0.95 |
| J 2 | 0.27 | −0.97 | |
| J 3 | −15.63 | −16.97 | |
| Middle | J 1 | 0.14 | 0.50 |
| J 2 | −0.44 | −0.58 | |
| J 3 | −20.35 | −20.37 | |
| Bottom | J 1 | 1.03 | 1.31 |
| J 2 | 0.27 | 0.06 | |
| J 3 | −15.63 | −15.41 | |
| Inter-layers | |||
| Top-middle | J 1 | −0.72 | −0.22 |
| J 2 | −2.28 | −2.12 | |
| Bottom-middle | J 1 | −0.73 | 0.38 |
| J 2 | −2.28 | −2.08 | |
| Top-bottom | J 3 | −33.45 | −27.04 |
In Fig. 3 we report the local changes of the exchange couplings and magnetic moments of the surface layer induced by the FePc adsorption, with respect to the pristine substrate. The modification of the exchange parameters is more pronounced in the region covered by the molecule, with the relative change in the range of [−92%, +35%]. In terms of the inner layers, the changes of the in-plane interactions are negligible.
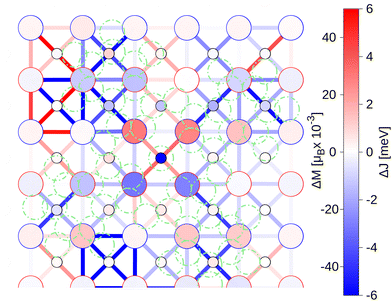 | ||
| Fig. 3 Changes in the exchange couplings ΔJ and in the atomic magnetic moments ΔM of the substrate of FePc/NiO(0001) with respect to the pristine substrate. The big (small) circles represent the Ni (O) atoms. The color of each circle indicates a variation in the magnetic moment ΔM of the corresponding atom. The color of the contour of each Ni circle indicates the direction of its initial magnetization before the molecule adsorption (red for up, blue for down). The colored lines between pair of atoms indicate the variations in the exchange couplings ΔJ between the pair of Ni atoms. The positions of the molecule's atoms are marked with green circles. See Fig. S5 (ESI†) for the detailed values. | ||
To rationalize the modification of the J3 super-exchange couplings, we search for correlations with either electron densities or magnetic moments of the substrate atoms (such variations are reported in Fig. S4, ESI†). In particular, we perform a rank correlation analysis and report the results in Table 2. The changes of the top-layer J3 are weakly correlated to local variations of the O electron densities ΔρO (Spearman's correlation coefficient ∼0.40 with a p-value of <0.01). We also investigated the correlation with the local redistribution of charge in the p orbitals of the O atoms, defined as ROi = ‖pi − p0i‖/‖pi + p0i‖, where p0i and pi are the charge densities of the p orbital of i-th O atom before and after adsorption, respectively. In this case, the correlation of J3 is opposite in sign, showing a Spearman's correlation coefficient of ∼−0.33 with a p-value of 0.03 for the redistribution of charge. The obtained correlation coefficients indicate that ΔρO and RO are good descriptors to rationalize the variations of the magnetic exchange in the top layer. Indeed, both relate to the charge displacement around the O atoms. We found that in the presence of the molecule the charge reduces in the first layer (see Fig. S4, ESI†), and redistributes from the in-plane p orbitals to the out-of-plane one (see Fig. S6 and S7, ESI†), hence charge migrates towards the molecule. Analyzing the changes of the J3 between the top and bottom layers, we found a weak negative correlation with the local variations of the electron densities in the Ni atoms (Spearman's correlation coefficient −0.36 with a p-value of 0.03) and a weak positive correlation with the local redistribution of charge in the p orbitals of the O atoms (Spearman's correlation coefficient 0.38 with a p-value of 0.02). Hence, we attribute the variations of the super-exchange couplings to two main effects: (i) the depletion of electron density around the O atoms, and its shift towards the molecule, which increases the magnitude of the super-exchange couplings in the top layer, and (ii) the redistribution of the electron density in the O atoms of the middle layer, along the direction of the top-bottom layer super-exchange (on average, charge migrates from the px and py to the pz orbitals, see Fig. S7, ESI†), which instead decreases the magnitude of the super-exchange coupling between the top and bottom layer. The latter effect is in part mitigated by the accumulation of charge density in the Ni atoms and consecutive reduction of their magnetic moments. The increased density at the interface slightly above the O atoms appears to favour the super-exchange coupling between the Ni atoms, even if the charge of the O atoms decreases. In summary, FePc adsorption modifies the J3 couplings via (i) localization of the charge at the interface; (ii) shift of the charge from the top O towards the Ni atoms and the molecule; (iii) reorganization of the charge in the sub-surface O atoms.
| Layer | Quantity | Spearman's c.c. | p-value |
|---|---|---|---|
| Top | ΔρO | 0.40 | <0.01 |
| Top | R O | −0.33 | 0.03 |
| Top | ΔρNi | 0.14 | 0.16 |
| Top-bottom | ΔρO | −0.02 | 0.91 |
| Top-bottom | R O | 0.38 | 0.02 |
| Top-bottom | ΔρNi | −0.36 | 0.03 |
Finally, we explore the effect of the modified exchange couplings on the magnon band structure of NiO, considering their average values from Table 1. The number of magnon bands, reported in Fig. 4, corresponds to the number of Ni atoms in the unit cell. A clear energy shift along almost the whole k-path (∼10 meV) induced by the FePc molecule is observed in the high energy magnons (optical modes). On contrary, no significant effect can be noticed for the acoustic magnons (around Γ). Moreover, modification of the magnon bands clearly shows the breaking of the degenerate points and thus the reduction of the magnetic symmetry of the system due to the proximity of the molecule.
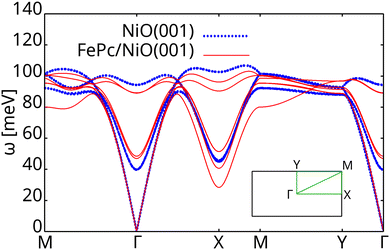 | ||
| Fig. 4 Magnon band structure of the NiO(001) substrate before (blue dotted line) and after adsorption of the FePc molecule (red continuous line). Inset show the k path. | ||
Therefore, magnon dispersion can be selectively modified, given that charge transfer processes in the spinterface can be manipulated through light excitation or chemical funcionalization, among others. In particular, to obtain stronger in-plane super-exchange couplings in TMOs at the surface, one should favor the formation of interface states.9 On the other hand, a weakening of the out-of-plane coupling in the sub-surface will occur if the charge is redistributed in the direction of the super-exchange, or if the magnetic moment of the TMOs atoms is increased. Notice that the former effect would be larger in TMOs with more electronegative metals, while the latter would be enhanced in TMOs with metals that are less than half-filled, such as Cr2O3, where an enhance of the electron density around the metallic centers results in an increase of their magnetic moments. Thus, taking advantage of the different electronic configuration of transition metals one could obtain various effects on the magnon properties. Thus, the molecular tuning of the exchange interactions in magnetic materials offers a big playground where the versatility of chemistry can be exploited, making it possible to selectively modify the magnon frequencies of potential devices based on these hybrid heterostructures. In addition, increasing the coverage of the substrate by creating molecular overlayers may induce more pronounced effects.
4. Conclusions
We have studied the effect of depositing FePc on the magnetic properties and magnon dispersion of NiO(001) from first-principles, extracting the local exchange couplings through a perturbative approach. In summary, the adsorption of the molecule induces a charge transfer redistribution where the electron density is depleted from the O atoms and accumulated on the Ni atoms and at the interface. In particular, the reduction in the O electron density and its displacement towards the interface correspond to a strengthening in the super-exchange couplings at the surface. On contrary, the redistribution of charge in the direction along the super-exchange coupling corresponds to its weakening inside the substrate. The effects of the molecule on the exchange couplings manifests itself in the the coherent spin excitations. All in all, proximity effects result in a breaking of the degeneracy in the magnon dispersion due to a loss of symmetry of the substrate.Author contributions
conceptualization, M. M., J. J. B. and G. F.; formal analysis, M. M., G. R. C. and A. R.; investigation, M. M., G. R. C., A. R. and G. F; validation, M. M., J. J. B. and G. F.; visualization, M. M.; writing – original draft, M. M.; writing – review, M. M., G. R. C., J. J. B. and G. F.; editing, M. M, G. R. C., J. J. B. and G. F. All authors have read and agreed to the published version of the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Union (Project SINFONIA, Grant 964396 and the ERC-2021-StG-101042680 2D-SMARTiES). We acknowledge the CINECA award under the ISCRA initiative (grants IscrC-HOAMI-HP10CJW8ZE, IscrB-ORGAFINT-HP10BC1AM9, IscrC-2OAFExch-HP10CKV3Q2), for the availability of high performance computing resources and support. J. J. B. and A. R. acknowledge the Generalitat Valenciana (grant CIDEXG/2023/1, and a PhD fellowship GRISOLIAP/2021/038, respectively). G. R. C. thanks the University of Valencia (grant Atracció de Talent INV23-01-13).Notes and references
- V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono and Y. Tserkovnyak, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- J. Hortensius, D. Afanasiev, M. Matthiesen, R. Leenders, R. Citro, A. Kimel, R. Mikhaylovskiy, B. Ivanov and A. Caviglia, Nat. Phys., 2021, 17, 1001–1006 Search PubMed.
- V. V. Kruglyak, S. O. Demokritov and D. Grundler, J. Phys. D: Appl. Phys., 2010, 43, 260301 CrossRef.
- B. Lenk, H. Ulrichs, F. Garbs and M. Münzenberg, Phys. Rep., 2011, 507, 107–136 CrossRef.
- I. Bergenti and V. Dediu, Nano Mater. Sci., 2019, 1, 149–155 CrossRef.
- F. Djeghloul, F. Ibrahim, M. Cantoni, M. Bowen, L. Joly, S. Boukari, P. Ohresser, F. Bertran, P. Le Fèvre and P. Thakur, et al. , Sci. Rep., 2013, 3, 1272 CrossRef CAS PubMed.
- M. Cinchetti, V. A. Dediu and L. E. Hueso, Nat. Mater., 2017, 16, 507–515 CrossRef CAS PubMed.
- M. Marino, E. Molteni, S. Achilli and G. Fratesi, Inorg. Chim. Acta, 2024, 562, 121877 CrossRef CAS.
- L. Gnoli, M. Benini, C. Del Conte, A. Riminucci, R. K. Rakshit, M. Singh, S. Sanna, R. Yadav, K.-W. Lin, A. Mezzi, S. Achilli, E. Molteni, M. Marino, G. Fratesi, V. Dediu and I. Bergenti, ACS Appl. Electron. Mater., 2024, 6, 3138–3146 CrossRef CAS PubMed.
- N. M. Caffrey, P. Ferriani, S. Marocchi and S. Heinze, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155403 CrossRef.
- M. Wagner, F. Calcinelli, A. Jeindl, M. Schmid, O. T. Hofmann and U. Diebold, Surf. Sci., 2022, 722, 122065 CrossRef CAS.
- R. Karstens, T. Chassé and H. Peisert, Beilstein J. Nanotechnol., 2021, 12, 485–496 CrossRef CAS PubMed.
- L. Liu, W. Zhang, P. Guo, K. Wang, J. Wang, H. Qian, I. Kurash, C.-H. Wang, Y.-W. Yang and F. Xu, Phys. Chem. Chem. Phys., 2015, 17, 3463–3469 RSC.
- T. Schmitt, P. Ferstl, L. Hammer, M. A. Schneider and J. Redinger, J. Phys. Chem. C, 2017, 121, 2889–2895 CrossRef CAS.
- M. Glaser, H. Peisert, H. Adler, M. Polek, J. Uihlein, P. Nagel, M. Merz, S. Schuppler and T. Chassé, J. Phys. Chem. C, 2015, 119, 27569–27579 CrossRef CAS.
- M. Marino, E. Molteni, S. Achilli, G. Onida and G. Fratesi, Molecules, 2024, 29, 2889 CrossRef CAS PubMed.
- P. Yuan, S. Catalano, W. Skowronski, R. Llopis, F. Casanova and L. E. Hueso, ACS Appl. Electron. Mater., 2024, 6, 4232–4238 CrossRef CAS.
- A. M. Ruiz, G. Rivero-Carracedo, A. Rybakov, S. Dey and J. J. Baldovi, Nanoscale Adv., 2024, 6(13), 3320–3328 RSC.
- G. Rivero-Carracedo, A. Rybakov and J. J. Baldov, Chem. – Eur. J., 2024, 30, e202401092 CrossRef CAS PubMed.
- K. Wang, K. Ren, Y. Cheng, M. Zhang, H. Wang and G. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 22047–22054 RSC.
- G. S. Kumar, A. M. Ruiz, J. Garcia-Oliver, Y. Xin, J. J. Baldov and M. Shatruk, Angew. Chem., Int. Ed., 2024, e202412425 Search PubMed.
- H. Meer, O. Gomonay, A. Wittmann and M. Kläui, Appl. Phys. Lett., 2023, 122(8), 080502 CrossRef CAS.
- J. Kunesš, V. I. Anisimov, S. L. Skornyakov, A. V. Lukoyanov and D. Vollhardt, Phys. Rev. Lett., 2007, 99, 156404 CrossRef PubMed.
- R. Logemann, A. N. Rudenko, M. I. Katsnelson and A. Kirilyuk, J. Phys.: Condens. Matter, 2017, 29, 335801 CrossRef CAS PubMed.
- I. V. Solovyev, Phys. Rev. B, 2021, 103, 104428 CrossRef CAS.
- D. Betto, Y. Y. Peng, S. B. Porter, G. Berti, A. Calloni, G. Ghiringhelli and N. B. Brookes, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 020409 CrossRef.
- L. Kyusup, L. Dong-Kyu, Y. Dongsheng, M. Rahul, K. Dong-Jun, L. Sheng, X. Qihua, K. S. Kwon, L. Kyung-Jin and Y. Hyunsoo, Nat. Nanotechnol., 2021, 16, 1336–1341 Search PubMed.
- C. Guo, C. Wan, X. Wang, C. Fang, P. Tang, W. Kong, M. Zhao, L. Jiang, B. Tao and G. Yu, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 134426 CrossRef CAS.
- J. M. Gottfried, Surf. Sci. Rep., 2015, 70, 259–379 CrossRef CAS.
- A. M. Serra, A. Dhingra, M. C. Asensio, J. A. Real and J. F. S. Royo, Phys. Chem. Chem. Phys., 2023, 25, 14736–14741 RSC.
- N. Konstantinov, A. Tauzin, U. N. Noumbé, D. Dragoe, B. Kundys, H. Majjad, A. Brosseau, M. Lenertz, A. Singh, S. Berciaud, M.-L. Boillot, B. Doudin, T. Mallah and J.-F. Dayen, J. Mater. Chem. C, 2021, 9, 2712–2720 RSC.
- R. Torres Cavanillas, M. Morant-Giner, G. Escorcia-Ariza, J. Dugay, J. Canet-Ferrer, S. Tatay, S. Cardona-Serra, M. Giménez-Marqués, M. Galbiati, A. Forment-Aliaga and E. Coronado, Nat. Chem., 2021, 13, 1–9 CrossRef PubMed.
- I. Cojocariu, S. Carlotto, H. M. Sturmeit, G. Zamborlini, M. Cinchetti, A. Cossaro, A. Verdini, L. Floreano, M. Jugovac, P. Puschnig, C. Piamonteze, M. Casarin, V. Feyer and C. M. Schneider, Chem. – Eur. J., 2021, 27, 3526–3535 CrossRef CAS PubMed.
- I. Cojocariu, S. Carlotto, H. M. Sturmeit, G. Zamborlini, M. Cinchetti, A. Cossaro, A. Verdini, L. Floreano, M. Jugovac and P. Puschnig, et al. , Chem. – Eur. J., 2021, 27, 3526–3535 CrossRef CAS PubMed.
- F. Petraki, H. Peisert, U. Aygul, F. Latteyer, J. Uihlein, A. Vollmer and T. Chassé, J. Mater. Chem. C, 2012, 116, 11110–11116 CAS.
- M. Glaser, H. Peisert, H. Adler, M. Polek, J. Uihlein, P. Nagel, M. Merz, S. Schuppler and T. Chasse, J. Mater. Chem. C, 2015, 119, 27569–27579 CAS.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. D. Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.:Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.:Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. Fischer, M. Däne, A. Ernst, P. Bruno, M. Lüders, Z. Szotek, W. Temmerman and W. Hergert, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014408 CrossRef.
- V. Cooper, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 161104 CrossRef.
- K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310 CrossRef CAS.
- X. He, N. Helbig, M. J. Verstraete and E. Bousquet, Comput. Phys. Commun., 2021, 264, 107938 CrossRef CAS.
- T. Holstein and H. Primakoff, Phys. Rev., 1940, 58, 1098–1113 CrossRef.
- J. Colpa, Phys. A, 1978, 93, 327–353 CrossRef.
- S. Hüfner, J. Osterwalder, T. Riesterer and F. Hulliger, Solid State Commun., 1984, 52, 793–796 CrossRef.
- G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1984, 53, 2339–2342 CrossRef CAS.
- B. E. F. Fender, A. J. Jacobson and F. A. Wedgwood, J. Chem. Phys., 1968, 48, 990–994 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- A. K. Cheetham and D. A. O. Hope, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 6964–6967 CrossRef CAS.
- R. W. Cairns and E. Ott, J. Am. Chem. Soc., 1933, 55, 527–533 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1950, 79, 350–356 CrossRef.
- S. Kwon and B. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 73 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04547e |
| This journal is © the Owner Societies 2025 |