¹H isotropic chemical shift metrics for NMR crystallography of powdered molecular organics

Abstract

Hydrogen magnetic shielding values from gauge including projector augmented wave (GIPAW) density functional theory (DFT) calculations, when combined with experimental solid-state ¹H nuclear magnetic resonance (NMR) chemical shift data collected on powdered microcrystalline organics, have been used to perform various crystal structure characterization tasks (e.g., refinements, verifications, determinations). These tasks fall under the umbrella of ‘NMR crystallography’. In several instances, an isotropic ¹H chemical shift (δ_iso) root-mean-squared deviation (RMSD) metric has been applied during these studies (including the first de novo crystal structure determination: M. Baias, J.-N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, De Novo Determination of the Crystal Structure of a Large Drug Molecule by Crystal Structure Prediction-Based Powder NMR Crystallography, J. Am. Chem. Soc., 2013, 135, 17501–17507). While it is assumed that the ¹H δ_iso RMSD metrics are converged, our study probes the robustness of these metrics. Specifically, we consider how the structure of the δ_iso(¹H) RMSD metric varies depending on: (i) selected GIPAW DFT input parameters; (ii) the number of fitting parameters used during linear mapping; and (iii) the GIPAW DFT computational software. These δ_iso(¹H) RMSD metrics were produced from a set of 24 benchmark crystal structures (428 crystallographically unique hydrogen atom environments). Interestingly, we find that the δ_iso(¹H) RMSD metric structures are very robust to substantial degradation in the quality of the GIPAW DFT computations, which is unexplored in the NMR crystallography literature as prior studies focus on convergence rather than divergence. We then briefly consider the impact of our findings using the structure determination of thymol as an illustrative example and our results strongly suggest that if δ_iso(¹H) RMSD metrics are being used, then the GIPAW DFT computations can be performed much more efficiently than at present. Overall, this should allow for more efficient NMR crystallography characterization tasks of important materials that contain ¹H nuclei, such as organic pharmaceuticals.

---

Introduction

Nuclear magnetic resonance (NMR) crystallography approaches regularly use solid-state NMR experiments and computational modelling to elucidate aspects of chemical structure.^1,2 Over the past decade or so, isotropic ¹H chemical shift values (δ_iso) measured with solid-state NMR experiments have been used to help determine,^3–6 verify,^7–9 predict,^10,11 refine,^12–16 and/or discriminate amongst^17–21 crystal structures of molecular organic compounds. To perform these tasks, experimental δ_iso values are often associated with computed hydrogen magnetic shielding values (σ_iso) using linear regression or a linear mapping. When properties of solids are being considered, σ_iso values may be computed in a number of ways, such as gauge including projector augmented wave density functional theory (GIPAW DFT),^22–27 fragment- or molecular-correction-based methods (which can include GIPAW DFT),^19,28–33 and by using machine learning (ML) algorithms.^34–36

In some NMR crystallography studies, computed σ_iso values are mapped to predicted isotropic chemical shift values (δ_iso,calc.) using a linear function (vide infra). In this process, it is common (though not required) to use experimental ¹H δ_iso values (δ_iso,expt.) that have been assigned. Assignment means that the ¹H NMR signal positions are known to be associated with specific hydrogen atomic sites in the structure under consideration. In one approach, the linear mapping is generated by minimizing the root-mean-squared deviation (RMSD, sometimes also called the ‘root-mean-squared difference’) between the δ_iso,calc. and δ_iso,expt. values (the RMSD definition is provided in the ESI†). Further specifics of the linear mapping process, and calculation of δ_iso(¹H) RMSD values, will be provided in the Results and discussion section.

So, if experimental and computational δ_iso(¹H) data exist, a given crystal structure may be associated with a δ_iso(¹H) RMSD value. A lone δ_iso(¹H) RMSD value is not particularly useful; rather, by comparing that δ_iso(¹H) RMSD value with other δ_iso(¹H) RMSD values, insight regarding the appropriateness of a crystal structure can potentially be gained. These ‘other’ δ_iso(¹H) RMSD values are typically associated with other crystal structures. For example, a δ_iso(¹H) RMSD value may be used for crystal structure determination when it is compared against the δ_iso(¹H) RMSD values of other plausible crystal structures.^{3–5,10,11,37,38} Sets of plausible crystal structures may be generated in different ways, including crystal structure prediction (CSP),^39–43 and genetic/ML algorithmic approaches.^6,44 Beyond this information, additional complexities may be considered. For example, recent interesting accounts include the effects of temperature and nuclear quantum effects on ¹H σ_iso values,^32,45,46 although in the present study, these aspects are not discussed.

Structural characterization tasks can be associated with a degree of confidence if one has access to the typical range that δ_iso(¹H) RMSD values may take. By using high-quality crystal structures and available δ_iso(¹H) NMR data on powdered samples associated with these crystal structures, an estimate of the distribution of δ_iso(¹H) RMSD values may be generated. In several literature accounts, it has been stated that δ_iso(¹H) RMSD values fall in the range of 0.33 ± 0.16 ppm^{3,7,9–11,37,38,47} when using the GIPAW DFT approach to compute hydrogen magnetic shielding values. Unfortunately, the details needed to verify this δ_iso(¹H) RMSD distribution have not been made available. This is potentially problematic as key articles in the literature, including the first de novo NMR crystallography structure determination of a powdered sample,³ cannot be exactly reproduced using available literature data. However, we clearly emphasize that our inability to precisely verify an individual δ_iso(¹H) RMSD metric does not imply a serious concern regarding the accuracy of that RMSD metric, nor in any of the conclusions arrived at by their use. This is partly because more fulsome disclosures have since been made for δ_iso(¹H) RMSD distributions that were established using other approaches (e.g., ML-based approaches). Importantly, the ML approaches produced δ_iso(¹H) metrics that did not differ very significantly from the GIPAW DFT ¹H shift metric.^5,35 However, while the GIPAW DFT and ML δ_iso(¹H) RMSD metrics are similar, they are not equivalent. Unsurprisingly, every δ_iso(¹H) RMSD metric depends on a variety of parameters: for example, the training data used for ML approaches, or the level of theory at which the GIPAW DFT calculations were performed. We therefore place some focus here on the transparent development of a δ_iso(¹H) RMSD metric using only the GIPAW DFT approach so that this information can be easily accessed and independently verified. Secondly, and to the best of our knowledge, no literature example assesses how sensitive GIPAW DFT δ_iso(¹H) RMSD metrics are to the inputs that were used to derive them. However, reasonably detailed disclosures of δ_iso(¹H) RMSD metric structure and convergence have been made available for fragment-based and cluster/fragment-based approaches,²⁹ and for other NMR crystallography metrics (for example, ¹³C).⁴⁸

In the first sections of this contribution, we provide the relevant GIPAW DFT-computed hydrogen σ_iso values, including all necessary data (i.e., input structures, input files, and output files) that were used to arrive at various new δ_iso(¹H) RMSD metrics (see ESI†). Consequently, we collect and summarize the measured experimental ¹H δ_iso values and assignments from the prior literature. We then consider how δ_iso(¹H) RMSD metrics vary as a function of: (i) the DFT software used to compute the hydrogen magnetic shielding tensors; (ii) the choice of experimental data used to generate the metric; (iii) the linear mapping process selected; (iv) the quality of the DFT calculation. We conclude by briefly considering an application of select newly developed δ_iso(¹H) RMSD metrics in the structure determination of thymol.

Experimental

Crystal structures were obtained from the Cambridge Structural Database (CSD),⁴⁹ which was developed and is maintained by the Cambridge Crystallographic Data Centre (CCDC). Each crystal structure is associated with a CSD refcode, which is an alphanumeric string typically composed of 6 letters followed by 0 or 2 numbers. Here, 24 crystal structures (with references included, where possible) were chosen for this study and they correspond to the following CSD refcodes: ACSALA07,⁵⁰ AMBACO10,⁵¹ AMCILL,⁵² BAPLOT01,⁵³ CIMETD,⁵⁴ COCAIN10,⁵⁵ COYRUD13,⁵⁶ FPAMCA11,⁵⁷ FURSEM01,⁵⁸ GLUTAS07,⁵⁹ GLYCIN28,⁶⁰ HISTCM01,⁶¹ HXACAN35,⁶² IBPRAC,⁶³ INDMET,⁶⁴ IPMEPL,⁶⁵ LABHEB,⁶⁶ LTYRHC10,⁶⁷ LTYROS10,⁶⁸ URACIL,⁶⁹ VOSREC,¹⁴ WEZCOT,⁷⁰ ZIVKAQ,⁷¹ ZZZUEE01.⁷² All selected structures were such that their R-factor was <10% (only exception was AMCILL, whose R-factor is 10.6%). Such R-factors are understood to represent good agreement between the measured diffraction response and the crystal structure model. Further, to ensure that the NMR and diffraction data were acquired under highly similar temperature conditions, all selected structures had their diffraction data measured near room temperature. Specific details can be found in the ESI† (for example, ‘Summary_Outputs_1Param_Map.xlsx’). For images of the building blocks associated with these crystal structures, please see Schemes S1 and S2 in the ESI.†

All DFT calculations used either the Quantum opEn Source Package for Research in Electronic Structure, Simulation, and Optimization (Quantum ESPRESSO, QE)⁷³ (version 6.7 or 6.8) or the CAmbridge Serial Total Energy Package (CASTEP)⁷⁴ (version 19.1). Input files required for performing calculations with QE and CASTEP were generated using CIF2CELL.⁷⁵ Software-generated (i.e. ‘structure-dependant’) Monkhorst-Pack⁷⁶k-point grids were obtained by setting the resolution to 0.25 Å⁻¹ for QE calculations and 0.05 × 2π Å⁻¹ for CASTEP calculations. CASTEP calculations were performed using a single plane wave energy cut-off (E_cut) of 1225 eV (90.04 Ry), while QE computations were run under a variety of E_cut values (all in units of Ry): 90, 55, 45, 35, 25, 15, 10, and 5. While all CASTEP calculations used ‘structure-dependent’ k-point grids, for QE, a second set of calculations was done using a k-point grid of 1 × 1 × 1. For more clarity regarding the types of calculations performed in this study, please consult the ESI.†

To obtain the various ¹H δ_iso RMSD metrics (each known informally as a ‘grey band’), the δ_iso(¹H) RMSD values describing the differences between experimental and calculated δ_iso(¹H) values were generated. To obtain δ_iso,calc. values for the unique hydrogens in each crystal structure, the structures obtained from the CSD were geometry optimized (H atoms only) and then magnetic shielding calculations were performed. This two-step process was done using QE⁷³ or CASTEP.⁷⁴ Both pieces of software use a plane wave basis set to describe the valence electrons, and pseudopotentials to describe the core electrons. For QE computations, pseudopotentials were sourced from the ‘pslibrary.1.0.0’,⁷⁷ and are of the form outlined by Dal Corso.⁷⁸ The following pseudopotentials were used: C.pbe-n-kjpaw_psl.1.0.0.UPF, H.pbe-kjpaw_psl.1.0.0.UPF, N.pbe-n-kjpaw_psl.1.0.0.UPF, O.pbe-n-kjpaw_psl.1.0.0.UPF, F.pbe-n-kjpaw_psl.1.0.0.UPF, Cl.pbe-n-kjpaw_psl.1.0.0.UPF, and S.pbe-n-kjpaw_psl.1.0.0.UPF. In contrast, CASTEP calculations used ultrasoft pseudopotentials that were generated ‘on-the-fly’. In all cases, hydrogen σ_iso values were obtained with the GIPAW²³ approach as it is an efficient method to calculate magnetic shielding tensors in crystalline solids.^73,74 Based on the hydrogen σ_iso values obtained, the δ_iso,calc. values were determined using a linear mapping (vide infra). The mapping process generates a single δ_iso(¹H) RMSD value for each crystal structure which describes how the calculated ¹H shifts compare to the experimental ¹H shifts.

A full disclosure of the information used to derive the various δ_iso(¹H) metrics is provided in the ESI† (‘Summary_Outputs_1Param_Map.xlsx’ and ‘Summary_Outputs_2Param_Map.xlsx’); however, a few general points are noted here. First, all experimental solid-state ¹H NMR data are taken from literature accounts where measurements were under ambient conditions. These conditions can impact the δ_iso(¹H) RMSD metric generation. For example, methyl group H atoms are expected to undergo rapid exchange with respect to the timescale of the ¹H Larmor frequency. Hence, ¹H NMR chemical shifts measured for methyl group hydrogens are dynamically averaged at room temperature. This is reflected in the metric generation by averaging the three GIPAW DFT-computed hydrogen σ_iso values for each methyl group. Further, this group of three hydrogens is assigned a relative weight of one (rather than say, three). A similar averaging and re-weighting procedure can be performed on methylene group hydrogen atoms if they are either dynamic or not resolved in the available solid-state NMR experimental data. Accordingly, methylene groups may reasonably be weighted as two or one. For methylene groups, we have tested both approaches in this study. When these groups are not averaged and therefore are weighted as two, it yields δ_iso(¹H) RMSD values that are slightly larger on average than when they are averaged (and thus weighted as one). Other chemical groups subjected to the same principles as above are R-NH₂ and R-NH₃⁺ group H atoms.

Among the 24 structures examined in this study, CIMETD, FURSEM01, HISTCM01, and LTYROS10 crystal structures contain CH₂ and NH₂ groups whose isotropic ¹H chemical shifts have not been experimentally resolved in the literature. Therefore, depending on the averaging method employed, we derived two distinct types of metrics: ‘loose’ and ‘tight’. ‘Loose’ denotes the case where these types of hydrogens were not averaged, while ‘tight’ represents the scenario where averaging was applied to them. For complete details, please refer to the Excel spreadsheets provided in the ESI.† In the main text, results from the ‘loose’ type of averaging were selected and used exclusively.

Results and discussion

Rationale for constructing additional ¹H chemical shift metrics

Proton δ_iso RMSD metrics for NMR crystallography can be found in numerous places in the literature.^{3,5,9–11,35,37,38,47} What distinguishes this study from prior work is the attention paid to the variation in the metric structure as a function of computational parameter settings and subsequent analysis variables. We are not aware of prior studies that perform such a detailed evaluation; rather, the δ_iso(¹H) RMSD metric is often presented ‘as-is’ with little understanding as to whether the metric is, for example, stable (by ‘stable’ we mean that the parameters used to characterize the metric, for example, its RMSD and the standard deviation of the RMSD, do not change significantly upon a variation in how the computations or analysis were performed). Further, we provide all necessary information for others to independently verify our findings. This last point is crucial as the δ_iso(¹H) RMSD metric appearance and subsequent utility depends on the information used in its derivation. In Table 1 we list the 24 crystal structures we selected in terms of their CSD refcodes. We additionally provide literature references where more information can be found regarding the various crystal structures and corresponding experimental ¹H δ_iso values measured on powdered samples associated with those crystal structures.

Table 1 CSD reference codes, structure references, and references for ¹H δ_iso,expt. values

CSD Refcode	Crystal structure ref.	^1H δiso,expt. ref.
ACSALA07	50	79
AMBACO10	51	80
AMCILL	52	5
BAPLOT01	53	38
CIMETD	54	81
COCAIN10	55	38
COYRUD13	56	82
FPAMCA11	57	38
FURSEM01	58	9
GLUTAS07	59	83
GLYCIN28	60	84
HISTCM01	61	85 and 86
HXACAN35	62	87
IBPRAC	63	87
INDMET	64	88
IPMEPL	65	12
LABHEB	66	89
LTYRHC10	67	90
LTYROS10	68	90
URACIL	69	91
VOSREC	14	14
WEZCOT	70	38
ZIVKAQ	71	92
ZZZUEE01	72	93

---

Generating ‘benchmark’ ¹H RMSD metrics (E_cut = 90 Ry, ‘structure-dependent’ k-point grid spacing) and software output comparison

As mentioned in the Introduction, a computational method generates the hydrogen σ_iso values for each unique hydrogen in each crystal structure being considered. Computed σ_iso values may then be mapped to calculated ¹H isotropic chemical shift values (δ_iso,calc.) according to the following linear equation:

δ_iso,calc. = mσ_iso + b

where there are (as expected) up to two adjustable parameters, which are the slope of the line (m) and the intercept (b). We will explore scenarios where m is fixed to a value of −1 and b is variable, and when both parameters may vary. In either case, the optimal value is established by minimizing the ¹H δ_iso RMSD that results when comparing δ_iso,expt. values against the various δ_iso,calc. values output from the linear mapping process.

One-parameter linear mapping of computed σ_iso values to computed δ_iso values. We begin by discussing δ_iso(¹H) RMSD metrics where the associated σ_iso values were derived from GIPAW DFT computations that used ‘structure-dependent’ k-point grids (as indicated in the Experimental section and detailed extensively in the ESI†) and E_cut ≅ 90.0 Ry. These calculations were performed using both QE⁷³ and CASTEP⁷⁴ to observe if there are any substantive differences between the outputs from these two computational software packages. We also clarify that for these benchmarks, we used a one-parameter linear mapping. In subsequent discussions, we will refer to these as our ‘benchmark’ δ_iso(¹H) RMSD metrics.

Transferability is very important in NMR crystallography when metrics are used,⁴³ and it would be concerning if different programs using similar computational approaches lead to fundamentally different results. While reasonable attempts were made to ensure that the quality of calculations were similar between CASTEP and QE (for example, similar k-point grid choice and E_cut values), they are not identical. We stress here that the main purpose of this section is not to establish rigorous equivalence, but rather, we hope it demonstrates a similarity between the δ_iso(¹H) RMSD metrics generated using either piece of software. A visual comparison of the two benchmark δ_iso(¹H) RMSD metrics (i.e., one for QE and another for CASTEP) is provided below in Fig. 1.

Fig. 1 Violin distribution plots for the ‘benchmark’ δ_iso(¹H) RMSD metrics. For each, the median is specified using a white horizontal line and the interquartile range is indicated using thick black boxes. The thin black lines protruding from the black boxes indicate 1.5 times the interquartile range. Left: The δ_iso(¹H) RMSD metric generated with the CASTEP program; right: the δ_iso(¹H) RMSD metric generated with the QE program. Both used E_cut ≅ 90.0 Ry, a ‘structure-dependent’ k-point grid, and a one-parameter linear mapping.

The δ_iso(¹H) RMSD metric structures for CASTEP and QE are virtually identical upon visual inspection. In terms of their average δ_iso(¹H) RMSD values and associated standard deviations, the CASTEP ¹H RMSD shift metric is 0.39 ± 0.17 ppm, while the QE ¹H RMSD shift metric is 0.40 ± 0.18 ppm. In all future discussions, we have decided to focus on outputs from the QE software as it is freely available and open source, which we believe is more congruent with our attempts to provide transparent δ_iso(¹H) RMSD metrics.

To assess the stability of the QE-derived benchmark δ_iso(¹H) RMSD metric with respect to the set of structures used to create the metric, we re-generated it, but using randomly selected subsets of the 24 crystal structures. For this purpose, 100 000 randomly selected subsets of 18 structures (out of the possible 24) were considered using a Python script. For each iteration, we re-calculated the average δ_iso(¹H) RMSD and associated standard deviation. Fig. 2A illustrates the resulting distribution of average δ_iso(¹H) RMSDs and Fig. 2B contains the distribution of the standard deviations.

Fig. 2 Discrete histogram distributions (100 bins) from 100 000 randomly selected subsets of 18 structures out of the possible 24 structures. In (A), the average δ_iso(¹H) RMSDs are displayed (in green), while in (B), the standard deviations associated with the δ_iso(¹H) RMSDs are displayed (in teal). For both plots, the δ_iso(¹H) RMSDs were derived from Quantum ESPRESSO outputs, E_cut = 90.0 Ry, ‘structure-dependent’ k-point grids, and a one-parameter linear mapping. Continuous normal distributions (red curves in (A) and (B)) were also generated for sake of comparison. They used the parameters: μ = 0.400 ppm ± 0.021 ppm (A), and μ(s) = 0.179 ppm ± 0.012 ppm (B). As we are considering multiple standard deviations in the above, we clarify that s refers to the standard deviation associated with an individual average δ_iso(¹H) RMSD, while ‘SD’ in the legends indicate the standard deviations in the distributions of the average δ_iso(¹H) RMSD and s(δ_iso(¹H) RMSD).

From Fig. 2A, the standard deviation in the average δ_iso(¹H) RMSD as a function of the set of structures used to generate the δ_iso(¹H) RMSD metric is roughly 0.02 ppm, which is well within the standard deviation of the benchmark metric (i.e., ±0.18 ppm). This underscores that the set of structures used to generate the δ_iso(¹H) RMSD metric does not strongly influence the resulting metric structure under ‘benchmark’ conditions, although there is some modest variability. Further, it can be observed that the discrete distribution we have generated closely resembles a continuous normal distribution (see Fig. 2A). This is suggestive that our selected number of random samples (i.e., 100 000) is sufficient. From Fig. 2B, we show that the average standard deviation (i.e., μ(s)) is equal to approximately 0.18 ppm and does not stray terribly far from this value. The distribution is slightly skewed to the left-hand side (skewness = −0.4) and so it is slightly more likely to find a particular s as < μ(s). As the standard deviation associated with this distribution is quite small (i.e., order of ±0.01 ppm), we do not read deeply into this finding. Rather, we simply report that the set of input structures selected do not influence the standard deviation of the benchmark QE δ_iso(¹H) RMSD metric in a pronounced fashion.

Two-parameter linear mapping of computed σ_iso values to computed δ_iso values. To see how the benchmark δ_iso(¹H) RMSD metrics change when performing a two-parameter (rather than a one-parameter) linear mapping, please refer to Fig. 3.

Fig. 3 Violin distribution plots for the δ_iso(¹H) RMSD metrics when using a two-parameter linear mapping. Left: The δ_iso(¹H) RMSD metric generated with the CASTEP program; right: the δ_iso(¹H) RMSD metric generated with the QE program. Both used E_cut ≅ 90.0 Ry and a ‘structure-dependent’ k-point grid.

By comparing Fig. 1 with Fig. 3, it can be concluded that the average δ_iso(¹H) RMSD and the standard deviations are significantly reduced when performing two-parameter linear mappings, which is expected. However, we are unaware of literature accounts that attempt to quantify the amounts of change when disclosing δ_iso(¹H) RMSD metrics resulting from one- and two-parameter linear mappings. We clarify that this is very different from the situation with other nuclei (e.g., ¹³C and ¹⁵N), where a two-parameter mapping is routinely used.^29,48,94 Quantitatively, the δ_iso(¹H) RMSD metric generated using CASTEP and a two-parameter linear mapping is 0.27 ± 0.14 ppm, while it is 0.26 ± 0.13 ppm for QE. However, this reduction in values does not immediately infer that the two-parameter linear mapping is superior for all structural characterization tasks (e.g., structure determination, vide infra).

¹H δ_iso RMSD metric structure variation with respect to E_cut value

The δ_iso(¹H) RMSD metrics for different plane wave energy cutoff values (i.e., E_cut = 90 Ry, 55 Ry, 45 Ry, 35 Ry, 25 Ry, 15 Ry, 10 Ry, and 5 Ry) were created by performing GIPAW DFT calculations using QE.⁷³ The rationale was to see how much key computational parameters related to the quality of the calculation influenced the resulting δ_iso(¹H) RMSD metric structure. The E_cut value is related to the number of plane waves used to describe the electron density. Theoretically, an endless number of plane wave basis functions are needed. However, for practical reasons, a cutoff energy is applied. With the use of lower E_cut values, fewer computational resources are used; however, the quality of the calculations is reduced. We thus wish to assess by how much we could reduce the E_cut value without altering the δ_iso(¹H) RMSD metric structure in a meaningful way. What is ‘meaningful’ is potentially subjective, and so we define that a metric is meaningfully altered if the change in the parameters describing it are greater than 0.05 ppm. This (admittedly arbitrary) value was selected as it is comfortably less than solid-state ¹H NMR linewidths under favourable measurement conditions (i.e., assuming an applied field and MAS frequency on the order of 10 T and 100 kHz, respectively, solid-state ¹H NMR linewidths of about 0.1–0.2 ppm are commonly observed).⁹⁵ We note in passing that interesting mathematical approaches to reduce apparent ¹H MAS NMR linewidths have been presented,^86,96 but they appear to suggest that the ultimate accuracy of measured ¹H MAS NMR peaks is roughly about 0.03 ppm under currently accessible measurement conditions.

The δ_iso(¹H) RMSD values were calculated for each structure at each E_cut value. Subsequently, the average ¹H RMSDs for the set of 24 crystal structures, and the standard deviations, were also calculated for each E_cut while using ‘structure-dependent’ k-point grids. Relevant information has been provided in Table 2.

Table 2 δ _iso(¹H) RMSD values for 8 different E_cut values (1-param.)^a

CSD Refcode	90 Ry^b	55 Ry	45 Ry	35 Ry	25 Ry	15 Ry	10 Ry	5 Ry
a All numerical values in this Table correspond to δiso(^1H) RMSD values, in ppm. Here, ‘Structure-dependent’ k-point grids were used. The k-point grids used for each crystal structure are provided in the ESI. b Excepting the first column, in this row the Ecut value used is indicated.
ACSALA07	0.632	0.625	0.621	0.653	1.194	2.905	2.410	2.673
AMBACO10	0.472	0.470	0.465	0.490	0.855	2.957	2.681	3.209
AMCILL	0.173	0.172	0.169	0.167	0.174	0.577	0.532	1.856
BAPLOT01	0.227	0.224	0.209	0.219	0.304	0.446	0.178	0.367
CIMETD	0.688	0.684	0.681	0.684	0.724	0.687	0.873	1.786
COCAIN10	0.283	0.289	0.282	0.277	0.251	0.384	0.609	1.228
COYRUD13	0.649	0.641	0.638	0.671	0.880	0.607	1.328	0.949
FPAMCA11	0.349	0.340	0.335	0.362	0.698	1.973	0.855	2.584
FURSEM01	0.485	0.470	0.468	0.485	0.761	1.730	1.653	2.171
GLUTAS07	0.368	0.362	0.360	0.366	0.625	0.592	0.454	2.016
GLYCIN28	0.068	0.071	0.070	0.068	0.204	0.869	0.531	0.446
HISTCM01	0.342	0.333	0.326	0.328	0.608	1.317	0.477	1.147
HXACAN35	0.257	0.250	0.244	0.280	0.618	1.113	0.818	1.768
IBPRAC	0.463	0.456	0.452	0.477	0.783	1.973	1.924	2.176
INDMET	0.445	0.438	0.432	0.465	0.825	1.977	1.596	1.565
IPMEPL	0.093	0.094	0.094	0.106	0.535	1.261	0.518	1.302
LABHEB	0.539	0.536	0.531	0.533	0.566	0.547	0.741	1.980
LTYRHC10	0.356	0.347	0.346	0.377	0.877	1.525	1.059	0.769
LTYROS10	0.193	0.189	0.189	0.214	0.520	0.674	0.699	0.810
URACIL	0.395	0.389	0.384	0.373	0.459	0.788	0.819	3.149
VOSREC	0.527	0.520	0.513	0.521	0.567	0.633	0.422	2.328
WEZCOT	0.332	0.329	0.323	0.322	0.347	0.499	0.597	1.630
ZIVKAQ	0.614	0.606	0.602	0.616	0.947	1.731	1.147	1.675
ZZZUEE01	0.653	0.653	0.653	0.652	0.625	0.669	0.797	1.154
Avg. ^1H RMSD / ppm	0.400	0.395	0.391	0.404	0.623	1.185	0.988	1.697
s(^1H RMSD) / ppm	0.179	0.178	0.178	0.180	0.252	0.757	0.641	0.773

---

A visual representation of some of the data contained in Table 2 is provided in Fig. 4.

Fig. 4 Violin distribution plots for δ_iso(¹H) RMSD metrics as a function of the value of E_cut. Starting from the left, the earlier displayed ‘benchmark’ metric at 90 Ry is provided. Moving sequentially to the right, the E_cut value is reduced to 55 Ry, 35 Ry, 25 Ry, and finally 15 Ry. For all, a ‘structure-dependent’ k-point grid and a one-parameter linear mapping were used.

These results show that the average δ_iso(¹H) RMSDs and the standard deviations calculated while using E_cut values of 90, 55, 45, and 35 Ry are extremely similar. However, there is a modest divergence upon lowering the E_cut value to 25 Ry. Further reduction in the cutoff energy leads to the δ_iso(¹H) RMSD metric parameters changing drastically (for example, observe the 15 Ry violin distribution plot in Fig. 4). We also provide below a similar visual depiction of how the δ_iso(¹H) RMSD metrics vary as a function of the E_cut value, but when using a two-parameter linear mapping (Fig. 5).

Fig. 5 Violin distribution plots for δ_iso(¹H) RMSD metrics as a function of the value of E_cut. Starting from the left, the earlier displayed metric at 90 Ry is provided. Moving sequentially to the right, the E_cut value is reduced to 55 Ry, 35 Ry, 25 Ry, and finally 15 Ry. For all, a ‘structure-dependent’ k-point grid and a two-parameter linear mapping were used.

The full dataset used to arrive at the various violin distribution plots shown in Fig. 5 can be found in the ESI,† Table S1. It is again observed that the metric structures are very similar down to E_cut values of 35 Ry, with a reasonably substantive change when E_cut is reduced to 25 Ry. The change in metric structure when going from 35 Ry to 25 Ry is somewhat less dramatic here when compared against the same situation and using a one-parameter linear mapping. This might be suggestive that a two-parameter mapping can ‘counteract’ some of the degradation in the δ_iso(¹H) RMSD metric when E_cut = 25 Ry, however it remains to be seen if this is a useful finding (vide infra). Values of E_cut = 15 Ry (and lower, see ESI†) produce very large changes in the δ_iso(¹H) RMSD metric structure. We again note that the change in the metric structure upon going from 25 Ry to 15 Ry is less dramatic when a two-parameter linear mapping is used, and the very pronounced ‘tail’ of the 15 Ry metric seen in Fig. 4 is reduced considerably (Fig. 5). Regardless of the linear mapping used, the structures of the metrics appear stable at E_cut values of 35 Ry and larger. We therefore tentatively propose that an energy cutoff value as low as 35 Ry can be used for determining the δ_iso(¹H) RMSD values of organic molecular crystal structures without substantially influencing the value of the predicted δ_iso(¹H) RMSD.

¹H δ_iso RMSD metric structure variation with respect to the k-point grid used

The δ_iso(¹H) RMSD metrics were also calculated for various E_cut values with k-point grids set to 1 × 1 × 1 and with the QE software. The comparison between these results with the previous results that used structure-dependent k-point grids is meant to highlight the possible effect of the k-point grid on the δ_iso(¹H) RMSD metric structure. For example, assuming a one-parameter linear mapping and E_cut = 90 Ry, the δ_iso(¹H) RMSD metric was 0.40 ± 0.18 ppm when a structure-dependent k-point grid was used. In contrast, when a 1 × 1 × 1 k-point grid is employed (and all other computational parameters and analysis were otherwise unchanged), it is 0.50 ± 0.20 ppm. This is, under our earlier definition, a significant increase in the average δ_iso(¹H) RMSD since 0.10 ppm > 0.05 ppm. The change in the standard deviation is modest in absolute terms (i.e., +0.02 ppm), but has scaled in a proportionate manner when compared against the average δ_iso(¹H) RMSD value. Further details regarding the various δ_iso(¹H) RMSD values are provided in Table 3, while a complete disclosure can be found in the ESI.†

Table 3 δ _iso(¹H) RMSD values for 8 different E_cut values (1-param., 1 × 1 × 1 grid)^a

CSD Refcode	90 Ry^b	55 Ry	45 Ry	35 Ry	25 Ry	15 Ry	10 Ry	5 Ry
a All numerical values in this Table correspond to δiso(^1H) RMSD values, in ppm. Here, 1 × 1 × 1 k-point grids were used. b Excepting the first column, in this row the Ecut value used is indicated.
ACSALA07	0.650	0.645	0.640	0.669	1.157	2.662	3.030	2.849
AMBACO10	0.590	0.587	0.582	0.608	0.949	3.096	2.997	3.253
AMCILL	0.330	0.329	0.326	0.325	0.350	0.669	0.620	2.604
BAPLOT01	0.415	0.416	0.419	0.417	0.486	0.561	0.904	1.163
CIMETD	0.711	0.710	0.705	0.707	0.743	0.689	1.001	2.097
COCAIN10	0.275	0.274	0.274	0.270	0.256	0.450	0.757	1.409
COYRUD13	0.713	0.706	0.702	0.731	0.916	0.645	0.925	1.999
FPAMCA11	0.380	0.375	0.368	0.400	0.739	1.863	0.844	2.920
FURSEM01	0.493	0.484	0.479	0.490	0.760	1.651	1.477	2.014
GLUTAS07	0.811	0.807	0.803	0.810	1.058	0.945	1.122	2.123
GLYCIN28	0.191	0.191	0.175	0.183	0.315	1.152	0.649	3.887
HISTCM01	0.410	0.402	0.395	0.398	0.660	1.442	0.794	0.601
HXACAN35	0.793	0.786	0.781	0.828	1.325	2.230	1.799	3.369
IBPRAC	0.470	0.464	0.462	0.485	0.807	2.104	2.110	2.269
INDMET	0.435	0.427	0.423	0.451	0.843	1.939	1.717	1.903
IPMEPL	0.108	0.104	0.102	0.125	0.557	1.398	0.460	1.798
LABHEB	0.537	0.533	0.529	0.529	0.561	0.556	0.743	1.962
LTYRHC10	0.853	0.854	0.854	0.853	1.044	1.651	1.654	2.538
LTYROS10	0.440	0.437	0.436	0.456	0.696	0.851	1.303	1.726
URACIL	0.381	0.373	0.366	0.357	0.454	0.880	1.656	6.106
VOSREC	0.542	0.533	0.533	0.539	0.611	0.811	0.676	2.321
WEZCOT	0.321	0.317	0.316	0.311	0.264	0.319	0.636	1.389
ZIVKAQ	0.605	0.594	0.590	0.606	0.957	1.753	1.422	1.841
ZZZUEE01	0.642	0.642	0.641	0.641	0.613	0.648	0.763	1.272
Avg. ^1H RMSD / ppm	0.504	0.500	0.496	0.508	0.713	1.290	1.252	2.309
s(^1H RMSD) / ppm	0.195	0.195	0.196	0.199	0.286	0.751	0.704	1.105

---

Assuming a given value of E_cut, similar increases in the average δ_iso(¹H) RMSD value, and the standard deviations in the δ_iso(¹H) RMSD values hold true for all the other energies (Fig. 6 and 7). This indicates, unsurprisingly, that better results (i.e., lower average δ_iso(¹H) RMSDs and narrower δ_iso(¹H) RMSD metrics) can be obtained using the structure-dependent k-point grids as they always result in a k-point grid density that is greater when compared against the 1 × 1 × 1 k-point grid density.

Fig. 6 Violin distribution plots for δ_iso(¹H) RMSD metrics as a function of the value of E_cut. Starting from the left the metric at 90 Ry is provided. Moving sequentially to the right, the E_cut value is reduced to 55 Ry, 35 Ry, 25 Ry, and finally 15 Ry. For all, a 1 × 1 × 1 k-point grid and a one-parameter linear mapping were used.

Fig. 7 Violin distribution plots for δ_iso(¹H) RMSD metrics as a function of the value of E_cut. Starting from the left, the metric at 90 Ry is provided. Moving sequentially to the right, the E_cut value is reduced to 55 Ry, 35 Ry, 25 Ry, and finally 15 Ry. For all, a 1 × 1 × 1 k-point grid and a two-parameter linear mapping were used. Data used to generate these plots can be found in the ESI,† Table S2.

Application: crystal structure determination of thymol

We have provided discussion outlining how δ_iso(¹H) RMSD metrics change as a function of a few important parameters. However, it is uncertain how these findings might be applied in NMR crystallography studies. As an example, we consider the structure determination of thymol using the previously generated CSP crystal structures from Salager et al.¹⁰ After performing the calculations of hydrogen magnetic shielding tensors at 4 different E_cut values (i.e., 15, 25, 35, and 55 Ry) with a ‘structure-dependent’ k-point grid, followed by determining the δ_iso(¹H) RMSD values using a one-parameter linear mapping, we observed that reducing the E_cut value from 55 to 35 Ry produces essentially identical results when the task is structure selection (Fig. 8A and B). When comparing the CSP-generated candidate structures, their substantially different δ_iso(¹H) RMSD values enable the selection of a single candidate crystal structure with high confidence (as all other candidate structures are >2σ from the selected structure). In the case of thymol, structure #3 is selected, which agrees with the prior literature result.¹⁰ Decreasing the E_cut value to 25 Ry (Fig. 8C) and 15 Ry (Fig. 8D) results in a progressively less confident structure selection. This is most dramatic when E_cut = 15 Ry as many δ_iso(¹H) RMSD values are somewhat close to the RMSD value for the selected structure (i.e., 18 of 22 alternative crystal structures have a δ_iso(¹H) RMSD value within 2σ from the selected structure). So, while the structure selection process at E_cut = 25 Ry is broadly like that at larger E_cut values (though not identical), the structure selection process is strongly affected in a negative fashion when E_cut = 15 Ry. However, while our confidence in the structure selection process is reduced at progressively lower E_cut values, the outcome of the process is the same (i.e., selection of crystal structure #3).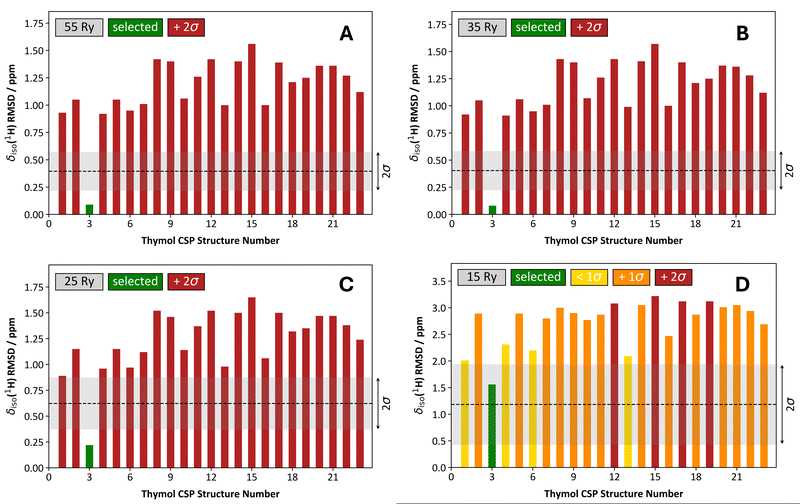

Fig. 8 Comparison of the structure selection process for 23 CSP-generated crystal structures of thymol using a one-parameter linear mapping, a structure-dependent k-point grid, and variable E_cut energies. The E_cut values used were: 55 Ry (A), 35 Ry (B), 25 Ry (C), and 15 Ry (D). In each quadrant, the associated δ_iso(¹H) RMSD metric is provided as a ‘grey band’, and they conform to the average values and standard deviations provided in, for example, Table 2. The structure selected is always the one with the lowest δ_iso(¹H) RMSD value and is consistently indicated with a green bar. For structures other than the selected structure, the color is variable. For example, when a given δ_iso(¹H) RMSD bar is red, it means that the selected structure’s δ_iso(¹H) RMSD is more than 2σ lower in comparison. If the δ_iso(¹H) RMSD bar is orange, it is more than 1σ above the selected structure, yet also <2σ. Lastly, a yellow δ_iso(¹H) RMSD bar indicates that the δ_iso(¹H) RMSD of the given structure is within 1σ of the selected structure.

When using a 1 × 1 × 1 k-point grid rather than the ‘structure-dependent’ k-point grids, the structure selection for thymol is similar so long as E_cut ≥ 25 Ry (Fig. 9 and Fig. S1, ESI†). When E_cut = 15 Ry, we find that the structure selection process is degraded to such an extent that we do not select the correct structure (Fig. 9C); however, this selection is done with low confidence as many other candidate structures have δ_iso(¹H) RMSD values that are very similar to the selected structure.

Fig. 9 Comparison of the structure selection process for 23 CSP-generated crystal structures of thymol using a one-parameter linear mapping, a 1 × 1 × 1 k-point grid, and variable E_cut energies. The E_cut values used were: 55 Ry (A), 25 Ry (B), 15 Ry (C). In each, the associated δ_iso(¹H) RMSD metric is provided as a ‘grey band’, and they conform to the average values and standard deviations provided in, for example, Table 3. The coloring scheme of the bars is unchanged from Fig. 8.

When these results for thymol are taken in concert, it is very tentatively suggested that E_cut values as low as 25 Ry can provide sufficiently reasonable estimates of the δ_iso(¹H) RMSD values that would be obtained under the ‘benchmark’ conditions (recall, the ‘benchmark’ values used E_cut = 90 Ry). Further, performing the computations at E_cut = 25 Ry does not substantially affect the structure selection process. For the unit cell dimensions typically associated with organics, it should be possible to use 1 × 1 × 1 k-point grids so long as the task is structure selection from a group of CSP-generated structures. If near quantitative convergence of the δ_iso(¹H) RMSD values is desired, it appears that 35 Ry is sufficient but combining E_cut = 35 Ry with a 1 × 1 × 1 k-point grid would not be appropriate (compare Fig. 8B with Fig. S1, ESI†). We underscore that further data and examples are required to strengthen these tentative suggestions into formal recommendations, and we are currently preparing a more fulsome discussion that involves several additional organic compounds and CSP-generated structure sets.

We next turn our attention to outcomes of the structure selection process for thymol when using a two-parameter linear mapping. When ‘structure-dependent’ k-point grids were chosen, the structure selection process is robust so long as E_cut ≥ 25 Ry (Fig. 10 and Fig. S2, ESI†). At E_cut = 15 Ry we observe something that was not seen in the case of the one-parameter linear mapping: the differences in the δ_iso(¹H) RMSD values between the selected structure and all other alternative crystal structures are almost always >2σ. This means that even when using E_cut = 15 Ry, we would confidently select CSP-generated structure #3. However, when we compare the set of 23 CSP-generated structures of thymol using the combination of conditions (i.e., E_cut = 15 Ry, structure-dependent k-point grid, two-parameter mapping) to the reference set of structures, even our selected structure would look comparatively poor. This leads us to a rather conflicted result and underscores the potential importance of comparing the δ_iso(¹H) RMSD values amongst: (i) all candidate structures and (ii) against the set of reference structures. In our present situation, if we (somehow) only had access to the data at E_cut = 15 Ry, we would conclude that while structure #3 is the best candidate structure by a considerable margin, we would wonder if a better structure could be found (perhaps by re-running the CSP process).

Fig. 10 Comparison of the structure selection process for 23 CSP-generated crystal structures of thymol using a two-parameter linear mapping, a structure-dependent k-point grid, and variable E_cut energies. The E_cut values used were: 55 Ry (A), 25 Ry (B), and 15 Ry (C). In each, the associated δ_iso(¹H) RMSD metric is provided as a ‘grey band’, and they conform to the average values and standard deviations provided in, for example, Table S1 (ESI†). The coloring scheme of the bars is unchanged from Fig. 8.

Considering now the outcomes of the two-parameter linear mapping with a 1 × 1 × 1 k-point grid and variable E_cut values (Fig. 11 and Fig. S3, ESI†), we generally observe trends that are similar to those observed previously. First, the structure selection process for thymol remains quite stable down to E_cut = 25 Ry, and so we can confidently select structure #3 even under these conditions where the computation quality is severely degraded relative to what would typically be considered as normal. In contrast to the case when a one-parameter linear mapping, E_cut = 15 Ry and 1 × 1 × 1 k-point grid is used (Fig. 9C), when the two-parameter linear mapping is used we are still able to select the correct structure for thymol, albeit with quite low relative confidence (Fig. 11C).

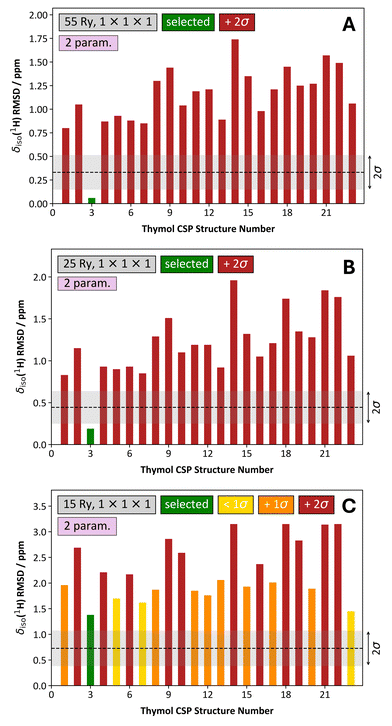Fig. 11 Comparison of the structure selection process for 23 CSP-generated crystal structures of thymol using a two-parameter linear mapping, a 1 × 1 × 1 k-point grid, and variable E_cut energies. The E_cut values used were: 55 Ry (A), 25 Ry (B), and 15 Ry (C). In each, the associated δ_iso(¹H) RMSD metric is provided as a ‘grey band’, and they conform to the average values and standard deviations provided in, for example, Table S2 (ESI†). The coloring scheme of the bars is unchanged from Fig. 8.

Conclusions

In this study, we assessed the robustness of ¹H isotropic chemical shift (δ_iso) RMSD metrics. This was achieved using a set of 24 high-quality crystal structures, associated assigned experimental ¹H δ_iso values, and gauge including projector augmented wave density functional theory (GIPAW DFT) computed hydrogen isotropic magnetic shielding (σ_iso) values. In all cases, a δ_iso(¹H) RMSD value for a crystal structure was generated by determining the linear mapping of σ_iso values to computed δ_iso values that minimizes the differences between experimental and calculated isotropic ¹H chemical shift values. We have probed the influence of the computational software used to generate the hydrogen σ_iso values and found that for high-quality ‘benchmark’ calculations there is no meaningful difference between CASTEP and Quantum ESPRESSO (QE) outputs. Additional items were considered using the QE software, such as variation in the plane wave energy cut-off (E_cut) and k-point grid. We find that so long as a linear mapping is used, the δ_iso(¹H) RMSD metrics are stable (i.e., any changes are below what we would consider as significant) until E_cut is below 35 Ry. Further, we find that δ_iso(¹H) RMSD metrics with E_cut = 35 Ry agree quantitatively with ‘benchmark’ δ_iso(¹H) RMSD metrics (both for one- and two-parameter linear mappings). This E_cut value is far lower than typically used in NMR crystallography studies and therefore hints that significant savings in computational resources can be gained without any discernible degradation in quality. The use of a sparse 1 × 1 × 1 k-point grid negatively impacts the robustness of the δ_iso(¹H) RMSD metric, but we find it to be of lesser importance when compared to the E_cut parameter. If qualitative results are sufficient, for example in the structure selection of thymol, we find that a two-parameter linear mapping, E_cut = 25 Ry, and a 1 × 1 × 1 k-point grid allows for the selection process to occur in an almost identical fashion compared to when a more dense k-point grid and much higher E_cut value is used. Further studies regarding the generality of these findings are well underway.

Author contributions

CMW: conceptualization, funding acquisition, select quantum chemical calculations, data verification, initial draft of manuscript (50%), and revisions (50%). FZ: most all quantum chemical calculations, initial data analysis, initial draft of manuscript (50%), and revisions (50%). Both authors have read and approved the final version of this manuscript.

Data availability

All data that support the findings of this study have been provided in the main text or as part of the ESI.†

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

CMW acknowledges the University of Regina, Faculty of Science for a startup grant, the Natural Sciences and Engineering Research Council of Canada (NSERC) for a Discovery Grant, and this research was enabled in part by support provided by Compute Ontario (https://www.computeontario.ca), the Prairies DRI Group, and the Digital Research Alliance of Canada (https://www.alliancecan.ca). FZ thanks the Department of Chemistry & Biochemistry and the Faculty of Graduate Studies and Research at the University of Regina for research stipends and a Saskatchewan Innovation and Excellence Graduate Scholarship.

References

1. R. K. Harris, NMR studies of organic polymorphs & solvates, Analyst, 2006, 131, 351–373.
2. C. Martineau, J. Senker and F. Taulelle, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, Elsevier Ltd, Oxford, UK, 2014, ch. 1, vol. 82, pp. 1–57.
3. M. Baias, J.-N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, De Novo Determination of the Crystal Structure of a Large Drug Molecule by Crystal Structure Prediction-Based Powder NMR Crystallography, J. Am. Chem. Soc., 2013, 135, 17501–17507.
4. D. V. Dudenko, P. A. Williams, C. E. Hughes, O. N. Antzutkin, S. P. Velaga, S. P. Brown and K. D. M. Harris, Exploiting the Synergy of Powder X-ray Diffraction and Solid-State NMR Spectroscopy in Structure Determination of Organic Molecular Solids, J. Phys. Chem. C, 2013, 117, 12258–12265.
5. A. Hofstetter, M. Balodis, F. M. Paruzzo, C. M. Widdifield, G. Stevanato, A. C. Pinon, P. J. Bygrave, G. M. Day and L. Emsley, Rapid Structure Determination of Molecular Solids Using Chemical Shifts Directed by Unambiguous Prior Constraints, J. Am. Chem. Soc., 2019, 141, 16624–16634.
6. M. Balodis, M. Cordova, A. Hofstetter, G. M. Day and L. Emsley, De Novo Crystal Structure Determination from Machine Learned Chemical Shifts, J. Am. Chem. Soc., 2022, 144, 7215–7223.
7. C. M. Widdifield, S. O. Nilsson Lill, A. Broo, M. Lindkvist, A. Pettersen, A. Svensk Ankarberg, P. Aldred, S. Schantz and L. Emsley, Does Z′ equal 1 or 2? Enhanced powder NMR crystallography verification of a disordered room temperature crystal structure of a p38 inhibitor for chronic obstructive pulmonary disease, Phys. Chem. Chem. Phys., 2017, 19, 16650–16661.
8. A. S. Tatton, H. Blade, S. P. Brown, P. Hodgkinson, L. P. Hughes, S. O. Nilsson Lill and J. R. Yates, Improving Confidence in Crystal Structure Solutions Using NMR Crystallography: The Case of β-Piroxicam, Cryst. Growth Des., 2018, 18, 3339–3351.
9. C. M. Widdifield, H. Robson and P. Hodgkinson, Furosemide's one little hydrogen atom: NMR crystallography structure verification of powdered molecular organics, Chem. Commun., 2016, 52, 6685–6688.
10. E. Salager, G. M. Day, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, Powder Crystallography by Combined Crystal Structure Prediction and High-Resolution ¹H Solid-State NMR Spectroscopy, J. Am. Chem. Soc., 2010, 132, 2564–2566.
11. J. Brus, J. Czernek, L. Kobera, M. Urbanova, S. Abbrent and M. Husak, Predicting the Crystal Structure of Decitabine by Powder NMR Crystallography: Influence of Long-Range Molecular Packing Symmetry on NMR Parameters, Cryst. Growth Des., 2016, 16, 7102–7111.
12. E. Salager, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, Powder NMR crystallography of thymol, Phys. Chem. Chem. Phys., 2009, 11, 2610–2621.
13. T. Pawlak and M. J. Potrzebowski, Fine Refinement of Solid-State Molecular Structures of Leu- and Met-Enkephalins by NMR Crystallography, J. Phys. Chem. B, 2014, 118, 3298–3309.
14. M. Sardo, S. M. Santos, A. A. Babaryk, C. López, I. Alkorta, J. Elguero, R. M. Claramunt and L. Mafra, Diazole-based powdered cocrystal featuring a helical hydrogen-bonded network: Structure determination from PXRD, solid-state NMR and computer modeling, Solid State Nucl. Magn. Reson., 2015, 65, 49–63.
15. I. Jastrzebska, T. Pawlak, R. Arcos-Ramos, E. Florez-Lopez, N. Farfán, D. Czajkowska-Szczykowska, J. Maj, R. Santillan, J. W. Morzycki and M. J. Potrzebowski, Synthesis, Structure, and Local Molecular Dynamics for Crystalline Rotors Based on Hecogenin/Botogenin Steroidal Frameworks, Cryst. Growth Des., 2016, 16, 5698–5709.
16. A. Scarperi, G. Barcaro, A. Pajzderska, F. Martini, E. Carignani and M. Geppi, Structural Refinement of Carbimazole by NMR Crystallography, Molecules, 2021, 26, 4577.
17. M. Kibalchenko, D. Lee, L. Shao, M. C. Payne, J. J. Titman and J. R. Yates, Distinguishing hydrogen bonding networks in α-D-galactose using NMR experiments and first principles calculations, Chem. Phys. Lett., 2010, 498, 270–276.
18. X. Filip, I.-G. Grosu, M. Miclăuş and C. Filip, NMR crystallography methods to probe complex hydrogen bonding networks: application to structure elucidation of anhydrous quercetin, CrystEngComm, 2013, 15, 4131–4142.
19. J. D. Hartman, G. M. Day and G. J. O. Beran, Enhanced NMR Discrimination of Pharmaceutically Relevant Molecular Crystal Forms through Fragment-Based Ab Initio Chemical Shift Predictions, Cryst. Growth Des., 2016, 16, 6479–6493.
20. J. Czernek, M. Urbanova and J. Brus, NMR Crystallography of the Polymorphs of Metergoline, Crystals, 2018, 8, 378.
21. C. M. Widdifield, J. D. Farrell, J. C. Cole, J. A. K. Howard and P. Hodgkinson, Resolving alternative organic crystal structures using density functional theory and NMR chemical shifts, Chem. Sci., 2020, 11, 2987–2992.
22. C. J. Pickard and F. Mauri, All-electron magnetic response with pseudopotentials: NMR chemical shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
23. T. Charpentier, The PAW/GIPAW approach for computing NMR parameters: A new dimension added to NMR study of solids, Solid State Nucl. Magn. Reson., 2011, 40, 1–20.
24. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, First-Principles Calculation of NMR Parameters Using the Gauge Including Projector Augmented Wave Method: A Chemist's Point of View, Chem. Rev., 2012, 112, 5733–5779.
25. S. E. Ashbrook and D. McKay, Combining solid-state NMR spectroscopy with first-principles calculations – a guide to NMR crystallography, Chem. Commun., 2016, 52, 7186–7204.
26. T. Pawlak, I. Sudgen, G. Bujacz, D. Iuga, S. P. Brown and M. J. Potrzebowski, Synergy of Solid-State NMR, Single-Crystal X-ray Diffraction, and Crystal Structure Prediction Methods: A Case Study of Teriflunomide (TFM), Cryst. Growth Des., 2021, 21, 3328–3343.
27. P. M. J. Szell, S. O. Nilsson Lill, H. Blade, S. P. Brown and L. P. Hughes, A toolbox for improving the workflow of NMR crystallography, Solid State Nucl. Magn. Reson., 2021, 116, 101761.
28. J. D. Hartman and G. J. O. Beran, Fragment-Based Electronic Structure Approach for Computing Nuclear Magnetic Resonance Chemical Shifts in Molecular Crystals, J. Chem. Theory Comput., 2014, 10, 4862–4872.
29. J. D. Hartman, R. A. Kudla, G. M. Day, L. J. Mueller and G. J. O. Beran, Benchmark fragment-based ¹H, ¹³C, ¹⁵N and ¹⁷O chemical shift predictions in molecular crystals, Phys. Chem. Chem. Phys., 2016, 18, 21686–21709.
30. J. D. Hartman, A. Balaji and G. J. O. Beran, Improved Electrostatic Embedding for Fragment-Based Chemical Shift Calculations in Molecular Crystals, J. Chem. Theory Comput., 2017, 13, 6043–6051.
31. M. Dračínský, P. Unzueta and G. J. O. Beran, Improving the accuracy of solid-state nuclear magnetic resonance chemical shift prediction with a simple molecular correction, Phys. Chem. Chem. Phys., 2019, 21, 14992–15000.
32. M. Dračínský, J. Vícha, K. Bártová and P. Hodgkinson, Towards Accurate Predictions of Proton NMR Spectroscopic Parameters in Molecular Solids, ChemPhysChem, 2020, 21, 2075–2083.
33. M. Shi, X. Jin, Z. Wan and X. He, Automated fragmentation quantum mechanical calculation of ¹³C and ¹H chemical shifts in molecular crystals, J. Chem. Phys., 2021, 154, 064502.
34. F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Chemical shifts in molecular solids by machine learning, Nat. Commun., 2018, 9, 4501.
35. M. Cordova, E. A. Engel, A. Stefaniuk, F. Paruzzo, A. Hofstetter, M. Ceriotti and L. Emsley, A Machine Learning Model of Chemical Shifts for Chemically and Structurally Diverse Molecular Solids, J. Phys. Chem. C, 2022, 126, 16710–16720.
36. S. Liu, J. Li, K. C. Bennett, B. Ganoe, T. Stauch, M. Head-Gordon, A. Hexemer, D. Ushizima and T. Head-Gordon, Multiresolution 3D-DenseNet for Chemical Shift Prediction in NMR Crystallography, J. Phys. Chem. Lett., 2019, 10, 4558–4565.
37. X. Li, M. A. Neumann and J. van de Streek, The application of tailor-made force fields and molecular dynamics for NMR crystallography: a case study of free base cocaine, IUCrJ, 2017, 4, 175–184.
38. M. Baias, C. M. Widdifield, J.-N. Dumez, H. P. G. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Powder crystallography of pharmaceutical materials by combined crystal structure prediction and solid-state ¹H NMR spectroscopy, Phys. Chem. Chem. Phys., 2013, 15, 8069–8080.
39. S. L. Price, Predicting crystal structures of organic compounds, Chem. Soc. Rev., 2014, 43, 2098–2111.
40. S. L. Price, From crystal structure prediction to polymorph prediction: interpreting the crystal energy landscape, Phys. Chem. Chem. Phys., 2008, 10, 1996–2009.
41. M. K. Dudek and K. Drużbicki, Along the road to crystal structure prediction (CSP) of pharmaceutical-like molecules, CrystEngComm, 2022, 24, 1665–1678.
42. J. E. Arnold and G. M. Day, Crystal Structure Prediction of Energetic Materials, Cryst. Growth Des., 2023, 23, 6149–6160.
43. G. J. O. Beran, Frontiers of molecular crystal structure prediction for pharmaceuticals and functional organic materials, Chem. Sci., 2023, 14, 13290–13312.
44. S. M. Santos, J. Rocha and L. Mafra, NMR Crystallography: Toward Chemical Shift-Driven Crystal Structure Determination of the β-Lactam Antibiotic Amoxicillin Trihydrate, Cryst. Growth Des., 2013, 13, 2390–2395.
45. E. A. Engel, V. Kapil and M. Ceriotti, Importance of Nuclear Quantum Effects for NMR Crystallography, J. Phys. Chem. Lett., 2021, 12, 7701–7707.
46. M. Dračínský, P. Bouř and P. Hodgkinson, Temperature Dependence of NMR Parameters Calculated from Path Integral Molecular Dynamics Simulations, J. Chem. Theory Comput., 2016, 12, 968–973.
47. J. Brus, J. Czernek, M. Hruby, P. Svec, L. Kobera, S. Abbrent and M. Urbanova, Efficient Strategy for Determining the Atomic-Resolution Structure of Micro- and Nanocrystalline Solids within Polymeric Microbeads: Domain-Edited NMR Crystallography, Macromolecules, 2018, 51, 5364–5374.
48. J. D. Hartman, S. Monaco, B. Schatschneider and G. J. O. Beran, Fragment-based ¹³C nuclear magnetic resonance chemical shift predictions in molecular crystals: an alternative to planewave methods, J. Chem. Phys., 2015, 143, 102809.
49. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, The Cambridge Structural Database, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
50. C. C. Wilson, Interesting proton behaviour in molecular structures. Variable temperature neutron diffraction and ab initio study of acetylsalicylic acid: characterising librational motions and comparing protons in different hydrogen bonding potentials, New J. Chem., 2002, 26, 1733–1739.
51. M. Nandhagopal and M. Narayanasamy, Private Communication to CSD, CCDC 1868172, 2018.
52. M. O. Boles and R. J. Girven, The structures of ampicillin: a comparison of the anhydrate and trihydrate forms, Acta Crystallogr., Sect. B, 1976, B32, 2279–2284.
53. Y. Ebisuzaki, P. D. Boyle and J. A. Smith, Methylxanthines. I. Anhydrous Theophylline, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, C53, 777–779.
54. E. Hädicke, F. Frickel and A. Franke, Die Struktur von Cimetidin (N′′-Cyan-N-Methyl-N′-[2-[(5-methyl-1H-imidazol-4-yl)methylthio]ethyl]guanidin), einem Histamin H₂-Rezeptor-Antagonist, Chem. Ber., 1978, 111, 3222–3232.
55. R. J. Hrynchuk, R. J. Barton and B. E. Robertson, The crystal structure of free base cocaine, C₁₇H₂₁NO₄, Can. J. Chem., 1983, 61, 481–487.
56. G.-M. Tang, J.-H. Wang, C. Zhao, Y.-T. Wang, Y.-Z. Cui, F.-Y. Cheng and S. W. Ng, Multi odd–even effects on cell parameters, melting points, and optical properties of chiral crystal solids based on S-naproxen, CrystEngComm, 2015, 17, 7258–7261.
57. H. M. Krishna Murthy, T. N. Bhat and M. Vijayan, Structure of a new crystal form of 2-{[3-(trifluoromethyl)phenyl]amino}benzoic acid (flufenamic acid), Acta Crystallogr., Sect. B: Struct. Sci., 1982, B38, 315–317.
58. J. Lamotte, H. Campsteyn, L. Dupont and M. Vermeire, Structure cristalline et moléculaire de l’acide furfurylamino-2 chloro-4 sulfamoyl-5 benzoïque, la furosémide (C₁₂H₁₁ClN₂O₅S), Acta Crystallogr., Sect. B, 1978, B34, 1657–1661.
59. C. B. Hübschle, C. Ruhmlieb, A. Burkhardt, S. van Smaalen and B. Dittrich, On avoiding negative electron density in Gram-Charlier refinements of anharmonic motion: the example of glutathione, Z. Kristallogr. - Cryst. Mater., 2018, 233, 695–706.
60. T. N. Drebushchak, E. V. Boldyreva, Yu. V. Seryotkin and E. S. Shutova, Crystal Structure Study of the Metastable β-Modification of Glycine and its Transformation into the α-Modification, J. Struct. Chem., 2002, 43, 835–842.
61. K. Oda and H. Koyama, A refinement of the crystal structure of histidine hydrochloride monohydrate, Acta Crystallogr., Sect. B, 1972, B28, 639–642.
62. R. Anitha, M. Gunasekaran, S. S. Kumar, S. Athimoolam and B. Sridhar, Single crystal XRD, vibrational and quantum chemical calculation of pharmaceutical drug paracetamol: a new synthesis form, Spectrochim. Acta, Part A, 2015, 150, 488–498.
63. J. F. McConnell, 2-(4-Isobutylphenyl) propionic acid, Cryst. Struct. Commun., 1974, 3, 73–75.
64. T. J. Kistenmacher and R. E. Marsh, Crystal and molecular structure of an antiinflammatory agent, indomethacin, 1-(p-chlorobenzoyl)-5-methoxy-2-methylindole-3-acetic acid, J. Am. Chem. Soc., 1972, 94, 1340–1345.
65. A. Thozet and M. Perrin, Structure of 2-isopropyl-5-methylphenol (Thymol), Acta Crystallogr., Sect. B, 1980, B36, 1444–1447.
66. A. L. Llamas-Saiz, C. Foces-Foces, I. Sobrados, J. Elguero and W. Meutermans, (4S,7R)-7,8,8-Trimethyl-4,5,6,7-tetrahydro-4,7-methano-1H(2H)-indazole (campho[2,3-c]pyrazole): comparison between the X-ray structure and carbon-13 NMR data in the solid state, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, C49, 724–729.
67. M. N. Frey, T. F. Koetzle, M. S. Lehmann and W. C. Hamilton, Precision neutron diffraction structure determination of protein and nucleic acid components. X. A comparison between the crystal and molecular structures of L-tyrosine and L-tyrosine hydrochloride, J. Chem. Phys., 1973, 58, 2547–2556.
68. A. Mostad, H. M. Nissen and C. Rømming, Crystal Structure of L-Tyrosine, Acta Chem. Scand., 1972, 26, 3819–3833.
69. R. F. Stewart and L. H. Jensen, Redetermination of the crystal structure of uracil, Acta Crystallogr., 1967, 23, 1102–1105.
70. J. M. Cense, V. Agafonov, R. Ceolin, P. Ladure and N. Rodier, Crystal and molecular structure analysis of flutamide. Bifurcated helicoidal C–H⋯O hydrogen bonds, Struct. Chem., 1994, 5, 79–84.
71. R. Sengupta and J. K. Dattagupta, A β-Adrenergic Agonist: Protonated Terbutaline Hemisulfate, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, C52, 162–164.
72. S. S. B. Glover, R. O. Gould and M. D. Walkinshaw, Structures of strychnine(I), C₂₁H₂₂N₂O₂, and a solvate of brucine(II), C₂₃H₂₆N₂O₄.C₂H₆O.2H₂O, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, C41, 990–994.
73. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
74. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570.
75. T. Björkman, CIF2Cell: Generating geometries for electronic structure programs, Comput. Phys. Commun., 2011, 182, 1183–1186.
76. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
77. Welcome to PSlibrary – A library of ultrasoft and PAW pseudopotentials, https://dalcorso.github.io/pslibrary/, (accessed June 2023).
78. A. Dal Corso, Pseudopotentials periodic table: From H to Pu, Comput. Mater. Sci., 2014, 95, 337–350.
79. R. Mathew, K. A. Uchman, L. Gkoura, C. J. Pickard and M. Baias, Identifying aspirin polymorphs from combined DFT-based crystal structure prediction and solid-state NMR, Magn. Reson. Chem., 2020, 58, 1018–1025.
80. R. K. Harris and P. Jackson, High-resolution ¹H and ¹³C NMR of solid 2-Aminobenzoic acid, J. Phys. Chem. Solids, 1987, 48, 813–818.
81. K. Maruyoshi, D. Iuga, A. E. Watts, C. E. Hughes, K. D. M. Harris and S. P. Brown, Assessing the Detection Limit of a Minority Solid-State Form of a Pharmaceutical by ¹H Double-Quantum Magic-Angle Spinning Nuclear Magnetic Resonance Spectroscopy, J. Pharm. Sci., 2017, 106, 3372–3377.
82. E. Carignani, S. Borsacchi, J. P. Bradley, S. P. Brown and M. Geppi, Strong Intermolecular Ring Current Influence on ¹H Chemical Shifts in Two Crystalline Forms of Naproxen: a Combined Solid-State NMR and DFT Study, J. Phys. Chem. C, 2013, 117, 17731–17740.
83. M. Sardo, R. Siegel, S. M. Santos, J. Rocha, J. R. B. Gomes and L. Mafra, Combining Multinuclear High-Resolution Solid-State MAS NMR and Computational Methods for Resonance Assignment of Glutathione Tripeptide, J. Phys. Chem. A, 2012, 116, 6711–6719.
84. L. Stievano, F. Tielens, I. Lopes, N. Folliet, C. Gervais, D. Costa and J.-F. Lambert, Density Functional Theory Modeling and Calculation of NMR Parameters: An ab Initio Study of the Polymorphs of Bulk Glycine, Cryst. Growth Des., 2010, 10, 3657–3667.
85. S. Li and M. Hong, Protonation, Tautomerization, and Rotameric Structure of Histidine: A Comprehensive Study by Magic-Angle-Spinning Solid-State NMR, J. Am. Chem. Soc., 2011, 133, 1534–1544.
86. P. Moutzouri, B. Simões de Almeida, D. Torodii and L. Emsley, Pure Isotropic Proton Solid State NMR, J. Am. Chem. Soc., 2021, 143, 9834–9841.
87. D. H. Zhou and C. M. Rienstra, Rapid Analysis of Organic Compounds by Proton-Detected Heteronuclear Correlation NMR Spectroscopy with 40 kHz Magic-Angle Spinning, Angew. Chem., Int. Ed., 2008, 47, 7328–7331.
88. J. P. Bradley, S. P. Velaga, O. N. Antzutkin and S. P. Brown, Probing Intermolecular Crystal Packing in γ-Indomethacin by High-Resolution ¹H Solid-State NMR Spectroscopy, Cryst. Growth Des., 2011, 11, 3463–3471.
89. A. L. Webber, L. Emsley, R. M. Claramunt and S. P. Brown, NMR Crystallography of Campho[2,3-c]pyrazole (Z′ = 6): Combining High-Resolution ¹H-¹³C Solid-State MAS NMR Spectroscopy and GIPAW Chemical-Shift Calculations, J. Phys. Chem. A, 2010, 114, 10435–10442.
90. J. Czernek and J. Brus, The covariance of the differences between experimental and theoretical chemical shifts as an aid for assigning two-dimensional heteronuclear correlation solid-state NMR spectra, Chem. Phys. Lett., 2014, 608, 334–339.
91. A.-C. Uldry, J. M. Griffin, J. R. Yates, M. Pérez-Torralba, M. D. Santa María, A. L. Webber, M. L. L. Beaumont, A. Samoson, R. M. Claramunt, C. J. Pickard and S. P. Brown, Quantifying Weak Hydrogen Bonding in Uracil and 4-Cyano-4′-ethynylbiphenyl: A Combined Computational and Experimental Investigation of NMR Chemical Shifts in the Solid State, J. Am. Chem. Soc., 2008, 130, 945–954.
92. R. K. Harris, P. Hodgkinson, V. Zorin, J.-N. Dumez, B. Elena-Herrmann, L. Emsley, E. Salager and R. S. Stein, Computation and NMR crystallography of terbutaline sulfate, Magn. Reson. Chem., 2010, 48, S103–S112.
93. M. Cordova, M. Balodis, B. Simões de Almeida, M. Ceriotti and L. Emsley, Bayesian probabilistic assignment of chemical shifts in organic solids, Sci. Adv., 2021, 7, eabk2341.
94. R. J. Iuliucci, J. D. Hartman and G. J. O. Beran, Do Models beyond Hybrid Density Functionals Increase the Agreement with Experiment for Predicted NMR Chemical Shifts or Electric Field Gradient Tensors in Organic Solids?, J. Phys. Chem. A, 2023, 127, 2846–2858.
95. U. Sternberg, R. Witter, I. Kuprov, J. M. Lamley, A. Oss, J. R. Lewandowski and A. Samoson, ¹H line width dependence on MAS speed in solid state NMR – Comparison of experiment and simulation, J. Magn. Reson., 2018, 291, 32–39.
96. M. Cordova, P. Moutzouri, B. Simões de Almeida, D. Torodii and L. Emsley, Pure Isotropic Proton NMR Spectra in Solids using Deep Learning, Angew. Chem., Int. Ed., 2023, 62, e202216607.

---

Footnote

† Electronic supplementary information (ESI) available: Root-mean-squared deviation (RMSD) definition; images of the building blocks, CSD refcodes, and numerical hydrogen labels for 24 compounds; δ_iso(¹H) RMSD values for 8 different E_cut values when using a two-parameter linear mapping; additional plots of the structure selection process for 23 CSP-generated crystal structures of thymol; Excel spreadsheets containing summaries of all calculated hydrogen magnetic shielding values and linear mapping processes; all DFT input and output files for both CASTEP and QE. See DOI: https://doi.org/10.1039/d4cp04354e

---