Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Direct route of ultrafast charge-pair generation upon below-band-gap excitation in P3HT: effect of external electric field†
Debkumar
Rana‡
 *,
Ayush Kant
Ranga
and
Arnulf
Materny
*,
Ayush Kant
Ranga
and
Arnulf
Materny
 *
*
School of Science, Constructor University, Campus Ring 1, 28759 Bremen, Germany. E-mail: debkumar.rana@mbi-berlin.de; amaterny@constructor.university
First published on 4th February 2025
Abstract
The generation and decay mechanism of polaron pairs (PPs) are relevant for a better understanding of photophysical processes in organic semiconductors such as poly 3-hexylthiophene-2,5-diyl (P3HT). A widely suggested model assumes that ultrafast PP generation occurs mainly from hot-exciton dissociation within <100 fs. In our experiments presented here, we have performed a wavelength-dependent transient pump–probe study to investigate the generation mechanism of the PP states. Interestingly, we have found that a below-band-gap excitation can generate the PP states efficiently even with a very low absorption strength at the pump-laser wavelength. This process has been found in neat P3HT thin film as well as in a P3HT-only diode configuration. In addition, besides the fast PP dynamics, we have also observed longer-lived species, which can tentatively be assigned to delocalized PP states. To gain more information, we have studied the PP dynamics under the influence of a static external field in reverse and forward bias for different excitation fluences. From this, we conclude that the bimolecular annihilation process of delocalized PPs states competes with a recombination process. The external electric field speeds up the rate of the recombination process when the annihilation process is saturated at high fluences.
Introduction
Grasping the mechanisms of charge photogeneration is crucial for the optimized design of new materials aimed at enhancing the power-conversion efficiency of organic thin-film solar cells.1,2 In an organic solar cell, the generation of charge happens in mainly three steps: the formation of bound electron–hole pairs in the form of excitons, the migration of excitons to the interface between electron donor and acceptor materials, and the dissociation of excitons into an interfacial charge-transfer state,3,4 with the hole and electron sitting on the neighboring donor and acceptor molecules. It is well-known that a significant amount of the electron–hole pairs can escape from their coulombic interaction to produce the charges as photocurrent. However, the mechanism of the efficient charge photogeneration remains unclarified. Different charge-photogeneration mechanisms have been proposed, such as “hot-excitons”5–8 or “cold-excitons”9–13 mechanisms, charge delocalization,14,15 high local charge mobility,16 and so forth, some of which lead to contradictory results.Transient absorption (TA) spectroscopy on a femtosecond time scale is a unique tool to investigate the charged species such as excitons and polarons. Poly(3-hexylthiophene-2,5-diyl) (P3HT) is widely explored as a promising donor material especially for solar-cell technology. P3HT has commonly been used as a donor material in the photovoltaic blends with phenyl-C61-butyric-acid methyl ester (PCBM).17–23 The ultrafast generation of photoexcited species in pure P3HT is well known. Excitons, polaron pairs (PPs), and polarons are observed after photoexcitation in P3HT based on their different photoinduced absorption (PA) bands.24–26 Here, the generation and decay mechanisms of the PPs is of great interest. It is well-established that upon the above-band-gap excitation, the hot-exciton dissociation process generates the PPs states within less-than 100 fs.24,26 However, different scenarios are also commonly invoked, like the rapid formation of PPs by exciton dissociation27 or the PP formation from delocalized coherent excitations.28 Recent theoretical work29,30 suggests that strong coherent coupling between electronic and vibrational degrees of freedom, that is, vibronic coupling, may generate the PPs very efficiently, similar to seminal models for polaron motion in solids.31 Antonietta et al.32 reported the origin of PPs from vibronic coupling of P3HT using two-dimensional spectroscopy with sub-20 fs pulses.
The different mechanisms of generating the PPs have been discussed in our earlier work.33,34 In our present work, we focus on the generation and the decay mechanisms of PPs after a below-band-gap excitation. The process of generation of PPs is still unclear when the system is excited with energies below the bandgap. Earlier, it has been reported that the absorption tail extending into the infrared may be due to the (1.35 eV/919 nm) triplet state previously seen in the electroluminescence spectra of polythiophenes.35,36 Although, the direct excitation of triplet states is spin forbidden, the presence of the heavy sulfur atom could provide the necessary spin–orbit coupling weakly allowing this transition. These triplet states might also be responsible for the generation of PPs. For P3HT:PCBM, Parkinson et al.37 have reported that the observation of a low-energy feature in absorption and photoluminescence measurements can lead to the suggestion that low-energy photons may create weakly bound PPs formed between the highest occupied molecular orbital HOMO of the polymer and the lowest unoccupied molecular orbital LUMO of PCBM. Matheson et al.38 and Simon et al.39 have investigated the charge-pair generation in P3HT:PCBM after below-band-gap excitation. Based on these two studies they concluded that interfacial dipoles at the donor/acceptor interface can cause the generation of charge pair states. The generation of PPs after below-band-gap excitation is of great scientific interest as the generation mechanism is very complex. To further investigate this process, we have performed experiments to study the dynamics of PPs arising from a low-energy excitation under varying conditions like different excitation fluences and external electric fields.
An organic solar cell device requires different layers of electrical contacts; the organic semiconducting material is sandwiched between an electron-transport and a hole-transport layer. Due to the potential difference of these asymmetric layers, the device behaves like a diode and exhibits an internal electric field. This internal field has an influence on the PP dynamics as we have demonstrated previously.33,34 Recent studies of the effect of an applied external electric field in P3HT have focused on the exciton and/or charge carrier dynamics using time-resolved photoluminescence spectroscopy.40,41 In order to obtain more information about the generation and decay mechanisms of the PPs generated after low-energy excitation, we further explore the role of external electric fields. In the first part of this manuscript, we discuss the generation and decay mechanism of PPs in a neat P3HT thin film. Later, the focus is going to be on the role of internal and external electric fields applied to a P3HT-only diode. Additionally, we have varied the excitation (pump) fluence to investigate the role of annihilation processes and to exclude the contribution of multi-photon excitations.
Experimental methods
Device fabrication
P3HT (Mw = 34–41k, average regioregularity = 89–94%, poly-dispersity index PDI = 1.5) was purchased from Rieke Metal and dissolved in chlorobenzene. The complete details of the device fabrication have been discussed in our earlier work.33 The solution of P3HT in chlorobenzene is used to prepare the thin film and the device. As substrate for the P3HT thin film a glass plate was utilized. We have fabricated the P3HT device under ambient conditions. The solar cell stack for this device, i.e., electron and hole-transport layers, glass substrate coated with ITO and the P3HT layer, was prepared step by step. The measured thickness of the deposited P3HT layer is 200 nm. As mentioned above, the device fabricated in the solar-cell configuration behaves like a diode due to the asymmetric contacts deposited on the two sides of the P3HT layer, which also result in an internal electric field of 0.8 V. More information on the sample and its properties can be found in the ESI.† The UV-vis absorption spectrum is shown in Fig. S1 (ESI†), the structure of the device in Fig. S2 (ESI†) and the curve resulting from an IV characterization in Fig. S3 (ESI†). In the IV curve, a small amount of current is present in our device also in the dark, which means that P3HT generates charges even in the absence of light. These charges may originate from the distortion of the P3HT side chain itself or the interface between ZnO and P3HT. After the sample preparation, in order to minimize oxygen doping, the fabricated layer-stack sample is immediately stored overnight in a glove box under N2 atmosphere where it is air-bubble-free encapsulated with a top layer consisting of epoxy resin and a glass sheet followed by 3 min curing in an UVA cube. The same process has been followed before and after each optical and electrical measurement. Still, a very low amount of oxygen doping might remain, but we did not find any significant change in our UV-vis absorption spectra or in the I–V characteristics. To see the effect of oxygen doping, one can intentionally dope the P3HT, as for example Herrmann et al.42 have demonstrated. They doped regioregular P3HT films in a FeCl3 solution to increase the level of oxidation-induced P3HT cations and observed changes of the optical absorption due to oxidation, which we do not observe.Femtosecond transient absorption spectroscopy
For the time-resolved TA measurements, we have used visible pump and probe wavelengths. The full-details of the experimental setup can be found elsewhere.33,43,44 In brief, a regenerative amplifier Ti:sapphire-based laser system (CPA 2010, Clark-MXR) producing laser pulses at 1 kHz repetition rate with 775 nm central wavelength, 1 mJ energy per pulse, and 150 fs pulse length was used to pump two optical parametric amplifiers (TOPAS, Light Conversion) in order to generate the pump and probe pulses with tunable wavelengths; the beam cross-sections used for the calculation of the fluences are 1256 and 1017 μm2, respectively. Both pump and probe beams were compressed to less than 120 fs using a set of prism compressors and then made parallel and kept with parallel polarizations for the measurements. A lens with a focal length of 20 cm was used to focus the pump and probe beam into the sample. The probe pulse is detected using a photodiode and the signal is integrated with a box-car amplifier.We have not used a reference beam to observe the stability of the laser beam fluctuation for each time delay since the fluctuation of our laser intensities is very small; it would have been bigger in a white-light experiment. The main beam of the Ti:sapphire laser of wavelength at 775 nm is monitored constantly and its power fluctuation is less than 1%. The optical parametric amplifiers used to generate the pump and probe wavelengths emit intensities with slightly more fluctuations (approx. 5–10%) due to the involvement of non-linear processes. However, these fluctuations could be minimized by averaging accumulating 1000 pulses per second and recording 30 loops. Therefore, the errors due to beam fluctuations were reduced considerably.
Results and discussion
Polaron-pair dynamics in neat P3HT thin film
At first, we considered the PP dynamics in a neat P3HT thin film. In the following, we present the results obtained for different pump and probe wavelengths and for varying pump-laser intensities. | (1) |
As mentioned earlier,33 P3HT shows a photoinduced (transient) absorption at 638 nm due to the PP species. Therefore, we measured the pump–probe dynamics of PPs by probing at 638 nm, using varying pump wavelengths. We started with excitations at 488 and 612 nm. As shown in panels (C) and (D) of Fig. 1, a sharp decrease in the transmission of the 638 nm probe pulse is observed. This is attributed to photoinduced absorption from the instantaneously photo-generated PPs. The signal intensity quickly recovers (indicated by reduced transmission) at positive time delays as most of the absorbing PPs decay. The observed photoinduced absorption decay dynamics consist of a fast and a very slow component. The latter component remains flat within our measurement window, since it is limited to a few hundred picoseconds due to the delay stages used in our experimental setup.
Next, we fixed the probe wavelength at 638 nm and adjusted the pump wavelength to 638 nm as well. Like for the 488 nm/488 nm and 612 nm/612 nm experiments discussed above, we expected a decay of the absorption, suggesting ground state bleach (GSB) dynamics. However, we observed a very strong TA signal, which can be assigned to the PPs (see panel (E) of Fig. 1). Finally, we moved the pump wavelength to 680 nm, where the P3HT absorption is quite low (see Fig. S1 in the ESI†). After excitation, a strong TA signal (see panel (F) of Fig. 1) was observed like for the 638-nm excitation. The probe wavelength is still in resonance with the PP absorption. Obviously, there is an efficient generation of PPs even when the pump laser wavelength is chosen such that the photon energies are less than the bandgap energy of P3HT. This was already observed by other groups,37 but has not yet been well understood. Therefore, we have carried out further investigations in this case.
Intensity-dependent pump–probe measurement. We continued our investigation to obtain more information about the origin of the PP signal when both the pump and probe wavelengths are set to 638 nm. By varying the excitation (pump) fluence from 4 to 36 μJ cm−2, we recorded the TA signal of the neat P3HT thin film, as shown in Fig. 2.
 | ||
| Fig. 2 Differential transient transmission dynamics (ΔT/T) obtained from the neat P3HT thin film at different excitation fluence where pump and probe both were at 638 nm. | ||
The experiments have been carried out starting at very low excitation intensity (4 μJ cm−2) where possible to avoid damages. In the case of the P3HT diode, the signal is very weak at this low pump fluence, as shown in Fig. 5(A). The parallel configuration provided more signal compared to the magic angle configuration. We also had more pump scatter in our transient signal. Considering the signal-to-noise ratio, we decided to continue the measurements in the parallel configuration. In general, the polarization between pump and probe pulses is usually set at magic angle (MA, ∼54.7°), to ensure isotropic signals. The kinetics measured at 638 nm could be different when measuring at the magic angle (different absolute numbers of t1 and t2). However, we were mainly interested in the origin and general behavior of the PP signal after excitation below band gap. Very recently, we also have performed polarization-dependent measurements of the anisotropy of the transient absorption signal, which still must be evaluated carefully and are not included in this work now.
It is very important to mention that we do not observe any thermal or heating effect causing a sample damage with below-band-gap excitation. In all our experiments we have carefully checked whether some permanent damage might occur, which would certainly falsify our results. We therefore have started with a rather small fluence of only 4 μJ cm−2. For all fluences applied for our experiments, we have firstly observed no “loop-to-loop” changes of the transients, and a repetition of the experiments also did not result in a loss of reproducibility. With our experiments, we are also on the “safe side” since the below-band-gap excitation sees a very low absorbance.
The inset shows the intensity of the TA signal at 0 ps, as a function of the pump intensity. We observed a linear increase in signal intensity with increasing excitation fluence. We applied a linear fit (y = a + b × x) to the ΔT/T signal, which is in an excellent agreement with our data. This linear dependence on the pump intensity excludes the possibility of a contribution from non-linear processes like a two-photon absorption, which could result in a PP generation from excited electronic states.
The dynamics shown in Fig. 2 are similar to those observed for PPs arising from above-band-gap excitation of hot excitons. The steep decrease in 638 nm probe pulse transmission is due to photo-induced absorption by instantaneously photo-generated PPs, most of which rapidly decay at positive time delay. The observed overall dynamics are rather well approximated by assuming two decay processes and is found to be well described by a bi-exponential decay fitting function, ΔT/T = Y0 + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/t1) + A1
exp(−t/t1) + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/t2). The fitting parameters Y0 (offset), A1/2 (amplitude), and t1/2 (time constant) are given in Table 1. The decay parameters in Table 1 represent an average value from three TA curves with each curve recorded as an average of 30 loops (statistical errors are given in each case). The observed behavior is reproduced in different experiments on different spots on the thin film. The fitting results of the decay kinetics are shown in Fig. S5 (ESI†).
exp(−t/t2). The fitting parameters Y0 (offset), A1/2 (amplitude), and t1/2 (time constant) are given in Table 1. The decay parameters in Table 1 represent an average value from three TA curves with each curve recorded as an average of 30 loops (statistical errors are given in each case). The observed behavior is reproduced in different experiments on different spots on the thin film. The fitting results of the decay kinetics are shown in Fig. S5 (ESI†).
| Excitation fluence (μJ cm−2) | t 1 (fs) | t 2 (ps) | A 1 (%) | A 2 (%) | Y 0 (%) |
|---|---|---|---|---|---|
| 4 | 613 ± 110 | 19.99 ± 3.6 | 60.51 ± 0.01 | 17.77 ± 0.05 | 21.72 ± 0.01 |
| 12 | 653 ± 90 | 15.49 ± 2.9 | 60.41 ± 0.01 | 21.69 ± 0.01 | 17.90 ± 0.01 |
| 20 | 740 ± 120 | 10.56 ± 1.1 | 59.85 ± 0.02 | 26.59 ± 0.01 | 13.56 ± 0.01 |
| 28 | 793 ± 140 | 14.95 ± 1.2 | 60.45 ± 0.01 | 28.85 ± 0.01 | 10.70 ± 0.01 |
| 36 | 656 ± 92 | 14.36 ± 0.7 | 61.46 ± 0.01 | 28.87 ± 0.01 | 09.67 ± 0.01 |
In our previous study,33 using TA experiments with a pump wavelength of 520 nm and probe wavelength of 638 nm, we observed that the PPs dynamics could be well described by a single exponential decay function with an offset, and the dynamics were independent of excitation intensity. However, in the present study, our analysis indicates that a mono-exponential function is insufficient to fit the decay kinetics – a second time constant is required.
The first time constant t1 represents the PPs dynamics, which remain independent of excitation fluence and are comparable to those observed with 520 nm excitation. We have presented the transient in Fig. S4 (ESI†). In contrast, the second time constant t2 is slower and shows a dependence on excitation intensity. As the excitation fluence increases, the decay rate associated with t2 accelerates within 20 μJ cm−2. At very high fluences (28 and 36 μJ cm−2), t2 starts to increase again and eventually saturates. The amplitude A1 of the PP signal corresponding to the t1 dynamics is bigger than A2 measuring the contribution of the t2 dynamics. A1 remains unchanged when the excitation fluence is varied from 4 to 36 μJ cm−2, however A2 increases; at the same time the constant background Y0 is decreasing.
The second time constant t2 is rather slow compared to t1, which we assign to the PP lifetime based on the observations made for above-band-gap excitation. It is difficult to unambiguously determine which species are contributing to these dynamics. It has been reported earlier that excimers, delocalized polarons (DP2), oxidized cations etc. all contribute to the TA at 638 nm.45,46 However, since the other species except for the DP2 are long lived (>100 ps), t2 can be likely assigned to the dynamics of DP2. The offset, Y0, can be attributed to trap states. As mentioned above, t2 is intensity dependent. Therefore, we propose a bimolecular annihilation process to explain the decay dynamics observed in the fluence range of 4–20 μJ cm−2. The bimolecular annihilation process is intensity dependent as two excitons interact with each other and transfer their energy. The probability for this interaction is proportional to the square of the exciton density. This quadratic dependence arises because the probability of two excitons meeting is related to the number of excitons present. We have used this concept here in case of the delocalized PPs. The decay kinetics can be modelled as described in eqn (2a),
 | (2a) |
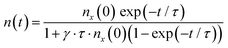 | (2b) |
| Excitation fluence (μJ cm−2) | n x (0) (cm3) | γ (cm3 s−1) | τ (ps) |
|---|---|---|---|
| 4 | 5.06 × 1016 | (1.08 ± 0.21) × 10−6 | 03.91 ± 0.86 |
| 12 | 2.65 × 1017 | (7.20 ± 0.11) × 10−7 | 06.01 ± 0.99 |
| 20 | 9.65 × 1017 | (2.70 ± 0.11) × 10−7 | 11.77 ± 1.20 |
| 28 | 2.02 × 1018 | (1.80 ± 0.11) × 10−7 | 16.08 ± 1.80 |
| 36 | 2.95 × 1018 | (1.80 ± 0.11) × 10−7 | 17.13 ± 1.50 |
The kinetic model of the bimolecular annihilation process fits the dynamics observed at 638 nm very well. We can estimate the excitation density, which is increasing with pump fluence. After 20 μJ cm−2 the annihilation process appears to be saturated. In the saturation regime, the dissociation process is slower. We have plotted the annihilation rate constant with the change of excitation fluence in Fig. S7 (ESI†).
As result from our P3HT thin film studies, we conclude that the generation of PPs in neat P3HT thin films occurs immediately after the pump excitation even with energies below the band-gap energy. The efficient production of PPs may arise from one of the following: (i) electronic states between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of P3HT, (ii) a vibronic coupling state or (iii) trap states within P3HT. In the neat P3HT thin film, we observe two distinct dynamics corresponding to two different species: the PP and the DP2. While the PP dynamics are independent of excitation intensity, the DP2 dynamics show intensity dependence pointing to a bimolecular annihilation process. This was supported by applying a bimolecular annihilation kinetic model, which helped us in understanding the annihilation and dissociation behaviour. Due to the increase in the annihilation rate constant with increasing pump intensity, the DP2 dynamics get faster until a saturation is reached. At the same time, some of the trap states seem to be released to DP2 states, which slows down the dynamics.
Polaron-pair dynamics in P3HT diode
After having investigated the dynamics in neat P3HT films, it is also of great interest to study the PP dynamics in a typical device. For this, we have prepared a P3HT device in a diode-like configuration. The P3HT layer is sandwiched between an electron (ZnO + ITO) and a hole transport layer (PEDOT:PSS + Ag), which also allow to apply an external electric field. Due to the potential difference of the asymmetric contacts, we have a built-in-potential in the diode resulting in a reverse bias of 0.8 V. In our experiment, we have applied an external electric field in reverse and forward bias. In forward bias, the external electric field can compensate the built-in-potential in the diode. First, we present the results from intensity-dependent pump–probe experiments on the P3HT diode without any external electrical field. Then, we show the outcome of our field-dependent studies.Intensity-dependent pump–probe measurement
Fig. 3 shows the PP dynamics of the P3HT diode probed at 638 nm after excitation with 638 nm pump wavelength where the pump fluence is varied from 4 to 36 μJ cm−2. In the inset, a plot of the TA signal at 0 ps as a function of the pump intensity is shown. Like for the neat thin film case, we again found a linear behavior, which excludes the possibility of two photon processes. At a first glance, the decay traces are like those observed for the neat P3HT thin film. However, as mentioned above, the diode has a built-in potential due to the different contacts, which should influence the dynamics. Like for the case of the neat P3HT film, we fit the overall decay dynamics in the P3HT device by applying exponential functions. A close analysis reveals that the PP dynamics in this case are well described by a bi-exponential decay model using a fitting function of the form of ΔT/T = Y0 + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/t1) + A1
exp(−t/t1) + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/t2), where again Y0 is the offset, A1 and A2 are the amplitudes, and t1 and t2 are the decay times characterizing the two exponential decay components. The decay parameters extracted from the fitting are shown in Table 3.
exp(−t/t2), where again Y0 is the offset, A1 and A2 are the amplitudes, and t1 and t2 are the decay times characterizing the two exponential decay components. The decay parameters extracted from the fitting are shown in Table 3.
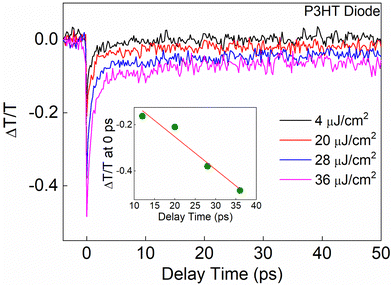 | ||
| Fig. 3 Differential transient transmission dynamics (ΔT/T) obtained from the neat P3HT diode at different excitation fluences where pump and probe both were at 638 nm. | ||
| Excitation fluence (μJ cm−2) | t 1 (fs) | t 2 (ps) | A 1 (%) | A 2 (%) | Y 0 (%) |
|---|---|---|---|---|---|
| 4 | 890 ± 171 | 34.27 ± 1.1 | 50.14 ± 0.01 | 29.85 ± 0.05 | 20.01 ± 0.01 |
| 20 | 751 ± 38 | 27.14 ± 3.1 | 77.14 ± 0.01 | 15.54 ± 0.05 | 07.32 ± 0.01 |
| 28 | 612 ± 67 | 09.91 ± 1.1 | 69.14 ± 0.03 | 20.85 ± 0.02 | 10.01 ± 0.01 |
| 36 | 833 ± 73 | 11.67 ± 0.9 | 68.21 ± 0.01 | 18.76 ± 0.05 | 13.03 ± 0.01 |
Table 3 shows that the first time constant t1, which represents the PP dynamics, seems to remain unchanged (within the error range) for different excitation fluences. However, the second time constant t2 exhibits a clear fluence dependence; the decay rate gets faster with increasing pump intensity. Between 4 and 20 μJ cm−2, the t2 dynamics are slower compared to those observed in the thin film. Interestingly, when the excitation fluence exceeds 20 μJ cm−2, the t2 dynamics become faster than those in the thin film. The differences are due to the internal electric field. Furthermore, at higher fluences, ranging from 28 to 36 μJ cm−2, t2 approaches a constant value. This saturation behavior has also been observed for the thin P3HT film.
While there are similarities between the film and diode decay dynamics, the deviation seems to be field-induced. In the following two sections, the decay dynamics under the influence of external electric fields are studied.
External-field-dependent pump–probe measurement: forward bias
In the above-mentioned diode experiment, for a 0 V external voltage, a non-zero internal field due to the built-in potential of −0.8 V remains active inside the P3HT device. To investigate the possibility of elimination of this field-induced effect, we have operated the P3HT device with an external voltage of 0.8 V in forward bias compensating the built-in potential. Fig. 4 shows the transient-absorption dynamics of the PPs observed under these conditions. Fitting the transients yields similar time constants for t1 and t2 for the different excitation fluences as in the neat-film case; the fitting results are summarized in Table 4. Despite the internal field compensation, the addition of various layers in the device of course influences the dynamics. However, a comparable behavior to the neat P3HT thin film is observed. Moreover, it is evident that the internal field changes the dynamics, which we already have reported earlier.33,34| Excitation fluence (μJ cm−2) | t 1 (fs) | t 2 (ps) | A 1 (%) | A 2 (%) | Y 0 (%) |
|---|---|---|---|---|---|
| 4 | 807 ± 140 | 18.02 ± 3.5 | 39.91 ± 0.01 | 32.85 ± 0.01 | 27.24 ± 0.01 |
| 20 | 749 ± 45 | 10.37 ± 2.8 | 76.16 ± 0.01 | 12.56 ± 0.02 | 11.28 ± 0.01 |
| 28 | 659 ± 140 | 14.30 ± 1.2 | 71.20 ± 0.01 | 18.56 ± 0.01 | 10.24 ± 0.01 |
| 36 | 903 ± 32 | 13.68 ± 0.6 | 65.20 ± 0.01 | 18.29 ± 0.01 | 16.51 ± 0.01 |
External-field-dependent pump–probe measurement: reverse bias
In the experiments presented in the last section, an external field was used to compensate the internal field. In this section, we discuss experiments where an external field in reverse bias is added to increase the internal field. Fig. 5 shows the TA dynamics observed from the P3HT diode after pump pulse excitation with different fluences and with different electric fields in reverse bias externally applied. In the insets of Fig. 5(A)–(D) we plot the ΔT/T signal at 0 ps as a function of the applied electric field.A field-induced quenching depending on the applied reverse bias is evident from the data presented. This is the first and clear evidence of an immediate field-induced dissociation, which occurs immediately after excitation with increasing efficiency for increasing electric field strength. An ultrafast field-induced dissociation of the primary pre-assembled states competes with the direct formation of the PPs and explains the PP absorption reduction at 0 ps. To support this assumption, we have carefully collected the data and repeated the experiments to ensure reproducibility. The field-dependent data are taken on different spots of the P3HT diode and averaged over 30 loops for each measurement. The collected information is an average from multiple scans. While the dynamics are reproducible, due to the inhomogeneity of the material, the absolute absorption values are varying, which might have to do also with reflection losses at the additional layers.
We first highlight the overall field-induced changes in the P3HT PP decay patterns before we discuss a possible physical interpretation later. As mentioned above, during the excitation-fluence-dependent study we found that there are two different regimes (below and above 20 μJ cm−2). This was already observed for the field-free case of the neat P3HT film. However, the t2 dynamics behave differently for the diode. Therefore, below we present the data analysis in two different subsections.
| PF (μJ cm−2) | EEF (V) | Net field (V) | t 1 (fs) | t 2 (ps) | A 1 (%) | A 2 (%) | Y 0 (%) |
|---|---|---|---|---|---|---|---|
| 4 | 0 | −0.8 | 890 ± 171 | 34.27 ± 1.1 | 50.14 ± 0.01 | 29.85 ± 0.05 | 20.01 ± 0.01 |
| −1.0 | −1.8 | 891 ± 130 | 15.24 ± 1.8 | 42.97 ± 0.01 | 29.72 ± 0.01 | 27.31 ± 0.01 | |
| −2.0 | −2.8 | 864 ± 119 | 13.14 ± 2.1 | 46.90 ± 0.02 | 26.65 ± 0.01 | 26.45 ± 0.01 | |
| 20 | 0 | −0.8 | 751 ± 038 | 27.15 ± 3.1 | 77.14 ± 0.01 | 15.54 ± 0.05 | 07.32 ± 0.01 |
| −1.0 | −1.8 | 692 ± 042 | 09.27 ± 2.9 | 75.40 ± 0.01 | 13.22 ± 0.01 | 11.38 ± 0.01 | |
| −2.0 | −2.8 | 769 ± 057 | 07.34 ± 0.7 | 74.37 ± 0.03 | 13.31 ± 0.02 | 12.32 ± 0.01 | |
Without external field (0 V) we only have the built-in-potential and the net electric field is −0.8 V. Similarly, the external electric fields −1 and −2 V represent net electric fields of −1.8 and −2.8 V, respectively. In our earlier study,33 with above-band-gap excitation of hot excitons, we have concluded that the field-induced PP dissociation makes the PP decay faster. Here, in our present study, when the PPs are generated due to below-band-gap excitation, we did not observe any influence of the external electric field on t1, i.e. the PP dynamics. Although there is a mild field induced quenching happening at 0 ps due to the loss of initial population, the PP dynamics remain constant. On the other hand, when we consider the effect of the external electric field on the dynamics of DP2, we have observed that the value of t2 is rather big (slow dynamics) at 0 V, which can be explained by the static polarization effect. Then, with the increment of the external electric field strength in reverse bias the value of t2 becomes smaller (faster dynamics). While the change from 0 to −1 V is drastic, it is almost negligible for the step from −1 to −2 V. This observation is true for both the excitation fluences, 4 and 20 μJ cm−2. The fitted curves for both the excitation fluences are provided in Fig. S8 and S9 (ESI†).
| PF (μJ cm−2) | EEF (V) | Net field (V) | t 1 (fs) | t 2 (ps) | A 1 (%) | A 2 (%) | Y 0 (%) |
|---|---|---|---|---|---|---|---|
| 28 | 0 | −0.8 | 612 ± 67 | 09.91 ± 1.1 | 69.14 ± 0.03 | 20.85 ± 0.02 | 10.01 ± 0.01 |
| −1.0 | −1.8 | 726 ± 87 | 16.62 ± 1.9 | 71.91 ± 0.01 | 18.87 ± 0.01 | 09.22 ± 0.01 | |
| −2.0 | −2.8 | 612 ± 67 | 21.47 ± 1.1 | 68.79 ± 0.03 | 21.10 ± 0.02 | 10.11 ± 0.01 | |
| 36 | 0 | −0.8 | 833 ± 73 | 11.67 ± 0.9 | 68.21 ± 0.01 | 18.76 ± 0.05 | 13.03 ± 0.01 |
| −1.0 | −1.8 | 981 ± 28 | 15.37 ± 0.6 | 66.74 ± 0.01 | 19.05 ± 0.01 | 14.21 ± 0.01 | |
| −2.0 | −2.8 | 912 ± 26 | 18.29 ± 0.7 | 67.34 ± 0.02 | 19.54 ± 0.01 | 13.12 ± 0.01 | |
We have observed that the PP dynamics, represented by t1, remains unchanged despite the increase of the external electric field strength. This behavior is consistent with the observations made at lower excitation fluences or under forward bias conditions. However, the dynamics the DP2 are of particular interest. The fitted curves for both these intensities are provided in Fig. S10 and S11 (ESI†). In our observation, we noticed that, as the external electric field strength increases in reverse bias, slower dynamics (increased t2 time constant) are observed at both 28 and 36 μJ cm−2. While the bi-exponential fitting provides a general view of the processes occurring on these different time scales, the possible mechanisms induced by the external electric field still must be discussed.
Discussion of results obtained for P3HT-only diode
As demonstrated above, the applied external electric field results in two different behaviors for the two regimes of excitation fluences. This raises the question: can the internal and external electric fields influence the bimolecular process? An electric-field effect on the annihilation rate constant has been discussed for polyfluorene by Gadermaier et al.50 for a fixed pump fluence. To investigate this further in P3HT with a broad range of excitation fluence, we have applied eqn (2b) to model the complete data set, which includes various excitation fluences and electric field strengths, to gain deeper insights. We have chosen three representative external electric voltages, −0.8, −1.8, and −2.8 V. Considering the thickness of the P3HT (200 nm), the effective fields are in the MV cm−1. The external electric fields cover a wide range from 4 to 14 MV cm−1. This should sufficiently demonstrate the influence of the fields on the dynamics. Using the annihilation model, we have extracted the dissociation time constants and annihilation rate constants for these different scenarios. Tables S1 and S2 (ESI†) list the time constants with their errors. At higher excitation fluences, the annihilation rate constant (Fig. 6(B)) decreases as the external field increases, indicating a slower annihilation process. However, the dissociation time constant (Fig. 6(D)) continues to increase, suggesting that dissociation is still happening more rapidly, even under stronger external fields. This contrasting behavior highlights the complex effect of the external field on the annihilation and dissociation processes at different fluences. | ||
| Fig. 6 (A) and (B) represent the annihilation rate constants and (C) and (D) the dissociation time constants obtained for the P3HT-only diode for different external applied fields in reverse bias with 0, −1, and −2 V (built-in-potential has to be added) at different excitation fluences. Errors for each point are listed in Tables S1 and S2, ESI†. | ||
When comparing the annihilation process in panel (A), we observed that the annihilation rate constant gets slower with the increase in the excitation fluence (smaller value of annihilation rate constant (γ) means that the annihilation is faster). However, at 4 μJ cm−2, the dissociation time constant in panel (C) is significantly higher than at other fluences. Additionally, the transmittance in the P3HT diode at 4 μJ cm−2 is quite low, which results in comparatively noisy data and affects the reliability of the measurements. The annihilation model works properly only when the time constant can be fixed in a particular range (shown in Fig. S12, ESI†). Therefore, the unusually high dissociation time constant derived from the 4 μJ cm−2 dataset is challenging to explain. Excluding the 4 μJ cm−2 data, the dissociation process becomes slower as the excitation fluence increases, which can be attributed to the more rapid annihilation process occurring at higher fluences. When comparing the annihilation process in panel (B), we have found that the annihilation gets faster with the increase in the excitation fluence. This results in making the dissociation process slower, which is shown in panel (D) with the increase in the excitation fluence from 28 to 36 μJ cm−2. The DP2 dissociation induced by the external electric field is still visible at higher excitation intensities.
Conclusion
We have performed transient absorption (TA) spectroscopy on a neat P3HT thin film and a P3HT-only diode to investigate the origin of the polaron pair (PP) state following a below-band-gap excitation. While previous studies have focused on PP generation from hot excitonic states after above-band-gap excitation, our observations demonstrate that PPs can be very efficiently generated also upon a below-band-gap excitation. We have confirmed that there are no nonlinear multi-photon processes involved as the TA signal exhibits a linear dependence on pump fluence.When P3HT is excited with a 638 nm pump pulse (below-band-gap excitation), both PPs and delocalized polaron states (DP2) are generated. The PP dynamics are independent of the pump excitation intensity, while the DP2 dynamics changes with excitation intensity. We found that DP2 are involved in bimolecular processes, with the annihilation rate constant increasing as the pump fluence rises, reaching saturation at very high fluences.
To explore the effect of electric fields, we have applied varying external fields to the P3HT-only diode. Increasing the internal reverse bias by a variable external field in reverse bias and also compensating it by applying an external field in forward bias resulted in interesting changes of the dynamics. Our aim was to better understand how the electric fields impact the PP and DP2 dynamics, given their inevitable presence in real semiconductor devices. We observed that at lower excitation fluences, the external electric field accelerates the DP2 decay, while at higher intensities, it slows down the process. These findings are crucial for optimizing device performance, as we show that on-band and below-band-gap excitation can help prevent device damage. Since the annihilation process observed serves as a loss channel for charge generation, controlling the balance between excitation fluence and external electric fields offers a way to regulate the charge generation process and enhance device efficiency. These results are of relevance for device applications because they open up a new direction to optimize the charge transport phenomena in organic semiconductor by controlling the excitation of charge pair species.
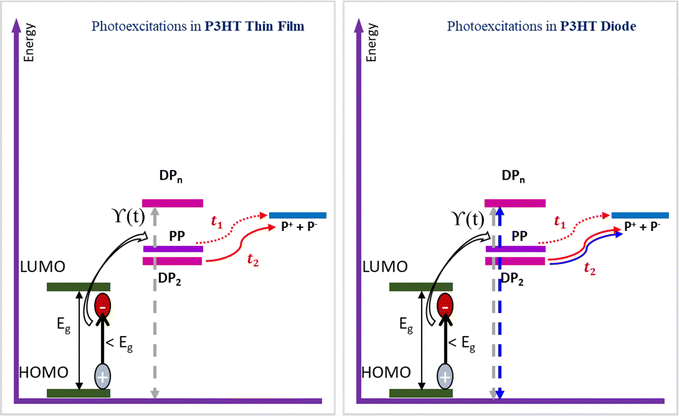
The different processes are summarized in Scheme 1.
Scheme 1 presents the generation and decay mechanism of polaron-pairs after photoexcitation in the P3HT thin film and diode. Based on our study, the polaron pair is generated directly for below band gap (Eg) excitation, which applies to both thin film and diode. We have not only seen the polaron-pair, but also the delocalized polarons after direct photoexcitation. In our earlier work,33,34 we found that the polaron pairs and delocalized polarons decay to localized polarons (presented by the full and dotted red lines and time constants t1 and t2 in the scheme, respectively). The energy levels of the polaron pair, delocalized polaron and localized polaron are included according to the results from our previous studies.33,34 In the diode, we must consider the additional electric field, which is influencing the dissociation and bimolecular annihilation processes. We have indicated the field dependent processes adding blue lines in our scheme.
In summary, we would like to list the important points in the following:
• Our study has shed light onto an interesting charge generation-process. We have focused on PPs, which have been little investigated in the past. Up to now, nearly exclusively dynamics induced by above-band-gap excitation have been studied. In our work, we demonstrated that below-band-gap excitation cannot only also result in PPs, but that this process is even more efficient than that considered up to now. This is interesting since it allows to create devices, which make use of a considerably wider light spectrum for charge generation.
• Below-band-gap excitation seeing only little absorbance at the same time results in less heat generation compared to the excitation at maximum absorption. Thermal stability is very important for organic semiconductors, which makes it even more attractive to also utilize the generation pathways below band gap.
• The addition of external electric fields and the variation of excitation fluence result in some additional information about the involved processes. Further experiments will however be required to better understand what states and what processes contribute.
• Upon below-band-gap excitation, we have seen two decay dynamics in both the P3HT thin film and the P3HT-only diode.
• If we compensate the built-in-potential (−0.8 V) by applying a forward bias to the diode, the observed dynamics in both samples are behaving equally.
• In reverse bias, the diode shows a clearly different behavior compared to the film for the delay times covered by our experiments. Varying the excitation intensity results in different contributing processes; one can distinguish between the low-excitation-fluence and the high-excitation-fluence case. For lower excitation fluences, we see a decrease of t2 assigned to the DP2 dynamics with increasing fluence, which is due to the bimolecular annihilation process becoming more efficient. At the same time, the PP dissociation is getting slower. For high excitation fluences, the annihilation reaches saturation. Depending on the excitation-fluence range, an applied electric field can speed up the dissociation and annihilation processes. This is an interesting result since electric fields might be useful for enhancing the efficiency of light-induced charge generation processes in practical applications.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Prof. Dr Veit Wagner and Dr Vladislav Jovanov (Constructor University) for supporting our work with sample preparation.References
- T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767 CrossRef CAS PubMed.
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Nat. Mater., 2018, 17, 119–128 CrossRef CAS PubMed.
- K. Vandewal, Annu. Rev. Phys. Chem., 2016, 67, 113–133 CrossRef CAS PubMed.
- Y. L. Lin, M. A. Fusella and B. P. Rand, Adv. Energy Mater., 2018, 8, 1702816 CrossRef.
- G. Grancini, M. Maiuri, D. Fazzi, A. Petrozza, H.-J. Egelhaaf, D. Brida, G. Cerullo and G. Lanzani, Nat. Mater., 2013, 12, 29–33 CrossRef CAS.
- Y. Xu, P. Xu, D. Hu and Y. Ma, Chem. Soc. Rev., 2021, 50, 1030–1069 RSC.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. Van Der Poll, G. C. Bazan and R. H. Friend, Science, 2014, 343, 512–516 CrossRef.
- V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- K. Vandewal, S. Albrecht, E. T. Hoke, K. R. Graham, J. Widmer, J. D. Douglas, M. Schubert, W. R. Mateker, J. T. Bloking and G. F. Burkhard, Nat. Mater., 2014, 13, 63–68 CrossRef CAS.
- H. Bässler and A. Köhler, Phys. Chem. Chem. Phys., 2015, 17, 28451–28462 RSC.
- D. Fazzi, M. Barbatti and W. Thiel, J. Phys. Chem. Lett., 2017, 8, 4727–4734 CrossRef CAS PubMed.
- Y. Pan, W. Li, S. Zhang, L. Yao, C. Gu, H. Xu, B. Yang and Y. Ma, Adv. Opt. Mater., 2014, 2, 510–515 CrossRef CAS.
- S. R. Yost and T. Van Voorhis, J. Phys. Chem. C, 2013, 117, 5617–5625 CrossRef CAS.
- B. Bernardo, D. Cheyns, B. Verreet, R. D. Schaller, B. P. Rand and N. C. Giebink, Nat. Commun., 2014, 5, 3245 CrossRef CAS PubMed.
- Y. Tamai, Polym. J., 2020, 52, 691–700 CrossRef CAS.
- D. Veldman, O. Ipek, S. C. Meskers, J. R. Sweelssen, M. M. Koetse, S. C. Veenstra, J. M. Kroon, S. S. van Bavel, J. Loos and R. A. Janssen, J. Am. Chem. Soc., 2008, 130, 7721–7735 CrossRef CAS PubMed.
- I. C. Ghosekar and G. C. Patil, Semicond. Sci. Technol., 2021, 36, 045005 CrossRef CAS.
- M. T. Dang, L. Hirsch and G. Wantz, Adv. Mater., 2011, 23, 3597–3602 CrossRef CAS.
- P. Berger and M. Kim, J. Renewable Sustainable Energy, 2018, 10, 013508 CrossRef.
- D. Rana and A. Materny, Spectrochim. Acta, Part A, 2021, 253, 119565 CrossRef CAS.
- S. Bom, M. Ortel and V. Wagner, Phys. Status Solidi A, 2014, 211, 1634–1639 CrossRef CAS.
- B. Gburek and V. Wagner, Org. Electron., 2010, 11, 814–819 CrossRef CAS.
- T. Z. Khan, P. Donfack, M. Namboodiri, M. M. Kazemi, S. Bom, V. Wagner and A. Materny, J. Phys. Chem. C, 2018, 122, 3454–3462 CrossRef CAS.
- J. Guo, H. Ohkita, H. Benten and S. Ito, J. Am. Chem. Soc., 2009, 131, 16869–16880 CrossRef CAS PubMed.
- X. M. Jiang, R. Österbacka, O. Korovyanko, C. P. An, B. Horovitz, R. A. Janssen and Z. V. Vardeny, Adv. Funct. Mater., 2002, 12, 587–597 CrossRef CAS.
- Y. Ogata, D. Kawaguchi and K. Tanaka, Sci. Rep., 2015, 5, 8436 CrossRef PubMed.
- R. D. Pensack and J. B. Asbury, J. Phys. Chem. Lett., 2010, 1, 2255–2263 CrossRef CAS.
- L. G. Kaake, J. J. Jasieniak, R. C. Bakus, G. C. Welch, D. Moses, G. C. Bazan and A. J. Heeger, J. Am. Chem. Soc., 2012, 134, 19828–19838 CrossRef CAS.
- C. M. Pochas and F. C. Spano, J. Chem. Phys., 2014, 140, 244902 CrossRef PubMed.
- H. Tamura, R. Martinazzo, M. Ruckenbauer and I. Burghardt, J. Chem. Phys., 2012, 137, 22A540 CrossRef.
- T. Holstein, Ann. Phys., 1959, 8, 325–342 CAS.
- A. De Sio, F. Troiani, M. Maiuri, J. Réhault, E. Sommer, J. Lim, S. F. Huelga, M. B. Plenio, C. A. Rozzi and G. Cerullo, Nat. Commun., 2016, 7, 13742 CrossRef CAS.
- D. Rana, P. Donfack, V. Jovanov, V. Wagner and A. Materny, Phys. Chem. Chem. Phys., 2019, 21, 21236–21248 RSC.
- D. Rana and A. Materny, J. Raman Spectrosc., 2023, 54, 1373–1382 CrossRef CAS.
- K. Sakurai, H. Tachibana, N. Shiga, C. Terakura, M. Matsumoto and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 9552 CrossRef CAS.
- P. D. Cunningham and L. M. Hayden, J. Phys. Chem. C, 2008, 112, 7928–7935 CrossRef CAS.
- P. Parkinson, J. Lloyd-Hughes, M. Johnston and L. Herz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 115321 CrossRef.
- A. B. Matheson, S. J. Pearson, A. Ruseckas and I. D. Samuel, J. Phys. Chem. Lett., 2013, 4, 4166–4171 CrossRef CAS.
- S. Sanden, N. M. Wilson, M. Nyman and R. Österbacka, Org. Electron., 2017, 42, 131–140 CrossRef CAS.
- T. Iimori, K. Awasthi, C.-S. Chiou, E. W.-G. Diau and N. Ohta, Phys. Chem. Chem. Phys., 2019, 21, 5695–5704 RSC.
- T. Iimori, K. Awasthi, C.-S. Chiou, E. W.-G. Diau and N. Ohta, ACS Appl. Energy Mater., 2018, 1, 6136–6151 CrossRef CAS.
- D. Herrmann, S. Niesar, C. Scharsich, A. Köhler, M. Stutzmann and E. Riedle, J. Am. Chem. Soc., 2011, 133, 18220–18233 CrossRef CAS.
- S. Ghosh, B. Pradhan, Y. Zhang, D. Rana, D. Naumenko, H. Amenitsch, J. Hofkens and A. Materny, J. Phys. Chem. C, 2021, 125, 7799–7807 CrossRef CAS.
- D. Rana, V. Jovanov, V. Wagner, A. Materny and P. Donfack, RSC Adv., 2020, 10, 42754–42764 RSC.
- R. Osterbacka, C. P. An, X. Jiang and Z. V. Vardeny, Science, 2000, 287, 839–842 CrossRef CAS.
- O. G. Reid, R. D. Pensack, Y. Song, G. D. Scholes and G. Rumbles, Chem. Mater., 2014, 26, 561–575 CrossRef CAS.
- D. Sun, Y. Rao, G. A. Reider, G. Chen, Y. You, L. Brézin, A. R. Harutyunyan and T. F. Heinz, Nano Lett., 2014, 14, 5625–5629 CrossRef CAS PubMed.
- N. Kumar, Q. Cui, F. Ceballos, D. He, Y. Wang and H. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 125427 CrossRef.
- H. Wang, H.-Y. Wang, B.-R. Gao, L. Wang, Z.-Y. Yang, X.-B. Du, Q.-D. Chen, J.-F. Song and H.-B. Sun, Nanoscale, 2011, 3, 2280–2285 RSC.
- C. Gadermaier, F. Grasse, S. Perissinotto, M. Graf, F. Galbrecht, U. Scherf, E. List and G. Lanzani, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045207 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: UV-Vis absorption of P3HT, P3HT-only diode structure, IV characteristics of P3HT-only diode, annihilation rate constant as function of excitation fluence, fitting results for the different observed dynamics, fitting results using annihilation model. See DOI: https://doi.org/10.1039/d4cp04342a |
| ‡ Present address: Max Born Institut für Nichtlineare Optik und Kurzzeitspektroskopie, Max Born Strasse 2A, 12489 Berlin, Germany. |
| This journal is © the Owner Societies 2025 |