Ferroelastic phase transition-modulated electronic transport and photoelectric properties in monolayer 1T′ ZrCl₂

Abstract

Monolayer 1T′ ZrCl₂ exhibits unique ferroelastic behavior with three structurally distinct variants (O1, O2, and O3), demonstrating potential for next-generation nanoelectronic and optoelectronic devices. This study investigates the electronic transport and optoelectronic properties of the O1 and O3 variants, with O3 serving as a representative for both O2 and O3 due to their structural symmetry. First-principles calculations and non-equilibrium Green's function analysis reveal that the O1 variant possesses exceptional electronic properties, including high electron mobility (1.44 × 10⁴ cm² V⁻¹ s⁻¹) and a large current on/off ratio (10⁶), while the O3 variant shows high conductivity in both crystallographic directions. Optoelectronically, the O1 variant demonstrates strong anisotropy with a maximum photocurrent density of 6.57 µA mm⁻², photo responsivity of 0.37 A W⁻¹, and external quantum efficiency of 41.08% along the a direction, outperforming many 2D materials, whereas there is negligible response along the b direction. In contrast, the O3 variant exhibits a more balanced photoresponse with comparable performance in both directions. These findings provide insights into structure–property relationships in ferroelastic 2D materials and pave the way for developing phase transition-based multifunctional devices for applications in information processing, energy conversion, and sensing.

---

1 Introduction

Research on two-dimensional (2D) materials has advanced considerably over the past two decades. These ultra-thin substances exhibit distinctive physical, chemical, and electronic properties compared to their bulk counterparts, thereby laying the foundation for the next generation of nanoelectronic and optoelectronic devices.^1–8 Within this diverse family of materials, transition metal dichalcogenides (TMDs) have attracted significant attention, with group VIB TMDs (e.g., MoS₂, WS₂) featuring layer-dependent direct bandgaps, strong light–matter interactions, and high on/off ratios for electronic and optoelectronic applications,^9–15 while group IVB TMDs (e.g., ZrS₂, ZrSe₂) exhibit exceptional carrier mobilities exceeding 2 × 10³ cm² V⁻¹ s⁻¹,¹⁶ and their nitrogen-based analogues (e.g., Zr₂N₃H) show promise for visible-light photocatalysis.¹⁷ 2D metal halides such as CuI and BiI₃ demonstrate unique properties including high photosensitivity and tunable bandgaps.^18–21 Halide-based materials have further emerged as a pivotal platform for studying magnetism at the atomic scale, exemplified by CrI₃ as the first reported 2D ferromagnet with strong perpendicular magnetic anisotropy and CrBr₃ with similar properties but lower Curie temperatures.²² Recent computational studies have further expanded this family by discovering promising halide-based materials including MeX₂/MeXY transition metal halides (e.g., CdI₂, ZnClI) for efficient photocatalysis and ternary alkaline-earth metal chlorides (e.g., CaSn₂Cl₆, CaPb₂Cl₆) as potential p-type transparent conductors, enriching the toolbox for fundamental physics exploration and device engineering at the atomic scale.^23,24

In recent years, the discovery of ferroic orders in 2D materials has opened up new avenues for next-generation multifunctional nanoelectronic and optoelectronic device applications.^25–27 One such class of materials that has emerged as a promising candidate is 2D ferroelastic materials, characterized by the presence of two or more orientation states that can be switched by applied mechanical stress. This phenomenon has been observed in several 2D materials, including 1T′-TMDs (MX₂, where X = S, Se, Te and M = Mo, W, Re),²⁸ phosphorene and its analogs (GeS, GeSe, SnS, SnSe),^29,30 honeycomb monolayers (graphene, BN, stanene),³¹ silver(II) fluoride (AgF₂),³² chromium dihalide (CrI₂),³³ β′-In₂Se₃,³⁴ and 2D perovskites (2L or thicker).³⁵ Their unique mechanical switching capability offers an additional degree of freedom for device engineering and functionality, making them promising candidates for future applications.

Recently, monolayer ZrCl₂ in its ground-state 1T′ phase has emerged as a novel 2D ferroelastic material, exhibiting an unprecedented 120° lattice rotation ferroelasticity.³⁶ This unique structural characteristic gives rise to three distinct ferroelastic variants (O1, O2, and O3), which fundamentally differ from the conventional 90° orthogonal transitions commonly observed in traditional ferroelastic systems.³⁶ The coupling between this distinctive ferroelastic behavior and the material's predicted anisotropic electrical and optical absorption properties opens up intriguing possibilities for property control through ferroelastic switching. The structural asymmetry-driven ferroelastic transitions can potentially enable tunable electrical states and controllable optical responses, making monolayer ZrCl₂ particularly promising for diverse applications, including programmable electronic devices, directional photodetectors, and other multifunctional instruments.^{28,34,37–43} However, while these initial findings are promising, a fundamental gap remains in our understanding of the collective influence of ferroelasticity and structural anisotropy on electronic transport and photocurrent characteristics.

To address the current research gap and unlock the potential of ZrCl₂ in programmable nanoelectronic and optoelectronic devices, we present a comprehensive investigation of monolayer 1T′ phase ZrCl₂, focusing on its carrier mobility, electronic transport properties, and photocurrent characteristics. Because O2 and O3 are rotated 120° relative to O1 and are mirror-symmetric to each other, our study focuses predominantly on the O1 variant, employing the O3 variant as a comparative reference to encompass all three variants effectively. Utilizing first-principles calculations and non-equilibrium Green's function theory, we aim to quantify the carrier mobility and electronic transport properties, characterize optoelectronic properties, and investigate the impact of ferroelastic phase transitions on these properties for both variants. By conducting this comprehensive study, we expect to bridge the gap between fundamental material science and practical device applications, potentially opening new avenues for programmable and adaptive nanoelectronic and optoelectronic technologies in fields such as information processing, energy conversion, and sensing.

2 Computational details

2.1 Calculational methods for the geometric and electronic structures of monolayer ZrCl₂

The geometric optimization and electronic properties of the monolayer ZrCl₂ were calculated using the QuantumATK (S-2021.06)⁴⁴ software based on density functional theory (DFT).⁴⁵ The Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA) and the linear combination of atomic orbitals (LCAO) methods were employed,⁴⁶ with the all-electron potential replaced by the PseuDodojo pseudopotentials⁴⁷ and a medium numerical basis for the wave function expansion. The real space density grid was truncated at 55 hartree, and a k-point grid density of 14 × 8 × 1 was utilized to sample the first Brillouin zone of ZrCl₂. Structural optimization convergence was achieved when the maximum force on each atom fell below 0.01 eV Å⁻¹. A vacuum spacing of 19 Å was implemented to prevent interlayer interactions. To comprehensively evaluate the electronic properties, calculations were performed both with and without spin–orbit coupling (SOC) effects. Since the SOC effects were found to be negligible on the electronic structure, subsequent calculations were conducted without SOC to optimize computational efficiency. For more precise bandgap results, the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional was employed.⁴⁸ Stability assessment of monolayer ZrCl₂ involved phonon spectrum calculations using an 11 × 9 × 1 supercell and ab initio molecular dynamics simulations with a 5 × 3 × 1 supercell. Molecular dynamics simulations were performed at 300 K using the NVT Nose–Hoover thermostat^49,50 with a thermostat time scale of 100 fs and a time step of 1 fs.

2.2 Calculational method of carrier mobility

The carrier mobility (μ) of 2D materials is evaluated using a modified formula within the framework of deformation potential (DP) theory.⁵¹ This model considers the anisotropy of the deformation potential, elastic constants, and effective mass, allowing for a more comprehensive description of the material's anisotropy. The formula for determining the carrier mobility of 2D materials is as follows:where k_B is Boltzmann's constant, T is the room temperature. 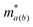C_a(b), E_1a(b) and corresponds to the elastic constant, deformation potential and effective mass in a and b directions, respectively. The two-dimensional elastic modulus C_a(b) was directly computed using the QuantumATK software. By linearly fitting the conduction band minimum (CBM) and valence band maximum (VBM) as a function of strain, we obtained E_1a(b). The effective mass at the CBM and VBM was calculated using the finite-difference (FD) representation of the E(k) derivative. This method was chosen for its superior accuracy compared to simple parabolic band fitting, especially for complex band structures.

2.3 Calculational method of I–V characteristics curve

The carrier transport was calculated by combining nonequilibrium Green's function (NEGF) and DFT methods.^52,53 Again, the PBE functional with LCAO methods and PseuDodojo pseudopotentials were employed for calculating carrier transport. The I–V characteristic curve calculations involved setting the Brillouin zone to 94 × 5 × 1 k-meshes and 8 × 151 × 1 k-meshes along the a and b directions, respectively. The I–V characteristics of the two-probe systems were then derived using the Landauer–Büttiker formalism:⁵⁴V_bias represents the bias voltage (eV_bias = ε_R − ε_L) applied at both ends of the two electrodes, T represents the carrier transport coefficient, f_L(E,ε_L) and f_R(E,ε_R) correspond to the Fermi Dirac distribution of the left and right electrodes, respectively.

2.4 Calculational method of photocurrent

Calculation of the photocurrent density J_ph involved integrating the NEGF methodology within the first-order perturbation theory framework, based on the first Born approximation.^55,56 The perturbation resulting from electron–light interaction is defined by a Hamiltonian, represented as:where Ĥ₀ is the Hamiltonian of the two-probe system, e represents the electron charge, m₀ is the free electron mass, p̂ denotes the momentum operator, and A is the electromagnetic vector potential. Transmission coefficients were calculated as:⁵⁷where G^<_ph and G^>_ph are the lesser and greater Keldysh Green's functions, respectively, while Γ_α and f_α correspond to the line width function and the Fermi distribution for the α (left or right) electrode. The J_ph is given by:⁵⁸

In addition, the functional, basis, pseudopotentials and k-meshes used in photocurrent calculations are consistent with those employed in carrier transport simulations.

3 Results and discussion

3.1 Structural and electronic properties of ZrCl₂

The monolayer O1 variant of 1T′ phase ZrCl₂, with a space group of P2₁/m, was obtained from the corresponding bulk (space group no. 31, Pmn2₁). We confirmed the phonon spectrum and molecular dynamics stability of the O1 variant (see Fig. S1, ESI†), in line with prior research.^36,59 Previous theoretical studies also supported its formation energy and mechanical stability.^36,59 The optimized cell, as shown in Fig. 1, exhibits lattice parameters of a = 3.33 Å and b = 6.23 Å, containing two Zr atoms and four Cl atoms. The bond lengths formed by Zr-1 and Cl-1 (2) atoms are 2.62 Å, and by Zr-2 and Cl-3 (4) atoms are 2.66 Å and 2.73 Å, respectively. These values are consistent with previous theoretical calculations.^36,59 The bond angles formed by Cl-2 and Zr-1 (2) atoms is 70.09°, and by Zr-2 and Cl-3 (4) atoms is 81.43°. These values closely match those obtained from the MatHub-2d database, which are 70.37° and 81.29°, respectively.⁶⁰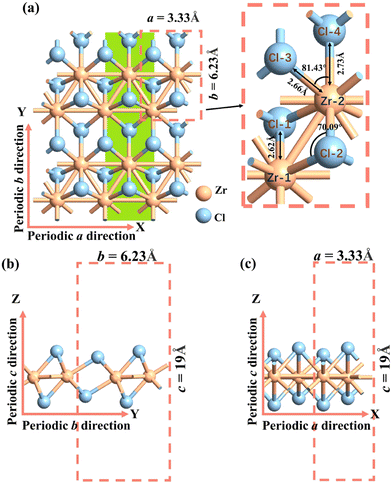

Fig. 1 Atomic structure of (a) top view, (b) and (c) side view of the O1 variants. a and b are the lattice constants of the 2D plane, and c is the lattice constant in the vacuum layer direction. In order to better illustrate how the O2 and O3 variants are obtained by rotating the O1 variant by 120° (Section 3.2.3, Fig. 5), we have highlighted the armchair Zr–Cl chain in green.

Monolayer O1 variant of ZrCl₂ exhibits a quasi-direct bandgap of 0.60/1.15 eV (PBE/HSE06) with a tiny difference between the direct and indirect bandgaps (E_direct − E_indirect = 6 meV), where both the VBM and the CBM lie between the Γ and X points as shown in Fig. 2(a) and (b). These computational results agree with previous research data.^36,59–61Fig. 2(c) illustrates the impact of spin–orbit coupling (SOC) on the band structure, revealing a minimal bandgap adjustment of 0.001 eV, while the general band structure remains largely unchanged. Hence, SOC effects are not considered in our subsequent research.⁶²

Fig. 2 The band structure of the O1 variant was calculated using the (a) PBE functional and (b) HSE06 functional, (c) PBE method considering the SOC effect, and (d) angular dependence of effective mass m* for holes and electrons. The inset in (a) shows the Brillouin zone.

3.2 Electronic transport properties

3.2.1 Anisotropic effective mass. Fig. 2(d) and Table 1 reveal significant anisotropy in the carrier's effective mass m* in the monolayer O1 variant of ZrCl₂ along the a and b directions. For electrons, the effective mass in the b direction is approximately twenty times higher than in the a direction, indicating a strong directional dependence. Conversely, for holes, the effective mass in the b direction is only 1.7 times higher than in the a direction. Comparing carrier types, in the a direction, is three times that of electrons, while in the b direction, this relationship inverts, with being about four times that of holes. The effective mass of electrons in the a direction is smaller compared to several other 2D materials, such as MoS₂ (0.47 m₀),⁶³ MoSe₂ (0.55 m₀),⁶³ As₂S₃ (1.70 m₀),⁶⁴ Zn₂VN₃ (2.15 m₀),⁶⁵ WS₂ (0.31 m₀),⁶³ WSe₂ (0.34 m₀),⁶³ VP (1.44 m₀),⁶⁶ GeAs₂ (0.27 m₀),⁶⁷ SiAs₂ (0.42 m₀).⁶⁸

Table 1 At 300 K, the effective mass m*, deformation potential E_l, elastic constant C_2D, and carrier mobility µ in a and b directions

Carrier	m* (m0)	E l (eV)	C 2D (N m^−1)	µ (cm^2 V^−1 s^−1)
e(a)	0.247	−0.262	82.83	1.44 × 10^4
e(b)	5.112	1.622	66.76	0.26 × 10^3
h(a)	0.726	3.014	82.83	0.48 × 10^3
h(b)	1.299	0.646	66.76	0.46 × 10^3

---

3.2.2 Anisotropic carrier mobility. Using eqn (1) and (2) to calculate the carrier mobility µ of the monolayer O1 variant of ZrCl₂, in which the E_l fitting is shown in Fig. S2 (ESI†). As shown in Table 1, the results reveal two significant characteristics: high µ and pronounced anisotropy along the a and b directions. In the a direction, the hole mobility is 0.48 × 10³ cm² V⁻¹ s⁻¹, while the electron mobility reaches 1.44 × 10⁴ cm² V⁻¹ s⁻¹, 30 times that of the hole mobility. In the b direction, the electron mobility decreases to 0.26 × 10³ cm² V⁻¹ s⁻¹, while the hole mobility is 0.46 × 10³ cm² V⁻¹ s⁻¹, nearly twice that of the electron mobility. Based on our first-principles calculations, we analyzed the spatial distribution of wavefunctions at CBM and VBM (see Fig. S3, ESI†) to understand the anisotropic transport behavior. Along the a direction (zigzag-like direction), the CBM wavefunction exhibits a delocalized nature, facilitating electron transport. In contrast, the VBM wavefunction shows strong localization in this direction, which significantly restricts hole movement. This distinct difference in wavefunction distribution directly accounts for the much higher electron mobility (1.44 × 10⁴ cm² V⁻¹ s⁻¹) compared to hole mobility (0.48 × 10³ cm² V⁻¹ s⁻¹) along this direction. This correlation between wavefunction distribution and carrier mobility has been well documented in similar 2D materials.^64,65 Along the b direction (armchair-like direction), although both CBM and VBM wavefunctions exhibit localized characteristics, their effective masses differ considerably: the electron effective mass (5.112 m₀) is notably larger than that of holes (1.299 m₀) in this direction, resulting in higher hole mobility (0.46 × 10³ cm² V⁻¹ s⁻¹) compared to electron mobility (0.26 × 10³ cm² V⁻¹ s⁻¹). The high carrier mobility of monolayer O1 variant of ZrCl₂, particularly its electron mobility of 1.44 × 10⁴ cm² V⁻¹ s⁻¹, surpasses that of various 2D materials, including MgZrN₂ (0.61 × 10³ cm² V⁻¹ s⁻¹),⁶⁹ SiAs (1.25 × 10³ cm² V⁻¹ s⁻¹),⁷⁰ GeAs (2.38 × 10³ cm² V⁻¹ s⁻¹),⁷⁰ Si₉C₁₅ (0.71 × 10³ cm² V⁻¹ s⁻¹),⁷¹ B₂N (1.01 × 10⁴ cm² V⁻¹ s⁻¹),⁷² and ZnPSe₃ (0.52 × 10³ cm² V⁻¹ s⁻¹).⁷³ The hole mobility, at 0.48 × 10³ cm² V⁻¹ s⁻¹, also exceeds that of several 2D materials, such as Si₉C₁₅ (0.43 × 10³ cm² V⁻¹ s⁻¹),⁷¹ CdPSe₃ (0.44 × 10³ cm² V⁻¹ s⁻¹),⁷³ ZnPSe₃ (0.41 × 10³ cm² V⁻¹ s⁻¹),⁷³ GeS (0.15 × 10³ cm² V⁻¹ s⁻¹),⁷⁴ and GeSe (0.51 × 10² cm² V⁻¹ s⁻¹).⁷⁴ This high µ suggests potential improvements in various electronic devices. For instance, it could enable the development of high-speed transistors with improved switching rates and reduced power consumption. In the context of optoelectronic devices, high µ could contribute to faster photodetectors with improved response times, which is crucial for applications requiring rapid light sensing or high-frequency optical communications. Moreover, the distinct anisotropic µ of the monolayer O1 variant of ZrCl₂ opens up unique application possibilities. It can serve as a versatile channel material in field-effect transistors (FETs),⁷⁵ capable of both n-type and p-type functionalities depending on the crystal orientation. Furthermore, this anisotropy shows promise for directional sensors with enhanced sensitivity and optoelectronic devices enabling polarized emission, potentially contributing to high-contrast displays and secure communication systems.

3.2.3 I–V characteristic curves. Given that electron mobility exceeds hole mobility in the a direction, while the opposite is true in the b direction, we constructed two-probe models to investigate transport properties along both crystallographic orientations. As illustrated in Fig. 3, these models consist of a 50 Å long ZrCl₂ channel with electrodes of the same material at both ends: heavily n-doped ZrCl₂ for electron transport studies and heavily p-doped ZrCl₂ for hole transport analyses. To optimize carrier transport and minimize electrode-induced effects, we precisely tailored the Fermi level of the ZrCl₂ electrodes. For electron transport along the a direction, the Fermi level was positioned 0.15 eV above CBM. Conversely, for hole transport along the b direction, it was set at 0.15 eV below VBM. This strategic adjustment resulted in comparable doping concentrations for both carrier types, with electron and hole densities in their respective transport directions reaching approximately 10¹⁴ cm⁻².

Fig. 3 Schematic diagrams of the two-probe system for computing the electric transport of monolayer O1 variant of ZrCl₂ in (a) the a direction and (b) the b direction. The channel length is 50 Å.

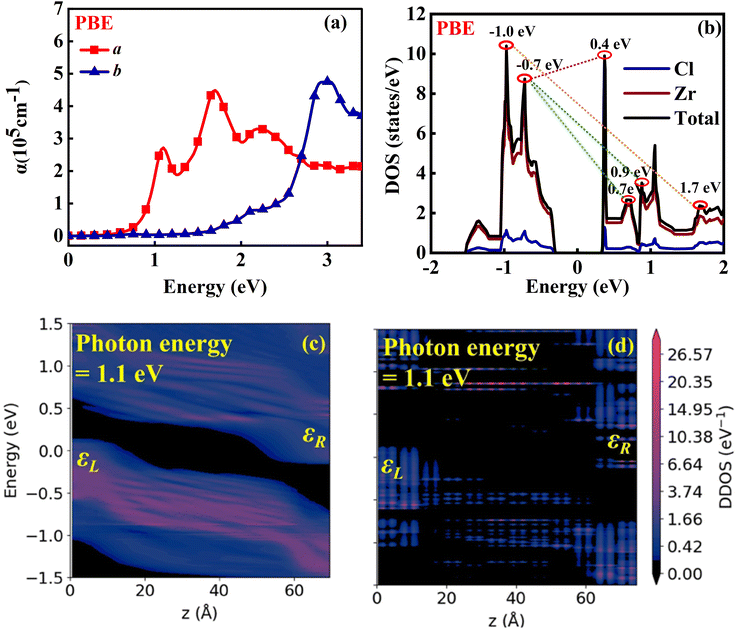
Fig. 4(a) displays the I–V curves in the a and b directions, indicating a noticeable anisotropy. The current in the a direction rises as the bias voltage increases, resulting in a conductive state; conversely, the current in the b direction remains in the off state. The maximum current on/off ratio occurs at −0.4 V, reaching 10⁶, which is comparable to or even better than those reported for other 2D materials or molecular devices, such as GeC₂ (10⁵),⁷⁶ GaPS (10⁵),⁷⁷ borophosphene (10⁵),⁷⁸ cyclo[18]carbon (10⁴).⁷⁹

Fig. 4 (a) The I–V characteristic curves of the O1 variants in the a direction and b direction, the inset is an enlarged view along the b direction at −0.4 V bias voltage. (b) Along the a direction and (c) b direction, the device of the density of states (DDOS) for the two-probe configuration of the O1 variant under −0.4 V bias.

To further explain the phenomenon of the maximum current on/off ratio observed at a bias of −0.4 V, we calculated the DDOS along the a and b directions under this bias. As shown in Fig. 4(b) and (c), the effective barrier height in the a direction ϕ_a is 0.21 eV, while in the b direction ϕ_b is 0.39 eV. This significant difference in barrier height directly influences carrier transport properties. The lower barrier in the a direction means that carriers more easily overcome the barrier in the a direction, leading to an “on” state in the a direction and an “off” state in the b direction. Further analysis of the DDOS distribution shows that the a direction exhibits a higher and more uniformly distributed density of states, which facilitates continuous electron transport and likely results in higher conductivity. In contrast, the uneven DDOS distribution in the b direction may increase carrier scattering, thereby reducing conductivity. These mechanisms account for the observed current maximum on/off ratio.

The monolayer 1T′ phase of ZrCl₂ under investigation is both its ground state and ferroelastic phase.³⁶ The formation of a ferroelastic phase typically arises from a reduction in the symmetry of the prototype structure, leading to a structural phase transition. This low-symmetry ferroelastic phase is characterized by multiple orientation states, manifesting as different spontaneous strains relative to the unit cell of the prototype phase. Specifically, the 1T′ phase of monolayer ZrCl₂ exhibits three energy-degenerate but structurally inequivalent variants O1, O2, and O3. These variants emerge from a Peierls distortion induced by the Fermi surface nesting in the prototype 1T structure, resulting in distorted octahedral coordination. This distortion causes spontaneous dimerization of Zr atoms along high-symmetry [100], [010], or [110] directions, thereby enabling a 2D three-state ferroelasticity. Fig. 5 depicts the O1, O2, and O3 variants of monolayer 1T′ phase ZrCl₂. The O1 variant displays intrinsic ferroelasticity, featuring an unusual 120° rotational transformation. It can convert to the O2 or O3 variants by overcoming a moderate energy barrier of 24–39 meV per atom. Notably, the O2 and O3 variants display mirror symmetry with respect to the Y-axis, highlighting the structural relationships among these ferroelastic states.^28,36 Given this symmetry and considering our device configuration, O2 and O3 are expected to produce equal but oppositely directed electric current (photocurrent). By analyzing O3 in detail, we not only gain direct insights into its behavior but can also infer the corresponding characteristics of O2 through simple directional inversion, enabling a comprehensive understanding of the entire system.

Fig. 5 The top views of the O1, O2, and O3 variants, respectively. The green, red, and purple highlighted portions represent the Zr–Cl chains of the O1, O2, and O3 variants. The illustration in the top right provides a simplified diagram of the 120° rotational relationship between the O1, O2, and O3 variants, as well as the Y-axis mirror symmetry between O2 and O3.

We further calculated the electron and hole transport properties of the O3 variant along the a and b directions. As shown in Fig. 6(a), in the voltage range of −0.4 V to 0.4 V, both directions exhibit high current values, peaking at approximately 500–600 nA, far exceeding the range observed in the O1 variant (80 nA). This indicates that the O3 variant demonstrates excellent conductivity for both electron and hole transport, with no distinct switching behavior. To better understand this phenomenon, we calculated the DDOS in both directions under −0.4 V bias, as shown in Fig. 6(b) and (c). The analysis reveals that the effective barrier height in the a direction ϕ_a is 0.05 eV, and in the b direction ϕ_b is 0.06 eV. The barrier heights are similar in both directions and significantly lower than those in the O1 variant, facilitating efficient carrier injection and transport. From the perspective of structural symmetry, the one-dimensional arrangement of Zr–Cl chains in the O1 variant leads to pronounced structural differences between the chain direction and the direction perpendicular to the chains, resulting in strong anisotropy in electrical transport. The O3 variant, with its 120° rotated Zr–Cl chains, forms a more uniform structure. In this configuration, Zr atoms are arranged into a hexagonal network, with Cl atoms symmetrically distributed around them. This structural homogeneity reduces directional anisotropy, yielding similar electron and hole transport properties along the a and b directions, respectively.

Fig. 6 (a) The I–V characteristic curves of the O3 variant along the a and b directions. (b) Along the a direction and (c) b direction, DDOS for the two-probe configuration of the O3 variant under −0.4 V bias.

The distinct electronic transport characteristics of the O1 and O3 variants open up exciting possibilities for designing versatile and high-performance nanoelectronic devices.^37,42 The O1 variant, with its high current on/off ratio (10⁶) and strong anisotropic conductivity, shows great potential for high-performance FETs, logic gates, and memory devices where precise current control and switching capabilities are crucial. Its anisotropic nature could also be exploited in the development of direction-sensitive sensors or in creating novel electronic circuits with directional conductivity. On the other hand, the O3 variant's high and nearly isotropic conductivity in both directions makes it an excellent candidate for applications requiring uniform current flow, such as transparent electrodes, interconnects in integrated circuits, or as channels in high-performance bipolar transistors. Its lack of distinct switching behavior could be advantageous in applications where consistent conductivity is needed across varying electric fields.

3.3 Photocurrent transport properties

To comprehensively understand the material's capabilities, we extended our investigation with a particular focus on the photocurrent characteristics of the monolayer O1 variant of ZrCl₂ in a practical device context. For this purpose, we designed and constructed a two-probe model of a ZrCl₂ photovoltaic p–i–n junction, as illustrated in Fig. 7. This structure consists of a p-doped region, an intrinsic (i) region, and an n-doped region. The central i region has a length of 50 Å. Both p and n regions have doping concentrations of 10¹⁴ cm⁻². At the heart of this device, the i region serves as the primary area for polarized light absorption, effectively capturing incident photons. The built-in electric field between the p and n regions spans the entire i region, promoting the separation of photogenerated electron–hole pairs. Subsequently, these separated electrons and holes move towards the n and p regions, respectively, generating a measurable photocurrent. This design utilizes the photovoltaic effect to achieve high-performance self-powered photodetection, providing an ideal platform for studying the complete physical process from photon absorption to charge separation and transport in ZrCl₂.

Fig. 7 The p–i–n junction diagram of the monolayer O1 variant of ZrCl₂ in (a) the a direction and (b) the b direction, θ is the polarization angle of linearly polarized light. e⃑ is the polarization vector of linearly polarized light.

The presence of heavily doped regions in our p–i–n structure significantly influences the choice of computational method for photocurrent calculations. While the GW method is known for its accuracy in predicting band gaps, it becomes less suitable for heavily doped 2D semiconductors as the GW band gap narrows due to enhanced screening of many-body effects. In such scenarios, DFT based on single-electron approximation, particularly the PBE functional, becomes more appropriate. Although PBE generally underestimates band gaps, heavy doping brings the effective band gap closer to PBE predicted values, making it a computationally efficient choice without significant loss of accuracy.^80,81 This approach is supported by previous studies, which have shown that GGA methods yield photocurrent results for 2D materials like MoS₂, WSe₂, and BP that are in high agreement with experimental data.^82–85 Considering these factors, we employed the PBE method for our photocurrent calculations, expecting it to provide reliable results for our heavily doped ZrCl₂ p–i–n structure while avoiding the computational intensity and potential inaccuracies of GW methods in this specific context (details in the ESI†).

Photocurrent density J_ph is a key performance metric in optoelectronic devices, representing the photocurrent generated per unit area under illumination. It directly reflects a material's light absorption and photoelectric conversion capabilities. To comprehensively evaluate device efficiency, photo responsivity R_ph and external quantum efficiency EQE are also crucial. These metrics are defined as:⁸⁶

where E is the photon energy, I_ω is the photon flux, h is Planck's constant, c is the speed of light, e is the electron charge, and λ is the wavelength.

R _ph (measured in A W⁻¹) quantifies the current output relative to incident light power, directly indicating the device's light-to-current conversion efficiency. EQE, a dimensionless ratio of generated electrons to incident photons, provides insight into the quantum efficiency of photoelectric conversion across different wavelengths. While R_ph offers a straightforward measure of device sensitivity, EQE accounts for photon energy, making it valuable for spectral performance analysis. Together, these metrics provide a comprehensive assessment of optoelectronic device performance.

Initially, we analyzed the J_ph generated under incident light with an in-plane θ of 0°. As depicted in Fig. 8(a), the O1 variant exhibits pronounced anisotropy in the J_ph along the a and b directions. In the a direction, the J_ph reaches two distinct peaks: 6.57 µA mm⁻² at a photon energy of 1.1 eV and 5.90 µA mm⁻² in the 1.5–1.6 eV range, which is even better than that of other 2D materials. For example NaCuTe (1.68 µA mm⁻²),⁸⁷ NaCuSe (0.65 µA mm⁻²),⁸⁷ NaCuS (0.66 µA mm⁻²),⁸⁷ and InSe (0.018 µA mm⁻²).⁸⁸ Additionally, a noticeable upward trend in J_ph is observed in the energy range of 2.8–3.0 eV. In contrast, the J_ph along the b direction is generally lower, with only a minor peak of 0.39 µA mm⁻² at a photon energy of 2.7 eV. Notably, these peaks coincide with the absorption peak of the material (Fig. 9(a)).

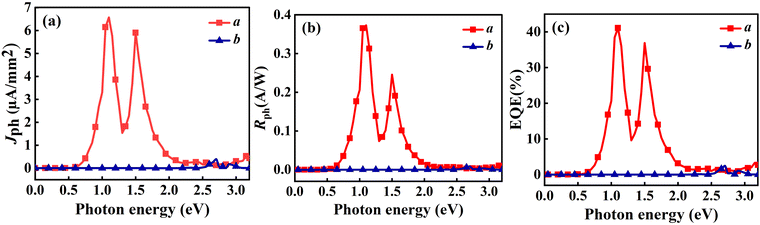Fig. 8 Linearly polarized light with θ of 0° incident on the O1 variant, showing (a) J_ph, (b) R_ph, and (c) EQE as functions of photon energy.

Fig. 9 (a) The optical absorption coefficient and (b) density of states (DOS) of the O1 variant calculated using the PBE methods. (c) Along the a direction and (d) b direction, DDOS for the two-probe configuration of the O1 variant under photon energy 1.1 eV.

To further understand the origin of the J_ph peaks, we calculated and analyzed the DOS for the O1 variant. According to Fermi's golden rule, the probability of electron transitions from the valence band to the conduction band is proportional to the DOS. Therefore, electron transitions between energy levels at DOS peaks are more likely, resulting in stronger photocurrent. By comparing the DOS (Fig. 9(b)) with the J_ph spectrum, we can elucidate the key photocurrent features along the a direction. The primary photocurrent peak around 1.1 eV is attributed to electron transitions from near the valence band (approximately −0.7 eV) to the CBM (around 0.4 eV), corresponding to the high DOS at these energy levels. The secondary peak around 1.5 eV likely results from transitions between states near the VBM (around −0.7 eV) and those slightly above the CBM (0.7–0.9 eV), aligning with the DOS distribution that shows an energy difference of approximately 1.4–1.6 eV. The photocurrent rise observed around 3.0 eV may correspond to electron transitions from the deeper valence band (around −1.0 eV) to higher energy states in the conduction band (around 2.0 eV). Although the DOS around 2.0 eV is relatively low, the energy alignment still facilitates a measurable photocurrent.

The pronounced anisotropy in J_ph can be explained by the band structure, partial charge density, and DDOS. As shown in Fig. 2(a), both the CBM and VBM are located along the Γ–X path, i.e., in the a direction. This band structure significantly enhances the probability of photon-induced electron–hole pair separation along the a direction compared to the b direction. The partial charge density analysis further confirms that electrons are primarily distributed along the a direction (see Fig. S4, ESI†). This allows the excited electrons to more easily transport in this direction, resulting in a much higher J_ph along the a direction than the b direction. Notably, under 1.1 eV photon illumination, the J_ph along the a direction is 10⁶ times greater than that along the b direction. Fig. 9(c) and (d) depicts the DDOS for the a and b directions under 1.1 eV photon energy, revealing a higher and more continuously distributed electron density along the a direction compared to the b direction, which elucidates the observed anisotropy in J_ph.

Fig. 8(b) and (c) illustrate the variation of R_ph and EQE with photon energy for the O1 variant along the a and b directions. Along the a direction, R_ph reaches peaks of 0.37 A W⁻¹ at 1.1 eV and 0.25 A W⁻¹ at 1.5 eV, respectively, significantly surpassing the maximum value of 0.009 A W⁻¹ observed in the b direction. Notably, the R_ph of ZrCl₂ along the a direction outperforms several reported 2D materials, including MoS₂ (0.016 A W⁻¹),⁸⁹ InS (0.13 A W⁻¹),⁸⁸ InSe (0.18 A W⁻¹),⁸⁸ NaCuTe (0.105 A W⁻¹),⁸⁷ and graphene (10⁻⁴ A W⁻¹).⁸⁴ In line with the responsivity, EQE peaks at 41.08% and 36.85% at 1.1 eV and 1.5 eV, respectively, along the a direction. In contrast, EQE in the b direction remains low across most of the energy spectrum, with a maximum of only 2.46%. This pronounced anisotropy further confirms the unique optoelectronic properties of the O1 variant. Moreover, the EQE along the a direction exceeds that of various 2D materials, such as SnS (22.01%),⁹⁰ NaCuTe (34.3%),⁸⁷ NaCuSe (8%),⁸⁷ and KagSe (17.9%).⁸⁹ In the higher energy range of 2.8–3.0 eV, although the increase in responsivity is less prominent, the EQE exhibits a noticeable rise, forming a small peak. In summary, the combination of high performance and anisotropic response also opens up possibilities for novel optoelectronic logic gates or optical switches based on polarization control. Additionally, the superior EQE compared to many other 2D materials indicates potential for high-efficiency photovoltaic devices, particularly in tandem solar cell architectures where specific wavelength ranges need to be targeted.

To gain a more comprehensive understanding of the optoelectronic properties of the O1 variant, we further investigated the relationship between J_ph, R_ph, and EQE with respect to the θ and photon energy, as shown in Fig. 10. All three parameters exhibit a strong dependence on both photon energy and θ, following a highly consistent pattern. The most prominent feature is the appearance of three distinct response peaks: a primary peak around 1.1 eV, a secondary peak near 1.5 eV, and a weaker but noticeable high-energy peak at approximately 2.8 eV. Notably, the variation of J_ph with θ in the ZrCl₂ photodetector follows the relation: J_ph(E) = A(E) + B(E)[sin(2θ + ϕ(E))],^91–94 where A, B and ϕ are coefficients related to energy and structure. Additionally, we observed that the angular dependence of R_ph and EQE follows a similar trend to that of J_ph.

Fig. 10 (a) J_ph, (b) R_ph, and (c) EQE of the O1 variant with respect to photon energy and θ for linearly polarized light incident along the a direction.

To further elucidate this behavior, we focused on three representative photon energies: 1.1 eV, 1.5 eV, and 2.8 eV (detailed angular dependence data are provided in Fig. S5, ESI†). The angular response shows distinct patterns at different photon energies. At 1.1 eV and 1.5 eV, a cosine-like distribution is observed, with maxima at θ ≈ 0° and 180°, and minima at θ ≈ 90°. In contrast, at 2.8 eV, an opposite sine-like behavior emerges, with peaks at θ ≈ 90° and minima at θ ≈ 0° and 180°. This angular dependence maintains symmetrical distribution over the 0° to 180° range across the entire measured energy spectrum, although the response intensity varies with photon energy. This unique omnidirectional photoresponse not only confirms the strong anisotropy of the O1 variant but also suggests potential applications in various advanced fields.⁹⁵ The device exhibits clear spectral selectivity, with primary high-sensitivity response in the near-infrared region (1.1 eV and 1.5 eV, corresponding to approximately 1129 nm and 828 nm), making it well-suited for near-infrared imaging, spectroscopy, and telecommunications. Additionally, a discernible response in the visible blue-violet spectrum (2.8 eV, ∼443 nm) extends the device's functionality to the visible light range. This multi-band detection capability, combined with strong angular dependence, enables effective operation across diverse optical environments spanning from near-infrared to visible light spectra, particularly for polarization-sensitive applications.

Fig. 11 illustrates J_ph, R_ph, and EQE characteristics of the O3 variant along the a and b directions under an in-plane θ of 0°. Both directions show significant responses, with notable features in both low and high-energy ranges. For the a direction (red curves), multiple prominent peaks are observed in the high-energy range (1.5–3.0 eV), which are generally larger than the peak in the low-energy range (approximately 0.8–1.0 eV), particularly for J_ph and EQE. In the R_ph plot, these peaks are comparable in magnitude. The b direction (blue curves) shows a stronger peak in the low-energy range but generally weaker response in the high-energy range compared to the a direction. Detailed analysis reveals that the J_ph along the b direction reaches its main peak (∼4 µA mm⁻²) at 0.95 eV, while the a direction displays several peaks in the high-energy region (∼2 µA mm⁻²). Similarly, R_ph follows a comparable trend, with a main peak of approximately 0.25 A W⁻¹ in the b direction. The EQE reaches a peak of about 23% at 0.95 eV in the b direction, while the highest EQE in the high-energy range along the a direction is around 15%. In contrast, the O1 variant demonstrates strong anisotropy, with significant response primarily along the a direction. Two distinct peaks appear at around 1.0 eV and 1.5 eV, with higher magnitudes (J_ph ∼ 6.57 µA mm⁻², R_ph ∼ 0.37 A W⁻¹ and EQE reaching up to 41.08%), while the b direction shows almost no response. This pronounced difference in structure-related optoelectronic properties opens new possibilities for developing innovative mechanical sensors. By accurately measuring changes in the optoelectronic response, it is possible to detect whether the material has undergone a phase transition from O1 to O3, enabling the detection of shear stress on the material surface. Most importantly, this type of sensor can be self-powered using sunlight, eliminating the need for an external power source, which offers a significant advantage for remote or hard-to-access environmental monitoring applications.

Fig. 11 Linearly polarized light with θ of 0° generates (a) J_ph, (b) R_ph, and (c) EQE in the O3 variant when incident in the a and b directions.

Furthermore, we investigated the relationships between the J_ph, R_ph, and EQE with θ and photon energy in both the a and b directions, as shown in Fig. 12 (additional angular dependence data for the b direction are provided in Fig. S6, ESI†). The distributions of J_ph, R_ph, and EQE exhibit similar patterns overall. All three quantities reach their maximum values in the low-energy region (approximately 0.8–1.0 eV). For the a direction, the maxima appear at θ between 110° and 130°, with J_ph reaching 4.96 µA mm⁻², R_ph at 0.34 A W⁻¹, and EQE at 31%. Similar behavior is observed in the b direction, where the maximum values occur within the range of 140°–160°, with comparable magnitudes (J_ph: 4.93 µA mm⁻², R_ph: 0.32 A W⁻¹, and EQE: 31%, see Fig. S6, ESI†).

Fig. 12 (a) J_ph, (b) R_ph, and (c) EQE of the O3 variant with respect to photon energy and θ for the linearly polarized light incident along the a direction.

Significant differences were observed in the angular and spectral dependencies of J_ph, R_ph, and EQE between the O1 and O3 variants. The O1 variant exhibits a characteristic symmetric pattern, with the response highly concentrated near 0° and 180° (a direction), and higher maximum values (J_ph 6.57 µA mm⁻², R_ph 0.37 A W⁻¹, EQE 41.08%), along with two distinct response bands at approximately 1.0 eV and 1.5 eV. In contrast, the angular and spectral dependencies of J_ph, R_ph, and EQE for the O3 variant show less symmetry, with the response distributed over a broader range of angles and photon energies. The O3 variant also demonstrates lower maximum values (J_ph 4.96 µA mm⁻², R_ph 0.34 A W⁻¹, EQE 31%) compared to the O1 variant, but exhibits a more balanced response across different angles and a wider spectral range. These differences reflect the distinct dimerization directions of Zr atoms in the two variants. The dimerization in the [100] direction of the O1 variant leads to strong anisotropy and specific energy responses, making it more suitable for applications requiring highly directional selectivity. Conversely, the [110] dimerization in the O3 variant results in a more balanced response, providing potential advantages in applications requiring wide spectral and multi-directional photodetection, such as omnidirectional sensors or broadband photodetectors. This distinction between the two variants opens up possibilities for designing tunable multifunctional optoelectronic devices. By switching between the O3 and O1 variants, it is possible to achieve dynamic transitions between omnidirectional response and high-sensitivity directional response, adapting to varying operational environments and requirements.

4 Conclusions

Our comprehensive study of monolayer 1T′ phase ZrCl₂ reveals striking differences between its O1 and O3 ferroelastic variants, demonstrating the profound impact of structural transitions on material properties. The O1 variant exhibits exceptional anisotropy, with ultra-high electron mobility (1.44 × 10⁴ cm² V⁻¹ s⁻¹) and current on/off ratio (10⁶) along the a direction, alongside strong photoresponse anisotropy (J_ph: 6.57 µA mm⁻², R_ph: 0.37 A W⁻¹, EQE: 41.08%). In contrast, the O3 variant shows more isotropic behavior, with high conductivity in both directions (500–600 nA at ±0.4 V) and a balanced photoresponse (J_ph: 4.96 µA mm⁻², R_ph: 0.34 A W⁻¹, EQE: 31%) across a broader spectrum. The ability to switch between these variants through ferroelastic transitions offers unprecedented opportunities for creating adaptive electronic and optoelectronic devices. By controlling Zr–Cl chain dimerization, we can potentially achieve dynamic regulation of material properties, leading to reconfigurable circuits, multi-state memory devices, and tunable sensors. Furthermore, the coexistence of variants with distinct properties opens possibilities for novel heterostructures and domain wall devices. This research not only deepens our understanding of 2D ferroelastic materials but also paves the way for new concepts in nanoelectronics and optoelectronics, positioning monolayer 1T′ ZrCl₂ as a promising platform for next-generation technologies in information processing, energy conversion, and sensing.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare that they have no conflict of interest.

Acknowledgements

Calculations were carried out in the High-Performance Computing Laboratory of Changzhou University and Hefei Advanced Computing Center. The authors extend their gratitude to the Stork's Writing Assistant (https://www.storkapp.me/writeassistant/) for its assistance in polishing some of the text in this article.

References

1. S. Joseph, J. Mohan, S. Lakshmy, S. Thomas, B. Chakraborty, S. Thomas and N. Kalarikkal, Mater. Chem. Phys., 2023, 297, 127332.
2. S. Chowdhury and D. Jana, Rep. Prog. Phys., 2016, 79, 126501.
3. X. Tang, Q. Hao, X. Hou, L. Lan, M. Li, L. Yao, X. Zhao, Z. Ni, X. Fan and T. Qiu, Adv. Mater., 2024, 36, 2312348.
4. P. Kumbhakar, C. Chowde Gowda and C. S. Tiwary, Front. Mater., 2021, 8, 721514.
5. J. Hu and M. Dong, J. Nanobiotechnol., 2024, 22, 63.
6. Y. Wu, W. Yuan, M. Xu, S. Bai, Y. Chen, Z. Tang, C. Wang, Y. Yang, X. Zhang, Y. Yuan, M. Chen, X. Zhang, B. Liu and L. Jiang, Chem. Eng. J., 2021, 412, 128744.
7. A. VahidMohammadi, M. Mojtabavi, N. M. Caffrey, M. Wanunu and M. Beidaghi, Adv. Mater., 2019, 31, 1806931.
8. S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 17033.
9. W. Zhang, Z. Huang, W. Zhang and Y. Li, Nano Res., 2014, 7, 1731–1737.
10. C. Li, D. Sang, S. Ge, L. Zou and Q. Wang, Molecules, 2024, 29, 3341.
11. X. Yin, C. S. Tang, Y. Zheng, J. Gao, J. Wu, H. Zhang, M. Chhowalla, W. Chen and A. T. S. Wee, Chem. Soc. Rev., 2021, 50, 10087–10115.
12. A. Ahmed, M. Zahir Iqbal, A. Dahshan, S. Aftab, H. H. Hegazy and E. S. Yousef, Nanoscale, 2024, 16, 2097–2120.
13. G.-B. Liu, D. Xiao, Y. Yao, X. Xu and W. Yao, Chem. Soc. Rev., 2015, 44, 2643–2663.
14. M. A. Khan and M. N. Leuenberger, Nanophotonics, 2018, 7, 1589–1600.
15. J. Zhang, L. Du, S. Feng, R.-W. Zhang, B. Cao, C. Zou, Y. Chen, M. Liao, B. Zhang, S. A. Yang, G. Zhang and T. Yu, Nat. Commun., 2019, 10, 4226.
16. M. Zhang, Y. Zhu, X. Wang, Q. Feng, S. Qiao, W. Wen, Y. Chen, M. Cui, J. Zhang, C. Cai and L. Xie, J. Am. Chem. Soc., 2015, 137, 7051–7054.
17. H. Zhang, F. Guégan, J. Wang and G. Frapper, Phys. Chem. Chem. Phys., 2024, 26, 14675–14683.
18. X. Huang, L. Yan, Y. Zhou, Y. Wang, H.-Z. Song and L. Zhou, J. Phys. Chem. Lett., 2021, 12, 525–531.
19. H. Han, M. Hong, S. S. Gokhale, S. B. Sinnott, K. Jordan, J. E. Baciak and J. C. Nino, J. Phys. Chem. C, 2014, 118, 3244–3250.
20. Y. Zhang, S. Li, W. Yang, M. K. Joshi and X. Fang, J. Phys. Chem. Lett., 2019, 10, 2400–2407.
21. A. Aji Suleiman, X. Zhou and T. Zhai, J. Phys. D: Appl. Phys., 2021, 54, 013002.
22. D. Torelli, H. Moustafa, K. W. Jacobsen and T. Olsen, npj Comput. Mater., 2020, 6, 158.
23. D. C. Hvazdouski, M. S. Baranava, E. A. Korznikova, A. A. Kistanov and V. R. Stempitsky, 2D Mater., 2024, 11, 025022.
24. L. Wang, T. Lin, J. Wang, C. Fang, Y. Li and Y. Qiao, Phys. Chem. Chem. Phys., 2024, 26, 26857–26870.
25. J. Kim, K.-W. Kim, B. Kim, C.-J. Kang, D. Shin, S.-H. Lee, B.-C. Min and N. Park, Nano Lett., 2020, 20, 929–935.
26. P. Man, L. Huang, J. Zhao and T. H. Ly, Chem. Rev., 2023, 123, 10990–11046.
27. H. Wang, Y. Wen, H. Zeng, Z. Xiong, Y. Tu, H. Zhu, R. Cheng, L. Yin, J. Jiang, B. Zhai, C. Liu, C. Shan and J. He, Adv. Mater., 2024, 2305044.
28. W. Li and J. Li, Nat. Commun., 2016, 7, 10843.
29. H. Wang and X. Qian, 2D Mater., 2017, 4, 015042.
30. Y. Yang, H. Zong, X. Ding and J. Sun, Appl. Phys. Lett., 2022, 121, 122903.
31. Z. Tu and M. Wu, Sci. Bull., 2020, 65, 147–152.
32. X. Xu, Y. Ma, T. Zhang, C. Lei, B. Huang and Y. Dai, Nanoscale Horiz., 2020, 5, 1386–1393.
33. L. Yang, Y. Gao, M. Wu and P. Jena, Phys. Rev. B, 2022, 105, 094101.
34. C. Xu, J. Mao, X. Guo, S. Yan, Y. Chen, T. W. Lo, C. Chen, D. Lei, X. Luo, J. Hao, C. Zheng and Y. Zhu, Nat. Commun., 2021, 12, 3665.
35. X. Xiao, J. Zhou, K. Song, J. Zhao, Y. Zhou, P. N. Rudd, Y. Han, J. Li and J. Huang, Nat. Commun., 2021, 12, 1332.
36. X. Huang, Z. Zhuo, L. Yan, Y. Wang, N. Xu, H.-Z. Song and L. Zhou, J. Phys. Chem. Lett., 2021, 12, 7726–7732.
37. X. Lu, Z. Chen, Y. Cao, Y. Tang, R. Xu, S. Saremi, Z. Zhang, L. You, Y. Dong, S. Das, H. Zhang, L. Zheng, H. Wu, W. Lv, G. Xie, X. Liu, J. Li, L. Chen, L.-Q. Chen, W. Cao and L. W. Martin, Nat. Commun., 2019, 10, 3951.
38. W. Lei, R. Hu, S. Han, H. Yuan, W. Jiao, Y. Luo and H. Liu, J. Phys. Chem. C, 2024, 128, 543–548.
39. Y. Shen and Q. Wang, Phys. Rep., 2022, 964, 1–42.
40. M. Wu and X. C. Zeng, Nano Lett., 2016, 16, 3236–3241.
41. S. Zhu, R. Duan, X. Xu, F. Sun, W. Chen, F. Wang, S. Li, M. Ye, X. Zhou, J. Cheng, Y. Wu, H. Liang, J. Kono, X. Li, Z. Liu and Q. J. Wang, Light: Sci. Appl., 2024, 13, 119.
42. T. Zhang, Y. Ma, L. Yu, B. Huang and Y. Dai, Mater. Horiz., 2019, 6, 1930–1937.
43. E. Salje, in Phase Transitions in Ferroelastic and Co-elastic Crystals, ed. E. K. Salje, Cambridge University Press, Cambridge, UK, 1993, p. 296, ISBN 0521429366.
44. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens. Matter, 2020, 32, 015901.
45. S. Smidstrup, D. Stradi, J. Wellendorff, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, T. Ghosh, E. Jónsson, H. Jónsson and K. Stokbro, Phys. Rev. B, 2017, 96, 195309.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G. M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
48. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
49. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
50. N. D. Mermin, Phys. Rev., 1965, 137, A1441–A1443.
51. H. Lang, S. Zhang and Z. Liu, Phys. Rev. B, 2016, 94, 235306.
52. C. A. Polanco, Nanoscale Microscale Thermophys. Eng., 2021, 25, 1–24.
53. M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
54. S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, 1995.
55. L. E. Henrickson, J. Appl. Phys., 2002, 91, 6273–6281.
56. J. Chen, Y. Hu and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155441.
57. L. Zhang, K. Gong, J. Chen, L. Liu, Y. Zhu, D. Xiao and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195428.
58. H. Haug and A. P. Jauho, Quantum kinetics in transport and optics of semiconductors, Springer, Berlin, 2008, vol. 2.
59. X. Wang, H. Qi, N. Wang, Z. Wang, W. Tang, Z. Tan, Z. Zhu, M. Zhang and C. Shen, J. Phys.: Condens. Matter, 2023, 35, 394001.
60. M. Yao, J. Ji, X. Li, Z. Zhu, J.-Y. Ge, D. J. Singh, J. Xi, J. Yang and W. Zhang, Sci. China Mater., 2023, 66, 2768–2776.
61. S. Sarikurt, T. Kocabaş and C. Sevik, J. Mater. Chem. A, 2020, 8, 19674–19683.
62. W. Shangguan, C. Yan, W. Li, C. Long, L. Liu, C. Qi, Q. Li, Y. Zhou, Y. Guan, L. Gao and J. Cai, Nanoscale, 2022, 14, 4271–4280.
63. A. Rawat, N. Jena, Dimple and A. De Sarkar, J. Mater. Chem. A, 2018, 6, 8693–8704.
64. B. Mortazavi, F. Shojaei, M. Azizi, T. Rabczuk and X. Zhuang, J. Mater. Chem. C, 2020, 8, 2400–2410.
65. I. V. Kosarev and A. A. Kistanov, Nanoscale, 2024, 16, 10030–10037.
66. Y. Xu, Q. Long, D. Li and P. Li, Phys. Chem. Chem. Phys., 2022, 24, 3379–3385.
67. T. Zhao, Y. Sun, Z. Shuai and D. Wang, Chem. Mater., 2017, 29, 6261–6268.
68. F. Shojaei, B. Mortazavi, X. Zhuang and M. Azizi, Mater. Today Energy, 2020, 16, 100377.
69. P. Li, Y. Xu, C. Liang and X. C. Zeng, J. Phys. Chem. Lett., 2022, 13, 10534–10542.
70. P. Li, W. Wu, Y. Xu, J. Liu, S. Wu, Y. Ye, C. Liang and X. C. Zeng, J. Phys. Chem. Lett., 2021, 12, 1058–1065.
71. Y. Xu and D. Li, Phys. Chem. Chem. Phys., 2024, 26, 21789–21800.
72. S. Lin, Y. Guo, M. Xu, J. Zhao, Y. Liang, X. Yuan, Y. Zhang, F. Wang, J. Hao and Y. Li, Nanoscale, 2022, 14, 930–938.
73. A. Kishore, H. Seksaria, A. Arora and A. De Sarkar, Phys. Chem. Chem. Phys., 2023, 25, 20337–20349.
74. M. Yang, S. Cao, Q. You, L.-B. Shi and P. Qian, Phys. E, 2020, 118, 113877.
75. Y. Xu, D. Li, H. Sun, H. Xu and P. Li, Phys. Chem. Chem. Phys., 2024, 26, 4284–4297.
76. W. Wu, D. Li, Y. Xu and X. C. Zeng, J. Phys. Chem. Lett., 2021, 12, 11488–11496.
77. P. Li, D. Li, Y. Xu, C. Liang and X. C. Zeng, J. Phys. Chem. Lett., 2024, 15, 3043–3054.
78. W. Yang, H. Wan and T. Chen, Mater. Sci. Semicond. Process., 2024, 181, 108653.
79. Y. Xu and W. Wu, J. Appl. Phys., 2020, 128, 194303.
80. S. Fang, C. Yang, Q. Li, B. Wu, L. Xu, S. Liu, J. Yang, J. Ma, J. Dong, Y. Li, J. Yang and J. Lu, Phys. Rev. Appl., 2023, 19, 024024.
81. S. Fang, Q. Li, C. Yang, B. Wu, S. Liu, J. Yang, J. Ma, Z. Yang, K. Tang and J. Lu, Phys. Rev. Mater., 2023, 7, 084412.
82. Y. Liu, J. Guo, E. Zhu, L. Liao, S.-J. Lee, M. Ding, I. Shakir, V. Gambin, Y. Huang and X. Duan, Nature, 2018, 557, 696–700.
83. Y. Liu, Y. Cai, G. Zhang, Y.-W. Zhang and K.-W. Ang, Adv. Funct. Mater., 2017, 27, 1604638.
84. A. Pospischil, M. M. Furchi and T. Mueller, Nat. Nanotechnol., 2014, 9, 257–261.
85. H. Tang, B. Shi, Y. Wang, C. Yang, S. Liu, Y. Li, R. Quhe and J. Lu, Phys. Rev. Appl., 2021, 15, 064037.
86. F. Wang, Z. Wang, K. Xu, F. Wang, Q. Wang, Y. Huang, L. Yin and J. He, Nano Lett., 2015, 15, 7558–7566.
87. H. Li, X. Jiang, X. Xu, G. Xu, D. Li, C. Li, B. Cui and D.-S. Liu, Phys. Chem. Chem. Phys., 2021, 23, 2475–2482.
88. H. Jin, J. Li, Y. Dai and Y. Wei, Phys. Chem. Chem. Phys., 2017, 19, 4855–4860.
89. Q. Wang, J. Li, Y. Liang, Y. Nie and B. Wang, ACS Appl. Mater. Interfaces, 2018, 10, 41670–41677.
90. P. Zhao, H. Yang, J. Li, H. Jin, W. Wei, L. Yu, B. Huang and Y. Dai, J. Mater. Chem. A, 2017, 5, 24145–24152.
91. S. Pal, N. V. Sarath, K. S. Priya and P. Murugavel, J. Phys. D: Appl. Phys., 2022, 55, 283001.
92. Y. Xie, L. Zhang, Y. Zhu, L. Liu and H. Guo, Nanotechnology, 2015, 26, 455202.
93. X. Tao, P. Jiang, H. Hao, X. Zheng, L. Zhang and Z. Zeng, Phys. Rev. B, 2020, 102, 081402.
94. S. N. Danilov, L. E. Golub, T. Mayer, A. Beer, S. Binder, E. Mönch, J. Minár, M. Kronseder, C. H. Back, D. Bougeard and S. D. Ganichev, Phys. Rev. Appl., 2021, 16, 064030.
95. F. Chu, M. Chen, Y. Wang, Y. Xie, B. Liu, Y. Yang, X. An and Y. Zhang, J. Mater. Chem. C, 2018, 6, 2509–2514.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04315d

---