Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermoelectric properties of the low-spin lanthanide cobalate perovskites LaCoO3, PrCoO3, and NdCoO3 from first-principles calculations†
Alveena Z.
Khan
 ,
Joseph M.
Flitcroft
,
Joseph M.
Flitcroft
 and
Jonathan M.
Skelton
and
Jonathan M.
Skelton
 *
*
Department of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK. E-mail: jonathan.skelton@manchester.ac.uk
First published on 2nd January 2025
Abstract
An ab initio modelling workflow is used to predict the thermoelectric properties and figure of merit ZT of the lanthanide cobalates LaCoO3, PrCoO3 and NdCoO3 in the orthorhombic Pnma phase with the low-spin magnetic configuration. The LnCoO3 show significantly lower lattice thermal conductivity than the widely-studied SrTiO3, due to lower phonon velocities, with a large component of the heat transport through an intraband tunnelling mechanism characteristic of amorphous materials. Comparison of the calculations to experimental measurements suggests the p-type electrical properties are significantly degraded by the thermal spin crossover, and materials-engineering strategies to suppress this could yield improved ZT. We also predict that n-doped LnCoO3 could show larger Seebeck coefficients, superior power factors, lower thermal conductivity, and higher ZT than SrTiO3. Our results highlight the exploration of a wider range of perovskite chemistries as a facile route to high-performance oxide thermoelectrics, and identify descriptors that could be used as part of a modelling-based screening approach.
1 Introduction
60–70% of global energy is currently lost as heat, and technologies to improve efficiency are a key enabler of the transition to sustainable energy.1 Thermoelectric (TE) power, which harnesses the Seebeck effect in a TE material to convert heat to electricity, is a leading contender to address this challenge.2 The performance of a TE material is typically defined by the dimensionless figure of merit ZT:3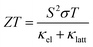 | (1) |
The majority of current high-performance TE materials are chalcogenides, including: Bi2Te3 (ZT up to approx. 1.2 from 300–400 K,7,8 and 1.4 between 400–500 K,9 in (Bi,Sb)2(Se,Te)3 alloys); PbTe (ZT ≈ 2.5 at T > 900 K in PbTe—SrTe alloys10,11); and SnSe (p-type ZT up to 3.1 at 773 K,12,13 n-type ZT up to 2.3 at 873 K14). Despite their performance, the current industry standards Bi2Te3 and PbTe are unsuitable for widespread application due to the scarcity of Te, which has a lower crustal abundance than Pt, and the environmental toxicity of Pb, which creates issues with end-of-life disposal.2 Chalcogenides can also be prone to poor thermal stability and oxidation at elevated temperature.15,16
Oxide-based TEs are highly desirable for their elemental abundance, high melting temperature and resistance to oxidation, but their ZT is often limited by high κlatt and low σ, the latter of which requires a high doping level to offset at the expense of a reduced absolute |S|.17 Nonetheless, reports of large thermoelectric power factors in the 1990s has spurred research into several families of oxide materials. Promising p-type oxides include the layered cobalates Na2Co2O418–20 (ZT = 0.92 at 900 K in NaxCo2O4/Ag composites21), Ca3Co4O922 (ZT = 0.87 at 973 K in single-crystal (Ca2CoO3)0.7CoO2,23ZT = 0.74 at 800 K in polycrystalline Ca3−xTbxCo4O9,24) and Bi2Sr2Co2Oy25 (ZT = 0.26 at 973 K in Bi2Sr2Co2Oy/Ag composites26). Candidate n-type oxides include ZnO27 (ZT = 0.65 at 1247 K in Zn0.96Al0.02Ga0.02O28) and the oxide perovskites SrTiO329–31 (ZT = 0.66 at 1100 K in Sr0.9La0.1Ti0.9Nb0.1O332) and CaMnO333,34 (ZT = 0.67 at 773 K in Ca2.97Bi0.03MnCu0.04O3−δ35). However, while perovskites, and in particular STO, have received considerable attention as prospective oxide TEs, they have yet to achieve a ZT competitive with flagship chalcogenide materials.17
The lanthanide cobalates LnCoO3 (Ln = La or a rare-earth metal Ce-Lu) are a family of perovskite oxides that, in contrast to the titanates and manganates, typically show p-type conductivity with relatively large Seebeck coefficients around room temperature.20,36 Reports of n-type lanthanide cobalates are uncommon, but n-type behaviour at low temperature has been observed in several LnCoO3.37–39 With the exception of LaCoO3, the LnCoO3 typically adopt the low-symmetry orthorhombic Pnma perovskite structure.37,40,41 The octahedral Co3+ have a low-spin magnetic arrangement at low temperature but progressively convert to a high-spin configuration at elevated T.42 This results in a significant increase in the electrical conductivity at high temperature, but at the cost of a large reduction in the Seebeck coefficient.36–39,43,44 Despite their potentially promising electrical properties, experiments have so far reported maximum ZT < 0.1,36,39,43,44 which are not competitive with more widely-studied perovskite oxides such as SrTiO3.
A recent theoretical study of the lanthanide cobalates LaCoO3 (LCO), PrCoO3 (PCO) and NdCoO3 (NCO) suggested the potential for high-temperature p-type ZT up to ∼0.75.45 However, this study modelled the high-symmetry cubic phases, which are not the ground state,37,40,41 determined the electrical properties with respect to an unknown relaxation time and without attempting to optimise the carrier concentration, and did not account for the κlatt in the predicted ZT. In this work, we apply a fully ab initio workflow for predicting thermoelectric performance, which we have previously shown to yield accurate predictions for the titanate perovskites,46 to better establish the potential of the LnCoO3 as oxide TEs. We find that the LnCoO3 benefit from a low κlatt and large |S|, the latter of which supports heavy doping and large σ and PFs. Comparison to experiments indicates that the electrical properties are severely degraded by the spin transition, and that exploring methods to suppress this may be a fruitful avenue for improving the ZT. More generally, by comparing to similar calculations on the titanate perovskites, including SrTiO3, we identify descriptors that could be indicative of good thermoelectric performance, and which could be used as the basis to explore a wider range of oxide perovskite chemistries.
2 Computational modelling
2.1 Prediction of thermoelectric properties
In this model, the macroscopic κp is an average over contributions κqj from individual phonon modes qj, with wavevector q and band index j, according to ref. 47:
 | (2) |
 | (3) |
 | (4) |
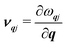 | (5) |
 | (6) |
In structurally-complex materials with small intraband frequency spacing, and/or in materials with short τqj (i.e. broad Γqj), there may be non-negligible heat conduction through the “wave-like” intraband tunnelling characteristic of amorphous materials (glasses).48 This contribution to the thermal conductivity, κw, can be obtained by solving the Wigner transport equation using the approach outlined in ref. 48. The (total) lattice thermal conductivity is then determined from:
| κlatt(T) = κp(T) + κw(T) | (7) |
Finally, we note that the κp, κw and κlatt are 3 × 3 tensors in which the three diagonal elements καα correspond to transport along the Cartesian directions α = x, y and z. Thermoelectric materials are rarely prepared as single crystals, and typically take the form of consolidated powders or thin films with randomly-oriented crystal grains. In this case, the measured (scalar) κlatt can be modelled as the average of the diagonal elements:
 | (8) |
The spectral conductivity Σ and generalised moments of the transport distribution function Ln are calculated according to:49,50
 | (9) |
 | (10) |
 | (11) |
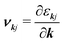 | (12) |
| τkj−1(T) = ΓADPkj(T) + ΓPOPkj(T) + ΓIMPkj(T) + ΓPIEkj(T) | (13) |
Once the Ln(T) have been calculated, the σ, S and κel can be determined from:49,50
| σ(εF, T) = L0(εF, T) | (14) |
 | (15) |
 | (16) |
We note that the Ln, and hence the σ, S and κel, depend on the Fermi energy. This can be adjusted to specify an extrinsic carrier concentration (“doping level”) n, under the assumption that the doping does not significantly affect the host band structure. This is termed the “rigid band approximation” (RBA).
We also note that, while we do not do so in this work, a common approximation used in electronic transport calculations is to replace the τkj with a (possibly temperature-dependent) constant value τel.49 In this case, the σ and κel are linearly proportional to the τel and the S, which is the ratio of two Ln (cf.eqn (15)), is independent of the lifetime.
Finally, as for the κlatt, the σ, S and κel are 3 × 3 tensors, and scalar averages σ, S and κel can be obtained in an analogous manner to eqn (8). The power factor S2σ in eqn (1) is also orientation dependent, and the PF along a given Cartesian direction can be calculated from:
| (S2σ)α = Sαα2σαα | (17) |
The ZT is orientation dependent and the values along the three Cartesian directions can be calculated as:
 | (18) |
2.2 Density-functional theory calculations
Calculations were performed using pseudopotential plane wave density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP) code.51Initial structures of LaCoO3 (LCO), PrCoO3 (PCO) and NdCoO3 (NCO) in the orthorhombic Pnma space group were taken from the Materials Project (MP) database52 (mp-1185232, mp-20090, mp-22599) and optimised to tight tolerances of 10−8 eV on the total energy and 10−3 eV Å−1 on the forces.
Electron exchange and correlation were modelled using the PBEsol generalised-gradient approximation (GGA) functional.53 The ion cores were modelled using projector-augmented wave pseudopotentials (PAW PPs).54,55 For La, Co and O, we used PPs with the valence configurations: La – 5s2 5p6 6s2 5d1; Co – 4s1 3d8 and O – 2s2 2p4. For Pr and Nd we used the Ln3+ PPs, which place two/three f electrons for Pr3+/Nd3+ in the pseudopotential core, resulting in the same valence configuration as the La PP. The valence wavefunctions were described using a plane-wave basis with an 800 eV kinetic-energy cutoff, and the electronic Brillouin zones were sampled using Γ-centred Monkhorst—Pack k-point meshes56 with 3 × 3 × 2 subdivisions. These parameters were chosen based on explicit testing to converge the absolute total energies to <1 meV atom−1 and the external pressure to <1 kbar (0.1 GPa).
The third-order (anharmonic) force constants were computed in 2 × 1 × 2 expansions of the conventional cells (80 atoms). The “particle-like” lattice thermal conductivities for band transport were calculated using the single mode relaxation time approximation (SM-RTA) to the phonon Boltzmann transport equation by combining the second- and third-order force constants to obtain modal heat capacities Cqj, group velocities νqj and lifetimes τqj on uniform Γ-centred 8 × 8 × 8 q-point sampling meshes. This mesh was chosen based on explicit testing to converge the scalar average of the κp tensors (eqn (2) and (8)) to within 5% of the values obtained with larger sampling meshes. We also solved the Wigner transport equation for the converged meshes to determine the κw contribution from intraband tunnelling.48
AMSET estimates the electronic relaxation times by summing scattering rates from four different processes, viz. acoustic deformation potential (ADP), polar optic phonon (POP), piezoelectric (PIE), and ionised impurity (IMP) scattering (eqn (13)), requiring a range of material properties to be calculated.
Deformation potentials were computed by performing a series of single-point energy calculations on deformed structures, generated using AMSET, with PBEsol.
High-frequency dielectric constants ε∞ were obtained using the linear-optics routines in VASP59 and non-self-consistent HSE06,60,62 where the electronic band energies are evaluated using PBE Kohn—Sham wavefunctions without updating the electron orbitals. The ionic contributions to the dielectric constants εionic, Born effective charges Z* and piezoelectric moduli e(0) were determined using DFPT with PBEsol.59 The ε∞ and εionic were used to obtain the static dielectric constants εs = ε∞ + εionic. The Z* were used with the phonon modes at q = Γ, evaluated with Phonopy, to calculate the polar optic phonon (POP) frequency ωpo. For both the linear-optics and DFPT calculations, convergence tests indicated that 3 × denser k-point sampling along each reciprocal-lattice vector, relative to the “base” meshes used for geometry optimisation, was required for convergence.
Finally, the elastic constants Cij were computed using PBEsol and the finite-differences routines in VASP (denser k-point sampling was not required for these calculations).
PIE scattering is not relevant to these systems, as the Pnma spacegroup is centrosymmetric and the piezoelectric moduli vanish, so we did not include this mechanism when estimating the scattering rates.
3 Results and discussion
3.1 Structure, phonon spectra and lattice thermal conductivity
The optimised structures of the three LnCoO3 are shown in Fig. 1. For PCO and NCO, the lattice parameters are in excellent agreement with experimental measurements, with maximum deviations of 0.8% in the lattice parameters and 1.2% in the unit-cell volume (Table S1, ESI†). For LCO, the Materials Project52 predicts the Pnma structure to be a low-lying metastable phase to the ground-state R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase,37 but our optimised lattice parameters and volume differ by up to 5.4% and 10.8% from those reported with ref. 37 (ICSD: 164459). However, it is not clear how this Pnma structure was obtained, and we are therefore unsure of the origin of this discrepancy.
c phase,37 but our optimised lattice parameters and volume differ by up to 5.4% and 10.8% from those reported with ref. 37 (ICSD: 164459). However, it is not clear how this Pnma structure was obtained, and we are therefore unsure of the origin of this discrepancy.
 | ||
| Fig. 1 Optimised structures of LaCoO3, PrCoO3 and NdCoO3 viewed along the crystallographic b direction. The Ln atoms are shown in dark blue, purple and yellow, the Co atoms are shown in light blue, and the O atoms are shown in green. These images were prepared using the VESTA software.63 | ||
The calculated phonon spectra of the three LnCoO3 are shown in Fig. 2 and Fig. S1/S2 (ESI†). The phonon spectra are broadly similar, as expected given the chemical similarity of La, Pr and Nd, with the exception that some of the higher-frequency modes of LCO and PCO show shallower dispersion and sharper features in the density of states (DoS) compared to NCO. The DoS curves of all three LnCoO3 show low- and mid/high-frequency groups of modes separated by a small “phonon bandgap”. The atom-projected DoS (PDoS) shows that modes in the low-frequency group are predominantly associated with motion of the Ln atoms, while the mid/high-frequency group corresponds to motion of the Co and O atoms, with Co and O making the largest contribution to the mid- and high-frequency modes, respectively. The form of the (P)DoS can therefore largely be explained by the difference in mass between the Ln, Co and O atoms. Finally, the calculated dispersions are free from imaginary modes, indicating all three LnCoO3 to be dynamically stable in the Pnma phase.
Turning now to the lattice thermal conductivity, the scalar-average “particle-like”’ conductivity, κp, of the three LnCoO3 are compared in Fig. 3(a). The κp is obtained by solving the Boltzmann transport equation for phonons, under the assumption that energy is carried by phonon quasiparticles, and, in most crystalline materials, is the dominant contributor to the κlatt.47
 | ||
| Fig. 3 Analysis of the “particle-like” (band) contribution κp to the averaged lattice thermal conductivity κlatt of LaCoO3 (LCO), PrCoO3 (PCO) and NdCoO3 (NCO) using the model developed in our previous work (eqn (19)).4 The κp is written as a the product of a harmonic term κ/τph, which at high temperature reflects differences in the phonon group velocities, and a weighted-average lifetime τph. Data for SrTiO3 (STO) and CaTiO3 (CTO) from our previous work46 are shown for comparison. | ||
At T = 1000 K, we predict values of κp = 0.66–0.94 W m−1 K−1, which are comparable at the higher end to our previous calculations on orthorhombic CaTiO3 (CTO, κp = 0.93 W m−1 K−1) and 30–50% smaller than we predicted for tetragonal SrTiO3 (STO, 1.4 W m−1 K−1).46 The κp are generally smallest along the b axis and largest along the c axis, but the anisotropy is small, with the axial conductivity differing by <10% of the scalar averages (Table S2, ESI†).
To establish the origin of the differences in the thermal transport, we used the analysis developed in our previous work4 and determined weighted-average lifetimes, τph, such that the κp can be written (cf.eqn (2)):
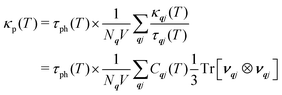 | (19) |
The summation on the right-hand side, κp/τph, is a useful metric for comparing differences in the group velocities, and saturates at high-temperature as the Cqj tend to the Dulong–Petit limit. Comparing the κp/τph of the three LnCoO3 to those of CTO and STO46 shows that the LnCoO3 have much lower group velocities (Fig. 3(b) and Table S3, ESI†). While the difference to STO may be partly due to the lower-symmetry orthorhombic structure,4 the fact that the values are 55–60% lower than the isostructural CTO likely indicates weaker chemical bonding compared to the titanate perovskites. A potential explanation for this is the weaker electrostatic interactions in the BO6 octahedra with Co3+ compared to Ti4+. On the other hand, we calculate τph = 0.38–0.58 for the three LnCoO3 at T = 1000 K, which are 1.6–2.4× longer than CTO and 2.4–4.5× longer than STO (Fig. 3(c) and Table S3, ESI†). It is also of note that the differences in the κp among the LnCoO3 are primarily due to differences in the τph (cf.Fig. 3(a) and (c)). At T = 1000 K, NCO and LCO have the largest and smallest κp, respectively, which is due to NCO having a 1.7% smaller κp/τph but a 1.5× longer τph (Table S3, ESI†).
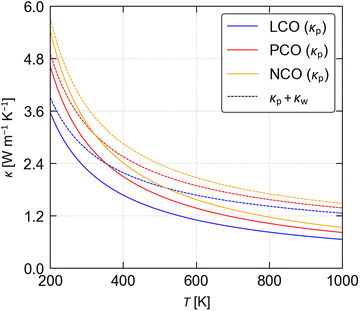
In materials where “dense” phonon dispersion curves and small intraband spacing, and/or broad linewidths due to short τph, lead to substantial energy overlap between phonon modes, there may be a significant “wave-like” intraband tunnelling contribution, κw, to the overall κlatt.48 Intraband tunnelling is typically the dominant heat-transport mechanisms in amorphous materials (glasses), and can be evaluated by solving the Wigner transport equation. We obtain values of κw = 0.55–0.6 W m−1 K−1 for the three LnCoO3, equal to ∼79–90% of the κp, which substantially increase the total κlatt to 1.27–1.49 W m−1 K−1 compared to the κp (Fig. 4 and Table S2, ESI†). This indicates that a large proportion of the heat transport in the three LnCoO3 is through this glass-like conduction mechanism. While perhaps surprising, our predicted (total) κlatt of 1.42 W m−1 K−1 for LCO at 800 K, and 1.49 and 1.61 W m−1 K−1 for PCO and NCO at 875 K, are reasonable matches to the measured values of 1.75 W m−1 K−1 for LCO44 and 1.25 W m−1 K−1 for PCO/NCO.43 (We tentatively attribute the underestimated κlatt of LCO to our modelling the metastable Pnma rather than the higher-symmetry R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase, and the overestimated κlatt of PCO and NCO to the morphology of the experimental samples and/or to differences in composition.)
c phase, and the overestimated κlatt of PCO and NCO to the morphology of the experimental samples and/or to differences in composition.)
In our previous calculations on the titanate perovskites46 we determined the κp using the same approach as in the present study, but we did not account for intraband tunnelling. To investigate whether this makes a significant contribution to the κlatt of the titanates, we solved the Wigner transport equation for STO and CTO to calculate the κw (Fig. S3/S4 and Table S4, ESI†). At T = 1000 K, the κw for CTO is 1.6× larger than the κp, whereas for STO the κw and κp are approximately equal and intraband tunnelling increases the predicted κlatt by almost a factor of two. We obtain total thermal conductivities of 2.47 and 2.73 W m−1 K−1 for CTO and STO, which are a much better match to the experimental measurements of 3.25 and ∼3–3.2 W m−1 K−1 (ref. 64–67) than the κp. While the calculations still underestimate the measured values, the discrepancy is on the order of 10–20%, which could easily be ascribed to, for example, incomplete separation of the lattice and electronic contributions to the total thermal conductivity κ or to the presence of (thermally-)conductive impurities.
This leads to the important result that intraband tunnelling likely makes a substantial contribution to the κlatt of the oxide perovskites, and it is necessary to solve the Wigner transport equation, rather than the more usual phonon Boltzmann transport equation, for these systems.48,57
3.2 Electronic structure and transport properties
The electronic band structure and density of states (DoS) of the three LnCoO3 are shown in Fig. 5 and Fig. S5/S6 (ESI†). In all three LnCoO3, the valence-band edge is formed of a roughly equal mix of Co 3d and O 2p states, while the conduction-band edge is primarily composed of Co states. Using the HSE06 hybrid functional, we predict indirect bandgaps Eg of between 2.59 eV for LCO and 2.87 eV for NCO, which are considerably larger than the predicted Eg in ref. 45 but consistent with the upper range of values measured in experiments (Table S5, ESI†). For all three LnCoO3 the valence-band maxima (VBM) lie along the Γ → Z path and the conduction-band minima (CBM) are close to U (Fig. 5 and Fig. S5/S6, ESI†). | ||
| Fig. 5 Calculated electronic band structure and atom-projected density of states (PDoS) of LaCoO3. In the band structure, the valence and conduction bands are shown in blue and orange, and the green and red markers show the positions of the valence-band maximum and conduction-band minimum. In the DoS plot, the total DoS is shown in black and the projections onto the Co d and O p states are shown in purple and green. This plot was generated using sumo.61 | ||
Fig. 6 shows the predicted average electrical conductivity σ, absolute Seebeck coefficient |S|, power factor S2σ (PF) and electronic thermal conductivity κel of the three LnCoO3, with both p-type (hole) and n-type (electron) doping, as a function of doping level n at a fixed T = 1000 K.
 | ||
| Fig. 6 Predicted electrical properties of LaCoO3 (LCO), PrCoO3 (PCO) and NdCoO3 (NCO) as a function of extrinsic carrier concentration n (“doping level”) at a fixed temperature T = 1000 K: (a) electrical conductivity σ, (b) absolute Seebeck coefficient |S|, (c) power factor S2σ(PF), and (d) electronic thermal conductivity κel. For all four quantities we show the scalar averages (cf.eqn (8) and (17)). Data for n-type SrTiO3 (STO) from our previous work is also shown for comparison.46 | ||
As for the titanate perovskites,46 we predict that high doping levels of n > 1020 cm−3 are required to obtain reasonable σ (Fig. 6(a)). Whereas most experiments on the LnCoO3 have examined p-type doping,37,39,43,44 our calculations predict that much larger σ can potentially be obtained with n-type doping. Taking n = 5 × 1021 cm−3 as a reference point, we predict that the n-type σ = 439–494 S cm−1 could be up to ∼6× larger than the p-type σ = 80–85 S cm−1 at T = 1000 K. Of the three titanate perovskites CaTiO3, SrTiO3 and BaTiO3 examined in our previous work,46 we predicted n-type STO to show the most favourable electrical properties. Compared to the three LnCoO3, STO shows a larger σ at n ≈ 1020 cm−3 and above, with a predicted 2.6 × larger σ = 1268 S cm−1 at n = 5 × 1021 cm−3.
The |S| are predicted to decrease monotonically from a relatively large value of around 900 μV K−1 to approx. 150 μV K−1 over the range of n = 1016–1022 cm−3 tested in our calculations (Fig. 6(b)). Unlike the electrical conductivities, we predict similar |S| for both p- and n-type doping, and we predict a near-constant increase of around 100 μV K−1 compared to n-type STO.46
The σ and |S| are related to the n and the carrier effective masses m* according to:68,69
 | (20) |
 | (21) |
 and
and  are the conductivity and Seebeck effective masses, respectively, and we have omitted the temperature dependence of the various parameters for brevity. We estimated the
are the conductivity and Seebeck effective masses, respectively, and we have omitted the temperature dependence of the various parameters for brevity. We estimated the  and
and  for a reference n = 5 × 1021 cm−3 and T = 1000 K using the procedure outlined in ref. 69, with a constant electron lifetime of τkj = τel = 10−14 s (Table S6, ESI,†cf.eqn (9)). We obtain
for a reference n = 5 × 1021 cm−3 and T = 1000 K using the procedure outlined in ref. 69, with a constant electron lifetime of τkj = τel = 10−14 s (Table S6, ESI,†cf.eqn (9)). We obtain  me and
me and  for p-type doping, and
for p-type doping, and  me and
me and 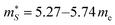 for n-type doping. The 3–4× larger
for n-type doping. The 3–4× larger  with p-type doping accounts for the majority of the ∼6× higher σ predicted for n-type doping, but indicates that stronger hole carrier scattering must also play a significant role. Similar calculations on n-type STO, with a more appropriate n = 1021 cm−3, yield
with p-type doping accounts for the majority of the ∼6× higher σ predicted for n-type doping, but indicates that stronger hole carrier scattering must also play a significant role. Similar calculations on n-type STO, with a more appropriate n = 1021 cm−3, yield 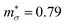 and
and  which qualitatively explain the higher σ and lower |S| compared to the three LnCoO3.
which qualitatively explain the higher σ and lower |S| compared to the three LnCoO3.
The band structures of all three LnCoO3 show low-energy secondary band extrema (VBM/CBM) that could be beneficial to the electrical properties (Fig. 5 and Fig. S5/S6, ESI†). To test this, we also computed the Fermi surface complexity factors  defined in ref. 69:
defined in ref. 69:
 | (22) |
 and K* are an effective valley degeneracy and effective anisotropy factor, respectively. The calculated
and K* are an effective valley degeneracy and effective anisotropy factor, respectively. The calculated 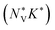 as a function of n and T for the three LnCoO3, for both p- and n-type doping, are shown in Fig. S7–S9 (ESI†). Across the three LnCoO3 we obtain values between 0.3–5.1 and 2.4–9.1 for p- and n-type doping, respectively, which are modest in comparison to high-performance chalcogenide thermoelectrics such as GeTe (
as a function of n and T for the three LnCoO3, for both p- and n-type doping, are shown in Fig. S7–S9 (ESI†). Across the three LnCoO3 we obtain values between 0.3–5.1 and 2.4–9.1 for p- and n-type doping, respectively, which are modest in comparison to high-performance chalcogenide thermoelectrics such as GeTe ( at the estimated n that maximises the PF) and PbSe (22).69 This suggests that, despite the multivalley electronic structure, Fermi surface complexity plays a minor role in the electrical properties of the LnCoO3, although it likely does contribute to the superior n-type transport.
at the estimated n that maximises the PF) and PbSe (22).69 This suggests that, despite the multivalley electronic structure, Fermi surface complexity plays a minor role in the electrical properties of the LnCoO3, although it likely does contribute to the superior n-type transport.
The rise in σ and decrease in |S| with n results in peak PFs between n = 1021–1022 cm−3 (Fig. 6(c)). The predicted maximum PFs for the p- and n-type LnCoO3, and for n-type STO,46 at T = 1000 K are listed together with the associated n, σ and |S| in Table S7 (ESI†). The p-type PFs range from 0.25–0.29 mW m−1 K−2 (n = 5–7 × 1021 cm−3), while the n-type PFs range from 1.4–1.6 mW m−1 K−2 (n = 6.5–8 × 1021 cm−3). In almost all cases, the maximum and minimum PFs are along the b and c axes, respectively, and align with the respective minimum and maximum in the κlatt (Table S8, ESI†). The anisotropy in the PFs is considerably larger than in the thermal conductivity, and the axial values differ from the averages by up to 25%.
Compared to our previous calculations on the titanate perovskites, we predict comparable n-type PFs to STO at the optimum n = 2 × 1021 cm−3 for this system, and considerably higher peak PFs at larger n, because the larger |S| allows the doping level to be increased to offset the lower σ. At T = 1000 K, the largest n-type S2σ = 1.6 mW m−1 K−1 for PCO (n = 7 × 1021 cm−3, S = −149 μV K−1, σ = 712 S cm−1) is 55% larger than the highest S2σ = 1 mW m−1 K−2 predicted for STO (n = 2 × 1021 cm−3, S = −139 μV K−1, σ = 524 S cm−1).
At large n the predicted κel follow the Widemann–Franz Law:
| κel = LσT | (23) |
The predicted temperature dependence of the σ, |S|, PF and κel of the LnCoO3 at n = 5 × 1021 cm−3 is shown in Fig. S10 (ESI†). At large n, the σ show a metallic-like drop with temperature consistent with degenerate semiconducting behaviour, while the |S| show a significant rise. For the p-type LnCoO3 this results in a relatively flat temperature dependence of the PFs, with a shallow maximum around 500 K. For the n-type systems, on the other hand, the PFs rise with T up to 1000 K. At the smaller n ≈ 1021 cm−3 that maximises the PF, n-type STO shows similar behaviour at low T, but the increase flattens out above ∼600 K. Finally, the κel is proportional to both σ and T through eqn (23). For the p-type LnCoO3, we predict a significant decrease from approx. 0.3 to 0.1 W m−1 K−1 between 200–1000 K, mirroring the behaviour of the σ, whereas for the n-type materials the two terms balance to yield a shallow temperature dependence. The κel of n-type STO shows intermediate behaviour, decreasing with T in line with the σ but maintaining a relatively high value of 0.4–0.6 W m−1 K−1.
Experimental measurements on p-type LnCoO3 typically show a large drop in S and increase in σ with temperature due to the thermal spin crossover from low-spin to high-spin Co3+.37,39,42–44 With reference to the electronic PDoS (Fig. 5 and Fig. S5/S6, ESI†), the spin crossover might be thought of as taking two electrons from the valence band and placing them in the conduction band, yielding two holes and two electrons per Co ion. With four Co ions per unit cell, this would correspond to a doping level of around 3.5 × 1022 cm−3, which is well above the ∼5 × 1021 cm−3 we predict would optimise the PF.
While crude, this picture is qualitatively supported by two observations. Firstly, extrapolating the data in Fig. 6, and considering the predicted temperature dependence in Fig. S10 (ESI†), suggests doping levels of this magnitude would yield p-type σ on the order of 100–1000 S cm−1 and S < 100 μV K−1, which are broadly consistent with measurements performed above the spin-transition temperature.36–39,42–44 Secondly, we might expect the large change in the (intrinsic) n through the transition to “swamp” a smaller extrinsic electron concentration, leading to a change in the sign of the Seebeck coefficient, which is seen in the measurements on n-type LCO in ref. 37 and 39.
On the other hand, comparison of the calculations to experimental measurements on p-type LnCoO337,39,44 show that, at the n that match the S, the calculations consistently overestimate the σ by 1–2 orders of magnitude (Table S9, ESI†). This suggests the spin-crossover may also induce changes to the band structure that affect the electrical conductivity. For example, a flattening of the valence bands could increase the  and/or increase the
and/or increase the  which would result in a lower σ/higher S for a given n. We defer a more detailed investigation of the effect of magnetic configuration on the electrical transport properties of the LnCoO3 to a future study.
which would result in a lower σ/higher S for a given n. We defer a more detailed investigation of the effect of magnetic configuration on the electrical transport properties of the LnCoO3 to a future study.
For present purposes, the comparison between our predictions for the low-spin LnCoO3 and experimental measurements suggest the electrical properties could be significantly improved if the spin transition can be suppressed. Experimental evidence suggests this might be possible with certain material modifications, such as in La(Mn1−xCox)O3 solid solutions and [LaCoO3]1−x[(La0.7Sr0.3)CoO3]x composites.37,44 The experiments in ref. 36 and 43 also show that the S is sensitive to the choice of Ln, which we speculate could be due to modulation of the spin transition temperature. More generally, the detremental impact of the spin transition, and the larger predicted |S| of the low-spin LnCoO3 compared to SrTiO3, motivates the exploration of alternative perovskite chemistries, perhaps based on B-site M3+ ions without unpaired electrons and/or with stronger crystal-field splitting.
3.3 Thermoelectric figure of merit
Fig. 7 shows the predicted averaged p- and n-type figure of merit ZT of PCO as a function of n and T, and data for all three LnCoO3 are provided in Fig. S11–S13 (ESI†). In general, the largest ZT are obtained at large n and high T, with the peak ZT at slightly lower n than the peak PFs due to the increase in the κel with n (cf.Fig. 6). We also predict considerably higher ZT for n-type doping than for p-type doping, due to the significantly higher PFs.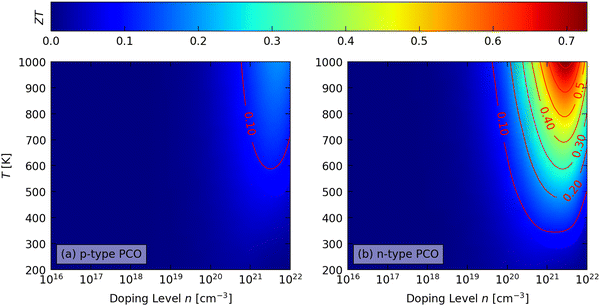 | ||
| Fig. 7 Predicted average figure of merit ZT of PrCoO3 (PCO) as a function of extrinsic carrier concentration n (“doping level”) and temperature with (a) p-type and (b) n-type doping. | ||
Considering the three heat-recovery scenarios set out in ref. 70, we predict maximum p-type ZTmax of 0.04–0.07 at 400 K, 0.09–0.12 at 600 K and 0.17–0.19 at 1000 K (Table S10, ESI†). While these are considerably lower than the ZT > 1 required for commercial application,2 they are also larger than the ZTmax < 0.1 reported in experiments on the LnCoO3,36,39,43,44 which highlights the scope for improved performance if the spin transition can be suppressed. Due to the significantly higher σ, we predict larger n-type ZTmax of 0.13–0.14, 0.28–0.31, and 0.66–0.73 at the three temperatures (Table S11, ESI†).
The ZT at 1000 K show modest anisotropy and vary by 7.5–15% around the averaged values (Fig. S11–S13, ESI†), due to a 5–25% variation in the PF and up to 10% variation in the κlatt. The maximum ZT are generally obtained along the b direction, where the maximum PFs tend to align with the minimum κlatt.
With the larger κlatt predicted by including the contribution from intraband tunnelling, we predict ZTmax = 0.06, 0.14 and 0.31 for n-type STO at the three temperatures.46 The latter value, and also the constituent properties of S = −196 μV K−1, σ = 258 S cm−1 and κel + κlatt = 3.17 W m−1 K−1, are a very reasonable match to the range of values obtained in experiments around this temperature (ZT = 0.27–0.37, S = −168 to −233 μV K−1, σ = 200–303 S cm−1, κ = 2.6–3.1 W m−1 K−1).71–73
The superior predicted performance of the n-type LnCoO3 are due to lower a κlatt and larger PFs, the latter predominantly from larger |S|, and also to larger σ at T = 1000 K. We predict the largest average n-type ZTmax = 0.73 at 1000 K for PCO, where the PF is ∼50% larger than predicted for STO.46 However, while these predictions are promising, realising them requires that the spin transition can be suppressed with n-type doping. This has not been demonstrated experimentally, and may be challenging, or even impossible, to achieve in practice.
Finally, we note that the κlatt is the majority contributor to the denominator in eqn (1) (Tables S10 and S11, ESI†), meaning that neglecting this contribution, as in the calculations in ref. 45, is a poor approximation. Indeed, the p-type ZTmax we predict are around 4× smaller than in ref. 45, and, given the relatively low ZT reported in experiments, we can confidently argue that the latter values are probably not realistic.
3.4 Discussion
In this study, we have applied an ab initio modelling workflow to investigate the thermoelectric performance of the lanthanide cobalates, LaCoO3, PrCoO3 and NdCoO3. Compared to the more widely-studied titanate perovskites, in particular SrTiO3, we predict the LnCoO3 could potentially show lower intrinsic lattice thermal conductivity, larger Seebeck coefficients and, with heavy doping to optimise the electrical conductivity, higher power factors and thermoelectric figures of merit. By exploiting the microscopic insight available from the calculations, we have also established the origin of these differences and identified potential descriptors for favourable thermoelectric performance in oxide perovskites.We first address the issue of the accuracy of our predictions relative to experimental measurements.
Our κlatt are obtained by using the single-mode relaxation-time approximation to the phonon Boltzmann transport equation to obtain the particle-like conductivity, κp,47 and by solving the Wigner transport equation to obtain the contribution from intraband tunnelling, κw.48 The SM-RTA is an approximation to the full solution to the linearised Boltzmann transport equation. Moreover, the perturbative approach to determining the linewidths is based on the harmonic frequencies and eigenvectors, and does not take into account thermal expansion nor anharmonicity beyond third order (e.g. four-phonon scattering processes). Despite these shortcomings, comparison to experiments suggests this approach is accurate enough to reproduce experimental measurements with small errors. Of note, however, is the large κw predicted for both the lanthanide cobalate and the group II titanate perovskites, which indicates that amorphous-like heat conduction makes an important contribution to the κlatt in these systems. It is likely that this may also be the case for other oxide perovskites, in which case this is an important general result.
The electrical transport properties are obtained by solving the electron Boltzmann transport equations within the rigid-band approximation, using approximate models for the electron scattering rates.49,50 Calculations comparing the RBA to atomistic models of doped PbTe and HfCoSb, with n up to 4.5 × 1021 cm−3, found 10–20% differences in the Seebeck coefficient.74 In our previous work, we compared predictions for SrTiO3 to measurements on heavily-doped single crystals (n = 5 × 1019–6.8 × 1020 cm−3), and found a tendency for the calculations to over- and underestimate the electrical conductivity at low and high temperature, respectively, and to underestimate the |S|.46,65 We also recently carried out a study where we used experimentally-measured relaxation times to predict the transport properties of STO, and found a similar tendency to underestimate the |S| and overestimate the σ.75 The models for electron scattering have been shown to work well across a wide range of systems, including the thermoelectrics SnS, SnSe, PbTe, Bi2Te3 and BiCuOSe and the hybrid halide perovskite (CH3NH3)PbI3.50 This approach also represents a significant conceptual improvement over using a fixed relaxation time.
We note that our predictions are for pristine single crystals, and do not take into account the impact of e.g. finite grain size and point defects on the transport properties.76 In previous work on the bismuth oxychalcogenides, using a similar approach to the present study, we found that the calculations gave a near-quantitative reproduction of measurements on doped single crystals, but that experiments on consolidated powders showed much larger variability.77
In the context of the LnCoO3 examined in the present work, the degradation of the |S| through the spin crossover makes it difficult to quantitatively assess the accuracy of our predictions. Based on our previous studies on the titanate perovskites46,75 we would expect the calculations to give reasonable “ballpark” predictions for the magnitude of the |S|, σ and PF, and of the n required to achieve them. As noted above, however, while several studies suggest it may be possible to control the spin transition chemically, at least to some extent,37,43,44 it is not clear whether this can be achieved with the heavy doping required to optimise the (p- or n-type) electrical properties.
With this in mind, we close our discussion by highlighting the key features of the LnCoO3 that the calculations predict could lead to superior thermoelectric performance compared to STO. The first is that the LnCoO3 show a significantly lower lattice lattice thermal conductivity, which, based on our analysis, can be attributed to weaker chemical bonding and lower phonon group velocities. This prediction is borne out in experiments,43,44,65–67 and the good reproduction of high-temperature measurements in our calculations suggests the low κlatt is not significantly impacted by the spin transition. A second key feature is the higher |S|, which we attribute to a larger Seebeck effective mass (cf.eqn (21)). In the LnCoO3, this is partially offset by a high conductivity effective mass, and the p-type S are severely degraded in the high-spin magnetic configuration.37,39,42–44 However, as a general observation, the possibility of superior electrical properties does motivate the exploration of a wider range of perovskite chemistries.
On this final point, modelling could be of considerable value in directing experiments towards the most promising candidates. In particular, the group-velocity metric κp/τph in eqn (19) can be obtained from inexpensive harmonic phonon calculations, while the effective masses  can be obtained from simple electronic-structure calculations using the CRTA.69 One can therefore envisage a screening study using these metrics to prioritise candidate perovskites for further study, whether by more detailed theoretical modelling such as performed in the present work, or by experiments.
can be obtained from simple electronic-structure calculations using the CRTA.69 One can therefore envisage a screening study using these metrics to prioritise candidate perovskites for further study, whether by more detailed theoretical modelling such as performed in the present work, or by experiments.
4 Conclusions
In summary, we have used an ab initio modelling workflow to obtain a comprehensive set of predictions for the thermoelectric properties and figure of merit of the orthorhombic low-spin lanthanide cobalate perovskites LaCoO3, PrCoO3 and NdCoO3.Compared to the more widely-studied titanate perovskites, and in particular SrTiO3, we predict the LnCoO3 to possess a beneficial lower lattice thermal conductivity, due to weaker chemical bonding and lower phonon group velocities. We find that glass-like intraband tunnelling makes a significant contribution to the κlatt of both the LnCoO3 and the titanate perovskites CaTiO3 and STO, which may indicate that this heat-conduction mechanism is important in oxides more generally.
We predict the LnCoO3 to have large carrier effective masses that result in high (absolute) Seebeck coefficients at the cost of reduced electrical conductivity, the latter of which requires heavier doping to offset. A combination of higher conductivity masses and stronger carrier scattering result in poor p-type conductivity, whereas the high |S| and reasonable conductivity predicted for the n-type LnCoO3 could yield superior power factors to STO if carrier concentrations on the order of ∼5 × 1021 cm−3 can be obtained. However, comparison to experiments suggests the electrical properties are negatively impacted by the thermally-activated transition from low- to high-spin Co3+, and that this behaviour may make it difficult or impossible to retain dominant n-type transport at elevated temperature.
If the spin transition can be suppressed, we predict modest p- and n-type ZT of up to 0.19 and 0.73 at 1000 K, the latter of which is competitive with other oxide materials. Although it is unclear whether these ZT can be achieved in practice, our results strongly motivate the exploration of alternative oxide perovskites, and we identify two descriptors, calculated from the harmonic phonon spectra and electronic structure, that could be used as a basis for this.
Author contributions
Conceptualization, methodology and writing – all authors; data curation, formal analysis and investigation – AZK and JMF; funding acquisition – JMS; software, project administration and supervision – JMF and JMS; resources – JMS.Data availability
Data will be made available after publication in an online repository at https://doi.org/10.17632/trx37mt89j. Our analysis code is available on GitHub at https://github.com/skelton-group/ZT-Calc-Workflow.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AZK is supported by a University of Manchester PhD studentship, and JMF and JMS are supported by a UK Research and Innovation (UKRI) Future Leaders Fellowship (MR/T043121/1, MR/Y033973/1). The calculations used the ARCHER 2 HPC facility via the UK Materials Chemistry Consortium, which is funded by the UK Engineering and Physical Sciences Research Council (EP/R029431, EP/X035859).Notes and references
- A. Firth, B. Zhang and A. Yang, Appl. Energy, 2019, 235, 1314–1334 CrossRef.
- R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441–463 RSC.
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- S. K. Guillemot, A. Suwardi, N. Kaltsoyannis and J. M. Skelton, J. Mater. Chem. A, 2024, 12, 2932–2948 RSC.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463 RSC.
- C. Li, J. Hong, A. May, D. Bansal, S. Chi, T. Hong, G. Ehlers and O. Delaire, Nat. Phys., 2015, 11, 1063–1069 Search PubMed.
- R. Deng, X. Su, Z. Zheng, W. Liu, Y. Yan, Q. Zhang, V. P. Dravid, C. Uher, M. G. Kanatzidis and X. Tang, Sci. Adv., 2018, 4, eaar5606 Search PubMed.
- H. Lee, T. Kim, S. C. Son, J. Kim, D. Kim, J. Lee and I. Chung, Mater. Today Phys., 2023, 31, 100986 Search PubMed.
- B. Zhu, X. Liu, Q. Wang, Y. Qiu, Z. Shu, Z. Guo, Y. Tong, J. Cui, M. Gu and J. He, Energy Environ. Sci., 2020, 13, 2106–2114 RSC.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- G. Tan, F. Shi, S. Hao, L.-D. Zhao, H. Chi, X. Zhang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nat. Commun., 2016, 7, 12167 CrossRef CAS PubMed.
- C. Zhou, Y. K. Lee, Y. Yu, S. Byun, Z.-Z. Luo, H. Lee, B. Ge, Y.-L. Lee, X. Chen, J. Y. Lee, O. Cojocaru-Mirédin, H. Chang, J. Im, S.-P. Cho, M. Wuttig, V. P. Dravid, M. G. Kanatzidis and I. Chung, Nat. Mater., 2021, 20, 1378–1384 CrossRef CAS PubMed.
- T. Kim, H. Lee and I. Chung, Bull. Korean Chem. Soc., 2024, 45, 186–199 CrossRef CAS.
- S. Byun, B. Ge, H. Song, S.-P. Cho, M. S. Hong, J. Im and I. Chung, Joule, 2024, 8, 1520–1538 CrossRef CAS.
- C. Jiang, X. Fan, B. Feng, J. Hu, Q. Xiang, G. Li, Y. Li and Z. He, J. Alloys Compd., 2017, 692, 885–891 CrossRef CAS.
- Y. Zheng, X. Y. Tan, X. Wan, X. Cheng, Z. Liu and Q. Yan, ACS Appl. Energy Mater., 2020, 3, 2078–2089 CrossRef CAS.
- R. Freer, D. Ekren, T. Ghosh, K. Biswas, P. Qiu, S. Wan, L. Chen, S. Han, C. Fu, T. Zhu, A. K. M. A. Shawon, A. Zevalkink, K. Imasato, G. J. Snyder, M. Ozen, K. Saglik, U. Aydemir, R. Cardoso-Gil, E. Svanidze, R. Funahashi, A. V. Powell, S. Mukherjee, S. Tippireddy, P. Vaqueiro, F. Gascoin, T. Kyratsi, P. Sauerschnig and T. Mori, J. Phys. Energy, 2022, 4, 022002 CrossRef CAS.
- I. Terasaki, Y. Sasago and K. Uchinokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R12685–R12687 CrossRef CAS.
- H. Yakabe, K. Kikuchi, I. Terasaki, Y. Sasago and K. Uchinokura, Proceedings of the 1997 16th International Conference on Thermoelectrics, 1997, pp. 523–527 Search PubMed.
- W. Koshibae, K. Tsutsui and S. Maekawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 6869–6872 CrossRef CAS.
- M. Ito and D. Furumoto, J. Alloys Compd., 2008, 450, 517–520 CrossRef CAS.
- Y. Miyazaki, Solid State Ionics, 2004, 172, 463–467 CrossRef CAS.
- M. Shikano and R. Funahashi, Appl. Phys. Lett., 2003, 82, 1851–1853 CrossRef CAS.
- S. Saini, H. S. Yaddanapudi, K. Tian, Y. Yin, D. Magginetti and A. Tiwari, Sci. Rep., 2017, 7, 44621 CrossRef CAS PubMed.
- R. Funahashi, I. Matsubara and S. Sodeoka, Appl. Phys. Lett., 2000, 76, 2385–2387 CrossRef CAS.
- S. Wang, Z. Bai, H. Wang, Q. Lü, J. Wang and G. Fu, J. Alloys Compd., 2013, 554, 254–257 CrossRef CAS.
- T. Tsubota, M. Ohtaki, K. Eguchi and H. Arai, J. Mater. Chem., 1997, 7, 85–90 RSC.
- M. Ohtaki, K. Araki and K. Yamamoto, J. Electron. Mater., 2009, 38, 1234–1238 CrossRef CAS.
- T. Okuda, K. Nakanishi, S. Miyasaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 113104 CrossRef.
- H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2003, 350, 292–295 CrossRef CAS.
- H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2005, 392, 306–309 CrossRef CAS.
- J. Wang, B.-Y. Zhang, H.-J. Kang, Y. Li, X. Yaer, J.-F. Li, Q. Tan, S. Zhang, G.-H. Fan, C.-Y. Liu, L. Miao, D. Nan, T.-M. Wang and L.-D. Zhao, Nano Energy, 2017, 35, 387–395 CrossRef CAS.
- T. Kobayashi, H. Takizawa, T. Endo, T. Sato, M. Shimada, H. Taguchi and M. Nagao, J. Solid State Chem., 1991, 92, 116–129 CrossRef CAS.
- D. Flahaut, T. Mihara, R. Funahashi, N. Nabeshima, K. Lee, H. Ohta and K. Koumoto, J. Appl. Phys., 2006, 100, 084911 CrossRef.
- X. Song, S. A. Paredes Navia, L. Liang, C. Boyle, C.-O. Romo-De-La-Cruz, B. Jackson, A. Hinerman, M. Wilt, J. Prucz and Y. Chen, ACS Appl. Mater. Interfaces, 2018, 10, 39018–39024 CrossRef CAS PubMed.
- J.-W. Moon, Y. Masuda, W.-S. Seo and K. Koumoto, Mater. Sci. Eng., B, 2001, 85, 70–75 CrossRef.
- C. Autret, J. Hejtmánek, K. Knížek, M. Maryško, Z. Jirák, M. Dlouhá and S. Vratislav, J. Phys.: Condens. Matter, 2005, 17, 1601 CrossRef CAS.
- V. Dudnikov, A. Fedorov, Y. Orlov, L. Solovyov, S. Vereshchagin, S. Y. Gavrilkin, A. Y. Tsvetkov, M. Gorev, S. Novikov and S. Ovchinnikov, Ceram. Int., 2020, 46, 17987–17991 CrossRef CAS.
- V. A. Dudnikov, Y. S. Orlov, L. A. Solovyov, S. N. Vereshchagin, Y. N. Ustyuzhanin, S. M. Zharkov, G. M. Zeer, A. A. Borus, V. S. Bondarev and S. G. Ovchinnikov, J. Taiwan Inst. Chem. Eng., 2024, 162, 105560 CrossRef CAS.
- J. A. Alonso, M. J. Martínez-Lope, C. de la Calle and V. Pomjakushin, J. Mater. Chem., 2006, 16, 1555–1560 RSC.
- K. Knížek, J. C. V. Hejtmánek, Z. C. V. Jirák, P. Tomeš, P. Henry and G. André, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 134103 CrossRef.
- J.-Q. Yan, J.-S. Zhou and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134409 CrossRef.
- H. Hashimoto, T. Kusunose and T. Sekino, J. Alloys Compd., 2009, 484, 246–248 CrossRef CAS.
- A. Kumar, D. Sivaprahasam and A. D. Thakur, Mater. Chem. Phys., 2021, 269, 124750 CrossRef CAS.
- H. Absike, N. Baaalla, L. Attou, H. Labrim, B. Hartiti and H. Ez-zahraouy, Solid State Commun., 2022, 345, 114684 CrossRef CAS.
- A. Z. Khan, J. M. Flitcroft and J. M. Skelton, Mater. Adv., 2024, 5, 652–664 RSC.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- M. Simoncelli, N. Marzari and F. Mauri, Phys. Rev. X, 2022, 12, 041011 CAS.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, J. Open Source Software, 2018, 3, 717 CrossRef.
- J. M. Skelton, D. S. D. Gunn, S. Metz and S. C. Parker, J. Chem. Theory Comput., 2020, 16, 3543–3557 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. Li, Y. Wang, X. Yang, H. Kang, Z. Cao, X. Jiang, Z. Chen, E. Guo and T. Wang, Chem. Eng. J., 2022, 428, 131121 CrossRef CAS.
- S. Ohta, T. Nomura, H. Ohta and K. Koumoto, J. Appl. Phys., 2005, 97, 034106 CrossRef.
- A. J. Ahmed, S. M. K. Nazrul Islam, R. Hossain, J. Kim, M. Kim, M. Billah, M. S. A. Hossain, Y. Yamauchi and X. Wang, R. Soc. Open Sci., 2019, 6, 190870 CrossRef CAS PubMed.
- S. P. Singh, N. Kanas, T. D. Desissa, M. Johnsson, M.-A. Einarsrud, T. Norby and K. Wiik, J. Eur. Ceram. Soc., 2020, 40, 401–407 CrossRef CAS.
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 CrossRef CAS PubMed.
- Z. M. Gibbs, F. Ricci, G. Li, H. Zhu, K. Persson, G. Ceder, G. Hautier, A. Jain and G. J. Snyder, npj Comput. Mater., 2017, 3, 8 CrossRef.
- S. LeBlanc, S. K. Yee, M. L. Scullin, C. Dames and K. E. Goodson, Renewable Sustainable Energy Rev., 2014, 32, 313–327 CrossRef CAS.
- A. Kikuchi, N. Okinaka and T. Akiyama, Scr. Mater., 2010, 63, 407–410 CrossRef CAS.
- H. Wang, C. Wang, W. Su, J. Liu, Y. Zhao, H. Peng, J. Zhang, M. Zhao, J. Li, N. Yin and L. Mei, Mater. Res. Bull., 2010, 45, 809–812 CrossRef CAS.
- D. Srivastava, C. Norman, F. Azough, M. C. Schäfer, E. Guilmeau, D. Kepaptsoglou, Q. M. Ramasse, G. Nicotra and R. Freer, Phys. Chem. Chem. Phys., 2016, 18, 26475–26486 RSC.
- M.-S. Lee and S. D. Mahanti, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165149 CrossRef.
- Y. Zhu, J. M. Skelton, D. J. Lewis and R. Freer, JPhys Energy, 2024, 6, 025027 CrossRef CAS.
- D. Narducci, E. Selezneva, G. Cerofolini, S. Frabboni and G. Ottaviani, J. Solid State Chem., 2012, 193, 19–25 CrossRef CAS.
- J. M. Flitcroft, A. Althubiani and J. M. Skelton, JPhys Energy, 2024, 6, 025011 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Includes additional data on the phonon spectra, lattice thermal conductivity, electrical-transport properties and thermoelectric figure of merit, and comparison of selected calculated properties to experimental measurements, to support the discussion in the text. See DOI: https://doi.org/10.1039/d4cp04303k |
| This journal is © the Owner Societies 2025 |