Unusual phase transition mechanism induced by shear strain in Si₂BN planar structures and comparison with graphene: an ab initio DFT study

Abstract

Using ab initio methods we show that by applying shear strain, a phase transition occurs between the AB and the AA Si₂BN planar sheets. Si–Si bonds stretch and bend towards the strain direction, causing an internal displacement of the remaining almost unchanged Si₂BN strips. As the shear strain increases, Si–Si bonds weaken and break, while leading to new Si–Si bond formation and causing the phase transition. The planar structure is maintained throughout the application of the strain, with no buckling, a phenomenon not reported so far in other 2D materials. Performing the same calculations for graphene we show that its structural deformations are strikingly different and result in buckling.

---

Recently, it was found that Si₂BN is a stable periodic two-dimensional (2D) structure, which; (i) although containing Si, is entirely planar, (ii) it has a honeycomb structure, very similar to graphene and (iii) it can be stable at temperatures of the order of 1000 K.¹ The structure is composed of alternating Si–Si and B–N bonds along the armchair chains, as shown in Fig. 1(a). Depending on the alternating orientation of the B–N bonds several stable allotropes of the Si₂BN structure may be considered. One of them is shown in Fig. 1(b), which is also planar, and was found to be slightly more stable than the one of Fig. 1(a) (see ref. 2). The two structures of Fig. 1(a) and (b) are the simplest Si₂BN allotropes, which are planar and their combination may produce several other mixed Si₂BN allotropes. In the former, the orientation of B–N bonds along an armchair chain is alternated (B–N and N–B) and the structure can be considered as having an AB stacking. On the other hand, in the latter, the orientation of the B–N bonds along an armchair chain is the same and the structure can be considered as having an AA stacking. More details for the crystalographic structure of those allotropes can be found in ref. 3 where their structural optimizations were performed using the density functional theory (DFT) in the generalized gradient approximation (GGA) with the Perdue–Burke–Ernzerhof (PBE) functional⁴ using the SIESTA code.⁵ Although Si₂BN has not been synthesized yet, it has been extensively studied for several of its properties, including its electronic,³ optical,⁶ thermoelectric⁷ and mechanical properties.⁸ It has been shown to be a promising candidate for hydrogen storage,^9–12 as anode materials for Mg-ion batteries,^13,14 as material for gas sensing applications,^15,16 as catalyst,¹⁷ for its interactions with DNA/RNA bases for biosensing applications¹⁸etc. These studies attest to the increasing interest of the scientific community in the properties of the Si₂BN structure.

Fig. 1 Si₂BN structures with (a) AB and (b) AA stacking. Blue, red, and green spheres represent Si, B, and N atoms, respectively.

In the present study we use DFT calculations to show that by applying in-plane shear strain either on the AA or the AB allotrope, the one allotrope can be transformed into the other. This is an unusual phase transition mechanism, belonging to a class of diffusionless (also called displacive) phase transitions, where due to shear strain, the atoms of the parent crystal structure are shifted in an organized manner, creating a new crystalline phase, without any atomic diffusion. These are the main characteristics of a Martensitic phase transition, which appears in many cases of three-dimensional materials, but it is rarely observed in 2D ones. For instance, the Martensitic phase transition in 2D materials has been reported in the transformation between black and blue phosphorene,¹⁹ the β-GeSe and α-SnTe monolayer multiferroics²⁰ and the SnSe monochalcogenide.²¹ In the case of Si₂BN, that phase transition can be achieved by overcoming a relatively small energy barrier, which is also studied, and shown to be due to the stretching and bending of the relatively weak Si–Si bonds. Under shear strain, each Si–Si bond is bent and eventually broken with a subsequent formation of another Si–Si bond, thus turning the AA structure into AB and vice versa. The corresponding mechanism for graphene is also studied for comparison, but no such behavior is observed. Instead, graphene under shear strain is found to buckle out of plane. This can be explained due to the equivalent strength of graphene bonds, which do not allow some of them to bend, without the bending of the others. This also explains that the observed phenomenon of phase change in Si₂BN may occur only in systems with bonds with inequivalent strengths. Therefore, this is not expected to be observed in binary 2D systems like the hexagonal BN, but it might be observed in other ternary 2D systems.

Usually, in the Martensitic phase transitions the atomic displacements are smaller than the spacing between adjacent atoms, and their relative arrangement topologically is preserved. This, however, is not the case for the presented transformation of Si₂BN, since the topology between the two phases is distinctly different in terms of the kind of atoms participating in each hexagonal ring containing the Si–Si bonds. Moreover, upon further application of the shear strain, the phase change will continue to alternate between the two phases. This phase transition mechanism has not been reported for any other 2D material.

For the DFT calculations, we use the SIESTA code⁵ in the PBE level⁴ and the same parameters as those described in ref. 8 In brief, we utilize (i) norm-conserving Troullier–Martins pseudopotentials²² in the Kleinman–Bylander factorized form,²³ (ii) an atomic-like double-zeta basis with polarization orbitals for the wave function expansion in real space, (iii) a 10 × 10 × 1 Monkhorst–Pack²⁴k-point grid, (iv) a 500 and 300 Ry mesh cutoff energy for Si₂BN and graphene, respectively, for the determination of charge densities and potentials. Starting from the optimized 32-atom rectangular unit cells of Si₂BN and graphene, which are reported in ref. 8 we gradually introduce in-plane shear strain, by modifying the tilting angle ϕ between the lattice vectors a and b, allowing the length of a and b to vary. In the unstrained structure, a = (a₀, 0, 0) and b = (0, b₀, 0), while in the strained ones, a = (a, 0, 0) and b = b(sin ϕ, cos ϕ,0), with ε_xy = tan ϕ being the shear strain. The vectors a and b, and the tilt angle ϕ are shown schematically in Fig. 2(a). Moreover, a 20 Å of vacuum is considered in the z direction, to simulate an isolated sheet of the structure. Optimizations are performed for increasing ϕ values with 1° increment and fixed lattice vector lengths using the conjugate gradient method. For each fixed ϕ value the structure is fully optimized both for the atomic positions and the lattice vector lengths. The structure is considered fully optimized if the maximum atomic force becomes smaller than 0.005 eV Å⁻¹, and both the in plane stress components σ_xx and σ_yy become smaller than 0.01 GPa, assuming that the thickness of the Si₂BN and graphene sheet is 3.34 Å (see ref. 25), which is the sheets' separation in graphene.

Fig. 2 (a) Lattice vectors a and b, and the tilt angle ϕ due to shear strain. (b) The evolution with tilt angle ϕ of the angles formed between B–N and Si–Si bonds with a in Si₂BN and the angle between the C–C bonds of graphene with a, which for ε_xy = 0 are normal to a. (c) and (d) Electron density for the unstrained AA Si₂BN and for the AB Si₂BN structure under shear strain for ϕ = 15°, respectively.

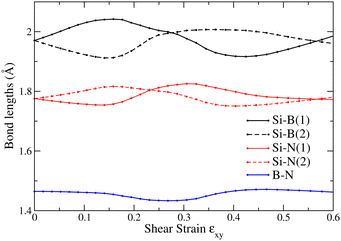
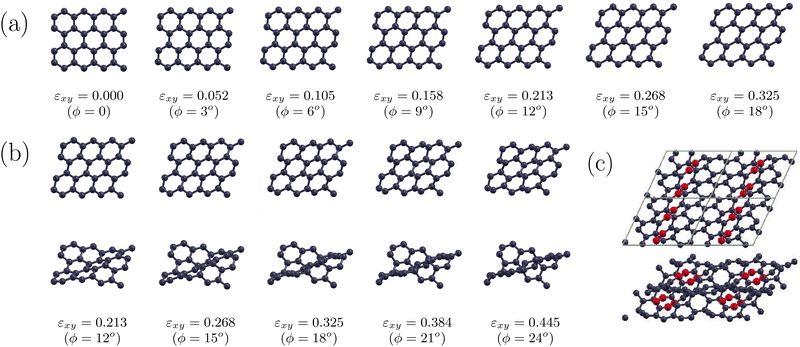
In Fig. 3 we show the optimized structures under shear strain of Si₂BN for ϕ = 0, 3°, 6°, 9°…. Below each snapshot, the tilting angle ϕ and the corresponding shear strain ε_xy= tan ϕ are shown. As one can see, shear strain causes a relatively large tilt in the Si–Si bonds, while the direction of B–N bonds remains almost intact. This can be seen in Fig. 2(b), which shows the angle Δϕ_bond = 90° − ϕ_bond as a function of ϕ, where ϕ_bond is the angle between the bond direction (B–N or Si–Si) and the lattice vector a. Indeed, Δϕ_B−N is very close to 0, while Δϕ_Si−Si increases with ϕ, taking values well above ϕ. This figure allows us to consider that Si₂BN consists of strips of hexagons containing the B–N bonds, which are interconnected through the Si–Si bonds and they slide with each other under shear strain. The bond lengths between the atoms of those stripes (i.e. the Si–B, Si–N, and B–N bond lengths) are shown in Fig. 4, where one can see that those bonds are deformed only slightly. It is worth noting that two different bonds appear between B and Si and between N and Si, which are shown in Fig. 4 as Si–N(1) and Si–N(2), and Si–B(1) and Si–B(2), respectively. From the bond length values of that figure, one can find that during the transformation from one phase to the other, the Si–N, Si–B, and B–N bonds are not shrunk by more than 3.6% and are not elongated by more than 3.0%.

Fig. 3 Transformation of Si₂BN structure with AB stacking into Si₂BN structure with AA stacking by applying shear strain. The snapshots represent the evolution of the optimized structure of AB Si₂BN as shear strain increases. Below each snapshot the shear strain ε_xy and the tilting angle between the lattice vectors a and b are shown. Blue, red, and green spheres represent Si, B, and N atoms, respectively.

Fig. 4 Si–B, Si–N and B–N bond lengths versus shear strain ε_xy.

As shear strain increases, the Si–Si bond tilts are accompanied by a Si–Si bond length increase, causing bond weakening and finally bond breaking. However, before bond breaking, each Si atom of the upper strip comes closer to the next Si atom of the lower strip forming a new Si–Si bond. This can be seen in Fig. 2(c) and (d), which show the electron density for the unstrained AA Si₂BN structure and the AB Si₂BN under shear strain for ϕ = 15°, respectively. In the former, the electrons tend to be in the middle of the Si–Si bond, indicating covalent bonding, which however, due to the small charge density in the area between the Si atoms, is not a very strong bond. In the latter, the electron density has a small valley between the Si atoms, indicating that the electrons prefer to be closer to the Si atoms rather than in the center of the bond and the Si–Si bond starts breaking. At the same time, however, a new Si–Si bond of similar strength has started to form between the Si atom of one strip with the next Si atom of the other strip. Thus, as the shear strain increases, the former Si–Si bond breaks while the new one strengthens, replacing the former, and transforms the AB Si₂BN structure into the AA one and vice versa. This bond weakening is shown in Fig. 3 as an absence of Si–Si bond sticks.

On the other hand, the corresponding snapshots for graphene, which are shown in Fig. 5, reveal a totally different behavior. In graphene, the strong C–C bonds allow only a small and uniform bond tilting which is not that large enough to cause any bond breaking. In particular, the corresponding angle Δϕ_C−C for graphene, which is also shown in Fig. 2(b), almost follows the line of identity Δϕ_C−C = δϕ, indicating that the bending of the C–C bonds follows the tilt angle. As ε_xy increases, the C–C bond lengths do not change significantly and the calculations show that the planar structure may be retained up to ε_xy = 0.36 (or ϕ = 20°) (see Fig. 5(a)). For larger ε_xy values the structure buckles to accommodate the strain, and for ε_xy = 0.466 (or ϕ = 25°), buckling brings closer some C atoms, (which in the unstrained structure would be far apart), which now form bonds and transform the structure into a totally new one with mixed sp¹/sp² bonding. This structure is shown in Fig. 5(c). Buckling however, may occur for even smaller ε_xy values and our results show that it may start at ε_xy ≈ 0.16 (or ϕ ≈ 10°). This result was obtained by optimizing the buckled graphene structure found for ϕ = 20°, for gradually decreasing ϕ values. According to our findings, the energy of the buckled structures is smaller than that of the planar ones for the same ε_xy values, and buckling disappears when ϕ drops down to ϕ = 9°. Snapshots of those buckled graphene structures are shown in Fig. 5(b).

Fig. 5 Snapshots of the optimized graphene structure under in-plane shear strain, (a) when planarity is retained, (b) when buckling occurs. Top and side views are shown in (b). Below each snapshot the shear strain ε_xy and the tilting angle between the lattice vectors a and b are shown. (c) Top view (top panel) and side view (bottom panel) of the optimized structure obtained for graphene under in-plane shear strain ε_xy = 0.466, corresponding to a tilting angle ϕ = 25°. The red-colored spheres represent sp¹ atoms, while all other atoms are sp².

Fig. 6(a) shows the strain energy ΔE = E − E_0,AB per formula unit for the Si₂BN structure with respect to the energy E_0,AB of the unstrained Si₂BN structure with AB stacking, while Fig. 6(d) shows the corresponding one for graphene. Fig. 6(d) shows also the energy curve of Si₂BN for comparison. As one can see in Fig. 6(a) the energy barrier for the transformation of Si₂BN with AB stacking into the Si₂BN structure with AA stacking is 0.54 eV per formula unit and corresponds to the value ε_xy = 0.22. This relatively small energy barrier indicates that this transformation is achievable. Considering that this process is reversible and the fact that the energy of the optimum Si₂BN structure with AA stacking is smaller than Si₂BN structure with AB stacking by 0.16 eV, the energy barrier for the conversion of AA into AB Si₂BN is 0.70 eV per formula unit. On the other hand, the energy curve for graphene takes much higher values than those for Si₂BN. It is worth noting that the energy to break the Si–Si bonds of Si₂BN by applying uniaxial tensile strain along the direction of Si–Si bonds is of the order of 0.5 eV per atom.⁸ Considering that there is one Si–Si bond per Si₂BN formula unit (four atoms), the energy to break a Si–Si bond is of the order of 2 eV.

Fig. 6 (a) Strain energy per formula unit ΔE, (b) shear stress σ_xy and (c) Si–Si interatomic distances versus shear strain ε_xy for the conversion of AB Si₂BN into AA Si₂BN. (d) Strain energy per 4-atom unit cell ΔE, (e) shear stress σ_xy and (f) C–C interatomic distances versus shear strain ε_xy for graphene.

Moreover, Fig. 6(b) and (e) show the shear stress σ_xy for Si₂BN and graphene, respectively, as a function of shear strain ε_xy. The stress–strain curve for Si₂BN is also shown in Fig. 6(e) for comparison. As one can see, for the conversion of AB Si₂BN into AA, or the opposite, the maximum shear stress that has to be applied is 11 GPa. Fitting the stress–strain curve to a cubic polynomial for ϕ in the range −5° ≤ ϕ ≤ 5° we found for Si₂BN, σ_xy = 119.612ε_xy + 0.600703ε_xy² − 960.050ε_xy³, while for graphene, σ_xy = 405.144ε_xy − 0.416954ε_xy² − 318.887ε_xy³. Using these polynomials, one can find the shear modulus G for Si₂BN and graphene, considering that for small strains G = σ_xy/ε_xy is equal to the coefficient of the linear term. Thus, for Si₂BN, G = 120 GPa and for graphene G = 405 GPa. This value for graphene is consistent with the one obtained using the formula G = E/(2(1 +ν)), which is valid for isotropic materials like graphene. In this formula, E is Young's modulus, and ν the Poisson's ratio. Considering that E and ν calculated with the same method,⁸ are E = 964 GPa and ν = 0.190, one finds exactly the same value for G (G = E/(2(1 + ν)) = 405 GPa).

In turn, Fig. 6(c) and (d) show the evolution of the Si–Si interatomic distances d₁, d₂ and d₃ for Si₂BN, and the C–C interatomic distances d₁ and d₂ for graphene as a function of ε_xy. These interatomic distances are shown in the insets. As Fig. 6(c) shows, the bond length d₁ increases as a function of ε_xy, while d₂ and d₃ decrease. For ε_xy = 0.27 (or ϕ ≈ 15°) the three interatomic distances become all equal and take the value d₁ = d₂ = d₃= 2.58 Å, corresponding to an increase of the Si–Si bond length of the order of 14%. For increasing ε_xy values, the new Si–Si bond is formed with bond length d₂ (or d₃), and the structure is transformed from AB into AA Si₂BN. On the other hand, Fig. 6(e) shows a totally different behavior for graphene, as already discussed above. The bond length d₁ does not change significantly versus ε_xy, while the change in the third neighbor distance d₂ is not enough to cause the breaking and the formation of new C–C bonds.

A useful practical application of the proposed phase transition would be in the field of micro-mechanical logic devices. This could be achieved by, say, assigning “0” and “1”, respectively, to AA and AB stacking. A key benefit of this is that Si₂BN based systems can be used to store data by means of mechanical applications without requiring electric power. Other applications may be considered by exploiting the practically infinite shear ductility of the structure (since the structural features are retained) either in the AA or AB stacking.

In conclusion, using first-principles calculations, we report the existence of an unusual phase transition in the novel Si₂BN 2D material, transforming Si₂BN with AB stacking into Si₂BN with AA stacking and vice versa. This is demonstrated via the application of in-plane shear strain which, contrary to other 2D materials, causes no buckling at any stage of the transformation process.

Author contributions

ZGF: conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, resources, supervision, validation, visualization, writing – original draft. MM: conceptualization, methodology, project administration, supervision, validation, visualization, writing – review & editing.

Data availability

All data that support the findings of this study are included in the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

ZGF wishes to acknowledge financial support from (i) the LESGO H2020-EIC-FETPROACT 2019–2020 project (agreement no. 952068) of the European Union and (ii) the project PRIN 2022 – Cod. 202278NHAM (PE11) CHERICH-C “Chemical and electrochemical energy storage materials from organic wastes: the treasure hidden in C-based materials” – CUP B53D23008590006, funded by the European Union – Next Generation EU in the context of the Italian National Recovery and Resilience Plan, Mission 4, Component 2, Investment 1.1, “Fondo per il Programma Nazionale di Ricerca e Progetti di Rilevante Interesse Nazionale (PRIN)”.

Notes and references

1. A. N. Andriotis, E. Richter and M. Menon, Phys. Rev. B, 2016, 93, 081413.
2. E. D. Sandoval, S. Hajinazar and A. N. Kolmogorov, Phys. Rev. B, 2016, 94, 094105.
3. Z. G. Fthenakis, M. Jaishi, B. Narayanan, A. N. Andriotis and M. Menon, J. Phys.: Condens. Matter., 2021, 33, 165001.
4. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
5. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter., 2002, 14, 2745.
6. H. R. Mahida, D. Singh, Y. Sonvane, P. B. Thakor, R. Ahuja and S. K. Gupta, J. App. Phys., 2019, 126, 233104.
7. C.-W. Wu, C. Xiang, H. Yang, W.-X. Zhou, G. Xie, B. Ou and D. Wu, Chin. Phys. B, 2021, 30, 037304.
8. Z. G. Fthenakis and M. Menon, Phys. Rev. B, 2019, 99, 205302.
9. S. Hu, Y. Yong, C. Li, Z. Zhao, H. Jia and Y. Kuang, Phys. Chem. Chem. Phys., 2020, 22, 13563–13568.
10. A. M. Satawara, G. A. Shaikh, S. K. Gupta, A. N. Andriotis, M. Menon and P. Gajjar, Int. J. Hydrogen Energy, 2023, 48, 25438–25449.
11. M. Jiang, J. Xu, P. Munroe, Z.-H. Xie and Z. Chen, Int. J. Hydrogen Energy, 2023, 50, 865–878.
12. R. Akilan, D. Ravichandran, S. Vinnarasi and R. Shankar, Mater. Lett., 2020, 279, 128487.
13. P. Panigrahi, Y. Pal, R. Ahuja and T. Hussain, Energy Fuels, 2021, 35, 12688–12699.
14. P. Panigrahi, S. B. Mishra, T. Hussain, B. R. K. Nanda and R. Ahuja, ACS Appl. Nano Mater., 2020, 3, 9055–9063.
15. V. Babar, A. Murat and U. Schwingenschlögl, J. Phys.: Cond. Matter., 2020, 32, 355602.
16. S. Thomas, A. K. Madam and M. Asle Zaeem, Phys. Chem. Chem. Phys., 2022, 24, 4394–4406.
17. D. Singh, S. Chakraborty and R. Ahuja, ACS Appl. Energy Mater., 2019, 2, 8441–8448.
18. D. S. Akilesh Muralidharan, M. Subramani and S. Ramasamy, J. Biomol. Struct. Dyn., 2023, 0, 1–32.
19. K. G. Reeves, Y. Yao and Y. Kanai, J. Chem. Phys., 2016, 145, 124705.
20. J. Zhou and S. Zhang, npj 2D Mater. Appl., 2021, 5, 16.
21. J. Zhou, S. Zhang and J. Li, NPG Asia Mater., 2020, 12, 2.
22. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
23. L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428.
24. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192.
25. Z. G. Fthenakis and N. N. Lathiotakis, Phys. Chem. Chem. Phys., 2015, 17, 16418–16427.

---