Discovering novel lead-free mixed cation hybrid halide perovskites via machine learning

Abstract

In our recent study (S. Alidoust, F. Jamalinabijan and A. Tekin, ACS Appl. Energy Mater., 2024, 7, 785–798), a thorough computational screening using density functional theory (DFT) was conducted on mixed cation halide perovskites with a general formula of AA′BX₃, aiming to identify promising lead-free candidates. Employment of 23 A/A′-cations, 29 B-ions, and 4 X-anions yielded approximately 29 000 possible perovskite combinations. However, while modern high-throughput DFT frameworks can handle large-scale calculations, treating the entire configurational space of 29 000 possible perovskite combinations remains computationally demanding. Leveraging machine learning (ML) approaches could provide a more efficient alternative for capturing this complexity. Therefore, by using two empirical criteria known as octahedral and tolerance factors, this huge number was narrowed to nearly 2700, and the corresponding decomposition energy and band gap calculations were performed for each one of them. However, the remaining nearly 26 300 perovskites, though not selected by the empirical criteria, could still hold valuable and potentially promising candidates. Therefore, an ML model has been trained on the DFT-calculated subset, which has been increased to 4181 to achieve molecular and elemental homogeneity in these data sets to predict and identify promising perovskites within the unexamined portion of the dataset. Remarkably, the ML approach identified 930 promising perovskites satisfying both the decomposition energy (≤0.025 eV per atom) and band gap (1.0 ≤ gap ≤ 2.0 eV) criteria. Among these, 20 perovskites were selected for further validation through DFT calculations, and a very nice agreement has been obtained between the predicted and calculated decomposition energy and band gap values. These findings highlight the effectiveness of ML in accelerating the discovery of materials with specific desirable properties.

---

1 Introduction

Energy has been a significant issue over the past few decades, with discussions highlighting the persistent challenges of both generating and storing it.¹ Oil, wood, and coal are examples of conventional energy sources that have been utilized for a long time because of their extensive availability, simplicity in storage and transportation, and low requirement for complex systems such as expensive energy storage plants.² On the other hand, these non-renewable energy resources produce greenhouse gases that endanger the globe.³ Therefore, there is a tremendous interest in the scientific community for finding environmentally friendly and renewable energy sources. In this respect, harvesting solar energy becomes an appealing candidate, even though the requirement of cutting-edge technological design solutions for the production and storage of solar energy.^4,5

In the photovoltaic (PV) industry, perovskite solar cells (PSCs) have recently gained extraordinary popularity for energy conversion. Perovskites are crystalline materials with a general formula of ABX₃, where A and B are inorganic cations and X is an anion.^6,7 Alternatively, hybrid organic–inorganic metal halide perovskites (HOIPs) are an emerging class of solar harvester materials due to their high efficiency and relatively low production costs.⁸ In 2009, Kojima et al.⁹ used HOIPs, in particular methylammonium (CH₃NH₃ = MA) lead iodide (MAPbI₃) and methylammonium lead bromide (MAPbBr₃), for the first time as visible-light sensitizers in photoelectrochemical cells. In 2011, Parks team fabricated a quantum-dot-sensitized solar cell based on MAPbI₃ nanocrystals with a power conversion efficiency (PCE) of 6.54%.¹⁰ The first solid-state HOIP, achieving 9.7% efficiency, was reported by Kim et al.¹¹ in 2012, followed by Lee et al.¹² with a 10.9% PCE using MAPbI₂Cl. Yu et al.¹³ improved this to 12% in 2014, while Im et al.¹⁴ reached 17.01% using a two-step spin-coating method. Breakthroughs continued with Yang et al.¹⁵ surpassing 20% efficiency with FAPbI₃ in 2015. Eperon et al.¹⁶ achieved 20.3% with a tandem structure in 2016, followed by Peng et al.,¹⁷ who reached 20.4% with a mixed-cation perovskite in 2017. In 2021, Yoo et al.¹⁸ attained a certified 25.2% efficiency using FAPbI₃ with MAPbBr₃, and Jeong et al.¹⁹ later reached 25.6% by suppressing anion-vacancy defects. As of now, single-junction PSCs have achieved a maximum certified PCE of 26.1%,²⁰ rivaling that of monocrystalline silicon solar cells.

The majority of these highly efficient PSCs are based on the toxic lead. Hence, searching for lead-free, efficient, and stable perovskite materials is so crucial for the PV industry.²¹ In order to find prospective lead-free HOIPs, new ingredients for both A and B sites have been experimentally investigated, and it has been found that promising lead-free perovskites can be obtained when B is replaced with less toxic ions such as Sn²⁺, Bi³⁺, Ge²⁺, Sb³⁺, Mn²⁺ and Cu²⁺.^22–29

In addition to these experimental studies, new promising perovskite candidates were obtained with the help of computational screening studies based on the expensive high-throughput density functional theory (DFT) calculations.^30–35 Meanwhile, data-driven research has recently attracted a lot of interest for accelerating this process by quickly screening candidates in the search for the new materials using materials repositories (such as materials project (MP),³⁶ Open Quantum Materials Database,³⁷ AFLOW,³⁸ and PAULING FILE³⁹) built from the DFT or experimental data.⁴⁰ In this context, machine learning (ML) algorithms have been widely used for the discovery of new materials.^41–44 For example, in 2016, Pilania et al.⁴⁵ used a support vector machines (SVM) classifier algorithm to illustrate the potent functionality and scalability of ML by assessing the formability of ABX₃ HOIPs using element-wise descriptors. By estimating the formability of 455 ABX₃ perovskites with ML, they found 40 promising new perovskites. Shuaihua et al.⁴⁶ chose the gradient boosting regression (GBR) algorithm from a comparison of six ML regression algorithms, including kernel ridge regression (KRR), SVM, Gaussian process regression (GPR), decision trees regression (DTR), and multi-layer perceptron (MLP), for the prediction of band gaps using a data set of 212 orthorhombic HOIPs, and they found 6 out of 5158 HOIPs with proper band gaps. A support vector classification model was developed in 2019 by Jain et al.⁴⁷ to predict the formability of 454 ABX₃ perovskites with the help of a dataset comprising 189 ABX₃ compounds mostly from the study of Li et al.⁴⁸ The developed model predicted 45 compounds as highly formable (with a formation probability greater than 0.8), and many of these were either experimentally synthesized or already published in the literature. Jino et al.⁴⁹ looked into the ML prediction of the band gap and decomposition energy of halide double perovskites using the gradient boosted regression trees (GBRT) approach. Specifically, the accuracy of GBRTs performance was comparable to the baseline error caused by the discrepancy between the experimental and DFT values. Ekaterina et al.⁵⁰ prepared a database of experimentally considered 515 two-dimensional (2D) HOIPs composed of 180 different organic cations, 10 metals (Pb, Sn, Bi, Cd, Cu, Fe, Ge, Mn, Pd, and Sb), and 3 halogens (I, Br, and Cl) and then used a Gradient Boosting Decision Tree (GBDT) approach to develop models to predict the band gap and partial atomic charges of 2D perovskites. In particular, they predicted the band gap and atomic partial charges with an accuracy of within 0.1 eV and 0.01 e, respectively. Zhang et al.⁵¹ trained several classifiers; the best performance was obtained with the extreme gradient boosting (XGBoost), using 44 HOIP and 58 non-HOIP samples collected from the literature to predict the formability of ABX₃ compounds, and they obtained 198 nontoxic perovskite candidates with a high probability of formability out of 18 560 virtual samples. Yang et al.²¹ used an ML technique to uncover promising double perovskites by training on the computed band gaps of 272 double perovskites. More recently, Lu et al.⁵² built a database containing experimentally synthesized 539 HOIPs and 24 non-HOIPs and then applied an imbalanced ML using elemental descriptors to predict the formability of 4320 ABX₃ candidates. In particular, they found that trifluoromethanaminium (TFMA) and azetidin-1-ium (AZ1) organic cations lead to the highly formable perovskites such as TFMAPbI₃, TFMASnI₃, TFMAPbBr₃, TFMABaI₃, TFMAPbCl₃, AZ1PbBr₃, and AZ1PbCl₃. In contrast to the previous studies, Wang et al.⁵³ collected the computed band gaps of 1747 double perovskites, not only halides but also oxides, from the MP database and then trained a classification predictive model using the GBDT algorithm. The resulting ML models have been used to predict the band gaps of 23 314 double perovskites and 6 perovskites (including Cs₂AgIrBr₆, Cs₂CdGeBr₆, and Rb₂AgIrBr₆) were found with promising optoelectronic properties.

In the literature, most of the ML studies focused on the perovskites with a general formula of ABX₃. However, the most efficient perovskites include either individual or complete mixing strategies of A, B, or X sites. In this regard, recently, a computational screening study has been performed in our research group to find promising perovskites with a general formula of AA′BX₃.⁵⁴ In this screening study, approximately 29 000 perovskite candidates, composed of 23 A/A′-cations, 29 divalent B-ions, and 4 X-anions, have been generated. By using empirical Goldschmidt tolerance (t)⁵⁵ and octahedral (μ) factors, it has been concluded that 2710 candidates tend to form stable perovskite structures, and then their corresponding decomposition energy (E_dec) and band gap (E_gap) were calculated at the DFT level.

However, it is known that the t does not always correctly discriminate between perovskite and nonperovskite materials. Bartel et al.⁵⁶ showed that using the Goldschmidt tolerance factor, only 74% of metal oxide and metal halide materials can be predicted as perovskite. They proposed a new tolerance factor as follows:

which offers a considerably better prediction of perovskite stability as seen in experiments.⁵⁶ Here, n_A is the oxidation state of A-cations and r_A, r_B, and r_X are the ionic radii of the A, B, and X sites, respectively. T < 4.18 indicates a promising perovskite structure.⁵⁶ Bartel et al.⁵⁶ showed that for around 1500 perovskite compounds, the T prediction is in agreement with the stability seen in experiments for more than 90% of the compounds.

Due to these facts, some of the left out perovskite candidates in our previous screening study,⁵⁴ ≃18 000 after the elimination of AA′BF₃ perovskites, which mostly lead to wide band gaps, could potentially be a favorable material. Therefore, revisiting and further investigating the potential of these left out perovskites is a necessity for the discovery of new promising perovskites. For this purpose, two different ML models have been trained based on the DFT outcomes of our previous study to predict the E_dec and E_gap of nearly 18 000 perovskite structures.

2 Method

2.1 Computational details

Structure optimizations have been performed by utilizing DFT as implemented in the Quantum Espresso (QE) simulation package.⁵⁷ The generalized gradient approximation (GGA) functional of Perdew–Becke–Ernzerhof (PBE)⁵⁸ was used as an exchange correlation (xc) functional. Electron–ion interactions were described by ultrasoft pseudopotentials (USPPs) available in the QE library.⁵⁹ Kinetic and charge density cutoffs of 40 and 320 Ry were set for all atoms, respectively. Structural relaxations were performed by sampling the Brillouin zone with a 4 × 4 × 4 k-point grid. Energy and force convergence criteria were chosen to be 10⁻⁵ and 10⁻⁴, respectively. In all DFT calculations, spin polarization was neglected.

As already detailed in our recent screening study,⁵⁴ metal halide perovskites can be synthesized by the spontaneous reaction of MAI and PbI₂ salts at room temperature:⁶⁰

MAI + PbI₂ → MAPbI₃ (2)

As similar to the mono-cation metal halide perovskites, dual-cation AA′BX₃ HOIPs (such as Cs_xMA1−xPbI₃^61,62 and MA_xFA1−xPbI₃⁶³) can be synthesized by mixing precursors of AX, A′X, and BX₂ as shown below:

For this reaction, the stability (E_dec or decomposition energy) can be assessed by using the following formula,^{32,33,64–70} which indicates the decomposition of AA′BX₃ into its corresponding binary constituents:

where is the total energy of AA′BX₃ and E_AX, E_A′X and E_BX2 are the total energies of AX, A′X, and BX₂, respectively. x and y depend on the stoichiometric ratio of the two cations, and their sum is 1. Negative E_dec denotes the stability of the perovskite. Perovskites are considered stable if their E_dec is below 0.025 eV per atom.⁷¹ While most of the AX, A′X, and BX₂ structures were taken from the open quantum materials database (OQMD)⁷² and the materials project (MP),⁷³ the ones that do not exist in these databases were manually generated with the help of known structures.

As is well-known, standard DFT tends to underestimate the band gaps of hybrid halide perovskites.⁷⁴ Although more accurate methods like hybrid functionals or GW approximations provide better estimates,³⁰ their high computational cost makes them unsuitable for large screening studies. In our previous work, we relied on the GLLB-SC (Gritsenko, O., Leeuwen, R., Lenthe, E., & Baerends, E.; SC stands for solid correlation) functional,⁷⁵ which has been shown to offer a reliable balance of accuracy and computational efficiency for predicting the band gaps of metal oxides and perovskites.^30,76 Due to its favorable performance in our earlier study,⁵⁴ we have continued to use this functional in the current work to perform band gap calculations efficiently as implemented in GPAW.⁷⁷ The band gaps produced by the GLLB-SC functional differ by 0.5 eV from the experimental ones.⁷⁸ In these band gap calculations, an 8 × 8 × 8 Monkhorst–pack k-point grid was employed. GLLB-SC band gaps were corrected by subtracting spin–orbit coupling (SOC), which is the interaction between an electron's spin and its orbital motion around the nucleus.⁷⁹

2.2 Data preparation: dual-cation AA′BX₃ perovskite data sets

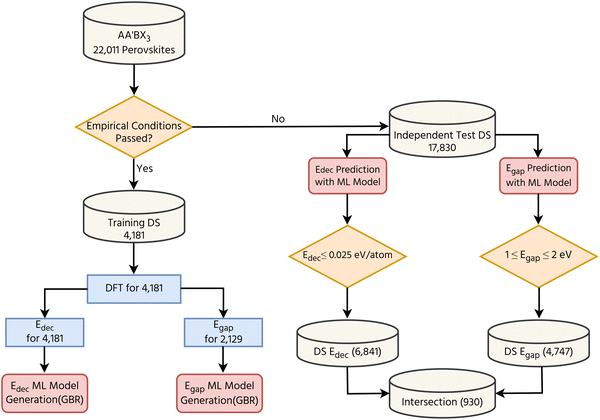
The flowchart shown in Fig. 1 summarizes the strategy used for the development of two ML models to predict the band gap and decomposition energy of AA′BX₃ perovskites. In our previous computational screening study,⁵⁴ nearly 29 000 AA′BX₃ perovskite combinations were considered. This number is reduced to 22 011 after the elimination of AA′BF₃ perovskites, which mostly have large band gaps. By applying empirical tolerance and octahedral factors, it has been found that 2710 candidates tend to form stable perovskites. To achieve molecular and elemental homogeneity in these data sets, additional decomposition energy and band gap calculations were also performed using the same DFT settings applied in our previous study.⁵⁴ This increased the number of considered perovskites in the data set to 4181. Out of the 4181 compounds, E_gap calculations were successfully completed for 2129 structures. As a result, two different data sets were built with the help of DFT calculations: DS^E_f holds 4181 E_dec values, and DS^E_gap comprises 2129 E_gap values. Two different ML models have been trained using these two data sets together with the GBR algorithm. As can be seen from the flowchart shown in Fig. 1, 17 830 AA′BX₃ perovskites do not satisfy the empirical conditions, and this set was called an independent test. Two different criteria, E_dec ≤ 0.025 eV per atom and 1 ≤ E_gap ≤ 2 eV, were used to select the promising perovskites. Finally, the perovskites satisfying both criteria at the same time have been collected.

Fig. 1 Data preparation and utilization workflow for ML models.

2.3 Machine learning

After testing several ML algorithms, such as DTR, K-nearest neighbors regression, and neural network regression from the scikit-learn ML library,⁸⁰ due to its better performance, the GBR algorithm was used to build ML models for the estimation of the decomposition energy and band gap of 17 830 AA′BX₃ perovskites included in the independent test.

The GBR algorithm was trained using the DFT-computed data sets, which were split into the training and test sets using a random selection process. The mean squared error (MSE), median absolute deviation (MAD), Root-mean-square deviation (RMSD), and R-squared (R²) were used as error metrics for the evaluation of the accuracy of the GBR model. The best models obtained at this step were dumped on Python pickles to use them for the independent test.

Feature (descriptor) selection is one of the most important steps in the ML model building process. Since the training of the ML models have been carried out using the DFT computed data sets, employment of features based on the crystal structures of AA′BX₃ perovskites such as lattice parameters, space group, cell volume and specific distances between A, B and X sites is more obvious. However, the corresponding structural features of the independent test are not known due to the lack of crystalline structural information. Therefore, obeying only the element-wise features is a necessity to establish a correlation between the chemical environment and the corresponding decomposition energies and band gaps. Particularly, some of these element-wise features were accumulated with the help of Pymatgen⁸¹ and Matminer⁸² open-source Python packages. Since these packages can produce a plethora of element-wise descriptors, only the most significant ones must be employed to increase the accuracy of the ML model and to avoid any possible overfitting/underfitting. As a result of these facts, feature engineering was also carried out during the ML model development. In this regard, an innovative method for hyperparameter tuning utilizing cross-validation (CV) via the GridSearchCV function within scikit-learn⁸⁰ was used to evaluate the performance of every combination of hyperparameters and identify the most optimal parameter values of the model. CV was implemented throughout the ML model construction phase. The value of “CV” in hyperparameter tuning specifies the number of folds in cross-validation, dividing data into subsets for training and evaluation. Through experiments with several CV values, the optimal CV value was determined, highlighting its pivotal role in improving model accuracy and robustness. Numerous combinations of hyperparameters, including loss function, learning rate, maximum depth, and number of estimators, were evaluated, and the most suitable ones were employed during the building of the highly accurate GBR models.

3 Results and discussion

3.1 Decomposition energy predictions

A dataset of DS^E_dec comprising 4181 compounds was utilized for the model generation to predict the decomposition energies. Fig. 2 illustrates a histogram analysis of the DS^E_dec dataset, where E_dec is changing between −0.4 eV per atom to 0.6 eV per atom, along with the frequency of A/A′, B, and X constituents within AA′BX₃ perovskites.

Fig. 2 Frequency of occurrences of E_dec, E_gap, A-cation, B-ion and X-anion of the DS^E_dec data set.

A total of 14 elemental descriptors, listed in the ESI,† were derived to characterize the E_dec of AA′BX₃ perovskites and were utilized as features in data sets for further analysis. The DS^E_dec data set was divided into two parts: 80% used for training and 20% for testing. The cross-validation method was applied by utilizing CV = 10 to identify the most appropriate parameters for the GBR model. As a result, ‘learning_rate’: 0.085, ‘loss’: ‘ls’, ‘max_depth’: 6, ‘min_samples_leaf’: 3, ‘min_samples_split’: 3, ‘n_estimators’: 300, ‘subsample’: 0.85 were selected and utilized for building the GBR model. In particular, an accuracy score of approximately 0.85 was reached for the test data set upon the employment of nearly 4000 data points. After creating and evaluating thousands of GBR ML models, the one exhibiting superior accuracy in predictions was selected as the best-performing GBR model. The following error metrics were obtained for the train and test data sets using the best GBR ML model. For the former, MSE: 0.063, R²: 0.983, RMSD: 0.251, and MAD: 0.169, and for the latter, MSE: 0.213, R²: 0.936, RMSD: 0.462, and MAD: 0.293, respectively. Fig. 3 shows the predicted decomposition energies of cubic AA′BX₃ perovskites in comparison to the calculated ones and the corresponding feature importance. It is obvious that the radius of the B site (r_B) has the greatest impact on the ML model performance, followed by the electronegativity of the B-ion and X-anion. The remaining features, especially the ones related to the perovskite structure, such as the tolerance factor (t), new tolerance factor (T),⁵⁶ and octahedral factor (μ) seem less important for the model performance. As it will be discussed in the next section, this best GBR ML model will be exploited to predict the decomposition energies of the independent data set comprising 17 830 perovskites.

Fig. 3 ML predicted decomposition energies of the cubic perovskites in the DS^E_dec dataset (left) and the corresponding feature importance (right).

3.2 Band gap predictions

For the prediction of band gap energies, the DS^E_gap data set, which contains 2129 band gaps of AA′BX₃ perovskites calculated at the GLLB-SC-SOC level, has been utilized. After conducting tests on over 30 different elemental descriptors, a total of 14 features, which were provided in Table S1 of the ESI,† were chosen for the GBR model generation. As similar to the E_dec predictions, the cross-validation approach has been utilized with the same settings to obtain the most suitable set of parameters. The data set has been divided into train and test sets with the following percentages: 75 and 25%, respectively. As the loss function, ‘lad’ has been selected, and the number of boosting stages (n_estimators) was set to 800. The maximum depth of the individual regression estimators, the minimum number of samples needed to split an internal node, and the learning rate (shrinkage factor) have been set to 5, 4, and 0.085, respectively. Fig. 4 shows the band gap prediction results of the cubic AA′BX₃ perovskites and the corresponding importance ranking of the features that have been used in the GBR ML model generation. As compared to the E_dec predictions, instead of only a few dominant features, it seems that all the considered features play a crucial role in making reliable band gap predictions. More specifically, the electronegativity of B-ion, which is also a dominant feature in the E_dec GBR ML model, is the most important descriptor in the band gap GBR ML model, followed by the standard deviation of the Mendeleev number (σ(MN)) and the tolerance factor (t). For the train data set, the following error metrics of MSE: 0.113, R²: 0.971, RMSD: 0.336, and MAD: 0.177 eV were obtained. In the case of the test data set, these errors were slightly increased to MSE: 0.202, R²: 0.946, RMSD: 0.449, and MAD: 0.319 eV. It should also be noted that the averaged RMSD of the test data set, 0.449 eV, was found quite comparable with the one (0.462 eV) obtained for the E_dec predictions. Nevertheless, it is apparent that the best GBR ML model demonstrated exceptional performance in the prediction of the band gaps.

Fig. 4 ML predicted band gap energies of the cubic perovskites in the DS^E_gap data set (left) and the corresponding feature importance (right).

Table 1 summarizes the error metrics obtained for the train and test data sets for both E_dec and E_gap predictions. Additionally, Table 2 shows the error values obtained for both E_dec and E_gap predictions of different materials in previous ML studies in the literature. It can be seen that the error values obtained in this study are within an acceptable range, especially when compared to those reported in similar studies.

Table 1 Error metrics obtained for the train and test data sets using the best GBRT ML model for both E_dec and E_gap predictions

Error metrics	E dec train	E dec test	E gap train	E gap test
MSE	0.063	0.213	0.113	0.202
R ^2	0.983	0.936	0.971	0.946
RMSD	0.251	0.462	0.336	0.449
MAD	0.169	0.293	0.177	0.319

---

Table 2 Error values from earlier research using various materials

Material (ML model)	Error
Double halide perovskites (GBRT)^49	RMSE (Edec) = 0.021 eV per atom
	RMSE (Egap) = 0.223
Double oxide perovskites (random forests)^83	MAE (Egap) = 0.180 eV
	R 2 (Egap) = 0.860 eV
MP-crystals-2018.6.1 data set (MEGNet)^84	MAE (Ef) = 0.028 eV per atom
	MAE (Egap) = 0.330 eV

---

The same E_dec and E_gap ML model generation and prediction procedure has also been applied to the orthorhombic and tetragonal perovskite phases, whose results are given in the ESI.†

3.3 Decomposition energy and band gap predictions for the independent data set

Following the development of accurate GBR ML models, these ML models have also been utilized to predict the decomposition energy and band gap of 17 830 AA′BX₃ perovskites included in the independent data set. In particular, the best GBR ML decomposition energy and band gap prediction models yielded that 6841 of 17 830 perovskites have a decomposition energy that is lower than 0.025 eV per atom, and 4747 perovskites have a desired band gap between 1.0 and 2.0 eV. Moreover, it has been found that a subset of 930 AA′BX₃ cubic perovskites meets both criteria simultaneously. Fig. 5 illustrates the distribution and frequency of occurrences of the A, B, and X components within the 930 compounds. Additionally, it provides a heatmap analysis showcasing the distribution pattern of A/A′-cations across these compounds. As can be seen from Fig. 5a, V is the most dominant B-cation, and it is followed by Ag. Among A-cations and X-anions, i-BuA, DiEA, and Cl were found to be the most favored ones. The heat-map in Fig. 5b highlights which A must be coupled with which A′ cation. The top mixing between A and A′ has been achieved with the following cation pairs: HY/i-BuA, HY/PhA, DiEA/HY, DiEA/HA.

Fig. 5 Frequency of occurrences of the A, B, and X components (left) and a heatmap analysis showing the distribution of A/A′-cations (right) within the 930 compounds.

In the final stage, a refined filtering process was applied to the predicted set of 930 perovskites using the new tolerance (0 < T < 4.18) and octahedral (0.414 < μ < 0.592) factors. This additional screening helped to further narrow down the subset, isolating the most promising candidates with the most favorable structural features. In particular, this filtration reduced the number of candidate structures to 485. Fig. S1 of the ESI† shows the frequency of occurrences of the A, B, and X components within the 485 compounds. Among them, 20 compounds were randomly selected to assess the accuracy of the GBR ML models. For this purpose, the decomposition and band gap energies of these 20 perovskites listed in Table 3 were calculated at the DFT level, and the obtained results were compared with the ML-predicted ones in Fig. 6. Specifically, very low MSEs of 0.160 and 0.098 have been obtained for the decomposition and band gap energies, respectively. This comparison highlights the accuracy of ML predictions, showing that the ML model's estimations for both the decomposition energy and band gap energy closely match the calculated values. Since ML models provide valuable insights for these 930 perovskites, integrating them into experimental workflows is essential to validate and explore their true potential in practical applications. Moreover, the performance of these ML models for the other perovskite formulas, such as AA′BB′X₃, might also be interesting.

Table 3 Predicted and calculated E_gap and E_dec values (in eV) and dimensionalities of 20 perovskites shown in Fig. 6

Perovskite	Predicted Egap	Calculated Egap	Predicted Edec	Calculated Edec	Dimension
3-Py DiMA SnBr3	1.72	1.62	−0.62	−0.24	3-D
3-Py FM InBr3	1.41	0.69	0.20	−0.42	Low-D
3-Py HA SnBr3	1.59	1.88	−1.67	−1.52	3-D
DiEA Cs InI3	1.91	1.70	0.05	−0.07	Low-D
DiEA HA PbI3	1.97	2.38	1.06	0.48	3-D
DiMA AA SnI3	1.16	1.10	0.67	0.59	3-D
DiMA TroP AgCl3	1.13	1.56	−0.45	−0.07	Low-D
EA AA SnI3	1.11	0.87	0.46	0.59	3-D
EA NH4SnBr3	1.66	1.44	−1.47	−1.56	3-D
FA HA SnBr3	1.35	1.14	−1.78	−1.95	3-D
FM HA SnBr3	1.50	2.20	−1.72	−1.78	3-D
FM i-BuA InI3	1.32	1.14	0.00	0.46	Low-D
FM TriMA SnBr3	1.84	2.20	−0.44	−0.82	3-D
GUA TiZ SnI3	1.32	1.19	0.52	0.36	3-D
HA i-BuA SnI3	1.68	1.63	−0.13	0.15	3-D
HA TetraMA SnBr3	1.87	1.85	−0.69	−1.05	3-D
HY i-BuA PbI3	1.95	1.85	0.49	0.22	3-D
HY i-BuA SnI3	1.67	1.60	0.03	−0.06	3-D
HY Py InI3	1.04	1.29	0.42	0.37	Low-D
TriMA GUA SnI3	1.19	1.42	−0.85	0.34	3-D

---

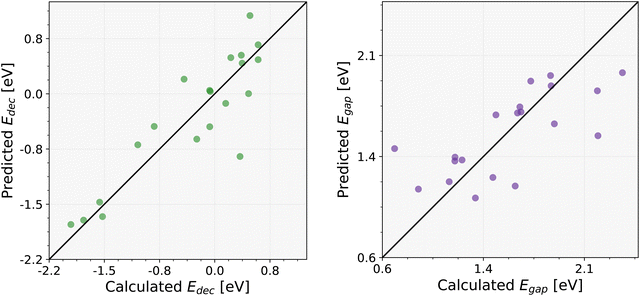Fig. 6 Comparison of predicted and computed decomposition energy (on the left panel) and band gap (on the right panel) for 20 new cubic perovskites.

4 Conclusions

In this study, we highlighted the potential of ML to accelerate the discovery of lead-free perovskite materials with the formula of AA′BX₃. We conducted a computational screening using high-throughput DFT to evaluate the decomposition energy and band gap of a vast set of mixed-cation halide perovskites. Initially, octahedral and tolerance factors were applied to reduce the number of candidates from approximately 29 000 to nearly 2700, for which DFT calculations were performed. Recognizing that the remaining 26 300 configurations might still contain promising materials, we trained ML models on the DFT-calculated data sets to predict the properties of these perovskites. After testing various ML algorithms, we selected GBR for its superior performance in predicting these properties. Separate GBR models were developed using elemental and structural features to predict decomposition energy and band gap. The GBR models demonstrated high accuracy with MSE errors of 0.063 and 0.113 for the decomposition energy and band gap GBR models, respectively. Our ML approach identified 930 potential perovskite candidates that met the criteria for decomposition energy (E_dec ≤ 0.025 eV per atom) and band gap (1.0 ≤ E_gap ≤ 2.0 eV). Out of 930, 20 perovskites were randomly selected for DFT calculations to validate the accuracy of our predictions, and very low MSEs of 0.160 and 0.098 eV have been obtained for the decomposition and band gap energies, respectively. These findings highlight the robustness of our ML approach and its potential to accelerate the discovery of new, environmentally friendly perovskite materials for optoelectronic applications.

Data availability

An open-source software implementation of our ML models and data sets are available at https://github.com/tccdem/Perosolar.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was financially supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK-119Z493). Computing resources are provided by the National Center for High Performance Computing of Turkey (UHeM), under Grant Number 1002132012, TÜBİTAK ULAKBİM, High Performance and Grid Computing Center (TRUBA resources), and Informatics Institute of İstanbul Technical University.

References

1. T. Kousksou, P. Bruel, A. Jamil, T. El Rhafiki and Y. Zeraouli, Sol. Energy Mater. Sol. Cells, 2014, 120, 59–80.
2. T. Mahlia, T. Saktisahdan, A. Jannifar, M. Hasan and H. Matseelar, Renewable Sustainable Energy Rev., 2014, 33, 532–545.
3. P. A. Owusu and S. Asumadu-Sarkodie, Cogent Eng., 2016, 3, 1167990.
4. O. Kaya, A. M. Klepacka and W. J. Florkowski, J. Environ. Manage., 2019, 248, 109309.
5. P. G. V. Sampaio and M. O. A. González, Renewable Sustainable Energy Rev., 2017, 74, 590–601.
6. G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988.
7. T. Brenner, D. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007.
8. K. P. Bhandari and R. J. Ellingson, in A Comprehensive Guide to Solar Energy Systems, ed. T. M. Letcher and V. M. Fthenakis, Academic Press, 2018, pp. 233–254.
9. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 , PMID: 19366264.
10. J.-H. Im, C.-R. Lee, J.-W. Lee, S.-W. Park and N.-G. Park, Nanoscale, 2011, 3, 4088–4093.
11. H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum, J.-E. Moser, M. Grätzel and N.-G. Park, Sci. Rep., 2012, 2, 591.
12. M. Lee, J. Teuscher, T. Miyasaka, T. Murakami and J.-H. Im, Science, 2012, 338, 643–647.
13. F. Wang, F. Xie, W. Li, J. Chen and N. Zhao, Adv. Funct. Mater., 2014, 24, 3417–3423.
14. J.-H. Im, I.-H. Jang, N. Pellet, M. Grätzel and N.-G. Park, Nat. Nanotechnol., 2014, 9, 927–932.
15. W. S. Yang, J. H. Noh, N. J. Jeon, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Science, 2015, 348, 1234–1237.
16. G. E. Eperon, et al. , Science, 2016, 354, 861–865.
17. J. Peng, et al. , Energy Environ. Sci., 2017, 10, 1792–1800.
18. J. J. Yoo, G. Seo, M. R. Chua, T. G. Park, Y. Lu, F. Rotermund, Y.-K. Kim, C. S. Moon, N. J. Jeon, J.-P. Correa-Baena, V. Bulović, S. S. Shin, M. G. Bawendi and J. Seo, Nature, 2021, 590, 587–593.
19. J. Jeong, et al. , Nature, 2021, 592, 381–385.
20. Best Research-Cell Efficiency Chart, 2023, https://www.nrel.gov/pv/assets/pdfs/best-research-cell-efficiencies.pdf.
21. Z. Yang, Y. Liu, Y. Zhang, L. Wang, C. Lin, Y. Lv, Y. Ma and C. Shao, J. Phys. Chem. C, 2021, 125, 22483–22492.
22. N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068.
23. N. Leblanc, N. Mercier, L. Zorina, S. Simonov, P. Auban-Senzier and C. Pasquier, J. Am. Chem. Soc., 2011, 133, 14924–14927 , PMID: 21866937.
24. W. Bi, N. Leblanc, N. Mercier, P. Auban-Senzier and C. Pasquier, Chem. Mater., 2009, 21, 4099–4101.
25. B.-W. Park, B. Philippe, X. Zhang, H. Rensmo, G. Boschloo and E. M. J. Johansson, Adv. Mater., 2015, 27, 6806–6813.
26. T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, Z. Zhang, M. Sherburne, S. Li, M. Asta, N. Mathews and S. G. Mhaisalkar, J. Mater. Chem. A, 2015, 3, 23829–23832.
27. C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 6804–6819 , PMID: 25950197.
28. B. Saparov, F. Hong, J.-P. Sun, H.-S. Duan, W. Meng, S. Cameron, I. G. Hill, Y. Yan and D. B. Mitzi, Chem. Mater., 2015, 27, 5622–5632.
29. D. Cortecchia, H. A. Dewi, J. Yin, A. Bruno, S. Chen, T. Baikie, P. P. Boix, M. Grätzel, S. Mhaisalkar, C. Soci and N. Mathews, Inorg. Chem., 2016, 55, 1044–1052 , PMID: 26756860.
30. I. Castelli, J. M. García-Lastra, K. Thygesen and K. Jacobsen, APL Mater., 2014, 2, 081514.
31. M. R. Filip and F. Giustino, J. Phys. Chem. C, 2016, 120, 166–173.
32. D. Yang, J. Lv, X. Zhao, Q. Xu, Y. Fu, Y. Zhan, A. Zunger and L. Zhang, Chem. Mater., 2017, 29, 524–538.
33. L. Jiang, T. Wu, L. Sun, Y.-J. Li, A.-L. Li, R.-F. Lu, K. Zou and W.-Q. Deng, J. Phys. Chem. C, 2017, 121, 24359–24364.
34. R. Ali, G.-J. Hou, Z.-G. Zhu, Q.-B. Yan, Q.-R. Zheng and G. Su, J. Mater. Chem. A, 2018, 6, 9220–9227.
35. S. Körbel, M. A. L. Marques and S. Botti, J. Mater. Chem. A, 2018, 6, 6463–6475.
36. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
37. S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010.
38. S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226.
39. E. Blokhin and P. Villars, in Handbook of Materials Modeling: Methods: Theory and Modeling, ed. W. Andreoni and S. Yip, Springer International Publishing, Cham, 2018, pp. 1–26.
40. J. Wei, X. Chu, X. Sun, K. Xu, H. Deng, J. Chen, Z. Wei and M. Lei, InfoMat, 2019, 1, 338–358.
41. Y. Liu, T. Zhao, W. Ju and S. Shi, J. Materiomics, 2017, 3, 159–177 , high-throughput experimental and modeling research toward advanced batteries.
42. J. Cai, X. Chu, K. Xu, H. Li and J. Wei, Nanoscale Adv., 2020, 2, 3115–3130.
43. R. Vasudevan, G. Pilania and P. V. Balachandran, J. Appl. Phys., 2021, 129, 070401.
44. E. O. Pyzer-Knapp, J. W. Pitera, P. W. J. Staar, S. Takeda, T. Laino, D. P. Sanders, J. Sexton, J. R. Smith and A. Curioni, npj Comput. Mater., 2022, 8, 84.
45. G. Pilania, P. Balachandran, C. Kim and T. Lookman, Front. Mater., 2016, 3, 19.
46. S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Nat. Commun., 2018, 9, 3405.
47. D. Jain, S. Chaube, P. Khullar, S. Goverapet Srinivasan and B. Rai, Phys. Chem. Chem. Phys., 2019, 21, 19423–19436.
48. C. Li, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 64, 702–707.
49. J. Im, S. Lee, T.-W. Ko, H. W. Kim, Y. Hyon and H. Chang, npj Comput. Mater., 2019, 5, 37.
50. E. I. Marchenko, S. A. Fateev, A. A. Petrov, V. V. Korolev, A. Mitrofanov, A. V. Petrov, E. A. Goodilin and A. B. Tarasov, Chem. Mater., 2020, 32, 7383–7388.
51. S. Zhang, T. Lu, P. Xu, Q. Tao, M. Li and W. Lu, J. Phys. Chem. Lett., 2021, 12, 7423–7430 , PMID: 34337946.
52. T. Lu, H. Li, M. Li, S. Wang and W. Lu, J. Phys. Chem. Lett., 2022, 13, 3032–3038 , PMID: 35348327.
53. Z. Wang, Y. Han, X. Lin, J. Cai, S. Wu and J. Li, ACS Appl. Mater. Interfaces, 2022, 14, 717–725 , PMID: 34967594.
54. S. Alidoust, F. Jamalinabijan and A. Tekin, ACS Appl. Energy Mater., 2024, 7, 785–798.
55. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
56. C. Bartel, C. Sutton, B. Goldsmith, R. Ouyang, C. Musgrave, L. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693.
57. P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
59. https://www.quantum-espresso.org/pseudopotentials .
60. D. B. Mitzi, Progress in Inorganic Chemistry, John Wiley & Sons, Ltd, 1999, pp. 1–121.
61. H. Choi, J. Jeong, H.-B. Kim, S. Kim, B. Walker, G.-H. Kim and J. Y. Kim, Nano Energy, 2014, 7, 80–85.
62. G. Niu, W. Li, J. Li, X. Liang and L. Wang, RSC Adv., 2017, 7, 17473–17479.
63. N. Pellet, P. Gao, G. Gregori, T.-Y. Yang, M. K. Nazeeruddin, J. Maier and M. Grätzel, Angew. Chem., Int. Ed., 2014, 53, 3151–3157.
64. M.-G. Ju, J. Dai, L. Ma and X. C. Zeng, J. Am. Chem. Soc., 2017, 139, 8038–8043.
65. Y.-Y. Zhang, S. Chen, P. Xu, H. Xiang, X.-G. Gong, A. Walsh and S.-H. Wei, Chin. Phys. Lett., 2018, 35, 036104.
66. C.-J. Yu, JPhys Energy, 2019, 1, 022001.
67. A. S. Thind, X. Huang, J. Sun and R. Mishra, Chem. Mater., 2017, 29, 6003–6011.
68. U.-G. Jong, C.-J. Yu, Y.-M. Jang, G.-C. Ri, S.-N. Hong and Y.-H. Pae, J. Power Sources, 2017, 350, 65–72.
69. U.-G. Jong, C.-J. Yu, J.-S. Ri, N.-H. Kim and G.-C. Ri, Phys. Rev. B, 2016, 94, 125139.
70. E. Tenuta, C. Zheng and O. Rubel, Sci. Rep., 2016, 6, 37654.
71. A. A. Emery and C. Wolverton, Sci. Data, 2017, 4, 170153.
72. S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 1–15.
73. A. Jain, J. Montoya, S. Dwaraknath, N. Zimmermann, J. Dagdelen, M. Horton, P. Huck, D. Winston, S. Cholia, S. Ong and K. Persson, in Handbook of Materials Modeling, ed. W. Andreoni and S. Yip, Springer, Cham, 2nd edn, 2020, pp. 1751–1784.
74. F. Brivio, K. T. Butler, A. Walsh and M. van Schilfgaarde, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155204.
75. O. Gritsenko, R. van Leeuwen, E. van Lenthe and E. J. Baerends, Phys. Rev. A, 1995, 51, 1944–1954.
76. I. E. Castelli, T. Olsen, S. Datta, D. D. Landis, S. Dahl, K. S. Thygesen and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 5814–5819.
77. J. J. Mortensen, et al. , J. Chem. Phys., 2024, 160, 092503.
78. I. Castelli, J. M. García-Lastra, K. Thygesen and K. Jacobsen, APL Mater., 2014, 2, 081514.
79. L. Jiang, W. Tao, L. Sun, Y. Li, A.-L. Li, R. Lu, K. Zou and W. Deng, J. Phys. Chem. C, 2017, 121, 24359–24364.
80. F. Pedregosa, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830.
81. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
82. L. Ward, et al. , Comput. Mater. Sci., 2018, 152, 60–69.
83. A. Talapatra, B. P. Uberuaga, C. R. Stanek and G. Pilania, Commun. Mater., 2023, 4, 46.
84. GitHub – materialsvirtuallab/megnet: Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals – github.com, https://github.com/materialsvirtuallab/megnet?tab=readme-ov-file, [accessed 17-08-2024].

---

Footnote

† Electronic supplementary information (ESI) available: Distribution and frequency of occurrences of the A, B, and X components and a heatmap analysis showing the distribution of A/A′-cations within the 485 compounds are provided. ML performance and feature importance on the decomposition energies and band gaps of both orthorhombic and tetragonal perovskites are also provided. Moreover, we have also provided a zip file including all data sets used in the ML model generation, the resulting best ML models and a csv file listing the 930 promising perovskites together with their predicted E_dec and E_gap values. See DOI: https://doi.org/10.1039/d4cp04218b

---