 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics of hydrogen adsorption on ruthenium fcc surfaces: a density functional theory study
Marietjie J.
Ungerer
 ab and
Nora H.
de Leeuw
ab and
Nora H.
de Leeuw
 *bc
*bc
aSchool of Chemistry, Cardiff University, Cardiff CF10 3AT, UK
bSchool of Chemistry, University of Leeds, Leeds LS2 9JT, UK. E-mail: M.J.Ungerer@leeds.ac.uk
cDepartment of Earth Sciences, Utrecht University, 3584 CB Utrecht, The Netherlands
First published on 28th February 2025
Abstract
Within the framework of the application of liquid organic hydrogen carriers (LOHC) to store, transport and re-generate hydrogen, ruthenium (Ru) is by far the most widely used catalyst. In its natural bulk state, the most abundant phase observed is the hexagonal close-packed (hcp) phase, but experimental studies on nanoparticles have shown that the face-centred cubic (fcc) phases are also present and are highly active in catalytic reactions. In this study, we have carried out calculations based on the density functional theory, with the generalized gradient approximation and long-range dispersion corrections, to investigate the behaviour of hydrogen adsorption at the fcc Ru (001), (011) and (111) surfaces. The Ru surfaces have been covered systematically with hydrogen (H), with a focus on the geometries, stabilities and adsorption energies. A detailed analysis has been performed of the energetic and electronic properties of a hydrogen monolayer on the Ru surfaces, combined with a thermodynamic analysis of the effect of temperature and pressure on the surface coverage, where the highest surface coverage observed was on the Ru (001) and (011) surfaces. The results indicate that the dissociation of H2 occurs readily and that the adsorption energies of single H atoms are between 0.4 and 0.6 eV. Neither recombination of H atoms to form molecular hydrogen (H2) or surface poisoning was observed.
1. Introduction
Among carbon-free energy sources, hydrogen (H2) technologies are a particularly attractive choice for sustainable energy production and storage.1 The production of clean H2 has been the focus of much investment and research. Some of these production technologies include the electrocatalytic splitting of water,2–6 steam methane reformation,7 the steam iron process,8 the sulphur–iodine cycle,9,10 the copper–chlorine cycle,10 and hydrogen from biomass.11,12In most of these technologies, metal catalysts, often platinum (Pt), are needed to facilitate H2 conversion and/or production. Several studies13–15 have shown that reducing the Pt content in catalysts by ruthenium (Ru) improved the material properties leading to enhanced hydrogen production.16 Small amounts of Ru can increase the hardness of Pt and palladium (Pd),17 thereby increasing corrosion resistance in superalloys,18 which are all attractive qualities in the highly corrosive environment of electrochemistry. Natural Ru has a hexagonal close-packed (hcp) crystal structure, but recent research19,20 has shown that it is also possible to produce stable and highly reactive face-centred cubic (fcc) nanoparticles.
Both experimental21,22 and theoretical studies23 have shown that for various catalytic systems using hcp Ru nanoparticles, high concentrations of dissociated hydrogen block the active sites, preventing subsequent reactions from occurring and thereby effectively poisoning the surfaces. If a more active fcc phase were to be considered, it is equally important to ascertain whether hydrogen poisoning would still occur. A detailed description is therefore needed of the interaction, i.e. adsorption, binding and reaction, of hydrogen on the catalytic surface.
In previous studies,24 we have focussed on different types of fcc Ru, Pt and Pd nanoparticles, including icosahedral, decahedral, cuboctahedral, cubic and spherical morphologies. We noted that the properties of the larger nanoparticles investigated resembled those observed in macro-surfaces, and in this work we will therefore focus on hydrogen adsorption at the ruthenium surfaces with Miller index (001), (011) and (111). We first present the STM (scanning tunnelling microscopy) images of the fcc Ru (001), (011) and (111) surfaces, before addressing the adsorption of elemental hydrogen (H) and molecular hydrogen (H2). Surface phase diagrams have also been generated through consideration of the surface free energies and the hydrogen chemical potential to determine the effects of temperature and pressure on the surface coverage.
2. Computational methods and calculations
As this work is part of an ongoing programme of research, the methods used are consistent with our previous work24 to enable direct comparison. Density functional theory (DFT) calculations were performed on the Ru surfaces using VASP version 5.4.1,25–28 within the generalized gradient approximation (GGA) in combination with the Perdew, Burke and Ernzerhof (PBE) exchange correlation functional,29–31 and we have applied the long-range dispersion approximation by Grimme with Becke–Johnson damping (DFT-D3(BJ)).32,33 In all calculations, projector augmented wave (PAW)34,35 pseudopotentials were used to describe the interactions between the valence and core electrons. The core electrons were defined up to and including 4s orbitals for the Ru atoms. Because Ru can form compounds from every oxidation state from −2, 0 and +1 to +8, all the 14 valence electrons in 4p6 4d7 5s1 are considered, leading to increased computational cost. For the H atoms, the electron was treated as a valence electron. Plane wave basis sets were applied to the valence electrons with the recommended cut-off of 400 eV. To ensure an electronic entropy of less than 1 meV atom−1, a smearing of 0.2 eV was used. The electronic and ionic optimisation criteria were set at 10−5 eV and 10−2 eV Å−1, respectively.Ru bulk metal has a Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m crystal structure, with a primitive face-centred cubic (fcc) cell, for which we used a Γ-centred 17 × 17 × 17 Monkhorst–Pack36k-point mesh. The resulting Ru fcc lattice constant was 3.778 Å, which correlates with the experimental value of 3.87.37 The low Miller index (001), (011) and (111) surfaces were created with the METADISE code,38 constructing the periodic p(3 × 3), p(3 × 4) and p(4 × 4) supercells, respectively. Each surface system consisted of a four-layer slab with a 15 Å vacuum space to ensure that no interaction would occur between the surfaces in neighbouring simulation cells as a result of the 3-dimensional boundary conditions. All three surfaces were bulk-terminated structures with four atomic layers, where the surface simulation cells comprised 72, 48 and 64 atoms with surface areas of the supercells of 128.46, 121.12, and 98.89 Å2 for the Ru (001), (011), and (111) surfaces, respectively. The Brillouin zone was sampled by a Γ-centred 7 × 7 × 1 Monkhorst–Pack k-point grid. During the optimisation of the surfaces, the bottom two layers of the supercells were frozen in their bulk locations, with the remaining two layers allowed to move until the set energy criteria were met. Spin polarisation was considered during these surface calculations to maintain consistency with future work, which will also include base metal dopants, where this setting will be essential.
m crystal structure, with a primitive face-centred cubic (fcc) cell, for which we used a Γ-centred 17 × 17 × 17 Monkhorst–Pack36k-point mesh. The resulting Ru fcc lattice constant was 3.778 Å, which correlates with the experimental value of 3.87.37 The low Miller index (001), (011) and (111) surfaces were created with the METADISE code,38 constructing the periodic p(3 × 3), p(3 × 4) and p(4 × 4) supercells, respectively. Each surface system consisted of a four-layer slab with a 15 Å vacuum space to ensure that no interaction would occur between the surfaces in neighbouring simulation cells as a result of the 3-dimensional boundary conditions. All three surfaces were bulk-terminated structures with four atomic layers, where the surface simulation cells comprised 72, 48 and 64 atoms with surface areas of the supercells of 128.46, 121.12, and 98.89 Å2 for the Ru (001), (011), and (111) surfaces, respectively. The Brillouin zone was sampled by a Γ-centred 7 × 7 × 1 Monkhorst–Pack k-point grid. During the optimisation of the surfaces, the bottom two layers of the supercells were frozen in their bulk locations, with the remaining two layers allowed to move until the set energy criteria were met. Spin polarisation was considered during these surface calculations to maintain consistency with future work, which will also include base metal dopants, where this setting will be essential.
The isolated H2 molecule was modelled in a periodic box of 7 × 8 × 9 Å3 to ensure negligible interaction with its images in neighbouring cells. The Gaussian smearing scheme39 was used during geometry optimisation and energy calculations with a smearing of 0.05 eV, with a Γ-centred 1 × 1 × 1 Monkhorst-Pack36k-point mesh. Dipole corrections were added in all directions and the H2 molecule was computed without symmetry constraints.
For the adsorption of hydrogen on the Ru surfaces, both H atoms and the optimised H2 molecule were added to the surface at various adsorption sites and in different configurations. A Γ-centred 7 × 7 × 1 Monkhorst–Pack k-point grid36 was used to sample the Brillouin zone in all the surface systems. During geometry optimisation, Gaussian smearing39 of 0.05 eV was applied in combination with the tetrahedron method, including Blöchl corrections40 in the final static simulations to obtain accurate total energies, charges, and densities of states. The electronic and ionic optimisation criteria were set at 10−5 eV and 10−2 eV Å−1, respectively. Perpendicular dipole corrections were added to account for the polarisation caused by the adsorption of the H atoms and the H2 molecule onto the Ru surfaces. To facilitate the calculation of any charge transfer during the hydrogen adsorption calculations, we have used spin-polarised DFT calculations. As the Ru metal is non-magnetic, the spin-polarised DFT calculations aid electron exchange during catalytic reactions.
To calculate the surface energies of the unrelaxed (γu) and relaxed (γr) surfaces we have used eqn (1) and (2), respectively:
 | (1) |
 | (2) |
To obtain the theoretical scanning tunnelling microscopy (STM) images, the Tersoff−Hamann41 approach was employed, where the tunnelling current is proportional to the local density of states (LDOS) of the surface at the position of the tip integrated between the Fermi level and the applied bias. The STM images (Fig. 2) were mapped in terms of the height as a function of the tip position over the surface using the HIVE42 program.
Atomic charges were obtained using the Bader analysis,43–46 which divides space into non-spherical atomic regions enclosed by local minima in the charge density.
The average adsorption energy (Eads) per H atom (i.e. half of an H2 molecule) adsorbed on the Ru surface was calculated as follows:47–50
 | (3) |
 is the energy of the Ru surface with adsorbed H atoms,
is the energy of the Ru surface with adsorbed H atoms,  is the energy of the clean Ru surface, EH2 is the energy of the isolated H2 molecule, and NH is the number of adsorbed H atoms. Another measure of adsorption is the energy of sequential adsorption (Seq. Eads), indicating the difference in energy for each additional hydrogen as the coverage increases in a stepwise fashion:
is the energy of the clean Ru surface, EH2 is the energy of the isolated H2 molecule, and NH is the number of adsorbed H atoms. Another measure of adsorption is the energy of sequential adsorption (Seq. Eads), indicating the difference in energy for each additional hydrogen as the coverage increases in a stepwise fashion: | (4) |
 and the previous system with one less adsorbate
and the previous system with one less adsorbate  .
.
To determine the thermodynamic effect of different H coverages on the Ru (001), (011), and (111) surfaces, the surface free energy (σ) is calculated for different temperatures (T) and the chemical potential (μH) of H. Previous publications51–53 have shown the relationship between the stabilities of the non-stoichiometric surfaces and the surface free energy (σ) which is calculated using the ab initio thermodynamics formalism. The resulting change in surface free energy upon H adsorption is denoted as
 | (5) |
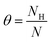 | (6) |
Assuming ideal gas behaviour, the integrated form of the Gibbs–Duhem54 equation relates the chemical potential of hydrogen in the gas phase as:
 | (7) |
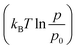 denotes the free energy change of H2 gas at constant temperature (T) when the partial pressure changes from p0 to p. To express the chemical potential, independent of the calculated quantities, the energy of hydrogen was omitted from eqn (5) and added to eqn (7).
denotes the free energy change of H2 gas at constant temperature (T) when the partial pressure changes from p0 to p. To express the chemical potential, independent of the calculated quantities, the energy of hydrogen was omitted from eqn (5) and added to eqn (7).
All the graphics for the surfaces and nanoparticles shown here were produced with the Visualization for Electronic and STructural Analysis (VESTA) v.3.5.556 software (Fig. 1, 3–9).
 | ||
| Fig. 1 Topographical view of the pristine fcc Ru (001), (011), and (111) surfaces. The lighter purple colour is used to distinguish more easily between the ruthenium atoms of different layers. | ||
3. Results and discussion
3.1. Pristine fcc ruthenium surfaces
In previous work,24 we have considered Ru in the fcc lattice arrangement and observed that Ru surface energies followed the observed trend Ru (111) < Ru (001) < Ru (011) for all three dispersion methods studied (i.e. DFT-D2, DFT-D3 and DFT-D3(BJ)). In another DFT study by Liu et al.57 the same trend was observed using GGA-PBE approximations to the exchange–correlation energy functional. Fig. 2 shows the topographical view of the pristine fcc Ru (001), (011), and (111) surfaces as constructed for our simulations. As in our previous work on Pt (001), (011) and (111) planes,47–50 all three surfaces are planar, bulk-terminated structures, comprising four layers in each slab. | ||
| Fig. 2 Simulated STM images of the pristine fcc Ru (001), (011), and (111) surfaces. The density (ϱ), tip distance (d), and bias (ΔV) are also indicated. | ||
Fig. 2 depicts the simulated STM images of the optimised Ru fcc surfaces, with reference to the primitive cells (shown in purple) of each of the (001), (011) and (111) surfaces. STM images were derived from the spatial distribution of the valence band states in the vicinity of the Fermi level (EF). On Ru (001), a chessboard-like structure can be seen, which is similar to the theoretical pattern we observed for Pt (001)47–50 and the experimental pattern reported for Cu (100).58 On Ru (011), the grooves formed in the [001] direction on the surface are evident. In our method we scanned from the top down, thus the atoms closer to the tip are lighter in colour, which highlights that every second row is higher in the surface. The alternating rows in the [010] direction are lower and therefore in a darker grey colour. This structure corresponds to the Pt (011) STM results,47 as well as the isostructural fcc Cu (110) surface.58 The STM image of the Ru (111) surface shows the typical fcc 3-folded honeycomb structure, similar to the theoretical Cu (111)58 and Pt (111)47 structures. None of the simulated surfaces showed deformation or had undergone reconstruction.
3.2. Elemental hydrogen adsorption
As part of our evaluation of the fcc Ru surfaces for the catalytic applications in liquid organic hydrogen carriers, we need to investigate the adsorption of hydrogen, both as elemental hydrogen (H) and molecular hydrogen (H2), onto the (001), (011) and (111) surfaces. Fig. 3 shows the top views of the Ru (001), (011), and (111) surfaces, where we have indicated all the possible unique adsorption sites available to H. The (001) surface has four-fold hollow (4F), atop (A) and bridge (B) sites, whereas the (011) surface also has 4F and A sites, but furthermore contains two types of bridge positions, the first in the top layer between neighbouring Ru atoms (B1) and the second in the valley of the exposed second layer (B2). The (111) surface has atop (A), bridge (B), face-centred cubic (fcc), and hexagonal close-packed (hcp) sites.Table 1 shows the adsorption energies (Eads in eV) with the resulting charge transfer (in e−) of H adsorbed onto the Ru (001), (011) and (111) surfaces. On the Ru (001) surface, the adsorption energy ranges between −0.44 and −0.66 eV, which correlates with previous results59 of H adsorption on Ru fcc nanoparticles. Both the HA and HB adsorption positions were semi-stable, in that if the atom placement deviated by 0.1 Å from the A or B site, the resulting position would be H4F after optimisation. When we compare these adsorption energies to other DFT results,57 we note a similar trend. The deviation in energy was 0.10, 0.05 and 0.09 eV respectively for the HA, HB and H4F sites, which falls within the error margin and could be due to the inclusion of dispersion corrections in our calculations. The dispersion correction accounts for dispersion forces, which are long-range interactions arising from the fluctuating dipoles of atoms or molecules. These forces are not adequately captured by standard DFT calculations.60 Even though the surface and the slab only consist of Ru atoms, the addition of a hydrogen atom creates a dipole. The functional and the dispersion correction method must be selected with great care depending on the complex to calculate sufficiently accurate interaction potentials. The performance of the D3 and D3(BJ) corrections is generally more accurate than the earlier D2 correction.47,61
| Ru (001) | HA | HB | H4F |
|---|---|---|---|
| E ads (eV) | −0.44 | −0.66 | −0.68 |
| Δq (e) | −0.17 | −0.26 | −0.21 |
| Ru (011) | HA | HB1 | HB2 | H4F |
|---|---|---|---|---|
| E ads (eV) | −0.07 | −0.55 | −0.24 | −0.30 |
| Δq (e) | −0.21 | −0.27 | −0.20 | −0.21 |
| Ru (111) | HA | HB | Hfcc | Hhcp |
|---|---|---|---|---|
| E ads (eV) | −0.20 | −0.55 | −0.69 | −0.63 |
| Δq (e) | −0.17 | −0.21 | −0.24 | −0.22 |
The charge analysis shows that between 0.17 and 0.26e− electron density was transferred from the Ru surface to the H atoms. Fig. 4 shows the iso-surfaces of the electron density difference between the adsorbed H and the Ru surfaces. Yellow and blue represent positive (electron-depletion) and negative (electron-gain) electron densities, respectively. The complex pattern on the Ru (001) surface indicates that electron transfer has occurred, confirming chemisorption of atomic H, but it does not definitively indicate ionic character. As was the case for H adsorption on fcc Ru nanoparticles,59 Ru readily donates electrons.
On the Ru (011) surface, the adsorption energy varies between −0.07 and −0.55 eV. The initially adsorbed HA hydrogen atom was highly mobile and ready to form either HB1 or HB2. Even though electron transfer occurred (Δq = −0.21e−), this would therefore be a meta-stable state. In an earlier ab initio study62 of hcp Ru, the atop H adsorption energy was calculated at −0.15 eV. This low adsorption energy indicates that H would readily adsorb to the surface, but it would be metastable and could easily desorb or take part in reactions, e.g. to form H2. The iso-surfaces of the electron density difference plot indicate that electron transfer is localised on the surrounding Ru atoms only. Our calculated adsorption energies show a similar trend to previous DFT results.57 Although Liu et al. did not find the HA adsorption, this site's adsorption energy was very similar to the very mobile position in the long bridge direction that they showed. The deviation in energy was less than 0.13 eV which falls within the error margin and could be due to the inclusion of the dispersion corrections used in our calculations.
When adsorbing onto the Ru (111) surface, the H adsorption energy ranges between −0.20 and −0.69 eV. Similar to the adsorption on Ru (011), the HA atom is highly mobile, whereas the most stable adsorption occurs in the hollow sites, i.e. Hfcc or Hhcp. Similar results were obtained in an ab initio study of hcp Ru,62 where the atop H adsorption energies were calculated at −0.15, −0.45, −0.57, and −0.63 eV for HA, HB, Hhcp, and Hfcc, respectively. Again, our adsorption energies are similar to previous DFT results.57 The deviation in energy was less than 0.10 eV which falls within the error margin and could be due to the inclusion of dispersion corrections in our calculations.
During the adsorption reactions, electron exchange occurred between the metal atoms and the adsorbate molecule. Charge transfer was found to be highly localised on the surface atoms and ranged between −0.17 and −0.24e−. Rivera Rocabado et al.63 showed that during H2 dissociation on the Ru153 nano-surface, the dissociated H atoms exhibited charges of −0.131 and −0.124e−. In a previous study,59 we observed a change in the resulting magnetic moment of the Ru13 nano-dot before and after H adsorption. However, in this surface study, no resulting magnetic moment was observed.
3.3. Molecular hydrogen adsorption
Fig. 5 shows the two different modes of H2 adsorption considered, i.e. (A) where only one H is bound to the surface with the second H pointing away from the surface into the vacuum space. In mode (B) the H2 molecule is adsorbed parallel to the Ru surface, where both H may interact with the surface atoms. Both modes were considered in all the inequivalent binding sites shown in Fig. 3. Fig. 6 shows the results of H2 adsorption on the Ru (001), (011) and (111) surfaces, with the resulting adsorption energies (Eads) listed in Table 2. | ||
| Fig. 5 Initial adsorption modes of molecular H2 on the metal surface, with (A) perpendicular and (B) parallel to the Ru surface. | ||
 | ||
| Fig. 6 Adsorption of molecular H2 on the Ru (001), (011) and (111) surfaces; Ru is purple, H is white. | ||
| (eV) | Ru(001) | Ru(011) | Ru(111) |
|---|---|---|---|
| A | −1.349 | −1.081 | −1.351 |
| B | −1.341 | −1.822 | −1.231 |
| C | −1.342 | −0.632 | −0.660 |
| D | — | — | −1.052 |
Results for the Ru (001) surface show that the H2 molecule dissociates spontaneously, with both atoms preferring to adsorb in the 4F position, closely followed by 4F-B or B-B combinations. This correlates well with the atomic H adsorption results, where the HA positions are only meta-stable adsorption sites where the H atoms remain mobile. The ΔEads per hydrogen was −0.67 eV, which corresponds to the single H adsorption in HB and H4F (Table 1).
H2 adsorption on the Ru (011) surface resulted in one case of dissociated 2H (A) and two cases of molecular H2 (B,C) adsorption. In the case of the dissociated hydrogen (A), both H atoms are in the bridge position. The average ΔEads per hydrogen was −0.54 eV, which corresponds to the single H adsorption in HB (Table 1). In one of the molecular H2 adsorptions (B), the molecule is sited in the channel space, in a bridge position but above the surface at a distance of 2.92 Å and 3.20 Å to the nearest Ru atop atoms. However, the fully occupied s-orbital of hydrogen has increased its bonding with the surface. The molecular adsorption and relatively long surface–adsorbate distances indicates physisorption, where any perturbation would allow the molecule to move across the surface for other reactions to take place. In the second type of molecular H2 adsorption (C) the molecule is located in the atop position. The relatively small Eads of −0.632 eV indicates physisorption, similar but weaker than molecular H2 in the (B) position. This mode of adsorption is meta-stable as even a 0.1 Å change in position results in dissociation.
On the Ru (111) surface, three cases of dissociated 2H adsorption (A, B, D) and molecular H2 (C) adsorption were observed. When we adsorbed a single H atom, Table 1, fcc adsorption was the most stable type, and similarly, when molecular hydrogen dissociates, the most stable position is for both H atoms to be sited in fcc positions, followed by fcc–hcp and hcp–hcp combinations. The ΔEads per hydrogen ranged between −0.53 and −0.68 eV, which corresponds to the single H adsorption in Hhcp and Hfcc (Table 1). In the case of molecular adsorption (C), H2 is physisorbed in the atop position, similar to the adsorption modes on the Ru (001) and (011) surfaces. In general, these findings show that H2 dissociates readily on the fcc Ru surfaces, with adsorption energies sufficiently small for desorption and evolution reactions to occur easily.
3.4. Hydrogen surface coverage
To consider the effect of surface coverage, the number of adsorbed H atoms (NH) was increased until a monolayer was obtained on all Ru surfaces. The lowest energy configurations for single H adsorption were used as the initial geometries for the increasing surface coverages. Various configurations for each surface and at different coverages were considered, with the lowest energy configurations shown below.Fig. 7 shows the coverage on the Ru (001) surface with H in the bridge position until a monolayer was reached. Interestingly we found high mobility of the H atoms toward the 4F binding sites. Up until a coverage of θ = 0.5, five out of the nine adsorbed H atoms were in the 4F position. In the fully covered surface (θ = 1.0) thirteen out of eighteen atoms were in the 4F position. One additional H atom was added (θ = 1.06) but from the side view it is evident that a second layer of hydrogen is started. No evidence of surface delamination or sub-surface hydrogen atoms was observed. Similar results were reported by Liu et al.57 who showed that the hydrogen atom in the HB position is very mobile and would change to the hollow site in some cases. Furthermore, Lui et al. showed that their system is of a similar size and although they report a 2 ML coverage, they did not actually show the formation of a second layer but meant that twice the amount of hydrogen was adsorbed onto the system compared to the 9 adsorption sites, i.e. 18 hydrogen atoms in a single layer.
Fig. 8 shows the coverage of the Ru (011) surface with H in the bridge position on the ridge (θ = 0.5), followed by the bridge positions in the valleys (light purple) until a monolayer (θ = 1.0) was reached. The hydrogen mobility observed on the Ru (001) surface was not observed here. All the H atoms stayed in the bridge positions until a monolayer was reached at θ = 1.0. One additional H atom was added (θ = 1.04) but from the side view it is evident that a second layer of hydrogen had started to form. Results by Liu et al.57 have shown a surface coverage of 0.75, i.e. lower than expected. Furthermore, the hydrogen mobility was much less than observed on the (100) surface.
Fig. 9 shows the coverage on the Ru (111) surface with H in the fcc position until θ = 0.5, then further coverage occurring in the hcp positions until a monolayer was reached. Up until a coverage of θ = 0.63, all the adsorbed H atoms stayed in the fcc/hcp positions. With the adsorption of an additional H atom θ = 0.66, a second layer started to form. Similar results were reported by Liu et al.57 but they only considered the lowest absorption in the fcc positions. They did not state if an additional hcp position was considered before determining when a full monolayer was obtained.
To determine if adsorption remains favourable as the surface coverage increases, the average adsorption energy as a function of surface coverage is shown in Fig. 10(a), whereas the sequential adsorption energy as a function of surface coverage is shown in Fig. 10(b). The Ru (001) surface had a maximum of 9 H2 adsorption sites (i.e. 18 H atoms) per 1.28 nm2 and the value of ΔEads decreases slightly with NH, which indicates that, although the average adsorption energy per hydrogen atom remains negative, the initial adsorption of isolated hydrogen was more favourable than the higher coverages. The trend on the (001) surface indicates that it has a high affinity to adsorption of a full monolayer of hydrogen atoms where the binding sites have little effect on the energetics. The maximum adsorption observed was at 14.01 H per nm2 Ru (θ = 1.0). The sequential adsorption energy is very stable until the final adsorption considered, where the onset of the second layer was endothermic.
 | ||
| Fig. 10 Average adsorption energies as a function of the H coverage for the Ru (001), (011), and (111) surfaces, (a) average adsorption energy per H and (b) sequential adsorption energy. | ||
The Ru (011) surface has a maximum of 12 H2 preferential adsorption sites per 1.21 nm2 Ru and ΔEads increased with NH up to a surface coverage of 9.92 H per nm2 Ru (θ = 0.5), after which the average adsorption energy decreased incrementally with increasing coverage. This trend indicates that this surface has a high affinity to adsorb hydrogen in all the bridge positions, whereas additional hydrogens also adsorb atop the surface, although less favourably. The maximum level of adsorption observed was at 19.83 H per nm2 Ru (θ = 1.0). The same trend is observed with the sequential adsorption where the lowest energy is at the bridge adsorption sites, followed by the change to atop positions. As soon as a second layer begins to form, the adsorption becomes endothermic.
On the Ru (111) surface, there was a maximum of 16 H2 preferential adsorption sites per 0.98 nm2 Ru. The ΔEads values are similar to that on Ru (001), but the trend follows that of Ru (011). It can be seen that up to 16.18 H per nm2 Ru (θ = 0.5), the fcc adsorption site was preferred, with a gradual decrease in Eads as the surface coverage increases. The adsorption of more H atoms (θ > 0.5) show a dramatic decrease in Eads with a second layer of H starting at 21.24 H per nm2 Ru. The sequential adsorption is stable as the number of H atoms increases, but the formation of the second layer is energetically unfavourable, as it was on the other two surfaces.
None of the surfaces showed any hydrogen poisoning in the form of deformation or delamination of Ru atoms, nor the occurrence of any sub-surface H atoms. However, the surfaces are highly susceptible to high coverages of H atoms, which could hinder H evolution across the surface.
3.5. Thermodynamics of hydrogen surface coverage
To determine the thermodynamic effect of H coverage on the different Ru surfaces, eqn (6) was used to quantify the relationship between the pressure and the chemical potential at different temperatures. In Fig. 11(a), we have plotted the H pressure against the chemical potential at different temperatures, while in Fig. 11(b)–(d) we present the effect of the coverage on the surface free energies in terms of the chemical potential (μH per eV) for adsorbed H on the Ru (001), (011) and (111) surfaces, respectively.The experimental conditions for LOHC depend not only on the hydrogenation or dehydrogenation reactions that occur, but also on the type of LOHC, catalyst and support systems used. For example, hydrogenation of dibenzyl toluene is performed at elevated pressures of 20–50 bar and temperatures of about 423.15–473.15 K.64 Its dehydrogenation is performed at ambient pressure (or slightly above) and temperatures of about 543.15–583.15 K. From Fig. 11(a) it is evident that pressure plays a significant role in the chemical potential range because H is a compressible gas. This means that the chemical potential range will fall between 0.0 and −0.2 eV even at the 5 bar we considered in our work.
In Fig. 11(b), each coloured line represents a different coverage of H on the (001) surface as a function of the surface energy and chemical potential. Overall, it was found that the pressure had a significant effect on the behaviour of the surfaces. As the chemical potential decreases (μH < −0.6 eV), the surface energy increases until total dehydrogenation of the surface occurs (θ = 0.0). The chemical potential versus surface energy graphs for the Ru (011) and (111) surfaces displays similar results. Under experimental conditions (−0.2 < μH (eV) < 0.0), the highest surface coverages were observed for each surface, indicating that an abundance of H atoms would be available for hydrogenation reactions to occur. However, it could also mean that the catalytic surface will be saturated with hydrogen, which may hinder the dehydrogenation of the LOHC.
In Fig. 12 we consider the effect of pressure and temperature on the H coverages of each Ru surface. The Ru (001) system shows that, at low temperatures (<250 K) and independent of pressure, full surface coverage (θ = 1.06) occurs. In the experimental region (up to 500 K) very high coverages of H are observed of θ = 0.94 (13.28 H per nm2 Ru). Complete H desorption occurs at around 1 bar and 970 K.
 | ||
| Fig. 12 Surface phase diagrams in terms of pressure and temperature for hydrogen adsorption at the Ru (001), (011), and (111) surfaces. | ||
The Ru (011) system shows full surface coverage θ = 1.0 (19.83 H per nm2 Ru) will occur in a temperature range between 500 and 700 K for all pressures considered. Complete H desorption occurs around at 1 bar and 1000 K. However, the Ru (111) surface shows only half-full coverage of θ = 0.5 (16.18 H per nm2 Ru) up to a temperature range between 870 and 970 K for all pressures considered. Complete H desorption only occurs at very high temperatures (>1000 K @ 1 bar). The theoretical study by Lui et al.57 included the influence of temperature and pressure on the coverage of hydrogen. Their study included a pressure range from 0 to 1 bar (0–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Pa) and showed that at low temperatures all the surfaces achieve the highest coverage, but as the temperature increases the hydrogen desorbs. Although their method included consideration of the surface area, they did not consider the chemical potential or surface free energy of the system. Thus, no direct parallel can be drawn between the two studies.
000 Pa) and showed that at low temperatures all the surfaces achieve the highest coverage, but as the temperature increases the hydrogen desorbs. Although their method included consideration of the surface area, they did not consider the chemical potential or surface free energy of the system. Thus, no direct parallel can be drawn between the two studies.
4. Conclusions
We have presented a systematic density functional theory study on the interaction of hydrogen atoms and molecules with the fcc Ru (001), (011) and (111) surfaces. An isolated H atom adsorbs preferentially in H4F, HB1 and Hfcc positions on the (001), (011) and (111) surfaces, respectively, where Bader analysis shows that charge transfer of between 0.17 and 0.27e− occurs from the surface to the adsorbate. When an H2 molecule is adsorbed, dissociation occurs readily but a few meta-stable sites were found where hydrogen binds molecularly.We have investigated surface coverages of H up to monolayer coverage, where Eads/H decreased with increasing H coverage on all three surfaces. The highest coverages were obtained on the (001) and (011) surfaces, followed by the (111) surface. When there is a steady supply of H molecules or atoms to the surface (e.g. during experimental conditions of hydrogenation and dehydrogenation), gradual H coverage causes the atoms to compete for surface sites. Owing to the barrier-less H2 dissociation, poisoning of the Ru catalyst can occur via physical blocking of the surface sites. Each of these conditions increases the likelihood of deeper penetration and catalyst poisoning.
Data availability
All data created during this research are openly available from Cardiff University's Research Portal: M. J. Ungerer and N. H. de Leeuw (2024). “Thermodynamics of Hydrogen Adsorption on Ruthenium fcc surfaces: A Density Functional Theory Study,” Cardiff University's Research Portal, V.1, Dataset. https://doi.org/10.17035/d.2024.0327648051.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Engineering and Physical Sciences Research Council (EPSRC grant EP/K009567/2) for funding. This research has used the Supercomputing Facilities at Cardiff University, UK, operated by ARCCA on behalf of Supercomputing Wales (SCW) projects, which is part-funded by the European Regional Development Fund (ERDF) via Welsh Government. This work has also used the Isambard2 UK National Tier-2 HPC Service (https://gw4.ac.uk/isambard/) operated by GW4 and the UK Met Office, and funded by EPSRC (EP/T022078/1).References
- M. van der Spek, C. Banet, C. Bauer, P. Gabrielli, W. Goldthorpe, M. Mazzotti, S. T. Munkejord, N. A. Røkke, N. Shah, N. Sunny, D. Sutter, J. M. Trusler and M. Gazzani, Perspective on the hydrogen economy as a pathway to reach net-zero CO2 emissions in Europe, Energy Environ. Sci., 2022, 15, 1034–1077 RSC.
- Z. Ge, B. Fu, J. Zhao, X. Li, B. Ma and Y. Chen, A review of the electrocatalysts on hydrogen evolution reaction with an emphasis on Fe, Co and Ni-based phosphides, J. Mater. Sci., 2020, 55, 14081–14104 CrossRef CAS.
- D. Bhalothia, L. Krishnia, S.-S. Yang, C. Yan, W.-H. Hsiung, K.-W. Wang and T.-Y. Chen, Recent Advancements and Future Prospects of Noble Metal-Based Heterogeneous Nanocatalysts for Oxygen Reduction and Hydrogen Evolution Reactions, Appl. Sci., 2020, 10, 7708 CrossRef CAS.
- N. Zaman, T. Noor and N. Iqbal, Recent advances in the metal–organic framework-based electrocatalysts for the hydrogen evolution reaction in water splitting: a review, RSC Adv., 2021, 11, 21904–21925 Search PubMed.
- J. Wang, F. Xu, H. Jin, Y. Chen and Y. Wang, Non-Noble Metal-based Carbon Composites in Hydrogen Evolution Reaction: Fundamentals to Applications, Adv. Mater., 2017, 29, 1605838 CrossRef PubMed.
- J. Cai, R. Javed, D. Ye, H. Zhao and J. Zhang, Recent progress in noble metal nanocluster and single atom electrocatalysts for the hydrogen evolution reaction, J. Mater. Chem. A, 2020, 8, 22467–22487 RSC.
- K. L. Hohn and L. D. Schmidt, Partial oxidation of methane to syngas at high space velocities over Rh-coated spheres, Appl. Catal., A, 2001, 211, 53–68 CrossRef CAS.
- M. Rydén and M. Arjmand, Continuous hydrogen production via the steam–iron reaction by chemical looping in a circulating fluidized-bed reactor, Int. J. Hydrogen Energy, 2012, 37, 4843–4854 CrossRef.
- Z. L. Wang, G. F. Naterer, K. S. Gabriel, R. Gravelsins and V. N. Daggupati, Comparison of sulfur–iodine and copper–chlorine thermochemical hydrogen production cycles, Int. J. Hydrogen Energy, 2010, 35, 4820–4830 Search PubMed.
- D. Doizi, V. Dauvois, J. Roujou, V. Delanne, P. Fauvet, B. Larousse, O. Hercher, P. Carles, C. Moulin and J. Hartmann, Total and partial pressure measurements for the sulphur–iodine thermochemical cycle, Int. J. Hydrogen Energy, 2007, 32, 1183–1191 Search PubMed.
- X. Xu, Q. Zhou and D. Yu, The future of hydrogen energy: bio-hydrogen production technology, Int. J. Hydrogen Energy, 2022, 47, 33677–33698 CrossRef CAS.
- G. Naterer, S. Suppiah, M. Lewis, K. Gabriel, I. Dincer, M. A. Rosen, M. Fowler, G. Rizvi, E. B. Easton, B. M. Ikeda, M. H. Kaye, L. Lu, I. Pioro, P. Spekkens, P. Tremaine, J. Mostaghimi, J. Avsec and J. Jiang, Recent Canadian advances in nuclear-based hydrogen production and the thermochemical Cu–Cl cycle, Int. J. Hydrogen Energy, 2009, 34, 2901–2917 CrossRef CAS.
- B. Lu, L. Guo, F. Wu, Y. Peng, J. E. Lu, T. J. Smart, N. Wang, Y. Z. Finfrock, D. Morris, P. Zhang, N. Li, P. Gao, Y. Ping and S. Chen, Ruthenium atomically dispersed in carbon outperforms platinum toward hydrogen evolution in alkaline media, Nat. Commun., 2019, 10, 631 Search PubMed.
- W. Li, Z. Wei, B. Wang, Y. Liu, H. Song, Z. Tang, B. Yang and S. Lu, Carbon quantum dots enhanced the activity for the hydrogen evolution reaction in ruthenium-based electrocatalysts, Mater. Chem. Front., 2020, 4, 277–284 RSC.
- J. Xu, W. Zhong, D. Gao, X. Wang, P. Wang and H. Yu, Phosphorus-enriched platinum diphosphide nanodots as a highly efficient cocatalyst for photocatalytic H2 evolution of CdS, Chem. Eng. J., 2022, 439, 135758 CrossRef CAS.
- H.-Y. Chen, H.-J. Niu, X. Ma, J.-J. Feng, X. Weng, H. Huang and A.-J. Wang, Flower-like platinum-cobalt-ruthenium alloy nanoassemblies as robust and highly efficient electrocatalyst for hydrogen evolution reaction, J. Colloid Interface Sci., 2020, 561, 372–378 CrossRef CAS PubMed.
- G. Rakhtsaum, Platinum Alloys: A Selective Review of the Available Literature, Platinum Met. Rev., 2013, 57, 202–213 Search PubMed.
- R. Darolia, Development of strong, oxidation and corrosion resistant nickel-based superalloys: critical review of challenges, progress and prospects, Int. Mater. Rev., 2019, 64, 355–380 CrossRef CAS.
- K. Kusada, H. Kobayashi, T. Yamamoto, S. Matsumura, N. Sumi, K. Sato, K. Nagaoka, Y. Kubota and H. Kitagawa, Discovery of Face-Centered-Cubic Ruthenium Nanoparticles: Facile Size-Controlled Synthesis Using the Chemical Reduction Method, J. Am. Chem. Soc., 2013, 135, 5493–5496 CrossRef CAS PubMed.
- M. Zhao and Y. Xia, Crystal-phase and surface-structure engineering of ruthenium nanocrystals, Nat. Rev. Mater., 2020, 5, 440–459 CrossRef CAS.
- F. Rosowski, A. Hornung, O. Hinrichsen, D. Herein, M. Muhler and G. Ertl, Ruthenium catalysts for ammonia synthesis at high pressures: preparation, characterization, and power-law kinetics, Appl. Catal., A, 1997, 151, 443–460 CrossRef CAS.
- S. Wu, Y.-K. Peng, T.-Y. Chen, J. Mo, A. Large, I. McPherson, H.-L. Chou, I. Wilkinson, F. Venturini, D. Grinter, P. Ferrer Escorihuela, G. Held and S. C. E. Tsang, Removal of Hydrogen Poisoning by Electrostatically Polar MgO Support for Low-Pressure NH3 Synthesis at a High Rate over the Ru Catalyst, ACS Catal., 2020, 10, 5614–5622 CrossRef CAS.
- D. S. Rivera Rocabado, M. Aizawa, T. G. Noguchi, M. Yamauchi and T. Ishimoto, Uncovering the Mechanism of the Hydrogen Poisoning on Ru Nanoparticles via Density Functional Theory Calculations, Catalysts, 2022, 12, 331 CrossRef CAS.
- M. J. Ungerer and N. H. De Leeuw, Computational Insights into Ru, Pd and Pt fcc Nano-Catalysts from Density Functional Theory Calculations: The Influence of Long-Range Dispersion Corrections, Catalysts, 2022, 12, 1287 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid–metalamorphous–semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zon integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- C. Song, O. Sakata, L. S. R. Kumara, S. Kohara, A. Yang, K. Kusada, H. Kobayashi and H. Kitagawa, Size dependence of structural parameters in fcc and hcp Ru nanoparticles, revealed by Rietveld refinement analysis of high-energy X-ray diffraction data, Sci. Rep., 2016, 6, 31400 CrossRef CAS PubMed.
- G. W. Watson, E. T. Kelsey, N. H. de Leeuw, D. J. Harris and S. C. Parker, Atomistic simulation of dislocations, surfaces and interfaces in MgO, J. Chem. Soc., Faraday Trans., 1996, 92, 433 RSC.
- M. Methfessel and A. T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- J. Tersoff and D. R. Hamann, Theory of the scanning tunneling microscope, Phys. Rev. B, 1985, 31, 805 CrossRef CAS PubMed.
- D. E. P. Vanpoucke and G. Brocks, Pt-induced nanowires on Ge(001), A density functional theory study, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81(8), 085410 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for Bader charge allocation, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- M. J. Ungerer, D. Santos-Carballal, A. Cadi-Essadek, C. G. C. E. van Sittert and N. H. de Leeuw, Interaction of H2O with the Platinum Pt(001), (011), and (111) Surfaces: A Density Functional Theory Study with Long-Range Dispersion Corrections, J. Phys. Chem. C, 2019, 123, 27465–27476 CrossRef CAS PubMed.
- M. J. Ungerer, D. Santos-Carballal, A. Cadi-Essadek, C. G. C. E. van Sittert and N. H. de Leeuw, Interaction of SO2 with the Platinum (001), (011), and (111) Surfaces: A DFT Study, Catalysts, 2020, 10, 558 CrossRef CAS.
- M. J. Ungerer, D. Santos-Carballal, C. G. C. E. van Sittert and N. H. de Leeuw, Competitive Adsorption of H2O and SO2 on Catalytic Platinum Surfaces: a Density Functional Theory Study, S. Afr. J. Chem., 2021, 74(1), 57–68 CAS.
- M. J. Ungerer, C. G. C. E. van Sittert and N. H. de Leeuw, Behavior of S, SO, and SO3 on Pt(001), (011), and (111) surfaces: A DFT study, J. Chem. Phys., 2021, 154, 194701 CrossRef CAS PubMed.
- X.-G. Wang, W. Weiss, S. Shaikhutdinov, M. Ritter, M. Petersen, F. Wagner, R. Schlögl and M. Scheffler, The Hematite (α-Fe2O3) (0001) Surface: Evidence for Domains of Distinct Chemistry, Phys. Rev. Lett., 1998, 81, 1038–1041 CrossRef CAS.
- K. Reuter and M. Scheffler, Composition, structure, and stability of RuO2 as a function of oxygen pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- D. Santos-Carballal, A. Roldan and N. H. de Leeuw, Early Oxidation Processes on the Greigite Fe3S4(001) Surface by Water: A Density Functional Theory Study, J. Phys. Chem. C, 2016, 120, 8616–8629 CrossRef CAS.
- R. B. Getman, Y. Xu and W. F. Schneider, Thermodynamics of environment-dependent oxygen chemisorption on Pt(111), J. Phys. Chem. C, 2008, 112, 9559–9572 CrossRef CAS.
- M. Chase, NIST-JANAF Thermochemical Tables, 4th edn, 1998, vol. Monograph Search PubMed.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- L. Liu, M. Yu, B. Hou, Q. Wang, B. Zhu, L. Jia and D. Li, Morphology evolution of fcc Ru nanoparticles under hydrogen atmosphere, Nanoscale, 2019, 11, 8037–8046 RSC.
- S. S. Tafreshi, A. Roldan and N. H. de Leeuw, Density Functional Theory Study of the Adsorption of Hydrazine on the Perfect and Defective Copper(100), (110), and (111) Surfaces, J. Phys. Chem. C, 2014, 118, 26103–26114 CrossRef CAS.
- M. J. Ungerer and N. H. de Leeuw, A DFT Study of Ruthenium fcc Nano-Dots: Size-Dependent Induced Magnetic Moments, Nanomaterials, 2023, 13, 1118 CrossRef CAS PubMed.
- J. Antony and S. Grimme, Density functional theory including dispersion corrections for intermolecular interactions in a large benchmark set of biologically relevant molecules, Phys. Chem. Chem. Phys., 2006, 8, 5287 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- C. Onwudinanti, G. Brocks, V. Koelman, T. Morgan and S. Tao, Hydrogen diffusion out of ruthenium—an ab initio study of the role of adsorbates, Phys. Chem. Chem. Phys., 2020, 22, 7935–7941 RSC.
- D. S. Rivera Rocabado, M. Aizawa, T. G. Noguchi, M. Yamauchi and T. Ishimoto, Uncovering the Mechanism of the Hydrogen Poisoning on Ru Nanoparticles via Density Functional Theory Calculations, Catalysts, 2022, 12, 331 CrossRef CAS.
- K. Müller, R. Aslam, A. Fischer, K. Stark, P. Wasserscheid and W. Arlt, Experimental assessment of the degree of hydrogen loading for the dibenzyl toluene based LOHC system, Int. J. Hydrogen Energy, 2016, 41, 22097–22103 CrossRef.
| This journal is © the Owner Societies 2025 |






