 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A protocol for the investigation of the intramolecular vibrational energy redistribution problem: the isomerization of nitrous acid as a case of study†
Leonardo J.
Duarte
 *ab,
Cláudio M.
Nunes
*ab,
Cláudio M.
Nunes
 b,
Rui
Fausto
b,
Rui
Fausto
 bc and
Ataualpa A. C.
Braga
bc and
Ataualpa A. C.
Braga
 *a
*a
aInstitute of Chemistry, Department of Fundamental Chemistry, University of São Paulo, Av. Prof. Lineu Prestes, 748 – Butantã, São Paulo, 05508-900, Brazil. E-mail: ljduarte@iq.usp.br; ataualpa@iq.usp.br
bUniversity of Coimbra, CQC-IMS, Department of Chemistry, 3004-535 Coimbra, Portugal
cSpectroscopy@IKU, Faculty of Sciences and Letters, Department of Physics, Istanbul Kultur University, Ataköy Campus, Bakirköy 34156, Istanbul, Turkey
First published on 22nd January 2025
Abstract
The conformational isomerization of nitrous acid (HONO) promoted by excitation of the νOH or νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching normal coordinates is the first observed case of an infrared-induced photochemical reaction. The energy captured by the excited normal modes is redistributed into a highly excited vibrational level of the τOH torsion normal coordinate, which is the isomerization reaction coordinate. Herein, we present simple numerical methods to qualitatively investigate the coupling between the normal coordinates and the possible gateways for vibrational energy redistribution leading to the isomerization process. Our methodology involves the generation of the relevant 2D potential energy surface (PES), by spanning the reaction coordinate and one of the 3N − 7 projected normal coordinates along the intrinsic reaction coordinate (IRC). Once the PES has been obtained, the time-independent wavefunctions are calculated using the standard discrete variable representation (DVR) approach. The reaction barrier is investigated using the interacting quantum atoms (IQA) decomposition scheme, evidencing an important contribution from the exchange–correlation energy to the isomerization. Coupling between normal coordinates indicates preferential normal modes to redistribute the vibrational energy. 1D deep tunneling rates were found to be negligible.
O stretching normal coordinates is the first observed case of an infrared-induced photochemical reaction. The energy captured by the excited normal modes is redistributed into a highly excited vibrational level of the τOH torsion normal coordinate, which is the isomerization reaction coordinate. Herein, we present simple numerical methods to qualitatively investigate the coupling between the normal coordinates and the possible gateways for vibrational energy redistribution leading to the isomerization process. Our methodology involves the generation of the relevant 2D potential energy surface (PES), by spanning the reaction coordinate and one of the 3N − 7 projected normal coordinates along the intrinsic reaction coordinate (IRC). Once the PES has been obtained, the time-independent wavefunctions are calculated using the standard discrete variable representation (DVR) approach. The reaction barrier is investigated using the interacting quantum atoms (IQA) decomposition scheme, evidencing an important contribution from the exchange–correlation energy to the isomerization. Coupling between normal coordinates indicates preferential normal modes to redistribute the vibrational energy. 1D deep tunneling rates were found to be negligible.
Introduction
Solving the Schrödinger equation for the movement of the nuclei yields plenty of information about a molecule and its normal modes, including vibrational frequencies, force constants and transition intensities. Not only the infrared spectra can be fully accurately calculated if the eigenvalues and dipole moment operators are known, but reliable estimates about the eigenstates’ lifetimes and thermally activated tunneling rates1 can also be recovered if one has access to the vibrational eigenspace. A plethora of numerical methods2 to solve the differential equations can be found in the literature, some of them being straightforward and easy to implement, while others are complex and require higher expertise in the field. Notably, even the simplest approaches have proven to be sufficiently accurate to be applied successfully to qualitative3,4 studies of intramolecular vibrational energy redistribution (IVR).5When a molecule interacts with an external radiation, it can absorb the field energy, reaching an excited “bright” state, and, subsequently, it may decay via radiationless pathways to lower energy “dark” states6 that are not directly accessible from the ground state. Within the harmonic approximation, transitions between eigenstates of different normal modes are forbidden, but when the eigenstates derive from an anharmonic potential there is a small, often significant probability of transferring the energy of one vibrational normal mode to others. Such an effect becomes even more intriguing when this redistribution of energy occurs alongside a chemical reaction or conformational change.
The first documented chemical reaction induced by infrared (IR) radiation, is the conformational isomerization of nitrous acid (HONO). The torsion of the dihedral angle of HONO defines an asymmetric double-well potential, with one minimum corresponding to the cis and the other to the trans conformer of the compound, the latter being slightly lower in energy than the first.7 By irradiating isolated molecules of HONO trapped in a solid nitrogen cryogenic matrix using broadband IR light, Hall and Pimentel7 were able to induce the conformational isomerization reaction. In their experiments, Hall and Pimentel used different optical filters with transmission over 10% in different regions within the 2210–5674 cm−1 range; irradiations were performed starting from diverse initial conformational compositions. Although the cis → trans isomerization appeared to be favored,7 both cis → trans and trans → cis processes were induced, as reflected by observation of photostationary states, which vary with the specific experimental conditions used (i.e., initial conformational composition of the sample and used wavelength irradiation band profile). The authors concluded on the nature of the excited modes, which they considered should mostly correspond to the νOH stretching fundamental vibration, observed for N2 matrix-isolated cis-HONO at 3410 cm−1 and for trans-HONO at 3558 cm−1.7
Although the rotational barrier for conformational isomerization (ca. 9–13 kcal mol−1 (ref. 7 and 8)) is low enough to be surpassed thermally at standard temperature and pressure (STP), the temperature of the cryogenic matrix in the Hall and Pimentel experiments, which was as low as 20 K, ensures that the isomerization could only occur via the IVR mechanism or by quantum mechanical tunneling (QMT) through the barrier.9
Experiments performed on deuterated nitrous acid (DONO)7 revealed that the isomerization rate of the deuterated molecule is ten times lower than that of the light isotopologue. On the other hand, calculations based on a rectangular potential model demonstrated that the isomerization rate should decrease by a factor of 105 if it took place only via QMT. Thus, tunneling rates alone cannot explain the observed isomerization rate, prompting consideration of excitation to an energy level above the torsional energy barrier.
In the one-dimensional torsional double-well potential of HONO, the only energy levels that are above the conformational isomerization barrier are high excited states (e.g., n ≥ 7), so that direct excitation from the ground state to any torsion energy level above the barrier is highly unlikely. The isomerization mechanism hypothesized by Hall and Pimentel7 relied on the transfer of energy from the excited νOH stretching coordinate, Q2, to the torsion, Q1, leading to the population of a torsional “dark” state with energy above the isomerization barrier. In line with this explanation, Somorjai and Hornig10 showed that, in a double potential well, the eigenstates above the energy barrier become highly delocalized between the two minima, i.e., once the system reaches one of these delocalized states, it can decay to both minima with roughly equal probability.
However, IVR can also induce chemical transformations even if the excited vibrational state is below the energy barrier for the process. This can be seen in the work of M. Lester et al.,11 where the excitation of the first overtone of the CH stretch of the Criegee intermediate (CH3)2COO triggers a 1,4 hydrogen shift followed by the decomposition to OH and (H2C2(CH3)O). Gas phase data for HONO12 have shown that the first excited state of Q2 may still be below the torsion barrier, so that a mechanism considering lower energy states of the reaction coordinate and involving vibrationally assisted QMT13 shall also be considered. In addition, more recently, it was also demonstrated that the isomerization in cryogenic matrix can also be induced by the first overtone of the νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch, Q3, although the efficiency of this process is 2.5 times lower than when the Q2 mode is pumped.14 This means that the isomerization can involve coupling between different normal modes, resulting in different paths, or gateways, for redistribution of the vibrational energy.
O stretch, Q3, although the efficiency of this process is 2.5 times lower than when the Q2 mode is pumped.14 This means that the isomerization can involve coupling between different normal modes, resulting in different paths, or gateways, for redistribution of the vibrational energy.
Perhaps the most advanced model that has been applied to describe IVR in the conformational isomerization of HONO is the multiconfigurational time-dependent Hartree (MCTDH) algorithm, developed by Meyer and coworkers.15–19 In this methodology, a six-dimensional potential energy surface, where each dimension corresponds to an internal coordinate, was obtained via single-point calculations at the CCSD(T)/cc-pVTZ level of theory. The single-point energies were then fitted with an analytic function describing the double-well potential of the cis and trans isomers, the internal coordinates force-field transformed into normal coordinates, and the spectroscopic constants calculated. After solving the Schrödinger equation for the nuclear motion in the 6D-PES, using a set of precontracted vibrational functions, a very precise description of each vibrational energy level was obtained.15–19 According to the MCTDH description, wavefunctions of the νOH stretch are localized in each minimum, whereas the wavefunctions of high excited states of the torsional normal mode delocalize completely between the cis and trans sides of the PES. The authors then argued that the isomerization process can only be understood if other vibrational modes besides νOH are included in the analysis.15–19 Time propagation of the wavepacket predicted the cis → trans isomerization to be more effective than the reverse process, as a consequence of the greater anharmonic coupling between the νOH stretching and the δHON bending modes in the cis conformer, which provides a more effective isomerization channel for the cis → trans process compared to the reverse one.15–19
Through an extensive investigation and comparison of the Local Random Matrix Theory (LRMT) with other models, Karmakar and Keshavamurthy20 demonstrated that a complete description of the IVR must account for the coupling between different normal modes, the density of states, combinations of normal modes, rotational contributions, as well as a statistical and/or probabilistic distribution of the transitions. Their model points to the classical-quantum correspondence involving the IVR in large molecules.
Considering the classical aspect of the IVR, a recent paper21 by Truhlar et al. reported a protocol to extract the energy flow between different normal modes from classical molecular dynamics. Using short-time Fourier transform and comparing the power spectra at different time, the authors were able to describe the energy transfer between the stretch and bending normal modes of water.
Interestingly, recent experiments22–24 have shown that infrared light can trigger not only conformational changes, but also lead to reactions involving cleavage of covalent bond(s). By the end of 2021, Nunes, Fausto and coworkers22 observed an IR-induced ring-opening reaction (i.e. a bond breaking process) in a benzazirine derivative, by excitation of the first overtone of the νOH stretching vibration of an OH substituent of the benzazirine that acts as a vibrational antenna capturing the excitation radiation energy and redistributing it towards the reaction coordinate. The existence of thermal activated processes can be ignored since studies were conducted in cryogenic matrices at 15 K.22 Such experiments pave the way for a new type of photochemical reaction, allowing the production and investigation of new molecules that are not accessible by conventional chemistry techniques. The emergence of new experimental techniques demands the development of new models that may explain and, more importantly, predict the phenomena observed in the laboratory.
Although as mentioned above theoretical investigations on IVR are relatively abundant in the literature, the need for models that are easy to interpret and quick to implement in the experimental pipeline has been limiting considerably the impact of these studies and their popularity among experimentalists. The objective of this work is to propose an easy-to-implement protocol to model IVR, and a physical interpretation of the phenomena through topological arguments. HONO has been chosen as a case study. We start by comparing the energy redistribution only between the νOH (Q2) or νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Q3) stretch normal modes and the intrinsic reaction coordinate (IRC) for the conformational isomerization, i.e., the minimal energy path connecting the two conformers and passing through the transition state structure (TSS) for conformational isomerization,24–26 which is coincident with νOH, (Q1).
O (Q3) stretch normal modes and the intrinsic reaction coordinate (IRC) for the conformational isomerization, i.e., the minimal energy path connecting the two conformers and passing through the transition state structure (TSS) for conformational isomerization,24–26 which is coincident with νOH, (Q1).
Herein, we adopt an approach based on numerical methods to obtain a description of the vibrational eigenstates of the Q1, Q2 and Q3 coordinates. A potential energy surface (PES) defined by the normal modes is first generated, and subsequently used to construct the vibrational Hamiltonian, the vibrational eigenstates being generated using discrete variable representation (DVR) techniques. In addition, we also analyze the double-well torsional potential and the contributions to its barrier and calculate the thermally activated tunneling rates.
Methodology
This work proposes the investigation of the IR-induced cis/trans isomerization of HONO at two different levels: (i) starting with the one-dimensional study of the isomerization barrier, which includes the characterization of the high energy torsional eigenstates, the Interacting Quantum Atoms (IQA) energy decomposition of the reaction barrier,27 the calculation of thermally activated cis → trans and trans → cis tunneling rates,1 and investigation of the IRC coupling with other normal modes; and then (ii) moving to a two-dimensional investigation of the PES generated by spanning the IRC together with the νOH or νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching normal modes, allowing the characterization of the vibrational eigenstates.
O stretching normal modes, allowing the characterization of the vibrational eigenstates.
Through this work, all calculations were done at the B3LYP/aug-cc-pVTZ level of theory, using the Gaussian16 software28 and atom in molecules parameters calculated with AIMAll.29 The construction of the potential energy surfaces and the solution of the vibrational problem were done using the numerical approaches described in the following sections. The DFT functional B3LYP is used due to its computational efficiency, enabling the calculation of a more resolved potential energy surface (PES), i.e., calculating the energy at more points along each normal coordinate. Additionally, this functional can reproduce experimental frequencies with a 2% error30 and supports IQA analysis, as it is implemented in the AIMAll software.
Normal modes of vibration
Atomic movements along the different normal modes of the two conformers of HONO are represented by the in-plane and out-of-plane red vectors in Fig. 1. The label of each normal mode is the same for both monomers. It is important to notice that normal modes are delocalized and the labeling presented considers the internal coordinates that contribute the most to the normal mode.The IRC vectors coincide with the imaginary normal mode at the transition state, and, at the minimum points, it coincides with the normal mode νOHQ1. At any other point, the IRC is orthogonal to 3N − 7 normal modes that are called “projected normal modes”.31
The projected normal mode intensities change along the IRC and are a measure of the coupling with the reaction coordinate. Their displacement vectors are used to construct the two-dimensional potential energy surface.
Constructing the potential energy surface
To calculate the decay rates between two normal modes, we need first to obtain the corresponding 2D Hamiltonian. Since it is known from experiments14 that both the νOH stretch (Q2) and the νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch (Q3) trigger the isomerization of HONO, we constructed two distinct Hamiltonians in terms of those coordinates, i.e., V(Q1, Q2) and V(Q1, Q3). This was done by defining a 2D grid of size 209 × 20 and generating distorted geometries in the direction of the projected Q2 and Q3 directions along the IRC. The molecular total energy was calculated at the B3LYP/aug-cc-pVTZ level of theory for each one of the 4180 points of the grid. The data were interpolated to a 300 × 300 grid for the generation of the contour plots of the PES, and for construction of the Hamiltonian operator for the nuclear motion. The interpolated grid spacing is: ΔQ1 = 0.184 Å amu1/2 and ΔQ2 and ΔQ3 = 0.006 Å amu1/2. As an example, the PES for V(Q1, Q2) is shown in Fig. 2a. The algorithm utilized to construct the PES is described in detail in the ESI,† where contour plots for V(Q1, Q3) are also found.
O stretch (Q3) trigger the isomerization of HONO, we constructed two distinct Hamiltonians in terms of those coordinates, i.e., V(Q1, Q2) and V(Q1, Q3). This was done by defining a 2D grid of size 209 × 20 and generating distorted geometries in the direction of the projected Q2 and Q3 directions along the IRC. The molecular total energy was calculated at the B3LYP/aug-cc-pVTZ level of theory for each one of the 4180 points of the grid. The data were interpolated to a 300 × 300 grid for the generation of the contour plots of the PES, and for construction of the Hamiltonian operator for the nuclear motion. The interpolated grid spacing is: ΔQ1 = 0.184 Å amu1/2 and ΔQ2 and ΔQ3 = 0.006 Å amu1/2. As an example, the PES for V(Q1, Q2) is shown in Fig. 2a. The algorithm utilized to construct the PES is described in detail in the ESI,† where contour plots for V(Q1, Q3) are also found.
The dotted line in Fig. 2a and b divides the PES into two domains, the one on the left containing the cis minimum and the right one containing the trans minimum. Such division is not arbitrary but is based on a topological analysis of the PES. Note in Fig. 2b that the negative of the gradient vector field, ![[capital Delta, Greek, vector]](https://www.rsc.org/images/entities/char_e13c.gif) V(Q1, Q2), does not cross the dotted line, which is called “zero-flux curve”. For a double minima PES, as is the case as that of HONO, such division is straightforward, but the definition of the frontiers between the different domains for a PES with 3 or more minima will demand a careful integration of the vector field in order to find the zero-flux curves. To find the border between different domains, we need to find a curve that satisfies the condition:
V(Q1, Q2), does not cross the dotted line, which is called “zero-flux curve”. For a double minima PES, as is the case as that of HONO, such division is straightforward, but the definition of the frontiers between the different domains for a PES with 3 or more minima will demand a careful integration of the vector field in order to find the zero-flux curves. To find the border between different domains, we need to find a curve that satisfies the condition:
 | (1) |
We take the negative of the gradient vector field, so that the vectors point towards the minima. The vectors in the Q1 direction point away from the TSS structure (the middle black dot in Fig. 2) since it is a maximum in such direction. Vectors in the Q2 direction point towards the TSS point, since it is a minimum along this coordinate. If the initial geometry of the molecule corresponds, for example, to the point (−2.0, 0.6), it will relax to the minimum of the cis conformer, while if the initial geometry of the molecule corresponds to the point (2.0, 0.6) it will end at the trans minimum. According to our calculations, the cis minimum is about 258 cm−1 (0.73 kcal mol−1) higher in energy than the trans minimum. The TSS the cis → trans isomerization stays around 4068 cm−1 (11.63 kcal mol−1) above the trans minimum.
Numerical solution to the 2D Schrödinger equation
Considering only the coordinates Q1 and Q2, the Hamiltonian for the nuclear movement is given by: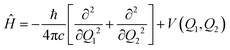 | (2) |
The Schrödinger equation is solved using the discrete variable representation (DVR). The potential energy term is written in diagonal matrix form, whose elements correspond to the value at each point of a 300 × 300 grid. The kinetic energy operator is also written in matrix form. Solutions to the time-independent Schrödinger equation are obtained by the diagonalization of Ĥ, yielding a set of orthonormal wavefunctions and their respective eigenvalues.
In Fig. 3, the probability density functions of the torsion mode eigenstates are drawn as contour plots. The eigenstates belonging to the cis isomer are colored in blue and those belonging to the trans isomer are colored in red. Note that the ground state |00〉 of both isomers has no nodes, and their energy eigenvalues are the sum of the zero-point energy of the normal modes Q1 and Q2. The next energy level, |10〉, presents one node in the Q1 direction. The lower energy eigenstates are localized in the domain of their corresponding isomers. However, the modes that approach the TSS energy delocalize over both domains. The delocalized normal modes are denominated by |*0〉, since there is no univocal way of defining their quantum number. As seen in the figure, Q1 eigenstates below the TSS energy may also delocalize, but the degree of such delocalization is smaller if compared to those staying above the barrier.
 | ||
| Fig. 3 Probability density functions (Ψ*Ψ) for the torsion mode of cis and trans isomers of HONO. High excited eigenstates becomes delocalized between the cis and trans domains. The eigenstates are overlaid on the PES contour plot only to show their delocalization over the cis and trans minima, as mentioned in Fig. 2a. | ||
In order to calculate the probability of the molecule, in any given state |n1n2〉, being observed at the cis conformation, we introduce the operator:
 | (3) |
 | (4) |
Eigenstates of the νOH stretching do not delocalize between the cis and trans domains, even if their energy eigenvalues are above the torsional barrier, the same occurring for eigenstates of the νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching, as shown in the ESI.† This result is expected since the normal coordinates are, by definition, orthogonal to each other. In Fig. 4. the probability density functions of the first (|01〉) and second (|02〉) excited states are shown. Although according to our calculations the energy eigenvalues of the |02〉 eigenstates of both isomers are greater than the energy of the isomerization barrier, the Q2 states are completely localized in their respective domains.
O stretching, as shown in the ESI.† This result is expected since the normal coordinates are, by definition, orthogonal to each other. In Fig. 4. the probability density functions of the first (|01〉) and second (|02〉) excited states are shown. Although according to our calculations the energy eigenvalues of the |02〉 eigenstates of both isomers are greater than the energy of the isomerization barrier, the Q2 states are completely localized in their respective domains.
 | ||
| Fig. 4 Probability density functions (Ψ*Ψ) for the OH stretch mode of cis and trans isomers of HONO. The eigenstates are overlaid on the PES contour plot only to show their delocalization over the cis and trans minima, as mentioned in Fig. 2a. | ||
The energy levels arising from the combination of the Q1 and Q2 modes are also eigenvectors of Ĥ. Those eigenstates are shown in Fig. 5. High-energy combination states also delocalize between the two domains, but their energies are higher than the second excited state of the νOH stretch, making it improbable that those states are populated during the IVR process.
 | ||
| Fig. 5 Probability density functions (Ψ*Ψ) for the combination of the torsion normal mode Q1 with the OH stretch mode of cis and trans isomers of HONO. The eigenstates are overlaid on the PES contour plot only to show their delocalization over the cis and trans minima, as mentioned in Fig. 2a. | ||
Mapping the dipole moment operator
In order to calculate the transition dipole moment between the different energy levels, it is necessary to construct the dipole moment operator using also a 2D grid. For each point on the PES grid, the molecular electric dipole moment vector was calculated, and the data were also interpolated to a 300 × 300 grid. The contour maps for each component, μx(Q1, Q2), μy(Q1, Q2) and μz(Q1, Q2) of the molecular dipole moment are shown in Fig. 6. The dipole moment operator for [Q1, Q3] coordinates space can be found in the ESI.†The advantage of mapping the dipole moment operator in this way is the possibility to identify atomic contributions to the transition dipole moment. Consider, for example, the transition |00〉 → |01〉, corresponding to the fundamental transition of the νOH stretch: the Q2 mode consists, mostly, of the displacement of the atom H in the xz plane. One should expect that such movement would result in a dipole moment variation on the x and z components, but not on the y direction, as the movement is perpendicular to this axis. The same interpretation can be derived from the dipole moment operator contour plot. The transition from |00〉 to |01〉 spreads the wavefunction in the Q2 direction. Notice that this direction is parallel to the contour lines of the molecular electric dipole moment y component, therefore this component does not contribute to the transition dipole moment. The transition from |00〉 to |10〉, on the other hand, occurs in the Q1 direction, perpendicular to the contour lines of the y component, which is the main contributor to the transition dipole moment.
Results and discussion
Experimental and theoretical IR spectra
The experimental spectrum of a mixture of the cis and trans isomers of HONO was taken from the HITRAN database32 (https://www.hitran.org). Such a spectrum was originally part of the NIST/PNNL library,33 which is known for its high quality. The spectrum was obtained using a modified FTIR apparatus, correcting for artifacts of the light source and for black-body radiation. The resolution of the spectrum is ∼0.06 cm−1, comparable to the width of most rotational–vibrational bands at 1 atm, so that a little pressure broadening is needed to obtain accurate intensity measurements. The HONO IR spectrum at room-temperature 298 K gas-phase is shown in Fig. 7. The spectrum ranges from 550 to 6500 cm−1, although the noise above 4500 cm−1 becomes too large and the determination of overtones in this region is impossible. In Fig. 7, the full lines below the spectrum mark the position of the anharmonic fundamental transitions, and the dotted lines the position of the overtones, both calculated at the B3LYP/aug-cc-pVTZ level. The assignment of the bands and their integrated intensities are given in Table 1. | ||
| Fig. 7 Infrared spectra of a mixture of the cis and trans isomers of HONO at 298 K gas-phase.32 The blue and red vertical lines mark the position of the anharmonic transitions calculated at the B3LYP/aug-cc-pVTZ level of theory for cis and trans isomers, respectively. Solid lines correspond to fundamental transition and dotted lines to overtones. | ||
| Mode | Harmonic calculation | Anharmonic calculation | DVR | Experimental | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Freq. | Int. | Corr. Int. | Freq. | Int. | Corr. Int. | Freq. | Int. | Corr. Int. | Band | Int. | |
| Q trans 1 | 581.28 | 98.48 | 75.41 | 553.41 | 96.12 | 73.60 | 564.48 | 121.04 | 92.68 | 550–730 | 179.78 |
| Q trans6 | 610.52 | 152.92 | 117.09 | 593.14 | 156.78 | 120.05 | 597.63 | 145.91 | 111.72 | ||
| Q cis 6 | 622.97 | 39.18 | 9.18 | 597.12 | 48.11 | 11.27 | 644.95 | 35.79 | 8.38 | ||
| Q cis 1 | 683.83 | 99.20 | 23.23 | 647.38 | 96.72 | 22.65 | 623.71 | 104.73 | 24.53 | ||
| Q trans 5 | 810.59 | 133.50 | 102.22 | 787.43 | 120.13 | 91.98 | 798.26 | 109.7 | 84.00 | 730–820 | 87.83 |
| Q cis 5 | 864.24 | 298.78 | 69.97 | 838.59 | 280.07 | 65.59 | 840.49 | 271.3 | 63.54 | 820–900 | 83.51 |
| Q trans 4 | 1295.51 | 177.91 | 136.22 | 1248.23 | 169.45 | 129.75 | 1337.63 | 174.51 | 133.62 | 1200–1321 | 111.43 |
| Q cis 4 | 1329.94 | 7.01 | 1.64 | 1312.95 | 6.12 | 1.43 | 1361.3 | 5.69 | 1.33 | ||
| Q cis 3 | 1708.54 | 207.97 | 48.71 | 1689.86 | 187.62 | 43.94 | 1703.49 | 213.04 | 49.89 | 1580–1668 | 52.58 |
| Q trans 3 | 1775.52 | 181.13 | 138.69 | 1750.85 | 189.53 | 145.12 | 1763.89 | 184.07 | 140.94 | 1668–1750 | 108.33 |
| Q cis 2 | 3577.59 | 24.88 | 5.83 | 3395.72 | 18.03 | 4.22 | 3437.19 | 20.07 | 4.70 | 3350–3390 | 7.79 |
| Q trans 2 | 3747.68 | 77.03 | 58.98 | 3573.47 | 63.95 | 48.96 | 3600.33 | 66.44 | 50.87 | 3540–3641 | 44.82 |
Considering that the experimental data were obtained for a mixture of the conformers at 298 K, a correction factor was applied to the calculated intensities to account for the conformers’ relative populations at this temperature. The free energy difference between the conformers was predicted by the performed calculations to be 0.73 kcal mol−1, with the trans isomer being the most stable form, which means that about 23% of the molecules are in the cis form and 77% in the trans form. The respective calculated intensities were then multiplied by 0.23 and 0.77, respectively.
Band intensities for normal modes Qcis1, Qtrans1, Qcis6 and Qtrans6 are overlapped in a way that individual quantification of their intensities is not possible. However, their sum can be compared with the theoretical data keeping in mind that a considerable part of the Qtrans1 band is out of the experimentally investigated range, therefore the experimental intensity sum is expected to be lower than the theoretical value. The sum of all Q1 and Q6 bands is 224.90 km mol−1 in the harmonic approximation, 227.56 km mol−1 as calculated considering anharmonicity, and 237.31 km mol−1 as predicted by our DVR methodology.
The bands for normal mode Q5 are partially overlapped, nevertheless allowing for a reasonable estimation of their experimental intensity. One can see that the anharmonic and DVR values are close to the experimental value of 87.83 km mol−1 of the Q5 normal mode of the trans isomer, while the harmonic model fails to reproduce the band intensity. On the other hand, all models underestimate in some amount the intensity of the Qcis5 band.
The models tend to overestimate the intensity of Qtrans3 and Qtrans4, while a good agreement is found for Qtrans2, which is isolated from all other fundamental bands and overtones, thus allowing a better estimation of the intensity. On the other hand, the Qcis2 band is mixed with both Qcis3 and Qtrans3 overtone bands, resulting in an integrated intensity larger than the actual value.
It is important to highlight that the DVR model is able to reproduce at a good level of approximation the experimental intensities, as this is a validation of the dipole moment operator calculations described in Section 2.3. Both the IR intensities and the decay rates between eigenstates depend on the transition dipole moment, so that if the mapping of the dipole moment operator could not reproduce well the fundamental IR intensities, then it would not also be able to produce a reliable description of the vibrational energy transference rate between different normal modes.
Considering only the fundamental transitions and using the maximum absorption wavenumber for each experimental band and excluding the Qcis1, Qtrans1, Qcis6, Qtrans6 and Qcis4 bands, the RMSD for the frequencies calculated by the harmonic model is about 106 cm−1, that for the anharmonic model is 30 cm−1, and the one for the DVR model 51 cm−1, representing 5.6%, 1.6% and 2.7% of the average frequency, respectively. The performance of our DVR method is, therefore, comparable to that of the conventional anharmonicity-corrected ab initio VPT2 calculations.34,35
Origin of the isomerization energy barrier
The IRC for the isomerization process was also obtained at the B3LYP/aug-cc-pVTZ level of approximation, as the use of DFT is necessary to perform the interacting quantum atoms (IQA) decomposition of the electronic energy.36 According to the IQA theoretical framework, the total energy is given by:27,37 | (5) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Oxc.
Oxc.
Wentzel–Kramers–Brillouin (WKB) thermally activated tunneling rates
The tunneling rates can be calculated once the vibrational eigenstates are known. Here, we do not consider tunneling through any direction but the IRC. Considering only the IRC, Q1, the Hamiltonian for the nuclear movement is given by: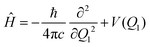 | (6) |
The IRC forms a double-well potential, where the minimum point on the left corresponds to the cis isomer and the right one to the trans isomer. By definition, the TSS is located at IRC = 0.0, and, like the 2D PES, the 1D potential can be divided into the cis domain, for Q1 = [−2.64, 0.00], and the trans domain, for Q1 = [0.00, 2.85]. Since the domains are well-defined, a cis probability can be assigned to each eigenvalue through simple integration:
 | (7) |
The probability, Pcis, not only is useful for the characterization of the vibrational levels, but it also applies as a measure of the eigenvalue delocalization between the cis and trans domains, which is relevant for the characterization of the tunneling probability.
In the Wentzel–Kramers–Brillouin (WKB) theory,42 the probability of a particle tunneling through a potential well depends on the ratio between the amplitudes of the wavefunction transmitted through and reflected by the barrier, which is determined by the momentum of the particle and the shape of the potential barrier. For a particle of energy E = hν on a double-well potential V(Q1), the tunneling rate, kWKB, can be calculated by integrating the barrier within the interval [a, b], where a and b are the coordinates where E = V(Q1). That is:
 | (8) |
Notice that the energy values in eqn (8) are given in units of cm−1 and the reduced mass is included in the Q1 coordinate. The dimensional analysis can be found in the ESI.†
The tunneling rate for each eigenstate is shown in Table 2. The lowest energy eigenstate of the trans isomer is below the zero-point energy level of the cis isomer, therefore tunneling from the lowest level of the trans isomer is not considered. As shown in Table 2, tunneling from low energy levels is negligible, but the tunneling rate increases as the levels become delocalized, near the top of the potential barrier.
| Eigenstate | cis | trans | ||||
|---|---|---|---|---|---|---|
| K WKB | P cis | Energy | K WKB | P cis | Energy | |
| 0 | 1.04 × 10−7 | 1.00 | 579.00 | — | 0.00 | 291.48 |
| 1 | 2.81 × 10−3 | 1.00 | 1190.96 | 1.34 × 10−5 | 0.00 | 854.36 |
| 2 | 9.85 × 100 | 1.00 | 1762.13 | 5.38 × 10−2 | 0.00 | 1390.18 |
| 3 | 1.10 × 104 | 1.00 | 2301.70 | 6.60 × 101 | 0.00 | 1904.07 |
| 4 | 5.11 × 106 | 1.00 | 2807.40 | 3.49 × 104 | 0.00 | 2394.25 |
| 5 | 1.14 × 109 | 1.00 | 3277.97 | 9.47 × 106 | 0.00 | 2859.90 |
| 6 | 1.30 × 1011 | 0.85 | 3709.50 | 1.42 × 109 | 0.00 | 3297.47 |
| 7 | 8.23 × 1012 | 0.77 | 4102.08 | 1.20 × 1011 | 0.16 | 3701.88 |
| 8 | 8.55 × 1013 | 0.59 | 4479.66 | 5.45 × 1012 | 0.25 | 4062.59 |
In cryogenic matrices, the population of excited vibrational states is unimportant and QMT can only take place essentially from the ground state (deep tunneling). However, at higher temperatures the population of excited states of modes of low energy like the torsional mode in HONO become non-negligible, leading to a more efficient tunneling involving also these states. In order to calculate the dependence of the tunneling rate with the temperature, the tunneling rate from each vibrational level is multiplied by a constant accounting for its Boltzmann population at a given temperature T, that is:
 | (9) |
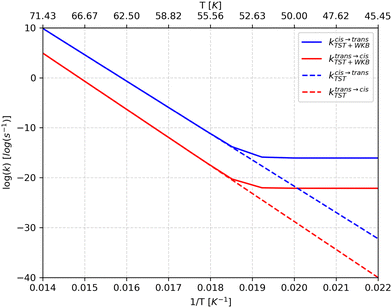 | ||
| Fig. 9 Rate constants for the conformational isomerization process in HONO predicted by the classical transition state theory (kTST) and using the WKB model (kWKB) as a function of temperature (T). | ||
At room temperature, the tunneling rate for the cis → trans isomerization is 1.09 × 106, and 2.9 × 105 for the reverse reaction. However, such temperature is enough for the thermal energy to surpass the torsion free energy barrier of about 10.3 kcal mol−1 (11.04 kcal mol−1 for the trans → cis isomerization). On the other hand, as seen in Fig. 9, the isomerization rate is negligible at low temperatures. The temperature of a cryogenic matrix is, in many of the experiments reported hitherto, below 20 K. Therefore, as already mentioned above, the population of excited states due to thermal energy is negligible, so that QMT, if operating, can only take place from the ground vibrational state (deep tunneling). Under these conditions, our calculations indicate that QMT cannot explain the nitrous acid conformational isomerization observed by Hall and Pimentel and others for the matrix-isolated compound.7,14 Since there is no thermal energy to surpass the torsion barrier and tunneling is inefficient, the isomerization process reported can only occur via the intramolecular vibrational energy redistribution (IVR) mechanism.
Possible isomerization gateways
As reported from experiments, the conformational isomerization in HONO can occur upon excitation of the fundamental Q2 or the first overtone of Q3.7,14 In both cases, the energy is captured by the vibrational antenna, either νOH or νN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and redistributed to a highly excited Q1 dark state via coupling between the normal modes. Once the dark state of Q1 is populated, the system may undergo isomerization by tunneling or/and by vibrational decay.
O, and redistributed to a highly excited Q1 dark state via coupling between the normal modes. Once the dark state of Q1 is populated, the system may undergo isomerization by tunneling or/and by vibrational decay.
In the harmonic approximation, the Hamiltonian for the vibrational movement of nuclei is separable, meaning that, for a molecule containing N atoms, the potential energy term can be expressed as:
 | (10) |
 | (11) |
The left panel of Fig. 10 shows the variation of the projected31,43 normal modes’ fundamental frequencies as a function of the IRC coordinate Q1 and the right panel shows the coupling elements between the normal modes and the IRC, BQn,Q1. As the system moves along the IRC, the internal coordinates change, modifying force constants and causing changes in the normal mode frequencies. Such changes are related to the coupling of the normal mode with the IRC, the greater the changes in the normal mode energy, the greater the coupling with the reaction coordinate.
The coupling elements, first introduced by Miler, Handy and Adams,44 are calculated by taking the dot product between the normal mode change and the IRC. Therefore, the coupling elements describe the curvature of the IRC considering the direction of the other normal modes. As the magnitude of the coupling element increases, the greater is the mixing and energy transfer between the normal coordinates.45 The total curvature of the IRC kIRC is given by:
 | (12) |
In this way, the contribution of each normal mode to the total curvature can be accessed and the main energy transfer channel can be identified.
The right panel of Fig. 10 shows the coupling elements for each normal mode along the IRC. As expected, the curvature at the critical points becomes maximum, but between the critical points, we see that the greatest coupling occurs for the Q2 normal mode, indicating a possible path to the energy redistribution. The coupling of Q3 in small, except at the trans domain.
The energy of normal modes Q2 and Q3 diminishes at the minimum, while the opposite is found for Q4, Q5 and Q6. The highest variation is found for Q4, however, this mode is low in energy and the energy redistribution from this mode can only take place to low energy states of Q1, which are still localized states, reducing the isomerization rate. The energies of the fundamental Q2 mode and first overtone of Q3 are about at the same as the isomerization barrier, so one can expect IVR from these levels to be more effective in promoting the isomerization reaction.
The frequency changes of Q2 and Q3 with respect to Q1 is greater for the cis conformer than for the trans, however the coupling elements for these modes are larger at the trans isomer. For the other modes, the highest coupling elements are found for the cis isomer. Q2 seems to be a good candidate for acting as antenna, in agreement with the experimental observation,7 as it presents greater coupling between the critical points. However, as the first overtone of Q3 is closer in energy to the fundamental Q2 transition, we also calculate the decay rates for this normal mode. Other normal modes also present a considerable coupling, however, they are too low in energy and cannot transfer energy to the delocalized “dark” eigenstate of Q1.
Obtaining a quantitative description of the isomerization mechanism demands a description of the cryogenic matrix phonon bath and a system-bath coupling term. As our calculations were performed in the gas-phase, we avoid the description of the phonons and considered only the Fermi Golden Rule (FGR) decay, which assumes an incidence of a homogeneous electromagnetic field spanning a continuum frequency range, that is:
 | (13) |
In eqn (13), I(νij→kl) is the intensity of the incident IR beam divided by a frequency range. The value of I(νij→kl) is set to 10 W m2 Hz−1. This will provide an estimation of the decay half-life, as it is related to the Einstein emission coefficient. However, such decays can be also mediated by coupling with the matrix phonons, which is a different mechanism, not involving the molecule transition dipole moment46 but still related to the overlap of the eigenstates. Therefore, it is here assumed that the possible decay paths found by this simple approximation include the decay mediated by matrix phonons.
Table 1 compares the transition frequencies obtained with the developed 2D model with those resulting from anharmonic ab initio calculations. For transitions occurring via excited νOH from Q2, the first excited vibrational level is still below the rotational barrier in the B3LYP/aug-cc-pVTZ level, but it can decay to torsion eigenstate that are delocalized enough in energy to promote the isomerization process. On the other hand, isomerization triggered by via excited νOH from Q3, can only occur from the correction overtones.
The DVR frequencies for both antenna modes are in good agreement with the anharmonic calculations, with a root mean squared deviation of about 45 cm−1 for the frequencies and 6 km mol−1 for intensities. The error in intensities, however, is increased by the large deviation of |00〉cis → |01〉cis. Disregarding this value, the RMSD value reduces to only 2 km mol−1. Such comparison is needed to validate the calculations of the dipole moment operator by the DVR methodology that are fundamental for the decay rate estimates calculated with eqn (13). The calculated decay rates for Q1–Q2 and Q1–Q3 (first fifty eigenstates) are provided in the ESI.† The data are summarized in the decay diagrams shown in Fig. 11.
The decay diagrams are interpreted as follows: starting from a high energy mode, one searches down the column for an eigenstate with a high decay rate, indicating a possible transition. From the new eigenstate, a horizontal line is drawn, reaching the diagonal line on the left. Again, one looks down the column for the next possible decay and repeats the process until it reaches a fundamental level.
Both diagrams shown in Fig. 11 show that the most probable channel allowing the cis → trans conversion must include a delocalized mode. Notice that even though such eigenstate is below the IRC barrier, it still has a small tunneling transmission probability, as shown in Fig. 8 Such small transmission not only allows tunneling once the eigenstate is occupied, either by increasing the temperature or by vibrational excitation, but also makes the integral with a localized state, e.g. 〈01|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |*0〉 in the Q1Q2 case, different from zero, thus initiating a cascade effect that leads to the isomerization. Notice that several decay paths can be traced, but some do not lead to isomerization. Therefore, the efficiency of the process depends on the number of isomerization paths pondered by the number of all possible decay paths.
|*0〉 in the Q1Q2 case, different from zero, thus initiating a cascade effect that leads to the isomerization. Notice that several decay paths can be traced, but some do not lead to isomerization. Therefore, the efficiency of the process depends on the number of isomerization paths pondered by the number of all possible decay paths.
The antenna normal mode intensity
In the previous section, the importance of the eigenstate delocalization was highlighted, since it ensures that the transition dipole moment is different from zero. However, as important as delocalization, the dipole moment operator must contribute to the non-nullity of the transition integral.Considering atomic charges and dipoles, the σ = x, y, z component of the molecular dipole moment is given by:
 | (14) |
 | (15) |
By analyzing the atomic polar tensor, it is possible to identify the main atomic contributions to the transition dipole moment, helping to understand the electronic effects determining the topology of the dipole moment operator. The relationship between the components of the dipole moment derivatives and the dipole moment operator is straightforward. Taking the fundamental transition for Q2 as example:
 | (16) |
Numerical values for the CCTDP contributions can be found in Table 3. For the torsion mode, the CT contributions in both isomers are zero as a consequence of their planar geometry.12 Note that, since Q1 corresponds to the movement of the hydrogen atom in the y direction (as depicted in Fig. 1), contributions from x and y directions are negligible, in accordance with the fact that the eigenstates are perpendicular to the contour-lines of the y component of the dipole moment contour map, as discussed in Section 2.4 The IR intensity of Q1 is approximately the same for both isomers: although the charge contribution is greater for the cis isomer, the dipolar polarization is also more negative, revealing a mechanism of counterpolarization.48,49
| Normal mode | Component | cis-HONO | trans-HONO | ||||
|---|---|---|---|---|---|---|---|
| C | CT | DP | C | CT | DP | ||
| Q 1 | x | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| y | 0.63 | 0.00 | −0.31 | 0.52 | 0.00 | −0.20 | |
| z | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Q 2 | x | 0.57 | −0.67 | 0.23 | 0.59 | −0.56 | 0.20 |
| y | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| z | 0.17 | −0.11 | 0.04 | −0.14 | 0.03 | −0.04 | |
| Q 3 | x | 0.22 | −0.47 | 0.48 | 0.21 | −0.49 | 0.56 |
| y | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| z | −0.16 | −0.04 | −0.20 | 0.06 | −0.11 | −0.28 | |
For Q2 and Q3, the movements of atoms occur in the xz plane, and contributions in the y direction are then negligible. The more intense νOH stretch band for the trans isomer results from the less effective cancelation of C and DP terms by charge-transfer effects compared with the cis isomer. The intensity of the Q3 band is determined mostly by dipolar polarization.
Conclusions
Here, we present a simple protocol to model the IVR phenomenon and its implementation to the vibrational isomerization of HONO. The IRC is defined as the minimum energy path connecting the TSS to minimum points representing equilibrium structures, this means that one of the normal modes of all minima will coincide with the IRC. Using the normal mode of the IRC (Q1, νOH) and a projected normal mode, a 2D PES can be constructed, allowing the calculation of solutions to the Schrödinger equation for the nuclear movement. The eigenstates can be then classified as belonging to the cis or trans conformer of HONO using topological criteria that divides the PES into two distinct domains. The energy eigenvalues obtained in this approach were shown to reproduce well the experimental data.The calculated eigenvectors can be classified in three groups: cis localized, trans localized and delocalized, depending on their position in the PES. As the energy level approaches the energy barrier, the eigenstates start to delocalize between the two isomers’ minima, allowing tunneling and transference of vibrational energy from other normal modes. There are, therefore, two mechanisms that can result in the isomerization reaction as represented in Figure:
1. The system is initially in the cis side of the barrier. Then, the energy captured by the antenna normal mode excites the molecule to a higher energy level from which IVR takes place, transferring the energy from the antenna mode to one dark eigenstate of the torsion normal mode that is still localized in the cis isomer domain. The system is then able to tunnel to the trans side of the barrier. This process is similar to the gateway tunneling process mentioned by Choudhury and coworkers46 and it is represented by the black arrows in Fig. 12;
2. The system initially in the cis domain is excited by the photon captured by the vibrational antenna. However, in this case, it decays directly to the trans side of the barrier during the IVR process via a delocalized eigenstate. This process is similar to the isomerization mechanism initially proposed by Hall and Pimentel,7 with the difference that the delocalized eigenstate can be below the isomerization barrier, i.e. even a small delocalization is sufficient to avoid the nullity of the transition dipole moment. This mechanism is pictured by the green arrows in Fig. 12.
The energy contribution for the isomerization barrier was found to be localized in the central N–O bond and is not correlated with any internal coordinate associated with the antenna normal modes. This suggests that the shape of PES is more important than its energetic origins when selecting the possible functional groups that will capture and redistribute the vibrational energy. The main factors for the IVR isomerization to occur are: (i) the existence of delocalized IRC eigenstates, which is determined by the PES topology and, (ii) a transition dipole moment different from zero. The latter can be modulated by analyzing the topology of the dipole moment operator, by identifying regions where the eigenstates of different normal modes overlap and performing the CCTDP analysis to identify the atomic contributions to the dipole moment derivative.
Considering the study of larger systems, the coupling elements of the projected normal modes with the IRC can aid in screening potential antenna groups for subsequent calculations of the eigenstate and decay rate. This approach helps reduce the dimensionality of the problem while maintaining the interpretability of the IVR mechanism.
Tunneling control is, already, considered the third paradigm for chemical reactivity,50 following thermodynamics and kinetics. The physical interpretation of eigenstates and their coupling mechanisms can offer the basis for an efficient control of the IVR process, thus unlocking a fourth paradigm for chemical reactivity.
Data availability
Data for this article, including the electronic energy, dipole operator map and potential energy surface characterization are available at LJD GitHub repository at https://github.com/ljduarte/hono_PES_data. Details about the methodology and algorithms have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. J. D. grant (postdoctoral fellowship #2022/09269-1 and #2023/13220-0) and A. A. C. B. (grant #2015/01491-3) are grateful to the São Paulo Research Foundation (FAPESP) for financial support. A. A. C. B. also thanks the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) of Brazil for academic support (Grant #313720/2023-1). CQC-IMS is supported by the Portuguese “Fundacão para a Ciencia e a Tecnologia” (FCT), through Projects UIDB/00313/2025 and UIDP/00313/2025 (national funds; DOI: 10.54499/UIDB/00313/2025 and 10.54499/UIDP/00313/2025) and LA/P/0056/2020. The ERA Chair Spectroscopy@IKU is funded by the European Research Agency under HORIZON-WIDERA-2023-TALENTS-01 (Grant No. 101184899).References
- E. M. Greer, K. Kwon, A. Greer and C. Doubleday, Tetrahedron, 2016, 72, 7357–7373 CrossRef CAS.
- H. Gharibnejad, B. I. Schneider, M. Leadingham and H. Schmale, Comput. Phys. Commun., 2020, 252, 106808 CrossRef CAS.
- C. Léonard, F. Le Quéré, P. Rosmus, C. Puzzarini and M. P. de Lara Castells, Phys. Chem. Chem. Phys., 2000, 2, 1117–1122 RSC.
- C. Léonard, G. Chambaud, P. Rosmus, S. Carter and N. C. Handy, Phys. Chem. Chem. Phys., 2001, 3, 508–513 RSC.
- V. Bondybey, Annu. Rev. Phys. Chem., 1984, 35, 591–612 CrossRef CAS.
- T. Uzer and W. Miller, Phys. Rep., 1991, 199, 73–146 CrossRef CAS.
- R. T. Hall and G. C. Pimentel, J. Chem. Phys., 1963, 38, 1889–1897 CrossRef CAS.
- P. Pham and Y. Guo, J. Chem. Phys., 2013, 138, 144304 CrossRef PubMed.
- M. Pettersson, E. M. Maçôas, L. Khriachtchev, R. Fausto and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 4058–4059 CrossRef CAS PubMed.
- R. L. Somorjai and D. Hornig, J. Chem. Phys., 1962, 36, 1980–1987 CrossRef CAS.
- F. Liu, J. M. Beames and M. I. Lester, J. Chem. Phys., 2014, 141, 234312 CrossRef PubMed.
- G. R. De Mare and Y. Moussaoui, Int. Rev. Phys. Chem., 1999, 18, 91–117 Search PubMed.
- R. Fausto, G. O. Ildiz and C. M. Nunes, Chem. Soc. Rev., 2022, 51, 2853–2872 RSC.
- L. Khriachtchev, J. Lundell, E. Isoniemi and M. Räsänen, J. Chem. Phys., 2000, 113, 4265–4273 CrossRef CAS.
- H.-D. Meyer, F. Le Quéré, C. Léonard and F. Gatti, Chem. Phys., 2006, 329, 179–192 CrossRef CAS.
- H.-D. Meyer, F. Gatti and G. A. Worth, Multidimensional quantum dynamics: MCTDH theory and applications, John Wiley & Sons, 2009 Search PubMed.
- F. Richter, M. Hochlaf, P. Rosmus, F. Gatti and H.-D. Meyer, J. Chem. Phys., 2004, 120, 1306–1317 CrossRef CAS PubMed.
- F. Richter, P. Rosmus, F. Gatti and H.-D. Meyer, J. Chem. Phys., 2004, 120, 6072–6084 CrossRef CAS PubMed.
- F. Richter, F. Gatti, C. Léonard, F. Le Quéré and H.-D. Meyer, J. Chem. Phys., 2007, 127, 164315 CrossRef PubMed.
- S. Karmakar and S. Keshavamurthy, Phys. Chem. Chem. Phys., 2020, 22, 11139–11173 RSC.
- R. M. Zhang, X. Xu and D. G. Truhlar, J. Phys. Chem. A, 2022, 126, 3006–3014 CrossRef CAS PubMed , PMID: 35522826.
- C. M. Nunes, N. A. M. Pereira, L. P. Viegas, T. M. V. D. Pinho e Melo and R. Fausto, Chem. Commun., 2021, 57, 9570–9573 RSC.
- C. M. Nunes, S. Doddipatla, G. F. Loureiro, J. P. L. Roque, N. A. M. Pereira, T. M. V. D. Pinho e Melo and R. Fausto, Chem. – Eur. J., 2022, 28, e202202306 CrossRef CAS PubMed , eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/chem.202202306.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- K. Yamashita, T. Yamabe and K. Fukui, Chem. Phys. Lett., 1981, 84, 123–126 CrossRef CAS.
- K. Yamashita, T. Yamabe and K. Fukui, Theor. Chim. Acta, 1982, 60, 523–533 CrossRef CAS.
- M. Blanco, A. Martn Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- T. A. Keith, Version 19.10.12, AIMAll (Version 19.10.12), Todd A. Keith, 2019, (aim.tkgristmill.com) Search PubMed.
- T. K. Roy, T. J. Carrington and R. B. Gerber, J. Phys. Chem. A, 2014, 118, 6730–6739 CrossRef CAS PubMed , PMID: 24977304.
- A. G. Baboul and H. B. Schlegel, J. Chem. Phys., 1997, 107, 9413–9417 CrossRef CAS.
- I. E. Gordon, L. S. Rothman, E. R. Hargreaves, R. Hashemi, E. V. Karlovets, F. M. Karlovets and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2022, 277, 107949 CrossRef CAS.
- S. W. Sharpe, T. J. Johnson, R. L. Sams, P. M. Chu, G. C. Rhoderick and P. A. Johnson, Appl. Spectrosc., 2004, 58, 1452–1461 CrossRef CAS PubMed.
- V. Barone, J. Chem. Phys., 2004, 122, 014108 CrossRef PubMed.
- V. Barone, J. Bloino, C. A. Guido and F. Lipparini, Chem. Phys. Lett., 2010, 496, 157–161 CrossRef CAS.
- P. Maxwell, Á. M. Pendás and P. L. Popelier, Phys. Chem. Chem. Phys., 2016, 18, 20986–21000 RSC.
- J. M. Guevara-Vela, E. Francisco, T. Rocha-Rinza and Á. Martn Pendás, Molecules, 2020, 25, 4028 CrossRef CAS PubMed.
- B. C. Symons, D. J. Williamson, C. M. Brooks, A. L. Wilson and P. L. Popelier, ChemistryOpen, 2019, 8, 560–570 CrossRef CAS PubMed.
- M. Gallegos, A. Costales and A. M. Pendas, ChemPhysChem, 2021, 22, 775–787 CrossRef CAS PubMed.
- A. F. Silva, L. J. Duarte and P. L. Popelier, Struct. Chem., 2020, 31, 507–519 CrossRef CAS.
- J. C. Thacker and P. L. Popelier, J. Phys. Chem. A, 2018, 122, 1439–1450 CrossRef CAS PubMed.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 158–168 Search PubMed.
- E. Bosch, M. Moreno and J. M. Lluch, Can. J. Chem., 1992, 70, 100–106 CrossRef CAS.
- W. H. Miller, N. C. Handy and J. E. Adams, J. Chem. Phys., 1980, 72, 99–112 CrossRef CAS.
- E. Kraka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 531–556 CAS.
- A. Choudhury, J. A. DeVine, S. Sinha, J. A. Lau, A. Kandratsenka, D. Schwarzer, P. Saalfrank and A. M. Wodtke, Nature, 2022, 612, 691–695 CrossRef CAS PubMed.
- A. F. Silva, W. E. Richter, A. B. Bassi and R. E. Bruns, Phys. Chem. Chem. Phys., 2015, 17, 30378–30388 RSC.
- L. J. Duarte and R. E. Bruns, J. Phys. Chem. A, 2018, 122, 9833–9841 CrossRef CAS PubMed.
- W. E. Richter, L. J. Duarte and R. E. Bruns, Spectrochim. Acta, Part A, 2021, 251, 119393 CrossRef CAS PubMed.
- P. R. Schreiner, J. Am. Chem. Soc., 2017, 139, 15276–15283 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The protocol for constructing the PES in normal coordinates, eigenstates of Q1 and Q3, dipole operator for Q1 and Q3, relative energy gradient analysis and minor notes on the WKB equation can be found in the ESI. See DOI: https://doi.org/10.1039/d4cp04130e |
| This journal is © the Owner Societies 2025 |








