Open Access Article
Open Access ArticleThe reaction of sulfenic acids with OH and HO2 radicals in different environments†
Josep M.
Anglada
 *a,
Ramon
Crehuet
*a,
Ramon
Crehuet
 *a,
Marilia T. C.
Martins-Costa
b,
Joseph S.
Francisco
*a,
Marilia T. C.
Martins-Costa
b,
Joseph S.
Francisco
 c and
Manuel F.
Ruiz-López
c and
Manuel F.
Ruiz-López
 b
b
aInstitute for Advanced Chemistry of Catalonia (IQAC) – CSIC, c/Jordi Girona 18-26, E-08034 Barcelona, Spain. E-mail: anglada@iqac.csic.es; rcsqtc@iqac.csic.es
bLaboratoire de Physique et Chimie Théoriques, UMR CNRS 7019, University of Lorraine, CNRS, BP 70239, 54506 Vandoeuvre-lès-Nancy, France
cDepartment of Earth and Environmental Science and Department of Chemistry, University of Pennsylvania, Philadelphia, PA, USA 19104-6316
First published on 2nd April 2025
Abstract
Sulfenic acids are involved in major chemical processes occurring in the atmosphere, in food chemistry and in biological systems. In these diverse environments, oxidation reactions caused by reactive oxygen species, especially hydroxyl (OH) and hydroperoxyl (HO2) radicals, are very important, but their mechanisms remain poorly understood. To address this question, in this paper we present high-level theoretical results on selected reactions in gas phase and in aqueous solution. The study shows that the abstraction of the acidic hydrogen by OH or HO2 is the most important process in all cases. It leads to the formation of sulfinyl radicals and H2O or H2O2, respectively, following a proton-coupled electron transfer (pcet) mechanism. The associated rate constants depend on sulfenic acid derivative when the oxidizing species is HO2, but all processes are diffusion controlled in the case of reaction with OH. From structurally simple systems to a cysteine-derived model peptide, this work provides a systematic study that contributes to a comprehensive understanding of the reactivity of sulfenic acids with radicals.
Introduction
Oxidation reactions are ubiquitous and play key roles in the chemistry of the atmosphere, in environmental chemistry and in biological systems. Among the most important oxidants in all these environments, the hydroxyl (OH) radical, the hydroperoxyl (HO2) radical and its associated superoxide anion O2−, hydrogen peroxide (H2O2) and ozone (O3) have special relevance and are commonly classified as reactive oxygen species (ROS). In the atmosphere, the gas-phase chemistry of the HOx radicals and ozone prevails. In living organisms, ROS can originate from pollutants in the environment,1,2 but they can also have an endogenous origin, initiated by electron reduction of molecular oxygen.3 They have important biological signaling activities, but cause oxidative stress when dysfunction within the antioxidant system occurs.4–6 Excess ROS in living organisms can lead to problems such as protein oxidation, through either cleavage of the polypeptide chain or modification of amino acid side chains, and lipid oxidation.3,7,8 The chemistry of ROS in the atmosphere and in biological systems has many similarities despite the different composition and thermodynamic conditions between these media, and this similarity has been discussed by bringing in data across the literature to highlight the common chemistry connections to all of these systems and chemical reaction environments.2 Here we report on our study of the reactivity of sulfenic acids with ROS species (i.e. OH and HO2) across different reaction environments, namely gas- and solution-phases.Sulfenic acids (R-SOH) have been of keen interest for more than three-quarters of a century and play important roles in different environments. They have been found to be key reaction intermediates in organic and bioorganic sulfur chemistry, as they can exhibit both nucleophilic and electrophilic character.9,10
In the atmosphere, dimethyl sulfide (CH3SCH3, DMS)11 and dimethyl disulfide (CH3SSCH3, DMDS)12 are major sources of atmospheric sulfur, with a great impact on the formation of aerosols, on climate and on air quality.13–15 The atmospheric oxidation of DMS and DMDS are mainly initiated by OH and the major products are methane sulfonic acid and sulfur dioxide, which further reacts with OH and H2O leading to sulfuric acid. However, between 3% and 7% of the DMS oxidation product forms methane sulfenic acid (CH3SOH, MSEA),16,17 and about 98% of the oxidation of DMDS by hydroxyl radical produces MSEA.18–20 Indeed, methane sulfenic acid is quite stable in the gas phase21 and has been characterized by microwave spectroscopy, by photoelectron spectroscopy, and by Fourier transform infrared spectroscopy,19,21,22 and its photochemistry has recently been investigated.23 However, its reactivity remains largely unexplored, with the exception of its reaction with ozone.20 Consequently, investigating the reactions of MSEA with OH and HO2, two of the primary atmospheric oxidants, is of significant interest.
In food chemistry, allium plants such as garlic, onion, leeks and shallots are known to play important roles in cure and prevention of human diseases, including bacterial, viral and fungal infections. These plants also show antioxidant, anti-blood pressure or even anticancer properties, which are mostly attributed to the sulfur compounds they contain, with sulfenic acids among them.24,25 In particular, the enzyme alliinase catalyzes the cleavage of S-allyl-L-cysteine S-oxide (in garlic)9 or S-alkenylcysteine S-oxide (in onion)26 producing 2-propenesulfenic acid (CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH2SOH) and 1-propensulfenic acid (CH3–CH
CH–CH2SOH) and 1-propensulfenic acid (CH3–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHSOH), respectively. These acids are potent antioxidants,27–31 having a much greater radical scavenger abilities than other sulfur compounds.32 It is worth mentioning that when onions are cut their cells are broken and release the enzyme alliinase and water, which react with S-alkenylcysteine S-oxide, producing 1-propenesulfenic acid. The oxidation of this sulfenic acid by lachrymatory factor synthase leads to the formation of syn-propanethial S-oxide (CH3CH2CHSO), which irritates the lachrymal glands, causing tears when peeling onions.26
CHSOH), respectively. These acids are potent antioxidants,27–31 having a much greater radical scavenger abilities than other sulfur compounds.32 It is worth mentioning that when onions are cut their cells are broken and release the enzyme alliinase and water, which react with S-alkenylcysteine S-oxide, producing 1-propenesulfenic acid. The oxidation of this sulfenic acid by lachrymatory factor synthase leads to the formation of syn-propanethial S-oxide (CH3CH2CHSO), which irritates the lachrymal glands, causing tears when peeling onions.26
Sulfenic acids are also formed by the oxidation of thiol groups (–SH),33 such as the cysteine residues of proteins,34 or by the oxidation of cysteine disulfides by hydroxyl radical. They play an important role in enzyme catalysis, redox homeostasis, and cell signaling.35–38 Consequently, they are crucial in the regulatory system and in combating elevated concentration of reactive oxygen species (ROS) under oxidative stress conditions.8,39 Sulfenic acids can also be formed by a two electron oxidation mechanism involving hydrogen peroxide, superoxide anion, hydroperoxides, nitric oxide, peroxynitrite, by hydrolysis and oxidation of disulfides or by reaction with monooxygenases.7,37,40,41 Sulfenic acids can either act as nucleophiles or electrophiles,36,37 reacting with hydrogen peroxide, thiols, thiolates, amines and others,42–47 and also act as radical trapping species.8,28–31 It has also been proposed that protein–SOH intermediates react with a secondary thiol group leading to the formation of a disulfide bond.36,37,48 However hydroxyl radical can also react with disulfide bonds leading to the back formation of sulfenic acids.37,41 Very interestingly, it has recently been shown that sulfenic acid can activate the decomposition of H2O2 producing OH radicals.49 Little is known about the evolution and degradation of these sulfenic acids, and we hypothesized that oxidation with HOx could be a relevant degradation route.
In this work we investigate the affinity of sulfenic acids 1 to 4 (Scheme 1) with OH and HO2 (HOx) radicals, both in gas phase and in water solvation. Compounds 1, 2, and 3 are important species in the atmosphere, in garlic, and in onion, respectively, whereas compound 4, which includes two peptide bonds, is chosen to model the sulfenic acid that would arise from oxidation of cysteine side-chain in proteins.
The goal is to provide insight into the molecular drivers behind the reactivity of sulfenic acids with OH and HO2 radicals, from fundamental, structurally simple sulfenic acids to more complex systems, and to develop a common reactivity scale that crosses atmospheric, environmental, and biological media, where this chemistry takes place.
Theoretical methods
All the reactions between compounds 1, 2, and 3 with OH and HO2 radicals have been investigated, in a first step, with the M06-2X50 density functional using the 6-311+G(2df,2p) basis set.51 In a second step, and in order to obtain accurate relative energies, we have performed single-point energy calculations at the optimized geometries using different theoretical approaches, depending on the system, namely:(1) The domain-based local pair natural orbital coupled cluster including perturbative triplet excitation DLPNO-CCSD(T)52 method with the aug-cc-pVTZ basis set,53 and
(2) the coupled cluster method with single and double excitations, and a perturbative treatment of all connected triplet excitations CCSD(T) method54 employing the aug-cc-pV(T+d)Z, aug-cc-pV(Q+d)Z and complete basis set (CBS) limit.51,53,55–57
For the reaction of compound 4 with OH and HO2 radicals, the computational methods employed include a combination of molecular mechanics (MM) methods,58ab initio density functional theory with the M06-2X density functional approach followed by single point energy calculations at DLPNO-CCSD(T).52,59
The solvation effects have been considered by re-optimizing and characterizing all stationary points employing the M06-2X functional using a polarizable implicit solvent model (PCM)60 with water as solvent, where the solvation free energies have been calculated taken into account the conversion between the gas phase standard state at 298 K and 1 atm to 1 M reference state in solvation (see ESI†). The role of explicit water molecules has also been discussed using a combined implicit–explicit model.
For the reactions involving compounds 1, 2, and 3 with HO2 radical, the rate constants have been calculated according to conventional transition state theory taking into account tunneling effects for an unsymmetrical Eckart barrier.61 For reactions with compound 4 with HO2 radical, the kinetics calculations have been computed according to conventional transition state theory, but in the framework of multi-conformer transition state theory (MC-TST). In this case we have taken into account the tunneling effects according to the Wigner approach The reactions of sulfenic acids with OH radical are predicted to be diffusion controlled, and we have computed the association rate constants of 1, 2, and 3 with OH radical employing the VRC-VTST (variable reaction coordinate – variational transition state theory).62,63 Further details of theoretical approaches used are described in the ESI.†
Results and discussion
All reactions investigated begin with the formation of a pre-reactive complex between the corresponding sulfenic acid and the hydroxyl or hydroperoxyl radical. The reactions continue through a transition state and lead to the formation of a post-reactive complex before the release of the products. We have named every stationary point by a number, which identifies the compound as in Scheme 1, followed for the letter A or B, identifying that the reaction takes place with HO2 of HO radicals respectively, followed by the letters R for reactant, CR for pre-reactive complex TS for transition states, or CP for post-reactive complex, and followed by a number. Thus, for instance, 1ATS2 identifies the transition state number 2 for the reaction of compound 1 (CH3SOH) with HO2, while 3BCR1 identifies the pre-reactive complex number 1 of the reaction of compound 3 (CH3CHCHSOH) with OH.We will begin analyzing some properties of the 1–4 sulfenic acids, and continue by discussing the reaction mechanisms. First, we will pay attention to the reaction of the parent methane–sulfenic acid (1) with hydroperoxyl and hydroxyl radicals, and will discuss the main electronic features. We will continue analyzing the reactivity of compounds 2, 3, and 4. Finally, we will discuss the effects of water solvation, and we will report the computed rate constants.
In a previous work, we investigated the reactivity of hydropersulfide (CH3SSH) with hydroxyl radical,64 showing that there is a competence between the addition of the radical to one of the sulfur atoms and the abstraction of the acidic hydrogen atom. Because CH3SSH and CH3SOH have the same number of valence electrons, we have also considered both possibilities for the reaction of sulfenic acids with OH and HO2 radical. In addition, we have also considered the possible abstraction of one hydrogen atom of the methyl group for the reaction of 1 + OH and the addition of the OH radical to the π bonds in the reactions of 2 and 3 with OH.
A. The sulfenic acids 1–4
Little is known about the acidity of sulfenic aids, and the few available values in the literature cover a wide range of pKa, from 4.8 for lumazine–sulfenic acid and 6.3 for 1-methyluracil-4-sulfenic acid,36 to 12.5 for triptycenyl sulfenic acid65 and 10.47 for 2-methyl-2-propanesulfenic acid.66 Therefore, we have first calculated the gas phase acidity and estimated the corresponding pKa in water. The pKa values have been calculated by considering the thermodynamic cycle reported in the ESI.† Absolute pKa values are obtained by taking the experimental pKa of 2-methyl-2-propanesulfenic acid, (CH3)3SOH, as the reference, and calculating relative δpKa values from the process R-SOH + (CH3)3-SO− → R-SO− + (CH3)3-SOH. Our results are displayed in Table 1. Note that our computed gas phase acidity of compound 1 compares very well with the experimental value. The estimated pKa values of compounds 1–4 range between 8.4 and 11.3 implying that all these species will be in an unionized form aqueous environments, such as in atmospheric clouds or in biological conditions, and that therefore they can react with OH and HO2 radicals.| Compound | ΔGacidityb (gas phase) | ||||
|---|---|---|---|---|---|
| Calculated | Exp.c | ΔGsolv (RSOH) | ΔGsolv (RSO−) | pKa | |
| a Calculated taking the CCSD(T) energies (DLPNO-CCSD(T) in the case of compound 4) and free energy corrections at M06-2X level. b Corresponds to the R-SOH → RSO− + H+ reaction. c Taken from ref. 67. d Experimental value from ref. 66. e Calculated by adding to the experimental values the δpKa according the R-SOH + (CH3)3-SO− ⇌ R-SO− + (CH3)3-SOH equilibrium. | |||||
| (CH3)3SOH | 349.0 | — | −3.7 | −61.5 | 10.47d |
| 1 | 352.5 | 352.0 ± 3.0 | −4.0 | −66.1 | 9.90e |
| 2 | 349.0 | — | −3.7 | −63.8 | 8.88e |
| 3 | 345.7 | — | −4.1 | −61.4 | 8.46e |
| 4 | 334.6 | — | −12.2 | −54.5 | 11.30e |
B. Reaction of sulfenic acid compounds with HO2 radical
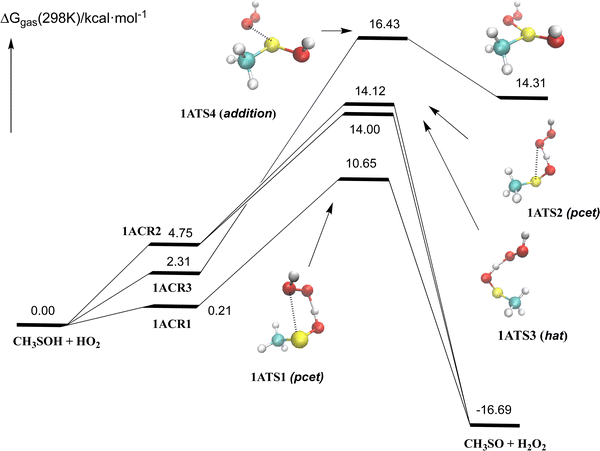
Our results, presented in Fig. 1–3 and Table 1, provide new insights into the reaction of methane sulfenic acid with HO2, complementing previous studies on sulfenic acids reacting with HO2 and methoxy radicals reported in the literature.28–31,68Fig. 1 illustrates the free energy profile of the gas-phase reaction of methane sulfenic acid with HO2, offering a representation of the reaction pathway. Fig. 2 highlights the most relevant electronic features of the processes involved, revealing details that enhance our understanding of the reaction mechanisms. Further data can be found in Table 1 and the ESI.† | ||
| Fig. 2 Electronic features for the different elementary reaction of the hydrogen abstraction of CH3SOH by HO2. | ||
 | ||
| Fig. 3 Relative free energy differences at 298 K between the different conformers of the transition states with the lowest reactant 4. Each elementary reaction involves the acidic hydrogen abstraction by HO2 following the pcet mechanism with the same electronic features as described for 1ATS1 above. The free energies are computed at DLPNO-CCSD(T)/aug-cc-pVTZ level of theory, with free energy corrections obtained at M06-2X level, and corrected by −3.8 kcal mol−1. See (ESI†). | ||
We have found three different kinds of processes for the abstraction of the hydrogen acid by the radical, with free energy barriers at 298 K of 10.65, 12.00, and 14.12 kcal mol−1 (via1ATS1, 1ATS2, and 1ATS3, respectively), all of them leading to the formation of methylsulfinyl radical (CH3SO) radical69 and H2O2. The reaction is calculated to be exoergic by 16.69 kcal mol−1. We have also found an additional reaction path involving the addition of the HO2 radical to the sulfur atom (via1ATS4) with a computed energy barrier of 16.43 kcal mol−1, producing the CH3S(OH)2 radical which is endoergic by 14.31 kcal mol−1. Further work (not displayed in Fig. 1) has shown that the CH3S(OH)2 radical easily hydrolyzes to CH3SO + H2O2 + H2O (see the ESI†). The analysis of the electronic structure, displayed in Fig. 2, shows that 1ATS1 and 1ATS2 follow a proton coupled electron transfer (pcet) mechanism and 1ATS3 involves a conventional hydrogen atom transfer mechanism (hat).
1ATS1 has the same electronic features described for the reaction of HSOH + HO2 and the reaction of sulfenic acids with methoxy and alkoxy radical,28–30 and involves the transfer of one electron from the sulfur atom 2 to the oxygen atom 6 and simultaneously the jump of the proton 4 to the oxygen atom 7 (see Fig. 2 for atom numbering). On the other side, in 1ATS2 the electron is transferred from the sulfur atom 2 to the oxygen atom 5 and the proton is transferred to the same oxygen atom. Please note that the distance of the atoms with which the electron is transferred is much larger in 1ATS2 (3.01 Å) than in 1ATS1 (2.83 Å), having the latter a smaller free energy barrier by 3.6 kcal mol−1 (see ESI† for more details). The elementary reaction through 1ATS3 (hat mechanism) occurs by the simultaneous breaking and forming of the (RS)O–H and H–(OOH) bonds requiring a much higher energy barrier than in 1ATS1.
Substitution of the –CH3 by –CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 and –CH
CH2 and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH3 groups (compounds 2 and 3) in the reaction with HO2 does not lead to significant differences, neither in the reaction mechanisms nor in the corresponding energy barriers. Table 2 shows that the reaction free energy of the lowest reaction path differ in these cases by tens of kcal mol−1, and the free energy barrier compare very well with that reported in the literature.31 The addition of the radical to the sulfur atom lies higher in energy and differs by less than 1 kcal mol−1 compared with the reaction of CH3SOH, and is described in the ESI.†
CH–CH3 groups (compounds 2 and 3) in the reaction with HO2 does not lead to significant differences, neither in the reaction mechanisms nor in the corresponding energy barriers. Table 2 shows that the reaction free energy of the lowest reaction path differ in these cases by tens of kcal mol−1, and the free energy barrier compare very well with that reported in the literature.31 The addition of the radical to the sulfur atom lies higher in energy and differs by less than 1 kcal mol−1 compared with the reaction of CH3SOH, and is described in the ESI.†
| Δ(E + ZPE)gas | ΔGgas | ΔGsol | k gas | k solv | |
|---|---|---|---|---|---|
| a Computed at CCSD(T)/aug-cc-pV(T+d)Z level, with zero point energy and free energy corrections obtained at M06-2X level. b Computed at DLPNO-CCSD(T)/(aug-cc-p)Z level, with zero point energy and free energy corrections obtained at M06-2X level. The corresponding values are corrected by −3.8 kcal mol−1. See ESI. c Relative energy between the reactant having the lowest free energy and the transition state with the lowest energy. d Gas phase rate constants are given in M−1 s−1 to allow comparison with solvation. The values in cm3 molecule−1 s−1 are given in parenthesis. e Gas phase rate constant computed at VRC-VTST level of theory. f Rate constant of VRC-VTST association reaction of three pre-reactive complexes (2BCR1 = 7.37 × 10−10 cm3 molecule−1 s−1, 2BCR1a = 1.2 × 10−9 cm3 molecule−1 s−1 and 2BCR1b = 6.48 × 10−10 cm3 molecule−1 s−1, see ESI). | |||||
| RSOH + HO2 → RSO + H2O2 | |||||
| 1ATS1 | 0.17 | 10.65 | 11.35 | 3.84 × 106 | 8.74 × 104 |
| (6.38 × 10−15) | |||||
| 2ATS1 | −0.45 | 10.11 | 11.19 | 1.39 × 107 | 2.14 × 105 |
| (2.31 × 10−14) | |||||
| 3ATS1 | 0.37 | 10.98 | 11.62 | 2.12 × 106 | 6.87 × 104 |
| (3.52 × 10−15) | |||||
| 4ATS1 , | −4.33 | 6.76 | 6.86 | 1.15 × 108 | 5.37 × 107 |
| (7.37 × 10−15) | |||||
The results for the reaction of the model 4 with HO2, are summarized in Fig. 3, which collects the relative free energy barrier of the different conformers of the transition states with respect to the free energies of the most stable R-SOH + HO2 reactants. The figure shows differences up to 11 kcal mol−1 in the energy barrier of the hydrogen abstraction process along the different compounds studied. Our results show that the free energy barrier of the most favorable path is computed to be about 4 kcal mol−1 smaller than in the reaction of compounds 1, 2, and 3 with HO2 (see Table 2). A detailed analysis of the different transition states indicates that in all cases considered, the processes have the same electronic features as described for 1ATS1 above, and the differences in the energy barriers may be associated to side interactions. In Fig. 3 we have also included the structures of the transition states of the reaction paths with the lowest and highest energy barrier (4ATS1_1, and 4ATS1-33, numbers 1 and 29 in Fig. 3). Fig. 3 shows that the 4ATS1_1 is stabilized by a strong hydrogen bond (d(H–O) = 1.65 Å) between the terminal hydrogen atom of the hydroperoxyl moiety and one oxygen atom of the carbonyl group, which does not exist in 4ATS1_33, and these results clearly highlight the importance of further interactions on the energy barriers of these processes. Again, other elementary reactions, such as the addition of the radical to the S atom, do not have any impact in the reaction rate and are discussed in the ESI.†
C. Reaction of sulfenic acid compounds with OH radical
Fig. 4 contains a schematic potential free energy surface for the reaction of methane sulfenic acid with hydroxyl radical. Again, and as mentioned above, each elementary reaction begins with the formation of a pre-reactive complex before the transition state and the release of the products.As pointed out above, we have considered three different elementary reactions, namely the abstraction of the acidic hydrogen by the OH radical (via1BTS1), the addition of the radical to sulfur atom (via1BTS2), and the abstraction of one hydrogen atom of the methyl group (via1BTS3). Our results show that the two first elementary processes begin with the 1BCR1 pre-reactive complex, and the free energy of the transition state for the hydrogen abstraction by the OH radical (1BTS1) lies below the free energy of the reactants (−5.41 kcal mol−1), which means that the reaction is controlled by diffusion, in contrast with the reaction of CH3SOH with HO2 described above, and any encounter between methane sulfenic acid and hydroxyl radical will produce the CH3SO radical and H2O. We predict this reaction to be exoergic by 48.08 kcal mol−1. Fig. 4 shows that the free energy barrier fort the addition of the OH radical to CH3SOH (via1BTS2) is isoergonic with respect to the separate reactants, producing CH3S(OH)2, which, although not shown in Fig. 4, easily hydrolyzes producing CH3SO + 2H2O (see the ESI†). Finally, the abstraction of one hydrogen atom of the methyl group by the OH radical (via1BTS3) requires a much higher free energy barrier (8.61 kcal mol−1), producing either CH2SOH + H2O or through a double proton transfer (via1BTS4) leading to CH3SO + H2O. Because the abstraction of the acidic hydrogen atom by OH is predicted to be diffusion controlled, we can conclude that the abstraction of the hydrogen atom of the methyl group will not occur.
Fig. 5(a) shows that the abstraction of the acidic hydrogen atom (1BTS1) follows a pcet mechanism, which is characterized by a system of three electrons in two orbitals and involve the transfer of one electron from the sulfur atom 2 to the oxygen atom (5) of the radical and the simultaneous transfer for the proton 4 from the oxygen of the CH3SOH to the oxygen of the radical. This kind of pcet processes described by a system of three electrons in two orbitals has been already described for other kind of reactions.64,70–74
It is also worth comparing the reactions of sulfenic acid and hydropersulfide (CH3SSH) with hydroxyl radical. Both compounds show great similarities as they have the same number of valence electrons and behave as good antioxidants with great ability to scavenge radicals.75,76 Moreover, RSSH can be also a precursor of sulfenic acids by reacting with OH radicals.64 In the case of the oxidation of CH3SSH with OH, results from the literature indicate that there is a competition between the addition of the radical to one sulfur atom and the hydrogen abstraction, the latter, taking place via a pcet mechanism.64 For the purposes of the present work, we have compared the H abstraction process in both reactions. Fig. 5(a) and (b) reveal that both reactions follow a pcet mechanism, having the same electronic features at the transition states as described above. However, there are significant differences in their energetics. Whereas the reaction of OH with RSSH needs to surmount a free energy barrier of 6.41 kcal mol−1 with respect to the reactants, the substitution of SH by OH in CH3SOH results in a drop of the relative free energy of the transition state by 11.8 kcal mol−1 so that the reaction becomes diffusion controlled as discussed above. The differences in these energy barriers can be rationalized considering a thermodynamic cycle following Mayer and co-workers77 and also applied in ref. 72. As described in Fig. 5(c) and (d), the first step correspond to the deprotonation energy of the reactants, which requires more energy for the CH3SOH compared with CH3SSH (17.6 kcal mol−1). The second step consist in bringing the anions and the hydroxyl radical to the structure of the transition state without the proton (1BTS1* and STS1*), which is more favorable in the case of sulfenic acid by 7.5 kca mol−1, and the third step consist in calculating the energy liberated in bringing the proton to the structure of the transition state (1BTS1 and STS1), favorable by 21.7 kcal mol−1 for the sulfenic acid with hydroxyl radical process, so that the formation of 1BTS1 is more favorable by 11.7 kcal mol−1 than the formation of STS1.
The potential impact of these reactions in the chemistry of the atmosphere deserves some comments. In one hand, for the CH3SOH + HO2 reaction, our calculations predict a rate constant of 6.38 × 10−15 cm3 molecule−1 s−1, at 298 K, and an Arrhenius equation  in the range of 200–320 K temperatures. Although the atmospheric concentration of HO2 is about two orders of magnitude greater than that of OH,1 the reaction of sulfenic acid with HO2 cannot compete with the reaction with OH, which is predicted to be diffusion controlled. Table 2, Fig. 4 and Table S2 (ESI†) show that the free energy at 298 K of 1BTS1 lies 5.41 kcal mol−1 below the free energy of the separate reactants and therefore the rate constant depends on the association between CH3SOH and OH. Calculations at VRC-VTST62 predict a rate constant of 6.31 × 10−10 cm3 molecule−1 s−1 (see Table 2).
in the range of 200–320 K temperatures. Although the atmospheric concentration of HO2 is about two orders of magnitude greater than that of OH,1 the reaction of sulfenic acid with HO2 cannot compete with the reaction with OH, which is predicted to be diffusion controlled. Table 2, Fig. 4 and Table S2 (ESI†) show that the free energy at 298 K of 1BTS1 lies 5.41 kcal mol−1 below the free energy of the separate reactants and therefore the rate constant depends on the association between CH3SOH and OH. Calculations at VRC-VTST62 predict a rate constant of 6.31 × 10−10 cm3 molecule−1 s−1 (see Table 2).
On the other hand, recent work has shown that in the troposphere, methane sulfenic acid reacts with ozone, with a reported rate constant of 2 × 10−12 cm3 molecule−1 s−1.20 It is therefore expected that this reaction is the major cause of atmospheric CH3SOH oxidation in ozone polluted areas, where the atmospheric concentration of ozone may be 5 to 7 orders of magnitude greater that the concentration of hydroxyl radical. However, in O3 free atmospheres, where the OH radical is formed by photolysis of HONO,78 the reaction of methane sulfenic acid with hydroxyl radical should play the major role.
The reaction of compounds 2, 3, and 4 with OH follows the same trends as for the reaction of compound 1. In all cases, the hydrogen abstraction by the radical involves a pcet mechanism, and we have found three different elementary reactions for the reaction between 2 and OH and one elementary reaction for the reaction between 3 and OH (see Table 2 and Tables S5, S6 of the ESI†). In all these processes, the free energy barrier lies below the free energy of the reactants indicating that all these reactions are diffusion controlled. For reactions of 2 and 3 with OH radical we have also calculated the association rate constant at VRC-VTST level of theory and the computed values are 2.51 × 10−9 and 7.96 × 10−10 cm3 molecule−1 s−1, respectively (see Table 2).
Beyond the acidic hydrogen abstraction by the hydroxyl radical, we have also considered the addition of the radical to the S atom of the sulfenic acid and for the reactions of 2 and 3 with OH the addition of the radical to the π bond. In all these cases, these processes require to surmount a free energy barrier and therefore are expected not to occur (see Tables S3–S6 of the ESI†).
In Fig. 6 we have collected the free energy barriers of all elementary reactions involving the abstraction of the acidic hydrogen of the sulfenic acid by the hydroxyl radical, along the structures of the transition state of the elementary reaction having the smaller and larger energy barrier. In line with the reaction of 4 with HO2 discussed above, we have found differences up to 10.83 kcal mol−1 in the energy barriers which depend on the interaction of the reacting group with other groups. Thus, in the transition state with the highest energy barrier, there is a repulsive interaction between the oxygen atom of the radical moiety and one nitrogen atom of the peptide bond which makes this stationary point less stable.
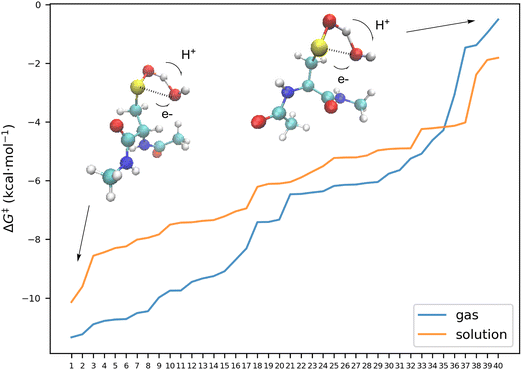 | ||
| Fig. 6 Free energy barriers at 298 K of the different conformers of the transition states relative to their reactants for the reaction of 4 with OH. Each elementary reaction involves the acidic hydrogen abstraction by OH following the pcet mechanism with the same electronic features as described for 1BTS1 above. The free energies are computed at DLPNO-CCSD(T)/aug-cc-pVTZ level of theory, with free energy corrections obtained at M06-2X level, and corrected by −3.8 kcal mol−1. See the (ESI†). | ||
D. Aqueous environments
The kinetics of the oxidation reactions described above in the gas phase involving sulfenic acids and HOx radicals may change when the processes take place in aqueous environments, such as aqueous aerosols in the atmosphere, surface waters (rivers, lakes, etc.) or biological systems. To estimate the importance of solvent effects in such conditions, we have made systematic calculations for these processes in water solution using the PCM implicit solvent model. All structures have been reoptimized in solution and the free energies have been calculated according to the methodology described in the computational section.As shown in Table 1 and Fig. 3, 6, the inclusion of solvent effects through the PCM model modifies the activation free energies of the different mechanisms and systems, but the changes are small. Again, the most favorable reaction involves the abstraction of the acidic hydrogen by the radical, via a pcet mechanism. The values in Table 1, which summarizes the activation free energies, illustrate the main trends. In the case of the reactions in aqueous solution with HO2, the barriers are slightly higher compared to gas phase values, with the largest difference amounting about 0.7 kcal mol−1, in line with the data reported for the reaction of 2 with HO2.31 Again, the free energy barriers for compounds 1–3 are very close to each other, but it is smaller by about 3.5 kcal mol−1 for compound 4 in the same way as discussed for the gas phase.
In the case of the reactions with OH, which all display negative energy barriers, with differences in the free energy barrier smaller than 1.0 kcal mol−1 compared to the gas phase, all abstraction reactions are expected to be diffusion controlled.
Overall, Table 1 shows that our calculated rate constants obtained for the reaction between compounds 1–3 with HO2, using a continuum solvent model are between 31 and 65 times smaller than in gas phase, and range between 6.87 × 104 and 2.15 × 105 M−1 s−1, compared with the 2.60 × 107 M−1 s−1 reported for the 2 + HO2.31 For the reaction between compound 4 with HO2, the computed rate constant in solvation is just 2.14 times smaller than that in gas phase, and the reaction is predicted to be much faster than for compounds 1–3, with a computed rate constant of 5.37 × 107 M−1 s−1 in liquid phase.
Nevertheless, the reactive systems contain several polar bonds that are likely to exhibit specific solute–solvent interactions such as hydrogen-bonds, and these interactions bring an additional stabilizing contribution to the solvation energies of the structures. The effect of solute–solvent hydrogen-bond formation with the reactants and the transition state was examined before in the case of the reaction 2 + HO2 using a similar quantum level as the one used in ref. 31. The authors used a discrete-continuum solvation model in which one explicit water molecule is included in the calculations, and the PCM model is used to account for the interactions with the dielectric continuum. They reported a barrier of 11.65 kcal mol−1, which is close to the value obtained with a pure PCM model (10.17 kcal mol−1). In order to see if this effect could be extended to our systems, we have also carried out a similar calculation on the most stable conformer of the reaction between 4 and HO2, and our results indicate that using a discrete-continuum solvation model with one explicit water molecule, the free energy barrier increases by 1.5 kcal mol−1 compared to the calculations with a pure PCM model in a similar way as reported for 2 + HO2, (see the ESI† for more details), and therefore we conclude that this effect is small.
In addition, as the reactions studied involve the transfer of H atoms carrying a varying degree of positive charge, it is also conceivable that water molecules actively assist the processes by participating to the reaction coordinate as proton relays. In order to take into account this possibility we have looked for processes where one water molecule acts as an intermediate in the proton transfer, namely one electron is transferred from the S atom to the terminal O atom of OH or HO2, whereas the acidic proton of the sulfenic acid is transferred to the water molecule and simultaneously, one proton from water is transferred to the OH or HO2 moiety. Our results are detailed in the ESI† and predict that the reactions with HO2 radicals require higher energy barriers, so that this mechanism should not be operative. For the reaction with OH, all transition states still have a negative energy barrier, and consequently, the reactions remain diffusion controlled.
The high reactivity of sulfenic acids with hydroxyl radical in different environments suggests a strong antioxidant ability of these species, in line with the antioxidant capacity of disulfide compounds, whose reaction with OH radicals41 contributes to the defense of biological systems against ROS species. Besides, one may note that one of the products of the reactions investigated are sulfinyl radicals (R-SO), which are less reactive than HOx, thiyl and perthiyl radicals, and have interest in environmental, organic and biochemical chemistry.11,79–83 Finally, it must be emphasized that in aqueous environments, the reaction of sulfenic acids with hydroperoxyl radical, whose pKa is 4.8, will have relevance in acidic media.
Conclusions
In summary, we explored the structure–function relationship for a series of sulfenic acids reacting with OH and HO2 in both gas phase and aqueous environments. We identified two main mechanisms: hydrogen abstraction (hat) and proton-coupled electron transfer (pcet), and our findings indicate that pcet predominates.The reactions with either OH or HO2 can proceed via two pathways: addition or abstraction. For the CH3SOH (1) + HO2 reaction, the two pathways lead to the same product, which is consistent with the existing literature, and favors H2O2 production, which has significant biochemical implications. For the CH3SOH (1) + OH reaction, the major products are CH3SO (H abstraction) and CH3S(OH)2 (OH addition), with the latter compound easily hydrolyzing to CH3SO and water. Abstraction of the hydrogen from the methyl group of CH3SOH will not occur; this step was found to have the largest activation energy among the collective steps in the mechanism. The CH3SOH + OHx reaction has relevance in the atmosphere and we predict a rate constant of 6.38 × 10−15 cm3 molecule−1 s−1 at 298 K for the reaction with HO2 and diffusion control for the reaction with OH, implying that the latter will be the most important oxidation process of CH3SOH in ozone free atmosphere.
An important finding is that the reactions of all sulfenic acids with hydroxyl radical are diffusion controlled, even when a water molecule participates as reactant in the whole process. Their rate constants depend on the association process between the sulfenic acid and the hydroxyl radical, and have been calculated to be 6.31 × 10−10, 2.51 × 10−9, and 7.96 × 10−10 cm3 molecule−1 s−1, for the gas phase reactions of 1, 2, and 3 with OH respectively. Our results suggest that in O3 free atmospheres, where the OH radical is formed by photolysis of HONO, the reaction of methane sulfenic acid with hydroxyl radical should play the major role.
For the reaction of 2, and 3 with HO2, our calculations predict rate constants 6.87 × 104 and 2.14 × 105 M−1 s−1, which is not very different from the rate constant for compound 1, but a much larger value is obtained for the reaction of the model system 4 with HO2 (5.37 × 107 M−1 s−1). In the last case, the interaction of the reacting group with the peptide bond patterns in the molecule produces a significant stabilization effect of the transition state that can be translated to the reaction of sulfenic acids in proteins. The very high reactivity of sulfenic acids with the hydroxyl radical suggests a strong antioxidant capacity of these species.
Data availability
The data supporting the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
JMA and RC thank the Spanish Ministerio de Ciencia e Inovación (grant PID2022-138040OB-I00) for financial support, and the Consorci de Serveis Universitaris de Catalunya (CSUC) and the Centro de Supercomputación de. Galicia (CESGA) for providing computational resources.References
- Paul S. Monks, Chem. Soc. Rev., 2005, 34, 376–395 Search PubMed.
- J. M. Anglada, M. Martins-Costa, J. S. Francisco and M. F. Ruiz-Lopez, Acc. Chem. Res., 2015, 48, 575–583 CrossRef CAS PubMed.
- S. Parvez, M. J. C. Long, J. R. Poganik and Y. Aye, Chem. Rev., 2018, 118, 8798–8888 CrossRef CAS PubMed.
- B. Halliwell, Plant Physiol., 2006, 141, 312–322 Search PubMed.
- M. Iriti and F. Faoro, Water, Air, Soil Pollut., 2008, 187, 285–301 CrossRef CAS.
- O. Sorg, C. R. Biol., 2004, 327, 649–662 CrossRef CAS PubMed.
- G. Xu and M. R. Chance, Chem. Rev., 2007, 107, 3514–3543 CrossRef CAS PubMed.
- K. U. Ingold and D. A. Pratt, Chem. Rev., 2014, 114, 9022–9046 CrossRef CAS PubMed.
- E. Block, Angew. Chem., Int. Ed. Engl., 1992, 31, 1135–1178 Search PubMed.
- E. Block, Reactions of Organosulfur Compounds: Organic Chemistry: A Series of Monographs, Academic Press, 2013, vol. 37 Search PubMed.
- I. Barnes, J. Hjorth and N. Mihalopoulos, Chem. Rev., 2006, 106, 940–975 Search PubMed.
- S. Meinardi, I. J. Simpson, N. J. Blake, D. R. Blake and F. S. Rowland, Geophys. Res. Lett., 2003, 30, 1454 CrossRef.
- G. A. Novak, D. B. Kilgour, C. M. Jernigan, M. P. Vermeuel and T. H. Bertram, Atmos. Chem. Phys., 2022, 22, 6309–6325 Search PubMed.
- J. Zhao, G. Sarwar, B. Gantt, K. Foley, B. H. Henderson, H. O. T. Pye, K. M. Fahey, D. Kang, R. Mathur, Y. Zhang, Q. Li and A. Saiz-Lopez, Atmos. Environ., 2021, 244, 117961 CrossRef CAS PubMed.
- S. Li, G. Sarwar, J. Zhao, Y. Zhang, S. Zhou, Y. Chen, G. Yang and A. Saiz-Lopez, Earth Space Sci., 2020, 7, e2020EA001220 CrossRef PubMed.
- J. Shen, W. Scholz, X.-C. He, P. Zhou, G. Marie, M. Wang, R. Marten, M. Surdu, B. Rörup, R. Baalbaki, A. Amorim, F. Ataei, D. M. Bell, B. Bertozzi, Z. Brasseur, L. Caudillo, D. Chen, B. Chu, L. Dada, J. Duplissy, H. Finkenzeller, M. Granzin, R. Guida, M. Heinritzi, V. Hofbauer, S. Iyer, D. Kemppainen, W. Kong, J. E. Krechmer, A. Kürten, H. Lamkaddam, C. P. Lee, B. Lopez, N. G. A. Mahfouz, H. E. Manninen, D. Massabò, R. L. Mauldin, B. Mentler, T. Müller, J. Pfeifer, M. Philippov, A. A. Piedehierro, P. Roldin, S. Schobesberger, M. Simon, D. Stolzenburg, Y. J. Tham, A. Tomé, N. S. Umo, D. Wang, Y. Wang, S. K. Weber, A. Welti, R. Wollesen de Jonge, Y. Wu, M. Zauner-Wieczorek, F. Zust, U. Baltensperger, J. Curtius, R. C. Flagan, A. Hansel, O. Möhler, T. Petäjä, R. Volkamer, M. Kulmala, K. Lehtipalo, M. Rissanen, J. Kirkby, I. El-Haddad, F. Bianchi, M. Sipilä, N. M. Donahue and D. R. Worsnop, Environ. Sci. Technol., 2022, 56, 13931–13944 CrossRef CAS PubMed.
- J. Chen, J. R. Lane, K. H. Bates and H. G. Kjaergaard, Environ. Sci. Technol., 2023, 57, 21168–21177 CrossRef CAS PubMed.
- S. Hatakeyama and H. Akimoto, J. Phys. Chem., 1983, 87, 2387–2395 CrossRef CAS.
- I. Barnes, K. H. Becker and N. Mihalopoulos, J. Atmos. Chem., 1994, 18, 267–289 CrossRef CAS.
- T. Berndt, J. Chen, K. H. Møller, N. Hyttinen, N. L. Prisle, A. Tilgner, E. H. Hoffmann, H. Herrmann and H. G. Kjaergaard, Chem. Commun., 2020, 56, 13634–13637 RSC.
- S. Lacombe, M. Loudet, E. Banchereau, M. Simon and G. Pfister-Guillouzo, J. Am. Chem. Soc., 1996, 118, 1131–1138 CrossRef CAS.
- R. E. Penn, E. Block and L. K. Revelle, J. Am. Chem. Soc., 1978, 100, 3622–3623 Search PubMed.
- X. Shao, J. Xue, J. Jiang and X. Zeng, J. Phys. Chem. Lett., 2024, 15, 7327–7334 Search PubMed.
- C. Jacob, Nat. Prod. Rep., 2006, 23, 851–863 Search PubMed.
- A. N. Jikah and G. I. Edo, Pharmacol. Res. – Mod. Chin. Med., 2023, 9, 100323 CrossRef.
- R. Kubec, R. B. Cody, A. J. Dane, R. A. Musah, J. Schraml, A. Vattekkatte and E. Block, J. Agric. Food Chem., 2010, 58, 1121–1128 CrossRef CAS PubMed.
- Y. Okada, K. Tanaka, I. Fujita, E. Sato and H. Okajima, Redox Rep., 2005, 10, 96–102 CrossRef CAS PubMed.
- P. T. Lynett, K. Butts, V. Vaidya, G. E. Garrett and D. A. Pratt, Org. Biomol. Chem., 2011, 9, 3320–3330 RSC.
- R. Amorati, P. T. Lynett, L. Valgimigli and D. A. Pratt, Chem. – Eur. J., 2012, 18, 6370–6379 CrossRef CAS PubMed.
- V. Vaidya, K. U. Ingold and D. A. Pratt, Angew. Chem., Int. Ed., 2009, 48, 157–160 CrossRef CAS PubMed.
- A. Galano and M. Francisco-Marquez, J. Phys. Chem. B, 2009, 113, 16077–16081 CrossRef CAS PubMed.
- K. Seki, J. Ishikawa and Y. Okada, J. Food Sci., 2018, 83, 1265–1270 CrossRef CAS PubMed.
- J. M. Fukuto, L. J. Ignarro, P. Nagy, D. A. Wink, C. G. Kevil, M. Feelisch, M. M. Cortese-Krott, C. L. Bianco, Y. Kumagai, A. J. Hobbs, J. Lin, T. Ida and T. Akaike, FEBS Lett., 2018, 592, 2140–2152 CrossRef CAS PubMed.
- D. Garrido Ruiz, A. Sandoval-Perez, A. V. Rangarajan, E. L. Gunderson and M. P. Jacobson, Biochemistry, 2022, 61, 2165–2176 CrossRef CAS PubMed.
- L. B. Poole, P. A. Karplus and A. Claiborne, Annu. Rev. Pharmacol. Toxicol., 2004, 44, 325–347 CrossRef CAS PubMed.
- V. Gupta and K. S. Carroll, Biochim. Biophys. Acta, 2014, 1840, 847–875 CrossRef CAS PubMed.
- N. J. Kettenhofen and M. J. Wood, Chem. Res. Toxicol., 2010, 23, 1633–1646 Search PubMed.
- D. E. Heppner, Y. M. W. Janssen-Heininger and A. van der Vliet, Arch. Biochem. Biophys., 2017, 616, 40–46 Search PubMed.
- A. T. Saurin, H. Neubert, J. P. Brennan and P. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17982–17987 Search PubMed.
- D. Mansuy and P. M. Dansette, Arch. Biochem. Biophys., 2011, 507, 174–185 CrossRef CAS PubMed.
- S. Adhikari, R. Crehuet, J. M. Anglada, J. S. Francisco and Y. Xia, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 18216–18223 CrossRef CAS.
- J.-P. R. Chauvin and D. A. Pratt, Angew. Chem., Int. Ed., 2017, 56, 6255–6259 CrossRef CAS.
- L. Turell, M. Steglich, M. J. Torres, M. Deambrosi, L. Antmann, C. M. Furdui, F. J. Schopfer and B. Alvarez, Free Radical Biol. Med., 2021, 165, 254–264 CrossRef CAS PubMed.
- J. T. Petroff, S. M. Omlid, N. Haloi, L. Sith, S. Johnson and R. D. McCulla, Comput. Theor. Chem., 2020, 1189, 112979 CrossRef CAS.
- L. A. H. van Bergen, G. Roos and F. De Proft, J. Phys. Chem. A, 2014, 118, 6078–6084 CrossRef CAS PubMed.
- B. Balta, G. Monard, M. F. Ruiz-López, M. Antoine, A. Gand, S. Boschi-Muller and G. Branlant, J. Phys. Chem. A, 2006, 110, 7628–7636 CrossRef CAS.
- E. Thiriot, G. Monard, S. Boschi-Muller, G. Branlant and M. F. Ruiz-López, Theor. Chem. Acc., 2011, 129, 93–103 Search PubMed.
- N. W. Pirie, Biochem. J., 1933, 27, 1181–1188 CrossRef CAS.
- L. Mao, Z.-S. Liu, C.-H. Huang, T.-S. Tang, H.-Z. Zhang, S.-Y. Chen and B.-Z. Zhu, Chem. Eng. J., 2024, 483, 148731 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- K. Roos, C. Wu, W. Damm, M. Reboul, J. M. Stevenson, C. Lu, M. K. Dahlgren, S. Mondal, W. Chen, L. Wang, R. Abel, R. A. Friesner and E. D. Harder, J. Chem. Theory Comput., 2019, 15, 1863–1874 CrossRef CAS PubMed.
- S. Mallick, B. Roy and P. Kumar, Comput. Theor. Chem., 2020, 1187, 112934 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- T. N. Truong and D. G. Truhlar, J. Chem. Phys., 1990, 93, 1761 CrossRef CAS.
- Y. Georgievskii and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 9776–9781 CrossRef CAS.
- J. Zheng, S. Zhang and D. G. Truhlar, J. Phys. Chem. A, 2008, 112, 11509–11513 Search PubMed.
- J. M. Anglada, R. Crehuet, S. Adhikari, J. S. Francisco and Y. Xia, Phys. Chem. Chem. Phys., 2018, 20, 4793–4804 Search PubMed.
- A. J. McGrath, G. E. Garrett, L. Valgimigli and D. A. Pratt, J. Am. Chem. Soc., 2010, 132, 16759–16761 CrossRef CAS PubMed.
- T. Okuyama, K. Miyake, T. Fueno, T. Yoshimura, S. Soga and E. Tsukurimichi, Heteroat. Chem., 1992, 3, 577–583 CrossRef CAS.
- https://webbook.nist.gov/cgi/cbook.cgi?ID=C62965224&Units=CAL&Mask=8#Thermo-React .
- L. Vereecken and J. Peeters, J. Chem. Phys., 2003, 119, 5159–5170 CrossRef CAS.
- H. P. Reisenauer, J. Romański, G. Mlostoń and P. R. Schreiner, Chem. Commun., 2013, 49, 9467–9469 RSC.
- S. Olivella, J. M. Anglada, A. Sole and J. M. Bofill, Chem. – Eur. J., 2004, 10, 3404–3410 CrossRef CAS PubMed.
- J. M. Anglada, S. Olivella and A. Solé, J. Am. Chem. Soc., 2014, 136, 6834–6837 CrossRef CAS PubMed.
- J. M. Anglada, M. T. C. Martins-Costa, J. S. Francisco and M. F. Ruiz-López, J. Am. Chem. Soc., 2024, 146, 14297–14306 Search PubMed.
- J. M. Anglada, J. Am. Chem. Soc., 2004, 126, 9809–9820 CrossRef CAS PubMed.
- J. M. Anglada, M. T. C. Martins-Costa, J. S. Francisco and M. F. Ruiz-López, Phys. Chem. Chem. Phys., 2019, 21, 9779–9784 Search PubMed.
- C. H. Switzer and J. M. Fukuto, Redox Biol., 2022, 57, 102486 CrossRef CAS PubMed.
- U. Barayeu, D. Schilling, M. Eid, T. N. Xavier da Silva, L. Schlicker, N. Mitreska, C. Zapp, F. Gräter, A. K. Miller, R. Kappl, A. Schulze, J. P. Friedmann Angeli and T. P. Dick, Nat. Chem. Biol., 2023, 19, 28–37 CrossRef CAS PubMed.
- J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147 CrossRef CAS PubMed.
- Q. Zhang, P. Liu, Y. Wang, C. George, T. Chen, S. Ma, Y. Ren, Y. Mu, M. Song, H. Herrmann, A. Mellouki, J. Chen, Y. Yue, X. Zhao, S. Wang and Y. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2302048120 CrossRef CAS PubMed.
- L. Tan and Y. Xia, J. Am. Soc. Mass Spectrom., 2013, 24, 534–542 CrossRef CAS PubMed.
- M. D. Sevilla, D. Becker and M. Yan, Int. J. Radiat. Biol., 1990, 57, 65–81 Search PubMed.
- Z. Zhang, X. Wang, P. Sivaguru and Z. Wang, Org. Chem. Front., 2022, 9, 6063–6076 RSC.
- K. L. Durand, X. Ma and Y. Xia, Analyst, 2014, 139, 1327–1330 Search PubMed.
- K. L. Durand, X. Ma and Y. Xia, Int. J. Mass Spectrom., 2015, 378, 246–254 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04106b |
| This journal is © the Owner Societies 2025 |