Isotope effects in Eley–Rideal abstraction of hydrogen from tungsten surfaces: the role of dissipation

Abstract

Molecular dynamics simulations are performed to investigate the influence of isotope substitutions on the Eley–Rideal recombination dynamics of hydrogen isotopes from the (100) and (110) surfaces of tungsten. Dissipation of electrons and phonons is taken into account by, respectively, the local density friction approximation and the general Langevin oscillator, effective models which have been intensively used in recent years. As the coupling to surface phonons and electrons might be altered by the mass combination, the main objective of the paper is to assess the role of dissipation to the surface in the course of abstraction.

---

1. Introduction

Despite great advances in surface science in the last 50 years, understanding elementary heterogeneous reactivity is still a vivid field. A molecular-level detailed understanding of these processes¹ provides relevant insights for catalysis,^2–4 the chemistry of the atmosphere and the interstellar medium,^5–7 plasma–wall interaction in atmospheric entries,^8,9 nuclear fusion,^10–12 among others.

Since the nineties, the Eley–Rideal (ER) recombination process, in which an atom colliding from the gas-phase (projectile) directly abstracts a pre-adsorbed atom on a surface (target), has been extensively studied on metals, both experimentally^13–26 and theoretically.^27–44 Most of the studies have focused on the recombination of hydrogen (and its isotopes). If many theoretical studies have overlooked possible energy transfer to the surface, recent works have analyzed dissipation to phonons and/or electron–hole pair excitations upon hydrogen scattering on clean and pre-covered surfaces,^45–60 using effective models, ab initio molecular dynamics or high-dimensional neural networks.

In the context of nuclear fusion, the interaction of hydrogen isotopes with tungsten is of great interest as the fusion fuel consists of D and T atoms. Tungsten is the main candidate for the armor material of the ITER fusion reactor divertors, which must control the escape of exhaust gases and impurities from the reactor and withstand the highest surface heat loads.¹² Moreover, the ER mechanism is of great importance in this regard, as its large exothermicity (approx. 1.75 eV) produces highly excited molecules, which are important for the production of negative ions.⁶¹ The present work focuses on the fundamental aspects of ER reactions, in particular the influence of energy dissipation upon isotopic substitutions.

Almost one decade ago, the H(D, T) + H(D, T)/W(110, 100) ER processes were studied via quasi-classical trajectory (QCT) simulation using density functional theory (DFT) based potential energy surfaces (PESs)⁶² within the Born–Oppenheimer approximation. It was observed that for all isotopes, ER abstraction occurred following a rebound of the projectile off a tungsten atom. Notably, significant isotope effects were detected on both W(100) and W(110) planes. When considering collision energies ranging from 0.1 to 5 eV at normal incidence, the cross sections followed an order based on the ratios of projectile mass m_p to target mass m_t. Specifically, the cross sections increased with the m_p/m_t ratios.

Furthermore, two main mechanisms were identified. The contribution of the sideway mechanism, where the projectile bounces off a tungsten atom at a similar altitude as the target, decreased significantly with the m_p/m_t ratio. As a consequence, the push-up mechanism, where the projectile bounces off a tungsten atom at an altitude below that of the target, became the main recombination mechanism for those isotopic combinations. The final energy partition also depended on the heavy-light/projectile-target combination. The translational energy of the formed molecules increased with the m_p/m_t ratio at the expense of the vibrational excitation. However, these conclusions are derived from an approximation that disregards the energy dissipation of the projectile during its interaction with the surface. Given that energy dissipation can influence both the projectile's dynamics and the behavior of the resulting molecule, we investigate the interplay between energy dissipation and isotopic effects upon Eley–Rideal abstraction for this system.

On the other hand, the effect of energy dissipation was also studied on both surfaces using the same PESs^45,63 for H₂ ER recombination. Dissipation produced variations of the cross section for H₂ recombination which were rationalized as a reduction in the effective collision energy. In the regions where the ER cross sections increased (decreased) with energy, electronic excitation reduced (enhanced) the recombination probability. Therefore, disregarding the isotopic effect, it was predicted that energy transfer is governed by electron–hole pair (ehp) excitations and energy transfer to phonons can safely be neglected due to the unfavorable mass mismatch between hydrogen and tungsten. These studies, however, ignored the random forces in the friction models, which were shown to influence the details of energy transfers upon atom scattering on metal surfaces.⁵⁷

More recently, isotope effects have been investigated for H scattering off clean fcc metals through experiments and simulations, which were found in very close agreement.⁵⁶ Inelastic energy losses were found to be very similar regardless of the impinging isotope, for all studied metals and different incidence energies ranging from 1 to 3 eV. This was explained by the compensation of the energy losses to electron and phonon excitation.

The goal of the present paper is to assess the influence of energy dissipation to the surface electrons and phonons upon the ER recombination of hydrogen isotopes on both the (100) and (110) tungsten surfaces. To achieve this, we employ molecular dynamics simulations that incorporate dissipation channels using well-established and widely adopted effective models.^45,63 The paper is organised as follows: in the next section, the employed methodology is presented, then the results are presented and discussed. Finally, the main conclusions of the work are summarized.

2. Methodology

QCT is performed to simulate the scattering of H isotopes onto the (110) and (100) reticular planes of tungsten in the zero coverage limit (single adsorbate). Global DFT-based potential energy surfaces (PESs) have been previously developed^47,49,64 for both surface symmetries, within the framework of the corrugation reducing procedure (CRP).^65,66 These PESs are six-dimensional as they explicitly consider the motions of the two hydrogen atoms with respect to a static surface with the tungsten atoms in their equilibrium position.

The simulations are carried out within three different models. In the first one, referred to as the Born–Oppenheimer static surface (BOSS) model, energy dissipation to the surface is not accounted for. In the second one, coupling to electron–hole pair excitations is modeled within the local density friction approximation (LDFA).^67,68 The effect of non-adiabaticity on hydrogen isotopes is introduced through dissipative and random forces into the classical equations (Langevin equation) as:

where m_i is the mass of the considered hydrogen isotope, i. The first right-hand side term corresponds to the adiabatic force, derived from the PES, V_6D({r_i, r_j}). Note that the indexes i and j refer to the recombining atoms. The friction force, proportional to the atom velocity, depends on the position vector, r_i, of the atom i, through the friction coefficient, η_el(r_i). Within the LDFA, η_el(r_i) corresponds to that of the same atom moving in a homogeneous free electron gas with an electron density equal to that of the bare surface at the same position r_i.^55,67–69 The random force, F_L(t), related to the friction force by the second fluctuation–dissipation theorem, accounts for electron temperature and is taken here as a Gaussian white noise.⁶⁸ In the present calculations, electronic temperature is set at T_s = 300 K. Details about the specific implementation of the LDFA can be found in ref. 46 and 47. In the third model, dissipation to surface phonons is added via a generalized Langevin oscillator (GLO) model^70,71 as implemented in ref. 72. Coupling with the metal phonons is introduced through a three-dimensional surface oscillator connected to a thermal bath that accounts for energy dissipation into the bulk.^70–75 This model including both the dissipation to phonons and electrons is referred to as the LDFA-GLO model.

Normal scattering is simulated for collision energies sampling the 0.1–5 eV range. The initial in-plane coordinates of the projectile atom (X_p, Y_p) are randomly sampled in a reduced section of the unit cell (green areas in Fig. 1) taking advantage of the symmetry. The initial altitude of the projectile is Z_p = 7.0 Å, which corresponds to the asymptotic region of the atom-substrate interaction potential.

Fig. 1 Representations of the (a) W(110) and (b) W(100) surfaces. The positions of the adsorption sites, respectively, 3-fold hollow and bridge are highlighted as red circles. Blue circles indicate the positions of the topmost tungsten atoms. The sampling areas of initial positions (X_p, Y_p) of the projectiles are highlighted in green and the lattice constant a is equal to 3.17 Å.

The target is initially located at its adsorption site and has random initial vibrational phases corresponding to the quantum zero-point energy for each (x, y, z) mode within the harmonic approximation, as done in previous studies.^76,77 The values, displayed in Table 1,⁷⁸ are in reasonable agreement with experiments for both studied surfaces. As illustrated as a red point in Fig. 1, the adsorption site is a 3-fold hollow site for the (110) surface while it is the bridge site for the (100) surface. The atom-surface potential energy surface is defined down to approximately Z = −3.9 Å.

Table 1 Adsorption energies Q_A, zero point energies (ZPE) in the x, y, and z modes, and positions of the adsorption sites (AS) for hydrogen (H), deuterium (D) and tritium (T)^62,79

		ZPE (meV)			AS (Å)
System	Q A (eV)	x	y	z	X	Y	Z
H/W(110)	3.06	47	60	71	1.585	0.6503	1.07
D/W(110)	3.06	33	42	50	1.585	0.6503	1.07
T/W(110)	3.06	26	35	42	1.585	0.6503	1.07
H/W(100)	3.09	69	40	67	1.585	0.0	1.107
D/W(100)	3.09	49	28	47	1.585	0.0	1.107
T/W(100)	3.09	40	23	39	1.585	0.0	1.107

---

All possible outcomes resulting from the projectile scattering have been detailed elsewhere.^80,81 Here, we focus only on the Eley–Rideal abstraction process which is assumed to take place when the formed H₂ molecule reaches the initial altitude of the projectile with a positive center-of-mass velocity towards the vacuum. It is also checked that the molecule is formed after only one rebound of its center-of-mass, following the first collision of projectile off the surface.

To achieve convergence, 640 000 trajectories were run for the W(110) plane and 320 000 for the W(100) one, with a maximum propagation time of 0.5 ps, for each collision energy. All trajectories are integrated with a Beeman algorithm using a fixed time step of 10⁻⁵ ps, which results in an average energy conservation in the BOSS simulations better than 1 meV. Since the ER process is ultra-fast, increasing the integration time beyond 0.5 ps did not modify the results. All possible isotope combinations have been considered on both crystallographic planes. The rotational and vibrational energy of the formed molecules have been classically averaged.

3. Results and discussion

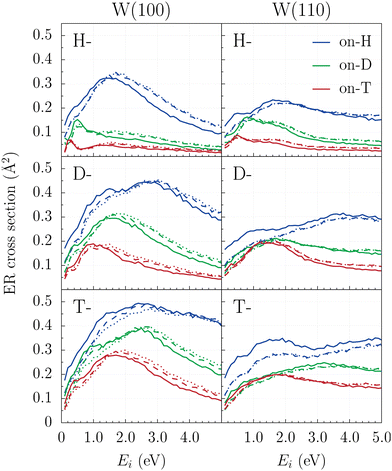
The ER abstraction cross sections (CSs) for all nine possible combinations of hydrogen isotopes are displayed in Fig. 2 as a function of collision energy, for both W(100) and W(110) symmetries within the framework of the BOSS, LDFA and LDFA-GLO models. “Proj-on-Targ” refers to “Proj” as the projectile and “Targ” as the target (“Proj” and “Targ” will be the H, D or T isotopes in the following). Note that H₂ CSs (blue lines in the top panels) are consistent with previous studies.^49,78

Fig. 2 ER cross sections (in Ų) as a function of incidence energy of the projectile E_i (in eV) for ER recombination on W(100) (left panels) and W(110) surfaces (right panels) within the BOSS (solid lines), LDFA (dashed lines) and LDFA-GLO (dotted lines) models. Top, middle and bottom panels correspond respectively to H, D and T projectiles recombining with the three different isotopes as a target.

Two striking features are extracted from Fig. 2. First, the inclusion of ehp excitations through LDFA may significantly affect ER cross sections. In contrast, accounting for energy dissipation to phonons via the GLO model shows only minor effects on this magnitude for both tungsten surfaces. As observed in H₂ recombination studies,⁴⁵ for different isotope combinations, the inclusion of ehp excitations generally shifts the maxima of the curves towards higher energies (compare solid lines corresponding to the BOSS model and dashed lines corresponding to LDFA results). Consequently, at low incident energies (E_i < 1 eV), where the curves exhibit steep slopes, including ehp excitations reduces the predicted CS by up to approximately 40%.

The second notable feature is that the influence of ehp excitations depends on the target's mass, with more pronounced effects when lighter H isotope is the target. This trend is evident for both crystallographic faces below 1 eV. However, at higher incident energies, this behavior persists only for D-on-H and T-on-H interactions on the W(110) surface, and for H-on-H interactions on W(100). Although the projectile loses more energy to ehp excitations due to its higher kinetic energy on average during the reaction, the effect of this energy dissipation on the CS does not correlate with the projectile mass.

Nevertheless, the main conclusions from previous work examining the isotopic effect on ER reactivity on both W surfaces within the BOSS model⁶² remain unchanged. Fig. 3 compares the ER cross sections for the nine isotopic combinations on each surface, using both the BOSS and LDFA-GLO models. On the one hand, all models predict small CS regardless of the isotope combination. On the other hand, the cross sections generally scale with the mass ratio (m_p/m_t) between the projectile and the adsorbed atom. However, the inclusion of energy loss channels to the surface reduces the pronounced isotope effect at low collision energies (E_i < 1 eV). At higher energies, the effect is essentially the same across both models. Consequently, for H₂, D₂ and T₂, the CSs are nearly identical in the 0.1–5.0 eV range.

Fig. 3 ER cross sections (in Ų) as a function of incidence energy of the projectile E_i (in eV) for ER recombination on W(110) (top panels) and W(100) surfaces (bottom panels) within the BOSS (left panels) and LDFA-GLO (right panels) models.

However, due to the use of different PESs in the present study compared to the work of Petuya et al.,⁶² discrepancies arise when comparing reactivity on the two tungsten surface faces. Quasi-classical dynamics performed on the earlier constructed FPLEPS PESs predicted higher ER reactivity at the W(100) crystallographic plane for each isotopic combination across the entire range of projectile kinetic energies (0.1–5.0 eV). In contrast, same calculations on the more accurate CRP PESs (with respect to DFT data) predict this behavior only for intermediate energies (1.0–2.0 eV) and when m_p/m_t ≥ 1. Otherwise, W(110) is predicted to be more reactive. This study confirms that the differences previously observed for H₂ recombination between the two PESs^49,78 also apply to other isotopic combinations. For W(110), the reactivity predicted by the CRP PES is higher than that of the FPLEPS PES, while for W(100), the reactivity differs only at high incident energies (E_i > 3 eV), with the CRP PES being less reactive at those energies.

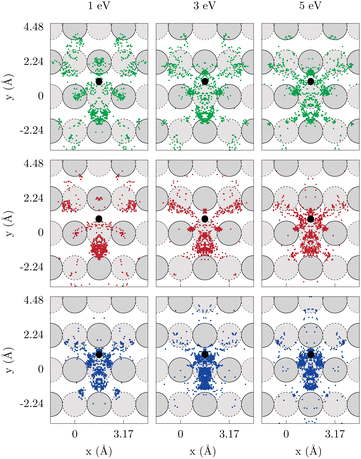
To confirm that the reaction dynamics remain unaffected by the inclusion of energy loss channels in the model, Fig. 4 and 5 display the distributions of (X_p, Y_p) in-plane coordinates of the projectile at the first rebound (opacity maps) within the LDFA-GLO model for W(100) and W(110), respectively. In the ensuing discussion, the following color coding is used: blue to denote H-on-T, red to denote H-on-H, and green to denote T-on-H.

Fig. 4 Opacity maps for the W(100) plane: (X, Y) first rebound positions of the projectiles for the trajectories leading to ER recombination at E_p = 1.0 (left) E_p = 3.0 (middle) and 5.0 eV (right) for T-on-H (up), H-on-H (middle) and H-on-T (down) within the LDFA-GLO model. Gray circles represent tungsten atoms of the first (solid line) and second layer (dashed line). The black disk represents the adsorbed isotope.

Fig. 5 Same as Fig. 4 but for W(110).

As previously found for the BOSS model,^62,64,78 the contribution to the total ER cross section of collisions where the projectile bounces on top of the initial position of the target remains marginal, even with the inclusion of energy dissipation channels. Therefore, ER recombination occurs after a redirection of the projectile off a nearby tungsten atom. This is reflected in the rebound positions of the projectiles, which are focused near lines connecting the adsorption site with its closest surrounding surface/subsurface atoms. Within this scenario, two mechanisms can be distinguished depending on whether the projectile bounces off a surface or a subsurface atom.

When comparing different isotopic combinations, it is observed that the reaction proceeds through higher impact parameters of the projectile as the m_p/m_t ratio increases. Concomitantly, the contribution to the ER cross section stemming from a projectile's rebound on the closest surface atoms from the adsorbate decreases with m_p/m_t. Notably, this contribution completely disappears for H-on-T on both tungsten surfaces. This trend holds true for both tungsten surfaces and cross the range of kinetic energies studied. Importantly, this behavior is not influenced by the inclusion of ehp excitations, as a comparison of average impact parameters in the BOSS and LDFA-GLO models (Table 2) shows that the addition of energy dissipation channels has almost no effect on this measure/magnitude.

Table 2 Average impact parameters (Å) for H-on-T, H-on-H and T-on-H recombinations on W(100) and W(110) at E_i = 1.0, 3.0, and 5.0 eV within LDFA-GLO (BOSS) model

E i	1.0 eV	3 eV	5 eV
H-on-T/W(110)	2.04 (1.94)	1.82 (1.88)	1.91 (1.98)
H-on-H/W(110)	2.20 (2.20)	2.00 (2.02)	1.96 (1.97)
T-on-H/W(110)	2.55 (2.58)	2.38 (2.42)	2.25 (2.33)
H-on-T/W(100)	1.57 (1.47)	1.25 (1.35)	1.54 (1.67)
H-on-H/W(100)	1.98 (1.86)	1.53 (1.49)	1.43 (1.47)
T-on-H/W(100)	2.28 (2.29)	1.91 (1.98)	1.83 (1.91)

---

The dynamics of these reactions can be rationalized, as previously done,⁶² in terms of two main pathways based on the projectile's rebound position Z_p: (i) a sideway mechanism (Z_p > 0.75 Å), where the projectile rebounds at the same altitude as the target is and (ii) a push-up mechanism (Z_p < 0.75), where the projectile extracts the target from bellow. Fig. 6 shows the distributions of the projectiles altitude (solid lines) and the targets altitude (dotted lines) at the moment of the first rebound. In general, the majority of reactive trajectories proceed via the push-up mechanism. The highest contribution of the sideway mechanism is observed for the T-on-H combination on both surfaces, which exhibits a gradual reduction as the m_p/m_t ratio decreases. For T-on-H on the 110 (100) tungsten surface, at 1 eV, 70% (35%) of the reactivity follows the sideway mechanism, whereas for H-on-T this pathway represents only 18% (8%) of the CS.

Fig. 6 Normalized distributions (area values) of the projectile altitude Z_p (solid lines) and target altitude Z_t (dotted lines) (in Å) at the projectiles first rebound of ER abstractions trajectories on W(100) (left panels) and W(110) (right panels) for various isotopic substitutions (H-on-T in blue, H-on-H in red, and T-on-H in green) at E_i = 1.0 (upper panels), 3.0 (middle panels) and 5.0 eV (bottom panels) within the LDFA-GLO model.

For all isotope combinations, the contribution of ER reactions following a rebound from subsurface atoms increases with collision energy. On the less compact W(100) surface, a significant portion of the reactivity occurs after the projectile rebounds off second-layer atoms. This is because the bridge position of the adsorbed atom makes the four-fold hollow position of the second-layer atoms easily accessible to the projectile. In contrast, on the more compact W(110) surface, the majority of reactive projectiles rebound off first-layer atoms.

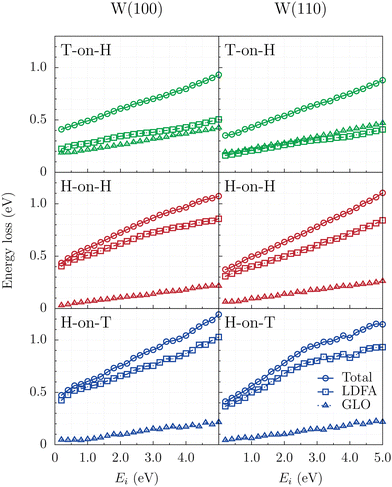
Although the reactivity and the dynamics of these ER processes do not change significantly with the inclusion of energy loss channels to the model, the analysis of the total energy dissipation during ER reaction in Fig. 7 shows that substantial amount of energy is transferred to the surface in all cases studied. At E_i = 0.1 eV approximately 0.45 eV are transferred from the two recombining atoms to the surface, with this value increasing steadily to around 1 eV at E_i = 5 eV. When comparing the two W surfaces, the energy losses are slightly higher on W(100) than on W(110), likely due to the lower average rebound altitude of the projectile on W(100) since higher electronic densities are found beneath the surface. However, these differences are small, under 0.1 eV. Additionally, energy losses are predicted to be slightly higher when hydrogen is the projectile, and for a given projectile, energy losses are marginally larger when the target is heavier.

Fig. 7 Average total energy losses (circles), average energy losses into phonons (triangles) and into e–h pair excitations (squares) as a function of the projectiles collision energy E_i. Results for W(100) (left panels) and W(110) (right panels) are shown for T-on-H (top panels), H-on-H (middle panels) and H-on-T (bottom panels) isotope combinations.

As previously stated, the energy transfer from the molecule to the surface can happen via ehp or phonon excitation, whose contributions to the total energy dissipation is highlighted in Fig. 7 by squares and triangles, respectively. When the projectile is an H isotope, the majority of energy is lost through e–h pair excitations (squares in bottom and middle panels for H-on-T and H-on-H, respectively). In contrast, for T-on-H (top panels), the total amount of energy transferred to the surface is similar, but half of the energy loss proceeds through phonon excitations, that is, it is drained by the GLO model (triangles). Similar behavior was observed experimentally and predicted by classical dynamics calculations for H and D scattering from several fcc (111) metal surfaces.⁵⁶

As a result, the internal energy of the formed molecules is lowered when including energy loss channels within the model. The final average translational, vibrational and rotational energies of the formed molecules are displayed in Fig. 8, for H-on-T, H-on-H and T-on-H combinations and both crystallographic planes within the framework of the BOSS and LDFA-GLO models. The final modes of motion are energetically excited as the process is exothermic by about 1.75 eV. In all cases at low energies (E_i < 1 eV) the translational energy is roughly twice the vibrational and the rotational energies. Increasing the projectile initial energy results mainly in a higher translational excitation of the molecules. While the translational energy roughly quadruples from E_i = 0.1 eV to E_i = 5 eV, the rotational energy is duplicated and the vibrational energy is duplicated or triplicated depending on the isotopic combination.

Fig. 8 Final average translational 〈E_tra〉, rotational 〈E_rot〉 and vibrational 〈E_vib〉 energies (in eV) of the formed molecules as a function of E_i (in eV). Left and right panels correspond to BOSS and LDFA-GLO models. Results for H-on-T (blue circles), H-on-H (red up-triangles) and T-on-H (green down-triangles) on both W(100) (solid lines and filled symbols) and W(110) (dotted lines and open symbols) surfaces are shown.

While formed molecules for H-on-T and H-on-H combinations show basically the same energy partitions for each incidence energy of the projectile in both surfaces, in the case of T-on-H, differences are observed with respect to the former as well as depending on the surface in which the ER reaction takes place. The TH molecules formed on W(110) are vibrationally more excited than on W(100), while on the former surface formed molecules have in average less translational energy than on the later surface. Similarly, at high incident energies (E_i > 1 eV), translationally more excited molecules form in the T-on-H combination at the expense of vibrational energy. Previous work with the FPLEPS PESs also observed lower vibrational excitation of the formed molecules for the D-on-H combination.⁶²

The comparison of the partition of average energy within the BOSS (left panels) and LDFA-GLO (right panels) models reveals that the energy dissipated into the surface is essentially removed from the translational energy for all isotope combinations, as previously observed for homonuclear isotope combination.^45,63 Thus, differences in average rotational and vibrational energies are negligible.

4. Conclusions

The Eley–Rideal recombination of hydrogen isotopes on W(110) and W(100) has been investigated by molecular dynamics simulation on DFT-based interpolated potential energy surfaces. The influence of the energy losses to the surface has been analyzed accounting for dissipation to electrons and phonons employing the local density friction approximation (LDFA) and the generalized Langevin oscillator (GLO) models, respectively.

It is observed that energy dissipation to the metallic surfaces has a very minor effect on the main observables of the reaction and as a consequence the main conclusions ignoring dissipation remain.⁶² The cross-sections for reaction are ordered by the (m_p/m_t) ratios, m_p and m_t being the masses of the projectile and the target respectively. Eley–Rideal reactions on these systems involve the rebound of the projectile off a surface or subsurface atom before abstracting the target, the subsurface contributions being more important in the case of the less compact (100) surface. As the m_p/m_t ratio of the isotopic combination increases the formed molecules tend to be more excited translationally at the expense of vibrational energy.

The energy dissipation channels competition depends mainly on the projectile's mass. While for the H projectile it is mainly governed by electron–hole pair excitations, for the heavier T isotope an identical amount of energy is dissipated to ehp and phonon excitations. Despite these differences, the total amount of energy dissipated is very similar for all isotopic combinations due to a compensation effect between the two channels. As a consequence, the LDFA-GLO model predicts molecules with lower average translational energies, while the average rotational and vibrational energies are basically unaffected.

Data availability

Data for this article, including results related to the Eley–Rideal recombination of hydrogen isotopes on tungsten surfaces, are available at Zenodo at https://doi.org/10.5281/zenodo.13970565.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

O. G. acknowledges financial support from the Gobierno Vasco-UPV/EHU Project No. IT1569-22 and from the Spanish MCIN/AEI/10.13039/501100011033 (PID2022-140163NB-I00). P. E. I.-A., M. M.-M., J. D. C., Y. S.-S. and J. R.-S. would like to thank the funding provided by the PNAP of the InSTEC/UH NAP223LH001-055 and the PN CBN of the CITMA PN223LH010-069 and would also like to thank the Advanced Computational Team at Instituto Superior de Tecnologías y Ciencias Aplicadas (InSTEC), University of Havana, for the support provided during the realization of this work. R. M.-B. and P. L. acknowledge funding from the University of Bordeaux, the CNRS, and the Transnational Common Laboratory QuantumChemPhys: Theoretical Chemistry and Physics at the Quantum Scale (ANR-10-IDEX-03-02) and the DALTON ANR project (ANR-22-CE30-0013). Computer time was provided by the Pole Modélisation HPC facility of the Institut des Sciences Moléculaires, UMR 5255, CNRS, Université de Bordeaux, cofunded by the Nouvelle Aquitaine region as well as the MCIA (Mésocentre de Calcul Intensif Aquitain).

References

1. R. Díez Muiño and H. Busnengo, Dynamics of Gas-Surface Interactions: Atomic-level Understanding of Scattering Processes at Surfaces, Springer, 2013.
2. G. A. Somorjai and Y. Li, Introduction to surface chemistry and catalysis, John Wiley & Sons, 2010.
3. F. Zaera, Prog. Surf. Sci., 2001, 69, 61.
4. J. M. Thomas and W. J. Thomas, Principles and Practice of Heterogeneous Catalysis, WCH, Weinheim, 1997.
5. M. J. Molina, L. T. Molina and D. M. Golden, J. Phys. Chem., 1996, 100, 12888–12896.
6. J. M. Greenberg, Surf. Sci., 2002, 500, 793.
7. J. S. Mathis, Rep. Prog. Phys., 1993, 56, 605.
8. B. Halpern and D. E. Rosner, J. Chem. Soc., Faraday Trans. 1, 1978, 78, 1883.
9. L. Martin-Gondre, PhD thesis, Université Bordeaux 1, 2009.
10. J. Roth, E. Tsitrone, A. Loarte, T. Loarer, G. Counsell, R. Neu, V. Philipps, S. Brezinsek, M. Lehnen and P. Coad, et al. , J. Nucl. Mater., 2009, 390, 1–9.
11. A. Kleyn, N. L. Cardozo and U. Samm, Phys. Chem. Chem. Phys., 2006, 8, 1761–1774.
12. J. Marian, C. S. Becquart, C. Domain, S. L. Dudarev, M. R. Gilbert, R. J. Kurtz, D. R. Mason, K. Nordlund, A. E. Sand, L. L. Snead and T. Suzudo, Nucl. Fusion, 2017, 57, 092008.
13. C. T. Rettner, Phys. Rev. Lett., 1992, 69, 383.
14. C. T. Rettner, J. Chem. Phys., 1994, 101, 1529.
15. C. T. Rettner and D. J. Auerbach, Phys. Rev. Lett., 1995, 74, 4551.
16. J. Y. Kim and J. Lee, Phys. Rev. Lett., 1999, 82, 1325.
17. J. Y. Kim and J. Lee, J. Chem. Phys., 2000, 113, 2856.
18. T. Kammler, S. Wehner and J. Küppers, Surf. Sci., 1995, 339, 125–134.
19. J. Kammler, T. Lee and J. Küppers, J. Chem. Phys., 1997, 106, 7362–7371.
20. B. Zecho, T. Brandner and J. Küppers, Surf. Sci. Lett., 1998, 418, L26–L30.
21. J. Wehner and S. Küppers, Surf. Sci., 1998, 411, 46–53.
22. J. Wehner and S. Küppers, J. Chem. Phys., 1998, 108, 3353–3359.
23. J. Wehner and S. Küppers, J. Chem. Phys., 1998, 109, 294–300.
24. T. Kammler, S. Wehner and J. Küppers, J. Chem. Phys., 1998, 109, 4071–4077.
25. J. Kammler and T. Küppers, J. Chem. Phys., 1999, 111, 8115–8123.
26. T. Kolovos-Vellianitis, D. Kammler and J. Küppers, Surf. Sci., 2000, 454–456, 316–319.
27. P. Kratzer and W. Brenig, Surf. Sci., 1991, 254, 275–280.
28. B. Jackson and M. Persson, Surf. Sci., 1991, 269, 195–200.
29. B. Jackson and M. M. Persson, J. Chem. Phys., 1992, 96, 2378.
30. H. K. Shin, Chem. Phys. Lett., 1995, 244, 235–244.
31. M. Persson and B. Jackson, Chem. Phys. Lett., 1995, 237, 468.
32. B. Caratzoulas, S. Jackson and M. Persson, J. Chem. Phys., 1997, 107, 6420–6431.
33. B. Shalashilin, D. V. Jackson and M. Persson, Faraday Discuss., 1998, 110, 287–300.
34. B. Shalashilin, D. V. Jackson and M. Persson, J. Chem. Phys., 1999, 110, 11038–11046.
35. D. Kalyanaraman, C. Lemoine and B. Jackson, Phys. Chem. Chem. Phys., 1999, 1, 1351–1358.
36. D. Jackson and B. Lemoine, J. Chem. Phys., 2001, 114, 474–482.
37. X. Guvenc, Z. B. Sha and B. Jackson, J. Chem. Phys., 2001, 115, 9018–9027.
38. J. D. Lemoine, D. Quattrucci and B. Jackson, Phys. Rev. Lett., 2002, 89, 268302.
39. X. Jackson, B. Sha and Z. B. Guvenc, J. Chem. Phys., 2002, 116, 2599–2608.
40. X. Guvenc, Z. B. Sha and B. Jackson, J. Phys. Chem. B, 2002, 106, 8342–8348.
41. B. Quattrucci, J. G. Jackson and D. Lemoine, J. Chem. Phys., 2003, 118, 2357–2365.
42. R. Martinazzo, S. Assoni, G. Marinoni and G. F. Tantardini, J. Chem. Phys., 2004, 120, 8761–8771.
43. G. Lanzani, R. Martinazzo, G. Materzanini, I. Pino and G. F. Tantardini, Theor. Chem. Acc., 2007, 117, 805–825.
44. M. Rutigliano and M. Cacciatore, Phys. Chem. Chem. Phys., 2011, 13, 7475–7484.
45. O. Galparsoro, R. Petuya, J. Juaristi, C. Crespos, M. Alducin and P. Larrégaray, J. Phys. Chem. C, 2015, 119, 15434–15442.
46. O. Galparsoro, R. Péétuya, H. F. Busnengo, J. I. Juaristi, C. Crespos, M. Alducin and P. Larregaray, Phys. Chem. Chem. Phys., 2016, 18, 31378.
47. O. Galparsoro, H. F. Busnengo, J. I. Juaristi, C. Crespos, M. Alducin and P. Larregaray, J. Chem. Phys., 2017, 147, 121103.
48. O. Galparsoro, J. I. Juaristi, C. Crespos, M. Alducin and P. Larrégaray, J. Phys. Chem. C, 2017, 121, 19849–19858.
49. O. Galparsoro, H. F. Busnengo, A. E. Martinez, J. I. Juaristi, M. Alducin and P. Larregaray, Phys. Chem. Chem. Phys., 2018, 20, 21334–21344.
50. G.-J. Kroes, M. Pavanello, M. Blanco-Rey, M. Alducin and D. J. Auerbach, J. Chem. Phys., 2014, 141, 054705.
51. M. Pavanello, D. J. Auerbach, A. M. Wodtke, M. Blanco-Rey, M. Alducin and G.-J. Kroes, J. Phys. Chem. Lett., 2013, 4, 3735–3740.
52. L. Zhou, X. Zhou, M. Alducin, L. Zhang, B. Jiang and H. Guo, J. Chem. Phys., 2018, 148, 014702.
53. J. Chen, X. Zhou and B. Jiang, J. Chem. Phys., 2019, 150, 061101.
54. L. Zhu, H. Ce, J. Chen and B. Jiang, Phys. Chem. Chem. Phys., 2023, 25, 5479.
55. O. Bünermann, H. Jiang, Y. Dorenkamp, A. Kandratsenka, S. M. Janke, D. J. Auerbach and A. M. Wodtke, Science, 2015, 350, 1346–1349.
56. Y. Dorenkamp, H. Jiang, H. Köckert, A. Janke, S. M. Kandratsenka, A. M. Wodtke and O. Bünermann, J. Chem. Phys., 2018, 148, 034706.
57. N. Hertl, R. Martin-Barrios, O. Galparsoro, P. Larrégaray, D. J. Auerbach, D. Schwarzer, A. M. Wodtke and A. Kandratsenka, J. Phys. Chem. C, 2021, 125, 14468–14473.
58. N. Hertl, A. Kandratsenka and A. M. Wodtke, Phys. Chem. Chem. Phys., 2022, 24, 8738–8748.
59. R. Martin Barrios, O. Galparsoro, A. Martinez Mesa, L. Uranga-Piña, C. Crespos and P. Larregaray, J. Phys. Chem. C, 2021, 125, 14075–14081.
60. R. Martin-Barrios, N. Hertl, O. Galparsoro, A. Kandratsenka, A. M. Wodtke and P. Larrégaray, Phys. Chem. Chem. Phys., 2022, 24, 20813–20819.
61. Physics and Applications of Hydrogen Negative Ion Sources, ed. M. Bacal, Springer, 2023.
62. R. Pétuya, M. A. Nosir, C. Crespos, R. Díez Muiño and P. Larrégaray, J. Phys. Chem. C, 2015, 119, 15325.
63. O. Galparsoro, J. Juaristi, C. Crespos, M. Alducin and P. Larregaray, J. Phys. Chem. C, 2017, 121, 19849–19858.
64. R. Pétuya, C. Crespos, E. Quintas-Sanchez and P. Larrégaray, J. Phys. Chem. C, 2014, 118, 11704–11710.
65. H. Busnengo, A. Salin and W. Dong, J. Chem. Phys., 2000, 112, 7641–7651.
66. R. A. Olsen, H. F. Busnengo, A. Salin, M. F. Somers, G. J. Kroes and E. J. Baerends, J. Chem. Phys., 2002, 116, 3841–3855.
67. J. I. Juaristi, M. Alducin, R. Diéz-Muino, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2008, 100, 116102.
68. M. Alducin, R. Diéz-Muino and J. I. Juaristi, Prog. Surf. Sci., 2017, 92, 317–340.
69. S. M. Janke, D. J. Auerbach, A. M. Wodtke and A. Kandratsenka, J. Chem. Phys., 2018, 143, 124708.
70. S. Adelman and J. Doll, J. Chem. Phys., 1976, 64, 2375–2388.
71. J. C. Tully, J. Chem. Phys., 1980, 73, 1975–1985.
72. J. I. Juaristi, M. Alducin, R. Díez Muiño, H. F. Busnengo and A. Salin, Phys. Rev. Lett., 2004, 93, 236103.
73. S. A. Adelman, J. Chem. Phys., 1979, 71, 4471.
74. P. Dohle, M. Saalfrank and T. Uzer, J. Chem. Phys., 1998, 108, 4226–4236.
75. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 1555.
76. R. Pétuya, M. A. Nosir, C. Crespos, R. Díez Muiño and P. Larrégaray, J. Phys. Chem. C, 2015, 119, 15325–15332.
77. R. Pétuya, P. Larrégaray, C. Crespos, P. Aruel, H. F. Busnengo and A. E. Martínez, J. Phys. Chem. C, 2015, 112, 3171–3179.
78. R. Pétuya, P. Larrégaray, C. Crespos, H. F. Busnengo and A. E. Martinez, J. Chem. Phys., 2014, 141, 024701.
79. R. Pétuya, P. Larrégaray, C. Crespos, P. Aurel, H. F. Busnengo and A. E. Martinez, J. Phys. Chem. C, 2015, 119, 3171–3179.
80. E. Quintas-Sánchez, P. Larregaray, C. Crespos, L. Martin-Gondre, J. Rubayo-Soneira and J.-C. Rayez, J. Chem. Phys., 2012, 137, 064709.
81. E. Quintas-Sánchez, C. Crespos, P. Larrégaray, J. Rayez, L. Martin-Gondre and J. Rubayo-Soneira, J. Chem. Phys., 2013, 138, 024706.

---