Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Estimating advancing and receding contact angles for pure and mixed liquids on smooth solid surfaces using the PCP-SAFT equation of state
Aliakbar
Roosta
 *a,
Sohrab
Zendehboudi
*a,
Sohrab
Zendehboudi
 b and
Nima
Rezaei
b and
Nima
Rezaei
 a
a
aDepartment of Separation Science, School of Engineering Science, LUT University, Lappeenranta, Finland. E-mail: aliakbar.roosta@lut.fi
bDepartment of Process Engineering, Memorial University, St. John's, NL, Canada
First published on 19th February 2025
Abstract
Contact angle is an important measure of wetting in systems involving liquid–solid interfaces. This study focuses on estimating advancing and receding contact angles of pure and mixed liquids on smooth solid surfaces using perturbed-chain polar statistical associating fluid theory equation of state (PCP-SAFT EoS). For the receding contact angle, we propose a model in which the surface energy of a solid covered by a liquid film is approximated by the geometrical average of the surface energies of the solid and liquid. The PCP-SAFT model is used to calculate the ratio of dispersion-to-total surface energy for diverse pure and mixed liquids. The results are validated against 104 experimental data point contact angles, showing an average absolute relative deviation (AARD) of 7.4% for the advancing angle and 10.6% for the receding angle. The contact angle model uses an α-parameter, acting as a weighting factor for the solid and liquid effects on the work of adhesion. The model uses 0.75 and 0.5 for the advancing and receding contact angles, respectively. To assess the reliability of this α-parameter, we also optimized it using experimental data of contact angle. The optimized parameter was found to be 0.74 for advancing and 0.48 for receding contact angle, and the AARD values slightly reduced to 7.2% and 10.5%, respectively. The value of optimized model parameter are similar to those obtained based on the model assumptions, showing that the film surface energy is correctly represented by the geometrical average both in advancing and receding processes. The contact angle model combined with the PCP-SAFT framework also allowed to accurately predict the advancing and receding contact angles of binary liquid mixtures.
1 Introduction
The wettability of liquid–solid interfaces significantly influences the properties and behavior of materials.1 A common way to quantify wetting is by observing the contact angle of liquid droplets on solid surfaces.2 Advancing and receding contact angles are crucial variables in surface science and provide insights into the wetting behavior of liquids, which is pivotal in various industrial and scientific applications such as pore condensation,3 immersion lithography,4 fiber coatings,5 drag reduction,6 oil production,7 oil/water separation,8 agricultural pesticide sprays,9 desalination,10 and inkjet printing.11The measurement of advancing and receding contact angles can be performed using several experimental techniques, such as sessile drop, titling plate, Wilhelmy plate, capillary rise, and centrifugation.12 A common method involves the sessile drop technique, where a liquid droplet is deposited on a solid surface, and the contact angles are measured as the droplet volume is increased or decreased.13 In the tilting plate method, a droplet is placed on a surface that is gradually tilted until the droplet begins to move, from which the advancing and receding angles are measured.14 The Wilhelmy plate method involves dipping and withdrawing of a thin plate from a liquid to measure these angles by analyzing force–distance curves.15 The capillary rise method measures contact angles by observing the behavior of a liquid in a thin capillary tube placed on a surface. For the advancing and receding contact angles, the liquid rise and fall are measured in the tube, respectively.16 The centrifugal method involves spinning a liquid droplet on a surface. The advancing contact angle is determined by measuring the angle at the front edge of the droplet, and the receding contact angle is measured at the rear edge.14
While these experimental measurements are invaluable, they are time-consuming, laborious, and sensitive to surface heterogeneity and contamination.17 Therefore, theoretical models and correlations are developed based on hydrodynamic molecular-kinetics to estimate the advancing and receding contact angles, offering a complementary approach to experimental techniques.18 There are two main approaches to explain the contact angle hysteresis: the dynamic model describes the contact angle behavior have not the contact line motion, and the other model describes the static contact angle hysteresis.18 The dynamic models are of three types: (1) hydrodynamic models, which assume that viscous dissipation within the liquid phase is the dominant factor influencing the contact angle dynamics, including friction in the liquid film;19,20 (2) molecular-kinetic models, which focus on the adsorption and desorption processes of molecules at the liquid–substrate interface, explaining how these molecular interactions impact the contact angle by considering the rate at which molecules attach to and detach from the surface;21 and (3) hybrid hydrodynamic-molecular kinetic models consider both wetting line friction and viscous dissipation contributions to the dynamic contact angle.22 The static models for advancing and receding contact angles focus on the liquid–solid interfaces under equilibrium conditions and are typically based on Young's equation.18 Previous studies offer diverse perspectives on the static modeling of advancing and receding contact angles. Joanny and de Gennes23 focused on the impact of surface heterogeneity on contact angle hysteresis, attributing it to defects on the solid surface. Marmur and Krasovitski24 introduced line tension as a factor influencing the contact angle hysteresis behavior, particularly on curved surfaces. Tadmor25 extended this concept by relating line energy to hysteresis and contact angle values. In contrast, Chibowski26 challenged the conventional view of hysteresis as solely resulting from the surface roughness or heterogeneity. By examining liquid film formation behind the receding contact line, they proposed a new approach to estimating the solid surface free energy based on contact angle hysteresis. However, there is still no definitive consensus or complete understanding of the hysteresis phenomenon on smooth homogeneous surfaces.27
In our previous work,28 we proposed a novel approach to successfully estimate the equilibrium contact angle of pure and mixed liquids on smooth solid surfaces using the perturbed chain polar statistical associating fluid theory (PCP-SAFT) equation of state and with a good acuracy. This paper presents a follow-up study and provides new correlations based on thermodynamic modelling to estimate the receding contact angle of pure and mixed liquids on smooth solid surfaces using the PCP-SAFT model. In the current study, we use a similar methodology to estimate the advancing contact angle. Commonly in literature, the receding contact angle models relate it to the advancing and equilibrium contact angle values, making its accuracy dependent on the latter estimates. The strength of our model is that the advancing and receding contact angles are estimated independently. By decoupling the advancing, receding, and equilibrium contact angle models, the uncertainty propagation from prior models is eliminated. Also, our model allows for more precise predictions across a broader range of liquid types (non-polar, polar, and associating) and solid surfaces with varying surface energies.
Our paper is structured as follows: after the introduction section, Section 2 provides background on estimating advancing and receding contact angles. Section 3 details the proposed methodology for calculating these contact angles based on the extended Young's equation.29 In Section 4, the conditions under which the experimental data gathered from the literature are presented. Section 5 presents the results of estimations of the advancing and receding contact angles for pure and binary mixed liquids on various solid surfaces under ambient conditions. Finally, Section 6 provides the concluding remarks.
2 Theoretical background
Contact angle hysteresis is the difference between the advancing and receding contact angles and is affected by the surface pore structure and wetting history. In successive advancing–receding contact angle measurement experiments, Chibowski26 proposed hysteresis to be primarily caused by the presence of a residual liquid film left behind the receding contact line of a droplet. This liquid film changes the effective surface free energy of the solid when calculating the receding contact angle. Chibowski26 applied Young's equation to calculate both advancing and receding contact angles, assuming that the only difference between them is attributed to the surface energy of the solid, as demonstrated by eqn (1):| γSF = γS + π | (1) |
By knowing the surface energy of the solid and the liquid, Chibowski26 established a relationship between the advancing and receding contact angles, as shown in eqn (2):
 | (2) |
Good et al.33–35 proposed that the free energy of adhesion is equal to the geometric mean of the free energies of cohesion for the two phases in contact. At the molecular level, the geometric mean represents the average interaction strength between the solid and liquid molecules at the interface. So, it is expected that the interfacial tension can be obtained from the geometric mean of the surface energies of the two phases. Recent studies36,37 combined the Good's geometrical mean approximation with the molecular dynamics framework to predict key parameters such as interfacial tensions and contact angles for various liquids and substrates. These studies support the validity of Good's assumption.
In developing eqn (2), Chibowski26 used the following work of adhesion terms based on the Good's model assumption:33
 | (3) |
 | (4) |
 | (5) |
 | (6) |
 by calculating the dispersion and non-dispersion (polar or hydrogen bonding) contributions to the Helmholtz free energy. We used the Owens–Wendt–Kaelble29 equation shown in eqn (6), as an extention of Young's equation, to estimate the equilibrium contact angle for various pure and mixed liquids on diverse solid surfaces. This includes 24 solids and 15 liquids, encompassing polar, non-polar, and associating liquids. However, our previous work28 is limited to cases where the surface energy of the liquid exceeds that of the solid.
by calculating the dispersion and non-dispersion (polar or hydrogen bonding) contributions to the Helmholtz free energy. We used the Owens–Wendt–Kaelble29 equation shown in eqn (6), as an extention of Young's equation, to estimate the equilibrium contact angle for various pure and mixed liquids on diverse solid surfaces. This includes 24 solids and 15 liquids, encompassing polar, non-polar, and associating liquids. However, our previous work28 is limited to cases where the surface energy of the liquid exceeds that of the solid.
Inspired by Chibowski26 and following our previous work,28 a model is proposed to estimate the advancing and receding contact angles.
3 Methodology
Following Chibowski's hypothesis,26 we also include in the receding contact angle model the effect of the residual liquid film on the solid surface energy. This liquid film, as suggested by Chibowski,26 alters the effective surface free energy of the solid. Building upon Good's work33 and using interfacial tension as the geometric mean of the surface energies, we propose that the surface energy of the film-covered solid (γSF) can be approximated as the geometric mean of the surface energies of the solid and the liquid, which is implemented for both the dispersion and non-dispersion contributions to the surface energy as shown by eqn (7) and (8): | (7) |
 | (8) |
The geometric mean provides a balanced approximation that reflects the combined effects of the solid and liquid surface energies. A recent study38 shows that the physical properties of a thin film arise from both the solid and liquid phases, which is a further validation of our assumption.
While our approach is consistent with the previous studies, including Chibowski's work,26 further justification and validation of this assumption will be provided by comparing the results with experimental data of the receding contact angle.
By substituting eqn (7) and (8) into eqn (6), a new model is developed for calculating the receding contact angle as shown in eqn (9); after mathematical manipulations, eqn (10) is obtained:
 | (9) |
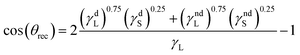 | (10) |
By comparing eqn (6) and (10), it follows that both equations are in the following form:
 | (11) |
In the current study, we evaluate eqn (10) to estimate the receding contact angle and compare it with the receding contact angle measurements from the literature. Furthermore, given that the advancing contact angle is commonly calculated using Young's equation in the literature,26,39–41 we employ eqn (6) to estimate the advancing contact angle and compare its results with experimental data available in the literature.
Moreover, we use the literature contact angle data to optimize the power parameter term of α in eqn (11) for calculating both the advancing and receding contact angles, aiming to develop more accurate models for estimating contact angle hysteresis. Also, this method will enable to check the validity of our assumption (eqn (7) and (8)) to obtain the dispersion and non-dispersion contributions to the liquid film surface energy as the geometric mean of the surface energies of the solid and liquid. The average absolute relative deviation (AARD) between the estimated contact angles and the literature data is minimized to determine the optimal α for calculating both the advancing and receding contact angles.
4 Data collection and sources
In this study, we have compiled 104 pairs of advancing and receding contact angle data points from various liquid–solid systems available in the literature.41–59 These data encompass contact angle measurements under the ambient conditions for a variety of liquid–solid pair combinations, including both pure and mixed liquids. We consider 26 different solid surfaces with a surface energy (γS) in the range of 9.5 mN m−1 to 64.7 mN m−1. For these solid surfaces, the contributions from dispersion forces (γdS) to the total surface energy are significant at room temperature which are listed from the literature sources, as detailed in Table 1.42,60–73| No. | Solid component (Tag) | γ S mN m−1 | γ dS mN m−1 | Ref. |
|---|---|---|---|---|
| 1 | Polytetrafluoroethylene (PTFE) | 19.1 | 18.6 | 60 |
| 2 | Paraffin wax (Wax) | 25.4 | 25.4 | 60 |
| 3 | Polychlorotrifluoroethylene (PCTFE) | 27.5 | 23.9 | 61 |
| 4 | Polyethylene (PE) | 33.1 | 32.0 | 60 |
| 5 | Polystyrene (PS) | 42.0 | 41.4 | 60 |
| 6 | Polycarbonate (PC) | 46.0 | 45.0 | 62 |
| 7 | Stainless steel-316 (SS-316) | 39.0 | 37.0 | 63 |
| 8 | Silicon rubber (SR) | 20.9 | 20.8 | 64 |
| 9 | Polypropylene (PP) | 30.4 | 30.4 | 65 |
| 10 | Polyvinylchloride (PVC) | 41.5 | 39.8 | 61 |
| 11 | Polymethyl methacrylate (PMMA) | 40.2 | 35.8 | 61 |
| 12 | Nylon 66 (Nylon-66) | 43.2 | 34.1 | 60 |
| 13 | Polyvinylidene fluoride (PVDF) | 30.0 | 23.2 | 60 |
| 14 | Polyethylene terephthalate (PET) | 41.3 | 37.8 | 60 |
| 15 | Fluorinated ethylene propylene (FEP) | 16.9 | 14.3 | 66 |
| 16 | Polydimethylsiloxane (PDMS) | 10.6 | 9.2 | 67 |
| 17 | FC-732 | 11.3 | 10.8 | This work |
| 18 | Nylon-12 | 35.8 | 30.3 | 68 |
| 19 | Polybutylene terephthalate (PBT) | 46.2 | 44.6 | 69 |
| 20 | Thermoplastic polyolefins (TPO) | 31.8 | 31.3 | 70 |
| 21 | Polyperfluoro alkoxyethylene (PFA) | 17.4 | 17.1 | 42 |
| 22 | Ethylene tetrafluoroethylene (ETFE) | 18.0 | 17.5 | 42 |
| 23 | Ethylene chlorotrifluoroethylene (ECTFE) | 30.2 | 29.7 | 42 |
| 24 | Perfluoroalkyl acrylate (PFAC) | 9.5 | 9.0 | 71 |
| 25 | Silica | 64.7 | 48.9 | 72 |
| 26 | Glass | 62.0 | 26.0 | 73 |
Furthermore, we examine 27 different liquids, including six polar, nine nonpolar, and 12 associating liquids, as listed in Table 2. The pure-component parameters of the PCP-SAFT model for these 27 liquids are gathered from the literature and are summarized in Table 2.74–76 These parameters are used to estimate the ratio  using the PCP-SAFT model, based on our previous work.28 Additionally, liquid surface tension data are obtained from the literature.77
using the PCP-SAFT model, based on our previous work.28 Additionally, liquid surface tension data are obtained from the literature.77
| Type of fluids | Component | CAS no. | PCP-SAFT pure component parameters | values by PCP-SAFT | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| m | σ | ε/k | μ D | Scheme | Ref. | ||||||
| Associating | Formamide | 75-12-7 | 1.4078 | 3.54 | 550 | 0 | 0.00647 | 2132.38 | 3B | 74 | 0.78 |
| Water | 7732-18-5 | 1.5000 | 2.6273 | 180.3 | 0 | 0.0942 | 1804.22 | 4C | 75 | 0.38 | |
| Ethylene glycol | 107-21-1 | 1.7108 | 3.7348 | 354.18 | 0 | 0.01627 | 2120.08 | 4C | 74 | 0.62 | |
| Glycerol | 56-81-5 | 1.7740 | 4.1223 | 408.60 | 0 | 0.01123 | 2063.85 | 3B | 74 | 0.66 | |
| Ethanol | 64-17-5 | 2.8866 | 2.9577 | 187.26 | 0 | 0.05533 | 2462.31 | 2B | 74 | 0.68 | |
| 1-Propanol | 71-23-8 | 3.6480 | 3.0135 | 213.87 | 0 | 0.03853 | 1980.97 | 2B | 74 | 0.84 | |
| 1-Butanol | 71-36-3 | 3.6639 | 3.2437 | 232.69 | 0 | 0.01435 | 2163.48 | 2B | 74 | 0.87 | |
| 1-Pentanol | 71-41-0 | 3.5903 | 3.4655 | 245.27 | 0 | 0.0139 | 2356.44 | 2B | 74 | 0.86 | |
| 1-Hexanol | 111-27-3 | 3.5476 | 3.6651 | 258.93 | 0 | 0.00722 | 2509.57 | 2B | 74 | 0.86 | |
| 1-Heptanol | 111-70-6 | 3.1954 | 3.9887 | 282.27 | 0 | 0.00298 | 2944.42 | 2B | 74 | 0.83 | |
| 1-Octanol | 111-87-5 | 3.431 | 4.0491 | 287.14 | 0 | 0.00239 | 2998.54 | 2B | 74 | 0.85 | |
| 1-Nonanol | 143-08-8 | 4.0538 | 3.9398 | 277.89 | 0 | 0.00254 | 2917.47 | 2B | 74 | 0.87 | |
| Polar | Dimethyl sulfoxide | 67-68-5 | 3.0243 | 3.2427 | 309.36 | 3.96 | 0 | 0 | — | 76 | 0.85 |
| Pyridine | 110-86-1 | 2.6491 | 3.4665 | 301.81 | 2.19 | 0 | 0 | — | 74 | 0.97 | |
| Nitrobenzene | 98-95-3 | 3.2851 | 3.5498 | 313.00 | 4.22 | 0 | 0 | — | 74 | 0.90 | |
| Methylene iodide | 75-11-6 | 2.4501 | 3.6152 | 381.06 | 1.22 | 0 | 0 | — | 74 | 0.99 | |
| Bromoform | 75-25-2 | 2.4337 | 3.6847 | 351.32 | 0.99 | 0 | 0 | — | 74 | 0.99 | |
| α-Bromonaphthalene | 90-11-9 | 3.4325 | 3.8980 | 369.79 | 1.29 | 0 | 0 | — | 74 | 0.99 | |
| Nonpolar | n-Hexane | 110-54-3 | 3.0651 | 3.7908 | 236.47 | 0 | 0 | 0 | — | 74 | 1.00 |
| n-Heptane | 142-82-5 | 3.4941 | 3.7926 | 238.11 | 0 | 0 | 0 | — | 74 | 1.00 | |
| n-Octane | 111-65-9 | 3.8607 | 3.8149 | 241.43 | 0 | 0 | 0 | — | 74 | 1.00 | |
| n-Nonane | 111-84-2 | 4.3188 | 3.7972 | 241.29 | 0 | 0 | 0 | — | 74 | 1.00 | |
| n-Decane | 124-18-5 | 4.6267 | 3.8411 | 244.92 | 0 | 0 | 0 | — | 74 | 1.00 | |
| n-Undecane | 1120-21-4 | 4.9114 | 3.8203 | 249.51 | 0 | 0 | 0 | — | 74 | 1.00 | |
| n-Dodecane | 112-40-3 | 5.4950 | 3.8329 | 244.84 | 0 | 0 | 0 | — | 74 | 1.00 | |
| n-Tetradecane | 629-59-4 | 6.0175 | 3.8261 | 252.66 | 0 | 0 | 0 | — | 74 | 1.00 | |
| n-Hexadecane | 544-76-3 | 6.9091 | 3.8784 | 250.17 | 0 | 0 | 0 | — | 74 | 1.00 | |
5 Results and discussion
5.1 Model validation through comparison with empirical data
The advancing and receding contact angle values obtained from our model under the room conditions are compared with experimental data, as shown in Table 3. This table includes 104 data points for various systems involving 27 pure liquids and 26 solid surfaces. As shown in Table 3, the AARD values for the advancing and receding contact angles are 7.4% and 10.6%, respectively, indicating good accuracy and model reliability for calculating the advancing contact angle (using eqn (6)), and the receding contact angle (using eqn (10)). Table 3 features solids with diverse surface energy values ranging from 9.5 to 64.7 mN m−1, with perfluoroalkyl acrylate (PFAC) having the minimum and silica having the maximum values (see Table 1). The list includes polar solids such as glass for which , and non-polar solids such as paraffin wax, with
, and non-polar solids such as paraffin wax, with  . Table 3 encompasses various types of liquids (associating, polar, and non-polar) with a broad range of surface tension values. For instance, at 293.15 K, water has a high surface tension of 72.74 mN m−1, while n-hexane has a low surface tension of 18.50 mN m−1.77 Furthermore, according to Table 3, the maximum relative deviations for the advancing and receding contact angles are 25.5% (for n-octane on PTFE) and 35.8% (for formamide on glass), respectively. Except for a few cases, the ARD% values are significantly low, demonstrating the high accuracy of our calculations, given a wide range of solid and liquid systems.
. Table 3 encompasses various types of liquids (associating, polar, and non-polar) with a broad range of surface tension values. For instance, at 293.15 K, water has a high surface tension of 72.74 mN m−1, while n-hexane has a low surface tension of 18.50 mN m−1.77 Furthermore, according to Table 3, the maximum relative deviations for the advancing and receding contact angles are 25.5% (for n-octane on PTFE) and 35.8% (for formamide on glass), respectively. Except for a few cases, the ARD% values are significantly low, demonstrating the high accuracy of our calculations, given a wide range of solid and liquid systems.
| No. | Fluids | Solids | Experiments | Model | |||||
|---|---|---|---|---|---|---|---|---|---|
| θ adv | θ rec | Ref. | θ adv | ARD | θ rec | ARD | |||
| 1 | Bromoform | PTFE | 74.0 | 54.0 | 42 | 73.5 | 0.7 | 53.0 | 1.8 |
| 2 | α-Bromonaphthalene | 75.0 | 54.0 | 42 | 73.0 | 2.7 | 52.7 | 2.5 | |
| 3 | Formamide | 92.3 | 75.1 | 43 | 84.8 | 8.1 | 63.5 | 15.5 | |
| 4 | Water | 122.0 | 94.0 | 42 | 104.7 | 14.2 | 85.2 | 9.4 | |
| 5 | Ethylene glycol | 85.4 | 68.7 | 43 | 84.4 | 1.1 | 66.1 | 3.8 | |
| 6 | Glycerol | 105.0 | 79.0 | 42 | 91.9 | 12.5 | 72.3 | 8.5 | |
| 7 | Pyridine | 72.0 | 54.0 | 42 | 64.6 | 10.3 | 46.3 | 14.2 | |
| 8 | Nitrobenzene | 74.0 | 52.0 | 42 | 72.3 | 2.3 | 52.5 | 1.0 | |
| 9 | Methylene iodide | 85.0 | 68.0 | 42 | 77.4 | 8.9 | 56.0 | 17.7 | |
| 10 | n-Octane | 41.5 | 25.9 | 44 | 30.9 | 25.5 | 21.9 | 15.3 | |
| 11 | n-Nonane | 43.5 | 27.1 | 44 | 36.7 | 15.6 | 26.1 | 3.8 | |
| 12 | n-Decane | 44 | 28.5 | 44 | 40.1 | 8.8 | 28.5 | 0.1 | |
| 13 | n-Undecane | 46 | 29.4 | 44 | 42.7 | 7.2 | 30.4 | 3.3 | |
| 14 | n-Dodecane | 46 | 30.1 | 44 | 44.7 | 2.9 | 31.8 | 5.6 | |
| 15 | n-Tetradecane | 47.5 | 30.5 | 44 | 47.8 | 0.5 | 34.0 | 11.6 | |
| 16 | n-Hexadecane | 47.5 | 30.5 | 44 | 49.9 | 5.1 | 35.6 | 16.7 | |
| 17 | Water | Wax | 115.0 | 110.0 | 78 | 106.2 | 7.6 | 105.2 | 4.3 |
| 18 | Formamide | PCTFE | 79.0 | 57.9 | 43 | 68.2 | 13.7 | 49.2 | 15.0 |
| 19 | Water | 99.6 | 73.6 | 43 | 87.3 | 12.4 | 67.3 | 8.5 | |
| 20 | Ethylene glycol | 80.0 | 58.0 | 43 | 64.0 | 20.0 | 47.7 | 17.8 | |
| 21 | Methylene iodide | 60.6 | 44.9 | 43 | 66.6 | 9.9 | 48.3 | 7.7 | |
| 22 | Formamide | PE | 75.0 | 48.0 | 45 | 63.6 | 15.2 | 47.9 | 0.3 |
| 23 | Water | 95.0 | 65.0 | 45 | 89.9 | 5.4 | 74.3 | 14.3 | |
| 24 | Ethylene glycol | 63.0 | 43.0 | 45 | 62.6 | 0.6 | 50.8 | 18.2 | |
| 25 | Glycerol | 81.0 | 63.0 | 45 | 73.2 | 9.6 | 58.8 | 6.6 | |
| 26 | Formamide | PS | 70.8 | 52.9 | 43 | 53.7 | 24.1 | 42.9 | 18.9 |
| 27 | Water | 91.0 | 83.0 | 45 | 86.4 | 5.0 | 75.3 | 9.3 | |
| 28 | Ethylene glycol | 60.5 | 57.5 | 45 | 54.1 | 10.6 | 48.6 | 15.5 | |
| 29 | Glycerol | 72.0 | 64.0 | 45 | 66.8 | 7.3 | 57.5 | 10.2 | |
| 30 | Formamide | PC | 57.5 | 43.0 | 45 | 46.9 | 18.4 | 37.6 | 12.6 |
| 31 | Water | 83.0 | 68.0 | 45 | 81.8 | 1.5 | 70.8 | 4.1 | |
| 32 | Ethylene glycol | 57.0 | 38.0 | 45 | 46.5 | 18.4 | 42.8 | 12.5 | |
| 33 | Glycerol | 71.0 | 57.0 | 45 | 60.9 | 14.2 | 52.5 | 7.9 | |
| 34 | Formamide | SS-316 | 60.4 | 45.2 | 46 | 53.9 | 10.8 | 40.3 | 10.8 |
| 35 | Water | 80.0 | 59.0 | 46 | 82.5 | 3.2 | 67.7 | 14.8 | |
| 36 | Glycerol | 82.0 | 65.0 | 46 | 64.3 | 21.6 | 51.5 | 20.7 | |
| 37 | Methylene iodide | 45.0 | 36.0 | 46 | 43.6 | 3.1 | 31.4 | 12.9 | |
| 38 | Water | SR | 109.0 | 90.0 | 47 | 107.4 | 1.5 | 93.0 | 3.3 |
| 39 | Glycerol | 95.0 | 90.0 | 47 | 93.4 | 1.7 | 78.0 | 13.4 | |
| 40 | Formamide | PP | 79.5 | 69.0 | 48 | 73.6 | 7.4 | 65.6 | 4.9 |
| 41 | Water | 99.0 | 87.5 | 48 | 102.2 | 3.2 | 103.2 | 18.0 | |
| 42 | Glycerol | 86.5 | 82.0 | 48 | 85.3 | 1.4 | 83.5 | 1.8 | |
| 43 | Dimethyl sulfoxide | 61.6 | 47.8 | 48 | 57.2 | 7.2 | 51.8 | 8.3 | |
| 44 | Methylene iodide | 65.7 | 52.4 | 48 | 57.1 | 13.2 | 41.0 | 21.8 | |
| 45 | Water | PVC | 82.0 | 67.0 | 49 | 81.8 | 0.2 | 68.2 | 1.8 |
| 46 | Water | PMMA | 78.0 | 66.0 | 50 | 76.0 | 2.5 | 60.2 | 8.7 |
| 47 | Ethylene glycol | 54.0 | 38.0 | 51 | 43.9 | 18.6 | 34.6 | 9.1 | |
| 48 | Water | Nylon-66 | 71.0 | 52.0 | 52 | 67.1 | 5.5 | 51.3 | 1.3 |
| 49 | Water | PVDF | 85.5 | 68.9 | 53 | 80.3 | 6.1 | 60.4 | 12.3 |
| 50 | Ethylene glycol | 54.1 | 32.1 | 53 | 56.8 | 5.0 | 41.2 | 28.3 | |
| 51 | Methylene iodide | 63.6 | 46.5 | 53 | 67.2 | 5.7 | 49.1 | 5.6 | |
| 52 | Formamide | PET | 51.7 | 27.9 | 43 | 48.6 | 5.9 | 35.7 | 27.9 |
| 53 | Water | 81.0 | 67.0 | 50 | 77.1 | 4.8 | 62.0 | 7.4 | |
| 54 | Methylene iodide | 38.1 | 25.7 | 54 | 41.5 | 8.9 | 30.1 | 17.1 | |
| 55 | Bromoform | FEP | 75.0 | 58.0 | 42 | 82.2 | 9.5 | 59.9 | 3.2 |
| 56 | α-Bromonaphthalene | 76.0 | 64.0 | 42 | 81.9 | 7.8 | 59.6 | 6.9 | |
| 57 | Formamide | 101.0 | 83.0 | 42 | 85.5 | 15.4 | 62.1 | 25.1 | |
| 58 | Water | 119.0 | 98.0 | 42 | 99.4 | 16.5 | 75.7 | 22.7 | |
| 59 | Ethylene glycol | 93.0 | 77.0 | 42 | 82.1 | 11.8 | 60.4 | 21.5 | |
| 60 | Glycerol | 104.0 | 82.0 | 42 | 89.1 | 14.3 | 66.1 | 19.4 | |
| 61 | Pyridine | 72.0 | 63.0 | 42 | 72.0 | 0.0 | 52.3 | 16.9 | |
| 62 | Nitrobenzene | 76.0 | 63.0 | 42 | 76.2 | 0.3 | 55.1 | 12.6 | |
| 63 | Methylene iodide | 84.0 | 74.0 | 42 | 85.3 | 1.5 | 62.3 | 15.8 | |
| 64 | Water | PDMS | 120.0 | 87.5 | 54 | 110.4 | 8.0 | 84.7 | 3.2 |
| 65 | n-Hexane | FC-732 | 52.9 | 40.7 | 41 | 58.2 | 10.1 | 41.6 | 2.3 |
| 66 | n-Heptane | 58.4 | 45.7 | 41 | 62.7 | 7.3 | 44.9 | 1.8 | |
| 67 | n-Octane | 61.9 | 51.5 | 41 | 65.4 | 5.7 | 46.9 | 8.8 | |
| 68 | n-Nonane | 65.4 | 60.1 | 41 | 68.1 | 4.1 | 48.9 | 18.6 | |
| 69 | 1-Propanol | 71.8 | 47.3 | 41 | 69.3 | 3.5 | 50.6 | 7.0 | |
| 70 | 1-Butanol | 72.7 | 47.5 | 41 | 71.5 | 1.6 | 52.0 | 9.4 | |
| 71 | 1-Pentanol | 74.4 | 48.8 | 41 | 72.3 | 2.8 | 52.6 | 7.9 | |
| 72 | 1-Hexanol | 76.3 | 54.3 | 41 | 82.1 | 7.6 | 60.0 | 10.4 | |
| 73 | 1-Heptanol | 76.6 | 51.2 | 41 | 81.2 | 6.1 | 59.6 | 16.3 | |
| 74 | 1-Octanol | 78.8 | 54.6 | 41 | 75.0 | 4.8 | 54.7 | 0.2 | |
| 75 | 1-Nonanol | 79.0 | 69.0 | 41 | 75.5 | 4.4 | 54.9 | 20.5 | |
| 76 | Water | Nylon-12 | 77.0 | 56.5 | 55 | 77.4 | 0.5 | 59.8 | 5.8 |
| 77 | Water | PBT | 84.0 | 64.0 | 69 | 79.2 | 5.7 | 67.2 | 5.1 |
| 78 | Water | TPO | 99.0 | 74.0 | 56 | 94.0 | 5.0 | 79.7 | 7.7 |
| 79 | Bromoform | PFA | 74.0 | 57.0 | 42 | 76.7 | 3.6 | 55.4 | 2.8 |
| 80 | α-Bromonaphthalene | 76.0 | 61.0 | 42 | 76.2 | 0.2 | 55.0 | 9.8 | |
| 81 | Formamide | 100.0 | 79.0 | 42 | 88.4 | 11.6 | 66.7 | 15.6 | |
| 82 | Water | 121.0 | 90.0 | 42 | 108.0 | 10.7 | 88.9 | 1.2 | |
| 83 | Ethylene glycol | 92.0 | 75.0 | 42 | 88.4 | 3.9 | 69.9 | 6.7 | |
| 84 | Glycerol | 103.0 | 80.0 | 42 | 95.5 | 7.2 | 75.9 | 5.1 | |
| 85 | Pyridine | 72.0 | 60.0 | 42 | 68.7 | 4.6 | 49.4 | 17.6 | |
| 86 | Nitrobenzene | 76.0 | 66.0 | 42 | 76.2 | 0.3 | 55.7 | 15.6 | |
| 87 | Methylene iodide | 84.0 | 68.0 | 42 | 79.5 | 5.3 | 57.6 | 15.3 | |
| 88 | Bromoform | ETFE | 68.0 | 51.0 | 42 | 75.8 | 11.5 | 54.8 | 7.4 |
| 89 | α-Bromonaphthalene | 70.0 | 47.0 | 42 | 75.3 | 7.6 | 54.4 | 15.8 | |
| 90 | Formamide | 94.0 | 71.0 | 42 | 86.4 | 8.1 | 64.5 | 9.2 | |
| 91 | Water | 108.0 | 84.0 | 42 | 105.5 | 2.3 | 85.3 | 1.6 | |
| 92 | Ethylene glycol | 82.0 | 63.0 | 42 | 85.9 | 4.7 | 66.8 | 6.0 | |
| 93 | Glycerol | 96.0 | 75.0 | 42 | 93.1 | 3.0 | 72.8 | 2.9 | |
| 94 | Pyridine | 58.0 | 41.0 | 42 | 67.2 | 15.8 | 48.2 | 17.6 | |
| 95 | Formamide | ECTFE | 79.0 | 65.0 | 42 | 69.4 | 12.2 | 53.2 | 18.1 |
| 96 | Water | 99.0 | 78.0 | 42 | 95.4 | 3.6 | 80.6 | 3.3 | |
| 97 | Ethylene glycol | 67.0 | 53.0 | 42 | 69.5 | 3.8 | 57.6 | 8.6 | |
| 98 | Glycerol | 83.0 | 69.0 | 42 | 79.2 | 4.5 | 65.0 | 5.8 | |
| 99 | Methylene iodide | 58.0 | 43.0 | 42 | 57.5 | 0.8 | 41.2 | 4.2 | |
| 100 | Water | PFAC | 130 | 91 | 71 | 116.2 | 10.6 | 91.6 | 0.7 |
| 101 | n-Dodecane | 77 | 60 | 71 | 79.0 | 2.6 | 57.1 | 4.8 | |
| 102 | Water | Silica | 42 | 29 | 58 | 41.5 | 1.2 | 33.7 | 16.0 |
| 103 | Water | Glass | 31.0 | 19.8 | 59 | 33.7 | 8.7 | 24.0 | 21.1 |
| 104 | Formamide | 23.5 | 15.6 | 59 | 21.7 | 7.6 | 21.2 | 35.8 | |
| Overall | — | — | — | 7.4 | — | 10.6 | |||
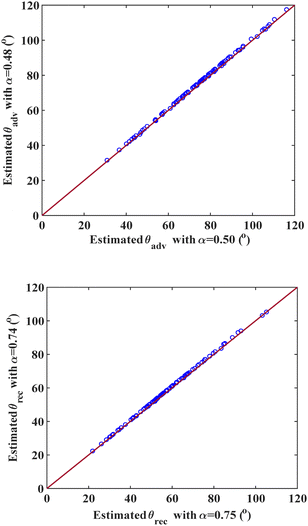
We compare our contact angle models (eqn (6) and (10)) with experimental data in Fig. 1. In Fig. 1a, the estimated advancing contact angle data are plotted against the experimental data for all 104 data points, using α = 0.50. This figure shows data scattering near the y = x reference line, indicating a good match between the estimated and experimental contact angle values. Overall, we slightly underestimate the advancing contact angle, especially for higher contact angle values. This deviation arises because our model relies on the Young's equation, which calculates the equilibrium contact angle, while the advancing contact angle is inherently larger. Similarly, the receding contact angle data estimated using α = 0.75 are depicted in Fig. 1b. Again, the agreement between the estimated and experimental data points is inferred by proximity to the reference line y = x, highlighting the accuracy and reliability of our model in estimating both advancing and receding contact angles. The trend shown in Fig. 1b shows a lower error for the receding contact angle in systems with a lower contact angle (better wetting).
 | ||
| Fig. 1 A comparison between estimated and experimental contact angles, (a) advancing contact angle data using α = 0.50, and (b) receding contact angle data, using α = 0.75. | ||
5.2 Tuning of the power term in the advancing and receding contact angle models
The contact angle model estimates (advancing and receding) depend on the magnitude of the parameter α that appears as the exponent in eqn (11). Promising results for the advancing contact angle are obtained by using α = 0.50, and for the receding contact angle by using α = 0.75. The receding contact angle values depend on a key-assumption that is formulated in eqn (7) and (8), which states that when a liquid film is present, the surface energy of the solid in contact with the liquid film is obtained as the geometric average of the solid and liquid surface energies, for both the dispersion (γdSF) and non-dispersion (γndSF) contributions. Furthermore, the advancing contact angle values calculated using eqn (6) rely on the assumption that the advancing contact angle is close to the equilibrium contact angle. To check the validity of these assumptions, the parameter α is set to be optimized based on the experimental data. If the assumptions are not correct, then the values of α obtained from optimization will be statistically different from those obtained by implementing our model assumptions. In the optimization, the objective function is the overall AARD between the predicted and experimental contact angle values to be minimized. We employ genetic programming, as a non-linear optimization technique, focusing on minimizing AARD between the model predictions and the experimental data. This iterative process will give fine-tuned power terms for both the advancing and receding cases.After optimization, the power term is obtained to be α = 0.48 for the advancing contact angle and 0.74 for the receding contact angle. These optimized values are remarkably close to the values 0.5 and 0.75, respectively, for advancing and receding contact angles that are obtained a priori based on our model assumption. Such an excellent agreement between the optimized and assumed α parameters shows the validity of our assumptions for estimating the receding contact angle (see eqn (7) and (8)) and also the applicability of eqn (6) for estimating the advancing contact angle. To assess the models’ accuracy, we compare AARD% values using the initial and optimized parameter. The AARD values for the initial power terms are 7.4% and 10.6% for the advancing and receding contact angles, respectively, while the optimized power terms of 0.48 and 0.74 result in slightly lower AARD values of 7.2% and 10.5%, respectively.
The power term (α) in eqn (11) acts as a weighting factor that applies the relative influences of the solid and liquid surface energies on contact angle. For the advancing contact angle α = 0.5; so, the solid and liquid surface energies have equal weights, consistent with Young's equation. A higher α value for the receding contact angle (α = 0.75) suggests that the influence of the liquid surface energy is more dominant compared to the solid's surface energy. When the liquid recedes, the drop contacts the solid in the receding tail through a thin liquid film, where its surface energy is approximated as the geometric mean of the solid and liquid surface energies.
Fig. 2 compares the advancing and receding contact angles estimated with the optimized α values against those estimated contact angles with initial α values. As illustrated in Fig. 2, the data closely follow the y = x line for the entire dataset for both advancing and receding contact angles. This suggests that using the original or optimized values of α for calculating advancing and receding contact angles yields no significant difference. To ensure this, we calculate and compare some statistical analysis parameters obtained from both the initial and optimized values of α.
The statistical analysis of the advancing and receding contact angle results with α values from optimization and that obtained a priori is summarized in Table 4, showing statistical parameters such as the coefficient of determination (R2), root mean square error (RMSE), average absolute relative deviation (AARD), minimum and maximum values of absolute relative deviation (min ARD and max ARD), mean absolute deviation (MAD), and minimum and maximum values of absolute deviation (min AD and max AD).
The analysis reveals that overall, the model for the advancing contact angle performs slightly better than that for the receding contact angle as it is evident in lower RMSE, AARD, and MAD values. Also, the contact angle model using the optimized power term (α) performs slightly better than that using the assumed power term values. In general, by comparing the statistical error parameters, it is evident that both the original values and optimized values of α yield nearly identical results, as the values of the statistical error parameters are similar. Hence, here on, we use α = 0.50 for the advancing contact angle and α = 0.75 for the receding contact angle in our calculations.
5.3 Simplified contact angle relationships for pure non-polar substances
When either the solid or liquid material is non-polar, the terms γndLγndS will become zero. Consequently, the advancing and receding contact angles will be simplified to eqn (12) and (13): | (12) |
 | (13) |
The mathematical manipulation will provide a simple relationship between the advancing and receding contact angles as follows:
 | (14) |
In eqn (14), the relationship between the advancing and receding contact angles only depends on the ratio of  . To verify this relationship for the advancing and receding contact angles when one of the substances is non-polar, eqn (14) is compared with experimental data from the literature for non-polar materials as shown in Fig. 3. The experiments include cases in which either solid or liquid is non-polar. As illustrated in Fig. 3, there is a good agreement between the experimental data and the predictions from eqn (14).
. To verify this relationship for the advancing and receding contact angles when one of the substances is non-polar, eqn (14) is compared with experimental data from the literature for non-polar materials as shown in Fig. 3. The experiments include cases in which either solid or liquid is non-polar. As illustrated in Fig. 3, there is a good agreement between the experimental data and the predictions from eqn (14).
 | ||
| Fig. 3 Comparison of simplified contact angle relations with experimental data for non-polar substances. Line: model (eqn (14)), (●) data from ref. 48, (■) data from ref. 41, (▲) data from ref. 71, (♦) data from ref. 42. | ||
 | (15) |
 | (16) |
The simplified relationships for the case of non-polar liquids, as given by eqn (15) and (16), indicate that both the advancing and receding angles depend solely on the ratio of 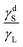 . These correlations are plotted in Fig. 4 and are compared with experimental contact angle data from the literature. Fig. 4 demonstrates that both equations correctly predict the trends in the advancing and receding contact angles with the the ratio
. These correlations are plotted in Fig. 4 and are compared with experimental contact angle data from the literature. Fig. 4 demonstrates that both equations correctly predict the trends in the advancing and receding contact angles with the the ratio  when the liquid is non-polar. Another observation from Fig. 4 is that the receding and advancing contact angles approach each other when the ratio
when the liquid is non-polar. Another observation from Fig. 4 is that the receding and advancing contact angles approach each other when the ratio 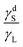 approaches either extreme values of zero or one. Based on these models, when
approaches either extreme values of zero or one. Based on these models, when  , the solid surface is completely wetted by the liquid and both contact angles approach zero.
, the solid surface is completely wetted by the liquid and both contact angles approach zero.
 | ||
| Fig. 4 Comparison of simplified contact angle models with experimental data for non-polar liquids. (▲) data from ref. 71, (■) data from ref. 41, (●) data from ref. 44. | ||
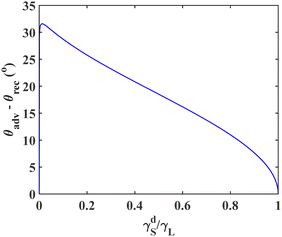
The effect of  on the contact angle hysteresis (θadv − θrec) for non-polar liquids is investigated and the results are shown in Fig. 5. According to Fig. 5, decreasing the ratio of
on the contact angle hysteresis (θadv − θrec) for non-polar liquids is investigated and the results are shown in Fig. 5. According to Fig. 5, decreasing the ratio of  initially increases the contact angle hysteresis; the hysteresis reaches a maximum of 31.6° at
initially increases the contact angle hysteresis; the hysteresis reaches a maximum of 31.6° at  , after which the it decreases sharply.
, after which the it decreases sharply.
5.4 Advancing and receding contact angles of a binary liquid
We demonstrated the models to effectively predict the advancing and receding contact angles for diverse combinations of pure liquids on pure solid surfaces. In this section, we evaluate the models’ capability to predict the advancing and receding contact angles for a binary liquid system, which, to the best of our knowledge, is the only available data for mixed liquids in the literature. According to our previous work,28 the surface energy ratio for mixtures can be determined by the PCP-SAFT model by calculating the residual Helmholtz energy contributions of the liquid mixture. This ratio can be used to estimate the contact angle of mixed liquids on solid surfaces. Fig. 6 illustrates the compositional dependency of the advancing and receding contact angles for ethanol + water solutions on a PTFE surface under the ambient conditions. We evaluate the models’ performance by comparing their predictions with experimental contact angle data from the literature. As it can be seen in Fig. 6, both contact angle models exhibit good accuracies in estimating the contact angles for a wide range of ethanol mole fractions in the ethanol + water mixture.
for mixtures can be determined by the PCP-SAFT model by calculating the residual Helmholtz energy contributions of the liquid mixture. This ratio can be used to estimate the contact angle of mixed liquids on solid surfaces. Fig. 6 illustrates the compositional dependency of the advancing and receding contact angles for ethanol + water solutions on a PTFE surface under the ambient conditions. We evaluate the models’ performance by comparing their predictions with experimental contact angle data from the literature. As it can be seen in Fig. 6, both contact angle models exhibit good accuracies in estimating the contact angles for a wide range of ethanol mole fractions in the ethanol + water mixture.
 | ||
| Fig. 6 Advancing and receding contact angle estimates for ethanol + water liquid mixtures on the PTFE surface vs. ethanol mole fraction; experimental data are obtained from ref. 57. | ||
6 Conclusions
This study has focused on estimating the advancing and receding contact angles for pure and mixed liquids on smooth solid surfaces of diverse materials, using the PCP-SAFT equation of state. To estimate the receding contact angle, we propose a novel approach in which the surface energy of a solid containing a liquid film is approximated by the geometrical average of the pure solid and liquid surface energy values. Also, using the PCP-SAFT model, we calculate the ratio of dispersion-to-total surface energy for diverse liquids. The models are validated against 104 pairs of experimental data for advancing and receding contact angles with average absolute relative deviations (AARDs) of 7.4% and 10.6% for the advancing and receding contact angles, respectively. Such small deviations from the experimental data verify the model to be reliable and accurate in diverse liquid–solid systems tested. In the advancing and receding contact angle models, there is an α-parameter which appears in the power term. Using the model assumptions, the α-parameters for the advancing and receding contact angle models are obtained to be 0.75 and 0.50, respectively. To check the reliability of the model assumptions leading to this α-parameter value, we vary α and find its optimal values by fitting to the experimental data. After parameter optimization, the optimal α values of 0.74 and 0.48 are obtained for the advancing and receding contact angle models which are close to their corresponding values (0.75 and 0.5, respectively) obtained a priori in the model. As expected, the AARD% values slightly decrease (from 7.4% to 7.2% for advancing and from 10.6% to 10.5% for receding) when the α-parameter is optimized. Interestingly, these optimized α-parameter values are close to those used originally in the model, verifying the model assumptions; furthermore, the low AARD values show good model accuracy when compared to experimental data. We also simplify the contact angle correlations for the case of non-polar systems where either the liquid or solid is non-polar. The simplified models are also validated against experimental data, demonstrating their effectiveness in predicting contact angles for non-polar liquids and solids. Additionally, we extend our analysis to the contact angle of binary liquid mixtures and study the compositional dependency of advancing and receding contact angles. The models show good accuracy in the full range of mole fractions of ethanol in ethanol/water mixtures on the PTFE surface, highlighting their applicability for liquid mixtures. Overall, the proposed advancing and receding contact angle models offer comprehensive and reliable methods for estimating the contact angles of pure and mixed liquids on smooth solid surfaces. The simplicity, versatility, and accuracy of our model make it a valuable tool for researchers and engineers working in fields related to surface science and wettability. Further research is needed, using molecular dynamics simulations and experimental studies on a wider range of systems, to deepen insights into the problem and to refine the model for more accurate predictions.Author contributions
Aliakbar Roosta: conceptualization, data collection, programming, analysis, and writing – review and editing. Sohrab Zendehboudi: analysis and writing – review and editing. Nima Rezaei: conceptualization, supervision, and writing – review and editing.Data availability
No new experimental data were generated for this study.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the funding received from the Jane and Aatos Erkko Foundation (JAES) in Finland for project 210053, which enabled this research.References
- Y. Wang, A. Kiziltas, P. Blanchard and T. R. Walsh, ContactAngleCalculator: An Automated, Parametrized, and Flexible Code for Contact Angle Estimation in Visual Molecular Dynamics, J. Chem. Inf. Model., 2022, 62, 6302–6308 CrossRef CAS PubMed.
- T. Huhtamäki, X. Tian, J. T. Korhonen and R. H. A. Ras, Surface-wetting characterization using contact-angle measurements, Nat. Protoc., 2018, 13, 1521–1538 CrossRef PubMed.
- N. K. Karna, E. Oyarzua, J. H. Walther and H. A. Zambrano, Effect of the meniscus contact angle during early regimes of spontaneous imbibition in nanochannels, Phys. Chem. Chem. Phys., 2016, 18, 31997–32001 RSC.
- K. G. Winkels, I. R. Peters, F. Evangelista, M. Riepen, A. Daerr, L. Limat and J. H. Snoeijer, Receding contact lines: From sliding drops to immersion lithography, Eur. Phys. J.-Spec. Top., 2011, 192, 195–205 CrossRef CAS.
- D. Quéré, Fluid coating on a fiber, Annu. Rev. Fluid Mech., 1999, 31, 347–384 CrossRef.
- L. Hauer, A. Naga, R. G. M. Badr, J. T. Pham, W. S. Y. Wong and D. Vollmer, Wetting on silicone surfaces, Soft Matter, 2024, 20, 5273–5295 RSC.
- A. Al-Shareef, P. Neogi and B. Bai, Dynamic contact angles in oil–aqueous polymer solutions, Phys. Chem. Chem. Phys., 2017, 19, 3337–3348 RSC.
- S. Rasouli, N. Rezaei, H. Hamedi, S. Zendehboudi and X. Duan, Superhydrophobic and superoleophilic membranes for oil-water separation application: A comprehensive review, Mater. Des., 2021, 204, 109599 CrossRef CAS.
- P. Shah and M. M. Driscoll, Drop impact dynamics of complex fluids: a review, Soft Matter, 2024, 20, 4839–4858 RSC.
- A. A. Jamali, M. I. Vohra, A. Ali, A. Nadeem, S. M. Attia, A. Hyder, A. A. Memon, F. Khan Mahar, R. B. Mahar, J. Yang and K. H. Thebo, Highly efficient mica-incorporated graphene oxide-based membranes for water purification and desalination, Phys. Chem. Chem. Phys., 2024, 26, 16369–16377 RSC.
- Á. G. Marín, H. Gelderblom, D. Lohse and J. H. Snoeijer, Rush-hour in evaporating coffee drops, Phys. Fluids, 2011, 23, 091111 CrossRef.
- H.-J. Butt, J. Liu, K. Koynov, B. Straub, C. Hinduja, I. Roismann, R. Berger, X. Li, D. Vollmer, W. Steffen and M. Kappl, Contact angle hysteresis, Curr. Opin. Colloid Interface Sci., 2022, 59, 101574 CrossRef CAS.
- X. Li, S. Silge, A. Saal, G. Kircher, K. Koynov, R. Berger and H.-J. Butt, Adaptation of a Styrene–Acrylic Acid Copolymer Surface to Water, Langmuir, 2021, 37, 1571–1577 CrossRef CAS PubMed.
- S. P. Evgenidis, K. Kalić, M. Kostoglou and T. D. Karapantsios, Kerberos: A three camera headed centrifugal/tilting device for studying wetting/dewetting under the influence of controlled body forces, Colloids Surf., A, 2017, 521, 38–48 CrossRef CAS.
- O. N. Tretinnikov and Y. Ikada, Dynamic Wetting and Contact Angle Hysteresis of Polymer Surfaces Studied with the Modified Wilhelmy Balance Method, Langmuir, 1994, 10, 1606–1614 CrossRef CAS.
- E. Schäffer and P. Wong, Contact line dynamics near the pinning threshold: A capillary rise and fall experiment, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5257–5277 CrossRef PubMed.
- T. T. Chau, W. J. Bruckard, P. T. L. Koh and A. V. Nguyen, A review of factors that affect contact angle and implications for flotation practice, Adv. Colloid Interface Sci., 2009, 150, 106–115 CrossRef CAS PubMed.
- H. B. Eral, D. J. C. M. ‘t Mannetje and J. M. Oh, Contact angle hysteresis: a review of fundamentals and applications, Colloid Polym. Sci., 2013, 291, 247–260 CrossRef CAS.
- O. V. Voinov, Hydrodynamics of wetting, Fluid Dyn., 1977, 11, 714–721 CrossRef.
- R. G. Cox, The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow, J. Fluid Mech., 1986, 168, 169 CrossRef CAS.
- Y. D. Shikhmurzaev, Moving contact lines and dynamic contact angles: a ‘litmus test’ for mathematical models, accomplishments and new challenges, Eur. Phys. J.-Spec. Top., 2020, 229, 1945–1977 CrossRef.
- H. B. Eral, D. J. C. M. ‘t Mannetje and J. M. Oh, Contact angle hysteresis: a review of fundamentals and applications, Colloid Polym. Sci., 2013, 291, 247–260 CrossRef CAS.
- J. F. Joanny and P. G. de Gennes, A model for contact angle hysteresis, J. Chem. Phys., 1984, 81, 552–562 CrossRef CAS.
- A. Marmur and B. Krasovitski, Line Tension on Curved Surfaces: Liquid Drops on Solid Micro- and Nanospheres, Langmuir, 2002, 18, 8919–8923 CrossRef CAS.
- R. Tadmor, Line Energy and the Relation between Advancing, Receding, and Young Contact Angles, Langmuir, 2004, 20, 7659–7664 CrossRef CAS PubMed.
- E. Chibowski, Surface free energy of a solid from contact angle hysteresis, Adv. Colloid Interface Sci., 2003, 103, 149–172 CrossRef CAS PubMed.
- D. Behnoudfar, M. I. Dragila, D. Meisenheimer and D. Wildenschild, Contact angle hysteresis: A new paradigm?, Adv. Water Resour., 2022, 161, 104138 CrossRef CAS.
- A. Roosta, S. Zendehboudi and N. Rezaei, Estimating contact angle of pure and mixed liquids on smooth solid surfaces using dispersive-to-attractive surface energy ratio from PCP-SAFT model, Chem. Eng. Sci., 2024, 300, 120607 CrossRef CAS.
- D. Y. Kwok and A. W. Neumann, Contact angle measurement and contact angle interpretation, Adv. Colloid Interface Sci., 1999, 81, 167–249 CrossRef CAS.
- D. H. Bangham and R. I. Razouk, Adsorption and the wettability of solid surfaces, Trans. Faraday Soc., 1937, 33, 1459 RSC.
- W. D. Harkins and H. K. Livingston, Energy Relations of the Surfaces of Solids II. Spreading Pressure as Related to the Work of Adhesion Between a Solid and a Liquid, J. Chem. Phys., 1942, 10, 342–356 CrossRef CAS.
- W. A. Zisman, Influence of constitution on adhesion, Ind. Eng. Chem., 1963, 55, 18–38 CrossRef CAS.
- L. A. Girifalco and R. J. Good, A Theory for the Estimation of Surface and Interfacial Energies. I. Derivation and Application to Interfacial Tension, J. Phys. Chem., 1957, 61, 904–909 CrossRef CAS.
- R. J. Good, Contact angle, wetting, and adhesion: a critical review, J. Adhes. Sci. Technol., 1992, 6, 1269–1302 CrossRef CAS.
- R. J. Good, Equilibrium Film Pressure on a Flat, Low-Energy Solid, Adsorption at Interfaces, 1975, pp. 28–47 Search PubMed.
- A. P. Sgouros, G. G. Vogiatzis, G. Kritikos, A. Boziki, A. Nikolakopoulou, D. Liveris and D. N. Theodorou, Molecular Simulations of Free and Graphite Capped Polyethylene Films: Estimation of the Interfacial Free Energies, Macromolecules, 2017, 50, 8827–8844 CrossRef CAS.
- A. Jarray, H. Wijshoff, J. A. Luiken and W. K. den Otter, Systematic approach for wettability prediction using molecular dynamics simulations, Soft Matter, 2020, 16, 4299–4310 RSC.
- K. Huang and R.-H. Yoon, Surface Forces in the Thin Liquid Films (TLFs) of Water Confined between n-Alkane Drops and Hydrophobic Gold Surfaces, Langmuir, 2019, 35, 15681–15691 CrossRef CAS PubMed.
- C. J. van Oss, R. F. Giese and W. Wu, On the Degree to which the Contact Angle is Affected by the Adsorption onto a Solid Surface of Vapor Molecules Originating from the Liquid Drop, J. Dispersion Sci. Technol., 1998, 19, 1221–1236 CrossRef CAS.
- C. N. C. Lam, N. Kim, D. Hui, D. Y. Kwok, M. L. Hair and A. W. Neumann, The effect of liquid properties to contact angle hysteresis, Colloids Surf., A, 2001, 189, 265–278 CrossRef CAS.
- C. N. C. Lam, R. Wu, D. Li, M. L. Hair and A. W. Neumann, Study of the advancing and receding contact angles: liquid sorption as a cause of contact angle hysteresis, Adv. Colloid Interface Sci., 2002, 96, 169–191 CrossRef CAS PubMed.
- S. Lee, J.-S. Park and T. R. Lee, The Wettability of Fluoropolymer Surfaces: Influence of Surface Dipoles, Langmuir, 2008, 24, 4817–4826 CrossRef CAS PubMed.
- C. W. Extrand and Y. Kumagai, An Experimental Study of Contact Angle Hysteresis, J. Colloid Interface Sci., 1997, 191, 378–383 CrossRef CAS PubMed.
- M. E. Diaz, J. Fuentes, R. L. Cerro and M. D. Savage, Hysteresis during contact angles measurement, J. Colloid Interface Sci., 2010, 343, 574–583 CrossRef CAS PubMed.
- F. D. Petke and B. R. Ray, Temperature dependence of contact angles of liquids on polymeric solids, J. Colloid Interface Sci., 1969, 31, 216–227 CrossRef CAS.
- K. Terpiłowski, L. Hołysz, D. Rymuszka and R. Banach, Comparison of contact angle measurement methods of liquids on metal alloys, Ann. Univ. Mariae Curie-Sklodowska, Sect. AA:Chem., 2016, 71, 89 Search PubMed.
- W. G. Pitt, B. R. Young and S. L. Copper, Measurement of advancing and receding contact angles inside polymer tubing, Colloids Surf., 1987, 27, 345–355 CrossRef CAS.
- E. Chibowski and K. Terpilowski, Surface free energy of polypropylene and polycarbonate solidifying at different solid surfaces, Appl. Surf. Sci., 2009, 256, 1573–1581 CrossRef CAS.
- K. M. McGinty and W. J. Brittain, Hydrophilic surface modification of poly(vinyl chloride) film and tubing using physisorbed free radical grafting technique, Polymer, 2008, 49, 4350–4357 CrossRef CAS.
- H. Y. Erbil, G. McHale, S. M. Rowan and M. I. Newton, Determination of the Receding Contact Angle of Sessile Drops on Polymer Surfaces by Evaporation, Langmuir, 1999, 15, 7378–7385 CrossRef CAS.
- B. A. Johnson, J. Kreuter and G. Zografi, Effects of surfactants and polymers on advancing and receding contact angles, Colloids Surf., 1986, 17, 325–342 CrossRef CAS.
- S. L. Schellbach, S. N. Monteiro and J. W. Drelich, A novel method for contact angle measurements on natural fibers, Mater. Lett., 2016, 164, 599–604 CrossRef CAS.
- C. A. Fuentes, L. Q. N. Tran, M. Van Hellemont, V. Janssens, C. Dupont-Gillain, A. W. Van Vuure and I. Verpoest, Effect of physical adhesion on mechanical behaviour of bamboo fibre reinforced thermoplastic composites, Colloids Surf., A, 2013, 418, 7–15 CrossRef CAS.
- W. S. Y. Wong, L. Hauer, A. Naga, A. Kaltbeitzel, P. Baumli, R. Berger, M. D’Acunzi, D. Vollmer and H.-J. Butt, Adaptive Wetting of Polydimethylsiloxane, Langmuir, 2020, 36, 7236–7245 CrossRef CAS PubMed.
- C. W. Extrand, Water Contact Angles and Hysteresis of Polyamide Surfaces, J. Colloid Interface Sci., 2002, 248, 136–142 CrossRef CAS PubMed.
- A. Nihlstrand, T. Hjertberg and I. K. Johansson, in First International Congress on Adhesion Science and Technology, ed. W. J. van Ooij and H. R. Anderson, CRC Press, 1998, pp. 287–307 Search PubMed.
- Y. Yonemoto and T. Kunugi, Experimental and theoretical investigation of contact-angle variation for water–ethanol mixture droplets on a low-surface-energy solid, Int. J. Heat Mass Transfer, 2016, 96, 614–626 CrossRef CAS.
- E. F. Ethington, Interfacial contact angle measurements of water, mercury, and 20 organic liquids on quartz, calcite, biotite, and Ca-montmorillonite substrates, USGS-OFR-90-409, 1990.
- M. P. Chodkowski, Significance of the receding contact angle in the determination of surface free energy, Ann. Univ. Mariae Curie-Sklodowska, Sect. AA:Chem., 2019, 73, 61 Search PubMed.
- D. K. Owens and R. C. Wendt, Estimation of the surface free energy of polymers, J. Appl. Polym. Sci., 1969, 13, 1741–1747 CrossRef CAS.
- S. Wu, Calculation of interfacial tension in polymer systems, J. Polym. Sci., Part C: Polym. Symp., 1971, 34, 19–30 CrossRef.
- Coatings Of Polymers And Plastics, ed. R. A. Ryntz and P. V. Yaneff, CRC Press, Boca Raton, 1st edn, 2003 Search PubMed.
- D. F. Williams, E. J. C. Kellar, D. A. Jesson and J. F. Watts, Surface analysis of 316 stainless steel treated with cold atmospheric plasma, Appl. Surf. Sci., 2017, 403, 240–247 CrossRef CAS.
- N. J. Hallab, K. J. Bundy, K. O’Connor, R. L. Moses and J. J. Jacobs, Evaluation of Metallic and Polymeric Biomaterial Surface Energy and Surface Roughness Characteristics for Directed Cell Adhesion, Tissue Eng., 2001, 7, 55–71 CrossRef CAS PubMed.
- K. Grundke and A. Augsburg, On the determination of the surface energetics of porous polymer materials, J. Adhes. Sci. Technol., 2000, 14, 765–775 CrossRef CAS.
- S. Ebnesajjad, Surface Treatment of Materials for Adhesive Bonding, Elsevier, 2nd edn, 2014, pp. 331–341 Search PubMed.
- E. J. Berger, Acid-Base Interactions: Relevance to Adhesion Science and Technology berger, VSP, Utrecht, The Netherlands, 1991 Search PubMed.
- S. Wu, in Polymer Handbook, ed. J. Brandrup, E. H. Immergut and E. A. Grulke, John Wiley & Sons, 4th edn, 1999, pp. 521–541 Search PubMed.
- C. Della Volpe, C. Migliaresi and G. Mari, Surface Modification of Polymeric Biomaterials, Springer, US, Boston, MA, 1996, pp. 107–115 Search PubMed.
- E. J. Berger, Acid-Base Interactions: Relevance to Adhesion Science and Technology, ed. K. L. Mittal, The Netherlands, 1991, p. 217 Search PubMed.
- E. Milnes-Smith, C. A. Stone, C. R. Willis and S. Perkin, Surface Reconstruction of Fluoropolymers in Liquid Media, Langmuir, 2022, 38, 4657–4668 CrossRef CAS PubMed.
- A. Shivamurthy, G. R. Prashanth, N. M. Renukappa, J. Sundara Rajan and S. Parameshwara, Study of surface energy of SiO2 and TiO2 on charge carrier mobility of rubrene organic field effect transistor, in 3rd International Conference on Theoretical and Applied Nanoscience and Nanotechnology, 2019.
- J. Comelles, M. Estévez, E. Martínez and J. Samitier, The role of surface energy of technical polymers in serum protein adsorption and MG-63 cells adhesion, Nanomedicine, 2010, 6, 44–51 CrossRef CAS PubMed.
- T. Esper, G. Bauer, P. Rehner and J. Gross, PCP-SAFT Parameters of Pure Substances Using Large Experimental Databases, Ind. Eng. Chem. Res., 2023, 62, 15300–15310 CrossRef CAS.
- E. Tsochantaris, X. Liang and G. M. Kontogeorgis, Evaluating the Performance of the PC-SAFT and CPA Equations of State on Anomalous Properties of Water, J. Chem. Eng. Data, 2020, 65, 5718–5734 CrossRef CAS.
- M. Kleiner and G. Sadowski, Modeling of Polar Systems Using PCP-SAFT: An Approach to Account for Induced-Association Interactions, J. Phys. Chem. C, 2007, 111, 15544–15553 CrossRef CAS.
- Surface Tension of Pure Liquids and Binary Liquid Mixtures, ed. M. D. Lechner, Springer-Verlag, Berlin/Heidelberg, 1997, vol. 16 Search PubMed.
- B. R. Ray and F. E. Bartell, Hysteresis of contact angle of water on paraffin. Effect of surface roughness and of purity of paraffin, J. Colloid Sci., 1953, 8, 214–223 CrossRef CAS.
| This journal is © the Owner Societies 2025 |