Benzylperoxy radical cation: an exceptionally stable and bound species

Abstract

The energetics of ionization and dissociation of the benzylperoxy radical have been investigated using explicitly correlated coupled-cluster methods. The theoretical values for the adiabatic ionization energy (9.331 eV) and cationic dissociation barrier (0.155 eV) harmoniously predict the elusiveness of the benzylperoxy radical in the contexts of photoionization and ion–molecule reactions. These properties make it an exception among unsaturated alkyl peroxy radicals, which typically undergo dissociative ionization. An in-depth scrutiny into the underlying electronic effects resposible for its elusiveness—predictably spanning photoionization mass spectrometry and ion–molecule reaction preparation—has profound implications, calling for a revised view of the valence bond perspective. By employing localized intrinsic bond orbital (IBO) methods in the study of the benzylperoxy radical cation, we present a case for reintroducing the Linnett double-quartet theory as the missing link between the theoretical basis and intuitive mechanisms involving triplet species, such as molecular oxygen.

---

1. Introduction

Organic peroxy radicals (ROO) are crucial intermediates in the low-temperature oxidation and photooxidation of hydrocarbons, drawing continuous interest due to their important roles in combustion and atmospheric chemistry.^1,2 In the troposphere, ROO can react with nitrogen oxides (NO_x) to control O₃ levels^3–5 and drive the formation of secondary organic aerosols (SOA).¹ Equally important in both atmospheric contexts and low-temperature combustion,² hydrogen atom migration in peroxy radicals leads to the regeneration of hydroxyl radicals (OH), the most critical species for initializing the self-cleansing of the troposphere by oxidizing volatile organic compounds (VOCs).^6,7 In a recent study reported by Chhantyal-Pun et al.,⁸ direct laboratory measurements and global modelling have shown that the reaction between ROO and monoterpene-derived Criegee intermediates can impart up to ∼1.3% of SOA generated in forested areas where biogenic VOCs (BVOCs) are abundant. The influence of ROO is categorically ubiquitous; these radicals play a consequential role in both global climate change and local air quality.^9,10 Accordingly, they have been the subject of numerous experimental^4,11–13 and theoretical studies.^14–16

Beyond the methyl peroxy radical (CH₃OO), which is the simplest and most abundant alkylperoxy species in the atmosphere, unsaturated peroxy radicals have also been gaining attention. In addition to fossil fuel-derived alkenes, BVOCs such as isoprene, which alone account for about one-third of annual global VOC emissions (with another one-third coming from methane) from all natural and anthropogenic sources,¹⁷ are prone to oxidation. The importance of BVOC-derived peroxy radicals in SOA formation has been addressed, and the ring-closure pathway leading to cycloperoxide formation, uniquely accessible to multi-unsaturated ROO radicals, has been scrutinized.^18–20 The reactivity of unsaturated alkylperoxy radicals is considered the key to understanding the effects of varying degrees of unsaturation on the combustion characteristics of biodiesel fuels.^21,22

Apart from BVOCs, unsaturated peroxy radicals can also be derived from aromatic compounds released into the atmosphere by anthropogenic sources, such as vehicle exhaust and paint solvents. Owing to concerns about pollution, considerable attention has been paid to the oxidation of toluene, and thus, the formation of the benzyl radical, which is a predominant intermediate in the early stages of the process, has been highlighted.^23–25 The oxidation of benzyl radical is particularly important in combustion, autoignition and the atmospheric degradation of alkylated aromatic hydrocarbons.^23–26 The temperature-sensitive formation of the adduct, benzylperoxy radical (BzOO), unlocks an extensive network of reactions, as outlined in prior theoretical studies.^27–30 However, the understanding of the kinetics and mechanisms of BzOO degradation is largely confined to its self-reaction, reactions with HOO or NO_x,^26,27,31 and a few laboratory studies.^23,24,32 Meanwhile, the unusually low O–O bond order in BzOO was identified at the MP2 level early on,³³ while Canneaux et al. demonstrated that the sophisticated CASPT2 method is necessary to model the BzOO isomerization kinetics in quantitative agreement with the available experimental results.^34,35

Although elusive and readily isomerized, peroxy radicals are of great importance. However, probing and identifying their isomers remain challenging, even with advanced techniques, such as cavity ring-down spectroscopy³⁶ and the universally applicable yet highly selective vacuum ultraviolet (VUV) synchrotron radiation photoionization mass spectrometry, due to their susceptibility to dissociative ionization.^37–39 On the other hand, for dissociative ionization specifically involving the cleavage of the C–O bond in ROO, measurement of the appearance energy (AE) of the daughter fragment R⁺ can be a remedy to issues with the detection of the parent ROO radical. Using a time-resolved technique, Meloni et al. successfully distinguished C₂H₅⁺ formed by dissociative ionization and concluded that C₂H₅OO⁺ was too weakly bound to be detected intact.³⁷ In a subsequent study, they extended their investigations to 1-cyclopentenylperoxy and propargylperoxy radicals. It has been generalized that the ground state of alkylperoxy cations is a triplet and these typically undergo dissociative ionization, with the sole exception being CH₃OO⁺, whereas the ground state of alkenylperoxy cations is a singlet.³⁸ This empirical rule has been ascribed to the strong hyperconjugation effect present in larger alkylperoxy cations, such as C₂H₅OO⁺ and C₃H₇OO⁺.³⁸ Here, we present the case of the BzOO⁺ ion, which can be reasonably stabilized by conjugation, and manages to exhibit a bound ground state as the triplet. The anomalies engendered by the aromatic ring are startlingly profound.

2. Results and discussion

2.1. Structures and molecular orbitals of BzOO and BzOO⁺

The optimized structures of the BzOO radical and its cationic states (singlet and triplet BzOO⁺) at the B3LYP/6-311++G(2df,p), M06-2X/6-311++G(2df,p), and CCSD(T)/6-311+G(d) levels are presented in Fig. 1. Our theoretical calculations pinpoint the substantial geometrical changes from a neutral structure to a cationic one. The ground state (X²A′′) of the BzOO radical features the peroxy moiety (on the σ plane) in an anti [dihedral angle ∠OOC_αC_β = 180°] orientation with respect to the phenyl ring. The ²A′′ electronic state can be readily understood as a single lone electron (α spin) occupying the low-lying HOMO−2 (Fig. 2), which is largely dominated by the π* orbital of the peroxy moiety, π*(O=O). Such an electronic configuration closely resembles that of the HOO radical,⁴⁰ where the π(O=O)²π*(O=O)¹ occupancy results in a nominal bond order of 1½. The C_α–O bond in the BzOO radical adopts a typical value of ≈1.47 Å.

Fig. 1 (a) The stable structures of BzOO and BzOO⁺ optimized at the M06/6-311++G(2df,p) (normal font), CCSD(T)/6-311+G(d) (bold font) and B3LYP/6-311++G(2df,p) (italic font). (b) The structure of BzOO⁺ (a¹A) overlaid on top of BzOO⁺ (X³A).

Fig. 2 The three highest occupied molecular orbitals and their energy levels (in Hartree) of the BzOO radical at the B3LYP/6-311++G(2df,p) level.

The MO diagram (Fig. 2) of BzOO presupposes that the singlet and triplet states of BzOO⁺ are very close in energy when the α or β electron is ionized from the aromatic π orbital in the HOMO or HOMO−1 level. Indeed, the lowest closed-shell singlet cation is formed by the removal of an α electron from HOMO−2 in the ionization process. The spin states decisively control the interaction between the peroxy moiety and the phenyl ring, resulting in markedly different “peroxy” dihedral angles. The acute angle ∠OOC_αC_β of −15.5° (at the B3LYP level) for the triplet BzOO⁺(X³A) suggests the quasi-equidistance of C_γ–O (2.418 Å) and C_β–O (2.512 Å) bonds, i.e., an isosceles geometry formed by the terminal O (i.e., O′), C_β, and C_γ atoms. The matching distances invite the presumption of 3-center-2-electron (3c–2e) bonding. By exploiting the feature of natural bond orbital (NBO) analysis^41–43 that allows for the selection of an alternative Lewis structure, we can enforce a 3c-bonding localization scheme for the terminal O atom interacting with the phenyl ring. By imposing this constraint, the percentage of the non-Lewis structure increases modestly from 2% to 2.7%, suggesting that the triangular moiety could be partially described by 3c–2e bonding as an alternative bonding picture to the single-electron C_γ–O′ bond. However, the α spin electron supposedly involved in this 3c–2e bond is largely confined to the terminal oxygen and is more appropriately regarded as a lone electron. Therefore, the framework of 3c–2e bonding only partially captures the interaction among these three atoms. We elaborate further on the bonding structure in the subsequent paragraphs. For the singlet-state BzOO⁺(a¹A), no interaction between the terminal O and the aromatic ring is permitted due to the significantly larger dihedral angle of −109.5°. The out-of-plane distortion of the phenyl ring is non-negligible in both states and becomes apparent when their molecular structures are overlaid (Fig. 1b). Evidently, such a distortion stems from the disparate C_γ–O′ interactions in BzOO⁺(a¹A) and BzOO⁺(X³A). Modest but no less noteworthy geometry changes could be observed in the C_α–OO bond length. The ionization to the singlet cationic state did not induce a significant geometrical change, causing only a light elongation from 1.474 Å (BzOO, at the B3LYP level) to 1.505 Å (BzOO⁺(a¹A)). The lengthening (0.020 Å) of the C_α–OO bond in the ionization transition for BzOO(X²A′′) → BzOO⁺(X³A) + e⁻ was somewhat indicative of the change in C_α–O bonding due to hyperconjugation. At the B3LYP/6-311++G(2df,p) level, the O–O distance in BzOO (1.313 Å) was comparable to that in hydroperoxyl radicals (HO–O, 1.325 Å), implying that the O–O bonding in BzOO and HOO is somewhat close. However, this was not the case for BzOO⁺. The O–O distances (1.240 Å for a¹A and 1.290 for X³A) were in contrast with the hydroperoxyl cation (HO–O⁺, 1.194 Å) and hydrogen peroxide cation (HO–OH⁺, 1.308 Å). These structural differences could be fully explained in the context of the corresponding ionization and dissociative ionization processes of the BzOO radical.

2.2. Ionization transition of BzOO

Treatment by the explicitly correlated coupled cluster (CCSD(T)-F12, variant b) could definitively and accurately predict IE(BzOO): it yielded IE values of 9.331 and 9.454 eV for the ionization transition: BzOO(X²A′′) → BzOO⁺(X³A) + e⁻ and BzOO(X²A′′) → BzOO⁺(a¹A) + e⁻, respectively. Despite the lack of experimental measurement for comparison, the accuracy of the current IE(BzOO) predictions could be substantiated by the agreement between the CCSD(T)-F12 prediction and experimental IE value of the benzyl (Bz) radical. The composite CCSD(T)-F12 value of IE(Bz) = 7.268 eV aligned well with the resonant two-photon ionization measurement, 7.2491 ± 0.0006 eV (ref. 44) and the value of 7.252 ± 0.005 eV obtained by imaging photoelectron photo-ion coincidence.⁴⁵ The CCSD(T)-F12 protocol even outperformed an earlier CCSD(T) prediction⁴⁶ of 7.284 eV, which was based on a complete basis set extrapolation (CBS) scheme. The smaller IE(Bz) compared to IE(BzOO) implies that the Bz⁺ produced by the dissociative ionization of BzOO distinguishable from the BzOO⁺ formed via direct ionization based on the distinct AE(Bz⁺) value in the time-resolved measurements.

The computed IEs for the transitions BzOO(X²A′′) → BzOO⁺(X³A) + e⁻ and BzOO(X²A′′) → BzOO⁺(a¹A) + e⁻ gave a triplet–singlet (X³A–a¹A) energy gap of 0.123 eV for BzOO⁺. As mentioned earlier, the ionization towards the triplet [singlet] state proceeded via the removal of a β[α] electron from the aromatic π [π*(O=O)] orbital (Fig. 2). In contrast to alkylperoxy radicals, where it has been reported that adiabatic ionization involves the removal of an electron from σ(C_α–O) and results in drastic elongation of the bonds, for instance, the respective C_α–OO bond distance increased by 0.21 Å and 0.72 Å (B3LYP/aug-cc-pVTZ predictions, see Table 2 in ref. 38) for CH₃OO and C₂H₅OO upon ionization,³⁸ the adiabatic ionization of BzOO plausibly yields cationic bound states. Evidently, BzOO⁺ stands out as an oddity that does not follow the empirical rule generalized by Meloni et al.³⁷ whereby the π conjugation from the phenyl ring, which should supposedly be much more capable of weakening the C_α–O bond than the hyperconjugation by alkyl groups, instead enhances the stability of the bound state of BzOO⁺(X³A). The Frank–Condon (FC) region related to the ionization of alkylperoxy radicals is here conceivably accessible along the r(C_α–O) coordinates. The ionization of BzOO can plausibly proceed via a mechanism similar to that of C₂H₅OO suggested by Wen and co-workers,¹² in which the singlet surface provides a predissociative state with more favorable FC factors, allowing for crossing into the repulsive region of the triplet surface. However, the substantial difference in the dihedral angle ∠OOC_αC_β between BzOO and its cations, particularly for BzOO⁺(X³A), may further complicate the ionization dynamics.

2.3. Dissociative ionization of BzOO → Bz⁺ + O₂ + e⁻

Understanding the comprehensive bonding structure of BzOO/BzOO⁺ is crucial for predicting the vulnerability of BzOO to dissociative ionization and, conversely, for anticipating the formation of stable BzOO⁺ ions. Refining this understanding could enable chemists to gain insights into the mechanisms governing the dissociative ionization of the neutral state and the subsequent stabilization of BzOO⁺ ions, which would be presumably obtained through the collision-induced association of precursor ions with O₂.³⁰Fig. 3 presents a schematic potential energy diagram for the energetics (Table 1) of BzOO/BzOO⁺ and Bz/Bz⁺ + O₂ computed using the composite CCSD(T)-F12 approach. While the BzOO radical has a theoretical D₀(Bz–OO) value of 0.900 eV, the spin-conserved dissociations of BzOO⁺ (X³A and a¹A) into Bz⁺ and O₂ (X³Σ_g⁻ and a¹Δ_g) were determined to be exothermic, with nominal D₀(Bz⁺−OO) values of −1.163 eV (triplet) and −0.304 eV (singlet). Notably, the experimental triplet–singlet splitting of 0.982 eV⁴⁷ for O₂ largely accounts for the difference between these two D₀(Bz⁺–OO) values. The negative D₀ values imply a fundamental difference in bonding between BzOO⁺ and alkylperoxy radical cations (ROO⁺), where the bonding can be partly described by means of NBO analysis. As summarized in Table S1 (ESI†), moderate perturbations were identified in the π orbitals of the phenyl ring toward the anti-bonding σ*(C_γ–O′) orbital, with E(2) values quantitatively ranging from ≈13–20 (β spin) to ≈33–41 (α spin) kcal mol⁻¹.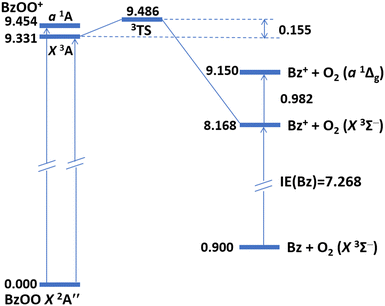

Fig. 3 Schematic potential energy diagram of BzOO/BzOO⁺ and Bz/Bz⁺ as computed using the CCSD(T)-F12 composite approach (see Table 1). All energies are in eV. The transition energy (0.982 eV) for O₂ a¹Δ_g ← X³Σ⁻ is taken from the NIST Webbook (ref. 47).

Table 1 Individual contributions (in eV) to the composite IEs, D₀ and barrier height of the TS

	IE[BzOO(X^2A′′) → BzOO^+(X^3A) + e^−]	IE[BzOO(X^2A′′) → BzOO^+(a^1A) + e^−]	IE(Bz)
a Single-point energy calculations at the CCSD(T)-F12/cc-pVQZ-F12 level. b Core-valence electronic corrections at the CCSD(T)/cc-pwCVTZ level. c Zero-point vibrational energy calculations at the B3LYP/6-311++G(2df,p) level. d Composite sum (EF12 + ΔECV + ΔEZPVE) for the IE, D0 values, and barrier height. e Resonant two-photon ionization measurement, see ref. 44 for details. f Vacuum ultraviolet threshold photoelectron measurement, see ref. 45 for details. g Previous IE prediction at the CCSD(T)/cc-pVQZ level with CV and ZPVE, see ref. 46 for details.
E F12	9.332	9.441	7.180
ΔECV^b	0.019	0.022	0.014
ΔEZPVE^c	−0.020	−0.009	0.074
Composite^d	9.331	9.454	7.268
Experimental or theoretical values			7.2491(6)^e
			7.252(5)^f
			7.284^g

---

	D 0(Bz^+–OO, X^3A)	D 0(Bz–OO)	Barrier height for the TS [BzOO^+(X^3A) → Bz^+ + O2(X^3Σ^−)]
E F12	−1.081	1.071	0.193
ΔECV^b	−0.006	−0.001	0.000
ΔEZPVE^c	−0.076	−0.170	−0.038
Composite^d	−1.163	0.900	0.155

---

Meloni et al.³⁸ ascribed the nonexistence of intact ROO⁺, where R is an alkyl group larger than ethyl (C₂H₅), to the vanishing D₀(R⁺–OO) value in photoionization mass spectrometry. The prediction of a bound BzOO⁺ herein necessitates there existing a transition state (TS) structure for the dissociation of BzOO⁺ into Bz⁺ and O₂. As revealed by the saddle point structure at the B3LYP[M06-2X] levels depicted in Fig. 1, the most prominent geometric change relative to the equilibrium structure manifested as a change in ∠OOC_αC_β from −15.5° [−12.6°] to −33.2° [−39.6°], entailing an imaginary vibrational frequency of 300i [278i] cm⁻¹. Intriguingly, this single imaginary normal mode corresponded to a stretching of the C_γ–O′ bond mixed with an internal rotation of the O=O moiety away from the phenyl ring, giving rise to a dubiously small barrier (without ZPVE correction) of ≈0.030 eV [0.049 eV]. To confirm the existence of this TS initially located with DFT, we successfully verified the structure with the more reliable coupled-cluster theory. At the CCSD(T)/6-311+G(d) level, ∠OOC_αC_βen route to the TS barely changed from −21.5° to −29.5°. However, the CCSD(T) barrier height (0.155 eV, Table 1) was 3–5 times larger than predicted by DFT, unambiguously confirming that BzOO⁺ (³A) is a stable and bound structure. In contrast, the ground-state structure of C₂H₅OO⁺ was barely bound with respect to C₂H₅⁺ and O₂, whereas CH₃OO⁺, being the only alkylperoxy cation detected so far, had an experimental D₀ estimated at ≈0.83 eV (80 kJ mol⁻¹),³⁷ making it over five times more strongly bound than BzOO⁺. Furthermore, given that the most stable conformation of the neutral BzOO places the OO group in an anti-orientation relative to the phenyl group, the FCF inevitably directs the cation toward the repulsive region of the PES upon photoionization. In this manner, we anticipate there would be a minimal detection of intact BzOO⁺ (X³A) species in photoionization mass spectrometry measurements.

2.4. Stability analysis of BzOO⁺(X³A)

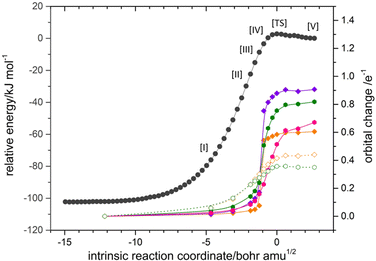
The NBO analysis provided eloquent justification for the weakening of the C_α–O bond in C₂H₅OO⁺ through hyperconjugation. As shown in Table S1 (ESI†), the donor–acceptor interaction σ(C_β–H) → σ*(C_α–O) gave rise to the highest stabilization energy, E(2) reaching up to 17.7 kcal mol⁻¹, thereby undermining the C_α–O bond strength in other ROO⁺ species, except for CH₃OO⁺, which lacks a C_β atom. In particular, the donor–acceptor interaction lowers the bond order of C_α–O, resulting in an exceptionally long bond length of approximately 2.2 Å. Intuitively, the perturbation by the π electrons on the phenyl ring towards σ*(C_α–O) should be more profound. However, there was a negligible influx of electrons into σ*(C_α–O) originating from the π conjugation system (Table S1, ESI†). Instead, the most prominent donation, via π(C_δ–C_ε) and π(C_β–C_γ′), occurred towards the anomalous C_γ–O′ bond, which was identified as a one-electron bond. These donor–acceptor interactions π(C_δ–C_ε) or π(C_β–C_γ′) → σ*(C_γ–O′) of β electrons are different (Table S1, ESI†) from BzOO⁺ to the optimized TS structure for BzOO⁺(³A) → Bz⁺ + O₂(³Σ⁻), mostly due to change in energy separation (ΔE, footnote a in Table S1, ESI†) of the concerned orbitals. Still, the E(2) values alone cannot illuminate the pathway of electron flow nor suggest a plausible mechanism for the generation of Bz⁺ and O₂ from BzOO⁺. To this end, it was necessary to apply intrinsic bond orbital (IBO) analysis,^48,49 which has been proven to be effective in directly linking the chemically intuitive “curly arrows” to the flow of electrons in chemical reactions. The transformation of IBOs along the reaction coordinate can unambiguously reveal the detailed mechanisms of bond rearrangement, and can even dispel the ambiguity between hydrogen atom transfer and concerted proton-coupled electron-transfer processes.⁵⁰ The IBO evolution along the IRC of the Bz⁺ + O₂ addition is shown in Fig. 4. The selected structures [I]–[V] and [TS] ensure that the energy profiles along the intrinsic reaction coordinate (IRC) pathway (black trace in Fig. 5) could be fittingly rendered. The IBOs depicted in Fig. 4 illustrate the most significant orbital change, which allows measuring the induced change of the charge distribution by the flow of electrons as the reaction proceeds along the IRC, as defined in ref. 51, in a way that quantitatively accounts for the participation of a specific IBO in the bonding rearrangement. The corresponding orbital changes of these IBOs at structures [I]–[V] and [TS] along the IRC were plotted, as shown in Fig. 5. The most dramatic orbital changes were mostly observed in the β-spin (1β–4β in Fig. 4) rather than the α-spin counterparts. As shown in a previous study on O₂,⁴⁰ the localized bond picture can still aptly describe the bonding of O₂ when the Linnett structure is invoked. The concept of the Linnett structure is an alternative to the Lewis structure as a representation of a valence bond, based on the Linnett double-quartet (LDQ) theory,^52–54 which describes the π-bonding of O₂ as two orthogonal, single β-electron bonds, while the overall triplet state is attained by allocating four α-electrons in non-bonding p-orbitals on both O atoms (see Fig. S1a, in the ESI†). In a similar fashion, IBO analysis was applied to BzOO⁺(³A) → Bz⁺ + O₂(³Σ⁻), and also suggested an interpretation based on Linnett structures. As already shown in the original article,⁴⁸ IBO analysis provides two equivalent bonding pictures for benzene, one of which directly corresponds to the Linnett structure so ingeniously proposed (Fig, S1a, ESI†).⁵⁴ Similarly, a Linnett structure for Bz⁺ (Fig. S1a, ESI†) is suggested. The Linnett representation does not invoke the concept of a resonance structure to account for the charge density. In Fig. 4, structure [I] represents the earlier stage of the IRC pathway, where the Linnett bonding pictures of both O₂ and Bz⁺ can be readily recognized. Progressing forward from [I] to [TS] to [V], one β-electron from the π-orbital (IBO-1β) and one α-electron from the lone p-orbital (IBO-1α) of O₂ contribute to form a new C_α–O bond pair. However, the transformation of the π-system seems more sophisticated. Here, two π-electrons, respectively in IBO-3β and IBO-4β undergo long-range migration to the opposite side of the phenyl ring, a distance that seems hardly conceivable to most chemists. Meanwhile, IBO-2β, wherein much of the perplexity arises, initially interacts with a π*(O=O) orbital of structure [III]. However, the density abruptly shifts to C_γ for structure [IV], ceasing its contribution to the newly formed C_α–O bond. Instead, the IBO-2β partially becomes the surrogate of IBO-1β at the [TS], preserving a certain degree of π character in the OO moiety. At structure [V] where the adduct is formed, the formation of a C_γ–O′ bond is evidently contributed by the p-orbitals on the terminal O and on the C_γ. To unravel the intricate rearrangement of Bz⁺ + O₂ → BzOO⁺, the orbital change of these IBOs along the IRC pathway were quantified and are plotted in Fig. 5. The IBOs discussed above could be categorized as, either purely residing within the π conjugation system (IBO-2α, IBO-3β, IBO-4β), or involved in C–O bonding interactions (IBO-1α, IBO-1β, IBO-2β). Evidently, the β electrons (IBO-2β and IBO-3β) were primarily responsible for most of the energy change, reflecting the rearrangement of π electrons prior to the formation of C_γ–O′, and leading to the sharp rise in energy in the vicinity of the [TS]. The electronic arrangements in the association of Bz⁺ + O₂ → BzOO⁺ are summarized in Scheme 1, which uses the intuitive ‘curly arrows’ depiction based on the Linnett structures.

Fig. 4 IBOs for alpha (1α–2α) and beta (1β–4β) electrons along the IRC for the addition reaction, O₂ + Bz⁺ → BzOO⁺.

Fig. 5 Energy profile of the IBOs along the IRC for O₂ + Bz⁺ → BzOO⁺. Legend: total energy (•), IBO-1α (), IBO-2α (), IBO-1β (), IBO-2β (), IBO-3β (), IBO-4β (). All energies are relative to the fully optimized energy of BzOO⁺ at the B3LYP/aug-cc-pVTZ level. IBO changes are measured and plotted as the root-mean-square deviation for the orbital partial charge distribution among the atoms with respect to the initial partial charge distribution.

Scheme 1 The speculated mechanism of O₂ addition to Bz⁺. The curly arrows in the Linnett structures (cross and dot represent α and β electrons, respectively) are drawn in accordance with the electron flow revealed in the IBO analysis.

Conceptual tools, such as inductive and mesomeric effects, are often very handy for predicting or rationalizing the stability of reactive species. While the hyperconjugation effect can sufficiently account for the absence of intact parent cations from larger alkylperoxy species in photoionization mass spectrometry, this reasoning cannot be readily extended to BzOO⁺, which features a π-conjugation system. In contrast to alkylperoxy cations, the conjugation stabilizes the bound structure of BzOO⁺(X³A), leading to a totally different outcome. Leveraging the distinct advantage of IBO analysis for bridging computational results and intuitive mechanisms, we identified highly disparate participations of α and β electrons in these stabilizing interactions, which could only be rationalized through the framework of the Linnett structure. The LDQ theory allowed outstanding predictions to be made even shortly after its introduction in 1961. Yet, despite its insightful bonding depiction for molecular oxygen and ozone, it has since faded into obscurity.⁵⁵ Another prevailing perception is that the curly-arrow depiction is unsuitable for reactions involving triplet species.⁵⁶ However, the current investigation tools not only facilitated the experimental study of BzOO and the potential observation of BzOO⁺, but also advocated for the revival of LDQ theory. This framework shows significant promise for understating similar molecular system, for instance, O₂ addition to polyaromatic hydrocarbons, cyclo[n]catbon,⁵⁷ and graphene.

3. Conclusions

We report on the potential existence of a stable and bound benzylperoxy cationic species (C₆H₅CH₂OO⁺ or BzOO⁺), which may serve as an exception to the generalization rule proposed previously.^37,38 The stability of BzOO⁺(X³A) was supported by the optimized minimum energy structures at the DFT and CCSD(T) levels, as well as the significant barrier height (0.155 eV) for the fragmentation of BzOO⁺ into Bz⁺ and O₂, determined at the CCSD(T) level. The formation of an anomalous C_γ–O′ bond in BzOO⁺, facilitated by interactions with the π electrons of the phenyl ring, was elucidated and understood through its electronic structure based on IBO analysis. Additionally, our CCSD(T)-F12 results show that the IE(BzOO(X²A′′) → BzOO⁺(X³A) + e⁻) value differed substantially from the AE(BzOO(X²A′′) → Bz⁺ + O₂ + e⁻) quantity, making it possible to detect BzOO⁺ ions experimentally. The discovery of this stable radical cation could inspire gas-phase spectroscopists to pursue the generation, detection, and characterization of BzOO⁺ in future photoionization experiments. Furthermore, the insights gained into the chemical bonding of BzOO⁺(X³A) pave the way for expanding the traditional curly-arrow depiction to represent reaction mechanisms involving π-electron systems in triplet oxygen.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K.-C. Lau acknowledges the financial support from the General Research Fund by the Hong Kong Research Grants Council (Grant No.: CityU 11307020). The computational studies were carried out using the High-Performance Computing facility, CityU Burgundy at the City University of Hong Kong.

References

1. J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317.
2. J. Zádor, C. A. Taatjes and R. X. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421.
3. R. G. Derwent, M. E. Jenkin and S. M. Saunders, Atmos. Environ., 1996, 30, 181–199.
4. T. J. Wallington, P. Dagaut and M. J. Kurylo, Chem. Rev., 1992, 92, 667–710.
5. B. J. Finlayson-Pitts and J. N. Pitts, Science, 1997, 276, 1045.
6. J. Peeters, T. L. Nguyen and L. Vereecken, Phys. Chem. Chem. Phys., 2009, 11, 5935–5939.
7. F. Rohrer, K. Lu, A. Hofzumahaus, B. Bohn, T. Brauers, C.-C. Chang, H. Fuchs, R. Häseler, F. Holland and M. Hu, et al. , Nat. Geosci., 2014, 7, 559–563.
8. R. Chhantyal-Pun, M. A. H. Khan, N. Zachhuber, C. J. Percival, D. E. Shallcross and A. J. Orr-Ewing, ACS Earth Space Chem., 2020, 4, 1743–1755.
9. D. J. Jacob and D. A. Winner, Atmos. Environ., 2009, 43, 51–63.
10. M. Glasius and A. H. Goldstein, Environ. Sci. Technol., 2016, 50, 2754–2764.
11. X. Tang, X. Gu, X. Lin, W. Zhang, G. A. Garcia, C. Fittschen, J.-C. Loison, K. Voronova, B. Sztáray and L. Nahon, J. Chem. Phys., 2020, 152, 104301.
12. Z. Wen, X. Lin, X. Tang, B. Long, C. Wang, C. Zhang, C. Fittschen, J. Yang, X. Gu and W. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 22096–22102.
13. H. B. Fu, Y. J. Hu and E. R. Bernstein, J. Chem. Phys., 2006, 125, 014310.
14. S. Lakshmanan, W. L. Hase and G. P. Smith, Phys. Chem. Chem. Phys., 2021, 23, 23508–23516.
15. Y. Xu, S. Xi, F. Wang and X. Li, J. Phys. Chem. A, 2019, 123, 3949–3958.
16. L. L. Lohr, J. R. Barker and R. M. Shroll, J. Phys. Chem. A, 2003, 107, 7429–7433.
17. A. Guenther, T. Karl, P. Harley, C. Wiedinmyer, P. I. Palmer and C. Geron, Atmos. Chem. Phys., 2006, 6, 3181–3210.
18. L. Vereecken, P. T. M. Carlsson, A. Novelli, F. Bernard, S. S. Brown, C. Cho, J. N. Crowley, H. Fuchs, W. Mellouki and D. Reimer, et al. , Phys. Chem. Chem. Phys., 2021, 23, 5496–5515.
19. F. Ma, X. Guo, D. Xia, H.-B. Xie, Y. Wang, J. Elm, J. Chen and J. Niu, Environ. Sci. Technol., 2021, 55, 4399–4409.
20. L. Vereecken, G. Vu, A. Wahner, A. Kiendler-Scharr and H. M. T. Nguyen, Phys. Chem. Chem. Phys., 2021, 23, 16564–16576.
21. P. Benjumea, J. R. Agudelo and A. F. Agudelo, Energy Fuel, 2011, 25, 77–85.
22. C. K. Westbrook, W. J. Pitz, S. M. Sarathy and M. Mehl, Proc. Combust. Inst., 2013, 34, 3049–3056.
23. B. Noziere, R. Lesclaux, M. D. Hurley, M. A. Dearth and T. J. Wallington, J. Phys. Chem., 1994, 98, 2864–2873.
24. G. El Dib, A. Chakir, E. Roth, J. Brion and D. Daumont, J. Phys. Chem. A, 2006, 110, 7848–7857.
25. G. da Silva, M. R. Hamdan and J. W. Bozzelli, J. Chem. Theory Comput., 2009, 5, 3185–3194.
26. B. Du, W. Zhang, L. Mu, C. Feng and Z. Qin, Chem. Phys. Lett., 2007, 445, 17–21.
27. O. N. Ventura, M. Kieninger, Z. Salta, A. M. Kosmas and V. Barone, Theor. Chem. Acc., 2019, 138, 115.
28. Y. Murakami, T. Oguchi, K. Hashimoto and Y. Nosaka, J. Phys. Chem. A, 2007, 111, 13200–13208.
29. L. Elmaimouni, R. Minetti, J. P. Sawerysyn and P. Devolder, Int. J. Chem. Kinet., 1993, 25, 399–413.
30. F. F. Fenter, B. Nozière, F. Caralp and R. Lesclaux, Int. J. Chem. Kinet., 1994, 26, 171–189.
31. B. Feng, C. Sun and S. Zhang, Atmos. Environ., 2019, 201, 18–27.
32. W. Sander, S. Roy, K. Bravo-Rodriguez, D. Grote and E. Sanchez-Garcia, Chem. – Eur. J., 2014, 20, 12917–12923.
33. I. Garcia, V. Uc, M. E. Ruiz, Y. G. Smeyers and A. V. Bunge, J. Mol. Struct. Theochem, 1995, 340, 149–158.
34. S. Canneaux, F. Louis, M. Ribaucour, R. Minetti, A. El Bakali and J.-F. Pauwels, J. Phys. Chem. A, 2008, 112, 6045–6052.
35. S. Canneaux, C. Hammaecher, F. Louis and M. Ribaucour, Chapter 2 Rate Constant Calculation of Benzylperoxy Radical Isomerization. In Reaction Rate Constant Computations: Theories and Applications, The Royal Society of Chemistry, 2013; pp 34–54.
36. H. Telfah, M. A. Reza, J. Alam, A. C. Paul and J. Liu, J. Phys. Chem. Lett., 2018, 9, 4475–4480.
37. G. Meloni, P. Zou, S. J. Klippenstein, M. Ahmed, S. R. Leone, C. A. Taatjes and D. L. Osborn, J. Am. Chem. Soc., 2006, 128, 13559–13567.
38. G. Meloni, T. M. Selby, F. Goulay, S. R. Leone, D. L. Osborn and C. A. Taatjes, J. Am. Chem. Soc., 2007, 129, 14019–14025.
39. X. Tang, X. Lin, G. A. Garcia, J.-C. Loison, Z. Gouid, H. H. Abdallah, C. Fittschen, M. Hochlaf, X. Gu and W. Zhang, et al. , Chem. Commun., 2020, 56, 15525–15528.
40. T. A. Corry and P. J. O’Malley, J. Phys. Chem. A, 2020, 124, 9771–9776.
41. F. Weinhold, Discovering chemistry with natural bond orbitals, John Wiley & Sons, 2012.
42. A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073.
43. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
44. G. C. Eiden, K. T. Lu, J. Badenhoop, F. Weinhold and J. C. Weisshaar, J. Chem. Phys., 1996, 104, 8886–8895.
45. J. D. Savee, J. Zádor, P. Hemberger, B. Sztáray, A. Bodi and D. L. Osborn, Mol. Phys., 2015, 113, 2217–2227.
46. K. C. Lau and C. Y. Ng, J. Chem. Phys., 2006, 124, 044323.
47. W. G. Linstrom and P. J. Mallard. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology: Gaithersburg MD, 20899, 2024.
48. G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843.
49. G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518–5522.
50. J. E. M. N. Klein and G. Knizia, Angew. Chem., Int. Ed., 2018, 57, 11913–11917.
51. J. E. M. N. Klein, G. Knizia and H. S. Rzepa, ChemistryOpen, 2019, 8, 1244–1250.
52. M. Green and J. W. Linnett, J. Chem. Soc., 1960, 4959–4965.
53. R. D. Harcourt, J. Chem. Educ., 1985, 62, 99.
54. J. W. Linnett, J. Am. Chem. Soc., 1961, 83, 2643–2653.
55. W. B. Jensen, Educ. Quim., 2017, 28, 74–83.
56. J. Andrés, P. González-Navarrete, V. S. Safont and B. Silvi, Phys. Chem. Chem. Phys., 2017, 19, 29031–29046.
57. J. Chen, L. Sun and R. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 17545–17552.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03905j

‡ Present address: Chemistry Research Laboratory, Department of Chemistry, University of Oxford, Oxford OX1 3TA, UK.

---