Simple carbenes as hydrogen bond acceptors: ab initio determination of nucleophilicities and reduced nucleophilicities

Abstract

Nucleophilicities for a range of simple carbene molecules acting as hydrogen bond acceptors B in forming complexes B⋯HX are reported. The carbenes chosen to fulfil the roles of a Lewis base are B = R₂M, cyclo-(CH)₂M, H₂C=C=M and two N-heterocyclic carbenes, where M is one of the group 14 tetrel atoms, C, Si, Ge or Sn and R = H, CH₃, and F. All the carbenes but CH₂ have a singlet electronic ground state. The Lewis acids, HX, involved are HF, HCl, HBr, HI and HCN, HCCH, and HCP. Nucleophilicities, N_B, of the carbenes were determined graphically from equilibrium dissociation energies, D_e, for the process B⋯HX = B + HX by using the equation D_e = c·N_B·E_HX, where c = 1.0 kJ mol⁻¹ and the E_HX are known numerical electrophilicities of the Lewis acids HX. D_e values were calculated ab initio at the CCSD(T)-F12c/cc-pVDZ-F12 level of theory, which for CH₂ refers to the singlet electronic excited state. It was established that NR₂M values lie in the order of M = C ≫ Si ∼ Ge ∼ Sn for a given R and in the order R = CH₃ > H > F for a given M. Reduced nucleophilicities, N_B/σ_axial, were determined by using the molecular electronic surface potential σ_axial at atom M (which lies on the C₂ axis) on the 0.001 e Bohr⁻³ iso-surface of each carbene molecule, as calculated at the MP2/aug-cc-pVTZ level. For R₂M having R = CH₃ and H and cyclo-(CH)₂-M carbenes, the determined values of N_B/σ_axial are shown to be independent of R and M.

---

1. Introduction

Carbenes fulfil an important role in synthetic organic chemistry. There exists a voluminous literature of books and reviews, with just one example of each^1,2 referred to here. Carbenes can act either as electrophiles or as nucleophiles and are known to be excellent hydrogen bond acceptors.^3–10 In this article, we examine the nucleophilicities of some simple carbenes when forming hydrogen-bonded complexes. Two groups of carbenes investigated here are shown in Fig. 1, which illustrates the specific examples with Si as the tetrel atom. The first group (A, B, and C in Fig. 1) can be represented by the general formula R₂M, where M is a group 14 (tetrel) atom, C, Si, Ge, or Sn, that is one from each of the first four rows of the Periodic Table. R is H, F or CH₃. The second group consists of the related cyclic C_2V molecules cyclo-(CH)₂M (together with their isomers H₂C=C=M), and two N-heterocyclic carbenes, cyclo-(CH)₂(NH)₂M (M = C and Si). Each carbene considered has C_2V symmetry. We investigate hydrogen-bonded complexes formed with the HX molecules (X = F, Cl, Br, I, CN, CCH, CP). In each case, the HX molecule lies along the C₂ axis of the carbene.

Fig. 1 Molecular diagrams of the carbenes discussed in this article. The molecules shown contain silicon as the ‘carbene’ atom but those based on other tetrel atoms C, Ge and Sn are also investigated. A = silylene, B = difluorosilylene, C = dimethylsilylene, D = silacyclopropenylidene, E = vinylidenesilanediyl (an isomer of D), and F = N-heterocyclic silylene.

It is well-known that CH₂ has a triplet electronic ground state, with energy separation from the singlet calculated by Schaefer et al.¹¹ to be 46(8) kJ mol⁻¹. The parent carbene CH₂ can be included in the present discussion however because the ab initio calculation carried out yields the singlet state. Evidently, carbenes (CH₃)₂C and F₂C have a singlet ground state, for which Hu¹² calculates the singlet states to be lower in energy than the triplet states by 224 and 3 kJ mol⁻¹, respectively. All other group 14 analogues of carbenes shown in Fig. 1 possess a singlet ground state. Consequently, the tetrel atom in each carbene considered here carries a non-bonding electron pair along the C₂ axis.

A convenient aid when discussing the propensity of a simple carbene to form hydrogen-bonded complexes is the so-called molecular electrostatic surface potential, MESP.¹³ Diagrams of the 0.001 e Bohr⁻³ iso-electron density surface for each of F₂Si, H₂Si and (CH₃)₂Si are shown in Fig. 2. The corresponding MESP diagrams for M = C (including H₂C), Ge and Sn are shown in Fig. S1 of the ESI.† The red regions in each case correspond to the negative (and therefore nucleophilic) regions of the iso-surface. The value of σ_axial of the MESP on the C₂ axis of each molecule is shown and coincides with the non-bonding electron pair of the R₂M molecule. Diatomic or linear Lewis-acid molecules HX (X = F, Cl, Br, I, CN, CCH or CP) are therefore likely form hydrogen-bonded complexes R₂M⋯HX in which the electrophilic H atom of HX interacts with the non-bonding electron pair. Hence, the equilibrium geometries of the R₂M⋯HX complexes should (like the parent molecules) have a C₂ axis of symmetry, with HX lying along that axis. It should be note that most of the F₂M are electrophilic (positive MESP) along the C₂ axis at M and are therefore expected to form, at best, weak complexes of the required symmetry with the HX molecules of interest.

Fig. 2 Molecular electrostatic surface potentials of F₂Si, H₂Si, and (CH₃)₂Si calculated at the MP2/aug-cc-pVTZ level of theory. The values of the MESP (the potential energy of a unit positive point charge on the 0.001 e Bohr⁻³ iso-surface) on the C₂ axis near the Si atom and its non-bonding electron pair are shown.

The nucleophilicity of a given carbene molecule acting as a Lewis base B is determined by the following method. It has been shown¹⁴ that the equilibrium energy D_e required for dissociation of a hydrogen-bonded complex B⋯HX of a Lewis base B and a Lewis acid HX into infinitely separated B and HX can be described by eqn(1), where N_B is the nucleophilicity of B and E_HX is the electrophilicity of HX:

D_e = c·N_B·E_HX (1)

The constant c is chosen as 1 kJ mol⁻¹ for convenience, so that, if D_e is given in kJ mol⁻¹, N_B and E_HX are dimensionless. Many N_B and E_HX values have been generated¹⁵ by least-squares fitting of ab initio-calculated D_e values to eqn (1), including the set of E_HX for HF, HCl, HBr, HI, HCN, HCCH and HCP. According to eqn (1), if, for a series of complexes B⋯HX in which B is fixed but HX is varied, D_e/c is plotted as the ordinate and E_HX as the abscissa, and then the gradient of the straight line gives the nucleophilicity N_B of B. By such means, new values of N_B not included in the initially generated set can be obtained. Recent applications of this approach include the series of Lewis bases ethyne, ethene and cyclopropane¹⁶ and monohydrides of group 13 elements B, Al and Ga.¹⁷ Alternatively, the gradient of the D_e/c versus N_B graph for a series of complexes B⋯A, in which A is a fixed Lewis acid and the B are a series of Lewis bases (such as N₂, CO, C₂H₂, C₂H₄, HCN, H₂O, and NH₃) of known N_B values, yielding the electrophilicity E_A of A. Applications of this type have recently generated the electrophilicities of various interhalogens (via halogen-bonded complexes B⋯XY¹⁸), and of the group 14 elements Si, Ge and Sn in tetrel-bonded complexes B⋯H₃M–X (M = Si, Ge, Sn).¹⁹

The nucleophilicities of the Lewis bases shown in Fig. 1 were calculated by using the approach set out in the preceding paragraph, namely by calculating the ab initio D_e values of the hydrogen-bonded complexes (e.g. R₂M⋯HX, where X = F, Cl, Br, I, CN, CCH, and CP) and finding the gradients of D_e/c versus E_HX plots. We also investigate here whether a reduced nucleophilicity can be defined by the gradient of a graph of D_e/σ_axialversus E_HX, as established for other series of Lewis bases.²⁰ This quantity is of interest because it has been shown to be a property only of the atom of the Lewis base B that is directly involved in, for example, a hydrogen bond and is independent of the remainder of B. Moreover, together with its analogous quantity reduced electrophilicity of a Lewis acid, it provides a method²¹ of calculating the D_e values from the properties of the separate molecules B and HX.

2. Theoretical methods

The geometries of the systems have been optimized at the CCSD(T)-F12c computational level^22,23 with the cc-pVDZ-F12 basis.²⁴ The CCSD(T) level of calculation is known as the gold-standard for the calculation of medium sized systems. The CCSD(T)-F12c approach has been shown to improve the basis set convergence of correlation and reaction energies²⁵ and thermochemistry²⁶ and provide results similar to those at the CCSD(T)/cc-pV(T/Q)Z level.²³ In addition, the cc-pVXZ-F12 basis set has shown broad applicability, including the estimation of interaction energies.²⁷ The standard frozen-core approximation was used for all the complexes, except for those containing tin, where 10 electrons have been correlated instead of the default (4 electrons). This avoids the mixing of the core and valence electrons in complexes where a tin atom is present. The inherent basis set superposition error (BSSE) has been corrected with the Boys and Bernardi full counterpoise method.²⁸ These calculations have been carried out with the scientific MOLPRO program.²⁹ The molecular electrostatic potentials on the 0.001 au electron density iso-surface (MESP) of the isolated monomers were calculated with the Gaussian-16 program³⁰ at the MP2/aug-cc-pVTZ level, analysed with the Multiwfn program³¹ and represented with the Jmol program.³²

3. Results

3.1. Comparison of the nucleophilicities along the C₂ axis direction of R₂M molecules (M = Si, Ge, Sn; R = CH₃, H and F)

Graphs of D_e/c versus the electrophilicities E_HX of the Lewis acids HX (X = F, Cl, Br, I, CN, CCH, and CP) are shown for the four series of complexes H₂M⋯HX (M = C, Si, Ge or Sn) in Fig. 3. Values of E_HX are from ref. 15, and except for HI and HBr, refined versions of which are reported in ref. 33. For the reason already discussed in Section 1, M = C can be included in Fig. 3 since the calculation refers to the singlet state. The gradients of the straight lines give the axial nucleophilicities N_H2M of the H₂M molecules and therefore of the non-bonding electron pair carried on the C₂ axis in each case. The determined values are 6.36(16), 2.71(7), 2.35(7) and 1.99(7) for M = C, Si, Ge and Sn, respectively. The value for M = C is higher than the rest, but the other three values are close to each other. It should be noted that the nucleophilicity decreases as the size of the atom M increases.

Fig. 3 Graphs of D_e/c versus E_HX for the four series of hydrogen-bonded complexes H₂M⋯HX, having M = C, Si, Ge or Sn and X = F, Cl, Br, I, CN, CCH, and CP. The gradients give the nucleophilicities of the non-bonding electron pair that lies along the C₂ axis of H₂M.

The corresponding diagram for the series (CH₃)₂M⋯HX when M = C, Si, Ge or Sn is shown in Fig. 4. It should be noted that, in Fig. 4, the origin is no longer included as a point for (CH₃)₂C⋯HX because of a significant non-zero intercept (This behaviour seems to be a characteristic of Lewis bases that have methyl groups attached, see for example Fig. 6 of ref. 16.). The points for (CH₃)₂C⋯HX when X = Cl, Br, and I are excluded because of unduly large D_e values resulting from significant (CH₃)₂CH⁺⋯X⁻ characters, as indicated by short distances r(C–H_axial) and lengthened distances r(H–X). The (CH₃)₂C⋯HX points having X = F, CN, CCH and CP seem to be better behaved and indicate that the axial nucleophilicity N_B of M = C in this series is considerably greater than those having M = Si, Ge and Sn. It is noted that the three molecules associated with rows 2, 3 and 4 of the Periodic Table again have very similar axial nucleophilicities. In fact, the ratios of N_B are 3.19(11)/1.36(8) : 1.18(8) : 1.00 for H₂C/H₂Si/H₂Ge/H₂Sn and 3.25(19) : 1.40(14) : 1.19(13) : 1.00 for (CH₃)₂C/(CH₃)₂Si/(CH₃)₂Ge/(CH₃)₂Sn; these ratios are therefore identical for H₂M and (CH₃)₂M within the standard errors.

Fig. 4 Graphs of D_e/c versus E_HX for the four series of hydrogen-bonded complexes (CH₃)₂M⋯HX, having M = C, Si, Ge or Sn and X = F, Cl, Br, I, CN, CCH, and CP. The gradients give the nucleophilicities of the non-bonding electron pair that lies along the C₂ axis of (CH₃)₂M.

Graphs of D_e/c versus E_HX for the series F₂C⋯HX, F₂Si⋯HX and F₂Ge⋯HX are shown in Fig. 5 (data are unavailable for F₂Sn⋯HX because the region of the MESP on the C₂ axis is positive and data are limited for F₂Ge⋯HX because of evidence of ionic characters for some of the HX complexes). The values of the nucleophilicity decrease from 3.39 for M = C, through small positive 0.93 for M = Si and becomes negative −0.39 for Ge. This is reflected in the MESPs at the tetrel atom on the C₂ axes of F₂C, F₂Si and F₂Ge which have the values (see Fig. S1, ESI†) of −85.0, +1.5 and +49.8 kJ mol⁻¹, respectively. Such MESP values indicate that the complexes with HX molecules are likely to be weak, except for F₂C⋯HX. This expectation is borne out by the gradients of the lines in Fig. 4. Presumably, for F₂Ge⋯HX, this is negative because of repulsion between the positive axial MESP at Ge on the C₂ axis of F₂Ge and the electrophilic atom H of the Lewis acids HX.

Fig. 5 Graphs of D_e/c versus E_HX for the three series of hydrogen-bonded complexes F₂M⋯HX having M = C, Si, or Ge and X = F, Cl, Br, I, CN, CCH, and CP. The gradients give the nucleophilicities at the non-bonding electron pair that lies along the C₂ axis of M. See the text for discussion of the negative gradient for the F₂Ge⋯HX series.

3.2. The inductive effects of R = CH₃ and R = F relative to R = H on the nucleophilicities of R₂M (M = Si, Ge, Sn)

Fig. 6 shows the D_e/c versus E_HX graphs for the three series (CH₃)₂C⋯HX, H₂C⋯HX and F₂C⋯HX. The gradients of the three straight lines are 9.41(22), 6.36(16) and 3.39(26), respectively. Thus, the substitution of the two H atoms by methyl groups increases the axial nucleophilicity near C by 3.1, while the substitution of two H atoms by F atoms decreases it by 3.0.

Fig. 6 Graphs of D_e/c versus E_HX for the three series of hydrogen-bonded complexes R₂C⋯HX having R = CH₃, H or F and X = F, Cl, Br, I, CN, CCH, and CP. The gradients give the nucleophilicities associated with the non-bonding electron pair that lies along the C₂ axis of C. They confirm that CH₃ has a +I effect relative to H while F has a −I (electron-withdrawing) effect.

The corresponding graphs for the R₂Si⋯HX series are shown in Fig. 7, while that for R₂Ge⋯HX is shown in Fig. S2 of the ESI.† The patterns in Fig. 7 and Fig. S2 (ESI†) are similar to those in Fig. 6, except that it decreases in nucleophilicity when CH₃ is replaced by H and then F becomes smaller from M = C to M = Si to M = Ge. As discussed in connection with Fig. 5, the gradient of the graph associated with the F₂Ge⋯HX line in Fig. S2 (ESI†) is negative. For the R₂Sn series, R = F is not available (for reasons discussed earlier), but the graphs for the (CH₃)₂Sn⋯HX and H₂Sn⋯HX are shown in Fig. S3 (ESI†). The axial nucleophilicity decreases by ∼0.8 in this case when CH₃ is replaced by H.

Fig. 7 Graphs of D_e/c versus E_HX for the three series of hydrogen-bonded complexes R₂Si⋯HX having R = CH₃, H or F and X = F, Cl, Br, I, CN, CCH, and CP. The gradients give the nucleophilicities associated with the non-bonding electron pair that lies along the C₂ axis of Si. They again confirm that CH₃ has a +I effect relative to H, while F has a −I (electron-withdrawing) effect.

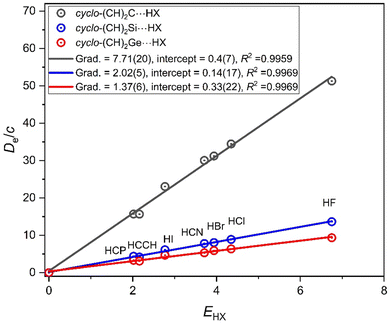
3.3. Axial nucleophilicities of the cyclic carbenes: cyclo-(CH)₂M (M = C, Si, Ge)

Replacing the two methyl groups in the (CH₃)₂M molecule by the HC=CH moiety leads to the cyclic carbene cyclo-(CH)₂M. Cyclo-(CH)₂C is the first member of cyclopropenylidenes,³⁴ was initially characterised by its microwave spectrum,³⁵ and is of significance in astrophysical spectroscopy. There is a singlet ground state for all M discussed here. To calculate ab initio the geometry of the cyclo-(CH)₂M molecules and their hydrogen-bonded complexes, cyclo-(CH)₂M⋯HX for M = C, Si and Ge is straight-forward, but for M = Sn there is evidence of ionic character and it is not included in what follows. Fig. 8 compares the plots of D_e/c versus E_HX for the three series cyclo-(CH)₂M⋯HX (M = C, Si, Ge). Fig. 8 illustrates clearly that, for the complexes cyclo-(CH)₂M, the order of the nucleophilicities is M = C ≫ Si ∼ Ge. It should also be noted that nucleophilicities are in the order (CH₃)₂M > cyclo-(CH)₂M for each of M = C, Si and Ge. Evidently, the inductive effect of two CH₃ groups is greater than that arising from the HC=CH moiety that replaces them.

Fig. 8 Graphs of D_e/c versus E_HX for the three series of hydrogen-bonded complexes cyclo-(CH)₂M⋯HX, where M = C, Si or Ge and X = F, Cl, Br, I, CN, CCH, CP. Each Lewis base is a carbene carrying the group 14 atom from the first three rows of the Periodic Table. The gradients give the nucleophilicities of the non-bonding electron pair on M that lies along the C₂ axis and cyclo-(CH)₂M can be viewed as generated from (CH₃)₂M by removing four H atoms and linking the two CH groups that remain.

3.4. Reduced nucleophilicities of carbene molecules acting as Lewis bases

In an earlier article,²⁰ we showed that the gradient of a graph of −D_e/σ_min plotted against E_HX for a series of hydrogen-bonded complexes B⋯HX in which X varies but B is the same Lewis base defines a reduced nucleophilicity И_B = N_B/σ_min of B. The term ‘reduced’ is taken to mean that И_B is a property only of the atom of B that is directly involved in the B⋯HX hydrogen bonds, independent of the remainder of B. In this section, we examine whether the reduced nucleophilicity is a term that can also be applied to the carbenes discussed earlier. The appropriate graphs here are those in which −D_e/σ_axial is plotted against E_HX, where σ_axial is the value of the MESP along the C₂ axis of each carbene, given that the HX molecules (X = F, Cl, Br, I, CN, CCH, CP) lie along the C₂ axes when B = R₂M (M = Si, Ge, Sn; R = H, CH₃, F). The values of σ_axial calculated at the MP2/aug-cc-pVTZ level of theory are set out in Table 1. Graphs of −D_e/σ_axialversus E_HX are shown in Fig. 9 for the complexes B⋯HX (X = F, Cl, Br, I, CN, CCH, CP) in which B = H₂M, (CH₃)₂M or cyclo-(CH)₂M for each of M = Si, Ge and Sn. None of the F₂M complexes is included in Fig. 9 because, as already discussed, σ_axial is positive or near-zero for these, resulting in very small (sometimes even negative) D_e values because of repulsion between the adjacent regions of the positive MESPs of B and HX.

Table 1 Values of the MESPs σ_axial on the 0.001 e Bohr⁻³ iso-surface near atoms M on the C₂ symmetry axis of Lewis-base carbenes, as calculated at the MP2/aug-cc-pVTZ level

	σ axial/(kJ mol^−1)
Carbene	M = C	M = Si	M = Ge	M = Sn
H2M	−151.0	−65.9	−60.1	−41.4
F2M	−85.0	+1.5	+49.8	+86.1
(CH3)2M	−178.7	−101.0	−91.1	−65.9
cyclo-(CH)2M	−186.9	−46.2	−32.8	−1.8
H2C=C=M	−168.0	−20.2	−17.8	+6
cyclo-NHM	−204.0	−87.1	—	—

---

Fig. 9 Graphs of −D_e/σ_axialversus E_HX for the ten series of hydrogen-bonded complexes H₂M⋯HX, (CH₃)₂M⋯HX, cyclo-(CH)₂M⋯HX when M = C, Si, Ge or Sn, and X = F, Cl, Br, I, CN, CCH, CP. Each Lewis base molecule is a group 14 carbene. The gradients give the reduced nucleophilicities of the non-bonding electron pair on M, which lies on the C₂ axis.

It is clear from Fig. 9 that the ten straight lines of differing gradients previously generated in D_e/c versus E_HX graphs have become parallel and effectively conflated when D_e is divided by σ_axial. The lines are of almost equal gradient (except perhaps for that of H₂Sn⋯HX). Otherwise, all gradient values fall within two standard errors of the mean value 0.0417 (standard deviation = 16).

This provides strong evidence that И_B = N_B/σ_axial can indeed be described as a reduced nucleophilicity that is common to the Lewis bases involved, namely, H₂M, (CH₃)₂M and cyclo-(CH)₂M, where M = C, Si, Ge or Sn. It should be noted that not only are the quantities И_B = N_B/σ_axial from Fig. 9 independent of the groups attached to a given tetrel atom, but they also appear to be independent of the group 14 atom.

Some series do not appear in Fig. 9. The cyclic carbene cyclo-(CH)₂Sn has the very low value of σ_axial of −1.8 kJ mol⁻¹. Clearly, the quantity И_B = N_B/σ_axial increases rapidly as the σ_axial value approaches zero and becomes infinite when the σ_axial value reaches zero. The И_B value is therefore very sensitive to small errors in σ_axial, is unreliable close to the singularity and becomes negative after the singularity. For these reasons, members of the series F₂M⋯HX, in addition to cyclo-(CH)₂Sn⋯HX, have been excluded from Fig. 9. For (CH₃)₂C⋯HX (as indicated earlier), there is evidence of ionic character in several points, with only four available, and consequently they are not included in Fig. 9.

3.5. H₂C=C=M (M = C, Si, Ge) as carbene Lewis bases

The molecules H₂C=C=C, H₂C=C=Si and H₂C=C=Ge are isomers of cyclo-(CH)₂–M (M = C, Si, Ge). They too are singlet carbenes and have also been characterised via their microwave spectra [see ref. 36 and 37, respectively]. In this section, the nucleophilicities of H₂C=C=M when forming hydrogen bonds with the HX series are determined and their reduced nucleophilicities examined.

Questions that arise for the carbenes H₂C=C=M are (a) whether a reduced nucleophilicity can be assigned to these molecules, and, if so, (b) whether it is identical to those determined viaFig. 9? To answer these questions, plots of D_e/c versus E_HX for the hydrogen-bonded complexes H₂C=C=M⋯HX (M = C, Si or Ge and X = F, Cl, Br, I, CN, CCH, and CP) are displayed in Fig. 10. The series H₂C=C=Sn⋯HX is excluded because the Lewis base has a small positive σ_axial (See Table 1 and earlier discussion). Fig. 10 indicates clearly that the order of the nucleophilicities of the three carbenes is N_H2C=C=C ≫ N_H2C=C=Si ∼ N_H2C=C=Ge.

Fig. 10 Graphs of D_e/c versus E_HX for the series of hydrogen-bonded complexes H₂C=C=M⋯HX (M = C, Si or Ge; X = F, Cl, Br, I, CN, CCH, and CP). Each Lewis base molecule is a carbene. The gradients give the nucleophilicities of these carbenes when forming a hydrogen bond to the series of HX molecules.

It is immediately obvious from Fig. 11 that the division of the points in Fig. 10 by the appropriate σ_axial values from Table 1 conflates only two of the straight lines (those associated with M = Si and Ge) to give a single gradient. Accordingly, the gradients are now the reduced nucleophilicities И_B = N_B/σ_axial of the two Lewis bases B = H₂C=C=Si and H₂C=C=Ge and this quantity is a property that is common to the atoms Si and Ge. Their values И_B = 0.0586(26) and 0.0562(29) are identical within their standard errors and yield a mean of 0.0574(28). The value for H₂C=C=C is certainly not identical to those for M = Si and Ge as shown in Fig. 9. Perhaps, this result is to be expected, given that the environment of the all the group 14 atoms C, Si and Ge in the Lewis bases in Fig. 9 consists of two single bonds at an angle of ∼90–110 degrees and, when the HX molecules are included, is in a trigonal environment. On the other hand, in the H₂C=C=M molecules, the tetrel atom is in a diagonal environment, created by a double bond on one side and the HX molecule on the other side. The non-bonding pair on M is also in close contact with the π electrons in these molecules. It is not clear why the gradient for the H₂C=C=C⋯HX graph is different from those with M = Si or Ge, but perhaps there is a stronger interaction between the axial non-bonding electron pair of C and the π-electron system than occurs with Si or Ge. It is interesting to note, however, that the value И_H2C=C=C = 0.0353(13) is identical (within standard errors) with those values of 0.0349(17) and 0.0337(18) obtained³⁸ by similar means for hydrogen bonds to the C atoms in OC, SC, and SeC and HNC, CH₃NC, and FNC, respectively.

Fig. 11 Graphs of −D_e/σ_axialversus E_HX for the three series of hydrogen-bonded complexes H₂C=C=M⋯HX. (M = C, Si and Ge; X = F, Cl, Br, I, CN, CCH, and CP). Each Lewis base molecule carries a group 14 atom and is a singlet carbene. The gradients yield the reduced nucleophilicity associated with the tetrel atom M, which lies on the C₂ axis of each H₂C=C=M molecule.

3.6. Cyclo-(CH)₂(NH)₂M (M = C or Si) acting as Lewis bases in forming hydrogen bonds

N-heterocyclic carbenes and N-heterocyclic silylenes, having formulae cyclo-(CH)₂(NH)₂M (M = C or Si) (hereafter referred to as NHC and NHSi, respectively), have recently fulfilled an important role in organic chemistry.^39,40 The D_e values of hydrogen-bonded complexes NHC⋯HX and NHSi⋯HX formed by these two Lewis bases were therefore calculated at the same CCSD(T)(F12c)/cc-pVDZ-F12 level of theory as other systems discussed here. The resulting graphs of D_e/c and −D_e/σ_axialversus E_HX are shown in Fig. 12 and 13, respectively. Each of NHC and NHSi has a C₂ symmetry axis, as do all other Lewis bases discussed in this article, and a high value of the MESP on the C₂ axis, favouring the geometry of NHM⋯HX complexes of the type illustrated in Fig. 12 and 13.

Fig. 12 D _e/c versus E_HX for the complexes cyclo-(CH)₂(NH)₂M⋯HX (M = C and Si; X = F, Cl, Br, I, CN, CCH, and CP).

Fig. 13 −D_e/σ_axialversus E_HX for the complexes cyclo-(CH)₂(NH)₂M⋯HX (M = C and Si; X = F, Cl, Br, I, CN, CCH, and CP).

Fig. 12 reveals that the nucleophilicity of the NHC molecule is three times that of its Si analogue, a ratio that is higher than that observed for other R₂M⋯HX series. Fig. 13 leads to the reduced nucleophilicities of 0.0388(11) for NHSi⋯HX and the higher value of 0.0483(9) for NHC⋯HX, indicating that the conflation of values is not as good as those reported in Fig. 9. The first value of the gradient И_NHSi falls within two standard errors of the mean of those in Fig. 9, but that for NHC⋯HX is somewhat higher. Whether it is significantly higher is not immediately clear and caution is necessary. First, there are only four different HX molecules involved, instead of the normal seven and moreover two of these points are essentially identical. Second, the small data set probably means that the standard error for И_NHC is too low. It is noted that there is a range of ∼0.01 in the И_B values as shown in Fig. 9.

4. Discussion and conclusions

The nucleophilicities N_B of several simple carbenes acting as Lewis bases B, namely H₂M, F₂M, (CH₃)₂M, cyclo-(CH)₂M, H₂C=C=M (M is one of the tetrel atoms C, Si, Ge, or Sn) and cyclo-(CH)₂(NH)₂M (M = C or Si only), have been reported in this article. According to eqn (1), graphs of D_e/c versus E_HX (the numerical electrophilicity of HX) for the series of hydrogen-bonded complexes B⋯HX (X = F, Cl, Br, I, CN, CCH, CP) are straight lines through the origin, having gradients N_B. All but one (the prototype H₂C) of the carbenes investigated possess a singlet electronic ground state, but H₂C was calculated ab initio as a singlet and was therefore not the electronic ground state molecule. Its properties were consistent with those of the others examined. The equilibrium dissociation energies D_e of the hydrogen-bonded complexes (each having a C₂ axis of symmetry) were calculated ab initio at the CCSD(T)(F12c)/cc-pVDZ-F12 level.

The results for the nucleophilicities are summarized in Table 2. These measure the propensity of the tetrel atoms involved to engage in hydrogen bonding to HX molecules. It is noted that for a given tetrel atom M, the order of the nucleophilicities for the R₂M carbenes is as follows: (CH₃)₂M > H₂M > F₂M, a result consistent with the accepted order of the inductive effects of the groups CH₃, H and F. The order across the (CH₃)₂M row in Table 2 is M = C ≫ Si ∼ Ge ∼ Sn; there are indications in the other R₂M rows that this is also true, even though the remaining rows are incomplete. The entries in Table 2 for cyclo-(CH)₂M and H₂C=C=M, respectively, reveal a similar pattern, while, for a given M, the nucleophilicity of the carbene for cyclo-(CH)₂M is greater than that of H₂C=C=M. Evidently, in passing from row 1 to row 2 of the Periodic Table, there is a large drop in the nucleophilicity of the tetrel atom in these carbenes, but the changes from rows 2 to 3 to 4 are much smaller. (CH₃)₂M has the largest nucleophilicity for a given M, followed by cyclo-(CH)₂M and H₂C=C=M. It has also been demonstrated that the carbenes investigated here exhibit the phenomenon of reduced nucleophilicity when each point on the straight line from the D_eversus E_HX plot is divided by the value of the MESP on the 0.001 e Bohr⁻³ iso-surface on the C₂ symmetry axis at the tetrel atom. In the present example, it appears that the reduced nucleophilicity is independent not only of the tetrel atom that participates in the hydrogen bond, but also of the remainder of the carbene molecule, at least for the R₂M and cyclo-(CH)₂M, which have a mean value И_B of 0.0417(16). This seems not to be the case for the H₂C=C=M carbenes which have the somewhat larger value of 0.0530(26) (based on only the Si and Ge values, however). H₂C=C=C is different. See Fig. 11 and associated discussion.

Table 2 Nucleophilicities for various Lewis-base carbenes B containing the tetrel atoms C, Si. Ge and Sn, as determined from the dissociation energies D_e of a series of hydrogen-bonded complexes B⋯HX (X = F, Cl, Br, I, CN, CCH, and CP)

Carbenes	M = C	M = Si	M = Ge	M = Sn^a
a As indicated in Table 1, the axial MESPs of the Sn-based carbenes discussed are low or even positive and as a result precluded the analysis being applied to complexes involving F2Sn, cyclo-(CH)2Sn and H2C=C=Sn. b All carbenes in this table have a singlet electronic ground state, except H2C which has a triplet ground state. The excited singlet state of H2C was that calculated ab initio and employed here. c Missing values in this column arise because of a repulsive interaction of a positive MESP at Sn on the C2 axis and the electrophilic H of HX. This leads to a distortion of results.
H2M	6.36(12)^b	2.71(7)	2.35(7)	1.99(7)
F2M	3.39(26)	0.93(11)	−0.39(2)^c	—
(CH3)2M	9.41(22)	4.05(18)	3.44(9)	2.89(16)
cyclo-(CH)2M	7.71(20)	2.02(5)	1.37(6)	—
H2C=C=M	5.93(22)	1.19(5)	0.90(5)	—
cyclo-NHM	9.86(18)	3.38(9)	—	—

---

A further property of interest in connection with the reduced nucleophilicity И_B of a Lewis base B, such as the H₂M discussed here, and its counterpart the reduced electrophilicity Ξ_HX of a Lewis acid is that they provide a route to the dissociation energy D_e from the properties of the separate component molecules. It was shown in ref. 21 that

D_e = {σ_max(HX)·σ_min(B)}·И_B·Ξ_HX (2)

To illustrate the use of eqn (2) in this context, Fig. 14 shows a graph of D_e values (as calculated by eqn (2)) plotted against the ab initio calculated values of D_e for 49 complexes H₂M⋯HX, (CH₃)₂M⋯HX, where M = C, Si, Ge and Sn. The F₂M⋯HX were excluded for reasons already discussed, as were the (CH₃)₂C⋯HX because only 4 points are available in Fig. 6 and there is a large intercept on the D_e/c axis. The mean value of И_B = 0.0417 for the 10 carbenes involved in Fig. 9 was used, while the Ξ_HX values are those listed in Table 2 of ref. 21.

Fig. 14 Graph of D_e values calculated by eqn (2) for the complexes R₂M⋯HX (R = H, CH₃; M = C, Si, Ge, Sn; X = F, Cl, Br, I, CN, CCH, CP) versus D_e values calculated ab initio at the CCSD(T)F12C/cc-pVDZ-F12 level.

Finally, the series of complexes H₂C⋯HX have been a part of the main investigation, even though the electronic ground state of H₂C is a triplet. However, the ab initio calculation for H₂C referred to the closed shell version, that is the electronic singlet state, which is higher in energy than the triplet. The value of σ_axial for singlet H₂C is in Table 1. Fig. 9 establishes unambiguously that for singlet H₂C the value of the reduced nucleophilicity is И_B = 0.0421(11), which is identical with the mean 0.0417(16) of the 10 values available from Fig. 9. This seems reasonable, as all the carbene molecules in Fig. 9 have singlet electronic ground states, even though all have different electronic energies.

Data availability

Some of the material associated with this article is made available in the ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

IA thanks the Ministerio de Ciencia, Innovación y Universidades (PID2021-125207NB-C32) for a grant of financial support and ACL is pleased to acknowledge the University of Bristol for the award of a University Senior Research Fellowship and for the award of an account on the Blue Pebble HPC.

References

1. R. A. Moss and M. P. Dyle, Contemporary Carbene Chemistry, (Volume 7 of the Wiley Series of Reactive Intermediates in Chemistry and Biology), 2013.
2. Y. Mizuhata, T. Sasamori and N. Takitoh, Chem. Rev., 2009, 109, 3479–3511.
3. J. A. Pople, Chem. Phys. Lett., 1986, 132, 141–146.
4. A. J. Arduengo, S. F. Gamper, M. Tamm, J. C. Calabrese, F. Davidson and H. A. Craig, J. Am. Chem. Soc., 1995, 117, 572–573.
5. I. Alkorta and J. Elguero, J. Phys. Chem., 1996, 100, 19367–19370.
6. M. Jabłoński and M. Palusiak, Phys. Chem. Chem. Phys., 2009, 11, 5711–5719.
7. P. Costa and W. Sander, Angew. Chem., Int. Ed., 2014, 5, 5122–5125.
8. J. M. Standard, J. Phys. Chem. A, 2017, 121, 381–393.
9. J. E. Del Bene, I. Alkorta and J. Elguero, Chem. Phys. Lett., 2017, 675, 46–50.
10. M. Jabłoński, Molecules, 2022, 27, 5712.
11. C. H. Bauschlicher, H. F. Schaefer III and P. S. Bagus, J. Am. Chem. Soc., 1977, 99, 7106–7110.
12. C.-H. Hu, Chem. Phys. Lett., 1999, 309, 81–89.
13. P. Politzer, J. S. Murray, T. Clark and G. Resnati, Phys. Chem. Chem. Phys., 2017, 19, 32166–32178.
14. A. C. Legon, Phys. Chem. Chem. Phys., 2014, 16, 12415–12421 ( See also Phys. Chem. Chem. Phys. , 2014 , 16 , 25199 ) , for correction.
15. I. Alkorta and A. C. Legon, Molecules, 2017, 22, 1786–1799.
16. I. Alkorta and A. C. Legon, Chem. Phys. Lett., 2023, 833, 140929.
17. I. Alkorta and A. C. Legon, ChemPlusChem, 2024, 89, e202400314.
18. I. Alkorta and A. C. Legon, ChemPlusChem, 2021, 86, 778–784.
19. I. Alkorta and A. C. Legon, J. Phys. Chem. A, 2024, 128, 5963–5968.
20. I. Alkorta and A. C. Legon, Phys. Chem. Chem. Phys., 2022, 24, 25822–25833.
21. I. Alkorta and A. C. Legon, J. Phys. Chem. A, 2023, 127, 4715–4723.
22. C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102.
23. C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74.
24. J. G. Hill and K. A. Peterson, J. Chem. Phys., 2014, 141, 094106.
25. T. B. Alder, G. Knizia and H. J. Werner, J. Chem. Phys., 2007, 127, 221106.
26. M. K. Kesharwani, N. Sylvetsky, A. Köhn, D. P. Tew and J. M. L. Martin, J. Chem. Phys., 2018, 149, 154109.
27. H. Kruse, R. Szabia and J. Šponer, J. Chem. Phys., 2020, 152, 214104.
28. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
29. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16, Revision, A.03, Gaussian, Inc., Wallingford, CT, USA, 2016.
31. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
32. Jmol: an open-source Java viewer for chemical structures in 3D, https://www.jmol.org.
33. I. Alkorta and A. C. Legon, Phys. Chem. Chem. Phys., 2022, 24, 12804–12807.
34. M. S. Schuurman, J. Giegerich, D. Lang, B. Kiendl, K. Pachner, R. J. MacDonell, A. Krüger and I. Fischer, Chem. – Eur. J., 2015, 21, 14486–14495.
35. J. M. Vrtilek, C. A. Gottlieb and P. Thaddeus, Astrophys. J., 1987, 314, 716–725.
36. M. C. McCarthy and P. Thaddeus, J. Mol. Spectrosc., 2002, 211, 235–240.
37. M. C. McCarthy and P. Thaddeus, J. Mol. Spectrosc., 2002, 211, 228–234.
38. I. Alkorta and A. C. Legon, ChemPlusChem, 2023, 88, e202300032.
39. N-Heterocyclic Carbenes, ed. S. P. Nolan, 2014, Wiley-VCH, Verlag GmbH & Co.
40. M. Haaf, T. A. Schmedake and R. West, Acc. Chem. Res., 2000, 33, 704–714.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03894k

---