A theoretical study of the molecular passivation of p-/n-type defects on tin- and germanium-mixed perovskite surfaces using Lewis base/acid

Abstract

Perovskite solar cells have been attracting considerable attention because of their high power conversion efficiency (PCE). However, their efficiency is compromised by the defect sites on the perovskite surfaces, where charge carriers (excitons) are trapped and recombined. In this study, based on the density functional theory method, we theoretically explore a molecular passivation process for coating a perovskite surface to reduce the defect concentration. This study focuses on Pb-free perovskite materials, such as MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃ (MA = CH₃NH₃), employing ethylenediamine and iodopentafluorobenzene as excellent passivation molecules. Our theoretical calculations show that the adsorption of these passivation molecules on the Pb-free perovskite surfaces could remove defect energy levels from the bandgap. Particularly, we discuss the effectiveness of a Lewis base to reduce deep defect levels for a Sn–Ge-mixed perovskite. Furthermore, we present a molecule-defect-level interaction model to understand the passivation mechanism, focusing on the chemical effects of Lewis bases/acids.

---

1. Introduction

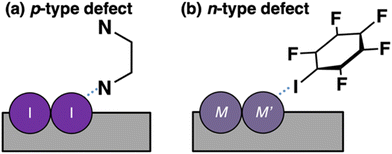
Recently, perovskite solar cells have been attracting considerable research interest because of their high power conversion efficiency (PCE), low production cost, lightweight, and flexibility.^1–3 Notably, Pb-based perovskite solar cells with high PCEs of over 20% have been reported, and further studies have been focusing on promoting their industrial applications.⁴ Conversely, due to the toxicity of Pb, Pb-free perovskites have been actively studied.^5–12 A perovskite crystal has the general form ABX₃, where A, B, and X represent a (organic) cation, (metal) cation, and halide anion, respectively. Sn and Ge have been explored as potential candidates for replacing Pb in the B site. Moreover, Pb-free perovskite solar cells have a considerable room for improvement in terms of their PCEs. This study focuses on Sn- and Ge-based perovskite materials.

To improve the PCE of solar cell devices, controlling the defects in perovskite materials is indispensable because defect sites trap excitons, promoting electron–hole recombination. Particularly, deep-level defects, whose energy levels are located near the center of the bandgap, work as efficient recombination sites and largely compromise the PCE of solar cell devices.^13–18 Furthermore, compared with the defects in the bulk, the defects at the interface between the perovskite layer and the electrode cause large PCE losses.¹⁹ Therefore, reducing the concentration of deep-level defects on the perovskite surfaces is critical for achieving a high PCE. For this purpose, molecular passivation is frequently employed, where a perovskite surface is coated with small molecules during device fabrication.^20–31 For this process, various types of molecules, such as acetylacetone, fullerene and its derivatives, pyridine, ethylenediamine (EDA), and iodopentafluorobenzene (IPFB), have been experimentally employed.^{10,20,21,30,32} In our previous study, we explored the molecular passivation mechanism of a Sn-based perovskite surface and reported that Lewis base (acid) molecules are effective for p-type (n-type) surface defects. To explain the passivation mechanism, we presented a molecule-defect-level interaction model, focusing on the interactions between the surface defect and the molecular orbital.³³

Notably, Ge doping has been actively studied for improving the properties of Sn-based perovskite materials.^34–36 Correspondingly, this study investigates the molecular passivation of perovskites containing Ge, such as MAGeI₃ and MASn_0.5Ge_0.5I₃, and compares the results with those for MASnI₃ (MA = CH₃NH₃). At present, various Ge dopant concentrations have been experimentally examined to improve the PCE of Sn-based perovskite solar cells, but it is difficult to precisely perform simulations for all of them. Thus, we present calculation results for a Ge-based perovskite to consider materials with high Ge dopant concentrations. Furthermore, we attempt to explain the molecular passivation process using the molecule-defect-level interaction model, evaluating the similarities and differences between Sn-based and Ge-based perovskites. Particularly, this study will show the effect of a Lewis base for not only Sn/Ge-based but also Sn–Ge-mixed perovskites on the removal of surface defect levels.

A variety of perovskite materials have been obtained through modifications of the ABX₃ perovskite structure with molecules, elements, and halogens. For example, the replacement of the A- and X-site elements with methylammonium, formamidinium or Cs and I, Br or Cl has been explored for solar cell materials. Thus, attempts to improve perovskites will lead to continuous development and modifications with materials of varying compositions. Correspondingly, it would be inefficient to explore optimal passivation molecules for various perovskite materials individually, underscoring the need for a transversal understanding of the molecular passivation mechanism. Our calculation results and discussions will provide insights for evaluating various types of perovskite materials.

In the following section, we explain the computational methodology, presenting perovskite surface models with a point defect. In Section 3.1, we discuss an approach for recognizing important surface defects that largely compromise the PCE of solar cells, considering both the defect formation energy and the defect level. From the computational results, we focus on V_Sn and I_Sn defects as p-type defects and MA_I as the n-type defect. In Section 3.2, we discuss the passivation mechanism against the p-type defects, achieved through the adsorption of EDA on MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃. In Section 3.3, we present the results of IPFB passivation against the n-type defect. Finally, we provide a summary in Section 4.

2. Computational models and method

We performed geometry optimization calculations to construct surface defect models and determined the structures of the passivation molecules adsorbed on surfaces using the density functional theory (DFT) method. Thereafter, we calculated the defect formation energy, adsorption energy, and density of states (DOSs) using single-point calculations for detailed analysis. We investigated several perovskites with different compositions, including MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃. For MASn_0.5Ge_0.5I₃, we employed a NaCl-like structure for the Sn and Ge geometrical compositions. For these perovskite materials, we prepared 2 × 2 × 3 slab surface models with the plane direction of (001), terminated by the SnI₂, GeI₂, or Sn_0.5Ge_0.5I₂ layer (Fig. 1). Conversely, the importance of I-MA termination has been addressed.³⁷ The calculation results using the I-MA-terminated models are provided in the ESI.†

Fig. 1 Clean surface model of the MASn_0.5Ge_0.5I₃ perovskite. Here, we employed 2 × 2 × 3 slab surface models with a plane direction of (001), terminated by the Sn_0.5Ge_0.5I₂ layer. For MASnI₃ (MAGeI₃), a similar clean surface model was adopted, terminated by SnI₂ (GeI₂).

Surface defect states such as density and type are not understood enough for the Sn-based perovskites, although those yield a large negative impact on the PCE of solar cell devices. Surfaces with high defect densities can have a significant negative impact on the PCE. The surface models used in this study may be considered a case where defects densely exist. In this study, we will discuss that the molecular passivation technique is effective in improving the PCE of Sn–Ge-mixed perovskites even against such situations.

For the DFT calculations, we employed the projector-augmented wave method with the pseudopotential approach,^38,39 using the Perdew–Burke–Ernzerhof functional⁴⁰ with Grimme's dispersion correction (D3).⁴¹ We adopted an energy cut-off of 450 eV and employed the k-point sampling of 2 × 2 × 1 based on the Monkhorst–Pack method⁴² for the optimization calculations. The k-point samplings of 4 × 4 × 1 and 5 × 5 × 1 with the Γ-centered mesh were employed for single-point and DOS calculations, respectively. Perovskites discussed in this study are not magnetic materials and the spin polarized calculation condition is not considered. All calculations were executed using the Vienna Ab initio Simulation Package 5.4.4.^43,44

3. Results and discussion

3.1. Important defects on the Sn-, Ge-based and mixed perovskite surfaces

To distinguish important surface defects that severely compromise the PCE of solar cells, we considered the defect formation energy in addition to the defect level. Here, the defect formation energy was employed to indicate whether the target defect is easily generated on the perovskite surface. We calculated the defect formation energy of 42 surface models with a point defect, considering 12 models for MASnI₃ (MAGeI₃) and 18 models for MASn_0.5Ge_0.5I₃. As point defects, we employed vacancy (V_X), interstitial (X_i), and substitution (Y_X) defects on perovskite surfaces with MA, Sn, Ge, I, and their combinations. These components (elements) are removed, added, or substituted with the neural charge state from the clean (pristine) surface models without defects. The clean perovskite surfaces are neutral, and hence the defect surfaces also become neutral. For the V_Sn model, an Sn atom is removed from the pristine perovskite surface.

The defect formation energy depends on the experimental conditions. To handle complicated experimental conditions theoretically, the chemical potential concept has been widely employed.^45,46 We describe the detailed procedure in the ESI,† where the chemical potentials of MA, Sn(Ge), and I are considered using phase diagrams. We examined three chemical potential conditions: Sn-rich (Ge-rich), I-rich, and moderate. In Table 1, we show the defect formation energies under which the most stable energies are achieved among these chemical potential conditions. Additionally, we show all the defect formation energies observed under these chemical conditions in the ESI.† From these calculations, we confirmed that p-type defects are more easily generated on the perovskite surface than n-type defects. Here, p-type defects are those with no electrons in the defect level, whereas the n-type defect possesses electrons in the defect level. Particularly, the generation of p-type surface defects of V_M, I_M, and MA_M on perovskite surfaces is energetically favorable, regardless of the Sn or Ge composition (here, “M” represents Sn or Ge). For example, the defect formation energies of V_Sn in MASnI₃ and MASn_0.5Ge_0.5I₃ are −0.21 and −0.02 eV, respectively. Formation energies of −0.16 and 0.02 eV are obtained for V_Ge on MAGeI₃ and MASn_0.5Ge_0.5I₃, respectively.

Table 1 Stable defect formation energies [eV] of MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃ under several chemical potential conditions

		MASnI3	MAGeI3	MASn0.5Ge0.5I3
p-type	VMA	0.60	0.86	0.80
	VSn	−0.21		−0.02
	VGe		−0.16	0.02
	Ii	0.02	0.34	0.21
	MASn	−0.44		0.12
	MAGe		0.20	−0.28
	IMA	1.58	1.20	1.85
	ISn	−0.06		0.16
	IGe		0.28	0.07
n-type	VI	0.84	1.12	1.13
	MAi	0.24	0.75	0.54
	Sni	1.32		1.71
	Gei		1.47	1.56
	MAI	0.69	1.15	1.22
	SnMA	1.68		1.56
	GeMA		1.77	1.94
	SnI	1.72		2.54
	GeI		2.18	2.35

---

Next, we consider the defect level to distinguish important surface defects. If the defect energy level is located between the valence band maximum (VBM) and the conduction band minimum, the defect behaves like an efficient recombination site and significantly compromises the PCE. We confirmed that the defect energy levels of V_M and I_M are located within the bandgap. Thus, we recognized eight p-type surface defects as particularly important: V_Sn and I_Sn for MASnI₃; V_Ge and I_Ge for MAGeI₃; and V_Sn, V_Ge, I_Sn, and I_Ge for MASn_0.5Ge_0.5I₃ (Fig. 2). In addition, by comparing these simulation results, we observed that similar defect structures are obtained, regardless of the Sn or Ge composition. However, this trend may be slightly different from those for Pb-based perovskites. Studies have shown that relatively shallow surface defects of I_MA, I_Pb, Pb_i, V_I, and Pb_I are easily generated on the Pb-based perovskite surface.^45,47 In this study, we discuss the Ge dopant effect for a Sn-based perovskite and hence pay attention to the MASn_0.5Ge_0.5I₃ model. For the Sn–Ge-mixed perovskite, the defect formation energies of −0.02 and 0.52 are obtained for the V_Sn defect on the Sn_0.5Ge_0.5I₂ and I-MA terminated surfaces, respectively. In addition, defect levels with the low formation energy are shallow or are not in the bandgap on the I-MA terminated surface. For example, V_Sn on the I-MA terminated surface does not have the defect level within the bandgap, although it has a deep defect level on the Sn_0.5Ge_0.5I₂ terminated surface. This tendency can be observed for other surface defects. This study discusses the removal of (deep) defect levels from the bandgap based on the molecular passivation technique. Thus, this study mainly discusses the Sn_0.5Ge_0.5I₂ terminated surface. We will show molecular passivation calculations next.

Fig. 2 Top view of the (a) p-type defects of V_M and I_M (M = Sn or Ge) on MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃ and the (b) n-type defect of MA_I on MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃.

3.2. Ethylenediamine (Lewis base) passivation against p-type surface defects

In this section, we discuss the passivation process against V_M and I_M surface defects, considering eight surface defect models for MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃. Here, EDA is examined as a passivation molecule, because the effectiveness of EDA passivation is experimentally confirmed for Sn–Ge-mixed perovskite solar cells. The geometrically optimized structures with EDA of these models are shown in Fig. 3. All EDA adsorptions on these surface defects are energetically favorable. For example, the EDA adsorption energy against V_Sn on MASnI₃ is −1.08 eV, and that against V_Ge on MAGeI₃ is −0.91 eV. Similarly, the adsorption energies against V_Sn and V_Ge on MASn_0.5Ge_0.5I₃ are −1.79 and −1.10 eV, respectively. Here, EDA has a monodentate structure, where a nitrogen atom is coordinated with the iodine atom on the perovskite surface for both V_M and I_M defects, regardless of the Sn or Ge composition.

Fig. 3 Passivated surface models with p-type defects of V_M and I_M (M = Sn or Ge) on (a) MASnI₃, (b) MAGeI₃, and (c) MASn_0.5Ge_0.5I₃. The adsorption energy of EDA is described below the label of each model. A schematic illustration of these models is also shown in Fig. 5a.

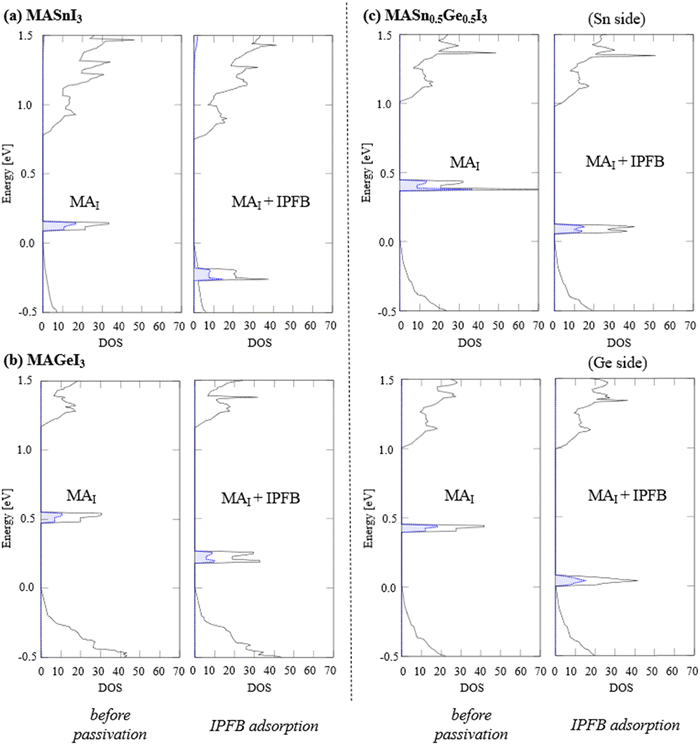
To investigate the molecular passivation mechanism, we present the DOSs of the surface defects of V_M before and after the EDA adsorption (passivation) in Fig. 4. The DOSs of I_M before and after the EDA adsorption are shown in the ESI.† The projected DOS (pDOS) for the I atoms around the defect site is also depicted with a filled red line. Here, the VBM energy of each system serves as the energy reference. Before the EDA adsorption, we confirmed that defect levels are located within the bandgap, mainly originating from the I atoms. In addition, we found that two I atoms form a dimer-like structure of I₂, as schematically illustrated in Fig. 5a. A similar dimer structure is observed on the Pb-based perovskite surfaces.¹³ These calculation results highlight the influence of surface halogens on p-type defects. After the EDA passivation, we confirmed that the defect levels were removed from the bandgap, as shown in Fig. 4. For the Sn-based perovskite, we have already demonstrated that the EDA passivation is effective against p-type defects, such as V_Sn and I_Sn.³³ In this study, we showed that the EDA passivation is also useful for p-type defects on MAGeI₃ and MASn_0.5Ge_0.5I₃. In the passivation process, EDA mainly interacts with the I site; consequently, we may observe similar passivation effects.

Fig. 4 The density of states (DOSs) before and after the EDA passivation (adsorption) against the p-type defect of V_M on (a) MASnI₃, (b) MAGeI₃, and (c) MASn_0.5Ge_0.5I₃. Here, the valence band maximum (VBM) energy of each system is adopted as the energy reference. The total DOS is depicted by the black line, and the pDOSs for the surface I atoms are drawn with the red dashed line.

Fig. 5 Schematic illustration of the (a) passivation mechanism against p-type defects using EDA and (b) against n-type defects using IPFB. For the p-type defect, EDA interacts with the I₂ dimer-like structure. For the n-type defect, IPFB interacts with the Sn–Sn, Ge–Ge, and Sn–Ge structures (M, M′ = Sn or Ge).

To elucidate the interaction between EDA and surface defects, we show the electron densities before and after the EDA adsorption. Fig. 6 shows the electron densities of each defect level at the Γ point. To determine the defect levels, we focus on the electron density localized around the defect sites. Before the EDA passivation (adsorption), the defect level is localized around I dimer atoms, which is consistent with the pDOS calculations without EDA (see Fig. 4). Conversely, the EDA adsorption significantly modifies the surface state. The hybridization with the highest occupied molecular orbital (HOMO) of EDA leads to a significant modification of the surface defect state. Furthermore, we observed significant changes in the HOMO of EDA before and after the molecular passivation, based on the pDOSs. These results demonstrate the importance of the interaction between the HOMO of EDA and the surface I atoms. To consider the interaction between the passivation molecule and the surface defect, it may be useful to pay attention to the energy difference between the HOMO energy of the passivation molecule and the defect level. For example, the energy difference of 0.20 (0.11) eV is obtained between the HOMO of EDA and the V_Ge defect level for MASn_0.5Ge_0.5I₃ (MAGeI₃). An energy difference of 0.27 (0.32) eV is calculated for V_Sn on MASn_0.5Ge_0.5I₃ (MASnI₃). Thus, such a small energy difference between the HOMO energy and the defect level leads to strong hybridization, and the defect level is removed from the bandgap.

Fig. 6 The electron density of the p-type defect of V_M before and after the EDA passivation (adsorption) on (a) MASnI₃, (b) MAGeI₃, and (c) MASn_0.5Ge_0.5I₃. (d) The electron densities of the HOMO and LUMO of EDA. The HOMO of EDA mainly contributes to the removal of p-type defect levels through interactions with surface defect states.

For the Sn-based perovskite, we have proposed a molecular-defect-level interaction concept to explain the removal of the surface defect. The passivation mechanism for the p-type defects is shown in Fig. 7a. In the p-type defect, there are no electrons; instead, the defect state is occupied by holes. In such a situation, the HOMO of the passivation molecule can more strongly interact with the defect state, donating an electron pair toward the p-type surface defect. In other words, the passivation molecule can work as a Lewis base. Our calculations demonstrated that the molecular-defect-level interaction concept is useful for various perovskite materials, including those containing Ge as a dopant. Thus, we discussed that p-type defects tend to be generated more easily on not only the Sn/Ge-based but also Sn–Ge-mixed perovskite surface, and hence the Lewis base can effectively work to remove p-type defect levels. In the next section, we discuss the Lewis-acid case against the n-type defect.

Fig. 7 Schematic diagram of the molecular passivation using the Lewis base and acid against (a) p-type and (b) n-type defects, respectively.

3.3. Iodopentafluorobenzene (Lewis acid) passivation against n-type surface defects

Here, we focus on the n-type surface defect, which is less easily generated on the perovskite surfaces compared with p-type defects. We previously investigated the passivation mechanism against MA_I on MASnI₃ and reported that the IPFB molecule is useful for removing the defect level from the bandgap, although EDA was not satisfactorily effective.³³ The effectiveness of IPFB passivation is confirmed to improve the PCE of the Sn–Ge-mixed perovskite solar cell devices. Here, IPFB behaves as a Lewis acid against the n-type defect. We describe the passivation process using IPFB against MA_I on MASn_0.5Ge_0.5I₃ and MAGeI₃ and compare the results with those for MASnI₃. In Fig. 2b, we show the MA_I defect structures on MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃. We observe that two Sn/Ge atom pairs are in proximity and are lifted from the surface (see Fig. 5b). The Sn–Sn(Ge–Ge) pair is formed on MASnI₃ (MAGeI₃) and the Sn–Ge pair on MASn_0.5Ge_0.5I₃. Several research groups have reported similar dimer-like structures observed on the Pb/Sn-based perovskite surface.^13,16–18

In Fig. 8, we show the IPFB-passivated surface structures. For MASnI₃ (MAGeI₃), IPFB adsorbs on the Sn(Ge) atom of the Sn–Sn(Ge–Ge) pair lifted from the perovskite surface. For MASn_0.5Ge_0.5I₃, either the Sn or Ge atom of the Sn–Ge pair becomes the adsorption site. The adsorptions of IPFB are energetically favorable, regardless of the Ge composition; adsorption energies of −0.88 and −0.67 eV are obtained for MASnI₃ and MAGeI₃, respectively. For MASn_0.5Ge_0.5I₃, −0.55 and −0.67 eV are obtained for the Sn and Ge site, respectively.

Fig. 8 Surface structures passivated with an IPFB molecule against the n-type defect of MAI on (a) MASnI₃, (b) MAGeI₃, and (c) MASn_0.5Ge_0.5I₃. The IPFB molecule adsorbs on the Sn or Ge site lifted from the surface. For MASn_0.5Ge_0.5I₃, we show the IPFB adsorptions on both of the Sn and Ge sites. The adsorption energy of IPFB is described below the label of each model. The schematic surface structure for these models is shown in Fig. 5b.

We summarize the DOS analyses before and after the IPFB passivation in Fig. 9. The black solid line depicts the total DOSs, and the filled blue dashed line indicates the pDOSs of the Sn/Ge atoms located on the perovskite surface. Here, the VBM of each system is employed as the energy reference. From these pDOS and electron density analyses, it is evident that the Sn/Ge atoms around the defect site mainly contribute to the MA_I defect level. Fig. 10 shows the electron density of the defect level at the Γ point before and after the IPFB passivation. Before the IPFB passivation (adsorption), the defect level is localized around the Sn/Ge atoms, which is consistent with the pDOS results (Fig. 9). After the IPFB adsorption (passivation) on the perovskite surfaces, the defect levels are tuned by shifting downward, where the lowest unoccupied molecular orbital (LUMO) of IPFB interacts with the defect sites. These results suggest that the interaction between the LUMO of IPFB and the defect state is essential for removing the n-type defect level from the bandgap. Here, we discuss the several effects exerted by the Ge component. For MASnI₃, the defect level is completely removed by the IPFB passivation. Conversely, for MAGeI₃ and MASn_0.5Ge_0.5I₃, the defect levels are still located within the bandgap, although those are improved by the IPFB passivation. These behaviors may be due to the bandgap differences of each material. The Ge composition slightly widens the bandgaps; for example, bandgaps of 0.71, 0.79, and 1.05 eV are obtained for clean surfaces of MASnI₃, MASn0_.5Ge_0.5I₃, and MAGeI₃, respectively. Therefore, the defect level may not have been pushed completely outside the bandgap in the Ge-containing materials. Moreover, the interaction with IPFB may also be different on the Sn and Ge sites.

Fig. 9 The density of states (DOSs) before and after the IPFB passivation (adsorption) against the n-type defect of MA_I on (a) MASnI₃, (b) MAGeI₃, and (c) MASn_0.5Ge_0.5I₃. Here, the valence band maximum (VBM) energy of each system is adopted as the energy reference. The total DOS is depicted by the black line, and the pDOSs for Sn and Ge are drawn with blue-dashed lines.

Fig. 10 The electron density of the defect level before and after the IPFB passivation (adsorption) against MA_I on (a) MASnI₃, (b) MAGeI₃, and (c) MASn_0.5Ge_0.5I₃. (d) The electron density of the HOMO and the LUMO of IPFB. The LUMO of IPFB mainly contributes to the removal of n-type defect levels through interactions with the surface defect states.

The passivation mechanism against the n-type surface defect may be explained using the molecule-defect-level interaction model in Fig. 7b. For the n-type defect, electrons exist in the defect site. Therefore, the LUMO of the passivation molecule can more easily interact with the n-type defect site. In other words, Lewis acids become effective for passivation against n-type defects. Conversely, the molecule-defect-level interaction model may be oversimplified to handle realistic surfaces. For example, understanding the overall interaction mechanism between the defect state and the orbital of the passivation molecule is important for effective passivation. However, a simple concept may be required to understand the passivation mechanism for various types of perovskites. The calculation results and discussion in this study will facilitate the exploration of passivation molecules against surface defects.

4. Conclusion

We discussed the molecular passivation effect of Lewis acids/bases on MASnI₃, MAGeI₃, and MASn_0.5Ge_0.5I₃ using the DFT method. Defect-formation-energy calculations showed that p-type surface defects are more easily generated on perovskite surfaces than n-type defects. This trend was observed for all surface models examined in this study, regardless of the Ge composition. Notably, we focused on V_Sn and I_Sn as p-type defects and MA_I as the n-type surface defect because they are easily generated with their defect levels lying within the bandgap.

To remove the defect level from the bandgap, we examined the passivation process of the p-type and n-type defects using EDA and IPFB molecules, respectively. For the p-type surface defects such as V_Sn and I_Sn, I atoms mainly contributed to the surface defect state. In the passivation process, EDA was adsorbed on the I (dimer-like) site, and it successfully removed the defect level from the bandgap. Thus, the I site became the main target in the p-type defect case. The experiments also revealed the effectiveness of EDA as a passivation molecule against Sn-based perovskites, aligning with our calculation results. For the n-type surface defect, the defect level was due to surface Sn(Ge) atom pairs. Thus, the Sn(Ge) site became the main target for the molecular passivation, and the IPFB passivation on the Sn(Ge) site proved effective for reducing the concentration of surface defects. To consider the passivation process, we presented a molecule-defect-level interaction concept. Therein, the interaction between the passivation molecule and the surface defect state was highlighted, focusing on the energy difference (match) between the molecular orbital and the surface state. Based on this concept, we also discussed the Lewis base (acid) passivation against the p-type (n-type) surface defect.

Perovskites exhibit high adaptability; consequently, various perovskite materials have been developed by replacing the constituent components with elements/molecules or introducing dopants. Particularly, based on the molecule-defect-level interaction model, we explained that a Lewis base can effectively remove p-type defect levels on the Sn–Ge-mixed perovskite surface as well as the Sn/Ge-based surface. The interaction model will be useful for comprehensively considering the passivation mechanism of various types of perovskites. We believe that our computational results and discussion will provide valuable insights for improving perovskite materials through molecular passivation.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is partly supported by Grant-in-Aid for Scientific Research (KAKENHI) of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Grant Number 21H00026 and 22K05038. We acknowledge financial support from NEDO project (“Development of materials for Pb free perovskite tandem solar cells”) on international collaboration. This work used computational resources of ITO provided by Research Institute for Information Technology, Kyushu University through the HPCI System Research Project (Project ID: hp220061) and Supercomputer Center, the Institute for Solid State Physics, the University of Tokyo. We would like to thank Prof. Hayase of The University of Electro-Communications for fruitful discussions based on experiments of Sn and Ge mixed perovskite solar cell devices.

References

1. M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514.
2. J. Y. Kim, J. W. Lee, H. S. Jung, H. Shin and N. G. Park, Chem. Rev., 2020, 120, 7867–7918.
3. M. R. Islam, Y. L. Wu, K. Liu, Z. J. Wang, S. C. Qu and Z. G. Wang, Adv. Mater. Interfaces, 2022, 9, 2101144.
4. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050.
5. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
6. Z. W. Xiao, Y. Y. Zhou, H. Hosono and T. Kamiya, Phys. Chem. Chem. Phys., 2015, 17, 18900–18903.
7. W. J. Ke, C. C. Stoumpos, I. Spanopoulos, L. Mao, M. Chen, M. R. Wasielewski and M. G. Kanatzidis, J. Am. Chem. Soc., 2017, 139, 14800–14806.
8. M. Ozaki, Y. Katsuki, J. W. Liu, T. Handa, R. Nishikubo, S. Yakumaru, Y. Hashikawa, Y. Murata, T. Saito, Y. Shimakawa, Y. Kanemitsu, A. Saeki and A. Wakamiya, ACS Omega, 2017, 2, 7016–7021.
9. Z. W. Xiao, Z. N. Song and Y. F. Yan, Adv. Mater., 2019, 31, 1803792.
10. M. A. Kamarudin, D. Hirotani, Z. Wang, K. Hamada, K. Nishimura, Q. Shen, T. Toyoda, S. Iikubo, T. Minemoto, K. Yoshino and S. Hayase, J. Phys. Chem. Lett., 2019, 10, 5277–5283.
11. K. Nishimura, M. A. Kamarudin, D. Hirotani, K. Hamada, Q. Shen, S. Iikubo, T. Minemoto, K. Yoshino and S. Hayase, Nano Energy, 2020, 74, 104858.
12. D. Meggiolaro, D. Ricciarelli, A. A. Alasmari, F. A. S. Alasmary and F. De Angelis, J. Phys. Chem. Lett., 2020, 11, 3546–3556.
13. M. L. Agiorgousis, Y. Y. Sun, H. Zeng and S. B. Zhang, J. Am. Chem. Soc., 2014, 136, 14570–14575.
14. S. van Reenen, M. Kemerink and H. J. Snaith, J. Phys. Chem. Lett., 2015, 6, 3808–3814.
15. E. Aydin, M. De Bastiani and S. De Wolf, Adv. Mater., 2019, 31, 1900428.
16. J. Wang, W. Li and W. J. Yin, Adv. Mater., 2020, 32, 1906115.
17. R. Sundheep and A. Jain, Surf Interfaces, 2022, 31, 102073.
18. J. Zhang, X. Zhang, M. E. Turiansky and C. G. Van de Walle, PRX Energy, 2023, 2, 013008.
19. R. J. Stewart, C. Grieco, A. V. Larsen, J. J. Maier and J. B. Asbury, J. Phys. Chem. Lett., 2016, 7, 1148–1153.
20. A. Abate, M. Saliba, D. J. Hollman, S. D. Stranks, K. Wojciechowski, R. Avolio, G. Grancini, A. Petrozza and H. J. Snaith, Nano Lett., 2014, 14, 3247–3254.
21. D. W. deQuilettes, S. M. Vorpahl, S. D. Stranks, H. Nagaoka, G. E. Eperon, M. E. Ziffer, H. J. Snaith and D. S. Ginger, Science, 2015, 348, 683–686.
22. H. R. Tan, A. Jain, O. Voznyy, X. Z. Lan, F. P. G. de Arquer, J. Z. Fan, R. Quintero-Bermudez, M. J. Yuan, B. Zhang, Y. C. Zhao, F. J. Fan, P. C. Li, L. N. Quan, Y. B. Zhao, Z. H. Lu, Z. Y. Yang, S. Hoogland and E. H. Sargent, Science, 2017, 355, 722–726.
23. R. Wang, J. J. Xue, K. L. Wang, Z. K. Wang, Y. Q. Luo, D. Fenning, G. W. Xu, S. Nuryyeva, T. Y. Huang, Y. P. Zhao, J. L. Yang, J. H. Zhu, M. H. Wang, S. Tan, I. Yavuz, K. N. Houk and Y. Yang, Science, 2019, 366, 1509.
24. Q. Jiang, Y. Zhao, X. W. Zhang, X. L. Yang, Y. Chen, Z. M. Chu, Q. F. Ye, X. X. Li, Z. G. Yin and J. B. You, Nat. Photonics, 2019, 13, 460.
25. F. Gao, Y. Zhao, X. W. Zhang and J. B. You, Adv. Energy Mater., 2020, 10, 1902650.
26. K. Hamada, R. Tanaka, M. A. Kamarudin, Q. Shen, S. Iikubo, T. Minemoto, K. Yoshino, T. Toyoda, T. L. Ma, D. W. Kang and S. Hayase, Acs Appl Mater Inter, 2020, 12, 17788–17794.
27. T. Nakamura, T. Handa, R. Murdey, Y. Kanemitsu and A. Wakamiya, Acs Appl Electron Ma, 2020, 2, 3794–3804.
28. S. F. Hu, K. Otsuka, R. Murdey, T. Nakamura, M. A. Truong, T. Yamada, T. Handa, K. Matsuda, K. Nakano, A. Sato, K. Marumoto, K. Tajima, Y. Kanemitsu and A. Wakamiya, Energy Environ. Sci., 2022, 15, 2096–2107.
29. S. F. Hu, J. Pascual, W. T. Liu, T. Funasaki, M. A. Truong, S. Hira, R. Hashimoto, T. Morishita, K. Nakano, K. Tajima, R. Murdey, T. Nakamura and A. Wakamiya, Acs Appl Mater Inter, 2022, 14, 56290–56297.
30. J. M. Xia, C. Liang, H. Gu, S. L. Mei, S. W. Li, N. Zhang, S. Chen, Y. Q. Cai and G. C. Xing, Energy Environ. Mater., 2023, 6, e12296.
31. S. F. Hu, P. Zhao, K. Nakano, R. D. J. Oliver, J. Pascual, J. A. Smith, T. Yamada, M. A. Truong, R. Murdey, N. Shioya, T. Hasegawa, M. Ehara, M. B. Johnston, K. Tajima, Y. Kanemitsu, H. J. Snaith and A. Wakamiya, Adv. Mater., 2023, 35, 2208320.
32. G. Giorgi, K. Yamashita and H. Segawa, Phys. Chem. Chem. Phys., 2018, 20, 11183–11195.
33. T. Naito, M. Takagi, M. Tachikawa, K. Yamashita and T. Shimazaki, J. Phys. Chem. Lett., 2023, 14, 6695–6701.
34. N. Ito, M. A. Kamarudin, D. Hirotani, Y. Zhang, Q. Shen, Y. Ogomi, S. Iikubo, T. Minemoto, K. Yoshino and S. Hayase, J. Phys. Chem. Lett., 2018, 9, 1682–1688.
35. C. H. Ng, K. Nishimura, N. Ito, K. Hamada, D. Hirotani, Z. Wang, F. Yang, S. Likubo, Q. Shen, K. Yoshino, T. Minemoto and S. Hayase, Nano Energy, 2019, 58, 130–137.
36. C. H. Ng, K. Hamada, G. Kapil, M. A. Kamarudin, Z. Wang, S. likubo, Q. Shen, K. Yoshino, T. Minemoto and S. Hayase, J. Mater. Chem. A, 2020, 8, 2962–2968.
37. A. Mirzehmet, T. Ohtsuka, S. A. Abd Rahman, T. Yuyama, P. Krüger and H. Yoshida, Adv. Mater., 2021, 33, 2004981.
38. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
39. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
42. H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
43. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558.
44. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
45. H. Uratani and K. Yamashita, J. Phys. Chem. Lett., 2017, 8, 742–746.
46. W. J. Yin, T. T. Shi and Y. F. Yan, Appl. Phys. Lett., 2014, 104, 063903.
47. F. Wang, S. Bai, W. Tress, A. Hagfeldt and F. Gao, Npj Flex Electron., 2018, 2, 22.

---

Footnotes

† Electronic supplementary information (ESI) available: We describe the (S1) chemical potentials and phase diagram, (S2) defect formation energies under each chemical potential condition, (S3) EDA passivation effect against p-type defects of I_Sn/I_Ge, (S4) pDOS for passivated perovskite surfaces using EDA and IPFB, (S5) interaction analysis between the molecule and defect state based on electron density, (S6) model size dependency, and (S7) calculation results for I-MA-terminated perovskite surface models. See DOI: https://doi.org/10.1039/d4cp03817g

‡ Emi Kino and Makito Takagi equally contributed to this study.

---