Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Systematic study of the structural, energetic and elastic properties of U1−yAmyO2−x compounds using empirical interatomic potentials
Baptiste
Labonne
 a,
Christine
Guéneau
b and
Marjorie
Bertolus
*a
a,
Christine
Guéneau
b and
Marjorie
Bertolus
*a
aCEA, DES, IRESNE, DEC, Cadarache, F-13108 Saint-Paul-Lez-Durance, France. E-mail: marjorie.bertolus@cea.fr
bUniversité Paris-Saclay, CEA, S2CM, Service de recherche en Corrosion et Comportement des Matériaux, 91191 Gif-sur-Yvette, France
First published on 29th January 2025
Abstract
Uranium–americium mixed oxides are envisaged as fuels or blankets for the transmutation of americium in fast neutron reactors, which requires an accurate knowledge of their properties. Here, the Cooper–Rushton–Grimes (CRG) potential terms related to Am4+ are reoptimized to lower the very high melting temperature of AmO2 predicted by the potential (≈3350 K) while keeping other properties unchanged. The resulting terms are used alongside U4+ parameters as well as previously optimized terms for the Am3+ and U5+ oxidation states in combination with molecular dynamics to perform a systematic study of the structural, thermodynamic and elastic properties of hypostoichiometric uranium–americium mixed oxides U1−yAmyO2−x with 0 ≤ y ≤ 1 and 0 ≤ x ≤ 0.1 over a wide temperature range (250–4500 K). The properties calculated include the lattice parameter and related properties (density, thermal expansion coefficient), the enthalpy increment and related properties (specific heat capacity, enthalpy of fusion), the melting temperature and the elastic constants. Our study shows a peculiar evolution of properties with the americium content with a change in the evolution for 50% americium due to the various oxidation states of the cations present in these compounds. Results presented in this paper provide significant insight into the properties of uranium–americium mixed oxides for all compositions, in particular for high americium contents, non-stoichiometric oxides and at high temperature and complement the few experimental data available for these materials.
I. Introduction
Uranium–americium mixed oxides are envisaged as fuels or blankets in fast neutron reactors to allow for the transmutation of americium in view of the reduction of its quantity in nuclear waste.1 In this context, the knowledge of thermodynamic, structural and elastic properties of (U,Am)O2 fuels is of crucial importance for fuel manufacturing, as well as for safe reactor operation. Beyond the use of low americium content fuel in reactor, highly Am-enriched uranium–americium oxides are being considered for space applications in radioisotope thermoelectric generators.2–10 The knowledge of thermodynamic properties for all Am contents, including high ones, is therefore crucial. In addition, the knowledge of elastic properties, in particular the elastic constants C11, C12 and C44, is necessary since these are direct parameters of micromechanical laws for single crystals, which are then homogenised for the simulation of the behaviour of the polycrystalline material.Experimental investigations on americium-bearing compounds are difficult due to the high radioactivity of this element and the data reported in the literature on uranium–americium oxides are relatively scarce. The U–Am–O ternary phase diagram data were obtained by Horlait et al.,11 Vălu et al.,12 Prieur et al.,13–15 Lebreton et al.16 and more recently Epifano et al.17–20 A CALPHAD model of the ternary system was then developed by Epifano et al. using these experimental data.21 This work pointed out that further investigations of this system are required, especially for high Am contents and oxygen to metal ratio (O/M) below 2 to improve the CALPHAD modelling of americium-bearing mixed actinide oxides.
Atomic scale modelling has proved itself to be an important complement to experimental characterizations to obtain data and bring insight into the behaviour of fuel materials over a wide range of compositions and conditions.22,23 We use it in this study to complement the few experimental data available on uranium–americium oxides.
The Cooper–Rushton–Grimes (CRG) potential24 has yielded excellent results on several pure and mixed actinide oxides,25–37 and was adapted for the study of uranium–americium mixed oxides in a previous paper.38 It yields, however, a very high melting temperature for AmO2 (≈3350 K), which could impact the results on uranium–americium mixed oxides with high Am content. We propose here an estimate of the probable melting temperature range for a hypothetical americium dioxide based on thermodynamic considerations and compare it to the very scarce data available.39,40
Based on this range estimate, we reoptimized the interaction terms related to Am4+ to lower the AmO2 melting temperature while keeping structural, thermodynamic and elastic properties virtually unchanged, as they are in line with experimental data. We then used the updated parameters in combination with U4+, Am3+ and U5+ terms to calculate the structural, thermodynamic and elastic properties of U1−yAmyO2−x with 0 ≤ y ≤ 1 and 0 ≤ x ≤ 0.1.
The paper is organized as follows. We briefly recall the potential formalism and calculation details, which are presented in detail in the paper dedicated to the optimization of the Am3+ and U5+ terms.38 We then describe precisely the method used to include the melting temperature in the fitting procedure and the generation scheme used to incorporate vacancies in our supercells. We then present and discuss the results of the systematic study of U1−yAmyO2−x compounds: the structural and energetic properties extracted directly from simulations, the derivative properties, i.e., thermal expansion coefficient and specific heat capacity, the melting temperatures, and the elastic properties. Finally, we conclude and present the outlooks of this work.
II. Methods
II.A. Potential formalism
The Cooper–Rushton–Grimes (CRG) potential24 is an embedded atom method (EAM) potential41,42 with the following formal definition for the potential energy of an atom i as follows: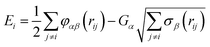 | (1) |
This potential formalism is remarkably good at reproducing known properties of actinide oxides, in particular the lattice parameter, the Cauchy violation of the elastic constants C12 ≠ C44 and the bulk modulus temperature dependence, probably due to the strongly ionic iono-covalent bonding in these systems. The terms originally published were optimized on experimental lattice parameters and elastic properties, while ensuring that fluorite was the most stable structure. The terms subsequently added for Am3+ and U5+ were optimized using lattice parameters and enthalpy increments12,17 for several stoichiometric uranium–americium mixed oxides at room temperature11,16 and at 1000 K.16,19
II.B. Calculation details
 | ||
| Fig. 1 Concentrations of the various cationic oxidation states in (U,Am)O2 compounds as a function of americium content, reproduced from ref. 45. | ||
For the study of hypostoichiometric oxides, oxygen vacancies were introduced randomly considering their relatively low concentration and the possibility for oxygen to diffuse. Moreover, DFT+U calculation results on AmO2−x showed that configurations with oxygen vacancies nearest neighbours to Am3+ were not necessarily the most stable.46 The charge neutrality was ensured by the reduction of one or several species. The order in which species are reduced is known from DFT+U calculations:45
• Below 50% Am, only U5+ can be reduced to U4+ since all americium cations are already in the (+III) oxidation state and U3+ terms are not included in the potential. This implies that there is a limit on the oxygen to metal ratio imposed by the americium content.
• Above 50% Am, Am4+ ions are reduced first to Am3+, followed by U5+ ions to U4+ if necessary. The latter occurs only for large deviations from stoichiometry for 0.50 < Am/(Am + U) ≤ 0.60.
II.B.2.a. Heat until it melts and moving interface methods. The Heat Until it Melts (HUM)48,49 and moving interface (MI)50,51 methods are presented in detail in our previous paper, only the main points are recalled here. The HUM method allows for the determination of the structural and energetic properties of interest as a function of temperature. We equilibrated the supercells for 100 ps in the NPT ensemble at 0 bar (as is standard in the community given the negligible pressure dependence of studied properties and to ensure U = H), from 250 K to 4500 K every 25 K, and averaged the properties over the last 50 ps for each temperature. These simulations were performed on 6 × 6 × 6 replications of the conventional fluorite cell, i.e., 2592-atom supercells for stoichiometric systems.
Due to overheating effects caused by the finite-size of the system, the melting temperature detected in a HUM run is overestimated by approximately 20%.52,53 The MI method is thus used to estimate a pseudo-melting temperature by simulating a solid–liquid interface, imposing the final temperature and pressure and monitoring the position of the interface. This monitoring was performed by computing the local entropy and the centro-symmetry parameter, as well as performing common neighbour analyses using LAMMPS to obtain the profile of these properties along the longest dimension of the supercell. The position of the interface at the end of the simulation indicates if the applied temperature is above or below the melting temperature yielded by the potential. The melting temperature is found when at the end of the simulation, both phases account for approximately half the supercell each. These simulations were performed in the NPT ensemble with a 25 K temperature step and 1 ns final relaxation time on 8 × 8 × 16 replications of the conventional fluorite cell, i.e., 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288-atom supercells for stoichiometric compounds.
288-atom supercells for stoichiometric compounds.
For both types of calculations, we used a 1 fs timestep, a 0.1 ps temperature damping parameter and a 0.5 ps pressure damping parameter for the Nosé–Hoover thermostat and barostat, respectively. Simulations were performed on five supercells with varying random configurations of U and Am positions in the cationic sublattice for each composition and on three seeds for the initialization of the velocities per supercell, totalling fifteen repetitions for a given set of conditions. Properties were then averaged over these simulations, taking twice the standard deviation as the uncertainty.
II.B.2.b. Calculation of elastic properties. The supercells equilibrated at a finite temperature for a given pressure using the HUM method can be used to compute the elastic constants. To do so, small deformations are applied to the simulation cell. These must be small enough so that the stress versus strain relationship respects Hooke's law, i.e., remains linear. This allows for the determination of the elastic tensor which, in the case of cubic materials, is entirely described by the C11, C12 and C44 constants using the Voigt notation. These can be used to compute various elastic moduli, as well as the Zener ratio, which measures the isotropy of cubic materials, in the Voigt–Reuss–Hill (VRH) scheme,54–56 therefore yielding a complete representation of the linear elastic properties of the material.
In practice, we used the lattice parameters yielded by the HUM method every 100 K to rescale the perfect supercell at each temperature before performing a 2 × 2 × 2 replication due to the sensibility of elastic properties on the supercell size. We then equilibrated the resulting 12 × 12 × 12 replication supercell at the corresponding temperature and zero pressure in the NPT ensemble for 30 ps to dislodge atoms from their equilibrium position. The LAMMPS “ELASTIC_T” script was used on the resulting structure to apply a ±4% deformation successively along all crystallographic axes and tilt factors in order to compute C11, C12 and C44. The Zener ratio A is then calculated as:
 | (2) |
III. Reoptimization and validation of Am4+ related potential parameters
III.A. Estimated melting temperature range
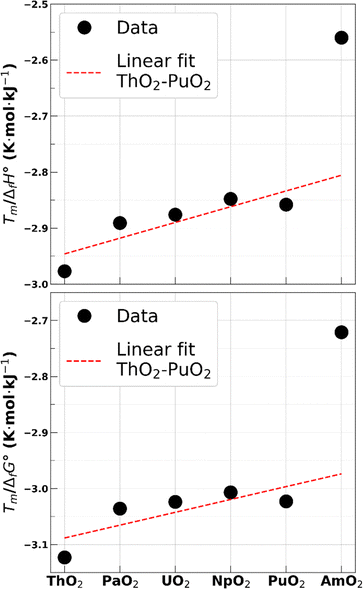
A single experimental value of AmO2 melting temperature was published by McHenry in 1965.57 The measurement was performed without control of the oxygen content and yielded 2386 K at standard pressure. CALPHAD-based calculations58,59 and experimental characterizations,17,58 however, show that the reduction process of AmO2 begins at temperatures as low as 1100 K. The calculated phase diagram also indicates that the melting should occur for an O/M ratio of approximately 1.76. The melting temperature of stoichiometric americium dioxide can therefore only be estimated. Casalta estimated the melting temperature of AmO2 at 2520 K without providing the method.39 More recently, Kato et al. proposed a value of 2773 K40 based on the effect of Am on the melting temperature of mixed actinide oxides.The melting temperature of stoichiometric americium dioxide predicted by the CRG potential using the MI method is about 3350 K. Since the melting temperature of AmO2 seems to have a strong influence on that of the mixed uranium–americium oxides with high Am contents60 and as a starting point for the precise modelling of AmO2−x compounds, a reoptimization of the Am4+ related parameters of the potential is needed to lower this value. We propose here a method to determine a probable melting temperature interval for a hypothetical stoichiometric AmO2. We use the enthalpy of formation and Gibbs free energy of formation of the actinide dioxides to infer the stability of these compounds. Using values from,61,62 we compute the ratios Tm/ΔfH° and Tm/ΔfG° for all actinide dioxides in the series ThO2 to AmO2. Results are reported in Table 1 and shown in Fig. 2. It is observed that the values are similar for all actinide dioxides except for AmO2, giving an additional hint that the experimental value by McHenry was not obtained on the stoichiometric compound.
| ThO2 | PaO2 | UO2 | NpO2 | PuO2 | AmO2 | |
|---|---|---|---|---|---|---|
| T m/ΔfH° (K mol kJ−1) | −2.977 | −2.891 | −2.876 | −2.848 | −2.858 | −2.560 |
| T m/ΔfG° (K mol kJ−1) | −3.123 | −3.036 | −3.024 | −3.007 | −3.023 | −2.721 |
Considering the various degrees of uncertainty associated to these ratios, a simple linear fit on the values of other actinide dioxides is used to determine a probable upper limit for these two ratios for americium dioxide. Values obtained are −2.81 K mol kJ−1 and −2.97 K mol kJ−1 for Tm/ΔfH° and Tm/ΔfG°, respectively, corresponding to a melting temperature of 2620 K and 2605 K, respectively. The latter is chosen as the lower bound for our melting temperature interval estimate.
The lower limit for these two ratios, which corresponds to the upper limit of the temperature interval, is more difficult to assess due to the transition in the chemical nature of cation-oxygen bonds taking place between plutonium and neptunium dioxides.63,64 It can be seen that the value of the two ratios decreases slightly from NpO2 to PuO2, but we have no indication on their behaviour for heavier actinides. We thus take the extreme values, i.e., those of ThO2, as being the lower limit for AmO2. The corresponding melting temperatures are 2780 K and 2735 K for Tm/ΔfH° and Tm/ΔfG°, respectively.
We thus consider that the melting temperature of a hypothetical americium dioxide is in the 2605–2780 K range. This rule of thumb gives results in line with the previous evaluations while diminishing the width of the interval spanned by the previous two estimates by Casalta and Kato et al. cited above. Despite the large uncertainties in this evaluation, it is clear that the current CRG potential largely overestimates the melting temperature of a hypothetical stoichiometric americium dioxide.
III.B. Fitting procedure
We used the DAKOTA software65 to reoptimize the potential parameters in order to lower the melting temperature of americium dioxide while keeping other properties such as the room-temperature lattice parameter and bulk modulus, the thermal expansion and the enthalpy increment unchanged, as they are in excellent agreement with the available experimental data. Based on previous work by Cooper et al. to lower the melting temperature of PuO2 predicted by the original potential parameters,25 we largely increased the N-body parameters of Am4+ while adjusting the Am4+–O terms to ensure that other properties were changed as little as possible. We employed the single-objective genetic algorithm (SOGA) using the JEGA package66 implemented in DAKOTA to optimize all parameters simultaneously, running the optimisation with five different initialisation seeds. Properties were calculated as follows: (1) room-temperature lattice parameter, (2) room-temperature bulk modulus, (3) melting temperature, (4) lattice parameter and enthalpy increment at 1000 K. After each step, the result was examined and the set of parameters was discarded if the computed properties were unacceptably far from their reference value. The tolerance for each property was chosen large enough to leave space for the subsequent optimization of the parameters, while rejecting sets having no chance of converging towards a valid solution. Values used for the optimization as well as tolerance criteria are reported in Table 2.We used several loss functions to guide the optimization: first the absolute relative error on numerical properties and second a 0 or 1 value corresponding to the identification of the solid to liquid phase transition or not, respectively. We applied various weights to the linear combination of these loss functions to find the best set of parameters. A weight value of 5 was chosen for the loss function regarding each room-temperature lattice parameter, bulk modulus and 1000 K lattice parameter. A weight value of 1 was used for the loss function of the enthalpy increment due to the rather high rigidity of the potential formalism with regard to energetic properties. A weight value of 10 was applied to the detection of the melting.
To decide on the “best” interatomic potential parametrization after the optimization, we selected the subset of all the sets of parameters predicting the melting in the estimated temperature range and defined a global objective function (GOF) combining the various loss functions:
 | (3) |
As for the optimization of the Am3+ and U5+ terms,38 simulations for the optimization of the interatomic potential coefficients were carried out on 2592-atom supercells with a time step of 2 fs. The Tdamp and Pdamp parameters of the Nosé–Hoover thermostat and barostat were fixed at 0.1 ps and 0.5 ps, respectively. For simulations at room temperature, the cells are equilibrated for 8 ps and the properties are averaged over the last 4 ps. For higher temperature properties, the equilibration time was set at 10 ps, with properties averaged over the last 4 ps. The room-temperature bulk modulus was determined by applying ±4% deformations on the supercell equilibrated at 300 K. The relatively high-cost of a moving interface calculation is incompatible with the iterative scheme of the parameters optimization. The alternative is to equilibrate the supercell at two temperatures corresponding to the lower and upper bounds of our acceptable interval multiplied by an overestimation coefficient calibrated on previous HUM and MI calculations. We found this coefficient to be extremely consistent over the melting temperatures calculated on low-concentration uranium–americium mixed oxides,38 with a value of 1.205 ± 0.005. We thus performed the two 30 ps equilibrations at 3100 K and 3400 K corresponding to corrected values of 2575 K and 2825 K, respectively. The interval was slightly broadened compared to the values determined in Section III.A to account for the uncertainties intrinsic to this method. We used the existence of the farthest peaks of the radial distribution functions or lack thereof to deduce the phase of the supercell. By ensuring that AmO2 was solid at the lower bound of the range and liquid at its upper bound, we successfully incorporated the melting temperature in the optimization procedure.
III.C. Final set of parameters
The final Am4+–O pair parameters as well as terms used for the other species are given in Table 3, while Table 4 regroups all the N-body terms with the updated values for Am4+.| Species α | Species β | A αβ (eV) | ρ αβ (Å) | C αβ (eV Å6) | D αβ (eV) | γ αβ (Å−1) | r 0 αβ (Å) |
|---|---|---|---|---|---|---|---|
| U4+ | U4+ | 18600 | 0.2747 | 0.0 | |||
| U4+ | O2− | 448.779 | 0.387758 | 0.0 | 0.6608 | 2.05815 | 2.38051 |
| U4+ | Am4+ | 18600 | 0.2677 | 0.0 | |||
| Am4+ | Am4+ | 18600 | 0.2609 | 0.0 | |||
| Am 4+ | O 2− | 361.3445 | 0.41441 | 0.0 | 0.85916 | 2.01777 | 2.31482 |
| O2− | O2− | 830.283 | 0.352856 | 3.884372 | |||
| Am3+ | U4+ | 18600 | 0.248879 | 0.0 | |||
| Am3+ | U5+ | 18600 | 0.234726 | 0.0 | |||
| Am3+ | Am3+ | 18600 | 0.286433 | 0.0 | |||
| Am3+ | Am4+ | 18600 | 0.272028 | 0.0 | |||
| Am3+ | O2− | 367.4422 | 0.381697 | 0.0 | 0.80836 | 2.16288 | 2.325338 |
| U5+ | U4+ | 18600 | 0.297631 | 0.0 | |||
| U5+ | U5+ | 18600 | 0.256063 | 0.0 | |||
| U5+ | Am4+ | 18600 | 0.286782 | 0.0 | |||
| U5+ | O2 | 1157.0704 | 0.357723 | 0.0 | 1.85097 | 1.917152 | 1.916728 |
| Species | G (eV Å1.5) | η (Å5) |
|---|---|---|
| U4+ | 1.806 | 3450.995 |
| U5+ | 1.7921 | 3448.0359 |
| Am3+ | 0.3553 | 1630.7277 |
| Am 4+ | 1.3726 | 6034.3348 |
| O2− | 0.690 | 106.856 |
III.D. Validation of the updated interaction terms
 | ||
| Fig. 3 Comparison of properties yielded by both sets of parameters and available experimental data for the lattice parameter58,67 (top), the enthalpy increment69 (middle) and the bulk modulus64,68,70,71 (bottom) as a function of temperature. | ||
We see that both the initial and new parametrizations are in excellent agreement with the available experimental data. They begin to behave differently above 2000 K and exhibit different melting temperatures, which can be identified by the discontinuity in the enthalpy increment. As expected, the new terms yield a much lower melting point. To confirm this, we used the moving interface method with fifteen different seeds for the initialization of the velocities and found the new melting point to be (2792 ± 5.7) K. This is slightly higher than the upper bound of the interval determined in Section III.A and in excellent agreement with the estimate by Kato et al.40
 | ||
| Fig. 4 Comparison of properties yielded by both sets of parameters and available experimental data for the lattice parameter19 (top) and the enthalpy increment17 (bottom) as a function of temperature for U0.3Am0.7O2. | ||
As a final validation, we investigate the difference between both parametrizations on the 0 K enthalpy of mixing, shown in Fig. 5. The enthalpy of mixing of uranium–americium mixed oxides is defined as:
| ΔHmix = HU1−yAmyO2 − (1 − y)HUO2 − yHAmO2 | (4) |
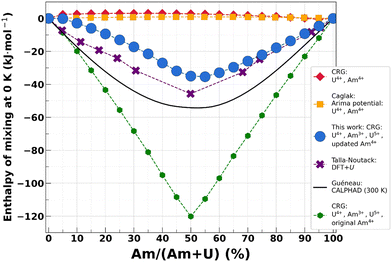 | ||
| Fig. 5 Comparison of the 0 K enthalpy of mixing computed using the original CRG potential (red diamonds), the Arima potential73 (yellow squares), the CRG potential augmented with Am3+ and U5+ oxidation states (green hexagons),38 the CRG potential with Am3+; U5+ and reoptimized Am4+ parameters (blue circles, this work), DFT+U45 (purple crosses) and CALPHAD74 (black line). | ||
It can be observed that only the interatomic potentials including the Am3+ and U5+ oxidation states yield negative values for the mixing enthalpy – indicative of a stable solid solution – also calculated in DFT+U,45 as values calculated with two potentials taking into account only the (+IV) oxidation states yield unphysical positive values.73 Moreover, the values obtained with the new parametrization are in much better agreement with the DFT+U-calculated ones due to the change in the absolute value of AmO2 enthalpy content. The results are also in good agreement with the calculated values at 300 K with the CALPHAD model.74 Since the enthalpy of mixing was not included in the fitting procedure, this is an important result for the validation of the reoptimized parameters.
IV. Results and discussion
We apply our parametrization to the calculation of properties of interest of (U,Am)O2−x oxides. We present here the results, separating the properties directly obtained as a function of temperature during HUM calculations, their derivative properties, the melting temperature estimates yielded by the MI method and the elastic properties.IV.A. Direct properties
 | ||
| Fig. 6 Room-temperature lattice parameter of (U,Am)O2−x compounds, including data of ref. 38, compared to experimental data measured by Lebreton16 and DFT+U calculations performed by Talla-Noutack.45 | ||
Fig. 7 shows the evolution of the lattice parameter and density as a function of temperature for stoichiometric uranium–americium mixed oxides. We can clearly see a change in the trend of the evolution of structural properties as a function of americium content occurring at an Am content of 50%: the lattice parameter (resp. the density) remains relatively similar from UO2 to U0.5Am0.5O2 while decreasing (resp. increasing) rapidly between 50% Am and AmO2. This is due to the change in the cationic oxidation states taking place at 50% Am, shown in Fig. 1, which impact the interatomic distances.38 At higher temperature, the two properties show a subtle inflection point with a temperature dependence on the americium content. This is associated with the Bredig transition predicted by the interatomic potential in these compounds. This transition is discussed in more detail in Section IV.B relative to the derivative properties.
 | ||
| Fig. 7 Evolution of the lattice parameter (top) and density (bottom) as a function of temperature for stoichiometric uranium–americium mixed oxides, including data of ref. 38. | ||
Then, around 3300–3600 K, the discontinuity in the density increment curves indicates the melting. Although the melting temperature Tm is overestimated by this simulation technique, it can already be seen that the melting temperature is very similar for all Am contents between 50% and 100% and that it is between the melting temperature of U0.5Am0.5O2 and that of UO2. Melting temperatures are discussed extensively in Section IV.C, which describes the results of the moving interface method.
The effect of the oxygen to metal ratio on the lattice parameter as a function of temperature is shown in Fig. 8 for three Am contents (20%, 50% and 80% Am). The same trend is observed in the variation of the cell parameter with the O/M ratio for the three Am contents: an increase up to approximately 1900 K and a decrease above this temperature. Quantitatively, however, these changes depend significantly on the americium content. Low americium contents are impacted both at low and high temperature; medium americium contents are virtually unaffected by the O/M ratio and high Am-contents are affected only at low temperature. We can also see O/M-dependent changes in the inflexion point associated with the Bredig transition (see Section IV.B).
 | ||
| Fig. 9 Enthalpy increment as a function of temperature for stoichiometric uranium–americium mixed oxides (top, magnification on bottom), including data of ref. 38. | ||
The impact of the oxygen to metal ratio on the enthalpy per atom is similar for all temperatures and compositions: the larger the deviation from O/M = 2.00 in the hypostoichiometric domain, the higher the enthalpy, as shown in Appendix A (Section A.1) for three Am/(Am + U). This is consistent with the enthalpy values calculated using the CALPHAD method in (U,Pu)O2−x by Fouquet-Métivier et al.79
IV.B. Derivative properties
The general thermal expansion coefficient α and specific heat capacity cp are defined as: | (5) |
 | (6) |
 | (7) |
The evolution of α and cp with respect to temperature is shown in Fig. 10 for stoichiometric (U,Am)O2 compounds.
 | ||
| Fig. 10 General thermal expansion coefficient (top) and specific heat capacity (bottom) as a function of temperature for (U,Am)O2 compounds. Values up to 50% Am/(Am + U) are taken from ref. 38. | ||
We consider both properties concurrently due to their nearly identical evolution as a function of temperature, focussing on americium contents above 50%. Their evolution with temperature is qualitatively identical to that of low americium contents mixed oxides:38 first a regular rise up to 1700 K, followed by a peak. The influence of the Am content up to 1700 K is more pronounced for the general thermal expansion coefficient than for the specific heat capacity. Medium americium contents have a generally higher thermal expansion coefficient than the pure oxides in this temperature region. The comparison of the specific heat capacity calculated with the values derived from enthalpy measurements performed by Epifano et al.17 is not conclusive due to the slight but systematic underestimation of this property by the CRG formalism, as well as to the possible changes in the experimental O/M ratio affecting the measurements.
The peaks observed in the derivative properties are related to the Bredig transition,80 observed in many compounds with fluorite structure including UO2.81–85 It is also predicted by atomic scale calculations using various interatomic potentials for UO2,24,86–88 including machine-learning potentials trained on DFT+U data,89 using the CRG potential for PuO2 and using ab initio molecular dynamics in UO2 and PuO2.90 The CRG potential also predicts this transition in (U,Pu)O2,25,32,35 (U,Th)O2,26 (U,Am)O234 and (U,Gd)O2.29 The Bredig transition is commonly admitted to be a superionic transition with the temperature TB of the maximum of the peak empirically considered to be approximately TB ≈ 0.8 × Tm, but the origin of the oxygen diffusion acceleration is still a matter of debate. Several modelling91–93 and experimental works81,83,84 were dedicated to the clarification of the underlying mechanisms with no consensus reached to this day.
In the case of (U,Am)O2 compounds, the amplitude and temperature of the peak are strongly dependent on the Am content. From UO2 to U0.5Am0.5O2, the temperature and amplitude of the peak decrease strongly and it becomes difficult to identify the peak for medium americium contents. For Am-rich compounds, the amplitude of the peak increases with the americium content while its temperature is relatively stable due to the low impact of the Am content on the melting temperature (see next section). The change in the trend of the evolution of the Bredig peak amplitude and temperature with americium content is a direct consequence of the change in the cationic oxidation states occurring at 50% Am, as seen in Fig. 1. The Bredig transition in pure americium dioxide is not a feature of the reoptimized Am4+ potential terms, it was yielded by the original CRG terms with the same amplitude at a higher temperature (2800 K).34 It is noteworthy that both parametrizations yield this behaviour, as it confirms that the only difference between the two sets of parameters is the melting temperature.
We also studied the effect of the O/M ratio on the derivative properties. Fig. 11 presents the general thermal expansion coefficient for all O/M ratios studied for two mixed oxides, as well as for AmO2−x. The effect of an increasing deviation from O/M = 2.00 on α is twofold. First, for temperatures below 1700 K, it results in a decreasing general thermal expansion coefficient. The intensity of this decrease depends on the americium content. Second, the Bredig peak is shifted at higher temperature, while its amplitude decreases. While all compositions seem to be affected qualitatively in the same manner, the temperature and amplitude of the peak also depends on the americium content, the peak disappearing entirely for AmO1.90. The fact that the Bredig peak disappears for low O/M ratios, which is also the case in the empirical potential calculations of (U,Pu)O2−x,94 could explain why this transition has not been observed yet in (U,Pu)O2 and (U,Am)O2 mixed oxides.
 | ||
| Fig. 11 General thermal expansion coefficient as a function of temperature for U0.8Am0.2O2−x (top), U0.2Am0.8O2−x (middle) and AmO2−x (bottom) for oxygen to metal ratios from 1.90 to 2.00. | ||
The evolution of the specific heat capacity as a function of temperature is shown in Fig. 12 for the same compositions. The effect of the O/M ratio on cp is different from what is observed for the thermal expansion α. The simulations show no impact of the O/M ratio on the specific heat capacity values up to the onset of the peak. When O/M decreases, the peak is shifted towards higher temperatures for all Am contents. This is in line with the experiments performed on UO2 by J. P. Hiernaut et al.,83 which showed that successive shots – associated to a reduction of the sample – yielded higher temperatures for the Bredig transition. The amplitude of the peak, however, evolves differently for the three Am contents. For 20% Am, the amplitude is virtually unchanged, as the difference between the cp values at the maxima corresponds to the difference between the cp values at the onset of the transition. For 80% Am, the peak decreases while flattening rapidly into a plateau. Finally, for AmO2−x, the decrease is more pronounced and the peak transforms into a plateau only at lower O/M values around 1.93.
 | ||
| Fig. 12 Specific heat capacity as a function of temperature for U0.8Am0.2O2−x (top), U0.2Am0.8O2−x (middle) and AmO2−x (bottom) for oxygen to metal ratios from 1.90 to 2.00. | ||
Based on our calculations as well as on the results of empirical potential calculations conducted on (U,Pu)O2−x94 and (U,Pu,Gd)O2−x29 using the same potential formalism, the conclusion as follows can be drawn concerning the evolution of the specific heat capacity with composition:
• As seen in AmO2−x, U1−yAmyO2−x with y > 0.5, (U,Pu)O2−x and (U,Pu,Gd)O2−x, the inclusion of oxygen vacancies associated with cations in the (+III) oxidation state results in a significant decrease of the Bredig peak amplitude, while increasing slightly its temperature.
• From the results on (U,Am)O2 and (U,Pu,Gd)O2 compounds, the inclusion of (+III) cations associated to (+V) ones while keeping O/M = 2.00 (without O vacancies) results in a decrease of both the amplitude and temperature of the Bredig transition.
• Compounds with a cationic sublattice composed of (+V) and (+III) cations in equal proportions, such as U0.5Am0.5O2, do not seem to exhibit a Bredig transition.
• Finally, as seen in U1−yAmyO2−x with y < 0.5, the inclusion of oxygen vacancies accommodated by the reduction of a (+V) cation to (+IV) results in a shift of the Bredig peak towards higher temperatures while leaving its amplitude unchanged.
From these we infer that, using the CRG formalism:
• The presence of (+III) cations tends to lower the amplitude of the Bredig peak.
• The presence of (+III) and/or (+V) cations tend to lower the Bredig peak temperature.
• Oxygen vacancies tend to increase the Bredig peak temperature.
Since we cannot perform simulations separating the effect of oxygen vacancies from that of changes in the oxidation states due to the charge neutrality of the supercells in our simulations, some of these effects could be coupled and/or could cancel each other out.
IV.C. Melting temperature estimates
Fig. 13 compares the estimates of the melting temperature for each composition yielded by the original Am4+ parameters and the reoptimized terms. The results for compounds with less than 50% Am are unaffected by Am4+ parameters since this oxidation state is not present for these compositions. The slope discontinuity exhibited by both parametrizations is once again due to the change in oxidation state at Am/(Am + U) = 0.5 (see Fig. 1). We observe a very large difference between the two sets of parameters on Tm for Am-rich compositions, our parametrization yielding much lower melting temperatures. For AmO2, the new value is (2792 ± 5.7) K, as opposed to (3346 ± 5.7) K with the original CRG potential. We can also see that the melting temperature of Am-rich compositions yielded by our parameters varies only slightly with Am content, with a possible local maximum reached for compositions around 70% Am for all studied O/M ratio. An important observation is that the melting temperature is close to the linear interpolation between UO2 and U0.5,Am0.5O2 for Am contents lower than 50% and between U0.5,Am0.5O2 U0.5 and AmO2 for higher contents. The confirmation of the melting temperatures for (U,Am)O2 with high Am contents could thus enable one to obtain a better estimate for the melting temperature of AmO2.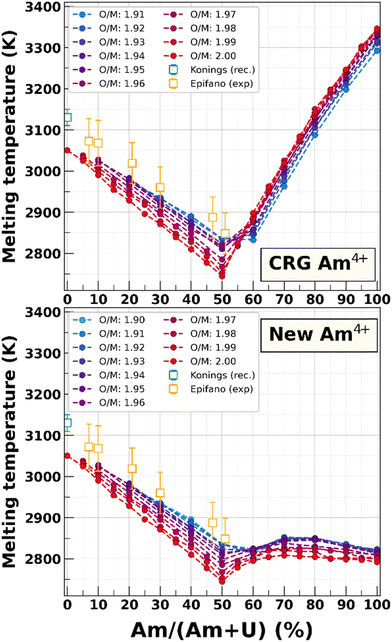 | ||
| Fig. 13 Estimates of the melting temperatures of U1−yAmyO2−x using the original CRG Am4+ parameters (top) and the set of terms obtained in this work (bottom). Available experimental data20,62 is shown as empty squares for comparison. | ||
The difference in the effect of the O/M ratio between the two parametrizations should also be noted. Using the original Am4+ parameters, the deviation from O/M = 2.00 had opposing effects on the melting temperature for low and high Am contents, increasing Tm for Am/(Am + U) ≤ 50% while decreasing it for Am-rich compositions. In contrast, the reoptimized potential predicts that a decrease in the O/M ratio increases the melting temperature for all Am contents, which is consistent with the shift of the Bredig transition temperature (see Section IV.B). This is in line with the results of the CALPHAD calculations using the TAF-ID database, which predict the congruent melting to be in the hypostoichiometric region for all Am contents in uranium–americium mixed oxides.74 This is also similar to the solid/liquid phase transition in MOX calculated using the CALPHAD method by Fouquet-Métivier et al.79 They proposed a stabilising mechanism due to an increase in the entropy that lowers the Gibbs free energy of the system and thus increases Tm for hypostoichiometric domains for all plutonium contents. They show that this entropy increase is due to the presence of plutonium in a mixed Pu4+/Pu3+ oxidation state to accommodate the oxygen vacancies in the hypostoichiometric compositions. Given the similarity in the oxidation states of plutonium and americium in actinide oxides, this explanation could also be valid for the U–Am–O system.
IV.D. Elastic properties
There is no measurement or first-principle calculation of the elastic properties of uranium–americium mixed oxides, these are therefore first estimates. The evolution with temperature of C11, C12, C44 and the Zener ratio for stoichiometric (U,Am)O2 compounds is shown in Fig. 14. The plots representing several isotherms of the elastic constants for (U,Am)O2 compounds can be found in Appendix B (Section B.1.1). | ||
| Fig. 14 Evolution with temperature of (a) C11 (b) C12 (c) C44 (d) the Zener ratio for (U,Am)O2 compounds. | ||
Elastic constants tend to decrease with temperature, indicating a softening of the materials. C12 exhibits a non-monotonous evolution with temperature: its value increases between 2300 K and 2800 K for UO2 and AmO2 as well as for low and high Am contents, in line with measurements by Hutchings on UO2,81 while it decreases steadily for U0.5Am0.5O2 from 300 K to 3000 K. We therefore infer that this increase is a direct consequence of the Bredig transition.
For all Am contents, the Zener ratio is low at room temperature, showing a significant anisotropy of the (U,Am)O2 compounds. It is higher for medium Am contents. For low and high Am contents, the Zener ratio remains relatively constant up to approximately to 2000 K, i.e., until the onset of the Bredig transition, due to the concomitant decrease of C11, C12 and C44. Above 2000 K, the Bredig transition affects the elastic constants in different ways, leading to a strong increase of the Zener ratio with temperature, which indicates a significant increase in the material isotropy. Medium compositions, in particular U0.5Am0.5O2, exhibit a rather steady evolution of all three independent elastic constants with temperature but with different temperature dependences, leading to a more progressive increase of the Zener ratio.
The variation of the elastic constants and Zener ratio as a function of the O/M ratio is similar for all Am contents. Fig. 15 shows the variation of the elastic constants and of the Zener ratio of U0.8Am0.2O2−x with temperature for all O/M ratio studied as an example. Additional results for two other americium contents (50% and 80% Am) can be found in Appendix B (Section B.1.2).
 | ||
| Fig. 15 Evolution with temperature of (a) C11 (b) C12 (c) C44 (d) the Zener ratio for U0.8Am0.2O2−x compounds with 0 ≤ x ≤ 0.1. | ||
The modifications induced by the O/M ratio on the lattice parameter cause an opposite variation in C11: the increase of the lattice parameter with decreasing oxygen content at low temperature induces a decrease in C11 and the opposite behaviour is observed at high temperature. The amplitude of the increase in C12 at high temperature can be correlated to the intensity of the Bredig peak in the general thermal expansion coefficient (see Fig. 11). The effect of the oxygen content on C44, indicative of the resistance to shear stress, is generally less significant but non negligible in particular for U0.5Am0.5O2−x. Finally, the Zener ratio increases when O/M decreases for temperatures lower than 2000 K, but the effect of the hypostoichiometry becomes negligible at higher temperatures for which stoichiometric materials are already nearly isotropic.
It can be noted that the behaviour of the elastic properties with the O/M ratio observed for Am contents below 50% is similar to that obtained by Porto et al. in (U,Pu)O2−x using the CRG potential.94 They took into account the same oxidation states as in (U,Am)O2−x for the cationic sublattice: U4+, U5+, and Pu3+ and Pu4+ instead of Am3+ and Am4+.
V. Conclusion
We reoptimized the interactions terms involving Am4+ cations of the CRG potential to lower the calculated melting temperature of AmO2 and used this parametrization in combination with U4+ parameters as well as previously optimized Am3+ and U5+ terms to perform a systematic study of the structural, thermodynamic and elastic properties of U1−yAmyO2−x with 0 ≤ y ≤ 1 and 0 ≤ x ≤ 0.1.Significant differences are observed between Am contents less than and greater than 50%, which can be correlated to the changes in the cationic oxidation states present in these compounds. Of particular interest is the prediction by the potential of a Bredig transition for the majority of the studied compositions, including AmO2, as well as for most hypostoichiometric compositions. The existence of a Bredig peak, however, is unclear for medium americium contents. In addition, the melting temperature is now more in line with basic thermodynamic data and the effect of the O/M ratio on this phase transition is consistent with CALPHAD predictions using the TAF-ID. Finally, elastic properties of (U,Am)O2−x compounds were evaluated for the first time.
These results will be useful for the CALPHAD modelling of Am-bearing oxides, as well as for the simulation of (U,Am)O2 fuel pellet at the mesoscopic and macroscopic scale. Additional experimental characterizations and/or electronic structure calculations on selected compositions, however, would be needed to confirm these results, especially for high americium contents and at high temperature.
Data availability
Data are available in the Zenodo repository of the PATRICIA H2020 European project: https://zenodo.org/communities/patricia/records?q=&l=list&p=1&s=10&sort=newest.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A
Appendix B
B.1.1. Isotherms. At low temperature, the elastic properties exhibit three types of evolution with the Am content, as shown in Fig. 17: a “V” (or “U”) shape, a “W” shape, or a “Δ” shape. This is consistent with the fact that the cationic concentrations in these oxides are linearly dependent on the americium content for the two sections UO2 to U0.5Am0.5O2 and U0.5Am0.5O2 to AmO2 (see Fig. 1).
B.1.2. Effect of the O/M ratio on the elastic properties. Fig. 18 shows the effect of the O/M ratio on the evolution with temperature of C11, C12, C44 and the Zener ratio in (U,Am)O2−x for 2 Am contents.
Acknowledgements
The authors would like to thank Bruno Michel and Anna Smith for fruitful discussions. This work was supported by the basic research Program (RTA) of the CEA Energy Division and is part of the PATRICIA project, which has received funding from the Euratom research and training programme 2019–2020 under grant agreement no 945077. It was performed using HPC resources from GENCI at TGCC and CINES under the allocations 2023 – A0150906922 and 2023 – R0151010339, as well as resources from CCRT funded by the CEA/DES simulation programme.References
- Homogeneous versus Heterogeneous Recycling of Transuranics in Fast Nuclear Reactors, Nuclear Energy Agency: Organisation for Economic Co-operation and Development, Paris, 2012 Search PubMed.
- A. Barco, et al., Design and Development of the ESA Am-Fueled Radioisotope Power Systems, 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2019, pp. 1–11 DOI:10.1109/AERO.2019.8741786.
- A. Barco, C. Fongarland, A. Group and R. M. Ambrosi, Safety Studies for the ESA Space Nuclear Power Systems: Accident Modelling and Analysis, 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2019, pp. 1–8 DOI:10.1109/AERO.2019.8741744.
- T. Wiss and D. Freis, Investigation on the use of Americium Oxide for Space Power Sources: Radiation Damage Studies, E3S Web Conf., 2017, 16, 05004 CrossRef.
- C. Barklay, E. J. Watkinson, R. Ambrosi, R. Mesalam, A. Barco and D. Kramer, Considerations for Utilising Alternative Radioisotopes in Radioisotope Power Systems, 2021 IEEE Aerospace Conference (50100), IEEE, Big Sky, MT, USA, 2021, pp. 1–6 DOI:10.1109/AERO50100.2021.9438353.
- E. J. Watkinson, et al., Thermal Properties and Behaviour of Am-Bearing Fuel in European Space Radioisotope Power Systems, Thermo, 2021, 1(3), 297–331, DOI:10.3390/thermo1030020.
- A. V. Mikhalev, D. O. Chernov and V. V. Korobeinikov, Use of Am-241 in RTGs, J. Phys.: Conf. Ser., 2020, 1689(1), 012063, DOI:10.1088/1742-6596/1689/1/012063.
- J.-F. Vigier, et al., Optimization of Uranium-Doped Americium Oxide Synthesis for Space Application, Inorg. Chem., 2018, 57(8), 4317–4327, DOI:10.1021/acs.inorgchem.7b03148.
- R. Ambrosi, et al., Americium-241 radioisotope thermoelectric generator development for space applications, International nuclear atlantic conference (INAC 2013), Recife, PE (Brazil), 24-29 Nov 2013, 2013 Search PubMed , https://inis.iaea.org/records/mp9hr-13a17.
- R. M. Ambrosi, D. P. Kramer, E. J. Watkinson, R. Mesalam and A. Barco, A Concept Study on Advanced Radioisotope Solid Solutions and Mixed-Oxide Fuel Forms for Future Space, Nucl. Technol., 2021, 207, 773–781 CrossRef.
- D. Horlait, F. Lebreton, P. Roussel and T. Delahaye, XRD Monitoring of α Self-Irradiation in Uranium–Americium Mixed Oxides, Inorg. Chem., 2013, 52(24), 14196–14204, DOI:10.1021/ic402124s.
- O. S. Vălu, D. Staicu, O. Beneš, R. J. M. Konings and P. Lajarge, Heat capacity, thermal conductivity and thermal diffusivity of uranium–americium mixed oxides, J. Alloys Compd., 2014, 614, 144–150, DOI:10.1016/j.jallcom.2014.05.083.
- D. Prieur, et al., Local Structure and Charge Distribution in Mixed Uranium–Americium Oxides: Effects of Oxygen Potential and Am Content, Inorg. Chem., 2011, 50(24), 12437–12445, DOI:10.1021/ic200910f.
- D. Prieur, et al., Accommodation of multivalent cations in fluorite-type solid solutions: case of Am-bearing UO2, J. Nucl. Mater., 2013, 434(1–3), 7–16, DOI:10.1016/j.jnucmat.2012.11.037.
- D. Prieur, et al., Melting behaviour of americium-doped uranium dioxide, J. Chem. Thermodyn., 2016, 97, 244–252, DOI:10.1016/j.jct.2016.02.003.
- F. Lebreton, Synthèse et caractérisation d’oxydes mixtes d’uranium et d’américium, Université de Limoges, 2014 Search PubMed.
- E. Epifano, et al., High temperature heat capacity of (U,Am)O2±x, J. Nucl. Mater., 2017, 494, 95–102, DOI:10.1016/j.jnucmat.2017.07.009.
- E. Epifano, et al., Extreme multi-valence states in mixed actinide oxides, Commun. Chem., 2019, 2(1), 59, DOI:10.1038/s42004-019-0161-0.
- E. Epifano, et al., Behaviour of (U,Am)O2 in oxidizing conditions: a high-temperature XRD study, J. Nucl. Mater., 2020, 531, 151991, DOI:10.1016/j.jnucmat.2020.151991.
- E. Epifano, et al., Melting behaviour of uranium–americium mixed oxides under different atmospheres, J. Chem. Thermodyn., 2020, 140, 105896, DOI:10.1016/j.jct.2019.105896.
- E. Epifano, Study of the U–Am–O ternary phase diagram, Université Paris-Saclay, 2017 Search PubMed.
- M. Bertolus and B. Michel, D7.6 Synthesis of INSPYRE results, INSPYRE Deliverables, 2022 Search PubMed.
- M. Bertolus, et al., Linking atomic and mesoscopic scales for the modelling of the transport properties of uranium dioxide under irradiation, J. Nucl. Mater., 2015, 462, 475–495, DOI:10.1016/j.jnucmat.2015.02.026.
- M. W. D. Cooper, M. J. D. Rushton and R. W. Grimes, A many-body potential approach to modelling the thermomechanical properties of actinide oxides, J. Phys.: Condens. Matter, 2014, 26(10), 105401, DOI:10.1088/0953-8984/26/10/105401.
- M. W. D. Cooper, S. T. Murphy, M. J. D. Rushton and R. W. Grimes, Thermophysical properties and oxygen transport in the (Ux,Pu1−x)O2 lattice, J. Nucl. Mater., 2015, 461, 206–214, DOI:10.1016/j.jnucmat.2015.03.024.
- M. W. D. Cooper, S. T. Murphy, P. C. M. Fossati, M. J. D. Rushton and R. W. Grimes, Thermophysical and anion diffusion properties of (Ux,Th1−x)O2, Proc. Phys. Soc., London, Sect. A, 2014, 470(2171), 20140427, DOI:10.1098/rspa.2014.0427.
- M. J. Rahman, B. Szpunar and J. A. Szpunar, Comparison of thermomechanical properties of (Ux,Th1−x)O2, (Ux,Pu1−x)O2 and (Pux,Th1−x)O2 systems, J. Nucl. Mater., 2019, 513, 8–15, DOI:10.1016/j.jnucmat.2018.10.038.
- P. S. Ghosh, et al., Melting behavior of (Th,U)O2 and (Th,Pu)O2 mixed oxides, J. Nucl. Mater., 2016, 479, 112–122, DOI:10.1016/j.jnucmat.2016.06.037.
- C. O. T. Galvin, M. Machida, H. Nakamura, D. A. Andersson and M. W. D. Cooper, Correlations for the specific heat capacity of (UxPu1−x)1 − yGdyO2−z derived from molecular dynamics, J. Nucl. Mater., 2022, 572, 154028, DOI:10.1016/j.jnucmat.2022.154028.
- C. O. T. Galvin, P. A. Burr, M. W. D. Cooper, P. C. M. Fossati and R. W. Grimes, Using molecular dynamics to predict the solidus and liquidus of mixed oxides (Th,U)O2, (Th,Pu)O2 and (Pu,U)O2, J. Nucl. Mater., 2020, 534, 152127, DOI:10.1016/j.jnucmat.2020.152127.
- I. Cheik Njifon and E. Torres, Phonons and thermophysical properties of U1−xPuxO2 mixed oxide (MOX) fuels, J. Nucl. Mater., 2020, 537, 152158, DOI:10.1016/j.jnucmat.2020.152158.
- C. Takoukam-Takoundjou, E. Bourasseau and V. Lachet, Study of thermodynamic properties of U1−yPuyO2 MOX fuel using classical molecular Monte Carlo simulations, J. Nucl. Mater., 2020, 534, 152125, DOI:10.1016/j.jnucmat.2020.152125.
- C. Takoukam-Takoundjou, E. Bourasseau, M. J. D. Rushton and V. Lachet, Optimization of a new interatomic potential to investigate the thermodynamic properties of hypo-stoichiometric mixed oxide fuel U1−yPuyO2−x, J. Phys.: Condens. Matter, 2020, 32(50), 505702, DOI:10.1088/1361-648X/abace3.
- E. Jossou, L. Malakkal, J. Ranasingh, B. Szpunar and J. Szpunar, Thermophysical properties of (UxAm1−x)O2 MOX fuel, Comput. Mater. Sci., 2020, 172, 109324, DOI:10.1016/j.commatsci.2019.109324.
- D. Bathellier, M. Lainet, M. Freyss, P. Olsson and E. Bourasseau, A new heat capacity law for UO2, PuO2 and (U,Pu)O2 derived from molecular dynamics simulations and useable in fuel performance codes, J. Nucl. Mater., 2021, 549, 152877, DOI:10.1016/j.jnucmat.2021.152877.
- M. J. D. Rushton and A. Chroneos, Impact of uniaxial strain and doping on oxygen diffusion in CeO2, Sci. Rep., 2014, 4(1), 6068, DOI:10.1038/srep06068.
- X.-Y. Liu, et al., Molecular Dynamics Simulation of Thermal Transport in UO2 Containing Uranium, Oxygen, and Fission-product Defects, Phys. Rev. Appl., 2016, 6(4), 044015, DOI:10.1103/PhysRevApplied.6.044015.
- B. Labonne, S. Orlat and M. Bertolus, Development of an interatomic potential for mixed uranium–americium oxides and application to the determination of the structural and thermodynamic properties of (U,Am)O2 with americium contents below 50%, J. Nucl. Mater., 2023, 579, 154390, DOI:10.1016/j.jnucmat.2023.154390.
- S. Casalta, Etude des propriétés du système Am-O en vue de la transmutation de l’Americium 241 en réacteur à neutrons rapides, Thèse Aix-Marseille I, 1996 Search PubMed , https://theses.fr/1996AIX11036.
- M. Kato, K. Morimoto, H. Sugata, K. Konashi, M. Kashimura and T. Abe, Solidus and liquidus temperatures in the UO2–PuO2 system, J. Nucl. Mater., 2008, 373(1–3), 237–245, DOI:10.1016/j.jnucmat.2007.06.002.
- M. S. Daw and M. I. Baskes, Semiempirical, Quantum Mechanical Calculation of Hydrogen Embrittlement in Metals, Phys. Rev. Lett., 1983, 50(17), 1285–1288, DOI:10.1103/PhysRevLett.50.1285.
- M. S. Daw and M. I. Baskes, Embedded-atom method: derivation and application to impurities, surfaces, and other defects in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29(12), 6443–6453, DOI:10.1103/PhysRevB.29.6443.
- P. M. Morse, Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels, Phys. Rev., 1929, 34(1), 57–64, DOI:10.1103/PhysRev.34.57.
- R. A. Buckingham, The classical equation of state of gaseous helium, neon and argon, Proc. Phys. Soc., London, Sect. A, 1938, 168(933), 264–283, DOI:10.1098/rspa.1938.0173.
- M. S. Talla Noutack, G. Jomard, M. Freyss and G. Geneste, Structural, electronic and energetic properties of uranium–americium mixed oxides U1−yAmy2 using DFT+U calculations, J. Phys.: Condens. Matter, 2019, 31(48), 485501, DOI:10.1088/1361-648X/ab395e.
- M. S. T. Noutack, M. Freyss, G. Jomard and G. Geneste, Electron polarons and donor point defects in americium dioxide AmO2, Phys. Rev. B, 2020, 101(2), 024108, DOI:10.1103/PhysRevB.101.024108.
- A. P. Thompson, et al., LAMMPS – a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171, DOI:10.1016/j.cpc.2021.108171.
- P. Carnevali, F. Ercolessi and E. Tosatti, Melting and nonmelting behavior of the Au(111) surface, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36(12), 6701–6704, DOI:10.1103/PhysRevB.36.6701.
- F. Ercolessi, W. Andreoni and E. Tosatti, Melting of small gold particles: mechanism and size effects, Phys. Rev. Lett., 1991, 66(7), 911–914, DOI:10.1103/PhysRevLett.66.911.
- J. R. Morris, C. Z. Wang, K. M. Ho and C. T. Chan, Melting line of aluminum from simulations of coexisting phases, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(5), 3109–3115, DOI:10.1103/PhysRevB.49.3109.
- A. B. Belonoshko, Molecular dynamics of MgSiO3 perovskite at high pressures: equation of state, structure, and melting transition, Geochim. Cosmochim. Acta, 1994, 58(19), 4039, DOI:10.1016/0016-7037(94)90265-8.
- F. Cricchio, A. B. Belonoshko, L. Burakovsky, D. L. Preston and R. Ahuja, High-pressure melting of lead, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(14), 140103, DOI:10.1103/PhysRevB.73.140103.
- J. Bouchet, F. Bottin, G. Jomard and G. Zérah, Melting curve of aluminum up to 300 GPa obtained through ab initio molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(9), 094102, DOI:10.1103/PhysRevB.80.094102.
- W. Voigt, Lehrbuch der Kristallphysik, 1928, vol. 962 Search PubMed.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 55 CrossRef.
- R. Hill, The Elastic Behaviour of a Crystalline Aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- R. E. McHenry, Melting Points of Curium and Americium Oxides, Trans. Am. Nucl. Soc., 1965, 8, 75 Search PubMed.
- E. Epifano, et al., Insight into the Am–O Phase Equilibria: A Thermodynamic Study Coupling High-Temperature XRD and CALPHAD Modeling, Inorg. Chem., 2017, 56(13), 7416–7432, DOI:10.1021/acs.inorgchem.7b00572.
- P. Gotcu-Freis, J.-Y. Colle, C. Guéneau, N. Dupin, B. Sundman and R. J. M. Konings, A thermodynamic study of the Pu–Am–O system, J. Nucl. Mater., 2011, 414(3), 408–421, DOI:10.1016/j.jnucmat.2011.05.014.
- M. Rochedy, A. L. Smith, M. Bertolus, B. Labonne, C. Guéneau and O. Beneš, D4.3 Measurements and atomic scale calculations in U–Pu–Am–Np–O systems, PATRICIA Deliverable, 2023 Search PubMed , https://cordis.europa.eu/project/id/945077/results/en.
- C. Guéneau, A. Chartier, P. Fossati, L. Van Brutzel and P. Martin, Thermodynamic and Thermophysical Properties of the Actinide Oxides, Comprehensive Nuclear Materials, Elsevier, 2020, pp. 111–154 DOI:10.1016/B978-0-12-803581-8.11786-2.
- R. J. M. Konings, et al., The Thermodynamic Properties of the f-Elements and their Compounds. Part 2. The Lanthanide and Actinide Oxides, J. Phys. Chem. Ref. Data, 2014, 43(1), 013101, DOI:10.1063/1.4825256.
- I. D. Prodan, G. E. Scuseria and R. L. Martin, Covalency in the actinide dioxides: systematic study of the electronic properties using screened hybrid density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(3), 033101, DOI:10.1103/PhysRevB.76.033101.
- L. Petit, A. Svane, Z. Szotek, W. M. Temmerman and G. M. Stocks, Electronic structure and ionicity of actinide oxides from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(4), 045108, DOI:10.1103/PhysRevB.81.045108.
- B. M. Adams, et al., Dakota, A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 6.15 User's Manual, Sandia Technical Report, SAND2020-12495, 2021.
- Eddy and John, JEGA V 2.3, 2009.
- J. A. Fahey, R. P. Turcotte and T. D. Chikalla, Thermal expansion of the actinide dioxides, Inorg. Nucl. Chem. Lett., 1974, 10(6), 459–465, DOI:10.1016/0020-1650(74)80067-X.
- M. Idiri, T. Le Bihan, S. Heathman and J. Rebizant, Behavior of actinide dioxides under pressure: UO2 and ThO2, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(1), 014113, DOI:10.1103/PhysRevB.70.014113.
- T. Nishi, A. Itoh, K. Ichise and Y. Arai, Heat capacities and thermal conductivities of AmO2 and AmO1.5, J. Nucl. Mater., 2011, 414(2), 109–113, DOI:10.1016/j.jnucmat.2011.01.019.
- M. S. Talla Noutack, G. Geneste, G. Jomard and M. Freyss, First-principles investigation of the bulk properties of americium dioxide and sesquioxides, Phys. Rev. Mater., 2019, 3(3), 035001, DOI:10.1103/PhysRevMaterials.3.035001.
- W. Huang and H. Chen, Investigation of the elastic, hardness, and thermodynamic properties of actinide oxides, Phys. B, 2014, 449, 133–137, DOI:10.1016/j.physb.2014.05.024.
- Y. Lu, Y. Yang, F. Zheng, B.-T. Wang and P. Zhang, Electronic, mechanical, and thermodynamic properties of americium dioxide, J. Nucl. Mater., 2013, 441(1–3), 411–420, DOI:10.1016/j.jnucmat.2013.06.043.
- E. Caglak and P.-E. Labeau, Lattice parameter of Am, Np bearing MOX fuel: an empirical potential study, J. Phys. Commun., 2021, 5(3), 035012, DOI:10.1088/2399-6528/abe921.
- M. Rochedy, A. Smith, M. Bertolus, B. Labonne, C. Guéneau and O. Benes, D4.4 Final report on thermodynamic models of U-Pu-Am-Np-O systems, PATRICIA H2020 Deliverable, to be published 2024.
- D. S. Aidhy, B. Liu, Y. Zhang and W. J. Weber, Chemical expansion affected oxygen vacancy stability in different oxide structures from first principles calculations, Comput. Mater. Sci., 2015, 99, 298–305, DOI:10.1016/j.commatsci.2014.12.030.
- R. A. Hein and P. N. Flagella, Technical Report GEMP-578, 1968 DOI:10.2172/4552169.
- L. Leibowitz, L. W. Mishler and M. G. Chasanov, Enthalpy of solid uranium dioxide from 2500 °K to its melting point, J. Nucl. Mater., 1969, 29(3), 356 CrossRef CAS.
- A. E. Ogard, Plutonium 1970 and Other Actinides, Metallurgical Society of the American Institute of Mining, 1970, p. 78 Search PubMed.
- P. Fouquet-Métivier, et al., Investigation of the solid/liquid phase transitions in the U–Pu–O system, Calphad, 2023, 80, 102523, DOI:10.1016/j.calphad.2022.102523.
- A. S. Dworkin and M. A. Bredig, Diffuse transition and melting in fluorite and antifluorite type of compounds. Heat content of potassium sulfide from 298 to 1260 degree K, J. Phys. Chem., 1968, 72(4), 1277–1281, DOI:10.1021/j100850a035.
- M. T. Hutchings, High-temperature studies of UO2 and ThO2 using neutron scattering techniques, J. Chem. Soc., Faraday Trans. 2, 1987, 83(7), 1083, 10.1039/f29878301083.
- J. Ralph and G. J. Hyland, Empirical confirmation of a bredig transition in UO2, J. Nucl. Mater., 1985, 132, 76 CrossRef CAS.
- J. P. Hiernaut, G. J. Hyland and C. Ronchi, Premelting transition in uranium dioxide, Int. J. Thermophys., 1993, 14, 609–612, DOI:10.1007/BF00566058.
- T. R. Pavlov, et al., Measurement and interpretation of the thermo-physical properties of UO2 at high temperatures: the viral effect of oxygen defects, Acta Mater., 2017, 139, 138–154, DOI:10.1016/j.actamat.2017.07.060.
- C. Ronchi, J. P. Hiernaut and G. J. Hyland, Laboratory Measurement of the Heat Capacity of Urania up to 8000 K: I. Experiment, Nucl. Sci. Eng., 1993, 113(1), 1 CrossRef CAS.
- C. B. Basak, A. K. Sengupta and H. S. Kamath, Classical molecular dynamics simulation of UO2 to predict thermophysical properties, J. Alloys Compd., 2003, 360(1–2), 210–216, DOI:10.1016/S0925-8388(03)00350-5.
- E. Yakub, C. Ronchi and D. Staicu, Molecular dynamics simulation of premelting and melting phase transitions in stoichiometric uranium dioxide, J. Chem. Phys., 2007, 127(9), 094508, DOI:10.1063/1.2764484.
- S. I. Potashnikov, A. S. Boyarchenkov, K. A. Nekrasov and A. Y. Kupryazhkin, High-precision molecular dynamics simulation of UO2–PuO2: pair potentials comparison in UO2, J. Nucl. Mater., 2011, 419(1–3), 217–225, DOI:10.1016/j.jnucmat.2011.08.033.
- E. T. Dubois, J. Tranchida, J. Bouchet and J.-B. Maillet, Atomistic simulations of nuclear fuel UO2 with machine learning interatomic potentials, Phys. Rev. Mater., 2024, 8(2), 025402, DOI:10.1103/PhysRevMaterials.8.025402.
- D. Bathellier, M. Freyss, I. Cheik Njifon, P. Olsson, E. Bourasseau and M. Bertolus, Heat capacity of UO2 and PuO2 from ab initio molecular dynamics simulations, To be published.
- A. Annamareddy and J. Eapen, Low Dimensional String-like Relaxation Underpins Superionic Conduction in Fluorites and Related Structures, Sci. Rep., 2017, 7(1), 44149, DOI:10.1038/srep44149.
- H. Zhang, X. Wang, A. Chremos and J. F. Douglas, Superionic UO2: a model anharmonic crystalline material, J. Chem. Phys., 2019, 150(17), 174506, DOI:10.1063/1.5091042.
- P. C. M. Fossati, A. Chartier and A. Boulle, Structural Aspects of the Superionic Transition in AX2 Compounds With the Fluorite Structure, Front. Chem., 2021, 9, 723507, DOI:10.3389/fchem.2021.723507.
- G. Porto, et al., Thermodynamic and thermoelastic properties of hypostoichiometric MOX fuels with molecular dynamics simulations, J. Nucl. Mater., 2024, 598, 155163, DOI:10.1016/j.jnucmat.2024.155163.
| This journal is © the Owner Societies 2025 |