Fluctuation-induced extensive molecular transport via modulation of interaction strength

Abstract

In our previous work, we studied the thermodynamics of two cases of intercompartmental transport through a carbon nanotube: one involving water molecules and the other involving nonpolar molecules. Free energy calculations indicate that transporting water molecules from one compartment to another via a narrow channel is impossible, whereas for nonpolar molecules, only approximately half can be transported. Therefore, the interaction strength between transported molecules significantly affects molecular transport. In this study, we examined the effect of interaction strength on molecular transport both kinetically and thermodynamically via simple models and molecular simulation methods. The results revealed that, depending on the interaction strength, the transport behavior can be categorized into three regimes: water-like, nonpolar-like, and transition regimes. Interestingly, the molecular fluctuations in the transition regime are so large that a significant number of molecules are transported between the compartments in an oscillatory manner, exceeding the transport of half of the molecules in the nonpolar-like regime. Thus, to induce molecular transport driven by large fluctuations, the interaction strength should remain within a moderate range. Moreover, potential of mean force (PMF) analysis supports this large fluctuating behavior, as the PMF profile exhibits a flat region that allows significant variation with no free energy cost. We elucidate the role of interaction strength in molecular transport, as well as the deep connection between molecular fluctuations and molecular transport.

---

1. Introduction

Chemical reactions in cells occur in complex environments where they are tightly regulated and precisely controlled, as observed in signal transduction via molecular transport, particularly through channels in membranes that separate the inner and outer cellular spaces.^1–9 To fundamentally understand the underlying physics of how these channels operate, it is essential to first comprehend the general principles that explain how and why molecular transport through channels occurs spontaneously. To investigate this issue, we studied simple models representing transport systems in which molecules are transferred between two separate compartments connected by a carbon nanotube (CNT).^10,11

In our previous study, we calculated the potential of mean force (PMF) for the complete transport of molecules from one compartment to another. We investigated two types of transported molecules, namely, water¹⁰ and nonpolar¹¹ molecules, which represent strong and weak interactions, respectively. We modeled nonpolar molecules by using water molecules whose partial charges were set to zero. In both cases, the transport of molecules into the initially empty inner space of the CNT was thermodynamically spontaneous. However, further transport from the CNT to the other compartment depended on whether the molecules were water or nonpolar molecules. For water molecules, the strong hydrogen-bonding interactions made it thermodynamically unfavorable to break these bonds, preventing the molecules from entering the empty space of the other compartment without compensation from the strong water–CNT interactions. In contrast, nonpolar molecules, without such strong interactions, exhibited spontaneous transport due to an increase in entropy, although only up to approximately half of all molecules were transported.

Given that the two model systems were identical except for the magnitude of the partial charges of the transported molecules, the observed differences in transport behavior highlight the significant influence of the interaction strength on the process. This naturally raises the following question: what happens if the interaction strength varies between the two extremes? Specifically, does the transport behavior in such cases resemble that of water or nonpolar molecules, or does it exhibit entirely new characteristics?

In this work, we addressed this question by performing unconstrained molecular dynamics (MD) simulations via a transport model in which all the molecules initially reside in one of two compartments connected by a CNT. We varied the magnitude of the partial charges, covering a range from water (charged) to nonpolar (neutral) molecules. Each trajectory was analyzed to observe the transport behavior across different interaction strengths. Through this analysis, we identified three categories of behavior, namely, the water-like regime, the nonpolar-like regime, and the transitional regime that has not been previously reported. To better understand these behaviors, we also calculated the PMFs for representative cases. The PMF results were consistent with the transport behaviors observed in the unconstrained MD simulations, providing a thermodynamic explanation for the different transport regimes.

Furthermore, understanding the conditions under which complete transport can occur is crucial for controlling molecular flow in industrial applications. For example, when aiming to transfer all molecules from one compartment to another, it is important to assess whether this is feasible. Our previous work indicated that neither water nor nonpolar molecules could be completely transported: transport rarely occurred for water molecules, whereas only partial transport (approximately half) was achievable for nonpolar molecules. Therefore, exploring whether complete transport can be achieved with an intermediate interaction strength is of practical interest, particularly in the context of engineering applications.

This paper is organized as follows: the next section provides the details of our models and simulation methods. The Results and Discussion section presents and explains the findings from our unconstrained MD simulations and PMF calculations. The final section summarizes our conclusions and their implications.

2. Computational models and methods

2.1. Computational models

To explore various transport cases of molecules with partial charges of different magnitudes, we used the model employed in our previous studies.^10,11 As shown in Fig. 1(A), the model comprises two compartments connected by a CNT, with molecules that move within the inner space created by the compartments and the CNT. The compartments and the CNT are fixed in space, while the transported molecules can move freely. Additionally, we generalized the model of transported molecules to allow variation in the strength of their interactions.

Fig. 1 (A) Molecular transport models with charge scaling factor (f) values of 0.6 (left) and 0.8 (right) for the transported molecules (orange or green). The blue lines represent the simulation boxes. (B) An example of molecular transport where all the molecules are transported from compartment 1 (left) to compartment 2 (right), with f = 0.6.

Specifically, in each case, all model parameters remained unchanged, except that the transported molecules exhibited partial charges of different magnitudes. The charge magnitude determines the strength of the electrostatic interactions between the transported molecules. The atoms in the other parts of the model, i.e., the compartments and the CNT, consist of carbon-based atoms with a partial charge of zero. Therefore, changes in the magnitude of the partial charges affect only the interactions between the transported molecules.

The models of transported molecules used in both our previous and current studies are based on the TIP3P water model,¹² which has been widely used in MD simulations involving CNTs and graphene plates.^13–16 In our previous research, we used the original TIP3P model for water molecules and a modified version in which all partial charges were set to zero for nonpolar molecules.^11,17 In this study, we introduced a charge scaling factor (f) for the partial charges in the TIP3P model. For example, the scaling factor for water molecules is 1, whereas for nonpolar molecules, the value is 0, as indicated in Table 1. For other types of transported molecules with arbitrary values of f, we adjusted the partial charges in the TIP3P model by applying the corresponding factor values. This method ensured that the net charge of any transported molecule remained zero. Using this approach, we modulated the strength of the electrostatic interactions. A similar method has previously been adopted to modulate the Lennard-Jones (LJ) interaction strength.^18,19

Table 1 The partial electric charges of atoms are determined by f for various transported molecules. Partial electric charges are calculated by multiplying the original partial charge values and the scaling factor f

Charge scaling factor (f)	Partial charge of oxygen atom	Partial charge of hydrogen atoms
1.0 (original TIP3P water model)	−0.834	0.417
0.9	−0.7506	0.3753
0.8	−0.6672	0.3336
0.7	−0.5838	0.2919
0.6	−0.5004	0.2502
0.5	−0.417	0.2085
0.4	−0.3336	0.1668
0.3	−0.2502	0.1251
0.2	−0.1668	0.0834
0.1	−0.0834	0.0417
0.0 (nonpolar molecule model)	0	0

---

We modeled the CNTs used as channels with the carbon atoms defined in the AMBER force field,²⁰ which is commonly employed alongside the TIP3P model.^13,14 The 6–12 LJ parameters of the carbon atoms in the CNTs were σ = 0.3400 nm, and ε = 0.3598 kJ mol⁻¹. The CNT used in this study was of the (6,6) armchair type with a length of 4 nm. The diameter of this CNT was small enough that only one molecule could fit across its cross section, although multiple molecules could be arranged along its length.

To create the compartments, we used modified graphene plates. These plates exhibited the same shape and molecular geometry as regular graphene plates, but their LJ interactions were weaker. Specifically, the LJ parameters for the atoms were σ = 0.3400 nm, and ε = 0.03598 kJ mol⁻¹. The σ value is the same as that for carbon atoms in the AMBER force field, but the ε value is 10 times lower. The reduced interaction strength prevented the adsorption of transported molecules onto the compartment walls. Each compartment had dimensions of 3.1 nm × 3.3 nm × 4 nm, as shown in Fig. 1(A). The two compartments were connected by the CNT, with each compartment containing an opening precisely sized to accommodate the CNT.

To calculate the LJ interactions within the model, we used the Lorentz–Berthelot rule,^21–23 and for long–range electrostatic interactions, we employed the particle–mesh Ewald (PME) method.²⁴ The cutoff distance for both the LJ and electrostatic interactions was set to 1.4 nm. Additional model details are described elsewhere.^10,11

2.2. Details of the MD simulations

We conducted MD simulations to investigate the effect of the interaction strength on the kinetics and thermodynamics of molecular transport for various molecules with different f values.

The simulations were performed under NVT (constant number, volume, and temperature) conditions at a temperature of 300 K. The number of transported molecules in the simulations was 400. To maintain the temperature, we employed a V-rescale thermostat²⁵ with a coupling constant of 0.1 ps. The integration time step was set to 2.0 fs.

Periodic boundary conditions (PBCs) were applied along all three Cartesian directions (x, y, and z). To minimize the interactions through PBCs along the z-axis, we used a simulation box with a length of 32 nm along the z-axis, which was significantly larger than the length of the transport system, i.e., 12 nm, as shown in Fig. 1(A).

For the MD simulations, we used the GROMACS simulation package (version 2023.3).²⁶ To fix the positions of the CNT and the two compartments, we utilized the freeze group option in GROMACS.²³ For trajectory analysis, we employed the MDAnalysis package (version 2.7.0).^27,28 To visualize the simulation results and prepare the figures for this paper, we employed VMD (version 1.9.4)²⁹ and xmgrace programs (version 5.1.25; https://plasma-gate.weizmann.ac.il/Grace/).

2.3. Unconstrained MD simulations

To observe the direct impact of interaction strength, we conducted a series of MD simulations with different f values without imposing any constraints on the transported molecules. In these transport simulations, all the transported molecules were initially placed in a single compartment (compartment 1), as shown in Fig. 1(B).

To prepare this initial state, we first carried out a 10-ns NVT MD simulation after placing the molecules in compartment 1 to achieve equilibrium within the compartment before initiating molecular transport. During this equilibration step, a molecular barricade—a six-carbon ring with a size comparable to the diameter of the CNT—was positioned at the boundary between the CNT and compartment 1 to prevent molecules from entering the CNT before the transport simulation began.¹⁷ After the 10-ns equilibration period, we removed the barricade to establish the initial state for the subsequent transport simulations, as illustrated in Fig. 1(B). Finally, we conducted unconstrained transport simulations with various f values to investigate whether molecular transport occurred and to quantify how many molecules moved to compartment 2.

2.4. PMF calculation

To better understand the unconstrained MD simulation results and calculate the free energy change during complete molecular transport (Fig. 1(B)), we used the PMF method previously applied to the water case¹⁰ and the nonpolar case.¹¹ In this study, we considered various f values for the PMF calculation. The PMF is represented as a function of the number of molecules in compartment 1 (N₁), because N₁ alone sufficiently represents the state of the transport process, as explained below.

The system state can generally be characterized by three variables, namely N₁, the number of molecules in the CNT (N_CNT), and the number of molecules in compartment 2 (N₂); however, these variables are not independent. Specifically, N_CNT remained almost constant during the simulations, as shown later, and, with its value varying between 10 and 15 depending on the value of f. Therefore, the state was primarily determined by N₁ and N₂. Furthermore, since N₁ + N₂ + N_CNT = 400, there was essentially only one independent variable: either N₁ or N₂. In our work, we chose N₁ as the variable for the PMF profile.

For the PMF calculation, N₁ can be controlled by blocking the passage of molecules to compartment 2. Specifically, for molecules to move to compartment 2, they must pass through the CNT. Therefore, by constraining one of the molecules within the CNT and fixing it in space, N₁ can be maintained at a certain value. For convenience, we denote this value as 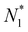. Now, if we slightly move the constrained molecule along the CNT toward compartment 2, we can obtain a new value of N₁, which is 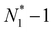. In this procedure, one molecule in the CNT, which occurs closest to compartment 2, is pushed into compartment 2 by the movement of the constrained molecule, resulting in an increase in the N₂ value and a decrease in the value of N₁, whereas the value of the N_CNT remains constant. We then fix the previously constrained molecule again and sample the state specified by . By continuing to move the constrained molecule toward compartment 2 step by step, we can sequentially push the molecules into compartment 2 and sample the states specified by , , 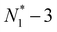etc.

Although the entire procedure described above is designed to calculate the PMF for molecular transport, if we focus solely on the constrained molecule, it can be considered a PMF calculation for moving this molecule from one point to another within the CNT. This is similar to a standard PMF calculation using umbrella sampling,^30,31 which was implemented in our work. In other words, we can map the change from to during transport to the translation of the constrained molecule over a certain distance along the CNT. This approach is feasible because, in our case, molecular transport is directly related to the translation of the molecule within the CNT.

Nevertheless, this PMF method, which is based on the translation of the chosen molecule for constraint purposes, is limited in the range of the N₁ domain due to the finite length of the CNT, which is 4 nm. Because of this limit, the maximum number of molecules that can reside in the CNT ranges from 10 to 15, depending on the value of f (refer to the available space in the CNT shown in Fig. 1 and other figures). This defines the domain size covered by the method (ΔN₁) as approximately 10 to 15. For example, if ΔN₁ is 10, using this method with a well-chosen molecule for constraint purposes, we obtain the PMF for 390 ≤ N₁ ≤ 400. To further determine the PMF for 380 ≤ N₁ ≤ 390, instead of the previously constrained molecule now in compartment 2, we must identify another molecule in the CNT for constraint purposes and subsequently calculate the PMF for that interval. This process can be repeated until we obtain the PMF for N₁ = 0.

However, the above description does not capture the full extent of the PMF method. Even with N₁ = 0, molecules remain in the CNT, specifically, 10 molecules if ΔN₁ is 10. For complete transport to compartment 2, all molecules within the CNT must also be transferred to compartment 2 (Fig. 1(B)). To describe this situation accurately, we must eventually record N_CNT. However, in this work, to plot the entire PMF using a single coordinate N₁, instead of directly using N_CNT, we defined negative N₁ values as N₁ = N_CNT − ΔN₁. Therefore, the state N₁ = −1 (or N_CNT = 9 for ΔN₁ = 10), which follows immediately after N₁ = 0 (or N_CNT = 10) in the transport sequence, represents the situation where one molecule, previously located in the CNT next to compartment 2, has moved into compartment 2, leaving 9 molecules in the CNT. Similarly, the state N₁ = −2 (or N_CNT = 8) indicates that, compared with the fully-occupied state of the CNT (N₁ = 0 and N_CNT = 10), two molecules have been transferred to compartment 2, leaving 8 molecules in the CNT. Thus, N₁ = −10 (or N_CNT = 0) indicates that all 10 molecules in the CNT have been transported to compartment 2, suggesting that the CNT is now empty and that all the molecules are in compartment 2, resulting in complete transport. Consequently, when ΔN₁ = 10, the entire N₁ domain ranges from −10 to 400 and can be divided into intervals of ΔN₁ = 10. For each interval of ΔN₁ = 10, we can separately calculate the partial PMF.

After calculating the PMF for each partial domain, we can combine these piecewise PMF values to create a complete PMF profile for the entire domain range of −10 ≤ N₁ ≤ 400 (for the case of ΔN₁ = 10). Technically, when two adjacent PMF profiles are combined, it is necessary to have overlapping regions in their domains. For example, in the case of ΔN₁ = 10 mentioned above, the domain of the second PMF profile could be 382 ≤ N₁ ≤ 392 to ensure overlap with the domain of the first PMF profile, which is 390 ≤ N₁ ≤ 400. Further details are provided in our previous works.^10,11

Finally, while we described the sampling procedure as involving the continuous movement of constrained molecules to achieve different N₁ values, alternative methods for establishing these states could be used. For example, instead of preparing states one by one via the movement of constrained molecules, we could utilize configurations obtained from osmosis MD simulations in which complete transport from compartment 1 to 2 is achieved. The detailed methodology for this approach is described in our previous work.¹⁰

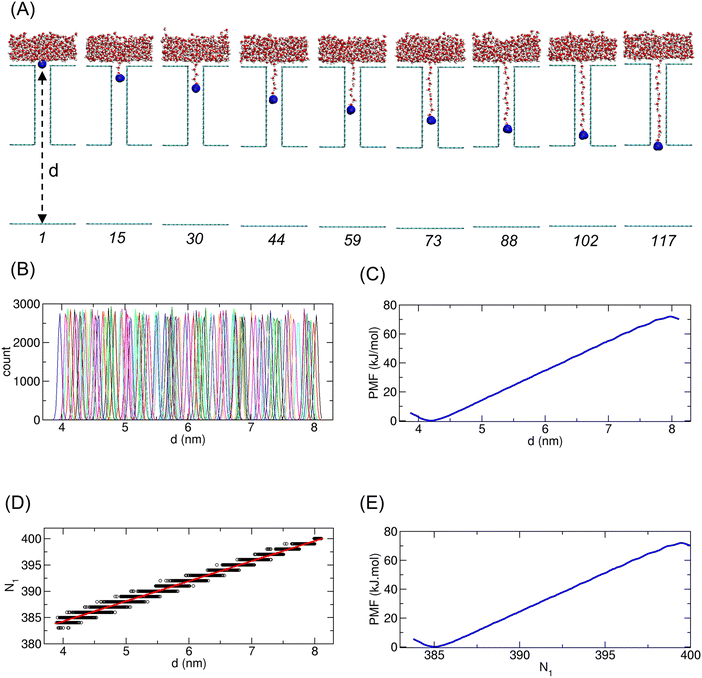
Now, let us consider the technical details of the PMF calculation. As mentioned earlier, to compute the PMF due to the change in N₁, we can equivalently calculate the PMF as a function of the translational distance d_CNT of the constrained molecule within the CNT. Note that, since the length of the CNT is 4 nm, the maximum distance d_CNT is 4 nm. However, for our convenience, we can use the distance d, not from the end of the CNT, but from the bottom graphene plate of compartment 2, such that d = d_CNT + 4 nm (Fig. 1(A) and 2(A)).

Fig. 2 PMF calculation for set 1 of the water case with f = 1. (A) Representative configurations of the nine windows selected from a total of 117 windows used for umbrella sampling. The numbers at the bottom indicate the window numbers. In each window, an umbrella potential was applied to the blue-colored water molecule to constrain the distance d from the bottom plate during the simulation. (B) Histograms of distances d of the constrained molecule from sampling across all 117 windows. (C) PMF as a function of d, which is calculated by solving the WHAM equation. (D) Plot of N₁versus d. The red line represents the regression curve obtained through nonlinear fitting, given by N₁ = 3.8206 d + 368.98 with a correlation coefficient of 0.9963. (E) PMF as a function of N₁, where the x-axis in (C) was converted from d to N₁via the regression curve in (D).

For the PMF calculation of a partial N₁ domain with ΔN₁, we employed the umbrella sampling method, introducing as many sampling windows as necessary to ensure sufficient overlap between adjacent windows and adequately cover the distance d_CNT. In each window, the constraining force on the chosen molecule was applied via an umbrella potential, namely, a harmonic potential with a force constant of 3000 kJ mol⁻¹ nm⁻². This force constant was chosen to be high enough to sample all desired states, regardless of the value of f; in fact, it was successfully employed in PMF calculations in our previous studies with f = 1¹⁰ and 0¹¹.

With this umbrella potential, we performed a 1500-ps NVT simulation for each window, using the first 500 ps for equilibration and the final 1 ns for PMF calculation. Before determining this simulation time, we carefully examined the convergence of the potential energy and other physical quantities, which reached equilibrium rapidly during equilibration. Furthermore, in our previous work with f = 1,¹⁰ we demonstrated the convergence of the PMF obtained from 1500-ps simulations using different time intervals.

We then obtained the PMF profile from the sampling data as a function of d by solving the equation of the weighted histogram analysis method (WHAM).^32,33 With the use of the strong linear relationship between N₁ and d, we converted the PMF profile into a function of N₁. This calculation was repeated for each partial domain of N₁, and the resulting PMF profiles were then merged into a single, final PMF profile. Finally, we adjusted the final PMF profile by shifting it along the y-axis so that the PMF value at N₁ = 0 was set to zero, allowing the use of the state at N₁ = 0 as a well-defined reference point. Further information can be found in our previous works.^10,11

2.5. Illustrative PMF calculation for f = 1

To illustrate the PMF calculation procedure described in Section 2.4, we detail the process using the water case with f = 1, as shown in Fig. 2. In this case, the occupation number of water molecules in the CNT was observed to be 15 on average; thus, ΔN₁ = 15. Accordingly, the N₁ domain of the first PMF profile spans approximately 385 ≤ N₁ ≤ 400, which we refer to as the set 1 domain.

In particular, for the PMF calculation of set 1, one water molecule was selected for constraint, highlighted in blue in Fig. 2(A). By applying constraints to the selected water molecule at various initial positions, we considered 117 windows for umbrella sampling. Snapshots of the system for representative windows are shown in Fig. 2(A). The histograms for the distance d of the constrained water molecule across all 117 windows are displayed in Fig. 2(B). Fig. 2(C) shows the PMF profile as a function of d. Using the linear relationship between d and N₁ (Fig. 2(D)), the final PMF for set 1 was obtained and is presented in Fig. 2(E).

Similarly, we performed PMF calculations for other domain sets, and the results for sets 2 to 5 are shown in Fig. 3(A). In the case of f = 1, the PMF of set 2 appears redundant because sets 1 and 3 together cover the domain region corresponding to set 2. However, for cases with lower f values, a small gap exists between sets 1 and 3, necessitating set 2 to fill this gap. For the entire PMF, a total of 72 sets were used.

Fig. 3 (A) PMF profiles for sets 1 to 5 of the water case with f = 1. To clearly illustrate the overlap between adjacent profiles, the profiles were shifted and arranged with spacing between them. (B) All PMF profiles from sets 1 to 72 (top colorful profiles) were merged into a single PMF (bottom profile shown as a thick black line). The region highlighted by the red dotted circle corresponds to the profiles shown in (A).

To combine the piecewise PMF profiles from all 72 sets into one single unified PMF, we merged the profiles sequentially. For two adjacent PMF profiles, one profile was shifted such that the average PMF values within the overlapping region matched. The two profiles were then averaged within the overlapping region to create a larger, merged PMF profile. Repeating this process across all sets resulted in a single unified PMF, as shown in Fig. 3(B).

In the above procedure, the total number of windows used across all 72 sets was 6144. Consequently, the total simulation time, calculated as 6144 × 1.5 ns, was 9216 ns or 9.216 μs. The same numbers of domain sets (72) and windows (6144) were used for the other cases with different f values.

To gain a deeper understanding of the molecular details within the CNT under the constraint force, we calculated the densities of individual water molecules along the principal axis (z-axis) of the CNT. The results are shown in Fig. 4. For each set, the constraint force results in a very narrow spatial distribution of the constrained water molecule, whereas the distributions of other water molecules, which are farther from the constrained molecule, are broader. Additionally, owing to strong intermolecular interactions, the water molecules remain close to one another, maintaining almost constant distances, which leads to the periodic patterns in the profile plots.

Fig. 4 Snapshots taken from the last frame and their individual water density profiles during the 1-ns production runs for selected windows from sets 1 to 4. The numbers at the bottom represent the corresponding window numbers. The constrained molecules in sets 1 to 5 are colored blue, green, violet, dark green, and cyan, respectively, corresponding to the colors of the PMF profiles in Fig. 3(A). In the density plots, the x-axis and y-axis represent the density (kg m⁻³) and the z-coordinate, respectively. Some window numbers are colored blue, green, and red to indicate that windows with the same color have similar density distributions for the constrained water molecules at the same z coordinates, resulting in overlap between their PMFs.

The water density profiles also provide insights into the molecular basis of the overlap between adjacent PMF profiles. Specifically, for each set in Fig. 4, as the window number increases, the narrow distribution of the constrained water molecules (constrained molecule 1) shifts downward. Before it reaches the end of the CNT at z = 14 nm, a broader distribution of the molecule chosen as the constrained molecule (constrained molecule 2) for the next domain set appears, ensuring overlap between adjacent PMFs. Therefore, the density profiles from some windows show the distributions of the two constrained water molecules: one from the current set (constrained molecule 1) and another from the following set (constrained molecule 2).

When considering the next set, we observe similar distributions of the aforementioned constrained water molecules (constrained molecules 1 and 2), but the relative broadness of the profiles is reversed. This occurs because the previously constrained molecule becomes unconstrained, causing its distribution to broaden, whereas the newly constrained molecule has a narrower distribution. Despite this difference, the presence of these common density profiles from two neighboring sets indicates the sampling of the same states of N₁, implying overlap between the adjacent PMF profiles.

More precisely in Fig. 4, for set 1, the density profile of the constrained molecule in set 1 (constrained molecule 1, blue) and the profile of the constrained molecule in set 2 (constrained molecule 2, green) are shown together for window 88. In set 2, similar density profiles (blue and green) at the same z locations are observed for window 31. The overlap between the same colored (blue and green) density profiles from different sets results in the overlap of their PMFs. Similarly, for sets 2 and 3, window 46 of set 2 and window 1 of set 3 have similar water density profiles (green and violet), whereas for sets 3 and 4, window 62 of Set 3 and window 18 of Set 4 have similar profiles (violet and dark green).

Although we discuss only the case with f = 0, the same discussion is applicable to other cases with different values of f.

3. Results and discussion

3.1. Trajectory analysis from unconstrained MD simulations

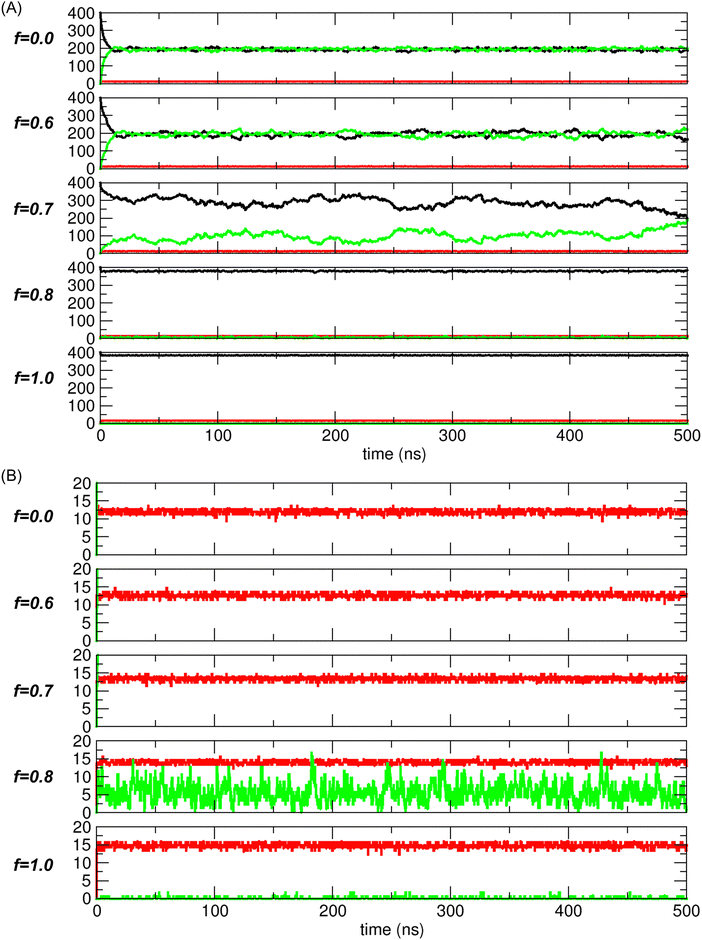
From the unconstrained MD simulations, we obtained the trajectories of systems under varying interaction strengths mediated by electrostatic interactions. Initially, all systems began with all transported molecules located in compartment 1, as shown on the left in Fig. 1(B). The system state was defined by N₁, N_CNT, and N₂, collectively expressed as a tuple, (N₁, N_CNT, N₂). Therefore, the initial state of the system was represented by (400, 0, 0) in the simulations.

As the simulation progressed, the system evolved toward a free-energy-minimized state, corresponding to the configuration with the lowest PMF value. Once this state was reached, the system stabilized, with thermal fluctuations around this configuration. For example, Fig. 5 shows the time evolution of the system state, with N₁ (black), N_CNT (red), and N₂ (green) plotted for different values of the scaling factor f (0.0, 0.6, 0.7, 0.8, and 1.0). Note that N₁ + N_CNT + N₂ = 400, as the total number of transported molecules remains constant at 400.

Fig. 5 (A) Trajectory analysis results for systems with f = 0.0, 0.6, 0.7, 0.8, and 1.0, displayed from top to bottom. The states, specified by the numbers of transported molecules in compartment 1 (N₁, black), CNT (N_CNT, red), and compartment 2 (N₂, green), are shown as functions of time. (B) The same plots as in (A), but with the y-axis range limited to values below 20 to better visualize the changes in N_CNT (red) and N₂ (green). Note that for f = 1.0, since N₁ + N_CNT + N₂ = 400 and N₂ ≈ 0, N₁≈ 400-N_CNT.

Fig. 5(A) shows two distinct regimes of f based on the trajectories. In one regime (f < 0.7), namely, for f = 0 (nonpolar) and f = 0.6, the dynamic behaviors are similar, with N₁ and N₂ converging to nearly equal values. However, the fluctuations for f = 0.6 are slightly larger than those for f = 0.0. In the other regime (f > 0.7), namely, for f = 0.8 and 1.0 (water), the common feature is that transport to compartment 2 is negligible. In contrast, for f = 0.7, which lies between these two regimes, the system does not converge to one of these characteristic states. Instead, it appears to explore a broader range of states, which will be further discussed later in relation to the PMF calculation.

The trajectories depicted in Fig. 5(B) indicate that the CNTs (red) are rapidly filled with molecules and remain in this state over time. Consequently, N_CNT remains nearly constant, typically at approximately 10 to 15, depending on the interaction strength or scaling factor f. This suggests that, after the initial period needed for the molecules to fill the CNT, the system state is once again essentially determined by N₁ (or N₂), as N₂ (or N₁) is simply given by 400-N₁-N_CNT (or 400-N₂-N_CNT).

To systematically analyze the change in N₁ with the f value, we calculated the average 〈N₁〉 and the standard deviation σ_N1. For this calculation, we disregarded the first 20 ns of the trajectory for equilibration and considered only the remaining 480 ns of the 500-ns simulation time for analysis. We examined various cases of f with intervals of 0.02, and within the range of f between 0.6 and 0.8, we used intervals of 0.001. The results are shown in Fig. 6.

Fig. 6 (A) Average number of N₁ (〈N₁〉) and (B) its fluctuation (σ_N1) from the 500-ns trajectories for various values of f. The error bars in (A) denote the fluctuations σ_N1.

Fig. 6(A) shows that when f < 0.65, the average number 〈N₁〉 is approximately 200-〈N_CNT〉/2 since 〈N₁〉 ≈ 〈N₂〉 (refer to Fig. 5(A) for f = 0 and 0.6) and 〈N₁〉 + 〈N_CNT〉 + 〈N₂〉 = 400. Moreover, 〈N₁〉 ≈ 200 since 〈N_CNT〉 ≪ 400. In the equilibrium state, the molecules are distributed equally between the two compartments, similar to nonpolar gas molecules. However, for f > 0.75, as f increases toward 1, 〈N₁〉 converges to 400-〈N_CNT〉 ≈ 400 since 〈N₂〉 ≈ 0 (refer to Fig. 5(B) for f = 0.8 and 1.0) and 〈N_CNT〉 ≪ 400. In this case, 〈N₁〉 ≈ 400 indicates that there is no transport to compartment 2, as observed in the water case. Between these two distinct regimes, there is a dramatic transition region where f ranges from 0.65 to 0.75.

In the transition regime (0.65 < f < 0.75), as shown in Fig. 6(A), with increasing f value, 〈N₁〉 does not change smoothly. Instead, it exhibits sharp and irregular variations. Consequently, 〈N₁〉 can decrease to 150 at certain f values, which is significantly less than the value of ∼200 observed for f < 0.65, whereas for other values, 〈N₁〉 can increase to 250. This result suggests the following: first, more than half of the molecules can be transported to compartment 2; second, in contrast to the nonpolar-like and water-like cases, where equilibrium is reached relatively quickly, the dynamics in this transition region are slower (also refer to Fig. 5(A) for f = 0.7), with various states explored in equilibrium, leading to large variations in 〈N₁〉.

To quantitatively understand the change in N₁ around 〈N₁〉, we show only the fluctuation in N₁, which is calculated from the standard deviation σ_N1, in Fig. 6(B). In Fig. 6(B), the maximum fluctuation occurs at f ≈ 0.7. This large fluctuation suggests substantial changes within the system, indicating the possibility of significant molecular transport. However, changes in N₁ that would directly support this transport are not observed in Fig. 5(A) for f = 0.7. To systematically investigate the possibility of such transport, we calculated the PMF.

Before we move to the PMF calculation, we must address the statistical significance of our results, which were based on a single simulation run for each value of f. To increase the statistical validity of our results, it would be ideal to perform multiple simulation runs and derive results from them. However, the objective of the fluctuation analysis is not to find statistically exact values of fluctuations but to gain insight into the system behavior as a function of f, allowing us to identify and estimate the transition regime. Moreover, instead of conducting multiple runs at sparse values of f, we performed single runs at very dense values of f, specifically at very closely neighboring values within the transition regime (f = 0.600, 0.601, …, 0.799, 0.800). Since we can approximate the results of two simulations from two very closely neighboring values of f as being equivalent to two simulations at a single value of f, this examination of very closely neighboring values of f in the transition regime compensated for the statistical error of single-run results.

Additionally, in the transition regime, the system behavior is more unpredictable than it is in the water-like and nonpolar-like states, which underscores the stochastic nature of the system. This unpredictability accounts for the irregular fluctuations observed in the transition regime. Consequently, a larger number of simulations may be required to accurately characterize the fluctuations as the stochastic nature of the system increases. However, determining the exact number of simulations necessary for statistical adequacy is challenging. This is why we chose to perform the PMF calculation, which provides a thermodynamic framework for understanding this stochastic behavior.

3.2. PMF

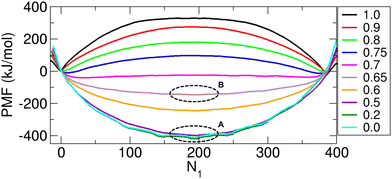
To better understand the molecular behaviors observed in the unconstrained MD simulations, we calculated the PMF, which represents the free energy change as a function of N₁. The PMF thermodynamically determines which dynamic processes occur spontaneously, and according to the minima of the PMF, we can predict the final system state reachable via these processes. The PMF results are shown in Fig. 7. The right and left ends of the N₁ axis correspond to the states where all the molecules reside in compartments 1 (or (400, 0, 0)) and 2 (or (0, 0, 400)), respectively.

Fig. 7 PMF profiles as a function of N₁ for various values of f ranging from 0.0 to 1.0.

To determine if the PMF results align with the observations from the unconstrained MD simulations, we can first examine the PMF value at the right end, where N₁ = 400, corresponding to the initial state in the simulations, and then progress toward the left end, reflecting decreasing values of N₁. As shown in Fig. 7, the PMF value at the right end is a local maximum, which leads the system to transition to states immediately to its left (N₁ < 400). This transition reflects the dynamic process in which molecules begin to fill the inner space of the CNT (Fig. 5(B)). Once the CNT is filled with molecules (at N₁ = 390 to 385, depending on f), further molecular transport to compartment 2 is determined by the value of f.

In Fig. 7, when f is greater than 0.7 (f = 0.75, 0.8, 0.9, and 1.0), as the system transitions further to the left (i.e., as N₁ decreases), it encounters barriers that are too high to overcome, causing fluctuations around the minimum value at N₁ = 390 to 385 (depending on f), as also shown in Fig. 5(A) (f = 0.8, 1.0). However, when f is less than 0.7 (f = 0.0, 0.2, 0.5, 0.6 and 0.65), no such barriers occur, and the system state changes with a monotonic decrease in N₁ until the PMF value reaches its global minimum at the center of the PMF profile. The system then fluctuates around this minimum (N₁ = 200-N_CNT/2 ≈ 200), as shown in Fig. 5(A) (f = 0.0, 0.6).

Finally, for f = 0.7, the PMF profile is almost flat, suggesting that N₁ can vary significantly with no free energy cost. This suggests that the system can explore a large configuration space (refer to Fig. 5(A) for f = 0.7) and that substantial molecular transport may be feasible. On the basis of this analysis, f = 0.7 represents a characteristic interaction strength, which we denote as f_c and refer to as the critical charge scaling factor.

Accordingly, the transport behaviors can be categorized into three distinct regimes on the basis of the value of f. When f is smaller than f_c (in our case, f < 0.7), the interactions between the transported molecules are relatively weak, and the transport behavior then resembles that of nonpolar molecules, as described in our previous study.¹¹ This regime is referred to as the nonpolar-like regime or the weak-interaction regime. In contrast, when f is sufficiently larger than f_c (in our case, f > 0.7), the system exhibits behavior analogous to that of water molecules, as reported in our previous study.¹⁰ We refer to this as the water-like regime or the strong-interaction regime. Between these two regimes lies a transition regime, occurring at approximately f = f_c. In this regime (0.65 < f < 0.75), the system transitions from a weak-interaction regime to a strong-interaction regime as f increases, resulting in a notable shift in transport dynamics.

Now, let us reconsider the fluctuations in Fig. 6(B) in relation to the PMF. The magnitude of these fluctuations is thermodynamically determined by the width of the PMF profile around the minimum, which reflects the range that can be explored by a system from the minimum to the height of thermal energy k_BT above the minimum, where k_B is the Boltzmann constant and T is the temperature. Specifically, if the PMF profile is narrow around the minimum, the fluctuation is small. Conversely, if the profile is wide, the fluctuation is large. Therefore, as f increases from 0, the PMF profile around the minimum widens (compare the profile width for f = 0 (the circle labeled A) with that for f = 0.65 (the circle labeled B) in Fig. 7), leading to larger fluctuations, as shown in Fig. 6(B). When f = 0.7, the PMF becomes nearly flat, indicating substantial fluctuations (Fig. 6(B)). However, for f values greater than 0.7, two minima emerge near the two ends of the profile in Fig. 7. These minima arise from the presence of a high barrier between them. The fluctuations in N₁ around these minima decrease with increasing f value due to the increasing barrier height. Consequently, the fluctuations shown in Fig. 6(B) decrease with increasing f.

To provide a greater understanding of the PMF profiles in relation to the system configurations, we show the PMF profiles alongside representative configurations in Fig. 8 and 9. In Fig. 8, the case of f = 0.6 once again represents nonpolar-like molecular transport behavior, with a single minimum in the PMF profile. The corresponding configurations in Fig. 8 indicate weak molecular interactions, resulting in the molecules filling the space as typical gas molecules do. Furthermore, the configurations show that as the system progresses from state I to state A, the molecules are transported into compartment 2 via the CNT. In state E, the molecules are evenly distributed between the two compartments, and the CNT is fully occupied.

Fig. 8 PMF for f = 0.6 as a function of N₁, along with the nine configurations corresponding to the points marked A through I in the PMF profile.

Fig. 9 PMF for f = 0.8 as a function of N₁, along with the nine configurations corresponding to the points marked A through I in the PMF profile.

Given that the PMF profile is symmetric, with a center at state E, the configurations also reflect this symmetry. Specifically, state D corresponds to F, state C corresponds to G, state B corresponds to H, and state A corresponds to I. Moreover, the overall transport process from state I to A can be divided into three subprocesses:¹¹ (1) the CNT filling process from I to H, (2) the intercompartment transport process from H to B while the CNT is fully occupied with molecules, and (3) the CNT emptying process from B to A (refer to the three regimes marked I, II, and III in Fig. 8). Importantly, the CNT filling and emptying processes are exactly opposite to each other.

In contrast to Fig. 8, Fig. 9 shows the PMF for f = 0.8, representing the case of water-like molecular transport behavior, where the interactions between molecules are relatively strong. Owing to these strong interactions, the molecules in the configurations are closely aggregated rather than scattered in space, as in the nonpolar case shown in Fig. 8. The configurations from state I through state A illustrate the transport process, during which the system overcomes the PMF barrier at E, leading to the complete transport of all molecules from compartment 1 to 2. In addition to the PMF symmetry, the configurations exhibit symmetry with a center at E. Specifically, if we exchange compartments 1 and 2 in the configuration at A, the resulting configuration closely resembles the one at I. This symmetry is also observed in the pairs of B and H, C and G, and D and F.

Similar to the three regimes I, II, and III in the PMF profile shown in Fig. 8, three distinct PMF regimes are identified in Fig. 9. Regimes I and III in Fig. 9 are associated with the CNT filling and emptying processes, respectively, whereas Regime II corresponds to the intercompartment transport process.¹⁰ In contrast to Fig. 8, Regime II features a barrier instead of a well.

3.3. Fluctuation-induced molecular transport

The PMF analysis results revealed that more than half of nonpolar-like molecules (f ≤ 0.65) or water-like molecules (f ≥ 0.75) cannot be transported from compartment 1 to 2 owing to the well at the center of the PMF profile and the barrier, respectively. However, the PMF profile at f ≈ 0.7, which lies in the transition regime between the nonpolar-like and water-like regimes, is nearly flat. This flat shape suggests that the system can explore a larger configuration space rather than being confined to a narrow region around the well. Consequently, a significant number of molecules—potentially more than half—may be transported between the two compartments in this regime. Therefore, it is important to carefully examine the transition regime, particularly around f ≈ 0.7.

Although the PMF profile at f ≈ 0.7 suggests large fluctuations, the magnitude of these fluctuations based on unconstrained MD simulations (σ_N1 ≈ 70 in Fig. 6(B)) is insufficient to ensure complete transport (ideally, σ_N1 ≈ 200 when N₁ oscillates between 400 and 0). More directly, the trajectory for f = 0.7 in Fig. 5(A) shows that the system has not yet converged and is still exploring other states. This suggests that the 500-ns simulation time is inadequate for the transition regime to fully explore all possible equilibrium states. Therefore, additional simulation time is needed to adequately sample all potential states.

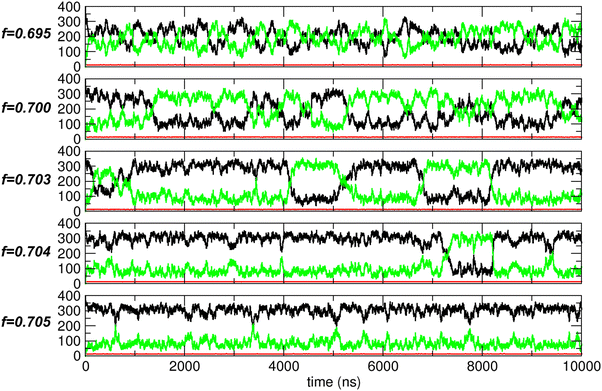
To address this issue, we conducted extended simulations up to 10 000 ns (10 μs) around f = 0.7. The trajectory analysis results are shown in Fig. 10. At f = 0.695, the behavior resembles that of nonpolar molecules (as shown for f = 0.0 in Fig. 5(A)) but with a much larger magnitude of fluctuations. In contrast, at f = 0.705, the behavior is more similar to that observed in the water-like regime (as shown for f = 1.0 in Fig. 5(A)). However, at f = 0.7, f = 0.703, and f = 0.704, the behavior exhibits characteristics of both nonpolar-like and water-like regimes. Specifically, the system experiences thermal fluctuations, causing N₁ and N₂ to fluctuate around their averages, similar to the nonpolar case. However, in contrast to the nonpolar-like case, these fluctuations emerge as oscillations between two distinct states: one where compartment 1 is more filled and one where compartment 2 is more filled. Furthermore, these two states exhibit thermodynamic stability, with N₁ (black) and N₂ (green) remaining constant over certain periods, indicating relatively stable aggregated states. In these states, relatively strong interactions prevent the molecules from scattering, as they do in the nonpolar-like regime, and cause them instead to aggregate, similar to the water-like regime. This combination of nonpolar-like and water-like behaviors leads to large fluctuations between the two compartments.

Fig. 10 Trajectory analysis results for systems with f values of 0.695, 0.7, 0.703, 0.704, and 0.705 (top to bottom). The states, represented by N₁ (black), N_CNT (red), and N₂ (green), are plotted as functions of time.

Since f = 0.703 exhibits pronounced characteristic behavior with large fluctuations and two stable states, we further examined the trajectory, with representative configurations shown in Fig. 11. To clearly illustrate the oscillatory behavior between these two stable states, we marked several points (1 through 5) in the PMF profile. These points correspond to states with maximal transport within specific time intervals, and the corresponding configurations are shown in Fig. 11. Although complete transport is not achieved, a significant number of molecules are spontaneously transported between the two compartments. Additionally, the transport process is bidirectional and reversible.

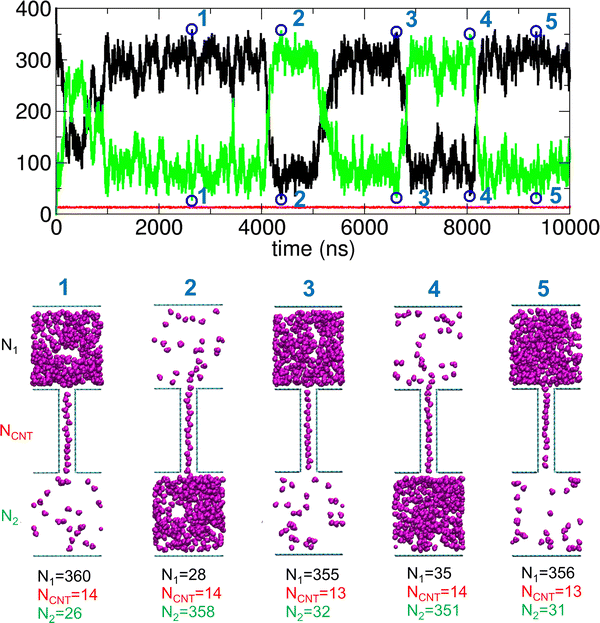Fig. 11 Trajectory analysis showing N₁, N_CNT, and N₂ for a system with f = 0.703, along with the five configurations corresponding to the points marked 1 through 5 in the plot.

In fact, compartment 1 (or, equivalently, compartment 2) alternates between filled and empty states, although it is never fully filled or completely empty. This behavior resembles that observed during dewetting transitions^34,35 between nanosized plates^18,19 or within CNTs,¹³ where oscillations between dry and wet states occur by adjusting the strength of solute–water LJ interactions. However, a key difference between our study and previous dewetting transition studies is the focus. While those studies primarily examined local water occupancy in confined spaces due to wall–water interactions, our work emphasizes how interactions between transported molecules influence global system-wide molecular transport between compartments.

As discussed in Section 3.1, this transport system exhibits stochastic behavior near f = 0.7. Therefore, what we observed for f = 0.703 is one of many thermodynamically possible results. In other words, in a different simulation, the transition could occur at an earlier or later time than the one we observed here. Likewise, while no transport is observed for f = 0.705, increasing the simulation time could yield transport similar to that observed for f = 0.703. However, as f increases further, the probability of such transport decreases, resulting in reduced fluctuations, as shown in Fig. 6(B). This is because as f increases, the attractive interaction strength between the transport molecules also increases, leading to a higher barrier in the PMF profile. Consequently, overcoming the barrier becomes more difficult, reducing the transport probability. Eventually, for sufficiently large f values, transport ceases altogether.

4. Conclusions

In this study, we investigated the effect of the interaction strength between transported molecules on molecular transport through a narrow channel connecting two compartments (compartments 1 and 2). To modulate the interaction strength, we adjusted the electrostatic properties of the model molecules being transported, using the TIP3P water model as a prototype. Specifically, we varied the electric charges of the molecules by a constant factor, referred to as the charge scaling factor f. A scaling factor of f = 1 corresponds to the original TIP3P model, whereas f = 0 represents nonpolar molecules. Previous studies have shown that with strong interactions (water case, f = 1), spontaneous transport does not occur. In contrast, with weak interactions (nonpolar case, f = 0), transport can occur, but only approximately half of the molecules are transported.

To systematically examine the dependence of molecular transport on f, we performed unconstrained MD simulations for various values of f. Interestingly, we found that at an intermediate interaction strength (f = 0.7), significant transport occurs, with more than half of the molecules transported. This intermediate regime of f represents a transitional phase between the strong-interaction regime (water-like case) and the weak-interaction regime (nonpolar-like case).

To better understand the underlying transport dynamics, we calculated the PMF (free energy change) as a function of the number of transported molecules in compartment 1 for various values of f. Specifically, the PMF profile for f = 0.7 exhibits a characteristic flat region, indicating that no thermodynamic force is required for the system to move between states in this region. This explains the extensive molecular transport observed, which results in large fluctuations in the number of molecules in each compartment, similar to the dewetting transition.

An interesting direction for further research would be a detailed thermodynamic analysis involving the decomposition of the PMF into its energetic and entropic contributions, as explored in our prior works.^10,11 While this analysis is beyond the scope of this study, one key aspect can still be discussed on the basis of previous research. In those works, we demonstrated that when the energetic contribution dominates the entropic contribution, a barrier forms at the center of the PMF profile, as observed in the water-like regime (strong-interaction case). Conversely, when the entropic contribution dominates, a well appears, as observed in the nonpolar-like regime (weak-interaction case). Therefore, the large flat region observed for f = 0.7 may be explained by the cancellation of these two opposing contributions.

Thus, to transport a large quantity of molecules between the compartments, the interaction strength should be moderate. If the interactions are too strong, the molecules will aggregate, making dissociation during transport energetically unfavorable. Conversely, if the interactions are too weak, the molecules are likely to scatter to maximize entropy. However, with moderately strong interactions, the entropic and energetic contributions become comparable and compete with each other. In such a case, molecules can either aggregate or scatter, maximizing fluctuations during the thermodynamic process. As a result, a significant number of molecules are transported. Further detailed thermodynamic analysis, including PMF decomposition, would be an important subject for future studies.

A primary concern in molecular transport for engineering applications is controlling molecular flow. Our study suggests that an optimal interaction strength could enable the transport of many molecules, but this process remains reversible, with molecules oscillating between compartments owing to the nature of fluctuations, which lack directionality. To achieve unidirectional molecular flow, additional methods, such as introducing osmolytes into the desired compartment or utilizing gated channels, are necessary.

Finally, as our study is based on a simplified model system, connecting our findings to realistic systems is important. In our model, transport molecules with f = 1 represent water molecules. Consequently, our results pertain directly to water transport between two compartments, which serves as a reference real system. However, as f decreases below 1, the transport molecules no longer represent water but can instead be interpreted as less polar molecules. For example, molecules with shapes similar to that of water but with lower polarity (corresponding to f = 0.7 in our model) could exhibit extensive fluctuation-driven molecular transport. This provides an opportunity for experimental validation in future studies.

Another extension of the reference water system involves modifying intermolecular interactions while maintaining f = 1. Specifically, hydrogen bonds between water molecules are responsible for strong intermolecular interactions that hinder transport between compartments. Thus, hydrogen bonding plays a critical role in modulating molecular transport. Tuning the strength of hydrogen bonds, for example, through the addition of salts, might provide a realistic means of controlling transport for a given molecule. Exploring how transport behavior changes with salt concentration would be particularly interesting, especially as it represents a more realistic system. Indeed, in our previous work,³⁶ we reported that osmolytes, which are not salts but exhibit strong LJ interactions with water molecules, can induce nearly complete transport to another compartment.

In our model, strong interactions are primarily electrostatic, but another potential source of strong interactions is LJ interactions. This raises an intriguing theoretical question: can strong LJ interactions substitute for strong electrostatic interactions? For example, if nonpolar molecules such as CO₂ exhibit sufficiently strong LJ interactions, comparable to the strength represented by f = 0.7 in our study, could fluctuation-driven extensive transport still be observed? Investigating this possibility would be an interesting topic for future work.

Furthermore, in realistic systems, the number of transport molecules may differ from the 400 molecules studied in our model. In our previous work for f = 1¹⁰ and f = 0¹¹, we observed that the PMF profile shapes were similar to those obtained with 400 molecules in this study when the periodic boundary effect was disregarded for water cases. Additionally, scaling behaviors for barrier heights in water systems and well depths in nonpolar systems were observed in relation to the number of molecules. However, for intermediate f values, such scaling behavior in the PMF profile remains unexplored. This presents another avenue for future research, particularly concerning fluctuation-driven transport, a process in which entropic and energetic contributions are expected to be balanced. For example, how does the critical value of f vary with the number of molecules? Is it still 0.7, as observed in our current model with 400 molecules?

Similarly, the shape of the transport molecules could influence transport behavior. Investigating how molecular shape affects fluctuation-driven transport would be another valuable direction for future studies.

Until this point, we have focused on the properties of the transport molecules. However, in real systems, the surface interactions between transport molecules and compartment walls can significantly influence the transport process. For example, as discussed in Section 2.1, we reduced the surface interaction strength to prevent adsorption. However, these surface interactions can range from repulsive to attractive in real systems. Our previous study³⁶ demonstrated that attractive surface interactions between regular graphene plates and water molecules led to the adsorption of molecules onto the walls, which resulted in reduced transport. Conversely, when the surface interactions were relatively weak, the transport molecules tended to stay away from the compartment walls, moving freely within the inner space without contacting the walls, including the CNT, which also reduced transport. Therefore, in the case of repulsive interactions, it is essential to consider effective strategies to drive the molecules toward the CNT, such as employing gravity or enhancing attractive interactions between the CNT and the transported molecules. In this study, we utilized a regular CNT that is more attractive to the transported molecules than the compartment walls.

Data availability

The data supporting the findings of this study are available within the article.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (no. RS-2023-00245362) and the Hankuk University of Foreign Studies Research Fund of 2024.

References

1. C. Chen, J.-D. Vincent and I. J. Clarke, Ion channels and the signal transduction pathways in the regulation of growth hormone secretion, Trends Endocrinol. Metab., 1994, 5, 227–233.
2. Y. J. Suzuki, H. J. Forman and A. Sevanian, Oxidants as stimulators of signal transduction, Free Radical Biol. Med., 1997, 22, 269–285.
3. J. M. Ward and J. I. Schroeder, Signal Transduction in Plants, Springer, 1997, pp. 1–22.
4. S. Zimmermann, T. Ehrhardt, G. Plesch and B. Müller-Röber, Ion channels in plant signaling, Cell. Mol. Life Sci., 1999, 55, 183–203.
5. B. Minke and B. Cook, TRP channel proteins and signal transduction, Physiol. Rev., 2002, 82, 429–472.
6. J. Iqbal and M. Zaidi, Molecular regulation of mechanotransduction, Biochem. Biophys. Res. Commun., 2005, 328, 751–755.
7. L. Tetsch and K. Jung, How are signals transduced across the cytoplasmic membrane? Transport proteins as transmitter of information, Amino Acids, 2009, 37, 467–477.
8. G. P. Bienert and F. Chaumont, Aquaporin-facilitated transmembrane diffusion of hydrogen peroxide, Biochim. Biophys. Acta, Gen. Subj., 2014, 1840, 1596–1604.
9. R. Mittler, S. I. Zandalinas, Y. Fichman and F. Van Breusegem, Reactive oxygen species signalling in plant stress responses, Nat. Rev. Mol. Cell Biol., 2022, 23, 663–679.
10. Y. Kwon and C. Eun, Free energy change in the complete transport of all water molecules through a carbon nanotube, Phys. Chem. Chem. Phys., 2023, 25, 7032–7046.
11. C. Eun, Free Energy Profile for the Complete Transport of Nonpolar Molecules through a Carbon Nanotube, Int. J. Mol. Sci., 2023, 24, 14565.
12. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 72, 926–935.
13. G. Hummer, J. C. Rasaiah and J. P. Noworyta, Water conduction through the hydrophobic channel of a carbon nanotube, Nature, 2001, 414, 6860.
14. A. Kalra, S. Garde, G. Hummer and T. P. Howard, Osmotic water transport through carbon nanotube membranes, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(18), 10175–10180.
15. S. R. Accordino, J. M. Montes de Oca, J. A. Rodriguez Fris and G. A. Appignanesi, Hydrophilic behavior of graphene and graphene-based materials, J. Chem. Phys., 2015, 143(15), 154704.
16. S. Dasetty, J. K. Barrows and S. Sarupria, Adsorption of amino acids on graphene: assessment of current force fields, Soft Matter, 2019, 15, 2359–2372.
17. C. Eun, Equilibration of molecules between two compartments through a nanochannel in the presence of osmolytes: a molecular dynamics simulation study, Phys. Chem. Chem. Phys., 2019, 21, 21136–21151.
18. N. Choudhury and B. M. Pettitt, The dewetting transition and the hydrophobic effect, J. Am. Chem. Soc., 2007, 129, 4847–4852.
19. C. Eun and M. L. Berkowitz, Fluctuations in number of water molecules confined between nanoparticles, J. Phys. Chem. B, 2010, 114, 13410–13414.
20. W. D. Cornell, P. Cieplak, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197.
21. H. A. Lorentz, Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase, Ann. Phys., 1881, 248, 127–136.
22. D. Berthelot, Sur le mélange des gaz, Compt. Rendus, 1898, 126, 15.
23. G. development Team, GROMACS 2023.3 Manual, https://www.gromacs.org, 2023.
24. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593.
25. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101.
26. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25.
27. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, MDAnalysis: a toolkit for the analysis of molecular dynamics simulations, J. Comput. Chem., 2011, 32, 2319–2327.
28. R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domanski, D. L. Dotson, S. Buchoux and I. M. Kenney, MDAnalysis: a Python package for the rapid analysis of molecular dynamics simulations, Los Alamos National Laboratory (LANL), Los Alamos, NM (United States), 2019.
29. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
30. T. Baştuğ, P.-C. Chen, S. M. Patra and S. Kuyucak, Potential of mean force calculations of ligand binding to ion channels from Jarzynski’s equality and umbrella sampling, J. Chem. Phys., 2008, 128(15), 155104.
31. J. A. Lemkul and D. R. Bevan, Assessing the stability of Alzheimer's amyloid protofibrils using molecular dynamics, J. Phys. Chem. B, 2010, 114, 1652–1660.
32. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13, 1011–1021.
33. J. S. Hub, B. L. De Groot and D. Van Der Spoel, G-whams-a free Weighted Histogram Analysis implementation including robust error and autocorrelation estimates, J. Chem. Theory Comput., 2010, 6, 3713–3720.
34. J. C. Rasaiah, S. Garde and G. Hummer, Water in nonpolar confinement: from nanotubes to proteins and beyond, Annu. Rev. Phys. Chem., 2008, 59, 713–740.
35. B. J. Berne, J. D. Weeks and R. Zhou, Dewetting and hydrophobic interaction in physical and biological systems, Annu. Rev. Phys. Chem., 2009, 60, 85–103.
36. C. Eun, Osmosis-Driven Water Transport through a Nanochannel: A Molecular Dynamics Simulation Study, Int. J. Mol. Sci., 2020, 21, 8030.

---