How does the polymer type affect the rate of water evaporation from polymer solutions?†
Masahiko
Tanaka
 a and
Susumu
Inasawa
a and
Susumu
Inasawa
 *ab
*ab
aGraduate School of Bio-Application and Systems Engineering, Tokyo University of Agriculture and Technology, 2-24-16 Naka-Cho, Koganei, Tokyo, 184-8588, Japan. E-mail: inasawa@cc.tuat.ac.jp
bDepartment of Applied Physics and Chemical Engineering, Tokyo University of Agriculture and Technology, 2-24-16 Naka-Cho, Koganei, Tokyo, 184-8588, Japan
First published on 19th November 2024
Abstract
Drying of aqueous polymer solutions is widely used to form polymer films. However, we do not fully understand how concentrated polymer near the drying interfaces decreases the rate of water evaporation. In addition, we do not know how the evaporation kinetics varies when we use different polymers. To understand these topics, we examined drying of polymer solutions with three different polymers, poly(vinyl alcohol) (PVA), poly(vinyl pyrrolidone), and poly(ethylene glycol) in unidirectional drying cells. In each case, the water evaporation rate (J) decreased to 1/10 of the initial rate during evaporation. J−1 was proportional to the amount of polymer transported to the drying interface during the drying time. The slope is defined as resistance factor A and the PVA solutions had larger A values than the other polymers, indicating that J decreased more noticeably in the PVA solutions. The molecular weights of the polymers did not explain A. Concentration profiles of polymers near the drying interfaces were quantified in situ with an optical microscope by exploiting differential interference contrast, from which we estimated the diffusion constants (Ds) of the polymers in the drying solutions. We found that A was negatively correlated with D. This result clearly indicates that the diffusivity and accumulation of dissolved polymer molecules near the drying interface governs the overall drying kinetics of their solutions.
1. Introduction
The drying kinetics of cast polymer solutions has been investigated for decades in terms of the drying rate,1 film deformation,2 crystallization,3 and the formation of defects such as bubbles.4 As the solvent evaporates, the polymer molecules become concentrated at the air–liquid interface and an elastic layer (skin) forms.5 This is thought to decrease the drying rate6 and increase mechanical instability during drying.2,4 Ciampi and McDonald investigated drying polymer films using magnetic resonance imaging (MRI).7 They found that the water concentration profile became inhomogeneous when a solution dried quickly.7 Daubersies et al. used Raman microscopy to determine polymer concentrations in drying polymer solutions confined in two-dimensional drying cells.8 They showed that an increase in polymer concentration at the air–solution interface caused a decrease in water chemical activity, which led to a decrease in the rate of water evaporation.8 These observations suggest that the transport of a polymer and its accumulation around drying interfaces are closely related to the water (solvent) evaporation rate. The accumulation of surfactant molecules also disturbs water evaporation.9,10 Roger et al. used small angle X-ray scattering (SAXS) and polarized microscopy to observe the formation of a lamellar layer of surfactant molecules near the drying interface.9,10 The thickness of the layer varied with the ambient humidity, and this further affected water evaporation.9,10 Progress in measurement techniques has enabled the elucidation of the relationship between the solvent evaporation rate and the evolution of structures and compositions in a solution.Solution flow caused by solvent evaporation transports dissolved solute toward the drying interface. Conversely, polarized (concentrated) solute molecules around the interface diffuse back to the bulk solution because of the concentration gradient. Therefore, the solute concentration profile is governed by the balance between flow and diffusion.11 Strong polarization of the solute near the drying interface is expected when the diffusion constant is small. This can severely retard water evaporation. This is the simple classical picture, but it could form the basis for an understanding of drying kinetics. Evaporation rates and concentration profiles in drying aqueous solutions have been investigated previously.8,9,12–14 However, to the best of our knowledge only one solute has been studied in most cases, and there has been no comparison of multiple solutes. Diffusivity varies depending on the solute: for example, in classical theory the diffusion constant of a polymer (e.g., a protein) is considered a function of its molecular weight (Mw),15,16 and we speculate whether it is possible to use the same relationship in drying polymer solutions.
In the present study, we examined the effects of the type of polymer and its Mw on the rate of water evaporation. We used a two-dimensional configuration for the drying experiments, as has been used in recent studies.9,10,13,17–20 This configuration enables the interpretation of the mass transport in drying films as quasi one-dimensional, whereas some papers report gravity-driven circulation flow even in thin liquid films.19–22 Several techniques have been utilized to quantitate the concentration change during drying: Raman microscopy,8,9,13,23 infrared spectroscopic imaging,12 SAXS,17 optical coherent tomography,19,24 MRI,3,7,23 and interferometry.14,25 However, it is still worth examining another technique with the same objective. Herein, we exploited differential interference contrast (DIC) using an optical microscope. This method has been used to improve the visibility of transparent samples such as cells26 and colloidal particles,27 and to characterize the structures of packed films of colloidal particles.28 In the DIC approach, the differences between the optical paths in transparent samples are visualized. The optical path is the product of the distance through which light travels and the refractive index of the sample. If a polymer is concentrated around the drying interface and polymer concentration is not homogeneous, there will be a distribution of the refractive index in the drying solution, because the refractive index of a polymer differs from that of water. Several papers report similar quantitative DIC, but phase mapping of single cell29 or lipid bilayer30 is a main target in those papers. Determination of concentration profiles in drying solutions by quantitative DIC, which we present in this paper, has never been reported so far. Because DIC is recorded as images, we could obtain concentration profiles in drying polymer solutions quickly. On the basis of DIC data, we will discuss herein the relevance of concentration increases to water evaporation kinetics.
2. Experimental
2.1 Sample preparation
We used three different polymers with various molecular weights: poly(ethylene glycol) (PEG, Mw = 3 × 102, 2 × 103, 2 × 104, and 4 × 105 g mol−1), poly(vinyl pyrrolidone) (PVP, Mw = 4.0 × 104, 3.6 × 105, and 1.3 × 106 g mol−1), and fully saponified poly(vinyl alcohol) (PVA, Mw = 1.8 × 104, 7.3 × 104, and 1.8 × 105 g mol−1). PVAs of Mw = 1.8 × 104 and 1.8 × 105 g mol−1 were purchased from JAPAN VAM & POVAL Co., Ltd (Osaka, Japan); PVP of 1.3 × 106 g mol−1 was purchased from Thermo Fischer Scientific/Alfa Aesar (MA, United States); and the other polymers were purchased from Fujifilm Wako Pure Chemical Industries, Ltd (Osaka, Japan). We added each solute to pure water to prepare the sample solution. The initial solute concentrations (C0s) in the samples were controlled in the range 0.2 to 0.9 vol%. Rheological measurements were conducted using a Cone/Plate Rheometer (DVNext, Brookfield, Toronto, Canada).2.2 Drying experiment
We used rectangular glass capillaries (0.1 × 2 × 100 mm3, 5012, VitroCom, NJ, USA) to measure the drying rates. Each capillary was partially filled with the sample solution by capillary suction and placed horizontally. We then placed a drop of water of volume ∼1 mL at the opposite edge of the capillary. The deposited water droplet also invaded the tube from the water side by capillary suction, and the air plug inside the capillary was compressed. As the polymer solution evaporated from the solution side, the air plug caused the water to flow toward the drying interface to compensate for the evaporation of water from the drying polymer solution. The drying air–water interface was pinned at the solution side during drying as shown in Fig. 1a (see also Fig. S1 in the ESI† for details). This method was first reported by Le Dizès Castell et al.31 We used a transparent glass heater (ST-91, Blast Co., Ltd, Kanagawa, Japan) to maintain a constant drying temperature of 50 °C to assume fast drying in industrial processes. Heating was conducted in ambient air that had a relative humidity of 26% to 84% at room temperature. The relative humidity at 50 °C is estimated to be 7% to 22%. Because of a large difference in the saturated vapor pressure of water (3.1690 kPa at 25 °C and 12.344 kPa at 50 °C),32 the variation in the relative humidity at 50 °C was small. Fig. 1b shows time evolution of the meniscus position xm in a drying cell. From the slope of the data, we obtained drying rate J. We conducted drying experiments at least three times for all samples.The transmission optical images of the capillaries were recorded using a digital camera equipped with an AZ 100 optical microscope (Nikon, Tokyo, Japan). The resolution of the observed images was estimated to be 12 μm, based on the numerical aperture of the objective lens (AZ Plan Apo 0.5×, Nikon, Tokyo, Japan), i.e., 0.05, and the pixels of the recorded images (2992 × 2000 pixels). The images were analyzed using the ImageJ software package (National Institutes of Health, MD, USA).
2.3 Measurement of the refractive index
We prepared aqueous solutions containing various concentrations (Cs) of each of the solutes which are shown as Table 1. We measured the refractive index (n) of each sample solution using a digital refractometer (HI96800, Hanna Instruments, RI, USA). We dried the polymer solutions to obtain polymer films, and measured the n of each film using a refractometer (160LED, Shibuya Optical Co., Ltd, Saitama, Japan). We then determined the polymer concentration in each dried film from the film weight before and after drying. The light sources were yellow LED (HI96800) or D line (591 nm, 160 LED). The measurements were conducted at room temperature (24 ± 3 °C). The n of each examined sample increased linearly with solute concentration, as shown in Fig. S2 (ESI†). We note that, owing to the high viscosity of the concentrated aqueous solutions of PVA and PVP, we were unable to prepare reference solutions above 25 vol% for PVA and 40 vol% for PVP, as shown in Fig. S2 (ESI†).| Sample | ρ [g cm−3] | M w [kg mol−1] | T m [°C] | r g [nm] |
|---|---|---|---|---|
| PEG | 1.13 | 0.3 | −15∼−8 | 0.69 |
| 2 | 45–55 | 1.4 | ||
| 20 | 56–68 | 4.6 | ||
| 400 | 35 | |||
| PVP | 1.2 | 40 | 225 | 5.1 |
| 360 | 17 | |||
| 1300 | 28 | |||
| PVA | 1.3 | 18 | >300 | 5.2 |
| 73 | 11 | |||
| 180 | 18 |
2.4 DIC observations
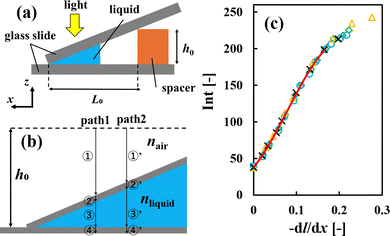
We used a hand-made glass cell (Fig. S3, ESI†) instead of a capillary tube for the investigations by DIC. This was because glass capillaries have a slight distortion that is apparent in DIC images. We placed two silicon spacers (each 0.1 mm thick) parallel to each other on a glass slide (Matsunami Glass Ind., Ltd, Japan). The spacers were 3 mm apart and we used a glass cover slide (Matsunami Glass Ind., Ltd, Japan) to cover them. The narrow gap surrounded by the glass slides and the spacers was used to hold each sample solution. A sample solution with an initial polymer concentration of 0.8–0.9 vol% was introduced from one edge of the cell, as shown in Fig. S3 (ESI†). We also put an aliquot of water on the other edge of the cell, as described in Section 2.2. This enabled the drying air–water interface to pin on the injection edge of the sample solution, as shown in Fig. S3 (ESI†). We obtained both transmission and DIC images of the drying samples using an Eclipse Ti-2 optical microscope (Nikon, Tokyo, Japan) equipped with a digital camera. The resolution was 0.7 μm, which was estimated from the numerical aperture of the objective lens (Plan Apo λ, 10×, Nikon, Tokyo, Japan), i.e., 0.45, and the pixels of the recorded images (2880 × 2048 pixels). Our objective in carrying out the DIC measurements was to obtain concentration profiles of the drying samples, so we recorded images around the drying interfaces. We note that we did not observe any clear circulation flow driven by gravity19–22 in drying polymer solutions. This may be owing to the small difference in density between examined polymer (Table 1) and water (1.0 g cm−3 (ref. 32)).In DIC images, changes in the gradient of the optical path length dl/dx are indicated by image brightness.26 Quantitative measurements require a calibration line that shows the relationship between image brightness I and dl/dx. To change the sample thickness h with a constant ratio, we made tilted glass cells with a constant gradient, as shown in Fig. 2(a). Liquid samples with a different refractive index were introduced into the gap. dl/dx changes with the gradient of the gap height in the x direction (dh/dx). The optical path changes in both air and water regions, as shown in Fig. 2(b). Thus dl/dx is described as (nliquid – nair) (dh/dx), wherein nliquid and nair are the refractive indices of the sample liquid and air, respectively. We analyzed the brightness of each image I using ImageJ software, and summarized the results as a calibration line that shows the relationship between I and −dl/dx, as shown in Fig. 2(c). We obtained the data using pure water, three aqueous solutions of PVA, PVP, and PEG, and approximately 10 different gradients of height dh/dx. All the intensity data were well summarized by −dl/dx, and demonstrated a curved increase. A cubic function describes the data from 0 ≤ −dl/dx ≤ 0.16 very well, and corresponds to the intensity range 38–200. Above that region, there was a plateau, as shown in Fig. 2(c). We only used the region where 38 ≤ I ≤ 200 to obtain the −dl/dx of each drying sample. We note that the cubic function does not have any physical meaning and we use it just to reproduce the relation of the calibration data in Fig. 2(c).
We used the same objective lens for the DIC investigations of the drying samples as we used for the calibration line measurements. We also kept all the investigation conditions, such as the intensity of the incident light, the exposure time, and the analog gain, that were used in the calibration line measurements. Drying was conducted at 50 °C using a transparent glass heater.
3. Results and discussions
3.1 Drying kinetics
Fig. 3(a)–(c) shows the evolution of the drying rates Js of pure water and the polymer samples over time. The corresponding time evolutions of the meniscus position xm in drying solutions are shown in the inset of Fig. 3(a)–(c). Whereas the drying rate of pure water remained almost constant during drying, the drying rates of the polymer samples decreased over time; they were approximately 1/10 of the drying rate of pure water after drying for 100 min. Each polymer sample exhibited a similar trend in J although the decrease in the drying rate was more rapid for larger C0 samples. It is reasonable to assume that polymer concentration around the drying interface caused the decrease because we did not observe any decrease in drying pure water. The polymer flows to the drying interface and becomes concentrated there. The amount of transported polymer dissolved in water that has evaporated up to drying time t is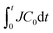 , with which we replotted J in Fig. 3(a)–(c), as shown in Fig. 3(d)–(f). All data with different C0s collapse to a single line, and 1/J is proportional to
, with which we replotted J in Fig. 3(a)–(c), as shown in Fig. 3(d)–(f). All data with different C0s collapse to a single line, and 1/J is proportional to  (insets in Fig. 3(d)–(f)). We have confirmed a similar relation in drying polymer solution at 25 °C. Salmon et al. have shown that J is proportional to the inverse of the total amount of polymer in the drying solution (1/ψ) when evaporation is in a steady state.33 In that work, all the polymer was transported to the vicinity of the drying interface and formed a concentration gradient.33 Furthermore, Tanaka and Inasawa have shown that an increased PVA concentration around the drying interface is closely related to
(insets in Fig. 3(d)–(f)). We have confirmed a similar relation in drying polymer solution at 25 °C. Salmon et al. have shown that J is proportional to the inverse of the total amount of polymer in the drying solution (1/ψ) when evaporation is in a steady state.33 In that work, all the polymer was transported to the vicinity of the drying interface and formed a concentration gradient.33 Furthermore, Tanaka and Inasawa have shown that an increased PVA concentration around the drying interface is closely related to 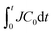 , which relates to a marked decrease in the drying rates of colloid–polymer suspensions.34 These studies suggest that the amount of polymer transported to the drying interface has a crucial effect on the rate of water evaporation.
, which relates to a marked decrease in the drying rates of colloid–polymer suspensions.34 These studies suggest that the amount of polymer transported to the drying interface has a crucial effect on the rate of water evaporation.
Herein, we introduce the resistance factor of drying A as in 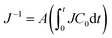 , as shown in Fig. 3(d)–(f). A larger A means a larger decrease in J when the same amount of water evaporates, even if C0 is the same. We plotted A using the molecular weights of the polymers Mws, as shown in Fig. 4(a). The A values of the PVAs were larger than those of the other polymers, even though their molecular weights were similar to those of the other polymers. This clearly suggests that the effect of the polymer on the decrease in drying rate is not explained by Mw alone. The concentration profile is determined by the balance between advection and diffusion in such thin cells. The polymer is transported by the drying-induced flow and is concentrated near the drying interface. Conversely, there is a concentration gradient that drives the diffusion of the polymer to the bulk. Therefore, the diffusion constant of the dissolved polymer is an important factor that explains the concentration profile, and further relates to the resistance factor A. In the following section, we estimate the diffusion constants of the polymers from DIC observation.
, as shown in Fig. 3(d)–(f). A larger A means a larger decrease in J when the same amount of water evaporates, even if C0 is the same. We plotted A using the molecular weights of the polymers Mws, as shown in Fig. 4(a). The A values of the PVAs were larger than those of the other polymers, even though their molecular weights were similar to those of the other polymers. This clearly suggests that the effect of the polymer on the decrease in drying rate is not explained by Mw alone. The concentration profile is determined by the balance between advection and diffusion in such thin cells. The polymer is transported by the drying-induced flow and is concentrated near the drying interface. Conversely, there is a concentration gradient that drives the diffusion of the polymer to the bulk. Therefore, the diffusion constant of the dissolved polymer is an important factor that explains the concentration profile, and further relates to the resistance factor A. In the following section, we estimate the diffusion constants of the polymers from DIC observation.
3.2 Diffusion constants of the polymers in the drying solutions
Fig. 5 shows transmission and DIC images of the drying polymer solutions. The images shown in Fig. 5(d)–(f) were obtained using the DIC system. The region near the drying interface became bright in drying polymer solutions (Fig. 5(d)–(f)), whereas there was no clear change in brightness as the pure water dried (Fig. S4, ESI†). In the close vicinity of the meniscus, as indicated by the red arrows in Fig. 5(a)–(c), each image was brighter than the background, even in bright field view. However, we do not observe such a brighter line around the meniscus in the drying pure water as shown in Fig. S4a and b (ESI†). This suggests that the light transmission increased near the meniscus of the drying polymer solutions, probably owing to the curved interface and an increase in the refractive index because of accumulated polymer around the meniscus. This enhancement was observed in a narrow region from the drying interface to a distance of x = 20 μm. The calibration line in Fig. 2(c) is not valid there, and we analyzed DIC images where x ≥ 20 μm. The intensity was constant in the x direction and did not change as the pure water dried (Fig. S4, ESI†). | ||
| Fig. 5 Transmission images of drying (a) PVA (Mw = 1.8 × 104 g mol−1, C0 = 0.80 vol%), (b) PVP (Mw = 3.6 × 105 g mol−1, C0 = 0.83 vol%), and (c) PEG (Mw = 4 × 105 g mol−1, C0 = 0.89 vol%) solutions. The corresponding DIC images for (a)–(c) are shown in (d)–(f). The red arrows indicate the bright regions near the menisci. (g)–(i) Intensity distributions measured along the dashed white lines in (d)–(f). The x axes in (g)–(i) correspond to those in Fig. 6. | ||
Polymer solutions evaporate in cells with a constant gap height of 0.1 mm. In these situations, the optical path only depends on the refractive index of the sample liquid. The optical path gradient in the drying sample is described by dl/dx = h(dn/dx). The intensity profiles in the DIC images in Fig. 5(g)–(i) were converted to dn/dx profiles, as shown in Fig. 6(a)–(c), using the relationships h = 0.1 mm and Fig. 2(c). Assuming that the bulk concentration is equal to the initial concentration of the polymer, the refractive index in the bulk region n0 is n(C0). We measured n0 for each sample solution (Section 2.3), and obtained the refractive index at position x, n(x), using:
 | (1) |
Finally, we obtained the concentration of the polymer C(x) using the calibration lines in Fig. S2 (ESI†). The concentration profiles of the drying polymer solutions are shown in Fig. 6(d)–(f). As drying progressed, the concentration of the polymer increased. The concentrations at x = 20 μm increased up to ≥30 vol% in all cases. PVP and PEG accumulated in broader regions than PVA.
We plotted dC/dx in Fig. 6(d)–(f), as shown in Fig. S5 (ESI†). We confirmed that all the data used for the analysis of the C profile exceeded the minimum resolution. A more detailed discussion is in the ESI.† The intensity of the irradiated light for DIC observation varied within 5%. The possible fluctuation ranges in C attributed to the variation in light intensity are represented by the error bars in Fig. 6(d)–(f).
In the one-dimensional advection–diffusion equation,11 the conservation of the polymer is described by:
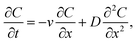 | (2) |
 | ||
| Fig. 7 (a) Ratios of (∂C/∂t) to v(∂C/∂x) in eqn (2) and (b) estimated values of D of PVA (Mw = 1.8 × 104 g mol−1) using the data shown in (a). The black dashed line in (a) represents y = 10−2. The drying times were 20 min (blue), 30 min (green), 60 min (yellow), and 90 min (red); (b) shows the data in which the ratios of (∂C/∂t) to v(∂C/∂x) were < 10−2. The purple line in (b) shows an approximated function33 based on the reported diffusion constant of PVA.1,35 | ||
Fig. 7(b) also suggests that D is dependent on the concentration. Interaction between polymer molecules would not be negligible at high concentrations and would decrease the diffusivity. It should be noted that the D values at concentrations of 1 vol% or smaller after drying for 60 min were scattered. This was because the corresponding second derivatives ∂2C/∂x2 were scattered. Although all the data satisfied the detection limit of dC/dx, as in Fig. S5 (ESI†), some of the data were insufficiently smooth or had insufficient signal-to-noise-ratios to calculate ∂2C/∂x2.
We analyzed the concentration profiles of all the drying samples and estimated the diffusion constants, which are summarized by Mw in Fig. S7(a) (ESI†). PVA exhibited low diffusivity compared with the other two polymers. We estimated the radius of gyration of polymer molecules rg (ref. 37) from the viscosity data as shown in Fig. S8 (ESI†) and replotted D in terms of rg (Fig. S7(b), ESI†). The values of rg do not summarize D of different polymers. These results suggest that neither Mw nor the size of polymer molecules (rg) is the main factor that governs D. The functional groups in the polymers would also affect the diffusivity. PVA molecules exhibit strong intermolecular interactions,38 and form clusters or agglomerates in water. In such situations, the effective diffusivity of the PVA molecules decreases. In addition, the persistence length that is a measure to show chain flexibility of polymer would relate to diffusion constant. Larger persistence length means a lower flexibility of polymer.39 Currently, we do not have information on the persistence length of the polymers we examined in this study. Understanding the interaction between polymer molecules and their flexibility is key to predicting their diffusivity.
We plotted the resistance factor A in terms of D, as shown in Fig. 4(b). We found that A was proportional to D−0.96 which is close to the slope of 1/D in Fig. 4(b). Qualitatively, this means that a large diffusivity reduces accumulation of the polymer around the drying interface, which leads to a lower decrease in the drying rate. The result shown in Fig. 4(b) is supported by the following simple derivation. Salmon et al. concluded that the drying rate is proportional to (D/tC0)1/2 when D is constant, and the liquid water is shielded by a skin layer of polymer on the drying interface.33 In the present study, the resistance factor was defined as  from the experimental results in Fig. 3. Substituting (D/tC0)1/2 into J in the definition gives A ∼ D−1, which is reasonably consistent with our result. This clearly shows that the resistance factor is determined by the diffusivity of the dissolved polymer in the drying solution. Dissolved polymer molecules are concentrated more when D is small, and a higher concentration in the immediate vicinity of the drying interface decreases the water potential.33 This relates to the formation of a skin layer of concentrated polymer. Unfortunately, we were unable to measure the concentration of the polymer when x < 20 μm in the present work. The relationship between the concentration of the skin layer and the resistance factor A requires further investigation.
from the experimental results in Fig. 3. Substituting (D/tC0)1/2 into J in the definition gives A ∼ D−1, which is reasonably consistent with our result. This clearly shows that the resistance factor is determined by the diffusivity of the dissolved polymer in the drying solution. Dissolved polymer molecules are concentrated more when D is small, and a higher concentration in the immediate vicinity of the drying interface decreases the water potential.33 This relates to the formation of a skin layer of concentrated polymer. Unfortunately, we were unable to measure the concentration of the polymer when x < 20 μm in the present work. The relationship between the concentration of the skin layer and the resistance factor A requires further investigation.
Finally, we shall briefly discuss the effect of viscosity on the resistance factor. In general, the viscosity of a polymer solution increases as C increases in two steps: gradually in the dilute region and rapidly in the concentrated region, as shown in Fig. S8(a) (ESI†). The overlap concentration Coverlap is defined as the concentration at which the slope of the viscosity increase changes on a double logarithmic scale.37 The viscosity data from polymer solutions are well summarized by the normalized concentration C/Coverlap,38 as shown in Fig. S8(b) (ESI†). This might suggest that the overlap concentration also provides a useful summary of A. However, this is incorrect. As shown in Fig. S9 (ESI†), we did not detect a good correlation between A and Coverlap. We conclude that an increase in viscosity and the subsequent increase in flow resistance in a drying polymer solution is not the main factor that affects the resistance factor A.
4. Conclusions
In the present study, we demonstrated that DIC can be exploited to determine the concentration profile of an aqueous drying solution of a polymer by optical microscopy. This method can be used when the gradient of the optical path is large owing to the large concentration gradient in the drying solution. Using the DIC method, we investigated the water evaporation kinetics of polymer solutions in a two-dimensional configuration. We found that the amount of transported polymer molecules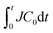 accurately represented the drying rate J, independently of the initial polymer concentration. J−1 was proportional to
accurately represented the drying rate J, independently of the initial polymer concentration. J−1 was proportional to  with a kinematic constant A
with a kinematic constant A . We estimated the diffusion constant (D) of the polymer molecules from the concentration profile of each drying sample. There was a clear negative correlation between D and A, suggesting that the accumulation of the polymer is key to understanding the decrease in the drying rate. These results illustrate how (involatile) polymer transport kinetics links to the overall drying kinetics of polymer solutions.
. We estimated the diffusion constant (D) of the polymer molecules from the concentration profile of each drying sample. There was a clear negative correlation between D and A, suggesting that the accumulation of the polymer is key to understanding the decrease in the drying rate. These results illustrate how (involatile) polymer transport kinetics links to the overall drying kinetics of polymer solutions.
The present DIC method can be used in combination with other techniques such as fluorescent observation. To understand mass transport kinetics inside a drying film, it is important to visualize the flow field in the solution. This can be achieved by, for example, tracking fluorescent particles. Therefore, by combining the DIC method with other techniques such as fluorescence tracking it is possible to simultaneously determine concentration and investigate the flow field.
Author contributions
Masahiko Tanaka: conceptualization, funding acquisition, investigation, formal analysis, writing – original draft and writing – review & editing; Susumu Inasawa: funding acquisition, writing – review & editing and supervision.Data availability
Data are available from the corresponding author upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Frank Kitching, MSc., from Edanz (https://jp.edanz.com/ac) for editing a draft of this manuscript. We also thank JAPAN VAM & POVAL Co., Ltd for providing the PVA granules. This work was partially financially supported by JSPS KAKENHI Grant Number JP 23K26435, JP 23H01742, JP24KJ1020 and the Institute for Fostering Leadership to create future value through Outstanding Research, Innovation and Sustainable Higher education (FLOuRISH) [grant number SP21-016-01].References
- Morio Okazaki, Katashi Shioda, Keizo Masuda and Ryozo Toei, Drying mechanism of coated film of polymer solution, J. Chem. Eng. Jpn., 1974, 7, 99–105, DOI:10.1252/jcej.7.99.
- Tadashi Kajiya, Eisei Nishitani, Tatsuya Yamue and Masao Doi, Piling-to-buckling transition in the drying process of polymer solution drop on substrate having a large contact angle, Phys. Rev. E, 2006, 73, 011601, DOI:10.1103/PhysRevE.73.011601.
- Sushanta Ghoshal, Paul Denner, Siegfried Stapf and Carlos Mattea, Study of the formation of poly(vinyl alcohol) films, Macromolecules, 2012, 45(4), 1913–1923, DOI:10.1021/ma2023292.
- Shunto Arai and Masao Doi, Skin formation and bubble growth during drying process of polymer solution, Eur. Phys. J. E, 2012, 35, 57, DOI:10.1140/epje/i2012-12057-2.
- Yuji Shimokawa, Tadashi Kajiya, Keiji Sakai and Masao Doi, Measurement of the skin layer in the drying process of a polymer solution, Phys. Rev. E, 2011, 84, 051803, DOI:10.1103/PhysRevE.84.051803.
- A. Babaie and B. Stoeber, Concentration field evolution during the drying of a thin polymer solution film near the contact line, Langmuir, 2015, 31, 9033–9040, DOI:10.1021/acs.langmuir.5b01960.
- E. Ciampi and P. J. McDonald, Skin formation and water distribution in semicrystalline polymer layers cast from solution: a magnetic resonance imaging study, Macromolecules, 2003, 36, 8398–8405, DOI:10.1021/ma034951j.
- Laure Daubersies, Jacques Lenga and Jean-Baptiste Salmon, Confined drying of a complex fluid drop: phase diagram, activity, and mutual diffusion coefficient, Soft Matter, 2012, 8, 5923–5932, 10.1039/C2SM25500F.
- Kevin Roger, Marianne Liebi, Jimmy Heimdal, Quoc Dat Pham and Emma Sparr, Controlling water evaporation through self-assembly, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(37), 10275–10280, DOI:10.1073/pnas.1604134113.
- K. Roger, E. Sparr and H. Wennerström, Evaporation, diffusion and self-assembly at drying interfaces, Phys. Chem. Chem. Phys., 2018, 20, 10430–10438, 10.1039/C8CP00305J.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport phenomena, John Wiley & Sons, Inc., 1960, ch. 18 Search PubMed.
- M. Lehtihet, E. Abisset, S. Chevalier, A. Sommier, C. Pradere and J. Leng, Thermospectroscopic infrared imaging of a confined drying process, Chem. Eng. J., 2021, 403, 126167, DOI:10.1016/j.cej.2020.126167.
- Kevin Roger and Jé.rôme J. Crassous, How the interplay of molecular and colloidal scales controls drying of microgel dispersions, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(46), e2105530118, DOI:10.1073/pnas.2105530118.
- Benjamin Sobac, Sam Dehaeck, Anne Bouchaudy and Jean-Baptiste Salmon, Collective diffusion coefficient of a charged colloidal dispersion: interferometric measurements in a drying drop, Soft Matter, 2020, 16, 8213–8225, 10.1039/D0SM00860E.
- M. E. Young, P. A. Carroad and R. L. Bell, Estimation of diffusion coefficients of proteins, Biotechnol. Bioeng., 1980, 22, 947–955, DOI:10.1002/bit.260220504.
- Myo T. Tyn and Todd W. Gusek, Prediction of diffusion coefficients of proteins, Biotechnol. Bioeng., 1990, 35, 327–338, DOI:10.1002/bit.260350402.
- Lucas Goehring, Joaquim Li and Pree-Cha Kiatkirakajorn, Drying paint: from micro-scale dynamics to mechanical instabilities, Philos. Trans. R. Soc., A, 2017, 375, 20160161, DOI:10.1098/rsta.2016.0161.
- Max Huisman, Paul Digard, Wilson C. K. Poon and Simon Titmuss, Evaporation of concentrated polymer solutions is insensitive to relative humidity, Phys. Rev. Lett., 2023, 131, 248102, DOI:10.1103/PhysRevLett.131.248102.
- Kohei Abe, Patrick Saul Atkinson, Chi Shing Cheung, Haida Liang, Lucas Goehring and Susumu Inasawa, Dynamics of drying colloidal suspensions, measured by optical coherence tomography, Soft Matter, 2024, 20, 2381–2393, 10.1039/D3SM01560B.
- Kai Inoue and Susumu Inasawa, Drying-induced back flow of colloidal suspensions confined in thin unidirectional drying cells, RSC Adv., 2020, 10, 15763–15768, 10.1039/D0RA02837A.
- Jean-Baptiste Salmon and Frédéric Doumenc, Buoyancy-driven dispersion in confined drying of liquid binary mixtures, Phys. Rev. Fluids, 2020, 5, 024201, DOI:10.1103/PhysRevFluids.5.024201.
- B. Selva, L. Daubersies and J.-B. Salmon, Solutal convection in confined geometries: Enhancement of colloidal transport, Phys. Rev. Lett., 2012, 108, 198303, DOI:10.1103/PhysRevLett.108.198303.
- Alena Bell, Jonas Kind, Maximillian Hartmann, Benjamin Kresse, Mark V. Hoefler, Benedikt B. Straub, Gü.nter K. Auernhammer, Michael Vogel, Christina Thiele and Robert W. Stark, Concentration gradients in evaporating binary droplets probed by spatially resolved Raman and NMR spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(15), e2111989119, DOI:10.1073/pnas.2111989119.
- Erik Sewalt, J. Kalkman, J. Ruud Van Ommen, Gabrie Meesters and V. van Steijn, Revealing how maltodextrin-containing droplets dry using optical coherence tomography, Food Res. Int., 2022, 157(4), 111049, DOI:10.1016/j.foodres.2022.111049.
- Douglas R. Vogus, Vincent Mansard, Michael V. Rapp and Todd M. Squires, Measuring concentration fields in microfluidic channels in situ with a Fabry–Perot interferometer, Lab Chip, 2015, 15, 1689, 10.1039/c5lc00095e.
- https://www.olympus-lifescience.com/en/microscope-resource/primer/techniques/dic/dicintro/ .
- Jiyun Han, Subeen Park, Mingizem Gashaw Seid, Byeongho Park, Soo Hyun Lee, Hyung Min Kim, Changha Lee, Jaesang Lee, Jae Hun Kim and Seok Won Hong, Real-time morphological detection of label-free submicron-sized plastics using flow-channeled differential interference contrast microscopy, J. Hazard. Mater., 2023, 459, 132207, DOI:10.1016/j.jhazmat.2023.132207.
- Hayato Miyazaki, Kohei Abe and Susumu Inasawa, Packing structures of colloidal silica particles formed by drying condensed suspensions, Drying Technol., 2020, 38, 385–394, DOI:10.1080/07373937.2019.1574813.
- Dan Fu, Seungeun Oh, Wonshik Choi, Toyohiko Yamauchi, August Dorn, Zahid Yaqoob, Ramachandra R. Dasari and Michael S. Feld, Quantitative DIC microscopy using an off-axis self-interference approach, Opt. Lett., 2010, 35, 2370–2372, DOI:10.1364/OL.35.002370.
- David Regan, Joseph Williams, Paola Borri and Wolfgang Langbein, Lipid bilayer thickness measured by quantitative DIC reveals phase transitions and effects of substrate hydrophilicity, Langmuir, 2019, 35(43), 13805–13814, DOI:10.1021/acs.langmuir.9b02538.
- Romane Le Dizès Castell, Marc Prat, Sara Jabbari Farouji and Noushine Shahidzadeh, Is unidirectional drying in a round capillary always diffusive?, Langmuir, 2023, 39(15), 5462–5468, DOI:10.1021/acs.langmuir.3c00169.
- D. R. Lide, Handbook of Chemistry and Physics, 83rd edn, 2002, CRC Press Search PubMed.
- Jean-Baptiste Salmon, Frédéric Doumenc and Bé.atrice Guerrier, Humidity-insensitive water evaporation from molecular complex fluids, Phys. Rev. E, 2017, 96, 032612, DOI:10.1103/PhysRevE.96.032612.
- M. Tanaka and S. Inasawa, Drying kinetics of colloid-polymer suspensions confined in a two-dimensional geometry, Colloids Surf., A, 2023, 672, 131693, DOI:10.1016/j.colsurfa.2023.131693.
- S. Jeck, P. Scharfer, W. Schabel and M. Kind, Water sorption in poly(vinyl alcohol) membranes: An experimental and numerical study of solvent diffusion in a crosslinked polymer, Chem. Eng. Process., 2011, 50, 543, DOI:10.1016/j.cep.2010.09.004.
- Kyle Anthony Baldwin, Manon Granjard, David I. Willmer, Khellil Sefiane and David John Fairhurst, Drying and deposition of poly(ethylene oxide) droplets determined by Péclet number, Soft Matter, 2011, 7, 7819–7826, 10.1039/C1SM05220A.
- M. Barcea, S. Morariu and D. Rusu, In situ gelation of aqueous solutions of entangled poly(vinyl alcohol), Soft Matter, 2013, 9, 1244–1253, 10.1039/C2SM26094H.
- Daniele Parisi, Colin D. Ditillo, Aijie Han, Seth Lindberg, Mark W. Hamersky and Ralph H. Colby, Rheological investigation on the associative properties of poly(vinyl alcohol) solutions, J. Rheol., 2022, 66, 1141–1150, DOI:10.1122/8.0000435.
- D. I. Bower, An introduction to polymer physics, Cambridge University Press, Cambridge, United Kingdom, 2002 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03457k |
| This journal is © the Owner Societies 2025 |