Chlorine gas and anion radical reactivity in molten salts and the link to chlorobasicity

Abstract

Next-generation nuclear power plants may include exciting novel designs in which molten salts are the coolant or a combination of the coolant and fuel. Whereas it is straightforward to see why having a low volatility coolant can be advantageous for safety, much is not understood about the production of volatile halogen gases as a result of radiation and even less is known about the distribution of these species at and away from interfaces. Using first principles molecular dynamics simulations, we investigate the product of the disproportionation reaction between chlorine anion radicals (nominally Cl₂˙⁻) in the bulk and slab configurations. We find that the product depends on the chlorobasicity of the medium. For example, in ZnCl₂, Cl₂ forms, but in a eutectic mixture of LiCl and KCl, Cl₃⁻ is formed as a product. We also find that Cl₃⁻ prefers to form at the vapor interface and this may have implications for corrosion and reactivity. Furthermore, the mechanisms of the mobility of Cl₂ and Cl₃⁻ are radically different, the first one being vehicular and the second Grotthus-like. Chlorobasicity is linked to the electronic structure of the host melt; ZnCl₂ forms extended networks along which metal ions and anionic counterions have significant electronic orbital overlap forming long, linear, molecular-like constructs; the opposite is true for the alkali metal eutectic salt.

---

1 Introduction

Modern molten salt reactors^1–3 to generate electricity are no longer a concept, but instead, are already starting to be built by different companies.^4,5 Depending on the salt mixture used,⁶ and in the high-temperature, high-radiation regimes these salt melts exist, radiolytic products are certainly expected.⁷ Part of the point of using molten salts in these systems is to avoid the high pressure environments of water-cooled reactors,⁸ and whereas molten salts achieve this, it is still important to understand off-gases,⁹ including those of halogenic nature that may be radiolytically produced as these are highly corrosive to surfaces.

In molten salts exposed to radiation, two general types of species will be initially generated, excess electron-type radicals and excess hole-type radicals,^7,10 which can subsequently undergo cascades of reactions. For example, in a recent article¹¹ we showed that in molten ZnCl₂ the excess electron-type species include ZnCl₃˙²⁻ and Zn₂Cl₅˙²⁻; the hole-type species can be Cl˙, Cl₂˙⁻, or some larger charge-deficient radical anion variation Cl_n+1˙⁽ⁿ⁻⁾. The most common reaction that one can follow experimentally by pulse radiolysis^12,13 in these systems is recombination,^7,14 where the excess hole species find and scavenge the excess electrons. From the point of view of molten salt reactors, this is excellent news, given that the final product of recombination is the original Cl⁻ or F⁻ ion and the original metal ion; in other words, such a reaction leads to no damage to the salt or other components. The resilience of the high-temperature molten salts toward harsh environmental conditions may be contrasted with the case of their room-temperature cousins, the ionic liquids, where for some but not for others, the existence of chemical bonds may result in a variety of reaction products.^15–24

This article focuses instead on a set of minority, but very important, disproportionation reactions, namely

2Cl₂˙⁻ → Cl₂ + 2Cl⁻ (1)

2Cl₂˙⁻ → Cl₃⁻ + Cl⁻, (2)

or their many possible variations corresponding to reactions between Cl_n+1˙⁽ⁿ⁻⁾ radical hole species. The reason why these reactions are so important is because they do not restore the salt to its original state; they instead create deleterious halogenic molecules which may preferentially appear at the gas interface.

Cl₂ + Cl⁻ → Cl₃⁻ (3)

Another way of thinking of reaction (2) is as a combination of reactions (1) and (3), in which Cl₂ acts as a Lewis acid and Cl⁻ as a Lewis base. Looking at it this way, we see that the more chlorobasic the melt, the more likely the reaction product will be the molecular anion Cl₃⁻.

Section 2, Computational methods, describes all methodological aspects of our calculations. We will show in Section 3 that in ZnCl₂, Cl₂ is a reaction product, and its mechanism of transport is vehicular. In contrast, in the eutectic mixture of LiCl and KCl, Cl₃⁻ forms, and its motion is Grotthuss-like^25,26 with the atoms that make Cl₃⁻ being constantly exchanged on a molecular time scale. While the disproportionation of Cl₂˙⁻ can be observed using time-resolved radiolysis techniques,⁷ the computational work presented here is of significant practical importance because the products of this reaction (Cl₂ or Cl₃⁻) are very difficult to observe via optical spectroscopy due to stronger overlapping absorptions of other transient species occurring on the same time scale.

2 Computational methods

This study includes simulations in the bulk and at the vacuum interface; for bulk simulations, the goal is to study the structure and dynamics of the equilibrium reaction product in the disproportionation reaction between two Cl₂˙⁻ radicals or other Cl_n+1˙⁽ⁿ⁻⁾-type analogs. Instead, for the interfacial studies, the goal is to better understand the preferred location where Cl₃⁻ forms and to some extent where it will prefer to reside on a longer time scale. Bulk studies were carried out in ZnCl₂ and in the eutectic mixture between KCl and LiCl; interfacial studies were carried out for multiple different initial conditions in the case of the eutectic mixture. Subsequent sections describe how these simulations were constructed and executed.

2.1 Classical molecular dynamics equilibration

In order to ensure appropriate liquid and interfacial structural behavior, initial snapshots for ab initio molecular dynamics (MD) trajectories were derived from well equilibrated MD runs using the polarizable ion model (PIM).^27,28 Historically, PIM models have been constructed from a combination of first principles data and structural experimental data, making them reliable for the reproduction of local structure and intermediate range order in molten salts; intermediate range order when multivalent metal ions are involved, is often not well captured with models that are not polarizable.

2.1.1 Polarizable ion model simulations to create initial conditions for first principles MD in the bulk phase. To study the LiCl–KCl eutectic mixture in the bulk phase, we created a simulation box containing 36 Li⁺, 25 K⁺, and 61 Cl⁻ ions, and to study bulk ZnCl₂, an initial frame was created with 36 Zn²⁺ and 72 Cl⁻ ions. These initial frames were then equilibrated using the PIM,^27,28 as coded in the FIST module of the CP2K software²⁹ version 7.1. Runs were 1 ns in duration at 1 bar and 673 K in the isothermal–isobaric³⁰ ensemble (NPT) using the Nosé–Hoover^31–33 method. The MD integration step was set to 1 fs, the cutoff for non-bonded interaction was set to 7 Å, and long-range electrostatic interactions were treated with the Ewald summation method.³⁴ Equilibrated liquid frames for the two systems were then selected from the final portion of each trajectory with the correct experimental density for each melt at 673 K (1.69 g cm⁻³ for LiCl–KCl from Ito et al.³⁵ and 2.48 g cm⁻³ for ZnCl₂ from Janz et al.³⁶). Box length values for the LiCl–KCl mixture melt and for the ZnCl₂ melt were 14.919 Å and 14.865 Å, respectively.

2.1.2 Polarizable ion model simulation to create the initial frame for first principles MD of LiCl–KCl at the interface. Because AIMD studies of interfacial systems are computationally expensive, to promote faster dynamics we chose to run these at a temperature higher than for our bulk studies. The equilibration process also starts with MD based on the PIM model²⁸ as coded in the Metalwalls software³⁷ release 20.05. Initial configurations were generated using the PACKMOL software³⁸ containing 89 Li⁺, 61 K⁺, and 150 Cl⁻ ions. We used a 1 fs timestep and a real-space cutoff of 12.0 Bohr (about 6.35 Å). The initial bulk liquid equilibration was performed for 1 ns in the isothermal–isobaric³⁰ ensemble at 1.0 bar and 773 K using the Nosé–Hoover thermostat^31–33 and barostat. The final configuration from the NPT equilibration run was then modified by extending the box length in the z direction by 3 times and centering the box in the z-direction with final box dimensions of 19.969 : 19.969 : 59.906 Å. We further equilibrated the system using these dimensions in the 2D-NVT ensemble (only x and y-axes are periodic and the Ewald³⁴ sum is performed in 2D) for an additional 1 ns. A single frame with low surface roughness was then chosen as input for AIMD.

2.2 First principles molecular dynamics simulations

First principles MD studies were carried out using the Quickstep module of the CP2K package. Initial conditions were the well equilibrated classical snapshots described in previous sections, except that melts needed to be modified to accommodate the formation or product, either Cl₂ or Cl₃⁻ (vide infra).

All AIMD calculations used the following parameters, 600 Ry CUTOFF, 60 Ry REL_CUTOFF, SCF convergence criteria and outer SCF convergence criteria equal to 10⁻⁶. For single point calculations derived from these trajectories and in order to compute properties, the CUTOFF and REL_CUTOFF were increased to 1200 Ry and 80 Ry respectively to improve accuracy in the computation of Bader charges.^39,40 We used the always stable predictor corrector integrator with EPS_DEFAULT set to 10 × 10⁻¹² and an extrapolation order of 4. The orbital transformation (OT) method^41,42 was used for all simulations together with the conjugate gradient minimizer and the FULL_ALL preconditioner. We used the Goedecker, Teter, and Hutter pseudopotentials⁴³ and the PBE functional^44–47 together with the D3 correction by Grimme,⁴⁸ for which R_CUTOFF was set to 40 Å. A list of elements and their respective basis sets are provided in Table 1. Unless otherwise noted, all our simulations were run as spin polarized.

Table 1 Basis sets⁴⁹ and GTH pseudo potentials

Element	Basis set	GTH potential
Li	TZVP-MOLOPT-SR-GTH	GTH-PBE-q3
K	TZVP-MOLOPT-SR-GTH	GTH-PBE-q9
Zn	TZVP-MOLOPT-SR-GTH	GTH-PBE-q12
Cl	TZVP-MOLOPT-GTH	GTH-PBE-q7

---

2.2.1 First principles molecular dynamics simulations in the bulk. The formation of Cl₂ or Cl₃⁻, both closed-shell species, required the introduction of a pair of charge-depleted Cl-based radical species with opposite spin. We achieved the desired configuration by (i) keeping the total system charge neutral, (ii) the multiplicity at a value of 1, and (iii) by swapping a Li⁺ ion with what nominally would be a Cl⁻ ion in the case of the eutectic mixture, and by removing a Zn²⁺ ion in the case of the ZnCl₂ melt; we also modified the distance of two Cl species so that these would be close to the typical bonding distance for Cl₂. Once these operations were performed, each system originally equilibrated as described in Section 2.1.1, was thoroughly re-equilibrated for 110 ps, this time using AIMD. Production trajectories after equilibration were 221 ps and 287 ps in duration for the ZnCl₂ and the LiCl–KCl eutectic mixture respectively. All AIMD simulations for bulk systems were carried out at 673.15 K in the constant temperature and volume ensemble (NVT) using a 1 fs time step and default parameters for the Nosé–Hoover chain thermostat, except that the time constant was set to 0.1 ps.

2.2.2 Interfacial AIMD simulations. We performed four different interfacial simulations of the LiCl–KCl eutectic melt (see Section 3.3); our goal was to establish the location (bulk or interface) where the formation of closed-shell Cl₃⁻ most likely occurred. An initial frame obtained from classical MD simulations (see Section 2.1.2) was further equilibrated using AIMD under 2D periodic boundary conditions for more than 100 ps using the wavelet-based Poisson solver^50,51 as coded in CP2K. Then a set of production simulations were run in which two Cl₂˙⁻ radicals were initially “created” in specifically chosen locations from what originally were Cl⁻ ions. The two initial Cl₂˙⁻ radicals were created by shortening the distance between Cl⁻ ions to about 1.90 Å and converging the wavefunction so that the α and β spins were primarily located on these two Cl₂˙⁻ radicals. Using the &BS section in CP2K, the initial electronic density guess was defined by specifying atomic orbital occupations in the initialization of the density matrix for these fragments; each of the fragments had one electron less than in a Cl⁻ ion and each had a different spin. Because two Cl⁻ ions were replaced by two Cl˙ radicals, production runs had an overall positive charge of +2 and a multiplicity of 1 (radical species had opposite spin values). The converged wavefunctions were then used to initialize non-equilibrium AIMD simulations.

By employing spin-polarized calculations to allow the spins of opposite sign to emerge (open-shell singlet formalism using the unrestricted Kohn–Sham method), four cases were studied, (i) when the two Cl₂˙⁻ radicals were initially created on opposite interfaces, (ii) when they were created on the same interface, (iii) when they were created in the middle of the system representing the bulk, and (iv) a case where a Cl₂ molecule from the gas phase collided with and attached to the interface forming Cl₃⁻. In each case we stopped our runs when we could identify the formation of product. Runs had a 1 fs time step and were carried out in the NVT ensemble at 773.15 K.

A final simulation of ∼40 ps extending scenario (iv) was run after the formation of Cl₃⁻. We did this to investigate if the product would remain in the vicinity of the interface or diffuse into the bulk. The system, which was now formally closed-shell after the hole species had reacted to form Cl₃⁻, was run using 3D periodic boundary conditions and as spin-restricted.

3 Results and discussion

In order to follow the identity and dynamics of the reaction product, Cl₂ or Cl₃⁻, along our first principles simulations, it was important to identify orbitals in the molecule that are well separated in energy from those in the band structure of the liquid. It turns out that these look very similar in the condensed phase and in the gas phase and because of this, we will use the same nomenclature for them as in the gas phase orbital diagrams provided in Fig. S1 (ESI†).

We start this section discussing the bulk phase and noticing how the equilibrium structure of the disproportionation reaction product differs depending on the nature of the host salt. We then consider dynamics and finally the location (bulk or interface) in which we find product in the case of the eutectic melt. This section also discusses intrinsic structural and electronic properties of the solvent,^11,52 making a connection between the nature and “availability” of Cl⁻ associated with the concept of chlorobasicity.^53–56

3.1 Formation of closed-shell halogenic molecules in bulk molten salts

When studying the product of the reaction between Cl-based hole species in ZnCl₂ and the LiCl–KCl eutectic mixture, a few points become apparent quickly. First, as can be gleaned from Fig. 1, in molten ZnCl₂, Cl₂ forms, and the identity of the two Cl atoms is fixed through our long first-principles production MD simulation. Furthermore, the electronic valence charge on each of the two individual Cl atoms is on average about the same and close to the ideal valence = 7; this can be seen from black and red lines in the top panel of Fig. 1. The situation is completely different when we consider the LiCl–KCl eutectic mixture. In this case, at most points in time, we observe three Cl atoms/ions that are separate in charge from the manifold of Cl⁻ ions with larger valence charge. This can be gleaned from the changes in line color, indicating changes in the identity of the atoms forming Cl₃⁻ on the bottom panel in Fig. 1.

Fig. 1 Bader charges for Cl-based atoms or ions in ZnCl₂ (top) and the LiCl–KCl eutectic mixture (bottom) as a function of time.

The second point we want to highlight is intrinsic to the host salt; the assigned Bader valence charge^39,40 of Cl⁻ ions in ZnCl₂ is in general lower than that in the eutectic melt by about 0.3. We interpret this to mean that in the eutectic mixture the behavior of Cl⁻ is more ionic; Cl⁻ is not significantly committed to sharing electrons with metal ions, and the mixture melt should be in general more chlorobasic (able to “donate” or share Cl⁻ with other species if these were to appear in the melt). The opposite is true in ZnCl₂ where Cl⁻ ions are strongly committed to extended Cl⁻-decorated Zn²⁺ charge networks in which the anions are significantly polarized.

To emphasize the more “molecular” nature of ZnCl₂, and how anions are committed to Zn²⁺ metal ions (in comparison to the eutectic melt, ZnCl₂ is not chlorobasic), we show in Fig. 2 a typical molecular orbital (MO) from the manifold of states in the band structure labeled “C” in Fig. S2a (ESI†). Fig. S2a and b (ESI†) show as a function of time orbital energies as well as labels for selected relevant states or bands in the cases of ZnCl₂ and the LiCl–KCl eutectic mixture respectively. What we mean to highlight in Fig. 2 is the clear formation of an extended molecular-style MO (many Zn²⁺ metal ions and many Cl⁻ anions) in which p orbitals of Cl⁻ overlap in a σ-bonding fashion with d orbitals of Zn²⁺. To be clear, what is unique in this picture is not the existence of large MOs but how these are correlated with liquid structure; orbitals of the ions are shared in a 1D fashion along the Cl⁻-decorated Zn²⁺ charge network. Other MOs in the same band each capture a different part of the ZnCl₂ charge network. In contrast, for the eutectic mixture, we see orbitals that can be either localized on specific ions or delocalized; these do not follow any significant longer-range molecular-style overlap pattern. This is not to say that there is no polarization of Cl⁻ by Li⁺ or K⁺; there certainly is, but based on the MOs it appears to be local.

Fig. 2 Cropped portion of a simulation frame highlighting extended but transient “σ-style” bonds between p orbitals of Cl⁻ ions and d orbitals in Zn²⁺ metal ions along a network. Notice the consistent four-coordination structure around Zn²⁺. This MO belongs to what we have labeled band C in Fig. S2a (ESI†); this is a band of similar MOs that encompass extended ZnCl₂ network structures; the bottom of the band has the most mixing between d orbitals in the metal ion and p orbitals on the anion with about 80–20%, respectively. Ions in the figure are not to scale and those within the network are shown larger for visual impact; ions not in the network are shown as transparent. Cl⁻ in green and Zn²⁺ in blue.

A third important observation when considering the bottom panel of Fig. 1 is the nature and time scale for charge transfer events when considering the Cl₃⁻ molecule in the eutectic melt. With an abundance of Cl⁻ ions available in a chlorobasic melt, we see that the identity of the atoms/ions that constitute Cl₃⁻ change on a scale that is between a few picoseconds to a few tens of picoseconds. Section 3.2 describes this charge transfer process and how it relates to motion. Interestingly, and supporting our findings, experimental studies by Andresen⁵⁷ on the molar absorptivity of Cl₂ and molten chloride melts saturated with Cl₂ (NaCl through CsCl melts as well as MgCl₂) indicate that, as opposed to the case in MgCl₂, the dissolved species in the alkali melts is not Cl₂.

3.2 Mechanisms of diffusion

The equilibrium reaction product of the disproportionation reaction between two Cl₂˙⁻ radicals in ZnCl₂ is the Cl₂ molecule. We can begin to recognize this by looking at the top panel in Fig. 1, which shows that the Bader charges of two Cl atoms are significantly lower and similar in value in comparison to those of all Cl⁻ ions in the melt. Furthermore, these are the exact same Cl atoms throughout our long AIMD production trajectory. This however, is not sufficient to guarantee that we are actually observing the product of the disproportionation reaction, given that these could be any two atoms that are not necessarily spatially linked. To verify that we are indeed creating Cl₂, we also identify and follow in real space and time the σ_g3s orbital of the neutral diatomic molecule. We are able to do this because the energy of σ_g3s is well separated from that of any other state in the band structure of the melt, as can be gleaned from Fig. S2a (ESI†). Because we are able to tell that the identity of the atoms forming Cl₂ does not change in time, we conclude that its motion is simply vehicular and we write no more about it here. Instead, we focus on the very interesting mechanism of motion for Cl₃⁻ in the LiCl–KCl eutectic mixture.

The reader is asked to once more inspect the bottom panel of Fig. 1 describing the number of valence electrons ascribed to Cl-based species in the eutectic mixture as a function of time. From the figure we see that at most points in time, there are three Cl species that have an assigned number of electrons that is lower than the rest of the Cl⁻ ions in the melt. Notice that the identity of these three atoms readily changes on the 10 ps time scale, and we see many of these changes on our long AIMD trajectory. In the case of the LiCl–KCl mixture, it is also important to verify that these three special atoms – which are in constant exchange – belong to a single molecule, and we can establish this by following the time history of σ_g3s and σ_u3p of Cl₃⁻ (see Fig. S1, ESI†). This is possible given that their energies do not fall close to bands of the melt as is shown in Fig. S2b (ESI†).

Fig. 3 shows time-stamped snapshots along a short segment of about 1 ps in our AIMD trajectory. Two things are important, (1) the atoms enclosed by the σ_g3s isosurface, and (2) the color-coded but semi-translucent shell around each Cl-based species in the melt. In the graph, Cl⁻ ions have a green shell, and this color shifts toward blue when the atom is more charge-depleted. For example, in the first frame of the sequence we see that the central atom within the σ_g3s isosurface is charge-depleted (more neutral as if it was a Cl atom) whereas the two terminal atoms are more negative. The color of the shells surrounding the three atoms, associated with their charge, very much change with changes in the symmetry of Cl₃⁻. The more asymmetric the molecule is, or, the larger the displacement along the anti-symmetric stretch coordinate, the more the negative charge localizes on the terminal atom that separates from the other two, which become Cl₂-like. This behavior is identical to what we described a couple of decades ago for I₃⁻ in water and to a lesser extent in acetonitrile.^58,59

Fig. 3 Time stamped frames showing motion of the Cl₃⁻ species. Li⁺ ions are in purple, K⁺ ions are in red, Cl⁻ ions are in green and their shell indicates charge. The bluer the shell surrounding Cl the more neutral the species, the more green the shell, the closer to anionic. Isosurfaces correspond to σ_g3s.

Notice that as opposed to the case of Cl₂ in ZnCl₂, the atoms forming Cl₃⁻ in the eutectic mixture are not conserved. In other words, if as a thought experiment we were to label radical hole species that react to form Cl₃⁻, the atoms in this molecule would not be the same a few tens of picoseconds later. In fact, the mechanism of motion of Cl₃⁻ is very reminiscent of the Grotthus mechanism. For example, at 233.2 ps we have the case were two terminal Cl species share the negative charge (greener shell) and the atom in the middle is more charge neutral (shell is blue); only a fraction of a ps later, one of the terminal atoms is lost as Cl⁻, which is then replaced from the other end of the molecule by a different Cl⁻ ion (see the snapshot at 233.5 ps). It is clear from the color of the translucent atomic shells within the σ_g3s isosurface that, at 233.5 ps the charge is significantly more localized on the terminal (green shell) atom than on the other two which are more akin to Cl₂ (each of these has a blue shell). However, already at 233.9 ps each terminal carbon in Cl₃⁻ has a green shell associated with it. In other words, the antisymmetric vibrational motion of this molecule, driven in significant part by polarization caused by adjacent ions in the melt, results in (i) concomitant fluctuations in charge localization within the molecule and (ii) the constant shedding and reacquisition of Cl⁻ ions (sometimes on the same side and sometimes on opposite sides). We emphasize that it is all the atoms in Cl₃⁻ that eventually get replaced, and not just a single polarizing Cl⁻-like terminal component. We can see this from Fig. S3 (ESI†) in which selected snapshots are shown with color-labeled Cl or Cl⁻ species that were, are, or will become part of Cl₂-like molecules. Fig. S3 (ESI†) focuses on Cl₂ because in the eutectic melt the process of swapping atoms in or out of Cl₃⁻ involves going through Cl₂-like intermediates.

Visual inspection of long “movies” generated from the trajectory of σ_g3s show that the motion of Cl₃⁻ appears faster than the vehicular motion of individual atoms. This is because, in addition to motion due to translation of atoms, we also have motion that is given by the independent translation of the σ_g3s isosurface. Put differently, the diffusion of Cl₃⁻ comes from a combination of the translational motion of atoms and the quantum mechanical change in identity of the atoms making the molecular ion.

3.3 Cl₃⁻ prefers to form at the vapor interface

Thus far, our discussion has been about disproportionation reactions (1) and (2) that, due to the nature of our simulations, were strictly constrained to occur in the bulk. However, the question arises of whether in the presence of interfaces (in our case the vapor interface), Cl₃⁻ which is charged, will prefer to form in the bulk or at the liquid–vapor boundary. This has obvious implications for off-gas behavior, solubility, and ultimately corrosion at surfaces. To explore this problem, we created four different initial scenarios as the starting point for first principles molecular dynamics simulations. In three of these, two Cl₂˙⁻ radical anions were introduced at different, but carefully selected, spatial locations on a slab of the eutectic LiCl–KCl melt; this slab had an upper and a lower boundary facing vapor interfaces. A fourth scenario introduced instead a single Cl₂ molecule from the gas phase that approaches and collides with the melt interface from above in the Z direction. Initial placement of the pair of Cl₂˙⁻ radicals was (i) at the same interface, (ii) at opposite interfaces, and (iii) in the middle of the bulk.

Fig. 4A1–C1, each show a different initial condition in which the atoms belonging to the two Cl₂˙⁻ radical anions are highlighted with blue shells. Fig. 4A2–C2 show the corresponding final frames after disproportionation viareaction (2); in this case the product is detected by considering the spatial location of σ_g3s. Fig. 4D1 and D2 are the frames before and after a vapor-phase Cl₂ molecule impacts the eutectic melt interface, respectively. The interpretation of all of these figures is clear and the same; in each case, no matter what the starting condition was, the product of the disproportionation reaction (2) forms at the vapor interface. We interpret this to mean that, even though Cl₃⁻ is charged, it is still charge-depleted in comparison to Cl⁻ ions in the melt and, there is a preference for it at the boundary for this reason.

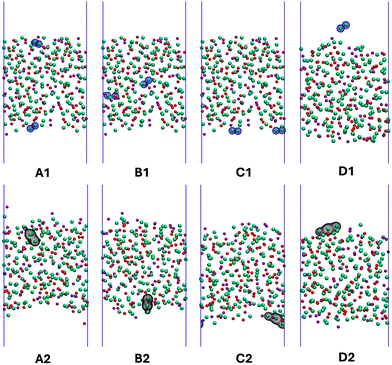Fig. 4 Upper panel figures show initial configurations for slab-based molecular dynamics runs and bottom panel snapshots after the disproportionation reaction occurred. In the upper panel blue shells around atoms indicate the initial location of Cl₂˙⁻ (A1)–(C1) and the location of Cl₂ (D1). In the bottom panel (A2)–(D2) the isosurfaces correspond to σ_g3s of the product Cl₃⁻. Notice that in all cases the product is at the interface independent of initial condition. Atomic color code is the same as in Fig. 3.

In an attempt to begin addressing the issue of formation of Cl₃⁻vs. longer-term localization of the species at the vapor interface, the simulation for the system in which a Cl₂ molecule was introduced from the gas phase (last column in Fig. 4) was further extended as closed-shell for an extra ∼40 ps during which Cl₃⁻ always remained interface-bound. This supports the conjecture that, at least on simulation time scales, Cl₃⁻ not only prefers to form at the boundary but also remains there. Just like we observe in the bulk, the species that forms at the interface alternates between Cl₃⁻ and Cl₂ as terminal atoms forming the triatomic species get continually swapped. If Cl₃⁻ molecular ions prefer to form at the interface instead of the bulk, salts that are not chlorobasic, and in which reaction (1) will be dominant, are expected to result in an even less favorable environment for Cl₂.

4 Conclusions

In molten salt reactors where the melt is the coolant, radiation will necessarily result in the formation of excess electron and excess hole type species. It is expected that, to a large extent, these species will recombine, resulting in the same original species in what amounts to a form of self-healing for the medium. Yet, other reactions may also occur, for example, excess electron species may end up reducing metal ions and excess hole species may react to form halogenic gas species. This is where the Lewis acid–base nature of the melt plays a significant role. Cl₂ can act as an acid and accept Cl⁻ to form Cl₃⁻, and this will happen readily in chlorobasic melts. Such a reaction will shift equilibria and make Cl₂-related species more soluble. In our study we find that ZnCl₂ is not chlorobasic in comparison to a eutectic mixture of LiCl and KCl. The product of the disproportionation between two hole species is accordingly different in the two systems and this difference is directly linked to the chlorobasicity of the medium. Interestingly, ZnCl₂ shows significant overlap between orbitals centered on cations and anions resulting in extended linear bonding patterns along Cl⁻-decorated Zn²⁺ charge networks. It will be interesting for future studies to explore the lability of these extended patterns of orbital overlap, given that ZnCl₂ is a low melting salt that is to some extent volatile, viscous, and of low electrical conductivity. Even in the case of the chlorobasic eutectic melt, we found that Cl₃⁻ prefers to form at interfaces; whether these species will significantly accumulate away from the bulk changing the composition of the interfacial melt is an interesting question that should be further investigated.

Author contributions

Supervision SR, VSB and CJM, conceptualization SR, VSB, CJM and HHN, investigation HHN, LDG, MSE, BB, SR and VSB, data curation HHN, formal analysis HHN, VSB and CJM, visualization HHN, writing – original draft CJM, writing – review and editing CJM and VSB.

Data availability

Data sets to reproduce figures in this article are made available within 30 days of the official acceptance date in the Zenodo repository under the Digital Object Identifier (DOI): https://doi.org/10.5281/zenodo.14736318.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported as part of the Molten Salts in Extreme Environments (MSEE) Energy Frontier Research Center, funded by the U.S. Department of Energy Office of Science, Office of Basic Energy Sciences. MSEE work at the University of Iowa was supported under a subcontract from Brookhaven National Laboratory, which is operated under DOE contract DE-SC0012704. Work at ORNL was supported under DOE contract DE-AC05-00OR22725. This research mainly used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility, and, in part, the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory, both supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. We also acknowledge the University of Iowa High Performance Computing Facility. This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://www.energy.gov/doe-public-access-plan).

Notes and references

1. C. Forsberg, G. T. Zheng, R. G. Ballinger and S. T. Lam, Nucl. Technol., 2019, 206, 1778–1801.
2. C. W. Forsberg, Nucl. Technol., 2020, 206, 1659–1685.
3. C. Andreades, A. T. Cisneros, J. K. Choi, A. Y. K. Chong, M. Fratoni, S. Hong, L. R. Huddar, K. D. Huff, J. Kendrick, D. L. Krumwiede, M. R. Laufer, M. Munk, R. O. Scarlat and N. Zweibau, Nucl. Technol., 2016, 195, 223–238.
4. I. L. Pioro, R. B. Duffey, P. L. Kirillov, G. V. Tikhomirov, N. Dort-Goltz and A. D. Smirnov, in Handbook of Generation IV Nuclear Reactors, Elsevier, 2nd edn, 2023, pp. 713–757.
5. J. Krepel and K. J. Kramer, in Molten Salt Reactors and Thorium Energy, Elsevier, 2nd edn, 2024, pp. 953–972.
6. J. Magnusson, M. Memmott and T. Munro, Ann. Nucl. Energy, 2020, 146, 107608.
7. K. Iwamatsu, G. P. Horne, R. Gakhar, P. Halstenberg, B. Layne, S. M. Pimblott and J. F. Wishart, Phys. Chem. Chem. Phys., 2022, 24, 25088–25098.
8. A. Ho, M. Memmott, J. Hedengren and K. M. Powell, Digit. Chem. Eng., 2023, 7, 100091.
9. H. B. Andrews, J. McFarlane, A. S. Chapel, N. D. B. Ezell, D. E. Holcomb, D. De Wet, M. S. Greenwood, K. G. Myhre, S. A. Bryan, A. Lines, B. J. Riley, H. M. Felmy and P. W. Humrickhouse, Nucl. Eng. Des., 2021, 385, 111529.
10. J. K. Conrad, K. Iwamatsu, M. E. Woods, R. Gakhar, B. Layne, A. R. Cook and G. P. Horne, Phys. Chem. Chem. Phys., 2023, 25, 16009–16017.
11. H. H. Nguyen, V. S. Bryantsev and C. J. Margulis, J. Phys. Chem. B, 2023, 127, 9155–9164.
12. J. F. Wishart, A. R. Cook and J. R. Miller, Rev. Sci. Instrum., 2004, 75, 4359–4366.
13. H. Hagiwara, S. Sawamura, T. Sumiyoshi and M. Katayama, Int. J. Radiat. Appl. Instrum., Part C, 1987, 30, 141–144.
14. A. Ramos-Ballesteros, R. Gakhar, G. P. Horne, K. Iwamatsu, J. F. Wishart, S. M. Pimblott and J. A. Laverne, Phys. Chem. Chem. Phys., 2021, 23, 10384–10394.
15. K. B. Dhungana, F. Wu and C. J. Margulis, J. Phys. Chem. B, 2017, 121, 8809–8816.
16. C. Xu, A. Durumeric, H. K. Kashyap, J. Kohanoff and C. J. Margulis, J. Am. Chem. Soc., 2013, 135, 17528–17536.
17. C. Xu and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 532–542.
18. F. Wu, C. Xu and C. J. Margulis, J. Chem. Phys., 2018, 148, 193831.
19. M. N. Knudtzon and D. A. Blank, J. Phys. Chem. B, 2020, 124, 9144–9153.
20. J. F. Wishart, A. M. Funston, T. Szreder, A. R. Cook and M. Gohdo, Faraday Discuss., 2012, 154, 353–363.
21. J. F. Wishart and P. Neta, J. Phys. Chem. B, 2003, 107, 7261–7267.
22. L. Das, R. Kumar, D. K. Maity, S. Adhikari, S. B. Dhiman and J. F. Wishart, J. Phys. Chem. A, 2018, 122, 3148–3155.
23. I. A. Shkrob, S. D. Chemerisov and J. F. Wishart, J. Phys. Chem. B, 2007, 111, 11786–11793.
24. I. A. Shkrob, T. W. Marin, S. D. Chemerisov and J. F. Wishart, J. Phys. Chem. B, 2011, 115, 3872–3888.
25. V. K. Thorsmølle, G. Rothenberger, D. Topgaard, J. C. Brauer, D. Kuang, S. M. Zakeeruddin, B. Lindman, M. Grätzel and J. Moser, ChemPhysChem, 2011, 12, 145–149.
26. N. P. Aravindakshan, C. Kuntz, K. Gemmell, K. Johnson and A. East, ECS Trans., 2016, 75, 575–583.
27. N. Ohtori, M. Salanne and P. A. Madden, J. Chem. Phys., 2009, 130, 104507.
28. Y. Ishii, S. Kasai, M. Salanne and N. Ohtori, Mol. Phys., 2015, 113, 2442–2450.
29. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
30. G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189.
31. S. Nosé, Mol. Phys., 1984, 52, 255–268.
32. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
33. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
34. A. Aguado and P. A. Madden, J. Chem. Phys., 2003, 119, 7471–7483.
35. H. Ito, Y. Hasegawa and Y. Ito, J. Chem. Eng. Data, 2001, 46, 1203–1205.
36. G. J. Janz, J. Phys. Chem. Ref. Data, 1988, 17, 325.
37. A. Marin-Laflèche, M. Haefele, L. Scalfi, A. Coretti, T. Dufils, G. Jeanmairet, S. K. Reed, S. Alessandra, R. Berthin and C. Bacon, et al. , J. Open Source Softw., 2020, 5, 2373.
38. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
39. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
40. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
41. J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118, 4365–4369.
42. V. Weber, J. VandeVondele, J. Hutter and A. M. N. Niklasson, J. Chem. Phys., 2008, 128, 084113.
43. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891.
46. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
47. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
49. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
50. L. Genovese, T. Deutsch, A. Neelov, S. Goedecker and G. Beylkin, J. Chem. Phys., 2006, 125, 074105.
51. L. Genovese, T. Deutsch and S. Goedecker, J. Chem. Phys., 2007, 127, 054704.
52. S. Sharma, A. S. Ivanov and C. J. Margulis, J. Phys. Chem. B, 2021, 125, 6359–6372.
53. L. Sharpless, J. Moon and D. Chidambaram, J. Phys. Chem. Lett., 2024, 15, 5529–5534.
54. J. H. V. Barner and N. J. Bjerrum, Inorg. Chem., 1973, 12, 1891–1896.
55. G. Letisse and B. Trémillon, J. Electroanal. Chem. Interfacial Electrochem., 1968, 17, 387–394.
56. B. Trémillon and G. Letisse, J. Electroanal. Chem. Interfacial Electrochem., 1968, 17, 371–386.
57. R. E. Andresen, T. Østvold and H. A. Øye, ECS Proc. Vol., 1976, 6, 111.
58. C. J. Margulis, D. F. Coker and R. M. Lynden-Bell, J. Chem. Phys., 2001, 114, 367–376.
59. C. Margulis, D. Coker and R. Lynden-Bell, Chem. Phys. Lett., 2001, 341, 557–560.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03285c

---