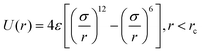Influence of polymer chain length and concentration on the deposition patterns of linear diblock copolymer solution nanodroplets

Abstract

We perform molecular dynamics simulations to study deposition patterns of linear diblock copolymer solution nanodroplets on a solid surface (a wall). The current work mainly investigates the influence of the polymer concentration, chain length, and solvent–wall interactions. Polymer block–wall interaction strengths (ε_Pa(Pb)W) are modified to simulate polymer blocks with different adsorption behaviors, such as weak adsorbable (ε_Pa(Pb)W = 0.6), moderate adsorbable (ε_Pa(Pb)W = 1.0), and strong adsorbable (ε_Pa(Pb)W = 1.2) polymer blocks. The deposition patterns are summarized into diagrams, including penetrating and nonpenetrating ridge-like structures, penetrating and nonpenetrating coffee-ring structures, and multilayer structures with and without defects. We determine factors that influence the deposition structure of the droplet and unveil the mechanism of the formation process of the pattern. This work helps in understanding the deposition pattern of linear diblock copolymer solution nanodroplets, which is beneficial for potential applications involving nanodroplet evaporation.

---

1 Introduction

The evaporation of droplets containing polymer solutions on solid substrates exhibits a variety of intricate deposition patterns, including coffee-ring, mountain-like, and volcano-like structures.^1–5 This phenomenon, commonly observed in everyday life, plays a crucial role in various practical applications.^6,7 It is also an efficient way to achieve surface patterning. By carefully manipulating variables like polymer concentration, solvent selection, and temperature, the desired deposition patterns can be achieved without the need for sophisticated equipment.^4,8–12 Among various polymer solutes, diblock block copolymers can be applied in the manufacturing of intelligent and programmable materials responsive to various stimuli.^13–15 Tailoring these copolymer features allows for the adjustment of the properties via incorporating different chemical groups into their blocks.^13,16,17 Thus, understanding the evaporation dynamics and deposition patterns of diblock copolymer solution droplets is of considerable scientific and practical interest.

Substantial progress has been achieved in understanding the evaporation dynamics of droplets on solid surfaces, including the analysis of static structures and evaporation processes.^9,18–22 Internal flows, such as capillary and Marangoni flows, profoundly influence the uniformity of these patterns.^9,19 The accumulation near interfaces alters the distribution of the polymer inside the droplet, which further induces mass transport. A typical example of an inhomogeneous pattern is the coffee-ring structure, characterized by solute accumulation at the periphery.^1,9,23 Among various factors, the initial polymer concentration and the chain length are crucial for the deposition pattern of the droplet. At a particular polymer concentration, the height in the middle of the deposition pattern can suddenly rise to form a central buckling.^24,25 In addition, a change in the chain length can alter the evaporation process and result in a variety of patterns.^26–29 The initial polymer concentration and the chain length are thus important factors controlling deposition patterns of the diblock copolymer solution droplet.

Most of these studies, however, focus on macroscale droplets, where established evaporation theories can be applicable. In contrast, nanoscale droplets exhibit unique evaporation dynamics, which is critical for technologies such as nano-printing, nano-coating, and microelectronics manufacturing.^30–33 For instance, nanoscale droplets do not exhibit the flux singularity typically seen in macroscale droplets and deviate from the d² law.³⁴ This phenomenon is evident in nanodroplets containing homopolymer solutions, where the evaporation rate tends to slow down toward the end of the process.⁸ The significantly smaller temporal and spatial scales involved in nanoscale droplet evaporation pose challenges for experimental observation.³⁵ To overcome these limitations, researchers have employed molecular dynamics (MD) and Monte Carlo (MC) simulations to elucidate the evaporation process on these smaller scales.^36–41 MD simulations, in particular, offer the ability to track particle positions, enabling a comprehensive view of the evaporation process.^8,42–49 For example, Katiyar et al.⁴⁰ and Zhang et al.⁵⁰ have investigated deposition patterns resulting from nanodroplet evaporation containing solvents and nanoparticles. Kravchenko et al. focused on deposition patterns induced by nanodroplets of homopolymer solutions.⁸ Cheng et al. employed a combination of implicit solvent MD and the moving interface method to study the evaporation dynamics of block copolymer solution nanodroplets.⁵¹ They also highlighted the challenge of observing coffee-ring structures without considering internal solvent flow. In our previous work, we utilized the explicit solvent simulation to study the influence of the solvent wettability and the interaction strength between polymer blocks and the wall on the deposition pattern and the evaporation dynamics of nanodroplets.⁵² However, the influence of the polymer concentration and the chain length remains unclear. As discussed above, they are important factors that alter the deposition pattern of the nanodroplet. It is thus necessary to study the evaporation process of the nanodroplet with chain lengths and concentrations from the nanoscale.

In the present work, deposition patterns of linear diblock copolymer solution nanodroplets are studied by coarse-grained molecular dynamics simulations. Factors such as the interaction strength, chain length, and polymer concentration, are analyzed systematically. The interactions in this study include polymer–wall (ε_Pa(Pb)W) and the wettability of the solvent (ε_SW). Influences of the concentration and the chain length are studied for the droplet with polymer blocks that have different adsorption behaviors on both the lyophilic and lyophobic walls. Following our previous definition,⁵³ the polymer blocks in the present work include the “adsorbable” (ε_Pa(Pb)W = 1.0), the “nonadsorbable” (ε_Pa(Pb)W = 0.6), and the “strong adsorbable” (ε_Pa(Pb)W = 1.2) ones. We focus on the nonadsorbable–adsorbable and the nonadsorbable–strong adsorbable copolymers. This work provides a reference for designing deposition patterns of linear diblock copolymer solution nanodroplets with different concentrations and chain lengths. Meanwhile, our work also helps to deepen the understanding of the droplet evaporation mechanism under the influence of the concentration and the chain length on the nanoscale. The study on formation processes broadens the understanding of polymer structures near solid substrates.

2 Models and simulation details

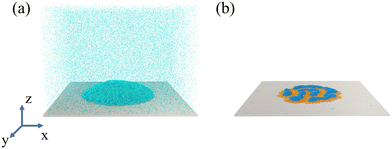
The simulation model consists of a droplet and a solid substrate (the wall) (Fig. 1a). The droplet is comprised of the linear diblock copolymer and the solvent. The polymer chain has two blocks (Pa and Pb) with the same length, while the solvent is a single bead. A wall is frozen under the droplet at the bottom of the simulation box, in which the wall beads are arranged in a face-centered-cubic lattice. On the top of the box, a virtual Lennard–Jones (LJ) wall is placed to prevent the beads from moving through the upper surface,
where z is the distance from the bead to the upper surface and z_c is the cutoff distance (3.0σ). For validation of the model, refer to ref. 8. The number of droplet beads (N_droplet) consists of 300 000 droplet beads in a reference simulation system. The concentration in the current work is defined by volume. The dimensions of the simulation box are 250 × 250 × 180σ³.

Fig. 1 An illustration of the simulation system: (a) a snapshot of the droplet before evaporation; (b) a snapshot of the deposition pattern after evaporation. The solvent bead, block Pa, and block Pb correspond to cyan, blue, and orange, respectively.

In the model, the LJ potential describes the nonbonded interaction between beads

with r_c = 3.0σ, and ε is the well depth of the potential, σ corresponds to the length unit, and r_c is the cutoff radius. By modifying the parameter of ε, the interaction strength is tuned between beads. The great value of ε corresponds to a strong interaction. We use symbols of “W”, “Pa”, “Pb”, and “S” to represent the wall, polymer block Pa and Pb, and the solvent. The ε of the same type is set as 1.0, namely ε_PaPa, ε_SS, and ε_PbPb. The interaction between the solvent and polymer blocks (ε_PaS and ε_PbS) is 1.0 to represent the same solvent environment for two blocks. The adjustment of interaction between the solvent and the wall (ε_SW) can change the wettability of the solvent on the wall. The contact angle of the solvent continuously changes with ε_SW.^54,55 In the current work, the low wettability (the lyophobic wall) is represented by setting ε_SW = 0.4, where the contact angle of the pure solvent is 99.8°. The lyophilic wall is simulated by setting ε_SW = 0.7, which corresponds to the contact angle of 52.8°.⁵² Polymer beads are connected via the harmonic potential
using conventional parameters of k_bond = 1111ε/σ² and l₀ = 0.967σ.⁵⁶ Here we define three block types based on their interaction with the wall.⁵² “Adsorbable” blocks denote the block that can form an adsorption layer (ε_Pa(Pb)W = 1.0), while “nonadsorbable” blocks do not form an adsorption layer (ε_Pa(Pb)W = 0.6). The “strong adsorbable” block denotes the block that is adsorbed by the wall due to the strong affinity (ε_Pa(Pb)W = 1.2). In the following sections, “N”, “A”, and “S” denote nonadsorbable, adsorbable, and strong adsorbable blocks. In addition, “I” and “O” denote the lyophilic and the lyophobic wall. “N-A-O”, “N-S-O”, “N-A-I”, and “N-S-I” represent the nonadsorbable–adsorbable copolymer solution droplet on the lyophobic wall, the nonadsorbable–strong adsorbable copolymer solution droplet on the lyophobic wall, the nonadsorbable–adsorbable copolymer solution droplet on the lyophilic wall, and the nonadsorbable–strong adsorbable copolymer solution droplet on the lyophilic wall, respectively.

To generate the initial structure, the droplet beads are randomly generated into a virtual spherical shell. The interaction between beads is then set as the soft potential to prevent the beads from being too close. The shell is finally removed and the simulation system is relaxed in the Nosé–Hoover thermostat for 1 × 10⁸ steps with the time step of at the temperature of T = 0.72ε/k_B, where m is the mass and k_B is the Boltzmann constant. The simulation temperature (0.72) is clarified in ref. 8. The glass transition temperature (T_g) of the pure polymer liquid is lower than the simulation temperature. The T_g is 0.42 with a chain length of 26 and ε_PaPb = 0.6. The current system is safe from the glass transition. Finally, the evaporation is simulated by deleting beads from the simulation box.^8,38,40 We place a virtual wall at a position that is 10σ below the upper surface. A solvent bead that reaches the wall has a probability of 10% of being deleted from the simulation box. Following the procedure, the solvent evaporates from the droplet (Fig. 1b). 5 independent simulations are performed for each state point. The simulations in our work are all conducted by the GALAMOST package.⁵⁷

3 Results and discussion

A striking feature of diblock copolymers is that their structures can be adjusted by building blocks. A systematic study is performed to investigate deposition patterns of the nonadsorbable–adsorbable and the nonadsorbable–strong adsorbable polymer solution droplets on the lyophilic and lyophobic walls. The influence of the concentration and the chain length is further investigated and summarized into 4 diagrams. The chain length varies from 10 to 52 with an interval of 6, while the concentration varies from 0.05 to 0.30 with an interval of 0.05. The block layer and the polymer layer are illustrated in Fig. S1 (ESI†). The number of layers is counted in the part where the number of block layers is greatest. If the boundary of the layer is unclear, the simulation is continued until the boundary is clear.

3.1 Number of solvent beads in droplets with time

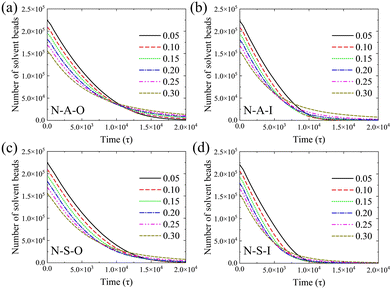
We trace the dynamics of the evaporation process based on the change in the number of solvent beads. The number of solvent beads decreases with time in Fig. 2. After the moment of 20 000τ, most of the curves tend toward zero. The evaporation rate can be estimated by the slope of the number of solvent beads with time. We calculate the slope of the number of solvent beads in the evaporation process (the curve in Fig. 2), and the evaporation rates at the beginning of evaporation are shown in Fig. S2 (ESI†). It is clearly seen that when the initial polymer concentration is no larger than ∼0.2, the evaporation rates only show a tiny decrease. However, when the concentration is greater than ∼0.2, the evaporation rates decrease sharply, resulting from the more concentrated polymers tending to reduce the diffusive ability of solvent beads towards the vapor phase. Nevertheless, in the low concentration regime, the influence of the concentration is weak. Evaporation rates deviate as the evaporation proceeds. All the evaporation rates decrease with time, which results from the increasing polymer concentration inside the droplet. Near the end of the evaporation, the evaporation rate is dominated by the diffusion of the solvent beads among polymer chains. In this period, polymer chains retard solvent beads from entering the vapor phase. In addition, the evaporation rate of the high initial concentration decreases with time more slowly than that of the low initial concentration (as shown in Fig. 2a). But it is greater than others at the end of the evaporation. Moreover, curves of various concentrations cannot overlap by translation. These results indicate the evaporation process changes the distribution of the polymer and the solvent flow inside the droplet.

Fig. 2 The time evolution of the number of solvent beads in the droplet with the evaporation process under various concentrations: (a) the nonadsorbable–adsorbable copolymer solution droplet on the lyophobic wall (N-A-O); (b) the nonadsorbable–adsorbable copolymer solution droplet on the lyophilic wall (N-A-I); (c) the nonadsorbable–strong adsorbable copolymer solution droplet on the lyophobic wall (N-S-O); (d) the nonadsorbable–strong adsorbable copolymer solution droplet on the lyophilic wall (N-S-I). The chain length of the polymer is 28.

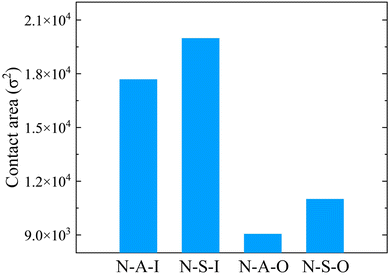
The end times of the evaporation are different for solvent wettabilities and copolymers. On the lyophobic wall, the number of solvent beads converges more slowly (Fig. 2a and c) than that on the lyophilic wall (Fig. 2b and d). The difference between evaporation end times on two types of walls is attributed to the size of the contact region between the droplet and the wall. When the wettability of the solvent is high, the droplet spreads over more area. The solvent is exposed to the vapor phase with a larger area. It is thus easier for solvent beads to escape from the droplet, which leads to the early end time (Fig. 3). Besides the solvent wettability, polymer adsorption is another factor that determines the shape of the droplet. The contact area of N-A-O is slightly less than that of N-S-O due to the relatively weak adsorption of the adsorbable block compared with the strong adsorbable block (Fig. 3). Although the polymer adsorption affects the contact area of the droplet, the influence of the solvent wettability is stronger than the polymer adsorption and thus a dominant factor. As shown in Table S1 (ESI†), the contact angle and the droplet radius are also different for these systems. The contact angle has an opposite trend with the contact area, while the radius has the same trend. On the same wall, the contact area of the nonadsorbable–strong adsorbable polymer is larger than that of the nonadsorbable–adsorbable one due to the increased affinity between the polymer and the wall.

Fig. 3 Contact areas of the nonadsorbable–adsorbable and the nonadsorbable–strong adsorbable copolymer solution droplets on the lyophobic and the lyophobic walls at 0τ. The concentration is 0.15 and the chain length is 28.

Furthermore, we compare the change in the number of solvent beads with the chain length. In Fig. S3 (ESI†), the influence of the chain length on the number of solvent beads and the evaporation rate is very weak for the nonadsorbable–adsorbable copolymer regardless of the solvent wettability. An exception is the slower evaporation rate on the lyophilic wall with a chain length of 10. This is attributed to the structure of the deposition pattern. There are three block layers in the pattern (in Section 3.2.3), which is difficult for the solvent bead to overcome before entering the vapor phase. However, the number of solvent beads with the short chain length decreases slightly faster than that with the long chain for the nonadsorbable–strong adsorbable copolymer (Fig. S3, ESI†). Compared with the nonadsorbable–adsorbable copolymer, the shape of the droplet can be greatly influenced by the strong adsorbable block. The number of long chains is less than that of the short chain due to the same number of total droplet beads. Meanwhile, the long chain is equivalent to bonding short chains and increases the interaction between beads. Accordingly, the contact area is smaller for the long chain since the adsorbed chains form two block layers on the lyophobic wall (except for a chain length of 10) and the lyophilic wall (Fig. S4, ESI†). The droplet is thus less flattened with the long chain during the evaporation, which decreases the area of the liquid–vapor interface.

Finally, we have estimated the Péclet number⁵⁸ in our simulation. We select a system with a chain length of 28 and a polymer concentration of 0.1. The diffusion coefficient D is estimated as 0.00431σ²/τ. The droplet radius R at the beginning of the evaporation is 32.1σ. The initial interface speed v_s is taken as the average value from 0τ to 800τ, which is 0.00256σ/τ. Thus, the Péclet number is calculated as Pe = Rv_s/D = 19.1. This shows that the interface moves much faster than the polymer diffusion.

3.2 Deposition patterns with changes in initial polymer concentration and chain length

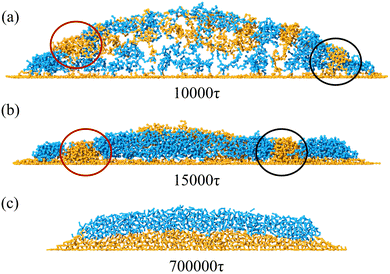
In the following sections, deposition patterns varying with the polymer concentration and the chain length are demonstrated for two types of copolymers on the lyophobic and the lyophilic walls. “Nonpenetrating coffee-ring structure” refers to the pattern whose central region is covered by layers of blocks (e.g.Fig. 4d). “Penetrating coffee-ring structure” refers to the pattern whose central region is not covered by any layers of blocks (e.g.Fig. 7a).

Fig. 4 Deposition patterns with various chain lengths and polymer concentrations on the lyophobic wall: (a) the snapshot and the side view (sliced) of the deposition pattern with a chain length of 34 and a concentration of 0.1; (b) the snapshot and side view (sliced) of the deposition pattern with a chain length of 16 and a concentration of 0.05; (c) the snapshot of the deposition pattern at 20 000τ (top) and 50 000τ (down) with a chain length of 28 and a concentration of 0.2; (d) the snapshot and side view (sliced) of the deposition pattern with a chain length of 10 and a concentration of 0.2. The blue, orange, and green symbols represent two, three, and four layers of the block in the deposition pattern, respectively. The half-filled circle (e.g. the system of (a)) denotes the multilayer structure with defects. The open circle is the nonpenetrating coffee-ring structure. The filled circle is the multilayer structure. The circle with a vertical bar marks the deposition pattern that transforms from 3 layers of the block to 2 or from 4 to 3. The color in the background is a guide to the eye. A sliced region is illustrated as the side view across the mass center of the deposition pattern along the X direction. The droplet consists of the nonadsorbable–strong adsorbable copolymer solution.

3.2.1 The nonadsorbable–strong adsorbable diblock copolymer solution droplet on the lyophobic wall. In this section, the lyophobic wall is simulated by fixing the interaction strength between the wall and the solvent (ε_SW) as 0.4. Parameters of the polymer blocks in a polymer chain are set as ε_PaW = 0.6 and ε_PbW = 1.2, respectively. In this way, we perform a study on a droplet of the nonadsorbable–strong adsorbable diblock copolymer (N and S blocks) solution on a lyophobic wall. Deposition patterns varying with chain lengths and concentrations are demonstrated in Fig. 4.

It is observed that the deposition patterns are mainly the multilayer structure with defects when the chain length becomes long (Fig. 4a). In this study, a defect specifically refers to structural irregularities that interrupt the formation of uniform layers, arising from the microphase separation of two polymer blocks during evaporation. Typical defects are shown in the circled regions in Fig. 5b, where they disrupt the formation of consistent multilayers, as illustrated in Fig. 5c. During evaporation, the strong affinity between block S and the wall facilitates the wetting of block S on the wall. This leads to an adsorption layer of block S on the wall as the evaporation proceeds. However, block N on the other end of the chain cannot occupy the same area as block S on the XY plane due to its weak interaction with the wall and the repellency against block S. This results in the spacing between aggregations of block N (e.g. structures in the red and black circles in Fig. 5). Polymer chains entering the spacing would aggregate with the neighboring same type blocks. These aggregations are beneficial for the formation of defects (e.g. dots among the multilayer structure). In Fig. 5a and b, a typical formation process of defects is illustrated at two moments. In the middle of the evaporation, aggregations of block S in the red and black circles (Fig. 5a) are induced by the accumulation of block N at the TPCL. In this process, the aggregation of block N at the TPCL interacts with block S of other chains from the solution. Block S in these chains further aggregate on the other end of the chains and finally form aggregations in the spacing between block N aggregations, as is shown in the red circle of Fig. 5a. This results in two defects in the deposition pattern (Fig. 5b). But the defect is a metastable state. All the defects disappear after a long-time relaxation (700 000τ), which leads to the formation of the multilayer structure (Fig. 5c).

Fig. 5 Regions are extracted from the droplet at the time of (a) 10 000τ, (b) 15 000τ, and (c) 700 000τ. The region is sliced from the center of the droplet along the X direction. The geometrical center of the region in the Y direction is equal to that of the droplet. The polymer concentration and the chain length are 0.1 and 34.

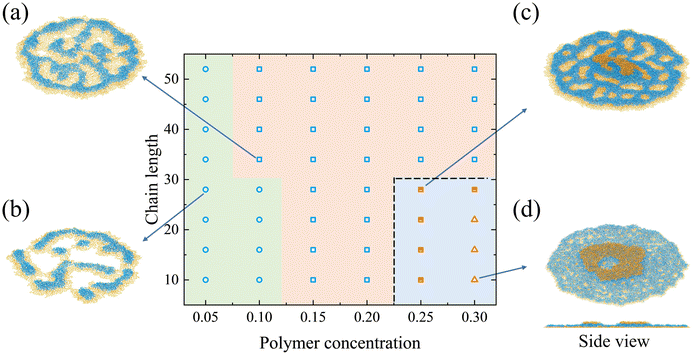
The number of polymer layers generally increases with the polymer concentration. At a higher concentration, more polymer chains can fill the liquid–solid interface to form a structure with several layers. The system with a chain length of 10 and a polymer concentration of 0.1 is an intermediate state between 3-block-layer and 2-block-layer structures. The deposition pattern consists of two layers of polymer. But the size of the top layer is small and it merges with the bottom layer within 5000τ. The pattern finally transforms into 2 layers of blocks.

For the polymer with a short length (e.g. a chain length of 10), the nonpenetrating coffee-ring forms when the polymer concentration increases (a polymer concentration of 0.2), as is shown in Fig. 4d. The diffusion of the short chain is faster than the long chain (Fig. S5, ESI†). This is beneficial for the chain to move with the internal flow, which facilitates the polymer accumulation at the periphery of the droplet. The small radius of gyration of the short chain length also prevents the peripheral polymer from interacting with other polymers on the other side of the pattern through the central area (Fig. S6, ESI†). Therefore, the polymer chains are less in the central region of the deposition pattern for short chain lengths, which facilitates the formation of the coffee-ring structure. The deposition pattern consists of two layers of polymer (side view in Fig. 4d). The bottom layer is a flat single layer structure with block S in contact with the wall. Polymers on the top form the ring structure. Block N in the top polymer layer is in contact with block N in the bottom layer. Different from the bottom layer in direct contact with the wall, the top layer does not have a strong affinity to fully spread over the bottom layer. The interaction between two layers of polymer is equal to the interaction strength of the same type of the polymer block. During the evaporation, the strong interaction strength of block S stabilizes the bottom layer. The bottom layer can be treated as a wall for the solvent and the polymer above it. The evaporation process above the bottom layer thus resembles that of the nonadsorbable–adsorbable on the lyophilic wall. The formation of the coffee-ring structure on the top layer is related to the concentration difference between the center and the periphery, the receding interfaces, and the polymer rearrangement near the end of the evaporation.⁵² In addition, the coffee-ring structure hardly forms on a lyophobic wall.^8,52 But the strong affinity between the polymer and the wall alters the droplet shape in the current simulation. It indicates that the contact angle of the droplet is smaller than 90°, which resembles a droplet on a lyophilic wall.

If the concentration further increases to 0.25, a multilayer structure forms since polymer chains just fill the central region of the deposition pattern in the top layer (the second layer). However, the third layer of polymer forms on the top of the deposition pattern when the concentration finally reaches 0.3. The polymer chains cannot fill the central region so the coffee-ring structure forms in the top layer. For the concentration of 0.3, the multilayer structure forms if the chain length increases from 10 to 16. The increased chain length is beneficial for the interaction between polymers and thus the central region is filled with polymers.

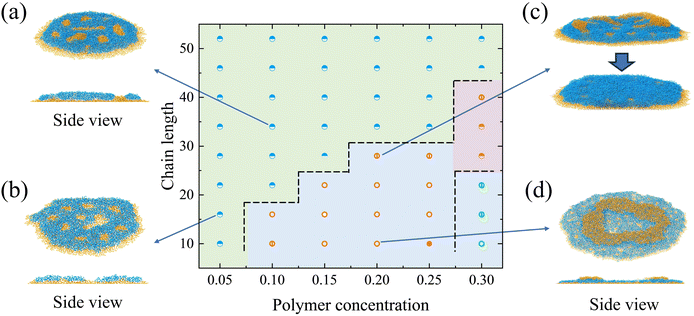
If the concentration is fixed as 0.2, the deposition pattern changes from the coffee-ring structure to the multilayer structure with defects with the increase in the chain length. The structure in Fig. 4c is an intermediate state since the number of layers of blocks would finally transform from 3 to 2, where 3 layers of block correspond to 2 layers of polymer. On the top layer of polymer, there are polymer aggregations in the periphery of the pattern (Fig. 4c). The peripheral polymer aggregation merges with the bottom layer within 5000τ after the end of the evaporation. It should be noted that all the structures would finally evolve into the multilayer structure after a long-time relaxation.

3.2.2 The nonadsorbable–strong adsorbable diblock copolymer solution droplet on the lyophilic wall. In this section, the lyophilic wall is simulated by fixing ε_SW as 0.7. Parameters of the polymer blocks (N and S blocks) are set as ε_PaW = 0.6 and ε_PbW = 1.2, respectively. Deposition patterns are shown in Fig. 6 with the changes in the concentration and the chain length. Due to the stronger interaction strength between the wall and the solvent, the contact area is larger than the lyophobic wall. For instance, the contact area of the system with a concentration of 0.1 and a chain length of 34 is 17 914.7σ² for the droplet on the lyophilic wall, while the contact area is 8986.98σ² for the lyophobic wall. This results from the fact that the greatest number of layers of block on the lyophilic wall (Fig. 6d) is less than that on the lyophobic wall (e.g. a chain length of 10 and concentration of 0.3). Interestingly, we find some ridge-like structures, which are defined as the deposition pattern with an incomplete single polymer layer for the N-S-I system. Two types of ridge-like structures can be designated, i.e., the “penetrating ridge-like structure”, where the pattern is not fully covered by polymer blocks (open circles in Fig. 6), and the “nonpenetrating ridge-like structure”, where the pattern is fully covered (open rectangles in Fig. 6). For structures with two polymer layers, they are categorized into intermediate structures that transform from two polymer layers into a single polymer layer (half-filled rectangles in Fig. 6) and a coffee-ring structure (open triangles in Fig. 6).

Fig. 6 Deposition patterns with various chain lengths and polymer concentrations on the lyophilic wall: (a) a snapshot of the deposition pattern with a chain length of 34 and a concentration of 0.1; (b) a snapshot of the deposition pattern with a chain length of 28 and a concentration of 0.05; (c) a snapshot of the deposition pattern with a chain length of 28 and a concentration of 0.25; (d) a snapshot and the side view (sliced) of the deposition pattern with a chain length of 10 and a concentration of 0.3. Blue and orange symbols represent two and three layers of blocks in the deposition pattern, respectively. The hollow rectangle is the nonpenetrating ridge-like structure. The half-filled rectangle is the structure that transforms from 3 layers of block to 2. The open circle is the penetrating ridge-like structure. The triangle is the nonpenetrating coffee-ring structure. The color in the background is a guide to the eye. A sliced region is illustrated as the side view across the mass center of the deposition pattern along the X direction. The droplet consists of the nonadsorbable–strong adsorbable copolymer solution.

When the concentration is low (0.05 and 0.1), the deposition pattern is mainly the penetrating ridge-like structure (Fig. 6b). The strong adsorbable block S tends to fill all the contact area. But the number of chains is so limited that the contact area cannot be covered by polymers. The nonadsorbable block N prefers to aggregate with the same type of blocks due to its weak affinity with the wall. Thus, stripes and dots of block N are formed above S blocks. With the increase in the concentration, there are enough polymer blocks to cover the area. The nonpenetrating ridge-like structure thus forms (Fig. 6a). The structure in Fig. 6c is an intermediate state between the coffee-ring structure and the nonpenetrating ridge-like structure. In Fig. 6c, the top layer of polymer would merge with the bottom layer after a short period of simulation.

If we keep the chain length as 10, the coffee-ring structure forms under a high concentration (Fig. 6d). The coffee-ring structure consists of two layers of polymer, which resembles the structure on the lyophobic wall. As the evaporation proceeds, the polymer forms an adsorption layer (the bottom layer) on the wall. The evaporation of the solvent and the polymer above the bottom layer resembles that of the nonadsorbable–adsorbable copolymer solution droplet. This is also attributed to the fact that the interaction between N blocks is equal to the interaction between the adsorbable block and the wall. Due to the high concentration, the polymer chain can form a dense adsorption layer at the bottom. There are enough polymers above the bottom layer to form the ring structure. But if the concentration is not high enough (e.g. 0.25), an intermediate state forms since the number of chains above the bottom layer is limited. In addition, compared with the polymer on the lyophobic wall, the deposition pattern on the lyophilic wall at a moderate concentration (from 0.15 to 0.20) cannot form a coffee-ring structure due to its larger contact area. The larger contact area facilitates the formation of ridge-like structures.

3.2.3 The nonadsorbable–adsorbable diblock copolymer solution droplet on the lyophilic and lyophobic walls. The influence of the concentration and the chain length on the deposition pattern is studied for the nonadsorbable–adsorbable diblock copolymer (N and A blocks) solution droplet on the lyophilic wall. The lyophilic wall is simulated by setting the interaction strength between the wall and the solvent (ε_SW) as 0.7. Parameters of the polymer blocks are set as ε_PaW = 0.6 and ε_PbW = 1.0. The deposition patterns are illustrated in Fig. 7. Starting from the left of the bottom row, the pattern generally changes from the penetrating coffee-ring structure to the multilayer flat structure with the increase in the concentration. When the concentration is 0.05, the coffee-ring structure consists of 1 layer of polymer (the side view in Fig. 7a). If the concentration increases to 0.15, more polymers can accumulate in the deposition pattern. The number of layers becomes two (the side view in Fig. 7b), accordingly. If the concentration further increases to 0.3, the multilayer structure forms since polymer chains fill the central region of the deposition pattern.

Fig. 7 Deposition patterns with various chain lengths and polymer concentrations on the lyophilic wall: (a) the top view and side view (sliced) of the deposition pattern with a chain length of 28 and a concentration of 0.05; (b) the top view and side view of the deposition pattern with a chain length of 10 and a concentration of 0.15; (c) the top view and side view of the deposition pattern with a chain length of 52 and a concentration of 0.15; (d) a snapshot of the deposition pattern with a chain length of 22 and a concentration of 0.15; (e) the top view and side view of the deposition pattern with a chain length of 16 and a concentration of 0.25. Blue, orange, and green symbols represent two, three, and four layers of block in the deposition pattern, respectively. The open circle is the penetrating coffee-ring structure. The blue circle with the orange center is the nonpenetrating coffee-ring structure. The circle with a central bar is the structure that transforms from 3 layers of blocks into 2. The filled circle is the multilayer flat structure. The half-filled circle is the multilayer structure with defects. The color in the background is a guide to the eye. A sliced region is illustrated as the side view across the mass center of the deposition pattern along the X direction. The region of (c) is sliced across the largest defect. The droplet consists of the nonadsorbable–adsorbable copolymer solution.

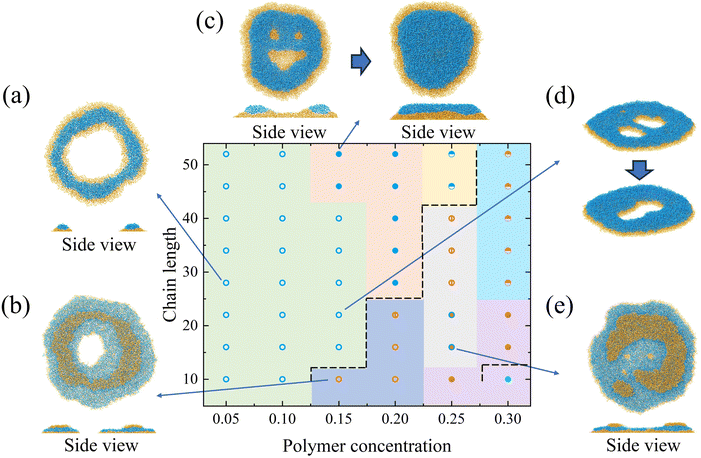
When the concentration is moderate (0.15 and 0.2), the multilayer structure with defects is observed if the chain length is long (e.g. 52). But the structure disappears in about 10 000τ and evolves to the multilayer structure. The transformation between two structures is illustrated in Fig. 7c. At ∼15 000τ, small defects have disappeared, leaving only one central defect in the pattern. The size of the central defect keeps shrinking and finally disappears. In this process, the potential energy in the pattern gradually becomes lower and tends to reach a plateau, as is shown in Fig. S7 (ESI†). This demonstrates that the multilayer flat structure is energetically favorable compared with the intermediate state of the structure with defects. When the concentration is 0.15, the coffee-ring structure would first have an intermediate state with more than 1 hollow, such as the structure in Fig. 7d. These hollows finally merge into a larger central hollow. When the concentration further increases to 0.25, the nonpenetrating coffee-ring structure is observed for the short chain length polymer due to the increased amount of polymers in the central region (Fig. 7e). The multilayer flat structure forms if the concentration is 0.25. The polymer can fill in the central area to suppress the formation of the central hollow. For the long chain, the multilayer structure is preferential. As shown in Fig. S5 (ESI†), the long chain diffuses more slowly than the short one. The long chain is less influenced by the flow inside the droplet. Besides, the long length shortens the distance between the chain at the periphery and the chain in the central region, which suppresses the formation of the coffee-ring structure. With the increase of the chain length, the number of layers of block decreases from 3 to 2.

As for systems on the lyophobic wall, all the deposition patterns are multilayer flat structures with or without defects. The difference between these structures is the number of layers of blocks in the structure. Deposition patterns on the lyophobic wall are shown in Fig. S8 (ESI†). With the increase in the concentration, the number of layers of blocks increases since there are more polymers in the deposition pattern. Similarly to the above systems, the number of layers decreases with the chain length.

Previous studies on symmetric diblock copolymers have shown that they tend to form lamellar structures on substrates when one block has preferential interactions with the substrate, and the two blocks are repulsive.^59–61 However, block copolymer nanodroplets exhibit a wider range of deposition patterns, influenced not only by block–wall and block–block interactions, but also by factors such as receding interfaces, the heterogeneity inside the droplet, and the self-assembly of polymer chains within the droplet.⁵³ These influences lead to diverse structures, including ridge-like, coffee-ring, and multilayer structures. The coffee-ring pattern, for instance, comprises polymer layers that resemble the lamellar structure seen in bulk simulations. However, unlike bulk lamellar formations, nanodroplet evaporation creates a central hollow as a result of mass transport during evaporation. Similarly, ridge-like structures share certain features with lamellar patterns, as both involve a layered arrangement. However, droplet evaporation causes the aggregation of block Pa into ridge patterns within the polymer layer, which is not observed in bulk lamellar structures. Among the observed structures, the multilayer and multilayer-with-defects patterns most closely resemble bulk lamellar formations, as they consist of multiple polymer layers. Nonetheless, defects often appear during the formation process, similar to bulk systems in early simulation stages, where incomplete layers with defects gradually develop into complete multilayers over extended simulation time. These comparisons provide further insight into the evaporation process of block copolymer nanodroplets and show promise for advancing potential technological applications.

4 Conclusions

In this work, coarse-grained molecular dynamics simulations are performed to study deposition patterns of linear diblock copolymer solution nanodroplets. Factors that influence the structure of the deposition pattern are systematically studied including the polymer chain length and the polymer concentration. We mainly focus on the combination of “adsorbable” (ε_Pa(Pb)W = 1.0), “nonadsorbable” (ε_Pa(Pb)W = 0.6), and “strong adsorbable” (ε_Pa(Pb)W = 1.2) polymer blocks. Two types of block copolymers are investigated in the study, namely nonadsorbable–adsorbable and nonadsorbable–strong adsorbable copolymers. The evaporation process of polymer solution nanodroplets is studied on both the lyophilic and lyophobic walls: (1) for the droplet with the nonadsorbable–strong adsorbable copolymer on the lyophobic wall, the multilayer structure with defects is observed for the polymer with the long chain. The nonpenetrating coffee-ring structure is a common pattern for the short chain polymer (e.g. ≤22). (2) For the droplet with the nonadsorbable–strong adsorbable copolymer on the lyophilic wall, the ridge-like structure is the most common. The coffee-ring structure forms only when the concentration is high. (3) For the droplet with the nonadsorbable–adsorbable copolymer on the lyophilic wall, the penetrating coffee-ring structure appears for the low concentration droplet. However, the nonpenetrating coffee-ring structure is observed when the concentration becomes high since the polymer fills the central region. Only for the droplet with the high concentration and the long chain length, does the multilayer structure with defects come into existence. (4) For the droplet with the nonadsorbable–adsorbable copolymer on the lyophobic wall, only the multilayer structure is observed. In addition, the evaporation rate is reflected by the change in the number of beads in the droplet with time. The evaporation of the droplet with the high initial polymer concentration is slower than that of the low one. The evaporation of the droplet on the lyophilic wall is faster than that on the lyophobic wall. The influence of the chain length is very weak for the nonadsorbable–adsorbable copolymer, while it is more obvious for the nonadsorbable–strong adsorbable copolymer.

Author contributions

Conceptualization (Z.-Y. S, H.-W. P.); methodology (H.-W. P.); investigation (H.-W. P, J. Z, Z.-Y. S.); visualization (H.-W. P.); funding acquisition (H.-W. P, Z.-Y. S.); project administration (Z.-Y. S.); supervision (Z.-Y. S.); writing – original draft (H.-W. P.); writing – review & editing (H.-W. P, Z.-Y. S.).

Data availability

The code for the calculation in this work is GALAMOST. Its python version is PYGAMD and can be found at https://github.com/youliangzhu/pygamd-v1. The version of the code employed for this study is version 3.0. Data in the work correspond to figures in the main text and the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the National Natural Science Foundation of China (No. 22103081, 52293471), and the support from the National Key R&D Program of China (No. 2022YFB3707303). The authors are grateful to the Network and Computing Center in Changchun Institute of Applied Chemistry for the hardware support. We also acknowledge the reviewers for their thoughtful suggestions, which have helped enhance the clarity and quality of this work.

Notes and references

1. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829.
2. A. G. Marín, H. Gelderblom, D. Lohse and J. H. Snoeijer, Phys. Rev. Lett., 2011, 107, 085502.
3. Y.-F. Li, Y.-J. Sheng and H.-K. Tsao, Langmuir, 2013, 29, 7802–7811.
4. X. Man and M. Doi, Phys. Rev. Lett., 2016, 116, 066101.
5. J. Xu, J. Xia, S. W. Hong, Z. Lin, F. Qiu and Y. Yang, Phys. Rev. Lett., 2006, 96, 066104.
6. M. Gonuguntla and A. Sharma, Langmuir, 2004, 20, 3456–3463.
7. H. Li, B. C.-K. Tee, J. J. Cha, Y. Cui, J. W. Chung, S. Y. Lee and Z. Bao, J. Am. Chem. Soc., 2012, 134, 2760–2765.
8. V. S. Kravchenko and I. I. Potemkin, Macromolecules, 2020, 53, 10882–10897.
9. S. Jafari Kang, V. Vandadi, J. D. Felske and H. Masoud, Phys. Rev. E, 2016, 94, 063104.
10. N. Basu and R. Mukherjee, Soft Matter, 2018, 14, 7883–7893.
11. Y.-F. Li, Y.-J. Sheng and H.-K. Tsao, Langmuir, 2014, 30, 7716–7723.
12. X.-Y. Yang, G.-H. Li, X. Huang and Y.-S. Yu, Langmuir, 2022, 38, 11666–11674.
13. H. Dau, G. R. Jones, E. Tsogtgerel, D. Nguyen, A. Keyes, Y.-S. Liu, H. Rauf, E. Ordonez, V. Puchelle, H. Basbug Alhan, C. Zhao and E. Harth, Chem. Rev., 2022, 122, 14471–14553.
14. C.-Y. Cheng, H. Xie, Z. Yuan Xu, L. Li, M.-N. Jiang, L. Tang, K.-K. Yang and Y.-Z. Wang, Chem. Eng. J., 2020, 396, 125242.
15. D. Wu, Y.-M. Leng, C.-J. Fan, Z.-Y. Xu, L. Li, L.-Y. Shi, K.-K. Yang and Y.-Z. Wang, ACS Sustainable Chem. Eng., 2022, 10, 6304–6312.
16. P. Ding, X. Yin, Q. Wang, X. Kang, M. Wu, K. Zhu, X. Wang, R. Wang and G. Xue, Langmuir, 2020, 36, 7289–7295.
17. C. Hu, T. Lu and H. Guo, J. Membr. Sci., 2018, 564, 146–158.
18. F. Wang, M. Wu, X. Man and Q. Yuan, Langmuir, 2020, 36, 8520–8526.
19. H. Hu and R. G. Larson, J. Phys. Chem. B, 2006, 110, 7090–7094.
20. H. Tan, C. Diddens, P. Lv, J. G. M. Kuerten, X. Zhang and D. Lohse, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8642–8647.
21. C. Diddens, J. Kuerten, C. van der Geld and H. Wijshoff, J. Colloid Interface Sci., 2017, 487, 426–436.
22. Y. Wen, P. Y. Kim, S. Shi, D. Wang, X. Man, M. Doi and T. P. Russell, Soft Matter, 2019, 15, 2135–2139.
23. S. Srivastava, Z. A. Wahith, O. Gang, C. E. Colosqui and S. R. Bhatia, Adv. Mater. Interfaces, 2020, 7, 1901954.
24. D. Willmer, K. A. Baldwin, C. Kwartnik and D. J. Fairhurst, Phys. Chem. Chem. Phys., 2010, 12, 3998–4004.
25. K. Baldwin and D. Fairhurst, Colloids Surf., A, 2014, 441, 867–871.
26. D. Zang, S. Tarafdar, Y. Y. Tarasevich, M. Dutta Choudhury and T. Dutta, Phys. Rep., 2019, 804, 1–56.
27. M. D. Choudhury, T. Dutta and S. Tarafdar, Colloids Surf., A, 2013, 432, 110–118.
28. M. Dutta Choudhury, T. Dutta and S. Tarafdar, Soft Matter, 2015, 11, 6938–6947.
29. B. Roy, M. D. Choudhuri, T. Dutta and S. Tarafdar, Appl. Surf. Sci., 2015, 357, 1000–1006.
30. M. Menétrey, L. Zezulka, P. Fandré, F. Schmid and R. Spolenak, ACS Appl. Mater. Interfaces, 2024, 16, 1283–1292.
31. J. Schneider, P. Rohner, D. Thureja, M. Schmid, P. Galliker and D. Poulikakos, Adv. Funct. Mater., 2016, 26, 833–840.
32. C. U. Hail, C. Höller, K. Matsuzaki, P. Rohner, J. Renger, V. Sandoghdar, D. Poulikakos and H. Eghlidi, Nat. Commun., 2019, 10, 1880.
33. S. Akin, P. Wu, J.-T. Tsai, C. Nath, J. Chen and M. B.-G. Jun, Surf. Coat. Technol., 2021, 426, 127788.
34. L. Ruiz Pestana and T. Head-Gordon, ACS Nano, 2022, 16, 3563–3572.
35. A. Hens, G. Biswas and S. De, J. Chem. Phys., 2015, 143, 094702.
36. S. N. Sun and H. M. Urbassek, J. Phys. Chem. B, 2011, 115, 13280–13286.
37. W. Chen, J. Koplik and I. Kretzschmar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052404.
38. J. Zhang, F. Leroy and F. Müller-Plathe, Langmuir, 2013, 29, 9770–9782.
39. S. Becker, H. M. Urbassek, M. Horsch and H. Hasse, Langmuir, 2014, 30, 13606–13614.
40. P. Katiyar and J. K. Singh, J. Chem. Phys., 2019, 150, 044708.
41. A. E. A. S. Evangelopoulos, A. N. Rissanou, E. Glynos, I. A. Bitsanis, S. H. Anastasiadis and V. Koutsos, Macromolecules, 2018, 51, 2805–2816.
42. J. Zhang, F. Müller-Plathe and F. Leroy, Langmuir, 2015, 31, 7544–7552.
43. J. J. Derksen, AIChE J., 2015, 61, 4020–4027.
44. M. Svoboda, A. Malijevský and M. Lísal, J. Chem. Phys., 2015, 143, 104701.
45. S. Becker, M. Kohns, H. M. Urbassek, M. Horsch and H. Hasse, J. Phys. Chem. C, 2017, 121, 12669–12683.
46. J. Zhang, J. Milzetti, F. Leroy and F. Müller-Plathe, J. Chem. Phys., 2017, 146, 114503.
47. S. Gao, Q. Liao, W. Liu and Z. Liu, J. Phys. Chem. Lett., 2018, 9, 13–18.
48. S. Gao, Q. Liao, W. Liu and Z. Liu, Langmuir, 2018, 34, 5910–5917.
49. L. Bi, B. Liu, Z. Zhu, P. E. Theodorakis, H. Hu and Z. Li, Phys. Fluids, 2023, 35, 012015.
50. J. Zhang, J. Milzetti, F. Leroy and F. Müller-Plathe, J. Chem. Phys., 2017, 146, 114503.
51. Y. Tang, J. E. McLaughlan, G. S. Grest and S. Cheng, Polymers, 2022, 14, 3996.
52. J. Zhang, H.-W. Pei and Z.-Y. Sun, Macromolecules, 2024, 57, 2574–2587.
53. H.-W. Pei, J. Zhang and Z.-Y. Sun, J. Chem. Phys., 2024, 161, 014711.
54. H.-W. Pei, H. Liu, Z.-Y. Lu and Y.-L. Zhu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 020401.
55. H.-W. Pei, H. Liu, Y.-L. Zhu and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2016, 18, 18767–18775.
56. B. Schnell, H. Meyer, C. Fond, J. P. Wittmer and J. Baschnagel, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 97.
57. Y.-L. Zhu, H. Liu, Z.-W. Li, H.-J. Qian, G. Milano and Z.-Y. Lu, J. Comput. Chem., 2013, 34, 2197–2211.
58. S. Cheng and G. S. Grest, ACS Macro Lett., 2016, 5, 694–698.
59. P. Petrus, M. Lísal and J. K. Brennan, Langmuir, 2010, 26, 3695–3709.
60. P. Petrus, M. Lísal and J. K. Brennan, Langmuir, 2010, 26, 14680–14693.
61. T. Geisinger, M. Müller and K. Binder, J. Chem. Phys., 1999, 111, 5241–5250.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02239d

---