Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quadrupolar NMR crystallography guided crystal structure prediction (QNMRX-CSP) of zwitterionic organic HCl salts
Carl H.
Fleischer
III
 ab,
Sean T.
Holmes
ab,
Sean T.
Holmes
 ab and
Robert W.
Schurko
ab and
Robert W.
Schurko
 *ab
*ab
aDepartment of Chemistry & Biochemistry, Florida State University, Tallahassee, FL 32306, USA. E-mail: rschurko@fsu.edu
bNational High Magnetic Field Laboratory, Florida State University, Tallahassee, FL 32310, USA
First published on 22nd October 2025
Abstract
In this work, we benchmark quadrupolar NMR crystallography guided crystal structure prediction (QNMRX-CSP) for determining the crystal structures of two zwitterionic organic HCl salts, L-ornithine HCl (Orn) and L-histidine HCl·H2O (Hist). These salts present an interesting challenge for QNMRX-CSP, as gas-phase geometry optimizations used to generate starting structures for the organic zwitterionic fragments fail to capture their correct solid-state geometries. To overcome this limitation, geometry optimizations using the COSMO water-solvation model are employed to generate initial structural models. Using this approach, QNMRX-CSP yields structural models of the two zwitterionic organic HCl salts that closely match experimentally determined crystal structures. In addition, the application of QNMRX-CSP to Hist represents a further step toward the de novo structural determination of solvated organic HCl salts, as Hist is the first benchmark system of this type to include a water molecule as a component of its crystal structure. This work is significant for its potential application to the structural determination of active pharmaceutical ingredients, which often feature complex organic components and solvated solid forms.
1. Introduction
NMR crystallography (NMRX) is a powerful approach for determining and refining the structures of crystalline solids, particularly when conventional methods face limitations. NMRX integrates solid-state NMR (SSNMR) spectroscopy, X-ray diffraction (most often powder X-ray diffraction, PXRD), and quantum chemical calculations to provide a comprehensive picture of atomic-level structure.1–5 SSNMR offers detailed information about local atomic environments, interatomic distances, and molecular conformations;6 XRD reveals long-range order, symmetry, space groups, and unit cell parameters;7,8 and quantum chemical calculations can be used to generate and refine candidate structures,9–16 as well as to calculate NMR interaction tensors, which can be used for screening and validation.17–19 Collectively, these enable the de novo structural determination of complex solids, including those with multiple components (i.e., organic molecules, inorganic ions, solvate molecules, etc.),20,21 structures with poorly defined hydrogen atom positions,22,23 and even disordered materials.24,25 Since the bonding and spatial arrangements of atoms directly relate to physicochemical properties such as solubility, stability, and bioavailability, NMRX provides a means of probing structure–property–function relationships in a wide range of organic solids, including active pharmaceutical ingredients and numerous other functional materials.1–5In NMRX methods, the choice of the most diagnostically relevant NMR interaction (e.g., chemical shifts,1,26–29 dipolar couplings,30–34 or the quadrupolar interaction35–41) is strongly sample-dependent. To date, most NMRX studies have employed isotropic chemical shifts due to their ease of measurement and wide availability;1–5 however, there are key limitations. First, calculating chemical shifts with first-principles quantum chemical computations can be computationally expensive, especially for structures featuring many atoms and/or for large datasets of candidate structures (we note that there are emerging machine-learning methods, such as the ShiftML software packages, that enable rapid computation of chemical shifts).19,42,43 Second, in certain cases, chemical shift assignment is fraught with difficulties due to broad patterns resulting from homo- and heteronuclear dipolar couplings44–47 and/or peak overlap due to the sample featuring multiple similar chemical environments – this is particularly problematic for complex molecules in organic solids, especially those with multiple low energy conformations.1
The quadrupolar interaction, which provides an alternative to chemical shifts for NMRX studies, manifests only in the SSNMR spectra of quadrupolar nuclides (i.e., nuclear spins I > ½). The quadrupolar interaction arises from the coupling between the nuclear quadrupole moment (Q) and the electric field gradients (EFGs) at the nucleus. EFGs are described by traceless, symmetric, second-rank tensors, which are defined by three principal components in their own principal axis systems, ranked such that |V33| ≥ |V22| ≥ |V11|. The EFG tensor components are most often expressed in terms of two parameters: the quadrupolar coupling constant, CQ = eQV33/h, and the quadrupolar asymmetry parameter, ηQ = (V11 − V22)/V33, where e is the elementary charge, h is Planck's constant, and 0 ≤ ηQ ≤ 1. Since EFGs depend solely on the ground state electron density, they are calculated from first principles more efficiently than chemical shifts.48,49
In light of this, as well as the abundance of quadrupolar nuclides in many solid organic compounds, our group developed a protocol for elucidating the solid-state structures of organic HCl salts, termed quadrupolar NMR crystallography guided crystal structure prediction (QNMRX-CSP).40,41 QNMRX-CSP employs powder X-ray diffraction (PXRD), 35Cl EFG tensors (both experimentally measured and calculated with DFT), Monte-Carlo simulated annealing (MC-SA),9 and dispersion-corrected density functional theory (DFT-D2*) geometry optimizations.50 To date, three studies have reported the development and application of QNMRX-CSP: (i) the initial study described the development of the protocol and its application to seven organic HCl salts, including five used as benchmarking systems, and two used in blind prediction tests;40 (ii) the second study extended the benchmarking of QNMRX-CSP to two organic HCl salts featuring organic components larger than those in the first set, and explored the application of QNMRX-CSP in the absence of PXRD data;41 and (iii) the most recent study demonstrated the application of QNMRX-CSP for the first de novo structure determination of an organic HCl salt for which no prior crystal structure was known.51 The studies highlight the necessity for continued benchmarking and the investigation of a more diverse range of organic HCl salts.
Herein, we extend QNMRX-CSP benchmarking calculations to zwitterionic organic HCl salts, including L-ornithine HCl (Orn) and L-histidine HCl·H2O (Hist) (Scheme 1). This study focuses on zwitterionic organic HCl salts, since they offer opportunities to tune the physiochemical properties of solid forms, while also presenting several challenges for the application of QNMRX-CSP. To this end, benchmarking calculations were carried out in two distinct scenarios: (i) to assess whether QNMRX-CSP can identify valid structural candidates for zwitterionic organic HCl salts using a known crystal structure as a starting point, and (ii) to evaluate its ability to generate accurate structural models using only the molecular formula, space group, and unit cell parameters. In the second scenario, geometry optimizations were performed using the COSMO water-solvation model to generate reasonable starting structural models. These two scenarios were explored independently: the first serves as a benchmarking exercise, while the second simulates a “real-world” application of QNMRX-CSP. Orn and Hist were chosen as structural models since they have known crystal structures and precisely measured 35Cl EFG tensors.52–57 Moreover, a water molecule is present in the crystal structure of Hist, which makes structural determination more difficult, but also opens the possibility of the de novo structure determination of solvated organic HCl salts by QNMRX-CSP.
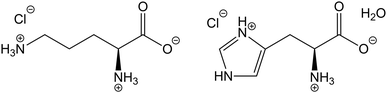 | ||
| Scheme 1 Molecular diagrams of the zwitterionic forms of L-ornithine HCl (Orn, left) and L-histidine HCl·H2O (Hist, right). | ||
2. Methods
2.1 QNMRX-CSP
QNMRX-CSP was developed and benchmarked for determining the crystal structures of organic HCl salts (Scheme S1 depicts a schematic diagram of QNMRX-CSP).40,41 QNMRX-CSP has three modules, each of which is divided into several steps: (i) module 1 (M1) involves the development of “chemically sensible” molecular fragments; (ii) module 2 (M2) uses the polymorph software to generate the initial candidate structures with MC-SA; and (iii) module 3 (M3) uses a QNMRX routine featuring DFT-D2* calculations to obtain geometry-optimized structural models and their concomitant 35Cl EFG tensors. In M2 and M3, benchmarked metrics are applied to retain candidate structures likely to converge to the “correct” crystal structure (§2.3). Lastly, the best candidate structures are validated using structural validation terms (§2.4).2.2 Computational details
QNMRX-CSP uses several software packages, including Amsterdam density functional (ADF),58 Polymorph9 and CASTEP59 within the BIOVIA Materials Studio R3 suite, and CASTEP Data Manager, an in-house program that automates CASTEP calculations.40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidate crystal structures per trial, where one trial consists of one complete iteration of (i) packing, (ii) clustering, (iii) force-field geometry optimization, and (iv) clustering (second round). The packing step uses a MC-SA algorithm to generate candidate crystal structures with maximum and minimum temperatures of 1.5 × 105 K and 300 K, respectively, using heating and cooling factors of 0.025 and 0.0005, and a minimum move factor of 10−10. Clustering removes duplicate structures using a radial distribution cut-off of 7.0 Å, tolerance of 0.13, and 140 bins. Dreiding force-field66 geometry optimizations were used to refine the candidate structures (the relative atomic positions for atom(s) in a molecular fragment are held constant) and calculate their static lattice energies. Convergence for these geometry optimizations is reached after maximum changes are achieved in energy of 2 × 10−5 kcal mol−1, force of 10−3 kcal mol−1 Å−1, stress of 10−3 GPa, and atomic displacement of 10−5 Å. Duplicate structures were removed in the second clustering step, using the same thresholds as the first. After ten trials of polymorph, a third round of clustering removed duplicate candidate structures generated across all trials.
000 candidate crystal structures per trial, where one trial consists of one complete iteration of (i) packing, (ii) clustering, (iii) force-field geometry optimization, and (iv) clustering (second round). The packing step uses a MC-SA algorithm to generate candidate crystal structures with maximum and minimum temperatures of 1.5 × 105 K and 300 K, respectively, using heating and cooling factors of 0.025 and 0.0005, and a minimum move factor of 10−10. Clustering removes duplicate structures using a radial distribution cut-off of 7.0 Å, tolerance of 0.13, and 140 bins. Dreiding force-field66 geometry optimizations were used to refine the candidate structures (the relative atomic positions for atom(s) in a molecular fragment are held constant) and calculate their static lattice energies. Convergence for these geometry optimizations is reached after maximum changes are achieved in energy of 2 × 10−5 kcal mol−1, force of 10−3 kcal mol−1 Å−1, stress of 10−3 GPa, and atomic displacement of 10−5 Å. Duplicate structures were removed in the second clustering step, using the same thresholds as the first. After ten trials of polymorph, a third round of clustering removed duplicate candidate structures generated across all trials.
2.3 Metrics
QNMRX-CSP uses metrics to retain candidate structures that are most likely to converge to the “correct” structure. Metrics include the experimental unit cell parameters, calculated static lattice energies, and 35Cl EFG tensors. The thresholds for these metrics were previously determined in benchmarking studies and further validated by two blind tests,40,41 as well as a de novo structure determination.51 Herein, four metric sets are used, which are combinations of metrics that are strategically positioned throughout the modules of QNMRX-CSP (see §3.1, Table 1, and Scheme S1). Candidate structures are only retained if both thresholds in each metric set are satisfied.| Metric set | Unit cell parametersa | E lat | Γ EFG (MHz) | E thresh (kJ mol−1) |
|---|---|---|---|---|
| a The unit cell parameters of the candidate structures are compared to the known unit cell parameters (Table 2) and are retained if those values are within ±20% or ±10% for Orn and Hist, respectively. b Candidate structures in the bottom 13.5% of Elat values are retained, i.e., such that: Elow ≤ Elat ≤ 0.865·Elow, where Elow is the Elat of lowest of all candidate structures. c Candidate structures are retained if their ΓEFG is equal to or below the benchmarked threshold. d Candidate structures are retained if their Elat is equal to or below Ethresh, such that: ΔE = Elat − Elow ≤ Ethresh. | ||||
| 1 | ±20%/±10% | 13.5% | — | — |
| 2 | — | — | 0.70 | 135 |
| 3 | — | — | 0.49 | 50 |
| 4 | — | — | 0.49 | 1 |
| Space group | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | C Q (MHz) | η Q | |
|---|---|---|---|---|---|---|---|---|---|
| a The crystallographic information of Orn and Hist was obtained from their known crystal structures, ORNHCL1252 and HISTCM12,53 respectively. b The experimental 35Cl EFG tensor parameters of Orn and Hist were obtained from previous studies.54–57 The quadrupolar coupling constant and asymmetry parameter are given by CQ = eQV33/h, and ηQ = (V11 − V22)/V33, respectively. The principal components of the EFG tensors are defined such that |V33| ≥ |V22| ≥ |V11|. The sign of CQ cannot be determined from the experimental spectra. | |||||||||
| Orn | P21 | 9.9480 | 7.9637 | 4.9826 | 90 | 99.87 | 90 | 2.99 | 0.36 |
| Hist | P212121 | 15.36 | 8.92 | 6.88 | 90 | 90 | 90 | 1.81 | 0.64 |
| Elow ≤ Elat ≤ 0.865·Elow | (1) |
| ΔElat = Elat − Elow ≤ Ethresh | (2) |
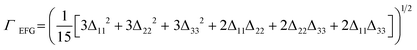 | (3) |
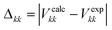 | (4) |
2.4 Structural validation
QNMRX-CSP validates candidate structures using two terms: the R-factor (R), which compares PXRD patterns, and an atomic position RMSD parameter, ΔRMSD, which compares atomic positions of the candidate structures to those of geometry-optimized structural models derived from experimental crystal structures. The CSD has over 1.3 million structures, of which ca. 90% have an R ≤ 10%; accordingly, we considered an R ≤ 10% to indicate a reasonable structural match.73 In the most recent CCDC blind tests, structures were considered a match if their ΔRMSD ≤ 1 Å.74,75 This relatively large threshold reflects the criteria used in these blind tests, which account for molecular size and flexibility, as well as the unique unit cell parameters of each structure. Herein, we adopted a stricter definition of a structural match, since the known unit cell parameters were used in the calculations. This resulted in smaller ΔRMSD values, with structures exhibiting ΔRMSD ≤ 0.2 Å considered to be good matches.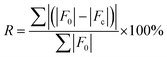 | (5) |
3. Results and discussion
3.1 QNMRX-CSP
To further develop QNMRX-CSP and expand its applicability to a wider array of systems, it is essential to refine benchmarking protocols, validate the thresholds used in its metric sets, and evaluate its performance for systems featuring a diverse selection of molecular fragments (e.g., organic zwitterions) and multiple motion groups (e.g., hydrates). Accordingly, QNMRX-CSP was applied in two different scenarios: first, to ascertain whether QNMRX-CSP can determine valid structural candidates using a fragment from the known crystal structure as a starting point, the steps outlined in module 1A (M1(A)) were followed (§3.2). Second, to demonstrate that valid structural candidates can be determined with knowledge of only the molecular formula, space group, and unit cell parameters (§3.3), the steps in module 1B (M1(B)) were used. Both scenarios subsequently used M2 and M3 in an identical manner. These two scenarios were investigated independently, with the first serving as a benchmarking and validation exercise, and the second as a practical application of QNMRX-CSP.3.2 QNMRX-CSP of zwitterionic organic HCl salts: starting from the known crystal structures
To demonstrate that QNMRX-CSP can be applied to organic zwitterionic HCl salts, we performed benchmarking calculations on Orn and Hist. A summary of the number of candidate structures retained by each metric set is provided in Table 3.| Hist | ||||||
|---|---|---|---|---|---|---|
| a The starting point for these calculations was geometry-optimized structures based on a known crystal structure. b The starting point for these calculations was ADF geometry-optimized structures based on isolated molecules. c The metric sets and their corresponding benchmarked metric values are detailed in Table 1. | ||||||
| Metric set 1 | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 952 |
→ | 166 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542 542 |
→ | 179 |
| Metric set 2 | 166 | → | 5 | 179 | → | 4 |
| Metric set 3 | 5 | → | 3 | 4 | → | 2 |
| Metric set 4 | 3 | → | 2 | 2 | → | 2 |
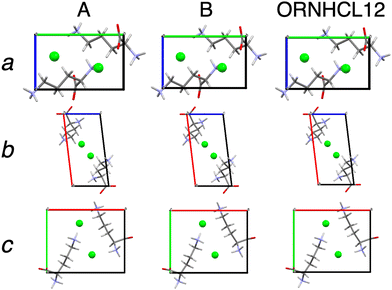
QNMRX-CSP, following M1(A), was first applied to Orn, which involved assigning molecular fragments consisting of an organic zwitterion and Cl− ion. Polymorph was then applied to generate 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 candidate structures. Of these, 71 were retained following the application of metric set 1. In M3, the 71 candidate structures underwent truncated geometry optimizations, followed by the application of metric set 2, which retained 18 candidate structures. These 18 candidate structures then underwent convergent geometry optimizations followed by the application of metric set 3, which retained 6 structures. These structures had their unit cell parameters adjusted to match those of the known crystal structure (Table 2) and were refined with a convergent geometry optimization. Of these, only 1 structure was retained by metric set 4, which is denoted as structure 6-11 (Fig. 1A). For structural validation (Table 4), the simulated PXRD pattern of 6-11 was compared to that of the DFT-D2* geometry-optimized ORNHCL12 structure, yielding an R value of 2.09%, well below the 10% threshold. Furthermore, a comparison of the atomic positions between the two structures yields ΔRMSD = 0.003 Å, well below the 0.2 Å threshold. Hence, 6-11 is an excellent structural match with the refined structure Orn (Fig. 1).
733 candidate structures. Of these, 71 were retained following the application of metric set 1. In M3, the 71 candidate structures underwent truncated geometry optimizations, followed by the application of metric set 2, which retained 18 candidate structures. These 18 candidate structures then underwent convergent geometry optimizations followed by the application of metric set 3, which retained 6 structures. These structures had their unit cell parameters adjusted to match those of the known crystal structure (Table 2) and were refined with a convergent geometry optimization. Of these, only 1 structure was retained by metric set 4, which is denoted as structure 6-11 (Fig. 1A). For structural validation (Table 4), the simulated PXRD pattern of 6-11 was compared to that of the DFT-D2* geometry-optimized ORNHCL12 structure, yielding an R value of 2.09%, well below the 10% threshold. Furthermore, a comparison of the atomic positions between the two structures yields ΔRMSD = 0.003 Å, well below the 0.2 Å threshold. Hence, 6-11 is an excellent structural match with the refined structure Orn (Fig. 1).
| Starting from refined isolated moleculese | ||||||
|---|---|---|---|---|---|---|
| a The calculated 35Cl EFG tensors for the candidate structures. b The ΓEFG of the candidate structures was derived using their calculated 35Cl EFG tensors and those reported from experiments (Table 2). c The R and ΔRMSD values were derived using the crystal structures determined from QNMRX-CSP and the methods outlined in §2.4. d The candidate structures were obtained from geometry-optimized structures based on the known crystal structures. e The candidate structures were obtained from ADF geometry-optimized structures based on isolated molecules. | ||||||
| Orn | 9-625 | 3.026 | 0.41 | 0.049 | 2.39 | 0.003 |
| Orn | 8-302 | 3.025 | 0.41 | 0.049 | 2.41 | 0.003 |
| Orn | 7-408 | 3.012 | 0.40 | 0.036 | 2.45 | 0.003 |
| Hist | 8-331 | 1.753 | 0.78 | 0.067 | 5.15 | 0.050 |
| Hist | 7-392 | 1.738 | 0.80 | 0.078 | 6.47 | 0.058 |
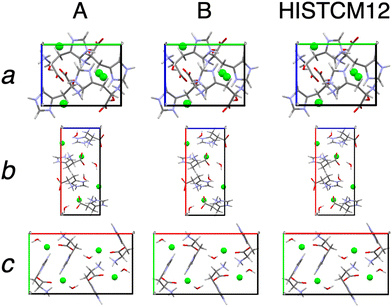
Application of QNMRX-CSP to Hist follows a similar routine; however, the resolution of final candidate structures was more challenging due to the presence of a water molecule as a third motion group. This is reflected by the higher number of unique candidate structures predicted in M2 with the Polymorph routine (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 structural candidates as opposed to 30
952 structural candidates as opposed to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 for Orn). Because of the larger phase space sampled by MC-SA due to the presence of a water molecule, we limited the unit cell parameter metric to ±10% rather than ±20%. The application of this modified metric set 1 resulted in the retention of 166 structures. After M3 was applied, 2 viable candidate structures remained (denoted 6-617 and 2-452), both of which have R and ΔRMSD values under the structural validation thresholds (Table 4; Fig. 2).
733 for Orn). Because of the larger phase space sampled by MC-SA due to the presence of a water molecule, we limited the unit cell parameter metric to ±10% rather than ±20%. The application of this modified metric set 1 resulted in the retention of 166 structures. After M3 was applied, 2 viable candidate structures remained (denoted 6-617 and 2-452), both of which have R and ΔRMSD values under the structural validation thresholds (Table 4; Fig. 2).
3.3 QNMRX-CSP of zwitterionic organic HCl salts: starting from an isolated molecule
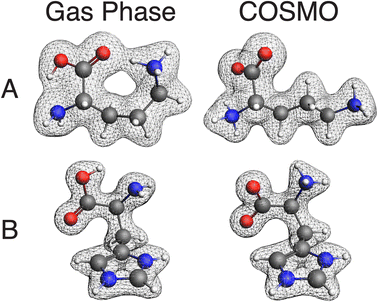
After benchmarking, we endeavored to use QNMRX-CSP for determining the crystal structures of Orn and Hist without reliance on their known crystal structures, in a manner that will be useful for future de novo structural predictions. Following the approaches of previous QNMRX-CSP studies,40,41 we followed the steps of M1(B) to obtain a set of molecular fragments by subjecting structural models of the organic zwitterions centered in a 15 × 15 × 15 Å3 unit cell of P1 space group symmetry to geometry optimizations. Although zwitterionic structural models were used as starting points, the geometry optimizations for both Orn and Hist converged to organic cationic forms (Fig. 3, left). To address this outcome, geometry optimizations were performed in ADF using the COSMO model (§2.2), which treats the solvent as a continuous polarizable medium that adjusts the electrostatic potential around the organic fragments to account for solvent-like stabilization of the charged functional groups. ADF (COSMO) calculations resulted in structural models representing organic zwitterionic cations (Fig. 3, right), which have distinct molecular conformations in comparison to the CASTEP-derived gas-phase models. In fact, the zwitterionic cations obtained from ADF (COSMO) optimizations are found to be similar to the zwitterionic cations from geometry-optimized ORNHCL12 and HISTCM12 structural models (§3.1, M1(A)), with comparative ΔRMSD values of 0.313 Å and 0.149 Å, respectively (Fig. 4). The remainder of the steps in M1(B) were then applied to both Orn and Hist.In the case of Orn, Polymorph generated 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 017 candidate structures, significantly exceeding the 30
017 candidate structures, significantly exceeding the 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 candidate structures predicted by the protocol described in §3.2. Furthermore, after the application of metric set 1, 749 candidates were retained, which is an order of magnitude greater than those in §3.2 (Table 3). This difference in the number of candidate structures is due, in part, to the distinct molecular configurations and electronic structures of the ADF (COSMO) zwitterionic cation and the geometry-optimized ORNHCL12 (Fig. 4). Despite the increase in the number of candidate structures, after M3 was applied, 3 candidate structures were retained, each with R and ΔRMSD values below the structural validation thresholds, thereby making them good matches to the geometry-optimized ORNHCL12 structure (Table 4; Fig. 1).
733 candidate structures predicted by the protocol described in §3.2. Furthermore, after the application of metric set 1, 749 candidates were retained, which is an order of magnitude greater than those in §3.2 (Table 3). This difference in the number of candidate structures is due, in part, to the distinct molecular configurations and electronic structures of the ADF (COSMO) zwitterionic cation and the geometry-optimized ORNHCL12 (Fig. 4). Despite the increase in the number of candidate structures, after M3 was applied, 3 candidate structures were retained, each with R and ΔRMSD values below the structural validation thresholds, thereby making them good matches to the geometry-optimized ORNHCL12 structure (Table 4; Fig. 1).
The application of Polymorph to the ADF (COSMO) zwitterionic cation of Hist resulted in 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542 candidate structures, which is similar to the 64
542 candidate structures, which is similar to the 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952 candidate structures described for benchmarking calculations in §3.2. This demonstrates that the zwitterionic fragments in each scenario are similar enough that M2 results in similar packing. After applying metric set 1 and M3, 2 candidate structures were retained and validated as good structural matches by calculating the R and ΔRMSD values (Table 4; Fig. 2).
952 candidate structures described for benchmarking calculations in §3.2. This demonstrates that the zwitterionic fragments in each scenario are similar enough that M2 results in similar packing. After applying metric set 1 and M3, 2 candidate structures were retained and validated as good structural matches by calculating the R and ΔRMSD values (Table 4; Fig. 2).
4. Conclusions
QNMRX-CSP can generate structural models of zwitterionic organic HCl salts that are consistent with known crystal structures, whether initiated from a known crystal structure or molecular fragments derived solely from a 2D molecular diagram. We have found that the proposed gas-phase DFT-D2* geometry optimization in M1 used in previous QNMRX-CSP applications is inadequate for generating reasonable starting molecular fragments for zwitterions. In contrast, geometry optimizations using the COSMO water-solvation model yield realistic molecular fragments. However, the use of COSMO comes with certain pitfalls, as illustrated by the Orn example, where initiating the QNMRX-CSP protocol from a molecular fragment with a slightly inaccurate conformation led to a substantial increase in the number of candidate structures requiring evaluation. Future studies should seek to remedy this issue by incorporating more sophisticated molecular conformational screening approaches to identify all possible conformations of a flexible molecule. At the front end of QNMRX-CSP, a broader range of SSNMR data would be integrated, such as 1H, 13C, and 15N chemical shifts, as well as 14N and/or 17O EFG tensors, to better identify plausible molecular conformations and protonation sites before using these models as starting points in CSP. Although this approach incurs an increased computational cost, QNMRX-CSP successfully identified a candidate structure for Orn that closely matches the known crystal structure. Lastly, QNMRX-CSP also determined, for the first time, a candidate structure for an organic HCl salt hydrate, Hist, showing promise for future investigations of solvated species. Finally, these results highlight the exciting prospect that QNMRX-CSP could enable the discovery of previously unobserved solid forms, including elusive polymorphs.Author contributions
C. H. Fleischer III conducted QNMRX-CSP, calculated the NMR tensors, and performed statistical analysis. C. H. Fleischer III, S. T. Holmes, and R. W. Schurko contributed to project conceptualization, as well as writing and editing the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The additional data sets supporting this article have been uploaded as part of the supplementary information (SI).Supplementary information is available. See DOI: https://doi.org/10.1039/d5ce00899a.
Acknowledgements
R. W. S. is grateful for research support from The Florida State University and the National High Magnetic Field Laboratory (NHMFL), which is funded by the National Science Foundation Cooperative Agreement (DMR-2128556) and by the State of Florida. This work was supported in part by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0022310, covering expenses related to postdoctoral salary.References
- R. K. Harris, NMR Crystallography: The Use of Chemical Shifts, Solid State Sci., 2004, 6(10), 1025–1037, DOI:10.1016/j.solidstatesciences.2004.03.040
.
-
R. E. Wasylishen, R. K. Harris and M. J. Duer, NMR Crystallography, A Wiley & Sons, New York, NY, 2009 Search PubMed
.
- C. Martineau, J. Senker and F. Taulelle, NMR Crystallography, in Annual Reports on NMR Spectroscopy, 2014, vol. 82, pp. 1–57, DOI:10.1016/B978-0-12-800184-4.00001-1.
- S. E. Ashbrook and D. McKay, Combining Solid-State NMR Spectroscopy with First-Principles Calculations – a Guide to NMR Crystallography, Chem. Commun., 2016, 52(45), 7186–7204, 10.1039/C6CC02542K
.
-
Modern NMR Crystallography, ed. D. L. Bryce, Royal Society of Chemistry, 2025, 10.1039/9781837673179
.
- B. Reif, S. E. Ashbrook, L. Emsley and M. Hong, Solid-State NMR Spectroscopy, Nat. Rev. Methods Primers, 2021, 1, 1–23, DOI:10.1038/s43586-020-00002-1
.
- A. A. Bunaciu, E. G. Udriştioiu and H. Y. Aboul-Enein, X-Ray Diffraction: Instrumentation and Applications, Crit. Rev. Anal. Chem., 2015, 45(4), 289–299, DOI:10.1080/10408347.2014.949616
.
- E. S. Ameh, A Review of Basic Crystallography and X-Ray Diffraction Applications, Int. J. Adv. Manuf. Tech., 2019, 105(7–8), 3289–3302, DOI:10.1007/s00170-019-04508-1
.
- R. L. C. Akkermans, N. A. Spenley and S. H. Robertson, Monte Carlo Methods in Materials Studio, Mol. Simul., 2013, 39(14–15), 1153–1164, DOI:10.1080/08927022.2013.843775
.
- J. D. Gale, GULP: A Computer Program for the Symmetry-Adapted Simulation of Solids, J. Chem. Soc., Faraday Trans., 1997, 93(4), 629–637, 10.1039/a606455h
.
- C. W. Glass, A. R. Oganov and N. Hansen, USPEX—Evolutionary Crystal Structure Prediction, Comput. Phys. Commun., 2006, 175(11–12), 713–720, DOI:10.1016/j.cpc.2006.07.020
.
- D. C. Lonie and E. Zurek, XtalOpt: An Open-Source Evolutionary Algorithm for Crystal Structure Prediction, Comput. Phys. Commun., 2011, 182(2), 372–387, DOI:10.1016/j.cpc.2010.07.048
.
- C. J. Pickard and R. J. Needs, Ab Initio Random Structure Searching, J. Phys.: Condens. Matter, 2011, 23(5), 053201, DOI:10.1088/0953-8984/23/5/053201
.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, CALYPSO: A Method for Crystal Structure Prediction, Comput. Phys. Commun., 2012, 183(10), 2063–2070, DOI:10.1016/j.cpc.2012.05.008
.
- T. Yamashita, S. Kanehira, N. Sato, H. Kino, K. Terayama, H. Sawahata, T. Sato, F. Utsuno, K. Tsuda, T. Miyake and T. Oguchi, CrySPY: A Crystal Structure Prediction Tool Accelerated by Machine Learning, Sci. Technol. Adv. Mater.: Methods, 2021, 1(1), 87–97, DOI:10.1080/27660400.2021.1943171
.
- J. Wang, H. Gao, Y. Han, C. Ding, S. Pan, Y. Wang, Q. Jia, H.-T. Wang, D. Xing and J. Sun, MAGUS: Machine Learning and Graph Theory Assisted Universal Structure Searcher, Natl. Sci. Rev., 2023, 10(7) DOI:10.1093/nsr/nwad128
.
- K. Wolinski, J. F. Hinton and P. Pulay, Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations, J. Am. Chem. Soc., 1990, 112(23), 8251–8260, DOI:10.1021/ja00179a005
.
- C. J. Pickard and F. Mauri, All-Electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(24), 245101, DOI:10.1103/PhysRevB.63.245101
.
- M. Cordova, E. A. Engel, A. Stefaniuk, F. Paruzzo, A. Hofstetter, M. Ceriotti and L. Emsley, A Machine Learning Model of Chemical Shifts for Chemically and Structurally Diverse Molecular Solids, J. Phys. Chem. C, 2022, 126(39), 16710–16720, DOI:10.1021/acs.jpcc.2c03854
.
- C. S. Vojvodin, S. T. Holmes, L. K. Watanabe, J. M. Rawson and R. W. Schurko, Multi-Component Crystals Containing Urea: Mechanochemical Synthesis and Characterization by 35Cl Solid-State NMR Spectroscopy and DFT Calculations, CrystEngComm, 2022, 24(14), 2626–2641, 10.1039/D1CE01610E
.
- C. S. Vojvodin, J. E. Sanchez, S. T. Holmes, X. Lin and R. W. Schurko, Mechanochemical Synthesis and NMR Crystallography of Multicomponent Crystals: New Perspectives from Chlorine and Alkali Metal Solid-State NMR Spectroscopy, Cryst. Growth Des., 2025 DOI:10.1021/acs.cgd.5c00540
.
- R. K. Harris, P. Y. Ghi, R. B. Hammond, C. Y. Ma and K. J. Roberts, Refinement of Hydrogen Atomic Position in a Hydrogen Bond Using a Combination of Solid-State NMR and Computation, Chem. Commun., 2003,(22), 2834–2835, 10.1039/b309302f
.
- J. Cui, D. L. Olmsted, A. K. Mehta, M. Asta and S. E. Hayes, NMR Crystallography: Evaluation of Hydrogen Positions in Hydromagnesite by 13 C{ 1 H} REDOR Solid-State NMR and Density Functional Theory Calculation of Chemical Shielding Tensors, Angew. Chem., 2019, 131(13), 4254–4260, DOI:10.1002/ange.201813306
.
- M. Cordova, P. Moutzouri, S. O. Nilsson Lill, A. Cousen, M. Kearns, S. T. Norberg, A. Svensk Ankarberg, J. McCabe, A. C. Pinon, S. Schantz and L. Emsley, Atomic-Level Structure Determination of Amorphous Molecular Solids by NMR, Nat. Commun., 2023, 14(1), 5138, DOI:10.1038/s41467-023-40853-2
.
- J. B. Holmes, D. Torodii, M. Balodis, M. Cordova, A. Hofstetter, F. Paruzzo, S. O. Nilsson Lill, E. Eriksson, P. Berruyer, B. Simões de Almeida, M. Quayle, S. Norberg, A. S. Ankarberg, S. Schantz and L. Emsley, Atomic-Level Structure of the Amorphous Drug Atuliflapon via NMR Crystallography, Faraday Discuss., 2025, 255, 342–354, 10.1039/D4FD00078A
.
- E. Salager, G. M. Day, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, Powder Crystallography by Combined Crystal Structure Prediction and High-Resolution1H Solid-State NMR Spectroscopy, J. Am. Chem. Soc., 2010, 132(8), 2564–2566, DOI:10.1021/ja909449k
.
- M. Baias, J.-N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, De Novo Determination of the Crystal Structure of a Large Drug Molecule by Crystal Structure Prediction-Based Powder NMR Crystallography, J. Am. Chem. Soc., 2013, 135(46), 17501–17507, DOI:10.1021/ja4088874
.
- C. M. Widdifield, S. O. Nilsson Lill, A. Broo, M. Lindkvist, A. Pettersen, A. Svensk Ankarberg, P. Aldred, S. Schantz and L. Emsley, Does Z ′ Equal 1 or 2? Enhanced Powder NMR Crystallography Verification of a Disordered Room Temperature Crystal Structure of a P38 Inhibitor for Chronic Obstructive Pulmonary Disease, Phys. Chem. Chem. Phys., 2017, 19(25), 16650–16661, 10.1039/c7cp02349a
.
- R. Toomey, L. Wang, E. C. Heider, J. D. Hartman, A. J. Nichols, D. A. A. Myles, A. S. Gardberg, G. J. McIntyre, M. Zeller, M. A. Mehta and J. K. Harper, NMR-Guided Refinement of Crystal Structures Using 15N Chemical Shift Tensors, CrystEngComm, 2024, 26(25), 3289–3302, 10.1039/d4ce00237g
.
- M. R. Chierotti and R. Gobetto, NMR Crystallography: The Use of Dipolar Interactions in Polymorph and Co-Crystal Investigation, CrystEngComm, 2013, 15(43), 8599–8612, 10.1039/c3ce41026a
.
- F. A. Perras, I. Korobkov and D. L. Bryce, NMR Crystallography of Sodium Diphosphates: Combining Dipolar, Shielding, Quadrupolar, Diffraction, and Computational Information, CrystEngComm, 2013, 15(43), 8727–8738, 10.1039/c3ce40875b
.
- P. Thureau, S. Sturniolo, M. Zilka, F. Ziarelli, S. Viel, J. R. Yates and G. Mollica, Reducing the Computational Cost of NMR Crystallography of Organic Powders at Natural Isotopic Abundance with the Help of 13C-13C Dipolar Couplings, Magn. Reson. Chem., 2019, 57(5), 256–264, DOI:10.1002/mrc.4848
.
- N. T. Duong, S. Raran-Kurussi, Y. Nishiyama and V. Agarwal, Quantitative 1H-1H Distances in Protonated Solids by Frequency-Selective Recoupling at Fast Magic Angle Spinning NMR, J. Phys. Chem. Lett., 2018, 9(20), 5948–5954, DOI:10.1021/acs.jpclett.8b02189
.
- P. Raval, J. Trébosc, T. Pawlak, Y. Nishiyama, S. P. Brown and G. N. Manjunatha Reddy, Combining Heteronuclear Correlation NMR with Spin-Diffusion to Detect Relayed Cl–H–H and N–H–H Proximities in Molecular Solids, Solid State Nucl. Magn. Reson., 2022, 120, 0–11, DOI:10.1016/j.ssnmr.2022.101808
.
- J. Dutour, N. Guillou, C. Huguenard, F. Taulelle, C. Mellot-Draznieks and G. Férey, Chiolite, a Case Study for Combining NMR Crystallography, Diffraction and Structural Simulation, Solid State Sci., 2004, 6(10), 1059–1067, DOI:10.1016/j.solidstatesciences.2004.07.031
.
- H. J. Jakobsen, A. R. Hove, R. G. Hazell, H. Bildsøe and J. Skibsted, Solid-state 14N MAS NMR of Ammonium Ions as a Spy to Structural Insights for Ammonium Salts, Magn. Reson. Chem., 2006, 44(3), 348–356, DOI:10.1002/mrc.1772
.
- H. Hamaed, J. M. Pawlowski, B. F. T. Cooper, R. Fu, S. H. Eichhorn and R. W. Schurko, Application of Solid-State 35 Cl NMR to the Structural Characterization of Hydrochloride Pharmaceuticals and Their Polymorphs, J. Am. Chem. Soc., 2008, 130(33), 11056–11065, DOI:10.1021/ja802486q
.
- D. L. Bryce, Calcium Binding Environments Probed by 43Ca NMR Spectroscopy, Dalton Trans., 2010, 39(37), 8593, 10.1039/c0dt00416b
.
- F. A. Perras and D. L. Bryce, Multinuclear Magnetic Resonance Crystallographic Structure Refinement and Cross-Validation Using Experimental and Computed Electric Field Gradients: Application to Na2Al2B2O7, J. Phys. Chem. C, 2012, 116(36), 19472–19482, DOI:10.1021/jp308273h
.
- A. A. Peach, C. H. Fleischer, K. Levin, S. T. Holmes, J. E. Sanchez and R. W. Schurko, Quadrupolar NMR Crystallography Guided Crystal Structure Prediction (QNMRX-CSP), CrystEngComm, 2024, 26(35), 4782–4803, 10.1039/D3CE01306E
.
- C. H. Fleischer, S. T. Holmes, K. Levin, S. L. Veinberg and R. W. Schurko, Characterization of Ephedrine HCl and Pseudoephedrine HCl Using Quadrupolar NMR Crystallography Guided Crystal Structure Prediction, Faraday Discuss., 2025, 255, 88–118, 10.1039/D4FD00089G
.
- F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Chemical Shifts in Molecular Solids by Machine Learning, Nat. Commun., 2018, 9(1), 4501, DOI:10.1038/s41467-018-06972-x
.
- M. Kellner, J. B. Holmes, R. Rodriguez-Madrid, F. Viscosi, Y. Zhang, L. Emsley and M. Ceriotti, A Deep Learning Model for Chemical Shieldings in Molecular Organic Solids Including Anisotropy, J. Phys. Chem. Lett., 2025, 8714–8722, DOI:10.1021/acs.jpclett.5c01819
.
- S. P. Brown, Applications of High-Resolution 1H Solid-State NMR, Solid State Nucl. Magn. Reson., 2012, 1–27, DOI:10.1016/j.ssnmr.2011.11.006
.
- U. Sternberg, R. Witter, I. Kuprov, J. M. Lamley, A. Oss, J. R. Lewandowski and A. Samoson, 1H Line Width Dependence on MAS Speed in Solid State NMR – Comparison of Experiment and Simulation, J. Magn. Reson., 2018, 291, 32–39, DOI:10.1016/j.jmr.2018.04.003
.
- M. Chávez, T. Wiegand, A. A. Malär, B. H. Meier and M. Ernst, Residual Dipolar Line Width in Magic-Angle Spinning Proton Solid-State NMR, Magn. Reson., 2021, 2(1), 499–509, DOI:10.5194/mr-2-499-2021
.
- B. Simões de Almeida, D. Torodii, P. Moutzouri and L. Emsley, Barriers to Resolution in 1H NMR of Rotating Solids, J. Magn. Reson., 2023, 355, DOI:10.1016/j.jmr.2023.107557
.
-
A. J. Vega, Quadrupolar Nuclei in Solids, in Encyclopedia of Magnetic Resonance, ed. D. M. Grant and R. K. Harris, John Wiley & Sons, Ltd, Chichester, UK, 2007, pp. 3869–3888, DOI:10.1002/9780470034590.emrstm0431
.
- J. Autschbach, S. Zheng and R. W. Schurko, Analysis of Electric Field Gradient Tensors at Quadrupolar Nuclei in Common Structural Motifs, Concepts Magn. Reson., Part A, 2010, 36(2), 84–126, DOI:10.1002/cmr.a.20155
.
- S. T. Holmes, C. S. Vojvodin and R. W. Schurko, Dispersion-Corrected DFT Methods for Applications in Nuclear Magnetic Resonance Crystallography, J. Phys. Chem. A, 2020, 124(49), 10312–10323, DOI:10.1021/acs.jpca.0c06372
.
- C. H. Fleischer, S. T. Holmes, X. Lin and R. W. Schurko, De Novo Crystal Structure Determination of L-Alaninamide HCl by Quadrupolar NMR Crystallography Guided Crystal Structure Prediction (QNMRX-CSP), Solid State Nucl. Magn. Reson., 2025, 140, 102034, DOI:10.1016/j.ssnmr.2025.102034
.
- B. Dittrich, P. Munshi and M. A. Spackman, Redetermination, Invariom-Model and Multipole Refinement of L -Ornithine Hydrochloride, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63(3), 505–509, DOI:10.1107/S0108768107014838
.
- H. Fuess, D. Hohlwein and S. A. Mason, Neutron Diffraction Study of L-Histidine Hydrochloride Monohydrate, Acta Crystallogr., Sect. B: Struct. Sci., 1977, 33(3), 654–659, DOI:10.1107/S0567740877004415
.
- S. T. Holmes, J. M. Hook and R. W. Schurko, Nutraceuticals in Bulk and Dosage Forms: Analysis by 35Cl and 14N Solid-State NMR and DFT Calculations, Mol. Pharmaceutics, 2022, 19(2), 440–455, DOI:10.1021/acs.molpharmaceut.1c00708
.
- O. Socha, P. Hodgkinson, C. M. Widdifield, J. R. Yates and M. Dračínský, Exploring Systematic Discrepancies in DFT Calculations of Chlorine Nuclear Quadrupole Couplings, J. Phys. Chem. A, 2017, 121(21), 4103–4113, DOI:10.1021/acs.jpca.7b02810
.
- M. K. Pandey, H. Kato, Y. Ishii and Y. Nishiyama, Two-Dimensional Proton-Detected 35Cl/1H Correlation Solid-State NMR Experiment under Fast Magic Angle Sample Spinning: Application to Pharmaceutical Compounds, Phys. Chem. Chem. Phys., 2016, 18(8), 6209–6216, 10.1039/c5cp06042g
.
- D. A. Hirsh, A. J. Rossini, L. Emsley and R. W. Schurko, 35Cl Dynamic Nuclear Polarization Solid-State NMR of Active Pharmaceutical Ingredients, Phys. Chem. Chem. Phys., 2016, 18(37), 25893–25904, 10.1039/c6cp04353d
.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22(9), 931–967, DOI:10.1002/jcc.1056
.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First Principles Methods Using CASTEP, Z. Kristallogr., 2005, 220(5–6), 567–570, DOI:10.1524/zkri.220.5.567.65075
.
- A. Klamt and G. Schüürmann, COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 5, 799–805, 10.1039/P29930000799
.
- C. C. Pye and T. Ziegler, An Implementation of the Conductor-like Screening Model of Solvation within the Amsterdam Density Functional Package, Theor. Chem. Acc., 1999, 101(6), 396–408, DOI:10.1007/s002140050457
.
- N. L. Allinger, X. Zhou and J. Bergsma, Molecular Mechanics Parameters, J. Mol. Struct., 1994, 312(1), 69–83, DOI:10.1016/S0166-1280(09)80008-0
.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals, Phys. Rev. B: Condens. Matter
Mater. Phys., 1999, 59(11), 7413–7421, DOI:10.1103/PhysRevB.59.7413
.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-Type Basis Sets for the Elements 1-118, J. Comput. Chem., 2003, 24(9), 1142–1156, DOI:10.1002/jcc.10255
.
- E. S. Sachs, J. Hinze and N. H. Sabelli, Frozen Core Approximation, a Pseudopotential Method Tested on Six States of NaH, J. Chem. Phys., 1975, 62(9), 3393–3398, DOI:10.1063/1.430993
.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, DREIDING: A Generic Force Field for Molecular Simulations, J. Phys. Chem., 1990, 94(26), 8897–8909, DOI:10.1021/j100389a010
.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, Relaxation of Crystals with the Quasi-Newton Method, J. Comput. Phys., 1997, 131(1), 233–240, DOI:10.1006/jcph.1996.5612
.
- J. R. Yates, C. J. Pickard and F. Mauri, Calculation of NMR Chemical Shifts for Extended Systems Using Ultrasoft Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(2), 024401, DOI:10.1103/PhysRevB.76.024401
.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, The Zero-Order Regular Approximation for Relativistic Effects: The Effect of Spin–Orbit Coupling in Closed Shell Molecules, J. Chem. Phys., 1996, 105(15), 6505–6516, DOI:10.1063/1.472460
.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192, DOI:10.1103/PhysRevB.13.5188
.
- P. Pyykkö, Year-2017 Nuclear Quadrupole Moments, Mol. Phys., 2018, 116(10), 1328–1338, DOI:10.1080/00268976.2018.1426131
.
- D. W. Alderman, M. H. Sherwood and D. M. Grant, Comparing, Modeling, and Assigning Chemical-Shift Tensors in the Cartesian, Irreducible Spherical, and Icosahedral Representations, J. Magn. Reson., Ser. A, 1993, 101(2), 188–197, DOI:10.1006/jmra.1993.1029
.
- G. Barr, W. Dong, C. J. Gilmore, A. Kern, A. Parkin and C. C. Wilson, Using the Cambridge Structural Database to Validate Powder Structures, Z. Kristallogr., 2007, 2007(suppl_26), 209–214, DOI:10.1524/zkri.2007.2007.suppl_26.209
.
- L. M. Hunnisett, N. Francia, J. Nyman, N. S. Abraham, S. Aitipamula, T. Alkhidir, M. Almehairbi, A. Anelli, D. M. Anstine, J. E. Anthony, J. E. Arnold and J. C. Cole,
et al., The Seventh Blind Test of Crystal Structure Prediction: Structure Ranking Methods, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2024, 80(6), 548–574, DOI:10.1107/S2052520624008679
.
- L. M. Hunnisett, J. Nyman, N. Francia, N. S. Abraham, C. S. Adjiman, S. Aitipamula, T. Alkhidir, M. Almehairbi, A. Anelli, D. M. Anstine, J. E. Anthony and J. C. Cole,
et al., The Seventh Blind Test of Crystal Structure Prediction: Structure Generation Methods, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2024, 80(6), 517–547, DOI:10.1107/S2052520624007492
.
| This journal is © The Royal Society of Chemistry 2025 |