Advances in atomistic modeling for epitaxial growth of nitride semiconductors: a DFT-based approach
Toru
Akiyama
 *ab
*ab
aGraduate School of Engineering, Mie University, Tsu 514-8507, Japan. E-mail: akiyama@phen.mie-u.ac.jp; Fax: +81 59 231 9724; Tel: +81 59 231 9724
bInnovation Center for Semiconductor and Digital Future, Mie University, Tsu 514-8507, Japan
First published on 1st July 2025
Abstract
The growth of high-quality epitaxial thin films of nitride semiconductors is essential for the development of energy-efficient power electronic devices as well as advanced optoelectronic applications. To enhance the performance of these materials, strict control over crystal growth conditions and a comprehensive understanding of surface structures and growth kinetics are indispensable. However, the mechanisms that govern epitaxial crystal growth remain incompletely understood due to the inherent complexity of surface structures and the dynamic nature of the growth processes. In this context, computational materials science, encompassing not only microscopic approaches such as density functional theory (DFT) and molecular dynamics but also mesoscale techniques like phase-field modeling, has emerged as an increasingly valuable tool adopted by both theorists and experimentalists for interpreting experimental results and predicting material properties. This highlight presents recent advances in computational studies of epitaxial crystal growth in nitride semiconductors, with a particular focus on state-of-the-art methods based on DFT. The techniques employed to investigate surface reconstructions and growth kinetics during epitaxial growth are introduced. Several case studies are discussed that reveal realistic surface reconstructions of nitride semiconductor surfaces such as GaN(0001) and AlN(0001). In addition, the growth processes involving adsorption, desorption, and migration behaviors of adatoms are examined. A key aspect of understanding epitaxial growth mechanisms is the presence of steps and kinks on the surface, which are inevitably formed during the growth process. Recent studies demonstrate that quantum-theory-based simulations provide a microscopic understanding of the complex phenomena associated with epitaxial crystal growth.
1 Introduction
Nitride semiconductors such as wurtzite gallium nitride (GaN) and aluminum nitride (AlN) are wide band gap (WBG) materials that play a significant role in optoelectronics, being widely used in blue and ultraviolet light-emitting diodes (LEDs) and laser diodes.1–5 The electronic properties derived from their wide band gaps, which enhance energy conversion efficiency, also make GaN particularly attractive for power electronics applications.6 With its high dielectric breakdown voltage and robustness in harsh environments, GaN shows strong potential as a next-generation power device capable of enabling energy-efficient systems. In addition, AlN and its related materials contribute significantly to the advancement of both optoelectronic and electronic devices, particularly in deep-ultraviolet (DUV) LEDs7,8 and high-electron-mobility transistors (HEMTs).9–11 Notably, DUV-LEDs based on aluminum gallium nitride (AlGaN) are emerging as promising alternatives to mercury-based lamps. Their potential applications include water and air purification, as well as sterilization of medical instruments.12–19 DUV-LEDs offer several advantages, including the use of non-toxic materials, relatively high efficiency, long operational lifetimes, and instant ignition. Moreover, AlN has garnered significant attention as a substrate material for the epitaxial growth of AlGaN-based light-emitting devices, owing to its outstanding properties, including a wide bandgap, excellent chemical stability, and high thermal conductivity.Although nitride semiconductors exhibit excellent material properties, their actual device performance often falls short of theoretical predictions. This discrepancy is largely attributed to the crystalline imperfections in the epitaxially grown thin films used in device fabrication. Structural defects such as dislocations, vacancies, and unintentional dopants can introduce electronic trap states, adversely affecting carrier transport and device reliability. Achieving high-quality epitaxial layers requires a thorough understanding of the fundamental atomic-scale phenomena governing epitaxial crystal growth. However, these processes remain only partially understood. Accordingly, advancing our knowledge of nitride epitaxy through atomistic simulations and computational materials science is both a technological necessity and a subject of significant scientific interest.
Fig. 1 shows the schematic of a surface including steps and kinks, along with various elemental processes resulting in the formation new crystalline layers. Surface steps, including kink sites, serve as critical stages for fundamental atomic-scale reactions in addition to the reaction in terrace regions. The significance of surface steps in thin-film growth has long been recognized,20 particularly in the context of step-flow growth,21 where new crystalline layers form through the incorporation of atoms or molecules near step edges. Therefore, to elucidate the atomic-scale mechanisms governing epitaxial growth, which is an essential step toward solving persistent challenges in semiconductor fabrication and driving advances in surface science and nanotechnology, the highest priority is to identify and characterize surface structures with steps and kinks at the atomistic level and unravel the detailed incorporation reactions occurring at these step edges.
 | ||
| Fig. 1 Schematic view of a surface including steps and kinks during epitaxial growth. Associated elemental processes involved in the growth are described. | ||
Significant efforts have been devoted to understanding surface steps, primarily on silicon surfaces, through both experimental22–27 and theoretical28–32 investigations. The insights gained from these studies have laid the foundation for Si-based technologies and have provided novel perspectives in the field of surface science. However, for wide band gap (WBG) semiconductors such as GaN and AlN, atomistic understanding of surface structures remains limited. Although the role of surface steps in epitaxial growth has been discussed from a phenomenological standpoint,33 a detailed, atomic-scale understanding is still lacking. Unveiling the atomic structure of surface steps and the associated surface reactions without empirical assumptions is essential for the further advancement of WBG semiconductor technology. Moreover, nitride semiconductors exhibit an ambivalent bonding character that includes both covalent and ionic components. This duality is expected to induce unique surface phenomena that are not present in conventional semiconductors such as silicon. Therefore, gaining a comprehensive understanding of surface step characteristics in nitride semiconductors is of paramount importance not only for advancing semiconductor device technology but also for deepening our fundamental understanding of surface science.
For nitride semiconductors, the most widely used technique for epitaxial growth is metal–organic vapor-phase epitaxy (MOVPE),34–36 in which metal–organic molecules (trimethylgallium and trimethylaluminum, for instance) and ammonia (NH3) serve as source gases for metals and nitrogen, respectively. The precursors are transported to the substrate growth surface within a reaction chamber using a carrier gas such as hydrogen and undergo surface diffusion to step edges. The technologically most relevant surface orientation of wurtzite nitride semiconductors is the (0001) plane. As a result, they are eventually incorporated into the crystalline film through a step-flow growth mechanism. From a physical perspective, the growth of thin films is governed by a series of processes at the gas–solid interface, including the adsorption of atoms or molecules onto the surface, their subsequent surface diffusion, molecular dissociation, and eventual desorption. It is well established that reconstructed atomic structures frequently form on the surfaces (growth fronts) of semiconductor materials. Consequently, a detailed understanding of these surface atomic structures is essential for controlling interfacial mass transfer during film growth.
It has been increasingly recognized through recent experimental findings that precise control of surface morphology during epitaxial growth is essential for the successful fabrication of high-performance nitride semiconductor devices, particularly those based on GaN and AlN.37–49 It is now widely recognized that the growth conditions, such as growth temperature and V/III ratio, are decisive factors influencing surface morphology. In general, a low V/III ratio typically leads to metal-rich conditions, promoting step-flow growth and increasing the likelihood of impurity incorporation. In contrast, a high V/III ratio suppresses the surface diffusion of group III adatoms, often resulting in rougher surfaces and reduced growth rates. In the case of MOVPE on the technologically relevant (0001) growth surface of wurtzite AlN, these conditions strongly affect the growth mode, leading to either step-flow or step-bunching behavior.45,46 Notably, step-bunching has been observed at elevated temperatures under MOVPE growth conditions on the AlN(0001) surface.45 The dependence of surface morphology on the substrate off-angle and the V/III ratio by constructing a phase diagram of growth modes that includes both step-flow and step-bunching regimes has been clarified.46 Since these morphologies stem from surface kinetic effects involving steps and kinks, understanding the relationship between growth conditions and growth kinetic behavior is essential for a deeper comprehension of epitaxial growth mechanisms.47–49
To this end, numerous theoretical studies have been conducted to investigate the surface structures of semiconductors using electronic structure calculations within the framework of density functional theory (DFT). DFT is a powerful and widely used approach due to its capability to calculate both electronic structures and total energies, making it particularly suitable for elucidating complex growth processes. In this highlight, recent advances in computational materials science related to the epitaxial growth of nitride semiconductors are presented, with a focus on state-of-the-art techniques based on DFT. Methods and techniques employed to evaluate surface structures and growth kinetics during epitaxial growth are introduced. Several case studies are discussed that provide insight into realistic surface reconstructions of nitride semiconductor surfaces such as GaN(0001) and AlN(0001). Furthermore, results of DFT calculations concerning growth processes including adsorption, desorption, and migration behaviors of adatoms are reviewed. A critical aspect in understanding epitaxial growth mechanisms is the role of surface features such as steps and kinks, which are inevitably formed during growth. Recent studies demonstrate that quantum-theory-based simulations offer a microscopic understanding of the complex phenomena associated with epitaxial growth.
2 Methodology
2.1 Density functional calculations
The term “DFT” originates from the fact that the central quantity in density functional theory is the electron density, which is itself a function of spatial and temporal variables. A detailed discussion of the theoretical background of DFT can be found in numerous references.50,51 The foundation of DFT lies in the Hohenberg–Kohn theorem,52 which states that the total ground-state energy of a many-electron system is uniquely determined by its electron density. The total energy of the system can thus be expressed as the sum of several components: the kinetic energy of non-interacting electrons, the external potential energy, the classical Coulomb (Hartree) energy, and the exchange–correlation energy, which captures the many-body interactions beyond classical electrostatics. The kinetic energy within DFT is evaluated using the Kohn–Sham orbitals,53 which are solutions to the effective single-particle equations derived from the Kohn–Sham formalism.The Kohn–Sham formalism maps a complex system of interacting electrons onto an equivalent system of non-interacting electrons moving in an effective potential, which is constructed to reproduce the exact ground-state electron density of the original many-body system. Within the framework of DFT, the exchange–correlation energy, which encapsulates essential many-body effects among electrons, plays a central role. In practical DFT calculations, exchange–correlation effects must be approximated due to the lack of an exact analytical form. Among the various exchange–correlation functionals, the Perdew–Burke–Ernzerhof (PBE) functional54 is one of the most commonly employed, representing a widely used formulation within the framework of the generalized gradient approximation (GGA). Compared to the local density approximation (LDA),55,56 GGA enhances accuracy by taking into account not only the local electron density but also its spatial variation, enabling a more reliable treatment of systems with inhomogeneous electron systems.
When using the plane-wave basis set formalism, representing the core electron wavefunctions or the oscillatory behavior of valence electron wavefunctions near the nucleus using plane waves becomes highly inefficient. To address this issue, the pseudopotential method is commonly employed. In the pseudopotential method, the complex and rapidly varying all-electron atomic potential is replaced with a smoother pseudopotential in the core region, thereby reducing the number of plane waves needed to represent the valence electron wavefunctions. If there are tightly bound orbitals that have a significant portion of their wavefunction weight located within the core region of an atom, the construction of smooth pseudopotentials57 becomes a considerable challenge. A more radical approach has been proposed by Vanderbilt.58 The resulting ultrasoft pseudopotentials allow for much smoother (softer) potentials in the core region, enabling a dramatic reduction in the number of required plane waves and, consequently, computational effort. In this highlight, N atoms of nitride semiconductors are described by ultrasoft pseudopotentials, while Al, Ga, and H atoms are treated by norm-conserving pseudopotentials.57 The presence of H atoms are taken into account for determining the surface structures under MOVPE growth conditions, since the surface interacts with H-rich ambient during vapor-phase epitaxy such as MOVPE.
Our work to date studying the surface structures of nitride semiconductors using DFT relies on the extended Tokyo Ab initio Program Package (xTAPP).59,60 In the xTAPP code, the conjugate-gradient minimization technique61,62 is employed for both the electronic-structure calculations and the geometry optimization; however, many DFT packages, such as VASP,63 quantum ESPRESSO,64 CASTEP,65 and PHASE/0,66 also have efficient schemes for calculating electronic structures of periodic systems.
2.2 Computational models
The plane-wave basis set calculations are, in principle, best suited for periodic crystalline solids. However, these calculations can also be applied to non-periodic systems such as those involving point defects or crystal surfaces by modeling them within a periodic supercell. In such cases, the unit cell is designed to replicate the target system within a periodic framework. To simulate surfaces and interfaces, the computational cell typically includes a crystal slab accompanied by a vacuum region. The slab is periodically repeated in the direction normal to the surface. To eliminate interactions between periodic images, a vacuum layer with a thickness of at least 10 Å is commonly introduced. The size of in-plane directions is often enlarged beyond the primitive cell to accommodate surface reconstructions. In the case of the AlN(0001) surface, the lattice vectors are conventionally defined as a1 = (2a, 0, 0), a2 = (−a, , 0), and a3 = (0, 0, 6c), where a and c represent the in-plane and out-plane lattice parameters, respectively. The computational model comprises a slab with four bilayers of wurtzite AlN and a vacuum spacing of approximately 10 Å, corresponding to four additional bilayers. To prevent unphysical states at the bottom surface, it is commonly passivated with fictitious hydrogen atoms that possess fractional charges. In the case of the AlN(0001) surface, each nitrogen atom at the bottom donates 5/4 electrons per bond; hence, each of these atoms is passivated by an artificial hydrogen atom with an effective valence of 0.75.67Fig. 2 shows typical reconstructions for GaN(0001) surfaces in the 2 × 2 periodicity under MOVPE conditions, along with the ideal surface.68 The presence of hydrogen atoms plays a critical role, as the formation of N–H bonds is energetically favorable due to their high bond strength. Under H-rich conditions, structures incorporating NH3 and NH2 species, as depicted in Fig. 2, become particularly stable. In the most favorable configuration, one NH3 molecule and three NH2 groups are attached onto the Ga-terminated surface at on-top sites. It is also essential to recognize that the (0001) and (000
, 0), and a3 = (0, 0, 6c), where a and c represent the in-plane and out-plane lattice parameters, respectively. The computational model comprises a slab with four bilayers of wurtzite AlN and a vacuum spacing of approximately 10 Å, corresponding to four additional bilayers. To prevent unphysical states at the bottom surface, it is commonly passivated with fictitious hydrogen atoms that possess fractional charges. In the case of the AlN(0001) surface, each nitrogen atom at the bottom donates 5/4 electrons per bond; hence, each of these atoms is passivated by an artificial hydrogen atom with an effective valence of 0.75.67Fig. 2 shows typical reconstructions for GaN(0001) surfaces in the 2 × 2 periodicity under MOVPE conditions, along with the ideal surface.68 The presence of hydrogen atoms plays a critical role, as the formation of N–H bonds is energetically favorable due to their high bond strength. Under H-rich conditions, structures incorporating NH3 and NH2 species, as depicted in Fig. 2, become particularly stable. In the most favorable configuration, one NH3 molecule and three NH2 groups are attached onto the Ga-terminated surface at on-top sites. It is also essential to recognize that the (0001) and (000![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) directions in the wurtzite crystal structure are crystallographically inequivalent. Thin films can be grown with either polarity: the (0001) surface corresponds to Ga-polar orientation, while the (000
) directions in the wurtzite crystal structure are crystallographically inequivalent. Thin films can be grown with either polarity: the (0001) surface corresponds to Ga-polar orientation, while the (000![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) surface is referred to as N-polar. The number of additional N and H atoms is carefully adjusted to effectively eliminate surface states and to compensate for partially filled electronic states, such that the resulting surface satisfies the electron counting (EC) rule.71,72
) surface is referred to as N-polar. The number of additional N and H atoms is carefully adjusted to effectively eliminate surface states and to compensate for partially filled electronic states, such that the resulting surface satisfies the electron counting (EC) rule.71,72
 | ||
| Fig. 2 Schematic top view of prevalent 2 × 2 reconstructions for GaN(0001) surfaces. Large open circles represent Ga atoms, solid circles N, and small open circles H. Reproduced from ref. 68 with permission from American Physical Society, copyright 2003. | ||
The surfaces with steps and kinks are simulated by constructing vicinal slab models, in which an upper terrace and a lower terrace appear alternately along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction. Fig. 3 shows top views of calculation models for the vicinal AlN(0001) surface.70 The lattice vectors for the vicinal AlN(0001) surface in Fig. 3 is defined as
00] direction. Fig. 3 shows top views of calculation models for the vicinal AlN(0001) surface.70 The lattice vectors for the vicinal AlN(0001) surface in Fig. 3 is defined as  , a2 = (0, 8a, 0), and a3 = (0, 0, 6c). Therefore, the lateral size of the vicinal surface model is denoted as
, a2 = (0, 8a, 0), and a3 = (0, 0, 6c). Therefore, the lateral size of the vicinal surface model is denoted as  . The slab models including the kinks (dashed red line in Fig. 3) are generated by removing the atoms from the slab models for a kink-free surface (dashed green line in Fig. 3). Due to the AB stacking order along the [0001] axis in the wurtzite lattice, the use of vicinal slab models with steps of one bilayer inevitably results in two different step-edge configurations, labeled as Step A and Step B in Fig. 3. As shown in Fig. 3(a), the step edges of Step A and Step B on the ideal surface consist of three Al–N bonds (threefold-coordinated N atoms) and two Al–N bonds (twofold-coordinated N atoms), respectively. To evaluate the stability of step edges with kinks compared with those without step edges, the models with and without kinks using the same unit cell are necessary.70,73 To simulate the vicinal surface including a single kink for each step edge, the slab models defined by different lattice vectors are employed. For instance, the lattice vectors are
. The slab models including the kinks (dashed red line in Fig. 3) are generated by removing the atoms from the slab models for a kink-free surface (dashed green line in Fig. 3). Due to the AB stacking order along the [0001] axis in the wurtzite lattice, the use of vicinal slab models with steps of one bilayer inevitably results in two different step-edge configurations, labeled as Step A and Step B in Fig. 3. As shown in Fig. 3(a), the step edges of Step A and Step B on the ideal surface consist of three Al–N bonds (threefold-coordinated N atoms) and two Al–N bonds (twofold-coordinated N atoms), respectively. To evaluate the stability of step edges with kinks compared with those without step edges, the models with and without kinks using the same unit cell are necessary.70,73 To simulate the vicinal surface including a single kink for each step edge, the slab models defined by different lattice vectors are employed. For instance, the lattice vectors are  ,
, 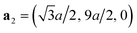 , and a3 = (0, 0, 6c), where the lateral size of vicinal surface model is denoted as
, and a3 = (0, 0, 6c), where the lateral size of vicinal surface model is denoted as  .74,75
.74,75
 | ||
Fig. 3 Top and side views of slab models for the vicinal surface with a single-bilayer step edge for (a) ideal and reconstructed AlN(0001) surfaces with (b) H-terminated N atoms and amino groups (Nad–H + NH2), (c) H-terminated N atoms and Al–H bonds (Nad + Al–H), and (d) partially terminated Al–H bonds (3Al–H). Blue, purple, and pink circles denote the Al, N, and H atoms, respectively. The atoms belonging to the lower, middle, and upper terraces are depicted by tiny, small, and large circles, respectively. Step edges with and without kinks are indicated by dashed red and green lines, respectively. The unit cell is represented by a black tetragon. The surface consists of (2 × 2) terrace regions (orange rhombus) and two single bilayer steps, which result in the  slab. Note that two types of bilayer (single layer) steps labeled as Step A and Step B are included in the unit cell owing to the stacking sequence of the wurtzite structure. Atomic structures are depicted using the VESTA visualization program.69 Reproduced from ref. 70 with permission from American Chemical Society, copyright 2024. slab. Note that two types of bilayer (single layer) steps labeled as Step A and Step B are included in the unit cell owing to the stacking sequence of the wurtzite structure. Atomic structures are depicted using the VESTA visualization program.69 Reproduced from ref. 70 with permission from American Chemical Society, copyright 2024. | ||
To construct the atomic configurations of the slab models, knowledge of previously reported surface reconstructions of flat GaN(0001) and AlN(0001) surfaces under MOVPE growth conditions,68,76–83 along with the electron counting (EC) rule,71,72 is utilized. The surface structures illustrated in Fig. 3(b) and (c) are derived from reconstructions observed in the terrace regions of the flat AlN(0001) surface. These models feature nitrogen atoms terminated by hydrogen in combination with either NH2 groups (Nad–H + NH2) or Al–H bonds (Nad–H + Al–H), both of which have been identified as representative (2 × 2) reconstructions under MOVPE conditions.77–81 Under Al-rich conditions, the lowest-energy reconstruction on the flat AlN(0001) surface corresponds to the (2 × 2) 3Al–H structure, where the surface is partially passivated by hydrogen atoms.78 As shown in Fig. 3(d), this 3Al–H configuration is adopted in the terrace region of the vicinal slab model, representing a plausible reconstruction under Al-rich growth conditions.70
2.3 Surface formation energy
To investigate the reconstructed structures on semiconductor surfaces under certain growth conditions, the relative stability among various reconstructions should be evaluated to select the candidate surfaces. The evaluation is accomplished by the surface formation energy according to the conventional thermodynamic formalism. To assess the relative stability on the AlN(0001) surface, for instance, the formation energy of Eform is calculated as a function of Al chemical potential μAl. The values of Eform are calculated as| Eform(μAl) = Etot − Eref + (ΔnAl − ΔnN)μAl − ΔnNEbulkAlN − ΔnHμH, | (1) |
| μAl + μN = EbulkAlN, | (2) |
| μbulkAl + ΔHf ≤ μAl ≤ μbulkAl, | (3) |
| μN2 + ΔHf ≤ μN ≤ μN2, | (4) |
For GaN, the relationship between the chemical potentials of Ga and N, μGa and μN, written as
| μGa + μN = EbulkGaN, | (5) |
2.4 Adsorption energy
The attachment of source gas on the reconstructed surface is evaluated by the adsorption energy Ead, which is obtained by the energy difference between the surfaces with and without adatoms. This is defined as| Ead = Etot+atom − Etot − Eatom, | (6) |
 | (7) |
3 Stability of the reconstructed surface
3.1 Reconstruction of the flat surface
On the basis of the formation energy in eqn (1), a surface phase diagram for flat GaN(0001) has been constructed and shows which surface is energetically most stable as a function of Ga and H chemical potentials, as shown in Fig. 4(a).68 The corresponding reconstructions are shown in Fig. 2. The calculated phase diagram unequivocally demonstrates that the structures obeying the EC rule71,72 are energetically favorable. Under H-poor conditions (i.e., low μH) the phase diagram reproduces the surface reconstructions for the bare GaN(0001) surface without H atoms.83,88–91 As the chemical environment shifts from N-rich to Ga-rich, the most thermodynamically stable configurations include an N atom, and finally the Ga bilayer structure is stabilized. In the presence of hydrogen, the most favorable surface configuration is the reconstruction with NH3 and NH2 (NH3 + 3NH2 in Fig. 2). In this structure, one NH3 molecule and three NH2 adsorb on-top positions, with their nitrogen atoms located directly above Ga surface atoms. This implies that at low temperatures, molecular NH3 and NH2 species are thermodynamically stable, and their dissociation is suppressed. | ||
| Fig. 4 (a) Phase diagram for the GaN(0001) surface in the presence of H atoms, as a function of μAl and μH. μH = 0 corresponds to the H2 molecule at T = 0 K; μGa = 0 corresponds to bulk Ga. Dots indicate experimental data from ref. 87; within the error bars, these data agree with the calculated NH3 + 3Ga–H/3Ga–H phase boundary highlighted by the thicker line. (b) Temperature dependence of μH for two different pressures. Reproduced from ref. 68 with permission from American Physical Society, copyright 2003. | ||
As the system moves towards H-poor conditions (i.e., decreasing μH), it becomes energetically unfavorable to retain all nitrogen atoms at the surface. Consequently, Ga–H bonds begin to form. The resulting surface structure is NH3 + 3Ga–H as shown in Fig. 2, where the three NH2 molecules in the original NH3 + 3NH2 are replaced by H atoms. In addition, the reconstruction with only H atoms (3Ga–H in Fig. 2) and a single NH group and H atom on the surface (Nad–H + Ga–H in Fig. 2) emerges under H-poor conditions. These findings lead to the important conclusion that NH3 dissociation occurs only under sufficiently low hydrogen chemical potential, and that the tendency for such dissociation is significantly enhanced under Ga-rich conditions.
Since an explicit expression for the hydrogen chemical potential is analytically given as a function of temperature and pressure,68,85,86 a direct connection between experimental growth conditions and surface structures is obtained in the calculated phase diagram shown in Fig. 4(b). At realistic growth temperatures ranging from 700 to 1100 °C and under not excessively N-rich conditions, surface configurations containing only NH3 and NH2 species are found to be thermodynamically unstable. This indicates that dissociation of NH3 molecules is energetically favorable in such regimes. The ability to compute the hydrogen chemical potential explicitly also allows for the incorporation of experimentally observed surface transitions into the phase diagram. This suggests the identification of the only experimentally confirmed transition between two distinct reconstructions, as indicated by the dotted line in Fig. 4(a).87 The experimental data align well with the transition between the NH3 + 3Ga–H and the 3Ga–H structures, effectively corresponding to the addition or removal of a single NH3 molecule.
A similar structural stability is recognized on the flat AlN(0001) surface, as shown in the phase diagram of energetically most stable structures shown in Fig. 5.78 When μH − μH2 is close to 0 eV, where μH2 is the chemical potential of the H2 molecule, the reconstruction with NH3 and NH2 (NH3 + 3NH2 shown in Fig. 2) is stabilized under N-rich conditions. In contrast, under Al-rich conditions, the reconstruction characterized by the formation of Al–H bonds (NH3 + 3Al–H in Fig. 5), which corresponds to NH3 + 3Ga–H in Fig. 2, becomes favorable. As the hydrogen chemical potential decreases to μH − μH2 ≤ −1.4 eV, the most stable surface structures shift to the 2 × 2 reconstruction with either the N atom (Nad) under N-rich conditions or Al atom(Alad) under Al-rich conditions, in agreement with the calculated results for the bare AlN(0001) surface without hydrogen.92–94 The Al bilayer structure is stabilized only under extremely Al-rich conditions, specifically when μAl − μbulkAl ≥ −0.04 eV. However, this structure is thermodynamically unstable during typical MOVPE growth, where the hydrogen partial pressure is 76 torr at temperatures between 1000 and 1400 °C corresponding to μH − μH2 values in the range of −1.6 to −1.1 eV. Within the hydrogen chemical potential range of −1.6 ≤ μH − μH2 ≤ −1.1 eV, Al–H bonds are favored under Al-rich conditions. Conversely, under N-rich conditions, reconstructions involving H-passivated N atoms such as NH and NH2 are stabilized, as labeled Nad–H + Al–H and Nad–H + NH2 in Fig. 5. The phase diagram results suggest that surface reconstructions incorporating H atoms, as well as those featuring N atoms, are likely to emerge under H-rich growth conditions.
 | ||
| Fig. 5 Phase diagram for the AlN(0001) surface in the presence of H atoms, as a function of μAl and μH. μH − μH2 = 0 corresponds to the H2 molecule at T = 0 K, and μAl − μbulkAl = 0 corresponds to bulk Al. Shaded area denotes the surface with H atoms. Reproduced from ref. 78 with permission from Japan Society of Applied Physics, copyright 2011. | ||
As depicted in Fig. 5, the surface phase diagram of AlN(0001) indicates that hydrogen-involved reconstructions such as 3Al–H and Nad–H + Al–H tend to be thermodynamically favorable under low-temperature conditions. However, the H-free surface structure (Nad in Fig. 5) can appear even under hydrogen-rich conditions when the temperature is sufficiently high. These findings suggest that various surface reconstructions can coexist on the AlN(0001) surface, leading to potentially diverse growth mechanisms that are highly sensitive to both temperature and the aluminum chemical potential. The nitrogen dangling bond in the Nad configuration exhibits greater chemical reactivity compared to the N–H and Al–H bonds present in the 3Al–H and Nad–H + Al–H reconstructions, respectively, so that surface adsorption processes are expected to proceed more readily at elevated temperatures. Moreover, since the Nad structure remains thermodynamically stable across a wide range of growth conditions under low H2 partial pressures, the growth rate under such low-pressure conditions is anticipated to surpass that observed at higher H2 pressures.
3.2 Reconstruction of the vicinal surface
Using the slab models including steps and kinks on the vicinal (0001) surface inclined to the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction as shown in Fig. 3 and considering a dozen of possible atomic configurations, stable step structures are identified. Fig. 6 shows the calculated formation energy in eqn (1) as a function of μAl for the
00] direction as shown in Fig. 3 and considering a dozen of possible atomic configurations, stable step structures are identified. Fig. 6 shows the calculated formation energy in eqn (1) as a function of μAl for the  vicinal AlN(0001) surface with a single-bilayer step edge including kinks.70 Although other stable structures cannot be entirely ruled out, the chemical potential dependence of the stable surface reconstructions is reflected by the lines with low formation energies in Fig. 6. The reconstruction labeled Nad–H + NH2, illustrated in Fig. 3(b), becomes thermodynamically favorable under N-rich conditions when μAl − μbulkAl ≤ −1.85 eV. In contrast, the Nad–H + Al–H reconstruction [Fig. 3(c)] is stabilized for −1.85 ≤ μAl − μbulkAl ≤ −1.1 eV. Furthermore, when μAl − μbulkAl ≥ −1.1 eV, the 3Al–H reconstruction shown in Fig. 3(d) becomes the most stable configuration. It is noteworthy that the formation energy for the kink-free surface (dashed line in Fig. 6) is lower than those with kinks [thick solid line in Fig. 6(a)], indicating that the kink-free step edge is energetically more favorable. This implies that step motion is likely to occur without kink formation, regardless of the specific atomic configuration at the step edge.
vicinal AlN(0001) surface with a single-bilayer step edge including kinks.70 Although other stable structures cannot be entirely ruled out, the chemical potential dependence of the stable surface reconstructions is reflected by the lines with low formation energies in Fig. 6. The reconstruction labeled Nad–H + NH2, illustrated in Fig. 3(b), becomes thermodynamically favorable under N-rich conditions when μAl − μbulkAl ≤ −1.85 eV. In contrast, the Nad–H + Al–H reconstruction [Fig. 3(c)] is stabilized for −1.85 ≤ μAl − μbulkAl ≤ −1.1 eV. Furthermore, when μAl − μbulkAl ≥ −1.1 eV, the 3Al–H reconstruction shown in Fig. 3(d) becomes the most stable configuration. It is noteworthy that the formation energy for the kink-free surface (dashed line in Fig. 6) is lower than those with kinks [thick solid line in Fig. 6(a)], indicating that the kink-free step edge is energetically more favorable. This implies that step motion is likely to occur without kink formation, regardless of the specific atomic configuration at the step edge.
 | ||
Fig. 6 Formation energy Eform as a function of μAl for the  vicinal AlN(0001) surface with a single-bilayer step edge including kinks at (a) Step A and (b) Step B. Each line corresponds to the formation energy dependence of different atomic configurations. Thick solid and dashed lines represent the formation energies of stable surfaces with and without kinks shown in Fig. 3(b)–(d), respectively. The values of hydrogen chemical potential μH − μH2 = −0.75 eV, which correspond to high H2 pressure (760 torr) at 1270 K (μH2 is the chemical potential of the single H2 molecule at 0 K) are considered for H-poor and H-rich conditions, respectively. Each line represents the formation energy of different atomic configurations. Reproduced from ref. 70 with permission from American Chemical Society, copyright 2024. vicinal AlN(0001) surface with a single-bilayer step edge including kinks at (a) Step A and (b) Step B. Each line corresponds to the formation energy dependence of different atomic configurations. Thick solid and dashed lines represent the formation energies of stable surfaces with and without kinks shown in Fig. 3(b)–(d), respectively. The values of hydrogen chemical potential μH − μH2 = −0.75 eV, which correspond to high H2 pressure (760 torr) at 1270 K (μH2 is the chemical potential of the single H2 molecule at 0 K) are considered for H-poor and H-rich conditions, respectively. Each line represents the formation energy of different atomic configurations. Reproduced from ref. 70 with permission from American Chemical Society, copyright 2024. | ||
By comparing the formation energies for the surfaces with kinks [solid lines in Fig. 6(a) and (b)], it is found that the formation energy of the surface with kinks at Step A is lower than that of the surface with kinks at Step B over a wide range of μAl. The stabilization of the surface with kinks at Step A, compared to that at Step B, can be intuitively understood by considering the number of dangling bonds and N–H bonds present on the surfaces. The kinks at Step A are formed by removing NH2 and H-terminated N atoms, in addition to Al and N atoms located at the lattice sites along the step edge. Although the introduction of kinks on the surfaces with Nad–H + NH2 and Nad–H + Al–H generates two new N dangling bonds, it also results in the formation of two new N–H bonds. In contrast, the introduction of kinks at Step B on the same surface results in only one new N dangling bond. Therefore, the number of N–H bonds formed around the kinks plays a crucial role in stabilizing the structure under N-rich conditions. It should be noted that Al–Al bonds can form at the kinks of Step A because twofold-coordinated N atoms appear at the kinks of the ideal surface, as shown in Fig. 3(a). By removing the N atoms at the kinks and forming Al–Al bonds between Al atoms on the lower and upper terraces, a different type of atomic configuration can emerge. However, the energy of the Al–Al bonds at the kinks is higher than that of Al–N–Al bonds by −3.80 eV per unit cell. Thus, similar to the stable atomic configuration found at Step B,95 the Al–N–Al bonding configuration at the kinks is energetically more favorable than the Al–Al bonding configuration.
For the reconstruction with 3Al–H, the formation of kinks at Step A leads to an increase in two N dangling bonds and one N–H bond. In contrast, kinks at Step B can be generated without changing the number of N dangling bonds and N–H bonds. Due to the smaller number of N dangling bonds, the surface with kinks at Step B is more stable than that with kinks at Step A under Al-rich conditions, specifically when μAl − μbulkAl ≥ −0.11 eV.
Similar trends in atomic structure and stability observed in AlN surfaces are also recognized in vicinal GaN(0001) surfaces.70 The reconstruction with Nad–H + NH2, which has the same atomic configuration as Nad–H + NH2 shown in Fig. 3(b), becomes stable under N-rich conditions. Alternatively, the Nad–H + Ga–H configuration is thermodynamically stabilized when the surface is exposed to conditions with a moderate nitrogen chemical potential. This reconstruction shares the same atomic arrangement as the Nad–H + Al–H structure illustrated in Fig. 3(c). The surface with kinks at Step B and Nad–H + Ga–H is always metastable. Furthermore, the energy of the reconstruction with 3Ga–H, which shares the same atomic configuration as 3Al–H shown in Fig. 3(d), is the lowest under Ga-rich conditions. The formation energy of the surface without kinks is lower than that of the surfaces with kinks, indicating that the kink-free surface is the most stable configuration.
Moreover, it is found that under N-rich conditions the formation energy of the surface including kinks at Step A is lower than that of the surface with kinks at Step B. As mentioned in the case of AlN surfaces, the stability of GaN surfaces with kinks can be intuitively understood by considering the number of dangling bonds and N–H bonds on the surfaces. In contrast, for the reconstruction with 3Ga–H, the surface including kinks at Step B becomes more stable than that including kinks at Step A under Ga-rich conditions. In the case of GaN surfaces, Ga–Ga bonds between Ga atoms located on the lower and upper terraces can be formed at the kinks of Step A by removing the N atoms at the kink sites of the ideal surface as shown in Fig. 3(a). However, the energy of Ga–Ga bonds at the kinks is higher than that of Ga–N–Ga bonds by −2.38 eV per unit cell, indicating that Ga–N–Ga bonds are energetically more favorable at the kink sites.
Based on the stability of kinks, implications can be drawn regarding the surface morphology observed in the atomic force microscopy (AFM) measurements. The calculated formation energies indicate that step edges with kinks are generally less stable than straight step edges. However, the kink formation energy can be reduced under certain growth conditions. In such cases, kinks may occasionally form during the adsorption process at the step edges, leading to a meandering-step morphology. Indeed, both hillock formation and step meandering have been observed by AFM in GaN MOVPE growth at low temperatures,96 which corresponds to the Ga-rich conditions. It is also expected that kinetic factors such as adatom incorporation into step edges, migration anisotropy around step edges,97,98 and kink dynamics99,100 can significantly influence the surface morphology, as discussed below.
4 Adsorption behavior and surface kinetics
4.1 Flat surface
To assess the interaction between the source gas and the reconstructed surface, contour maps of the potential energy surface (PES) is generated, following methods developed in previous calculations.77,101–103 The PES is constructed by calculating the adsorption energies defined in eqn (6), where the adatom is laterally positioned at multiple inequivalent sites across the surface, while vertical relaxation of the adatom and full relaxation of all other atoms in the system are allowed. By evaluating a sufficient number of distinct lateral positions, a detailed map of the adsorption energy landscape could be obtained.Fig. 7(a) and (b) show the PES for the Al and N adatoms on the reconstructed flat AlN(0001) surface with Nad–H + NH2, which is applicable for the MOVPE conditions under extreme N-rich conditions. To obtain the PES shown in Fig. 7, a 6 × 6 uniform mesh is generated on the (0001) plane of the 2 × 2 unit cell, resulting in 36 lateral positions for the flat surface with the 2 × 2 reconstruction. According to the PES contour plot for the Al adatom shown in Fig. 7(a), the most stable adsorption site for the Al atom on the surface with Nad–H + NH2 is located between the topmost Al–N bonds around the NH group. This configuration results in the formation of an Al–Al bond (bond length: 2.66 Å) between the Al adatom and the topmost surface Al atom. The adsorption energy is calculated to be −2.03 eV,104 representing the energy gain associated with Al–Al bond formation. This value corresponds to desorption temperatures ranging from 700 K to 900 K, depending on the Al vapor pressure (below 1 × 10−3 torr), as derived from eqn (7), suggesting that most of the additional Al atoms can readily desorb from the surface. The energetically most favorable transition sites for the Al adatom migration are located directly above the topmost Al atoms [arrow in Fig. 7(a)], with a calculated migration barrier of 0.42 eV. This energy barrier originates from the dissociation of the Al–N bond between the Al adatom and the adjacent NH group.
 | ||
| Fig. 7 Contour plots of the adsorption energy for (a) Al and (b) N adatoms on the reconstructed flat AlN(00001) surfaces with hydrogen passivated N atoms and amino groups (Nad–H + NH2) and the adsorption energy for (c) Al and (d) N adatoms on the reconstructed flat surfaces with hydrogen passivated N atoms and Al–H bonds (Nad–H + Al–H). The (2 × 2) unit cell reconstruction is enclosed by a dashed rhombus. Arrow indicates the saddle point for the migration. Notation of atoms are the same as those in Fig. 5. | ||
In the case of nitrogen adsorption, the most stable adsorption site on the Nad–H + NH2 surface is found between the topmost Al–N bonds surrounding the NH group, as shown in Fig. 7(b). The adsorption energy, reported as −3.24 eV,104 reflects the energetic gain associated with the formation of an additional N–N bond. The lowest-energy migration path for the N adatom lies above the second-layer N atoms [see arrow in Fig. 7(b)], with a corresponding migration barrier of 0.82 eV. This barrier arises from the dissociation of the N–N bond between the N adatom and the NH group. Given the significantly lower migration barrier for the Al adatom compared to N adatom, it can be inferred that Al adatoms predominantly migrate across the flat surface during growth.
As shown in Fig. 7(c), the PES contour plot for an Al adatom on the reconstructed flat AlN(0001) surface with the Nad–H + Al–H, which corresponds to MOVPE growth conditions under moderately N-rich conditions, is similar to that on the Nad–H + NH2 surface shown in Fig. 7(a). The most stable adsorption site for the Al atom on the Nad–H + Al–H surface is located between the topmost Al–N bonds near the NH group. The calculated adsorption energy is −1.83 eV,104 corresponding to the energy gain associated with the formation of an Al–Al bond. Therefore, even under moderately N-rich conditions, most of the additional Al atoms can be easily detached from the surface. The most favorable migration pathway for the Al adatom on this surface is found to lie above the topmost Al atoms, as indicated by the arrow in Fig. 7(c), which is similar to the pathway identified for the Nad–H + NH2-terminated surface. The calculated energy barrier for migration is 0.63 eV. This barrier originates from the need to break the Al–N bond between the Al adatom and the neighboring NH group during migration.
In contrast, for the N adatom on the reconstructed AlN(0001) surface with Nad–H + Al–H termination shown in Fig. 7(d), the most stable adsorption site differs from that on the Nad–H + NH2 surface in Fig. 7(b). On the Nad–H + Al–H surface, the most stable site is located near the Al–H bond. The adsorption energy of −4.17 eV104 corresponds to the energy gain associated with the formation of an additional NH group, which forms three Al–N bonds. The difference in the most stable adsorption sites between the Nad–H + NH2 and Nad–H + Al–H surfaces originates from the presence of the NH2 group in the former, which introduces steric hindrance. The energetically lowest transition sites for the migration of the N adatom are located above the second layer N atoms [arrow in Fig. 7(d)] and the energy barrier for migration is 1.28 eV. The difference in energy barrier between Nad–H + Al–H and Nad–H + NH2 is caused by the stability of the N adatom near the Al–H bond for the surface with Nad–H + Al–H.
Table 1 summarizes the calculated adsorption energies of Al and N adatoms at their most stable sites, as well as the energy barriers for migration on reconstructed AlN(0001) surfaces. For comparison, the corresponding values for Ga and N adatoms on the reconstructed GaN(0001) surface are also presented.95 The trends in migration energy barriers for GaN are found to be quite similar to those for AlN. However, a noticeable difference is observed in the adsorption energies, which can be attributed to the differences in the chemical bonding nature between Ga–N and Al–N. In particular, the adsorption energy of the N adatom on the GaN(0001) surface with Nad–H + Ga–H termination is significantly different. This is due to the formation of three Ga–N bonds between the N adatom and the topmost Ga atoms, which results in a stronger binding energy.
| Material | Reconstruction | Species | E ad | E b |
|---|---|---|---|---|
| AlN | Nad–H + NH2 | Al | −2.03 | 0.42 |
| N | −3.24 | 0.82 | ||
| AlN | Nad–H + Al–H | Al | −1.83 | 0.63 |
| N | −4.17 | 1.28 | ||
| GaN | Nad–H + NH2 | Ga | −2.09 | 0.46 |
| N | −3.39 | 0.69 | ||
| GaN | Nad–H + Ga–H | Ga | −1.88 | 0.70 |
| N | −3.66 | 0.91 |
Based on the calculated adsorption energies and migration energy barriers shown in Table 1, the behavior of adatoms can be inferred as follows. Since the adsorption energies of N adatoms are smaller in magnitude than those of Al adatoms, it is suggested that Al adatoms are more strongly bound to the surface. Since the migration probability is proportional to exp(−Eb/kBT), where Eb is the energy barrier, the difference in Eb of less than 0.2 eV for Al and Ga adatoms is unlikely to significantly affect their migration behavior or the resultant growth rate. However, this conclusion is drawn under the assumption that growth proceeds on a flat surface. The influence of surface features such as steps and kinks must be carefully examined to fully understand the adatom dynamics under realistic growth conditions.
4.2 Vicinal surface with steps and kinks
To investigate the interaction between source gas species and the vicinal surface featuring steps and kinks, the PES contour plots are constructed following the approach in ref. 74. The PES was obtained using the slab model briefly described in section 2.2, where the adatom is laterally fixed at different surface positions and relaxed along the surface-normal direction. Based on the adsorption energy defined in eqn (6), the PES maps are generated. Fig. 8(a) and (b) present the resulting PES for Al and N adatoms, respectively, on the vicinal AlN(0001) surface with Nad–H + NH2. Here, an 8 × 12 uniform mesh is generated on the vicinal (0001) plane of the
slab model briefly described in section 2.2, where the adatom is laterally fixed at different surface positions and relaxed along the surface-normal direction. Based on the adsorption energy defined in eqn (6), the PES maps are generated. Fig. 8(a) and (b) present the resulting PES for Al and N adatoms, respectively, on the vicinal AlN(0001) surface with Nad–H + NH2. Here, an 8 × 12 uniform mesh is generated on the vicinal (0001) plane of the  unit cell, and therefore the adsorption energies for 96 independent lateral positions are used. As illustrated by the potential energy surface (PES) contour plot for the Al adatom in Fig. 8(a), the vicinity of the kink site on Step A corresponds to the most energetically favorable adsorption site, exhibiting an adsorption energy of −4.88 eV. In contrast, both the step edge and the kink of Step B also act as energetically favorable adsorption sites. These adsorption energies are markedly lower than those on the terrace regions and notably smaller than the most stable adsorption energy (−2.03 eV in ref. 104) observed on the flat AlN(0001) surface with the Nad–H + NH2 reconstruction, as shown in Fig. 7(a). These findings suggest that vicinal AlN(0001) surfaces featuring steps and kinks preferentially incorporate Al adatoms at such defect sites, rather than on flat terrace regions.
unit cell, and therefore the adsorption energies for 96 independent lateral positions are used. As illustrated by the potential energy surface (PES) contour plot for the Al adatom in Fig. 8(a), the vicinity of the kink site on Step A corresponds to the most energetically favorable adsorption site, exhibiting an adsorption energy of −4.88 eV. In contrast, both the step edge and the kink of Step B also act as energetically favorable adsorption sites. These adsorption energies are markedly lower than those on the terrace regions and notably smaller than the most stable adsorption energy (−2.03 eV in ref. 104) observed on the flat AlN(0001) surface with the Nad–H + NH2 reconstruction, as shown in Fig. 7(a). These findings suggest that vicinal AlN(0001) surfaces featuring steps and kinks preferentially incorporate Al adatoms at such defect sites, rather than on flat terrace regions.
 | ||
Fig. 8 Contour plots of the adsorption energy for (a) Al and (b) N adatoms around steps and kinks for the reconstructed surface with hydrogen passivated N atoms and amino groups (Nad–H + NH2). Step edges and kinks are shown by blue dashed lines. The unit cell is enclosed by black rectangles. Dashed green and blue arrows represent migration pathways along the [1100] and [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] directions toward the stable adsorption site. The unit cells are multiplied for visual understanding. The notation of atoms are the same as those in Fig. 3. Reproduced from ref. 74 with permission from Japan Society of Applied Physics, copyright 2024. 0] directions toward the stable adsorption site. The unit cells are multiplied for visual understanding. The notation of atoms are the same as those in Fig. 3. Reproduced from ref. 74 with permission from Japan Society of Applied Physics, copyright 2024. | ||
The notably low adsorption energy at the kink site of Step A can be primarily ascribed to the formation of two Al–N bonds. Additionally, the migration energy barriers for Al adatoms around this kink exhibit slight anisotropy, measured as 3.05 eV along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction and 3.18 eV along the [11
00] direction and 3.18 eV along the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction. Such a minor energy difference and large energy barriers indicates that the kink Ehrlich–Schwoebel barrier (KESB)99,100 is effectively negligible. The migration probability estimated using exp(−Eb/kBT) at 1270 K is less than 1 × 10−13 regardless of the migration directions. This probability corresponds to a migration event occurring approximately once every 0.2 s at 1270 K. The negligible KESB, combined with the reduced adsorption energies at kinks and step edges, underscores the pivotal role of Al adatom incorporation at these defect sites in facilitating step-flow growth. Consequently, it is reasonable to conclude that the persistence of step-flow growth is predominantly governed by the preferential incorporation of Al adatoms into kink sites. The observed anisotropy in migration barriers is attributed to the fact that adatom diffusion along both the [1
0] direction. Such a minor energy difference and large energy barriers indicates that the kink Ehrlich–Schwoebel barrier (KESB)99,100 is effectively negligible. The migration probability estimated using exp(−Eb/kBT) at 1270 K is less than 1 × 10−13 regardless of the migration directions. This probability corresponds to a migration event occurring approximately once every 0.2 s at 1270 K. The negligible KESB, combined with the reduced adsorption energies at kinks and step edges, underscores the pivotal role of Al adatom incorporation at these defect sites in facilitating step-flow growth. Consequently, it is reasonable to conclude that the persistence of step-flow growth is predominantly governed by the preferential incorporation of Al adatoms into kink sites. The observed anisotropy in migration barriers is attributed to the fact that adatom diffusion along both the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] and [11
00] and [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] directions proceeds via adsorption sites situated on the terrace. Ultimately, the disparity in adsorption energies between kink and terrace sites emerges as the principal factor influencing the migration energy barriers.
0] directions proceeds via adsorption sites situated on the terrace. Ultimately, the disparity in adsorption energies between kink and terrace sites emerges as the principal factor influencing the migration energy barriers.
The PES contour plot for the N adatom, presented in Fig. 8(b), demonstrates energy variations of approximately 3 eV depending on its lateral position. The kink site at Step B emerges as the most energetically favorable adsorption site, with an adsorption energy of −4.00 eV. Nonetheless, multiple other stable adsorption sites are also found on the terrace, exhibiting adsorption energies only about 0.15 eV higher than that of the kink. These adsorption energies on the vicinal surface are comparable to those observed at the step edge (−4.11 eV) and on the flat surface [−3.24 eV104 in Fig. 7(b)]. The enhanced stability of the N adatom is primarily attributed to the formation of chemisorbed Al–N bonds with surface Al atoms and N–N bonds involving pre-adsorbed N atoms. Furthermore, the PES contour plot reveals that the migration energy barriers for the N adatom are 1.42 eV along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction and 1.50 eV along the [11
00] direction and 1.50 eV along the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction, indicating minimal anisotropy and suggesting that the kink Ehrlich–Schwoebel barrier (KESB) remains insignificant. In addition, specific adsorption configurations near the step edge, which facilitate N2 desorption through reactions with surface nitrogen atoms, have been identified. These findings imply that N adatoms may be removed from step edges via the formation and subsequent desorption of N2 molecules.
0] direction, indicating minimal anisotropy and suggesting that the kink Ehrlich–Schwoebel barrier (KESB) remains insignificant. In addition, specific adsorption configurations near the step edge, which facilitate N2 desorption through reactions with surface nitrogen atoms, have been identified. These findings imply that N adatoms may be removed from step edges via the formation and subsequent desorption of N2 molecules.
The PES contour plots for Al and N adatoms on the reconstruction with Nad–H + Al–H, which corresponds to the MOVPE conditions under moderately N-rich conditions, are illustrated in Fig. 9. The overall PES landscape for the Al adatom shown in Fig. 9(a) closely resembles that for the reconstruction with Nad–H + Al–NH2 presented in Fig. 8(a). The most stable adsorption site is located near the kink of Step A, with an adsorption energy of −3.82 eV. This energy is significantly lower than those in the terrace region, and also lower than that of the most stable adsorption site on the flat AlN(0001) surface, which has an adsorption energy of −1.83 eV104 in Fig. 7(c). Consequently, the vicinal surface with Nad–H + Al–H termination preferentially incorporates Al adatoms at kinks and step edges rather than at terrace sites. The adsorption behavior of Al adatoms exhibits a similar trend between the Nad–H + Al–NH2 and Nad–H + Al–H reconstructions.
 | ||
Fig. 9 Contour plots of the adsorption energy for (a) Al and (b) N adatoms around steps and kinks for the reconstructed surface with hydrogen passivated N atoms and Al–H bonds (Nad–H + Al–H). Step edges and kinks are shown by blue dashed lines. The unit cell is enclosed by black rectangles. Dashed green and blue arrows represent migration pathways along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] and [11 00] and [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] directions toward the stable adsorption site. The unit cells are multiplied for visual understanding. The notation of atoms are the same as those in Fig. 3. Reproduced from ref. 74 with permission from Japan Society of Applied Physics, copyright 2024. 0] directions toward the stable adsorption site. The unit cells are multiplied for visual understanding. The notation of atoms are the same as those in Fig. 3. Reproduced from ref. 74 with permission from Japan Society of Applied Physics, copyright 2024. | ||
The migration energy barriers for the Al adatom are calculated to be 2.03 eV along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction and 2.15 eV along the [11
00] direction and 2.15 eV along the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] direction. Although the absolute values of the barriers differ from those observed on the Nad–H + Al–NH2 surface, the overall migration behavior of Al adatoms on these vicinal surfaces can be regarded as qualitatively similar. The small energy barrier difference of 0.12 eV between the two directions and large energy barriers implies the absence of a significant KESB. Indeed, the migration probabilities estimated using exp(−Eb/kBT) at 1270 K are less than 1 × 10−9, regardless of the migration direction. This probability corresponds to a migration event occurring approximately once every 10−5 s at 1270 K. The calculated results highlight the importance of Al adatom incorporation at both kinks and step edges in sustaining step-flow growth. The adsorption energy at the step edge of Step B exceeds that at the most stable kink site by only 0.12 eV, so that the Al adatoms can also be incorporated at locations away from kinks. This off-kink incorporation likely contributes to the development of irregular step edges, potentially influencing the overall step morphology during epitaxial growth.
0] direction. Although the absolute values of the barriers differ from those observed on the Nad–H + Al–NH2 surface, the overall migration behavior of Al adatoms on these vicinal surfaces can be regarded as qualitatively similar. The small energy barrier difference of 0.12 eV between the two directions and large energy barriers implies the absence of a significant KESB. Indeed, the migration probabilities estimated using exp(−Eb/kBT) at 1270 K are less than 1 × 10−9, regardless of the migration direction. This probability corresponds to a migration event occurring approximately once every 10−5 s at 1270 K. The calculated results highlight the importance of Al adatom incorporation at both kinks and step edges in sustaining step-flow growth. The adsorption energy at the step edge of Step B exceeds that at the most stable kink site by only 0.12 eV, so that the Al adatoms can also be incorporated at locations away from kinks. This off-kink incorporation likely contributes to the development of irregular step edges, potentially influencing the overall step morphology during epitaxial growth.
The PES contour plot for the N adatom depicted in Fig. 9(b) indicates that the most energetically favorable adsorption site resides within the terrace region, rather than at kink or step edge locations. This site exhibits an adsorption energy of −5.40 eV, which is notably lower than that of the most stable site on the flat AlN(0001) surface [−4.17 eV104 in Fig. 7(d)]. The fact that the preferred adsorption occurs in the terrace region implies that the adsorption characteristics of vicinal and flat surfaces are similar. The strong binding at this site is primarily attributed to the formation of both a chemisorbed Al–N bond with a surface Al atom and an N–H bond. Furthermore, the PES contour plot reveals migration energy barriers of 2.67 eV and 2.85 eV for the N adatom along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] and [11
00] and [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] directions, respectively. These barriers are considerably higher than those found on the Nad–H + Al–NH2 reconstructed surface [Fig. 8(b)], reflecting the deeper adsorption potential characteristic of the Nad–H + Al–H surface. Such large migration barriers, exceeding 2.5 eV, suggest that N adatom mobility on the vicinal surface with the Nad–H + Al–H reconstruction is substantially hindered under MOVPE conditions featuring a low V/III ratio.
0] directions, respectively. These barriers are considerably higher than those found on the Nad–H + Al–NH2 reconstructed surface [Fig. 8(b)], reflecting the deeper adsorption potential characteristic of the Nad–H + Al–H surface. Such large migration barriers, exceeding 2.5 eV, suggest that N adatom mobility on the vicinal surface with the Nad–H + Al–H reconstruction is substantially hindered under MOVPE conditions featuring a low V/III ratio.
The adsorption energies and migration barriers for Al and N adatoms, calculated and depicted in Fig. 8 and 9, are summarized in Table 2. Considering that N2 molecules can form on the Nad–H + Al–NH2 reconstructed surface and that the migration barriers for N adatoms on the Nad–H + Al–H surface are relatively large, it is reasonable to conclude that the growth behavior is largely determined by the adsorption and diffusion of Al adatoms, as shown in Fig. 8(a) and 9(a). The migration barrier difference between the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] and [11
00] and [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] directions is less than 0.12 eV, indicating near isotropic diffusion and a negligible kink Ehrlich–Schwoebel barrier (KESB). This negligible KESB suggests effective suppression of step meandering. Conversely, on the Nad–H + Al–H surface, Al adatoms can incorporate at both kink sites and step edges distant from kinks. Such incorporation may lead to the formation of roughened step edges, which in turn could contribute to step meandering and bunching, offering a possible explanation for the experimentally observed step bunching under MOVPE conditions with a low V/III ratio.46
0] directions is less than 0.12 eV, indicating near isotropic diffusion and a negligible kink Ehrlich–Schwoebel barrier (KESB). This negligible KESB suggests effective suppression of step meandering. Conversely, on the Nad–H + Al–H surface, Al adatoms can incorporate at both kink sites and step edges distant from kinks. Such incorporation may lead to the formation of roughened step edges, which in turn could contribute to step meandering and bunching, offering a possible explanation for the experimentally observed step bunching under MOVPE conditions with a low V/III ratio.46
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] and [11
00] and [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] directions obtained by the contour plots shown in Fig. 8 and 9 for the reconstructed surfaces with hydrogen passivated N atoms and amino groups (Nad–H + NH2) and hydrogen passivated nitrogen atoms (Nad–H + Al–H) in ref. 74. The unit of energies is eV
0] directions obtained by the contour plots shown in Fig. 8 and 9 for the reconstructed surfaces with hydrogen passivated N atoms and amino groups (Nad–H + NH2) and hydrogen passivated nitrogen atoms (Nad–H + Al–H) in ref. 74. The unit of energies is eV
| Reconstruction | Species | E ad | Stable position | E b along the [1100] direction | E b along the [1120] direction |
|---|---|---|---|---|---|
| Nad–H + NH2 | Al | −4.88 | Kink of Step A | 3.05 | 3.18 |
| N | −4.00 | Terrace | 1.50 | 1.42 | |
| Nad–H + Al–H | Al | −3.82 | Kink of Step A | 2.03 | 2.15 |
| N | −5.40 | Terrace | 2.67 | 2.85 |
However, the extent to which variations in energy barriers due to different surface reconstructions affect the stability and linearity of step edges remains uncertain. As shown in Table 2, a difference of approximately 1 eV in migration energy for Al adatoms corresponds to a change in migration probability by a factor of more than 1000 at 1270 K. Therefore, growth-condition-dependent variations in migration barriers around kinks and steps may play a decisive role in determining the growth mode. Nevertheless, further investigations are required to quantitatively clarify the contributions of adsorption and migration behavior to surface morphology.
Most recently, the effect of surface potential energy landscape on the surface morphology has been examined using the cellular automaton model. Chabowska et al. have explored various factors affecting surface pattern dynamics using the vicinal cellular automaton model, which distinguishes surface diffusion from adatom incorporation into the crystal.105 The calculation model is based on a new approach employing the vicinal cellular automaton model106,107 to simulate the growth of vicinal crystal surfaces, modeling the diffusion of adatoms on the surface and their incorporation into the crystal lattice. The energy potential was derived from the results of DFT calculations for the AlN(0001) surface with step edges.104 An appropriate diagram of pattern formation as a function of depth of the potential well βEV (β is inverse temperature) and the height of the Ehrlich–Schwoebel barrier (ESB) βEES97,98 is illustrated in Fig. 10(a). The contour plots of the meander wavelength λ as a function of βEV and βEES, averaged over 10 simulation runs, are presented in Fig. 10(b). Based on the contour plots, the potential regions in which well-defined meanders of appropriate wavelength can form are identified. It is observed that meanders do not develop when both the potential well depth and the ESB are zero. When either parameter is non-zero, step meandering begins to occur, and the wavelength λ decreases with increasing potential well depth or increasing ESB height. A simultaneous increase in both βEV and βEES results in an even more pronounced reduction in meander wavelength. The isolines shown in Fig. 10(b), corresponding to λ values between 25 and 40, delineate the region in parameter space where well-developed meander patterns can form. These results provide insight into the optimal conditions for crystal growth, including suitable temperature ranges, flux rates, and other critical parameters. Moreover, it should be noted that successful guidance of the formation of core–shell InAlN nanorods at the mesoscopic level has recently been demonstrated by evolving the methodology to use DFT-derived parameters as input to mesoscale models, particularly those based on the phase-field method.108 This multiscale approach, grounded in a comprehensive investigation of DFT calculation results, has proven especially effective when applied to large-scale modeling frameworks for nitride semiconductors.
 | ||
| Fig. 10 (a) Diagram of pattern formation on the surface obtained for the adatom concentration c0 = 0.003, initial distance between steps l0 = 5, number of diffusional steps nDS = 5, and time steps t = 2 × 106 at different values of potential well βEV (β = 1/kBT) and Ehrlich–Schwoebel barrier βEES. Different colors correspond to different surface heights. (b) Diagram of meander wavelength λ as a function of βEV and βEES obtained for c0 = 0.003, l0 = 5, nDS = 5 and t = 2 × 106. Different colors correspond to different meander wavelengths. The presented green and black isolines correspond to λ = 25, 30, 35, 40 and are extracted from simulation data, respectively. Reproduced from ref. 105 with permission from American Physical Society, copyright 2024. | ||
To the best of my knowledge, there have been very few studies focusing on the GaN surfaces with steps and kinks. For GaN(0001) surfaces incorporating atomic steps (excluding kink sites), recent DFT studies109,110 have elucidated the fundamental atomic-scale mechanisms of nitrogen incorporation at step edges. These findings contribute to a deeper microscopic understanding of step-flow growth in GaN epitaxy. In their comprehensive investigation, Bui et al. explored a wide range of step-edge configurations on vicinal (0001) surfaces inclined along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] and [11
00] and [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0] directions. By systematically analyzing the stability of various combinations of terrace reconstructions and step-edge terminations, they identified the energetically most favorable step structures. Furthermore, by using hyperplane constraint method32,111 the reaction pathways for NH unit incorporation, where NH species are generated via NH3 decomposition on the terrace, were explored.109 A plausible reaction pathway was proposed in which NH units interact with Ga adatoms near the step edges, leading to the formation of N–Ga bonds and subsequent incorporation into the growing GaN crystal. The reactions are energetically favorable, particularly when the free-energy gain associated with H2 formation in the gas phase is taken into account. The proposed reaction pathway provides an atomistic understanding of the step-flow growth mechanism of GaN epitaxial growth.
0] directions. By systematically analyzing the stability of various combinations of terrace reconstructions and step-edge terminations, they identified the energetically most favorable step structures. Furthermore, by using hyperplane constraint method32,111 the reaction pathways for NH unit incorporation, where NH species are generated via NH3 decomposition on the terrace, were explored.109 A plausible reaction pathway was proposed in which NH units interact with Ga adatoms near the step edges, leading to the formation of N–Ga bonds and subsequent incorporation into the growing GaN crystal. The reactions are energetically favorable, particularly when the free-energy gain associated with H2 formation in the gas phase is taken into account. The proposed reaction pathway provides an atomistic understanding of the step-flow growth mechanism of GaN epitaxial growth.
5 Conclusions and prospects
This highlight critically reviews recent advancements in computational materials science, particularly the use of DFT calculations to deepen atomic-scale understanding of epitaxial growth mechanisms in nitride semiconductors, especially GaN and AlN. The focus is placed on surface structures, atomic configurations of steps and kinks, and adsorption and migration behaviors. For the identification of stable surface reconstructions, DFT calculations reveal stable surface reconstructions of GaN(0001) and AlN(0001) surfaces under growth conditions, such as the chemical potentials of Ga/Al and the presence of hydrogen: H atoms stabilize the surface through the adsorption of NH3 and NH2 species during the MOVPE; by modeling vicinal surfaces, the stability of surfaces containing steps and kinks has been evaluated. The reconstruction with Nad–H + NH2 is energetically favorable under the N-rich limit, whereas reconstruction with Nad–H + Al–H (Nad–H + Ga–H) is favorable for moderately N-rich conditions for the AlN (GaN) surface. For the adsorption behavior, the Al adatoms exhibit strong adsorption at kinks with relatively low migration barriers, indicating their critical role in step-flow growth, while the N adatoms also show strong adsorption on the terrace region. The results of DFT calculations imply that differences in kink formation and adsorption energies lead to variations in surface morphology, such as step-flow growth, step bunching, and step meandering. The findings obtained by DFT calculations underscore the importance of computational materials science as a tool for understanding the crystal growth mechanisms of nitride semiconductors. Furthermore, the combination of DFT-derived parameters with vicinal cellular automaton models and phase-field simulations has proven to be a powerful multiscale strategy for controlling growth across different length scales. The insights gained from these approaches contribute to the realization of high-quality epitaxial films for device applications via MOVPE.More recently, there have been several attempts to utilize information science technologies, such as artificial intelligence, in the field of materials science. As a novel approach to understanding epitaxial growth, entirely new methodologies have been explored to dramatically improve predictive performance beyond that of conventional simulations.112,113 To improve conventional small-scale DFT (density functional theory) calculations that impose short-range periodicity, such as the use of a (2 × 2) lateral cell, the stable structures of nanometer-scale GaN(0001) surfaces with Ga and H adsorbates, which serve as a fundamental basis for crystal growth modeling, have been identified. Fig. 11 shows the most stable structure discovered through large-scale DFT calculations combined with a machine learning-based Bayesian optimization technique.112 The configuration shown in Fig. 11 reveals that H atoms are distributed in such a way that they avoid the immediate vicinity of Ga atoms. It should be noted that the distribution of hydrogen atoms is asymmetric, leading to a highly complex adsorption structure. The ability to uncover complex and low-energy surface structures that lack symmetry is a significant advantage of employing machine learning approaches. To assess the flux of chemical species transported to the growth surface by the inert carrier gas during GaN crystal growth, sequential reaction routes for the synthesis of precursors have been proposed based on DFT calculations.114 For the quantitative evaluation, data assimilation of gas-phase reaction kinetics in GaN MOVPE has recently been carried out using a multi-objective optimization framework.113 By integrating insights from DFT calculations into the optimization process, the model is able to accurately reproduce not only the concentration of impurity precursor (CH4) as an objective variable, but also the underlying reaction mechanisms. Notably, the simulation predicted substantial formation of GaH3, a key GaN precursor species that remains challenging to detect experimentally.115 These advancements pave the way for a quantitatively predictive framework for crystal growth, driven by the integration of computational materials science and cutting-edge approaches from information science.
 | ||
| Fig. 11 Top view of the stable (6 × 6) surface structure by the arrangements of the hydrogen-covered surface (blue tiles) and the Ga adatom surface (red tiles), discovered by the Bayesian optimization. Brown, blue and white atoms correspond to Ga, N and H, respectively. Black dashed tile indicates a (6 × 6) area. Reproduced from ref. 112 with permission from American Institute of Physics, copyright 2022. | ||
Data availability
The author declares that there are no primary research results, software or code included in the highlight manuscript. No new data were generated or analyzed as part of this highlight.Author contributions
The author participated in conceiving and designing the highlight articles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
TA would like to thank Dr. T. Kawamura, Prof. Y. Kangawa, and Prof. H. Miyake for scientific discussion. The author is also thankful for the financial support by the JSPS KAKENHI Grant No. JP24K08268, JP24K01360, JP25K01680 and the EIG CONCERT Japan framework of JST-SICORP Grant No. JPMJSC22C1, and acknowledges Kyushu University and the National Institutes of Natural Sciences for providing access to the computational facilities at the Research Institute for Information Technology and the Research Center for Computational Science (Project: 25-IMS-C047), respectively.References
- S. Nakamura, T. M. T. Mukai and M. S. M. Senoh, Jpn. J. Appl. Phys., 1991, 30, L1998 CrossRef CAS.
- R.-H. Horng, D.-S. Wuu, C.-F. Lin and C.-F. Lai, Nitride Semiconductor Light-Emitting Diodes (LEDs), Woodhead Publishing, 2nd edn, 2018, pp. 209–241 Search PubMed.
- I. Akasaki, Rev. Mod. Phys., 2015, 87, 1119–1131 CrossRef.
- H. Amano, Rev. Mod. Phys., 2015, 87, 1133–1138 CrossRef CAS.
- S. Nakamura, Rev. Mod. Phys., 2015, 87, 1139–1151 CrossRef CAS.
- T. Ueda, Jpn. J. Appl. Phys., 2019, 58, SC0804 CrossRef CAS.
- M. Shatalov, W. Sun, R. Jain, A. Lunev, X. Hu, A. Dobrinsky, Y. Bilenko, J. Yang, G. A. Garrett, L. E. Rodak, M. Wraback, M. Shur and R. Gaska, Semicond. Sci. Technol., 2014, 29, 084007 CrossRef CAS.
- T. Takano, T. Mino, J. Sakai, N. Noguchi, K. Tsubaki and H. Hirayama, Appl. Phys. Express, 2017, 10, 031002 CrossRef.
- T. T. Mnatsakanov, M. E. Levinshtein, L. I. Pomortseva, S. N. Yurkov, G. S. Simin and M. Asif Khan, Solid-State Electron., 2003, 47, 111–115 CrossRef CAS.
- H. Tokuda, M. Hatano, N. Yafune, S. Hashimoto, K. Akita, Y. Yamamoto and M. Kuzuhara, Appl. Phys. Express, 2010, 3, 121003 CrossRef.
- N. Yafune, S. Hashimoto, K. Akita, Y. Yamamoto, H. Tokuda and M. Kuzuhara, Electron. Lett., 2014, 50, 211–212 CrossRef CAS.
- M. Kneissl, T.-Y. Seong, J. Han and H. Amano, Nat. Photonics, 2019, 13, 233–244 CrossRef CAS.
- H. Masuda, M. Kimura and A. Morita, J. Dermatol. Sci., 2017, 86, e81 CrossRef.
- S. Rattanakul and K. Oguma, Environ. Sci. Technol., 2017, 51, 455–462 CrossRef CAS PubMed.
- X. Zhou, Z. Li, J. Lan, Y. Yan and N. Zhu, Ultrason. Sonochem., 2017, 35, 471–477 CrossRef CAS PubMed.
- S. Rattanakul and K. Oguma, Water Res., 2018, 130, 31–37 CrossRef PubMed.
- M. Nakamura, A. Morita, S. Seite, T. Haarmann-Stemmann, S. Grether-Beck and J. Krutmann, Exp. Dermatol., 2015, 24, 407–411 CrossRef CAS.
- S. Yamazaki, A. Nishioka, S. Kasuya, N. Ohkura, H. Hemmi, T. Kaisho, O. Taguchi, S. Sakaguchi and A. Morita, J. Immunol., 2014, 193, 5488–5497 CrossRef CAS PubMed.
- M. Mori, A. Hamamoto, A. Takahashi, M. Nakano, N. Wakikawa, S. Tachibana, T. Ikehara, Y. Nakaya, M. Akutagawa and Y. Kinouchi, Med. Biol. Eng. Comput., 2007, 45, 1237–1241 CrossRef PubMed.
- W. K. Burton, N. Cabrera, F. C. Frank and N. F. Mott, Philos. Trans. R. Soc., A, 1951, 243, 299–358 CrossRef.
- N. Newman and M. Vahidi, Handbook of Crystal Growth, North-Holland, Boston, 2nd edn, 2015, pp. 835–868 Search PubMed.
- R. S. Becker, J. A. Golovchenko, E. G. McRae and B. S. Swartzentruber, Phys. Rev. Lett., 1985, 55, 2028–2031 CrossRef CAS PubMed.
- A. Latyshev, A. Aseev, A. Krasilnikov and S. Stenin, Surf. Sci., 1989, 213, 157–169 CrossRef CAS.
- B. S. Swartzentruber, N. Kitamura, M. G. Lagally and M. B. Webb, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13432–13441 CrossRef CAS PubMed.
- A. Baski, S. Erwin and L. Whitman, Surf. Sci., 1997, 392, 69–85 CrossRef CAS.
- J.-L. Lin, D. Y. Petrovykh, J. Viernow, F. K. Men, D. J. Seo and F. J. Himpsel, J. Appl. Phys., 1998, 84, 255–260 CrossRef CAS.
- A. Paszuk, O. Supplie, M. Nandy, S. Brückner, A. Dobrich, P. Kleinschmidt, B. Kim, Y. Nakano, M. Sugiyama and T. Hannappel, Appl. Surf. Sci., 2018, 462, 1002–1007 CrossRef CAS.
- D. J. Chadi, J. Vac. Sci. Technol., A, 1987, 5, 834–837 CrossRef CAS.
- T. W. Poon, S. Yip, P. S. Ho and F. F. Abraham, Phys. Rev. Lett., 1990, 65, 2161–2164 CrossRef CAS PubMed.
- J. A. Venables, Surf. Sci., 1994, 299–300, 798–817 CrossRef CAS.
- Q.-M. Zhang, C. Roland, P. Bogusławski and J. Bernholc, Phys. Rev. Lett., 1995, 75, 101–104 CrossRef CAS PubMed.
- S. Jeong and A. Oshiyama, Phys. Rev. Lett., 1998, 81, 5366–5369 CrossRef CAS.
- L. Liu and J. Edgar, Mater. Sci. Eng., R, 2002, 37, 61–127 CrossRef.
- H. Amano, N. Sawaki, I. Akasaki and Y. Toyoda, Appl. Phys. Lett., 1986, 48, 353–355 CrossRef CAS.
- S. Nakamura, Y. Harada and M. Seno, Appl. Phys. Lett., 1991, 58, 2021–2023 CrossRef CAS.
- D. Schiavon, E. Litwin-Staszewska, R. Jakieła, S. Grzanka and P. Perlin, Materials, 2021, 14, 1–9 Search PubMed.
- B. Heying, E. J. Tarsa, C. R. Elsass, P. Fini, S. P. DenBaars and J. S. Speck, J. Appl. Phys., 1999, 85, 6470–6476 CrossRef CAS.
- C. Adelmann, J. Brault, D. Jalabert, P. Gentile, H. Mariette, G. Mula and B. Daudin, J. Appl. Phys., 2002, 91, 9638–9645 CrossRef CAS.
- X.-Q. Shen, M. Shimizu and H. Okumura, Jpn. J. Appl. Phys., 2003, 42, L1293 CrossRef CAS.
- S. Vézian, F. Natali, F. Semond and J. Massies, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 125329 CrossRef.
- G. Koblmueller, J. Brown, R. Averbeck, H. Riechert, P. Pongratz and J. S. Speck, Jpn. J. Appl. Phys., 2005, 44, L906 CrossRef.
- A. L. Corrion, F. Wu and J. S. Speck, J. Appl. Phys., 2012, 112, 054903 CrossRef.
- N. A. Kaufmann, L. Lahourcade, B. Hourahine, D. Martin and N. Grandjean, J. Cryst. Growth, 2016, 433, 36–42 CrossRef CAS.
- A. Kimura, N. Futagawa, A. Usui and M. Mizuta, J. Cryst. Growth, 2001, 229, 53–57 CrossRef CAS.
- I. Bryan, Z. Bryan, S. Mita, A. Rice, J. Tweedie, R. Collazo and Z. Sitar, J. Cryst. Growth, 2016, 438, 81–89 CrossRef CAS.
- K. Bellmann, U. W. Pohl, C. Kuhn, T. Wernicke and M. Kneissl, J. Cryst. Growth, 2017, 478, 187–192 CrossRef CAS.
- K. Sato, S. Yasue, K. Yamada, S. Tanaka, T. Omori, S. Ishizuka, S. Teramura, Y. Ogino, S. Iwayama, H. Miyake, M. Iwaya, T. Takeuchi, S. Kamiyama and I. Akasaki, Appl. Phys. Express, 2020, 13, 031004 CrossRef CAS.
- Z. Zhang, M. Kushimoto, A. Yoshikawa, K. Aoto, C. Sasaoka, L. J. Schowalter and H. Amano, Appl. Phys. Lett., 2022, 121, 222103 CrossRef CAS.
- K. Uesugi, S. Kuboya, K. Shojiki, S. Xiao, T. Nakamura, M. Kubo and H. Miyake, Appl. Phys. Express, 2022, 15, 055501 CrossRef CAS.
- W. Kohn and P. Vashishta, in General Density Functional Theory, ed. S. Lundqvist and N. H. March, Springer US, Boston, MA, 1983, pp. 79–147 Search PubMed.
- E. Kiely, R. Zwane, R. Fox, A. M. Reilly and S. Guerin, CrystEngComm, 2021, 23, 5697–5710 RSC.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef PubMed.
- Y. Yoshimoto and S. Tsuneyuki, Surf. Sci., 2002, 514, 200–205 CrossRef CAS.
- J. Yamauchi, Y. Yoshimoto and Y. Suwa, Appl. Phys. Lett., 2011, 99, 191901 CrossRef.
- J. Yamauchi, M. Tsukada, S. Watanabe and O. Sugino, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 5586 CrossRef CAS PubMed.
- H. Kageshima and K. Shiraishi, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 14985–14992 CrossRef CAS.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- T. Yamasaki, A. Kuroda, T. Kato, J. Nara, J. Koga, T. Uda, K. Minami and T. Ohno, Comput. Phys. Commun., 2019, 244, 264–276 CrossRef CAS.
- K. Shiraishi, J. Phys. Soc. Jpn., 1990, 59, 3455 CrossRef CAS.
- C. G. Van de Walle and J. Neugebauer, Phys. Rev. Lett., 2002, 88, 066103 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- T. Akiyama and T. Kawamura, Cryst. Growth Des., 2024, 24, 5906–5915 CrossRef CAS.
- M. D. Pashley, K. W. Haberern, W. Friday, J. M. Woodall and P. D. Kirchner, Phys. Rev. Lett., 1988, 60, 2176–2179 CrossRef CAS PubMed.
- M. D. Pashley, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 10481–10487 CrossRef CAS PubMed.
- P. J. Feibelman, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11118–11122 CrossRef CAS.
- T. Akiyama and T. Kawamura, Jpn. J. Appl. Phys., 2024, 63, 02SP71 CrossRef CAS.
- T. Akiyama and T. Kawamura, Phys. Status Solidi B, 2024, 261, 2300573 CrossRef CAS.
- J. E. Northrup, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045313 CrossRef.
- T. Akiyama, K. Nakamura and T. Ito, Appl. Phys. Lett., 2012, 100, 251601 CrossRef.
- T. Akiyama, D. Obara, K. Nakamura and T. Ito, Jpn. J. Appl. Phys., 2011, 51, 018001 CrossRef.
- Y. Kangawa, T. Akiyama, T. Ito, K. Shiraishi and T. Nakayama, Materials, 2013, 6, 3309–3360 CrossRef CAS PubMed.
- T. Akiyama, in Fundamental Properties of III-Nitride Surfaces, ed. T. Matsuoka and Y. Kangawa, Springer International Publishing, Cham, 2018, pp. 55–92 Search PubMed.
- T. Akiyama, Y. Seta, K. Nakamura and T. Ito, Phys. Rev. Mater., 2019, 3, 023401 CrossRef CAS.
- P. Kempisty and Y. Kangawa, Phys. Rev. B, 2019, 100, 085304 CrossRef CAS.
- R. M. Feenstra, J. E. Northrup and J. Neugebauer, MRS Internet J. Nitride Semicond. Res., 2020, 7, 3 CrossRef.
- D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, J. Phys. Chem. Ref. Data, 1982, 11(Supplement No. 2), 129–131 Search PubMed.
- Y. Kangawa, T. Ito, A. Taguchi, K. Shiraishi and T. Ohachi, Surf. Sci., 2001, 493, 178–181 CrossRef CAS.
- Y. Kangawa, T. Ito, Y. Hiraoka, A. Taguchi, K. Shiraishi and T. Ohachi, Surf. Sci., 2002, 507–510, 285–289 CrossRef CAS.
- A. Munkholm, G. B. Stephenson, J. A. Eastman, C. Thompson, P. Fini, J. S. Speck, O. Auciello, P. H. Fuoss and S. P. DenBaars, Phys. Rev. Lett., 1999, 83, 741–744 CrossRef CAS.
- A. R. Smith, R. M. Feenstra, D. W. Greve, M. S. Shin, M. Skowronski, J. Neugebauer and J. E. Northrup, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 1998, 16, 2242–2249 CrossRef CAS.
- J. E. Northrup, J. Neugebauer, R. M. Feenstra and A. R. Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9932–9935 CrossRef CAS.
- D. Segev and C. G. Van de Walle, Surf. Sci., 2007, 601, L15–L18 CrossRef CAS.
- P. Kempisty, K. Kawka, A. Kusaba and Y. Kangawa, Materials, 2023, 16, 5982 CrossRef CAS PubMed.
- J. E. Northrup, R. Di Felice and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 13878–13883 CrossRef CAS.
- M. S. Miao, A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155319 CrossRef.
- P. Strak, K. Sakowski, P. Kempisty and S. Krukowski, J. Appl. Phys., 2015, 118, 095705 CrossRef.
- T. Ohka, T. Akiyama, A. M. Pradipto, K. Nakamura and T. Ito, Cryst. Growth Des., 2020, 20, 4358–4365 CrossRef CAS.
- N. A. Kaufmann, L. Lahourcade, B. Hourahine, D. Martin and N. Grandjean, J. Cryst. Growth, 2016, 433, 36–42 CrossRef CAS.
- G. Ehrlich and F. G. Hudda, J. Chem. Phys., 1966, 44, 1039–1049 CrossRef CAS.
- R. L. Schwoebel and E. J. Shipsey, J. Appl. Phys., 1966, 37, 3682–3686 CrossRef CAS.
- O. Pierre-Louis, M. R. D'Orsogna and T. L. Einstein, Phys. Rev. Lett., 1999, 82, 3661–3664 CrossRef CAS.
- M. Rusanen, I. T. Koponen, J. Heinonen and T. Ala-Nissila, Phys. Rev. Lett., 2001, 86, 5317–5320 CrossRef CAS PubMed.
- Y. Takemoto, T. Akiyama, K. Nakamura and T. Ito, e-J. Surf. Sci. Nanotechnol., 2015, 13, 239–243 CrossRef CAS.
- J. Neugebauer, T. K. Zywietz, M. Scheffler, J. E. Northrup, H. Chen and R. M. Feenstra, Phys. Rev. Lett., 2003, 90, 056101 CrossRef PubMed.
- V. Jindal and F. Shahedipour-Sandvik, J. Appl. Phys., 2009, 105, 084902 CrossRef.
- T. Akiyama, T. Ohka, K. Nagai and T. Ito, J. Cryst. Growth, 2021, 571, 126244 CrossRef CAS.
- M. A. Chabowska, H. Popova and M. A. Załuska-Kotur, Phys. Rev. B, 2025, 111, 155401 CrossRef CAS.
- M. Załuska-Kotur, H. Popova and V. Tonchev, Crystals, 2021, 11, 1135 CrossRef.
- M. A. Chabowska and M. A. Załuska-Kotur, ACS Omega, 2023, 8, 45779–45786 CrossRef CAS PubMed.
- M. A. M. Filho, W. Farmer, C. Hsiao, R. B. dos Santos, L. Hultman, J. Birch, K. Ankit and G. K. Gueorguiev, Cryst. Growth Des., 2024, 24, 4717–4727 CrossRef CAS PubMed.
- K. M. Bui, K. Shiraishi and A. Oshiyama, Appl. Surf. Sci., 2021, 557, 149542 CrossRef CAS.
- K. My Bui, K. Shiraishi and A. Oshiyama, Appl. Surf. Sci., 2023, 613, 155840 CrossRef CAS.
- F. Imoto, J.-I. Iwata, M. Boero and A. Oshiyama, J. Phys. Chem. C, 2017, 121, 5041–5049 CrossRef CAS.
- A. Kusaba, Y. Kangawa, T. Kuboyama and A. Oshiyama, Appl. Phys. Lett., 2022, 120, 021602 CrossRef CAS.
- A. Kusaba, S. Nitta, K. Shiraishi, T. Kuboyama and Y. Kangawa, Appl. Phys. Lett., 2022, 121, 162101 CrossRef CAS.
- R. B. dos Santos, R. Rivelino, F. D. B. Mota, A. Kakanakova-Georgieva and G. K. Gueorguiev, Dalton Trans., 2015, 44, 3356–3366 RSC.
- Z. Ye, S. Nitta, Y. Honda, M. Pristovsek and H. Amano, Jpn. J. Appl. Phys., 2020, 59, 025511 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |
