Structural evolution and bonding features of electron deficient copper chalcogenides

Abstract

A group of otherwise covalent ternary copper sulfides and selenides demonstrate metallic p-type conductivity and Pauli paramagnetism, which distinguishes them from semiconducting counterparts built up from the same elements. This difference originates from the electron deficiency delocalized over structural units of copper chalcogenides. Considering the significant technological importance of chalcogenide materials, we surveyed ternary copper sulfides and selenides with alkali and alkaline earth cations to provide insights into their crystal structures and transport properties. We found that the compositions and structures of many chalcogenides can be rationalized based on two 2D nets with honeycomb and square lattice net topologies, respectively. We have also shown how simple electron-orbital counts can be applied to metallic chalcogenides with formally charge unbalanced compositions and demonstrated that these compounds are indeed electron deficient. In agreement with experimental data and DFT calculations, such phases demonstrate metallic p-type conductivity.

---

Introduction

Electron-deficient covalent materials combine directional bonding and low coordination numbers typical for covalent phases with metallic type conductivity. These materials can be described by the term “covalent metals” that summarizes their structural and physical properties. The “covalent” part reflects on the nature of chemical bonding and local structure (i.e., a small difference in electronegativities), while the “metal” highlights the low electrical resistivity of the materials due to electron delocalization and deficiency. One common example of a compound with metallic properties and electronic delocalization is graphite, which is built of layers of covalently bonded carbon atoms with trigonal planar coordination and exhibits strong electron delocalization due to half-occupied bands with p_z character. Although strong electron delocalization is usually associated with bonds between elements that have a small electronegativity difference, Δχ, some chalcogenide compounds exhibit a significant electron delocalization in the presence of a relatively large Δχ. One such example is copper sulfides and selenides, which structures show features of covalently bound materials (low coordination numbers for copper and well-defined geometry of the Cu coordination polyhedra), while demonstrating metallic conductivity.

Numerous natural and synthetic copper chalcogenides with metallic conductivity and Pauli paramagnetism have been known for decades.^1–4 Unlike graphite, materials such as covellite CuS, klockmannite CuSe, or umangite Cu₃Se₂, are p-type conductors. While the physical properties of many chalcogenides have been thoroughly studied, the theoretical basis of their physical behavior has been developed afterwards. The common trait of these phases is a deviation from the oxidation state formalism. It became widely acknowledged that the oxidation state of Cu in these peculiar phases is +1, while mixed +1/+2 states were ruled out,^5–8 resulting in the deficit of the formal negative charge in binary (CuS, CuSe, Cu₃Se₂, CuS₂, CuSe₂) and ternary (NaCu₄S₃, NaCu₄Se₃, NaCu₄S₄, NaCu₄Se₄) phases. This distinguishes copper from other metals, demonstrating truly mixed oxidation states in chalcogenides.^9,10 DFT study of covellite confirmed the presence of holes in the valence band and the absence of a bandgap in CuS (more precisely Cu₆S₆, as the structure is built on stacking of CuS and Cu₂S₂ layers and has S–S bonds), and thus, the observed p-type metallic conductivity aligned perfectly with the experiments.¹¹ The holes originate from a mismatch between the number of molecular orbitals and the number of available valence electrons to fill them. The same study showed a significant level of hybridization between copper and sulfur valence orbitals near the Fermi level, indicating the delocalization of holes over Cu₃S₃ building blocks in the covellite structure. The delocalization of holes over copper chalcogenide slabs (hereinafter, slab is defined as a layer made by connecting the simplest layers) suggests slightly higher positive charges on both copper and chalcogenide atoms (in other words, more positive on copper, less negative on sulfur), which must not be confused with mixed valence on both copper and chalcogen atoms.¹² The same phenomenon was confirmed in the recently reported paramagnetic NaCu₄S₃ phase¹³ and a series of related electron deficient phases.^14–16

The unique electronic structure of covalent metals made them attractive for applications as a new class of catalyst for CO₂ conversion into value-added products.¹⁷ Apart from catalysis, metal chalcogenides were studied as prospective materials for a wide range of vital applications, including rechargeable batteries,^18–27 thermoelectric power generation,^28–35 heterogeneous photo- and electrocatalysis,^36–39 photovoltaics,^40,41 solar cells with unmatched performance,^42–46 radionuclides removal,⁴⁷ neuromorphic engineering,^48,49 cancer treatment,^50,51 and others.^52,53 Although most chalcogenide research focuses on the semiconductors, recent advances in understanding the electronic behavior of materials with an intermediate type of bonding challenged the traditional systematics of covalent/metallic/ionic bonding mechanisms.^54–56 This intermediate type of bonding, which has also been termed “metavalent”, is responsible for unconventional properties of materials such as GeTe, SnTe, and PbTe,^54–56 which have promising applications in thermoelectrics. Although these materials started attracting more interest, a detailed understanding of their electronic structures and crystal design principles is still missing.

The goal of this highlight is to illustrate electron deficiency in metallic covalent compounds by using the structural and electronic features of ternary copper sulfides and selenides with alkali and alkaline metals as an example. These materials are divided into two major groups: formally charge balanced and formally charge unbalanced (i.e. electron deficient). A common and most apparent indication of a potential chalcogenide covalent metal is the difficulty of assigning oxidation states in the composition using the common oxidation states formalism, which provides a starting point for their systematic analysis. Following a traditional crystallographic approach, we start with the local coordination of copper and chalcogenide atoms and consider building blocks in the structures to show how they can be arranged in more complex structures. While many hypothetical building unit stackings are possible, few of them have been realized in real materials, leaving this field awaiting the synthesis of many new compositions.

Synthesis of copper chalcogenides

Before discussing the electronic and structural properties of chalcogenide materials, we first briefly describe the synthetic methods for their preparation (Fig. 1). Ternary copper sulfides and selenides are very commonly synthesized by employing alkali polychalcogenide fluxes.⁵⁷ We use the term “flux” here to highlight the excess of polychalcogenide reagents compared to the stoichiometry of a product and the subsequent necessity of flux removal after reaction completion. Alkali polychalcogenide fluxes offer numerous advantages, including compositional versatility and low melting temperatures.^16,58–63 The major drawback of these compounds is high moisture sensitivity, as well as challenges associated with the tedious synthesis of these starting materials by reacting alkali metals with chalcogens in liquid ammonia. However, this disadvantage can be overcome by using metal chalcogenides (Na₂Q, K₂Q, etc., Q = S or Se) in combination with the respective chalcogens to generate polychalcogenide fluxes in situ. Copper can be introduced in the reaction in the elemental form or as a pre-made binary chalcogenide. Copper(II) oxide, used for the preparation of NaCu₄Se₄ phase is a rather unusual starting material.¹⁶ In most cases, the reagents are typically mixed in an inert atmosphere and sealed in a glass ampule (quartz or Pyrex, depending on reaction temperatures) under vacuum, then melted and slowly cooled for crystallization. To melt and react the starting materials, a wide temperature range of 350–1100 °C is employed.^16,58–63 Excess flux is removed by washing the reaction products with DI water and organic solvents, typically DMF. Some sulfides were synthesized using binary precursors combined with elemental sulfur in exact stoichiometric ratios to target certain compositions.^58,64,65 Overall, this approach employs the same apparatus as flux reactions (i.e., slow cooling of reactions in sealed tubes).

Fig. 1 Three main routes to the synthesis of copper chalcogenides.

Besides polychalcogenides, other sources of alkali cations, including carbonates, thiocyanates, and hydroxide–halide mixtures, can be employed to create fluxes. To avoid pressure buildup during the synthesis, reactions with carbonates are performed in open crucibles under an inert atmosphere.^14,66–71 Mixed alkali hydroxides-sodium iodide flux was successfully employed for the synthesis of charge unbalanced Na₃Cu₄Se₄ phase isostructural with K₃Cu₄Se₄.⁷² Such flux, however, is highly reactive and cannot be used for synthesis in a glass ampule or alumina crucible. Therefore, preparations of Na₃Cu₄Se₄ and some other phases were done in a glassy carbon boat under nitrogen flow in a tube furnace.⁷² Thiocyanate fluxes were used to prepare BaCu₂S₂ and CsCu₅S₃ phases in two-step processes.^73,74 Potassium thiocyanate, used for the synthesis of Ba phase, acted more like a solvent, as the resulting structure does not contain potassium. On the contrary, the synthesis of CsCu₅S₃ was assisted by cesium thiocyanate flux.

Although, in most cases reported so far, elemental starting materials are used as primary reagents, one can employ boron–chalcogen mixtures (BCM) to reduce oxides and form chalcogenide phases. This method is generally utilized for the synthesis of copper chalcogenides with elements that have high oxygen affinity and, thus, tend to oxidize in air. For example, NaCuUS₃ phase can be formed by reacting U₃O₈, Cu, Na₂CO₃, B, and S.⁷⁵ In this reaction, B binds oxygen in the system and S reacts with the metals, providing both metal chalcogenides to form the final phase and the polychalcogenide flux, NaS_n, to grow its single crystals. Similarly, the CsCu₄Q₃ phase has been prepared using BCM.⁷⁶ Unlike the previous report on the synthesis of CsCu₄S₃ phase, where the reaction was performed under an Ar atmosphere,⁷⁰ the BCM reaction was performed in a sealed silica tube. Alternatively, the CsCu₄Se₃ phase can be obtained by using a hydrothermal route, which is relatively less common for chalcogenides.⁷⁷ This phase formed in the reaction between ≈250 mg of a mixture of K₂Se₄, Cu, and CsCl in a sealed quartz ampoule with 0.5 ml of DI water at 120 and 170 °C.⁷⁷ These examples show interchangeability between the synthetic techniques. Additionally, new phases can be obtained by solid state postsynthetic modifications of the known phases. For example, a rare case of utilizing ternary sulfide as a starting material was the preparation of the CsCu₅S₃ phase via solid state reaction of the CsCu₄S₃ phase with extra copper.⁷⁸ Overall, rich variability of synthetic techniques offers a convenient playground for the synthesis of new copper chalcogenide phases with desired compositions and properties.

Naturally, the formation of solid solutions between isostructural sulfides and selenides can be assumed. As a recent report on this matter demonstrated, the mismatches of chalcogenide sizes and covalency result in the pronounced structural ordering in mixed chalcogenides.⁷⁹ This ordering was rationalized based on crystallographic data and hard–soft acid–base principles, which allows for the avoidance of costly DFT calculations. The results were confirmed experimentally, and the new KCuZrTe₂S ordered mixed anionic phase was prepared.

Copper chalcogenides building blocks and the electron count

In the structures of binary and ternary chalcogenides, copper atoms coordinate two to four Q atoms (Table 1), with the most common coordination numbers being 3 and 4, corresponding to trigonal planar and tetrahedral coordination, respectively (Fig. 2). By sharing Q atoms, CuQ_n units form discrete 0D ions, infinite 1D chains, 2D layers and slabs, or 3D frameworks. The reduction of structural dimensionality is commonly caused by additional cations, which divide copper chalcogenide units, and can be employed to decrease the thermal conductivity of materials.^80,81 Some structures of layered and quasi-layered chalcogenides can be described with two common 2D motifs. From the point of view of the structural topology, they are variations of honeycomb (hcb) and square lattice (sql) nets, with trigonally coordinated copper atoms predominantly forming basic hcb nets and tetrahedrally coordinated copper atoms – sql ones (Fig. 2). Both types of nets have the same CuQ stoichiometry of a basic single net; however, the formation of more complex structures through node connecting and sharing results in a variety of compositions in sulfides and selenides.

Table 1 Ternary copper chalcogenides with sql and hcb motifs in the structures

Composition	Orbital count	Electron count	Electron-orbital mismatch	Type	sql phases	hcb phases
A(CuQ)n, n = 1
A^+(CuQ)^−	18/2	17 + 1	0	Balanced	LiCuSe (ref. 82), NaCuSe (ref. 83)	KCuSe (ref. 83)
n = 2
A^+(Cu2Q2)^−	36/2	34 + 1	1	Unbalanced	KCu2Se2 (ref. 84)	—
A^2+(Cu2Q2)^2−	36/2	34 + 2	0	Balanced	t-BaCu2Q2 (ref. 73)	CaCu2S2 (ref. 85)
A^+(Cu3Q3)^−	54/2	51 + 1	2	Unbalanced	Likely unstable
A^2+(Cu3Q3)^2−	54/2	51 + 2	1	Unbalanced	—	—
n = 4
A^+(Cu4Q4)^−	72/2	68 + 1	3	Unbalanced	Likely unstable
A^2+(Cu4Q4)^2−	72/2	68 + 2	2	Unbalanced	Likely unstable
A^+(Cu4Q2(Q2))^−	70/2	68 + 1	1	Unbalanced	—	NaCu4Q4 (ref. 16 and 63)
A^+(Cu4Q3)^−	64/2	62 + 1	1	Unbalanced	ACu4Q3 (ref. 60, 71, 76 and 86)	NaCu4Q3 (ref. 13 and 15)
n = 6
A^+(Cu6Q4)^−	92/2	90 + 1	1	Unbalanced	—	NaCu6Se4 (ref. 61)

---

Fig. 2 (a) hcb copper selenide net with trigonal planar Cu coordination in KCuSe phase; (b) sql copper selenide net with tetrahedral Cu coordination in LiCuSe structure.

Basic single CuQ nets can be found in charge balanced A⁺CuSe phases (A⁺ = Li–K). The tetragonal structures of LiCuSe and NaCuSe phases are built of sql nets, whereas the hexagonal KCuSe is comprised of hcb nets (Fig. 2, Table 1). By doubling the basic structural units, one can derive the structures with [Cu₂Q₂]ⁿ⁻ stoichiometries. Depending on the counter cation (either alkali or alkaline earth metal), these compounds can represent either charge balanced (such as BaCu₂Q₂ series) or charge unbalanced compositions (for example, orthorhombic KCu₂Se₂ phase). Nevertheless, both examples feature isolated sql nets separated by the cations. Multiplying of the layers can also occur by connecting atoms between them and forming a slab. For example, the structure of charge balanced trigonal CaCu₂S₂ phase is built by connecting some nodes of two hcb nets to build Cu₂S₂²⁻ slabs (Fig. 3a–c). Interactions between two flat hcb layers change the local environment of both Cu and S atoms, leading to their distorted tetrahedral coordination environment. Ca atoms in this structure also have octahedral sulfur coordination and occupy the interlayer space. Two neighboring sql nets with common nodes form a Cu₄S₃⁻ slab in KCu₄S₃ phase (Fig. 3d–f).

Fig. 3 (a–c) Double hcb and (d–e) double sql slabs in the structures of charge-balanced CaCuS₂ and charge-unbalanced KCu₄S₃ phases, respectively.

The electron deficiency of copper chalcogenide phases can be easily calculated from the chemical composition and the knowledge about Q–Q bonds in the structure (Table 1). For a simple NaCuSe case, the total number of valence orbitals is given as a sum of five 3d orbitals from the Cu atoms, one 4s and three 4p orbitals from the Se atoms, resulting in a total of nine. In these orbital count calculations, we assume that Cu 4s and 4p orbitals have significantly higher energy and have only a marginal (yet, very important in some cases) contribution to the top of the valence band. For the electrons, each Cu atom provides 11 electrons, and each S atom offers six electrons, resulting in 17 electrons per (CuS) unit. For A⁺CuQ phases (A = Li–K), an additional electron is coming from the alkali metals, charge balancing the layers with one electron to result in nine orbitals with 18 electrons. Doubling the (CuS) units yields 18 orbitals with only 34 electrons, requiring an alkaline earth metal to charge balance it, as in BaCu₂Q₂. On the other hand, if only one alkali cation is balancing the layers in an A⁺Cu₂Q₂ composition, such as KCu₂Se₂, the layers are one electron short of the charge balanced state, resulting in a one-electron-deficient structure. Further increase in the number of stacking layers increases the electron deficiency. The copper chalcogenide phases reported to date exhibit a maximum of one electron deficiency per formula unit (or 0.5 electron per single CuS unit in NaCu₂S₂), allowing one to surmise that the structures with two or more electron deficiency sites per formula unit are unstable. Therefore, ternaries with A⁺Cu₃Q₃ stoichiometry have not been reported to date, with (CuQ)₃⁻ 2D units being likely unstable due to high electron deficiency, 2/3 electrons per CuS unit.

It is easy to see that the higher homologues of the (CuS)_n family should also be unstable. There are, however, ways to alleviate the electron deficiency in compositions with high copper content, by either forming dichalcogenide bonds or sharing atoms between layer units. A good example of the former is NaCu₄Q₄ compounds, which formulas can also be written as Na⁺[Cu₄Q₂(Q₂)]⁻. Forming a Q–Q bond effectively eliminates one orbital from the orbital count by shifting Q–Q antibonding state significantly above the Fermi level,¹³ resulting in 9 × 4 − 1 = 35 orbitals with 17 × 4 + 1 = 69 electrons. Such units are present in the NaCu₄Q₄ phases, which contain a slab of four hcb layers with a dichalcogenide bond connecting two inner ones. This dichalcogenide bond binds the layers into a double layer with a kagome dual net topology (Fig. 4, Table 1). The former approach to reducing orbital count achieves the stabilization of the structure by sharing atoms from different layers, typically a chalcogen atom. One common example is A⁺(Cu₄Q₃)⁻ and A²⁺(Cu₄Q₃)²⁻ compositions. In A⁺(Cu₄Q₃)⁻, 4 × 5 + 3 × 4 = 32 orbitals host 11 × 4 + 3 × 6 + 1 = 63 electrons, having a deficiency of one hole per formula unit. In the ACu₄Q₃ (A = K–Cs) series of charge unbalanced tetragonal phases, Cu₄Q₃⁻ slabs are formed by two sql nets with shared Q atoms. The slabs are separated by alkali cations in the structures. When a smaller Na⁺ cation occupies the A site, the resulting structure contains vertex-sharing hcb layers combined into Cu₄S₃⁻ slabs. Similar to the CaCu₂S₂ phase, the copper coordination number in the Cu₄S₃⁻ slabs is increased to four and the hcb layers are visibly corrugated. The way two inner hcb layers of a Cu₄S₃⁻ slab are connected also matches the topology of kagome dual net. Finally, the highest homologue reported so far has a NaCu₆Se₄ composition. In NaCu₆Se₄, two CuSe hcb nets are divided not by one but by two Cu₂Se double hcb, forming slabs with a Cu₆Se₄ composition. The formula unit contains 46 orbitals and 91 electrons, showing the same one hole per formula unit electron deficiency. To the best of our knowledge, no ternary phase built on more single and double hcb layers has been reported; however, a slab made of two single and three double layers can be found in the structure of Cu₉S₅ binary. Overall, shared atoms and dichalcogenide bonds are an efficient way to stabilize higher homologues of copper chalcogenide ternaries, enabling the formation of phases with lower hole concentration per Cu atom. Since higher homologues require using small A : Cu molar ratios, their synthesis may be challenging in the presence of commonly used polychalcogenide fluxes. Alternative synthetic routes using fluxes or solvents that dissolve the starting materials but do not incorporate into the final products are therefore required to stabilize those phases.

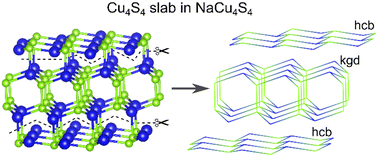Fig. 4 Cu₄S₄ slab in the NaCu₄S₄ structure made from four hcb layers. Two central layers are connected in kagome dual net motif (kgd).

The remaining ternary copper sulfide and selenide structures are not based on hcb and sql nets (Table 2), and their dimensionality varies from 0D to 3D. For example, unlike the A⁺(Cu₄Q₃)⁻ series, the charge balanced Na₂Cu₄S₃ phase, as well as both the orthorhombic primitive (oP) and base centered (oC) modifications of the BaCu₄S₃ phase, feature complex 2D (Na, oC Ba) and 3D (oP Ba) structures. Another example of isomerism among copper chalcogenide units appears in A₃⁺Cu₄S₄ phases (A⁺ = Na⁺ or K⁺) containing 1D Cu₄S₄ units with decreased dimensionality due to a high content of alkali cations. Besides oP BaCu₄S₃, anionic frameworks can be found in the structures of o-BaCu₂Q₂, ACu₅Q₃ (A = Na, Cs), and ACu₇S₄ (A = K, Rb) series with alkali and alkaline earth cations occupying channels of frameworks. 2D anionic slabs and layers are quite common among chalcogenides with various stoichiometries. Usually, alkali and alkaline cations separate 2D anionic units, however, in the recently reported K₃BaCu₇S₆ phase Ba²⁺ cations are inserted in Cu₇S₆ double layers, while K⁺ cations separate such layers.⁷² Interstitial sites in copper sulfides and selenides layers are usually vacant. However, in mixed anion ACu_4.2TeS₂ series of compounds isostructural to KCu₄S₃, there are additional copper atoms partially occupying the voids of the CuTeS₂ layers.⁹¹ The volume of the Voronoi polyhedron⁹² for the interstitial copper atom in the KCu_4.2TeS₂ structure is about 3.6 ų larger than the void in the KCu₄S₃ phases. This discrepancy volume is due to the larger size of the Te atom, which allows for the accommodation of additional Cu atoms. High content of cations per formula unit results in chalcogenides dimensionality reduction, while the presence of polychalcogenide anions facilitates the formation of 1D anionic chains: for example, CuQ₄ and CuS₆ chains contain Q₄²⁻ and S₆²⁻ anions, respectively (Table 2). Finally, the charge balanced Na₄Cu₂S₃ phase appears to be the only compound with discrete Cu₂S₃⁴⁻ 0D anions. As can be seen, the complexity of anionic units exceeds structures solely built on sql and hcb motifs in many chalcogenides. Nevertheless, the same principles of orbital and electron count can be applied to them (Table 2). Similar to phases built on CuQ fragments, the electron deficiency in phases without such fragments does not exceed one electron per formula unit.

Table 2 Ternary copper chalcogenides without sql and hcb motifs in the structures from highest to lowest Cu : Q ratio in formula unit

Composition	Orbitals count	Electron count	Electron-orbital count mismatch	Type	Dimensionality of CuxQy unit
Cu : Q = 1/6
CsCu((S6)^2−) (ref. 93)	58/2 − 10/2	47 + 1	0	Balanced	1D
Cu : Q = 1/4
A^+Cu(Q4^2−) (ref. 77, 94–96)	42/2 − 6/2	35 + 1	0	Balanced	1D
Cu : Q = 8/13
Ba4Cu8Se2(Se2^2−)4(Se3^4−) (ref. 97)	184/2 − 10/2	166 + 8	0	Balanced	2D
Na4Cu2S3 (ref. 64)	44/2	40 + 4	0	Balanced	0D
Cu : Q = 1
o-BaCu2Q2 (ref. 73)	36/2	34 + 2	0	Balanced	3D
KCuS (ref. 65)	18/2	17 +1	0	Balanced	1D
A3Cu4S4, A = Na, K (ref. 59 and 67)	72/2	68 + 3	1	Unbalanced	1D
Cu : Q = 7/6
K3BaCu7S6 (ref. 72)	118/2	113 + 5	0	Balanced	2D
Cu : Q = 6/5
Na7Cu12S10 (ref. 58)	200/2	192 + 7	1	Unbalanced	1D
Cu : Q = 5/4
Cs2Cu5Se4 (ref. 69)	82/2	79 + 2	1	Unbalanced	2D
Cu : Q = 4/3
BaCu4S3 (ref. 98), Na2Cu4S3 (ref. 99)	64/2	62 + 2	0	Balanced	3D (Ba), 2D (Na)
A3Cu8Q6, A = K–Cs (ref. 62, 66 and 68)	128/2	124 + 3	1	Unbalanced	2D
ACu3Q2, A = K–Cs (ref. 70 and 100–102)	46/2	45 + 1	0	Balanced	2D
Cu : Q = 5/3
ACu5Q3, A = Na, Cs (ref. 78 and 87–90)	74/2	73 + 1	0	Balanced	3D and 2D
Cu : Q = 7/4
ACu7S4, A = K, Rb (ref. 103)	102/2	101 + 1	0	Balanced	3D

---

Electronic structures of copper chalcogenides

DFT calculations and physical properties measurements of the copper chalcogenide phases can provide a more nuanced view on the electron deficiency than that derived from simple electron count. X-ray photoelectron spectroscopy, bond valence method, and structural data for a series of chalcogenides showed a +1 oxidation state for copper atoms exclusively, implying the formal oxidation states above −2 for chalcogen atoms.^{5–7,104–106} This evidence suggests the electron deficit being distributed over chalcogen np valence orbitals, resulting in the presence of holes on the chalcogenide atoms and ultimately in the metallic p-type conductivity. More detailed electronic structure calculations, however, show that the holes are distributed over bands with Cu 3d and S 3p character, indicating that the positive charge is distributed over both Cu⁺ and S²⁻ ions. For example, Fig. 5 shows the results of DFT calculations of electronic band structure and densities of states (DOS) for CuS,¹¹ NaCu₄S₃,¹³ NaCu₄S₄,¹³ and NaCu₄Se₄ (ref. 16) phases.

Fig. 5 Electronic band structure and DOS for (a and b) CuS, (c) NaCu₄S₃, (d) NaCu₄S₄, and (e) NaCu₄Se₄ phases. Adapted with permission from ref. 11, 13 and 16. Copyright: American Chemical Society.

DFT calculations show crucial common features of all four phases under consideration: first, the upper bands in the band structure cross the Fermi level in the proximity of the Γ point. This accounts for the metallic properties of the chalcogenides and agrees with the experimental data on electrical conductivity and magnetism. Second, the dispersion in the upper bands significantly depends on the direction. Bands contributed by Cu 3d_x²–y², 3d_xy, and S 3p_x, 3p_y orbitals are highly dispersed in directions parallel to Cu_xS_y slabs. This agrees with the structural data, as orbitals forming these bands participate in the copper–chalcogen bonding within the Cu_xS_y slabs. On the contrary, bands with predominant contributions from Cu 3d_xz and 3d_yz orbitals are weakly dispersed in all directions, as the corresponding orbitals do not participate in the bonding. Notable differences in the band structures of CuS,⁹ NaCu₄S₃,¹¹ NaCu₄S₄,¹¹ and NaCu₄Se₄ (ref. 14) phases are observed in the direction perpendicular to the slabs. Cu 3d_z² and Q np_z orbitals are oriented in this direction. In NaCu₄S₃, the overlap of these orbitals results in the bands crossing the Fermi level and their dispersion in the c direction in the crystal structure. In CuS, NaCu₄S₄ and NaCu₄Se₄ Q–Q bonds form, and the overlap of np_z orbitals significantly surpasses the overlap of 3d_z² and np_z orbitals. The resulting antibonding band has much higher energy and lies entirely above the Fermi level. DFT calculations confirm strong covalency of the Cu–Q bonds and the metallic nature of the electron deficient chalcogenides. It is important to note that this view agrees well with the XPS results, which only show that Cu atoms in a selected structure have the same oxidation state, which is different from the +2 oxidation state. Having a slight hole delocalized over Cu 3d orbitals only marginally increases the formal charge on Cu atoms.

Conclusions

Ternary copper sulfides and selenides can be divided into two broad groups, charge-balanced and charge unbalanced compounds. The combination of metallic p-type conductivities and covalent bonding makes charge unbalanced phases “covalent metals”. While the compositions of new phases vary significantly, the same square lattice and honeycomb 2D topological motifs persist in the structures of many layered and quasi-layered copper chalcogenides. The metallic nature of charge-unbalanced compounds originates from the presence of holes on the bands with 3d Cu and 3p S character, indicating hole distribution between them. Carrier concentration in the electron deficient phases can be estimated with a simple vacancy count approach, which shows good agreement with the experimental data. Since copper chalcogenides show a significant variability in their compositions, one can expect that more phases can be discovered when using a reaction mixture with an alkali metal deficit, leading to homologous series with higher Cu content. To date, no phases with Cu₃Q₃ stoichiometry of copper chalcogenide units have been reported. While Cu₃Q₃⁻ slabs are likely unstable due to high electron deficiency, the formation of Cu₃Q₃²⁻ units in the reactions with alkaline earth metals is worth investigating. Overall, electron count can be used to specifically target either metallic or semiconducting phases in the synthesis based on the charge balance. Moreover, conversion of p-type metal into a semiconductor can be done with compositional tuning, as it was demonstrated by charge unbalanced CsCu₄S₃ phase transition to charge balanced CsCu₅S₃.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Author contributions

Sergei A. Novikov: investigation, methodology, validation, writing – original draft, writing – review & editing; James Casey: writing – original draft, writing – review & editing; Hope A. Long: writing – original draft, writing – review & editing; Vladislav V. Klepov: conceptualization, funding acquisition, supervision, investigation, methodology, validation, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts of interest to report.

Acknowledgements

This work was supported by the University of Georgia Department of Chemistry, Franklin College of Arts and Sciences, and the Office of Provost.

References

1. K. Okamoto, S. Kawai and R. Kiriyama, Jpn. J. Appl. Phys., 1969, 8, 718.
2. F. Gautier, G. Krill, P. Panissod and C. Robert, J. Phys. C: Solid State Phys., 1974, 7, L170.
3. T. Kanashiro, T. Ohno, M. Satoh, K. Okamoto, A. Kojima and F. Akao, Solid State Ionics, 1981, 3–4, 327–330.
4. R. Berger and C. F. Van Bruggen, J. Less-Common Met., 1984, 99, 113–123.
5. J. C. W. Folmer and F. Jellinek, J. Less-Common Met., 1980, 76, 153–162.
6. G. van der Laan, R. A. D. Pattrick, C. M. B. Henderson and D. J. Vaughan, J. Phys. Chem. Solids, 1992, 53, 1185–1190.
7. S. W. Goh, A. N. Buckley and R. N. Lamb, Miner. Eng., 2006, 19, 204–208.
8. B. Raveau, Phys. C, 2023, 611, 1354295.
9. A. Mesbah and J. A. Ibers, J. Solid State Chem., 2013, 199, 253–257.
10. A. Mesbah, J. Prakash, J. C. Beard, E. A. Pozzi, M. S. Tarasenko, S. Lebègue, C. D. Malliakas, R. P. Van Duyne and J. A. Ibers, Inorg. Chem., 2015, 54, 2851–2857.
11. S. Conejeros, I. de P. R. Moreira, P. Alemany and E. Canadell, Inorg. Chem., 2014, 53, 12402–12406.
12. V. A. Starodub, Russ. Chem. Rev., 1999, 68, 801–820.
13. S. A. Novikov, J. Casey, H. A. Long, J. C. Bledsoe, J. J. Locklin and V. V. Klepov, Cryst. Growth Des., 2023, 23, 7243–7251.
14. Z. Peplinski, D. B. Brown, T. Watt, W. E. Hatfield and P. Day, Inorg. Chem., 1982, 21, 1752–1755.
15. M. Sturza, D. E. Bugaris, C. D. Malliakas, F. Han, D. Y. Chung and M. G. Kanatzidis, Inorg. Chem., 2016, 55, 4884–4890.
16. H. Chen, J. N. B. Rodrigues, A. J. E. Rettie, T.-B. Song, D. G. Chica, X. Su, J.-K. Bao, D. Y. Chung, W.-K. Kwok, L. K. Wagner and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 635–642.
17. H. Shin, Y. Ha and H. Kim, J. Phys. Chem. Lett., 2016, 7, 4124–4129.
18. E. Levi, G. Gershinsky, D. Aurbach, O. Isnard and G. Ceder, Chem. Mater., 2009, 21, 1390–1399.
19. E. Levi, M. D. Levi, O. Chasid and D. Aurbach, J. Electroceram., 2009, 22, 13–19.
20. H. S. Kim, T. S. Arthur, G. D. Allred, J. Zajicek, J. G. Newman, A. E. Rodnyansky, A. G. Oliver, W. C. Boggess and J. Muldoon, Nat. Commun., 2011, 2, 427.
21. A. Manthiram, Y. Fu and Y.-S. Su, Acc. Chem. Res., 2013, 46, 1125–1134.
22. Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627–631.
23. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 1–7.
24. P. Canepa, G. Sai Gautam, D. C. Hannah, R. Malik, M. Liu, K. G. Gallagher, K. A. Persson and G. Ceder, Chem. Rev., 2017, 117, 4287–4341.
25. Z. Hu, Q. Liu, S.-L. Chou and S.-X. Dou, Adv. Mater., 2017, 29, 1700606.
26. M. D. Regulacio, D.-T. Nguyen, R. Horia and Z. W. Seh, Small, 2021, 17, 2007683.
27. C.-B. Chang and H.-Y. Tuan, Chem. – Asian J., 2022, 17, e202200170.
28. W. Liu, K. C. Lukas, K. McEnaney, S. Lee, Q. Zhang, C. P. Opeil, G. Chen and Z. Ren, Energy Environ. Sci., 2013, 6, 552–560.
29. M. Ohta, D. Y. Chung, M. Kunii and M. G. Kanatzidis, J. Mater. Chem. A, 2014, 2, 20048–20058.
30. M. M. Kubenova, K. A. Kuterbekov, M. K. Balapanov, R. K. Ishembetov, A. M. Kabyshev and K. Z. Bekmyrza, Nanomaterials, 2021, 11, 2238.
31. G. Dennler, R. Chmielowski, S. Jacob, F. Capet, P. Roussel, S. Zastrow, K. Nielsch, I. Opahle and G. K. H. Madsen, Adv. Energy Mater., 2014, 4, 1301581.
32. M. M. Alsalama, H. Hamoudi, A. Abdala, Z. K. Ghouri and K. M. Youssef, Rev. Adv. Mater. Sci., 2020, 59, 371–398.
33. R. Mulla and M. H. K. Rabinal, Energy Technol., 2019, 7, 1800850.
34. Z. Yang, E. Smith, Y.-C. Tseng, K. Ciesielski, S. Novikov, T. Kalab, Y. Huang, E. Toberer and Y. Mozharivskyj, J. Mater. Chem. A, 2024, 12, 5357–5365.
35. Y. Shi, C. Sturm and H. Kleinke, J. Solid State Chem., 2019, 270, 273–279.
36. C. G. Morales-Guio, L.-A. Stern and X. Hu, Chem. Soc. Rev., 2014, 43, 6555–6569.
37. J. N. Hausmann and P. W. Menezes, Curr. Opin. Electrochem., 2022, 34, 100991.
38. K. Sharma, A. Kumar, T. Ahamad, Q. V. Le, P. Raizada, A. Singh, L. H. Nguyen, S. Thakur, V.-H. Nguyen and P. Singh, J. Mater. Sci. Technol., 2023, 152, 50–64.
39. Z. Chen, W. Wei and B.-J. Ni, Curr. Opin. Electrochem., 2022, 31, 100888.
40. A. Dey, J. Ye, A. De, E. Debroye, S. K. Ha, E. Bladt, A. S. Kshirsagar, Z. Wang, J. Yin, Y. Wang, L. N. Quan, F. Yan, M. Gao, X. Li, J. Shamsi, T. Debnath, M. Cao, M. A. Scheel, S. Kumar, J. A. Steele, M. Gerhard, L. Chouhan, K. Xu, X. Wu, Y. Li, Y. Zhang, A. Dutta, C. Han, I. Vincon, A. L. Rogach, A. Nag, A. Samanta, B. A. Korgel, C.-J. Shih, D. R. Gamelin, D. H. Son, H. Zeng, H. Zhong, H. Sun, H. V. Demir, I. G. Scheblykin, I. Mora-Seró, J. K. Stolarczyk, J. Z. Zhang, J. Feldmann, J. Hofkens, J. M. Luther, J. Pérez-Prieto, L. Li, L. Manna, M. I. Bodnarchuk, M. V. Kovalenko, M. B. J. Roeffaers, N. Pradhan, O. F. Mohammed, O. M. Bakr, P. Yang, P. Müller-Buschbaum, P. V. Kamat, Q. Bao, Q. Zhang, R. Krahne, R. E. Galian, S. D. Stranks, S. Bals, V. Biju, W. A. Tisdale, Y. Yan, R. L. Z. Hoye and L. Polavarapu, ACS Nano, 2021, 15, 10775–10981.
41. K. Srivastava, A. K. Ray, S. Yadav, M. Deepa and J. Prakash, New J. Chem., 2024, 48, 16869–16876.
42. P. Myagmarsereejid, M. Ingram, M. Batmunkh and Y. L. Zhong, Small, 2021, 17, 2100241.
43. R. S. Hall, D. Lamb and S. J. C. Irvine, Energy Sci. Eng., 2021, 9, 606–632.
44. X. Jin, Y. Fang, T. Salim, M. Feng, Z. Yuan, S. Hadke, T. C. Sum and L. H. Wong, Adv. Mater., 2021, 33, 2104346.
45. J. Kangsabanik, M. K. Svendsen, A. Taghizadeh, A. Crovetto and K. S. Thygesen, J. Am. Chem. Soc., 2022, 144, 19872–19883.
46. M. A. Scarpulla, B. McCandless, A. B. Phillips, Y. Yan, M. J. Heben, C. Wolden, G. Xiong, W. K. Metzger, D. Mao, D. Krasikov, I. Sankin, S. Grover, A. Munshi, W. Sampath, J. R. Sites, A. Bothwell, D. Albin, M. O. Reese, A. Romeo, M. Nardone, R. Klie, J. M. Walls, T. Fiducia, A. Abbas and S. M. Hayes, Sol. Energy Mater. Sol. Cells, 2023, 255, 112289.
47. S. Ma, L. Huang, L. Ma, Y. Shim, S. M. Islam, P. Wang, L.-D. Zhao, S. Wang, G. Sun, X. Yang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 3670–3677.
48. S. R. Bauers, M. B. Tellekamp, D. M. Roberts, B. Hammett, S. Lany, A. J. Ferguson, A. Zakutayev and S. U. Nanayakkara, Nanotechnology, 2021, 32, 372001.
49. K. C. Kwon, J. H. Baek, K. Hong, S. Y. Kim and H. W. Jang, Nano-Micro Lett., 2022, 14, 58.
50. F. Olawale, O. Oladimeji, M. Ariatti and M. Singh, J. Nanotechnol., 2022, 2022, 6176610.
51. M. Liu, Y. Liu, B. Gu, X. Wei, G. Xu, X. Wang, M. T. Swihart and K.-T. Yong, Chem. Soc. Rev., 2019, 48, 4950–4965.
52. T. Lu, S. Dong, C. Zhang, L. Zhang and G. Cui, Coord. Chem. Rev., 2017, 332, 75–99.
53. Y. Zhou, D. Wu, Y. Zhu, Y. Cho, Q. He, X. Yang, K. Herrera, Z. Chu, Y. Han, M. C. Downer, H. Peng and K. Lai, Nano Lett., 2017, 17, 5508–5513.
54. M. Wuttig, V. L. Deringer, X. Gonze, C. Bichara and J.-Y. Raty, Adv. Mater., 2018, 30, 1803777.
55. J.-Y. Raty, M. Schumacher, P. Golub, V. L. Deringer, C. Gatti and M. Wuttig, Adv. Mater., 2019, 31, 1806280.
56. M. Wuttig, C.-F. Schön, J. Lötfering, P. Golub, C. Gatti and J.-Y. Raty, Adv. Mater., 2023, 35, 2208485.
57. M. G. Kanatzidis, Chem. Mater., 1990, 2, 353–363.
58. K. O. Klepp, M. Sing and H. Boller, J. Alloys Compd., 1993, 198, 25–30.
59. D. P. Shoemaker, Y.-J. Hu, D. Y. Chung, G. J. Halder, P. J. Chupas, L. Soderholm, J. F. Mitchell and M. G. Kanatzidis, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10922–10927.
60. P. Stoll, C. Näther, I. Jeß and W. Bensch, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, 286–288.
61. M. Sturza, C. D. Malliakas, D. E. Bugaris, F. Han, D. Y. Chung and M. G. Kanatzidis, Inorg. Chem., 2014, 53, 12191–12198.
62. C. Näther, D. Röhnert and W. Bensch, Eur. J. Solid State Inorg. Chem., 1998, 35, 565–577.
63. X. Zhang, M. G. Kanatzidis, T. Hogan and C. R. Kannewurf, J. Am. Chem. Soc., 1996, 118, 693–694.
64. K. O. Klepp, M. Sing and H. Boller, J. Alloys Compd., 1992, 184, 265–273.
65. G. Savelsberg and H. Schäfer, Z. Naturforsch., B: J. Chem. Sci., 1978, 33, 711–713.
66. C. Burschka, Z. Naturforsch., B: J. Chem. Sci., 1979, 34, 675–677.
67. C. Burschka, Z. Naturforsch., B: J. Chem. Sci., 1979, 34, 396–397.
68. H. Schils and W. Bronger, Z. Anorg. Allg. Chem., 1979, 456, 187–193.
69. W. Bronger and H. Schils, J. Less-Common Met., 1982, 83, 279–285.
70. C. H. Burschka, Z. Anorg. Allg. Chem., 1980, 463, 65–71.
71. W. Rüdorff, H. G. Schwarz and M. Walter, Z. Anorg. Allg. Chem., 1952, 269, 141–152.
72. X. Zhou, V. S. C. Kolluru, W. Xu, L. Wang, T. Chang, Y.-S. Chen, L. Yu, J. Wen, M. K. Y. Chan, D. Y. Chung and M. G. Kanatzidis, Nature, 2022, 612, 72–77.
73. J. Huster and W. Bronger, Z. Anorg. Allg. Chem., 1999, 625, 2033–2040.
74. J. Huster and W. Bronger, Z. Anorg. Allg. Chem., 2001, 627, 1395–1400.
75. A. A. Berseneva, V. V. Klepov, K. Pal, K. Seeley, D. Koury, J. Schaeperkoetter, J. T. Wright, S. T. Misture, M. G. Kanatzidis, C. Wolverton, A. V. Gelis and H.-C. zur Loye, J. Am. Chem. Soc., 2022, 144, 13773–13786.
76. N. Ma, F. Li, J.-G. Li, X. Liu, D.-B. Zhang, Y.-Y. Li, L. Chen and L.-M. Wu, J. Am. Chem. Soc., 2021, 143, 18490–18501.
77. N. S. Hartig, P. K. Dorhout and S. M. Miller, J. Solid State Chem., 1994, 113, 88–93.
78. N. Ma, F. Jia, L. Xiong, L. Chen, Y.-Y. Li and L.-M. Wu, Inorg. Chem., 2019, 58, 1371–1376.
79. A. Tassanov, H. Lee, Y. Xia and J. M. Hodges, J. Am. Chem. Soc., 2024, 146, 32627–32639.
80. A. J. E. Rettie, C. D. Malliakas, A. S. Botana, J. M. Hodges, F. Han, R. Huang, D. Y. Chung and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 9193–9202.
81. E. Muzaffar, S. Azam, A. I. Bashir and M. Irfan, Mater. Sci. Eng., B, 2023, 292, 116448.
82. M. Valldor, D. Mikhailova, L. Giebeler, K. T. Lai, L. Spillecke, H.-J. Grafe and B. Büchner, Inorg. Chem., 2018, 57, 7201–7207.
83. G. Savelsberg, Z. Naturforsch., B: J. Chem. Sci., 1978, 33, 370–373.
84. O. Tiedje, E. E. Krasovskii, W. Schattke, P. Stoll, C. Näther and W. Bensch, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 134105.
85. A. P. Purdy, Chem. Mater., 1998, 10, 692–694.
86. D. B. Brown, J. A. Zubieta, P. A. Vella, J. T. Wrobleski, T. Watt, W. E. Hatfield and P. Day, Inorg. Chem., 1980, 19, 1945–1950.
87. H. Effenberger and F. Pertlik, Monatsh. Chem., 1985, 116, 921–926.
88. F. Li, X. Liu, N. Ma, Y.-C. Yang, J.-P. Yin, L. Chen and L.-M. Wu, J. Am. Chem. Soc., 2023, 145, 14981–14993.
89. Z. Xia, H. Fang, X. Zhang, M. S. Molokeev, R. Gautier, Q. Yan, S.-H. Wei and K. R. Poeppelmeier, Chem. Mater., 2018, 30, 1121–1126.
90. N. Ma, Y.-Y. Li, L. Chen and L.-M. Wu, J. Am. Chem. Soc., 2020, 142, 5293–5303.
91. J. M. Hodges, Y. Xia, C. D. Malliakas, T. J. Slade, C. Wolverton and M. G. Kanatzidis, Chem. Mater., 2020, 32, 10146–10154.
92. V. A. Blatov, A. P. Shevchenko and V. N. Serezhkin, J. Appl. Crystallogr., 2000, 33, 1193–1193.
93. T. J. McCarthy, X. Zhang and M. G. Kanatzidis, Inorg. Chem., 1993, 32, 2944–2948.
94. P. K. Dorhout, C. C. Raymond and S. M. Miller, Z. Kristallogr., 1995, 210, 776–776.
95. K. O. Klepp and C. Weithaler, Z. Naturforsch., B: J. Chem. Sci., 1995, 50, 1791–1793.
96. M. G. Kanatzidis and Y. Park, J. Am. Chem. Soc., 1989, 111, 3767–3769.
97. S. Maier, O. Perez, D. Pelloquin, D. Berthebaud, S. Hébert and F. Gascoin, Inorg. Chem., 2017, 56, 9209–9218.
98. J. E. Iglesias, K. E. Pachali and H. Steinfink, Mater. Res. Bull., 1972, 7, 1247–1258.
99. G. Savelsberg and H. Schäfer, Mater. Res. Bull., 1981, 16, 1291–1297.
100. C. Burschka and W. Bronger, Z. Naturforsch., B: J. Chem. Sci., 1977, 32, 11–14.
101. K. O. Klepp and M. Sing, Z. Kristallogr. - New Cryst. Struct., 2002, 217, 474–474.
102. A. J. E. Rettie, M. Sturza, C. D. Malliakas, A. S. Botana, D. Y. Chung and M. G. Kanatzidis, Chem. Mater., 2017, 29, 6114–6121.
103. T. Ohtani, J. Ogura, H. Yoshihara and Y. Yokota, J. Solid State Chem., 1995, 115, 379–389.
104. C. D. Malliakas, J. Yao, D. M. Wells, G. B. Jin, S. Skanthakumar, E. S. Choi, M. Balasubramanian, L. Soderholm, D. E. Ellis, M. G. Kanatzidis and J. A. Ibers, Inorg. Chem., 2012, 51, 6153–6163.
105. A. N. Buckley, W. M. Skinner, S. L. Harmer, A. Pring, R. N. Lamb, L.-J. Fan and Y. Yang, Can. J. Chem., 2007, 85, 767–781.
106. Y. Moëlo, A. F. Popa and V. Dubost, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2022, 78, 627–636.

---