DOI:
10.1039/D5CE00160A
(Paper)
CrystEngComm, 2025,
27, 4568-4581
Thermodynamics of the condensation of the Si8O20(SnMe3)8 building block with M–X (M = B, Al, Si, P, Ti, V, Zn, Sn, Sb, X = Cl, Me, Et) precursors by DFT-D3 calculations†
Received
14th February 2025
, Accepted 28th May 2025
First published on 29th May 2025
Abstract
Synthesis of porous metallosilicate materials from siloxane oligomers is a promising approach for constructing well-defined structures at a molecular level. Here, we use quantum chemistry DFT methods and demonstrate a computationally cheap method for screening potential precursors for synthesizing porous metallosilicates. We estimate the thermodynamic parameters of condensation reactions of the octakis(trimethyltin)spherosilicate Si8O20(SnMe3)8 (CUBE) building block with metal chlorides and alkyl metals. These reactions represent the initial steps in the non-hydrolytic synthesis of metallosilicate gels containing potentially uniform single-site metal centers. Our main emphasis was on the spontaneity and irreversibility of the condensation and the computational screening of potential metal center sources. The precursors previously reported in successful condensations with CUBE, such as AlCl3, [AlCl4]−, Si–Cl compounds, PCl3, TiCl4, and VOCl3, are shown to undergo sufficiently irreversible reactions, as are the untested precursors BCl3, VCl4, and POCl3. Interestingly, AlMe3 proves to be twice as exoergic as AlCl3. The first chloride in Cp2TiCl2 reacts readily, but the second may be partially reversible. SbCl3 and Ph3SbCl2 are borderline cases, and the reversibility of their condensations might pose a problem. SnCl4 was found unsuitable as a precursor to stannosilicates. It should be possible to prepare zincosilicates from ZnEt2, but not from ZnCl2, as the affinity of Zn for Cl− is so high that in the presence of a source of Cl−, zincosilicate structures will dissolve back to CUBE and ZnCl2. The oxophilicity of the metal in the precursor is the main factor in the driving force for the condensation with CUBE. Alkyl metals and lighter elements are more prone to the reaction than the corresponding metal chlorides and heavier analogs. The propensity of [SnMe3]+ to bind to Cl− in preference to CUBE has a supporting effect. At low temperatures, the condensation is slightly disfavored, while at the experimentally used temperature of 100 °C, this process contributes over 20 kJ mol−1 of the additional driving force and helps to complete the condensation. The reliability of B3LYP-D3 and PBE0-D3, together with the CBS extrapolation scheme, is also evaluated in calculations.
Introduction
Porous metallosilicates represent a diverse class of chemically simple yet powerful heterogeneous catalysts – partially hollow extended networks generally composed of [SiO4] and [MOx] (M = metal) polyhedra.1 The potentially omnidirectional bonding between the [SiO4] tetrahedra provides a chemically and thermally stable backbone that supports porosity and can withstand harsh reaction environments. The silicate networks can accommodate most chemical elements that can form stable bonds to oxygen, with the general trend of enhancing the electrophilic character of the resulting metal center, attributable to the negative inductive effect of the oxygen. The applicability in catalysis and viable synthesis routes depends entirely on the target metal, its oxidation state, its chemical environment, and the required porosity of the final material.
A spherosilicate consisting of a double 4-ring core (D4R, Si8O20) with every vertex functionalized with a suitable reactive group has attracted significant attention as a molecular building block for constructing a whole array of nanoporous materials.2–5 By direct crosslinking of these cubic units into 3-dimensional infinite networks, microporous materials have been obtained, while mesoporous systems can be prepared with templates or long-alkyl chain substituents.
Highly promising possibilities arise in the controlled synthesis of single-site catalysts from the well-behaved condensation chemistry of the octakis(trimethyltin)spherosilicate building block Si8O20(SnMe3)8 (CUBE), first reported by Feher and Weller.6,7 The trimethyltin functionalization provides high solubility in non-polar solvents and supports metathesis reactions with covalent d- and p-block element (M) chlorides and bromides as well as organometallic compounds, forming Me3SnCl, Me3SnBr, or Me3SnR as byproducts, respectively. Multiple silicate Si–O–M linkages are thus created by non-hydrolytic condensation, leading to the formation of gels. The metathesis is analogous to common proton-exchange reactions. However, due to the relatively low reactivity and weak coordinating nature of the [Me3SnOSi] moiety, it is highly compatible with other functional groups and ligands.
Increasingly more complex non-hydrolytic sol–gel schemes were reported by Ghosh et al.,8 Clark et al.,9 Lee et al.,10 Clark and Barnes,11 and Barnes et al.,12 utilizing TiCl4, Cp2TiCl2, ZrCl4, Cp2ZrCl2, VOCl3, WOCl4, and AlCl3 as metal sources and SiCl4, HSiCl3, MeSiCl3, and Me2SiCl2 as inert cross-linkers. This line of research has culminated in a flexible two-step, one-pot procedure (Fig. 1). The CUBE building block is first cross-linked by a limited amount of the metal precursor, providing ideal conditions for M–X group condensation, homogeneous incorporation of the metal sites, and structural relaxation. A true solution of oligomeric species is formed, which are then “knitted” together by further cross-linking with silyl chlorides to produce porous silicate matrices. The solvent and all reaction byproducts are then removed under vacuum to obtain pure materials. Subsequently, Styskalik et al.13 used the approach to prepare a series of porous Lewis acidic aluminosilicate matrices containing [R]+ [AlO4]− (R+ = lutidinium, NBu4+) and [L-AlO3] (L = pyridine, THF) sites starting from AlCl3 and its coordination compounds in THF. The method was improved by using longer hybrid silyl chlorides (ClMe2Si(CH2)nSiMe2Cl, where n = 1–3) for the final cross-linking. This resulted in increased average pore sizes and better diffusion properties, leading to superior activities in Lewis acid catalysis.
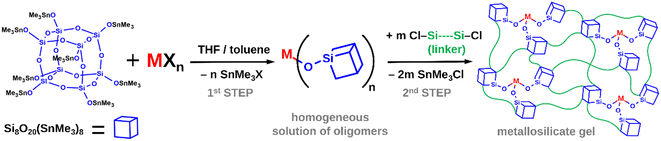 |
| | Fig. 1 General reaction scheme for the two-step one-pot synthesis of metallosilicate gels from CUBE. | |
Most recently, we used the first step of this procedure to prepare a series of Lewis acidic aluminosilicate oligomers starting from L-AlCl3 and L-AlMe3 compounds. We characterized the structure of the aluminosilicate sites by 27Al MQ/MAS NMR techniques and studied the conditions leading to single-site species.14
Since the first applications of CUBE to the synthesis of metallosilicate catalysts, it was presumed that the condensation reactions used to connect the metallosilicate networks are irreversible for all reported precursors. The validity of this assumption has far-reaching implications. The method of sequential additions assumes that the connections and structures formed in one cross-linking step remain unchanged during the next steps. Each subsequent cross-linking step only adds further connectivity through the residual –SnMe3 groups left at the CUBE vertices in the oligomeric structures. Under such conditions, no rearrangement or metal migration can occur, and the structures formed should be amorphous and purely statistical, allowing for the use of mean-field concepts, such as average connectivity and Vegard's law. Irreversibility should also result in better decoupling between the chemistries of the precursors used in the sequential cross-linking steps, and it would imply that the order of the steps strictly matters. This work aims to answer the question of reversibility for a broader spectrum of interesting metal site precursors using quantum chemistry DFT computational methods.
Computational methods
The input geometries were drawn and preoptimized by molecular mechanics in Avogadro 1.2.0 software.15 Further calculations were performed using the GAMESS 2019(R2) suite.16,17 The structures were optimized in delocalized internal coordinates18 by the B3LYP19,20 and PBE021,22 exchange–correlation functionals (DFT grid: 96 radial/302 angular points) with the correlation-consistent valence triple-ζ cc-pVTZ (default)23–25 and the augmented small-core pseudopotential-based aug-cc-pVTZ-PP (Sb, Sn) basis sets26,27 in vacuum. Grimme's empirical D3 dispersion correction with Becke–Johnson damping28–30 was used in all calculations. The following convergence criteria were used: 10−5 for the largest absolute change in the density matrix and 5·10−5 Hartree Bohr−1 for the largest component of the geometry gradient. Vibrational analyses with harmonic oscillator approximation were used to confirm the energy-minimum character of the obtained stationary point geometries and to calculate the thermodynamic corrections to the electronic energy at 0, 273.15, 298.15, and 373.15 K (ideal gas at 101.325 kPa and rigid rotor approximations). The structures were first optimized by B3LYP-D3, and the resulting geometries were used as inputs for the optimizations by PBE0-D3 to minimize the conformational variations between the two optimized geometries. Additional single-point energy calculations using the double- and quadruple-ζ cc-pVxZ + aug-cc-pVxZ-PP (Sn) (x = D, Q) basis sets were conducted with the corresponding method. The exponential complete basis set limit (CBS) extrapolation scheme developed by Halkier et al.31 was then used to obtain refined electronic energies (ECBS) with decreased effects of the basis set superposition error (BSSE) and the fitting parameters B and α according to eqn (1)–(3). The choice of temperatures was aimed to provide thermodynamic data (ΔH, ΔS, and ΔG) at two standard temperatures as well as a third set at a reasonable high-temperature limit (100 °C) for the practical use of the condensation reaction, given the thermal stability of CUBE (decomposes above ~120 °C). All the produced data is available in the ESI† (Tables S1–S46 for thermodynamic data by reaction; Tables S47 and S48 for the electronic energy and thermal corrections by structure; Tables S49–S57 for equilibrium geometries by structure).| |  | (1) |
| |  | (2) |
| |  | (3) |
Results and discussion
Reaction spontaneity
The reversibility of the condensation reaction of the Si8O20(SnMe3)8 building block (CUBE) with precursors of interest was characterized through the calculation of the Gibbs energy change for model reactions with truncated molecular representations of the polymeric products (metallosilicate networks). A single reactive group (corner) of the CUBE was modeled by either Me3SnOSiH3 (model A, reactions (1A)–(26A)) for all condensation steps with MXn precursors (x = 0,…, n–1) and by Me3SnOSi(OSiH3)3 (model B, reactions (1B)–(20B)) for the condensation of only the first X group (X = Cl, Me, Et).
This aimed to provide both precise thermodynamic data for the initial condensation reaction (the first substitution on the metal) and to get a sense of the level of precursor deactivation with subsequent condensation steps all the way to the completely condensed metallosilicate sites. Of course, this must be viewed as an approximation that reflects mainly the electronic effects on the central atom (metal) and excludes any steric repulsion between multiple connected CUBEs.
The driving force for the condensation reaction may be viewed as a sum of two contributions (positive or negative) – the exchange of the reactive group M–X for the silicate moiety M–O–Si on the metal (different for each precursor) and the exchange of the silicate moiety Sn–O–Si for Sn–X on the trimethyltin group (intrinsic driving force, common to all precursors). Reactions (26A) and (20B) model the latter process for precursors with Cl− as a leaving group to assess how much of the driving force (and more importantly, with what sign) comes intrinsically from the chemistry of the trimethyltin group.
As there is no sharp distinction between reversible and irreversible reactions, in the following discussion, as a rule of thumb, reactions with ΔG ≤ −30 kJ mol−1 shall be considered sufficiently irreversible to prevent any measurable extent of network equilibration over the reaction times of interest (≤1 week).
Reactions A.
| | |
py–BCl3−x(OSiH3)x + Me3SnOSiH3 → py–BCl2−x(OSiH3)1+x + SnMe3Cl (where: x = 0–2)
| (1A) |
| | |
py–AlMe3−x(OSiH3)x + Me3SnOSiH3 → py–AlMe2−x(OSiH3)1+x + SnMe4 (where: x = 0–2)
| (2A) |
| | |
py–AlMe3−x(OSiH3)x(THF) + Me3SnOSiH3 → py–AlMe2−x(OSiH3)1+x(THF) + SnMe4 (where: x = 0–2)
| (3A) |
| | |
py–AlCl3−x(OSiH3)x + Me3SnOSiH3 → py–AlCl2−x(OSiH3)1+x + SnMe3Cl (where: x = 0–2)
| (4A) |
| | |
py–AlCl3−x(OSiH3)x(THF) + Me3SnOSiH3 → py–AlCl2−x(OSiH3)1+x(THF) + SnMe3Cl (where: x = 0–2)
| (5A) |
| | |
[AlCl4−x(OSiH3)x]− + Me3SnOSiH3 → [AlCl3−x(OSiH3)1+x]– + SnMe3Cl (where: x = 0–3)
| (6A) |
| | |
SiCl4−x(OSiH3)x + Me3SnOSiH3 → SiCl3−x(OSiH3)1+x + SnMe3Cl (where: x = 0–3)
| (7A) |
| | |
Me3SiCl + Me3SnOSiH3 → Me3SiOSiH3 + SnMe3Cl
| (8A) |
| | |
PhMe2SiCl + Me3SnOSiH3 → PhMe2SiOSiH3 + SnMe3Cl
| (9A) |
| | |
PCl3−x(OSiH3)x + Me3SnOSiH3 → PCl2−x(OSiH3)1+x + SnMe3Cl (where: x = 0–2)
| (10A) |
| | |
POCl3−x(OSiH3)x + Me3SnOSiH3 → POCl2−x(OSiH3)1+x + SnMe3Cl (where: x = 0–2)
| (11A) |
| | |
TiCl4−x(OSiH3)x + Me3SnOSiH3 → TiCl3−x(OSiH3)1+x + SnMe3Cl (where: x = 0–3)
| (12A) |
| | |
Cp2TiCl2−x(OSiH3)x + Me3SnOSiH3 → Cp2TiCl1−x(OSiH3)1+x + SnMe3Cl (where: x = 0–1)
| (13A) |
| | |
VCl4−x(OSiH3)x + Me3SnOSiH3 → VCl3−x(OSiH3)1+x + SnMe3Cl (where: x = 0–3)
| (14A) |
| | |
VOCl3−x(OSiH3)x + Me3SnOSiH3 → VOCl2−x(OSiH3)1+x + SnMe3Cl (where: x = 0–2)
| (15A) |
| | |
ZnEt2−x(OSiH3)x + Me3SnOSiH3 → ZnEt1−x(OSiH3)1+x + SnMe3Et (where: x = 0–1)
| (16A) |
| | |
ZnEt2−x(OSiH3)x(THF) + Me3SnOSiH3 → ZnEt1−x(OSiH3)1+x(THF) + SnMe3Et (where: x = 0–1)
| (17A) |
| | |
ZnEt2−x(OSiH3)x(THF)2 + Me3SnOSiH3 → ZnEt1−x(OSiH3)1+x(THF)2 + SnMe3Et (where: x = 0–1)
| (18A) |
| | |
ZnCl2−x(OSiH3)x + Me3SnOSiH3 → ZnCl1−x(OSiH3)1+x + SnMe3Cl (where: x = 0–1)
| (19A) |
| | |
ZnCl2−x(OSiH3)x(THF) + Me3SnOSiH3 → ZnCl1−x(OSiH3)1+x(THF) + SnMe3Cl (where: x = 0–1)
| (20A) |
| | |
ZnCl2−x(OSiH3)x(THF)2 + Me3SnOSiH3 → ZnCl1−x(OSiH3)1+x(THF)2 + SnMe3Cl (where: x = 0–1)
| (21A) |
| | |
[ZnCl3−x(OSiH3)x]− + Me3SnOSiH3 → [ZnCl2−x(OSiH3)1+x]− + SnMe3Cl (where: x = 0–1)
| (22A) |
| | |
SnCl4−x(OSiH3)x + Me3SnOSiH3 → SnCl3−x(OSiH3)1+x + SnMe3Cl (where: x = 0–3)
| (23A) |
| | |
SbCl3−x(OSiH3)x + Me3SnOSiH3 → SbCl2−x(OSiH3)1+x + SnMe3Cl (where: x = 0–2)
| (24A) |
| | |
Ph3SbCl2−x(OSiH3)x + Me3SnOSiH3 → Ph3SbCl1−x(OSiH3)1+x + SnMe3Cl (where: x = 0–1)
| (25A) |
| | |
Cl− + Me3SnOSiH3 → H3SiO– + SnMe3Cl
| (26A) |
Reactions B.
| | |
py–BCl3 + Me3SnOSi(OSiH3)3 → py–BCl2OSi(OSiH3)3 + SnMe3Cl
| (1B) |
| | |
py–AlMe3 + Me3SnOSi(OSiH3)3 → py–AlMe2OSi(OSiH3)3 + SnMe4
| (2B) |
| | |
py–AlCl3 + Me3SnOSi(OSiH3)3 → py–AlCl2OSi(OSiH3)3 + SnMe3Cl
| (3B) |
| | |
[AlCl4]− + Me3SnOSi(OSiH3)3 → [AlCl3OSi(OSiH3)3]− + SnMe3Cl
| (4B) |
| | |
SiCl4 + Me3SnOSi(OSiH3)3 → SiCl3OSi(OSiH3)3 + SnMe3Cl
| (5B) |
| | |
Me3SiCl + Me3SnOSi(OSiH3)3 → Me3SiOSi(OSiH3)3 + SnMe3Cl
| (6B) |
| | |
PhMe2SiCl + Me3SnOSi(OSiH3)3 → PhMe2SiOSi(OSiH3)3 + SnMe3Cl
| (7B) |
| | |
PCl3 + Me3SnOSi(OSiH3)3 → PCl2OSi(OSiH3)3 + SnMe3Cl
| (8B) |
| | |
POCl3 + Me3SnOSi(OSiH3)3 → POCl2OSi(OSiH3)3 + SnMe3Cl
| (9B) |
| | |
TiCl4 + Me3SnOSi(OSiH3)3 → TiCl3OSi(OSiH3)3 + SnMe3Cl
| (10B) |
| | |
Cp2TiCl2 + Me3SnOSi(OSiH3)3 → Cp2TiClOSi(OSiH3)3 + SnMe3Cl
| (11B) |
| | |
VCl4 + Me3SnOSi(OSiH3)3 → VCl3OSi(OSiH3)3 + SnMe3Cl
| (12B) |
| | |
VOCl3 + Me3SnOSi(OSiH3)3 → VOCl2OSi(OSiH3)3 + SnMe3Cl
| (13B) |
| | |
ZnEt2(THF)2 + Me3SnOSi(OSiH3)3 → ZnEtOSi(OSiH3)3(THF)2 + SnMe3Et
| (14B) |
| | |
ZnCl2(THF)2 + Me3SnOSi(OSiH3)3 → ZnClOSi(OSiH3)3(THF)2 + SnMe3Cl
| (15B) |
| | |
[ZnCl3]− + Me3SnOSi(OSiH3)3 → [ZnCl2OSi(OSiH3)3]− + SnMe3Cl
| (16B) |
| | |
SnCl4 + Me3SnOSi(OSiH3)3 → SnCl3OSi(OSiH3)3 + SnMe3Cl
| (17B) |
| | |
SbCl3 + Me3SnOSi(OSiH3)3 → SbCl2OSi(OSiH3)3 + SnMe3Cl
| (18B) |
| | |
Ph3SbCl2 + Me3SnOSi(OSiH3)3 → Ph3SbClOSi(OSiH3)3 + SnMe3Cl
| (19B) |
| | |
Cl− + Me3SnOSi(OSiH3)3 → (H3SiO)3SiO− + SnMe3Cl
| (20B) |
Fig. 2 displays the values of the Gibbs energy change for the first step of the condensation of all the precursors of interest at 298.15 K as calculated by B3LYP-D3 and PBE0-D3 using both molecular models A and B. Fig. 3 and 4 show the comparisons of all the condensation steps (all steps represented by model A and the first step represented by model B) as calculated by the two DFT functionals, respectively. The results show that the reaction is sufficiently spontaneous and irreversible for most precursors, especially those reported to be utilized experimentally, thereby generally supporting the conclusions of Clark, Lee, Barnes, and Styskalik,10–13 and the validity of the method of sequential additions.
 |
| | Fig. 2 Gibbs energy change of the first step of the condensation of studied precursors with models A (light) and B (dark) of CUBE at 298.15 K, as calculated by B3LYP-D3/CBS (red) and PBE0-D3/CBS (blue). | |
 |
| | Fig. 3 Gibbs energy change of the condensation of selected precursors with models A and B of CUBE at 298.15 K, as calculated by B3LYP-D3/CBS. | |
 |
| | Fig. 4 Gibbs energy change of the condensation of selected precursors with models A and B of CUBE at 298.15 K, as calculated by PBE0-D3/CBS. | |
Fig. S1 and S2 (ESI†) show the corresponding values of the Gibbs energy change for the first step of the condensation at 0 and 373.15 K, respectively. The negligible differences between the two figures indicate that the effects of temperature do not affect the interpretation of the results in any significant way, and, therefore, the following discussion will deal primarily with the Gibbs energy change at 298.15 K (ΔG298.15).
PCl3 was the very first precursor reported in reactions with CUBE by Weller and Feher,7 and their experiments indicated a fast, highly exothermic reaction (10A)/(8B). Our calculations concur with the predicted ΔG298.15 < −80 kJ mol−1 for the first step and approximately equal to −70 kJ mol−1 for the third step (electronic effects-only approximation), making the condensation perfectly irreversible. Although the reported products were only partially condensed and inhomogeneous, this was likely only due to the crude reaction conditions (PCl3-rich stoichiometry, poor solvent, and fast mixing at room temperature), and if appropriately conducted, PCl3 should yield silicophosphate sites with the general formula [P(OSi≡)3]. Porous materials containing such sites would be interesting as strong Lewis bases and redox catalysts, with the added benefit of utilizing a light, abundant, non-toxic p-block element. Analogous to PCl3, silicophosphate sites with the general formula [PO(OSi≡)3] should be available through the condensation of POCl3(11A)/(9B). Calculations predict irreversible condensation (ΔG298.15 < −60 kJ mol−1) with very little change in the subsequent condensation steps.
The condensation reactions of CUBE with VCl4(14A)/(12B) and especially VOCl3(15A)/(13B) were reported initially by Ghosh et al.8 and later extensively studied by Lee et al.10 In the first condensation step, both precursors exhibit thermodynamic characteristics nearly identical to POCl3, however, compared to VOCl3, VCl4 is significantly deactivated as the condensation progresses, decreasing ΔG298.15 to mere −35.6/−33.8 kJ mol−1 by B3LYP-D3 and PBE0-D3, respectively.
The reaction of TiCl4(12A)/(10B) was reported (along with ZrCl4 and SiCl4) by Barnes et al.,12 who successfully used multistep template-free procedures to obtain micro-mesoporous titano- and zirconosilicates. Calculations showed that the condensation of TiCl4 is highly exoergic with ΔG298.15 ranging from nearly −80 kJ mol−1 for the first step to −57 kJ mol−1 for the last step, making it irreversible. Reactions of CUBE with Cp2TiCl2 were reported by Clark et al.,9 who obtained a molecular substitution product of CUBE Si8O20(Cp2TiCl)8 in high yield. In harmony with this experimental observation, our calculations show that the condensation of this precursor is nearly half as energetic as TiCl4, with ΔG298.15 ranging from over −40 kJ mol−1 to approximately −32 kJ mol−1. Since the steric repulsion between the cyclopentadienyl rings and the CUBE(s) is completely neglected by model A (and the results given by model B for the first condensation step do not significantly differ), this deactivation compared to TiCl4 is attributed in large part to electronic effects – the electron-donating ability of the Cp rings. The Cp rings will impose additional steric repulsion and, especially in the case of the second condensation, a large additional penalty can be expected, explaining the apparently high activation barrier of the reaction and the tendency for stepwise substitution.
SiCl4(7A)/(5B), Me3SiCl (8A)/(6B), and PhMe2SiCl (9A)/(7B) are relevant as inert cross-linking and capping agents. Alternatively, a precursor with the general formula RSiCl3, where R is a functional moiety, could be used for embedding. Clark and Barnes11 studied various cross-linking procedures by SiCl4, HSiCl3, and Me2SiCl2. Styskalik et al.13 used ditopic linkers with general formulas ClMe2Si(CH2)nSiMe2Cl (n = 1–3) as well as the very similar Me3SiCl directly as a capping agent to remove the residual –SnMe3 groups left in the prepared metallosilicate matrices. The results show that SiCl4 is one of the most exoergic precursors with estimated ΔG298.15 ranging from −102 to −75 kJ mol−1 while the condensation of Me3SiCl is moderated by the positive inductive effect of the methyl substituents to −60.2/−54.9 kJ mol−1 by B3LYP-D3 and PBE0-D3, respectively. Surprisingly, the condensation of PhMe2SiCl is predicted to be even slightly more energetic than that of Me3SiCl, despite our expectations that a positive mesomeric effect of the phenyl substituent would decrease the reactivity even further. The reactivity of compounds such as HSiCl3 and Me2SiCl2 is expected to range somewhere between the extremes of SiCl4 and Me3SiCl. In conclusion, there is no doubt about the irreversibility of the condensation reaction for any Si–Cl precursors.
The condensation of CUBE with py–AlCl3(4A)/(3B) and [AlCl4]−(6A)/(4B) was described by Styskalik et al.13 with reports of full condensation and undisturbed coordination environment around Al even after subsequent cross-linking by the Si–Cl linkers. We have recently employed both precursors, along with py–AlMe3(2A)/(2B) experimentally.14 The calculations show that while condensation for all three precursors is certainly irreversible, there are vast differences between py–AlCl3 and py–AlMe3. While the former is a moderately exoergic precursor (−70 to −50 kJ mol−1), the latter is the most energetic in the whole series (around −100 kJ mol−1). This agrees with our experimental observations of the relative reactivity of the two precursors.14 In our experience, py–AlMe3 is much more sensitive to concentration, proper cooling (−80 °C), and slow addition speed. Mismanagement of these conditions leads to the formation of particulate precipitates. This is attributed to the emergence of molecular hotspots – a behavior typical of highly exothermic, low activation barrier reactions. [AlCl4]− is comparable to py–AlCl3 with a greater degree of deactivation in the subsequent condensation steps.
Given the rather hard character of the Al-based Lewis acids, precursors based on B and Zn were screened as softer alternatives. Borosilicate Lewis acids differ from their aluminosilicate counterparts by the tendency of the [BO3] moiety to assume planar geometry with π-electron delocalization across the whole moiety. This results in much weaker, more reversible coordination to ligands and the fact that, in contrast to [Al(OSi≡)3], [B(OSi≡)3] is a well-defined and stable species.32 To facilitate maximally relevant comparison, py–BCl3(1A)/(1B) was chosen as the starting precursor, and the results show that its condensation with CUBE is highly exoergic (−99 to −77 kJ mol−1) with very little deactivation in subsequent steps. Therefore, B–Cl compounds, in general, are predicted to be perspective, irreversibly reacting precursors for the synthesis of CUBE-based borosilicate materials. The possibility of maintaining an undisturbed coordination environment throughout the condensation is, however, questionable given the aforementioned general lability of neutral ligands on [BO3] centers.
ZnCl2 represents another alternative and it is often used in synthetic organic chemistry as a milder analog to AlCl3 in reactions, such as the Friedel–Crafts methods.33 In analogy to Al, we also considered the use of the commercially available ZnEt2. Due to the weaker coordination to Zn, no special ligands were assumed, but rather the precursors were studied primarily in the state of saturation (coordination number 4) by THF – the aprotic solvent of choice to dissolve both ZnCl2 and CUBE. The results show that the condensation of ZnEt2(THF)2(18A)/(14B) is moderately energetic (−64 to −28 kJ mol−1) and thus quite irreversible, albeit with significant deactivation between the first and the second steps. In contrast, the condensation of ZnCl2(THF)2(21A)/(15B) is a clear example of the limits of the CUBE-based synthetic approach as the predicted ΔG298.15 is positive (+13 to +20 kJ mol−1). Therefore, the equilibrium is shifted towards CUBE + ZnCl2, and the condensation is not spontaneous. Moreover, this also implies, that even if [Zn(OSi≡)2] sites were generated from ZnEt2, the method of sequential additions could not be used because as soon as any SnMe3Cl was generated by subsequent steps, such as the inert cross-linking by Si–Cl compounds, the equilibrium of the CUBE/ZnCl2 system would lead to the dissolution of the Zn–O–Si bonds and leaching out ZnCl2. The presence of Cl− donors, such as SnMe3Cl, may also give rise to the anionic species [ZnCl3]−(22A)/(16B), which, according to the results, should behave in the same manner as ZnCl2, although model B predicts the condensation of the first Zn–Cl to be slightly spontaneous.
SbCl3(24A)/(18B) was chosen as a softer isoelectronic analog to the Lewis basic PCl3. The results show that its condensation thermodynamics are right on the established border of absolute irreversibility (−30 to −25 kJ mol−1).
Ph3SbCl2(25A)/(19B) was selected as an interesting antimony(V) precursor for computational screening because the obvious candidate, SbCl5, is unsuitable for several reasons. First, our recent work showed that fitting four CUBEs around an Al3+ center is strongly disfavored.14 It is doubtful that fitting five CUBEs around the 11% larger Sb5+ is possible. Second, SbCl5 is a strong oxidizing agent, and third, the extreme stability of the [SbCl6]− species implies a side reaction between unconsumed SbCl5 and the evolving SnMe3Cl byproduct, producing ionic compounds, such as [SnMe3][SbCl6]. In contrast, Ph3SbCl2 was expected to be much less energetic, and there is no doubt that two CUBEs can fit around Sb at 180° apart with the [Ph3Sb] moiety in an equatorial plane between them. Our calculations showed that this precursor is even slightly less exoergic than SbCl3, with ΔG298.15 of at most −30 and as little as −17 kJ mol−1, making its irreversibility questionable.
Finally, Clark and Barnes11 mentioned using SnCl4 to obtain stannosilicates (23A)/(17B). The possibility for an irreversible exchange of Cl− between different tin(IV) species appeared highly questionable to us. Our calculations show that although the condensation reaction is still spontaneous in this case, it is hardly irreversible with ΔG298.15 of at most −16 and as little as −7 kJ mol−1. A facile ligand exchange with SnMe3Cl, leading to a mixture of SnMe2Cl2 and SnMeCl3 is also a possibility. Therefore, SnCl4 is likely not a useful precursor, and this type of condensation reaction is generally not well suited for the synthesis of stannosilicates.
Examination of the results for (26A)/(20B) (Table 1) shows that at low temperatures, the driving force for the condensation of CUBE with M–Cl compounds comes exclusively from the preferences of the metal site precursors. Thermal corrections, however, have the effect of favoring the condensation, contributing over −20 kJ mol−1 at 373.15 K. Since, in this case, there is a large disparity between model A (26A) and B (20B), the latter is taken as more accurate and should be used for interpretation. This situation is favorable with respect to moderating the reactivity of highly energetic precursors, as cooling not only decreases the kinetic rates but also decreases the thermodynamic driving force.
Table 1 Gibbs energy change for the exchange of [SnMe3]+ between the models A and B of CUBE and Cl−
| Reaction |
Method |
ΔE (kJ mol−1) |
ΔG0 (kJ mol−1) |
ΔGCBS273.15 kJ mol−1) |
G
CBS
298.15 (kJ mol−1) |
ΔGCBS373.15 (kJ mol−1) |
|
(26A)
|
B3LYP-D3 |
52.5 |
45.4 |
32.9 |
31.8 |
28.9 |
| PBE0-D3 |
47.3 |
40.5 |
28.1 |
27.2 |
24.3 |
|
(20B)
|
B3LYP-D3 |
12.9 |
6.0 |
−15.5 |
−17.3 |
−22.8 |
| PBE0-D3 |
6.1 |
0.2 |
−20.5 |
−21.3 |
−27.4 |
Routes to Al- and Zn-silicates
The model A of CUBE was used to study the condensation with py–AlMe3/py–AlCl3 and ZnEt2/ZnCl2 with respect to the effects of the coordination of THF (one of the two most successful solvents for the CUBE-based systems) as both metals can exist in multiple coordination states.
For py–AlMe3/py–AlCl3, pentacoordinate states (5C) with THF donors in axial positions were assumed: py–AlMe3(THF) (3A) and py–AlCl3(THF) (5A). To visualize the interaction of the condensation with coordination, these two reactions, along with (2A) and (4A), were added up to form a system with total composition py–AlMe3 + py–AlCl3 + 3 Me3SnOSiH3 + THF, where either of the Al precursors can undergo condensation (evolving SnMe4 or SnMe3Cl, respectively) and both Al educt and Al product can coordinate to THF. The total Gibbs free energy of the system in various states is then displayed in Fig. 5 and 6 for 0 and 298.15 K, respectively. Starting from the left and right, the initial precursors py–AlMe3/py–AlCl3 (denoted as states Me3 and Cl3) can undergo three condensation steps towards the center of the diagrams. The energy scale is referenced with respect to the final state with the tetracoordinate (4C) aluminosilicate product py–Al(OSiH3)3, which is common to both precursors (states denoted as O). In parallel, states containing the pentacoordinate analogs (with additional THF at Al) are visualized in lighter colors (5C).
 |
| | Fig. 5 Relative Gibbs energy of the condensation of py–AlCl3/py–AlMe3 (dark, 4C) and py–AlCl3(THF)/py–AlMe3(THF) (light, 5C) with model A of CUBE at 0 K, as calculated by B3LYP-D3/CBS (red) and PBE0-D3/CBS (blue). | |
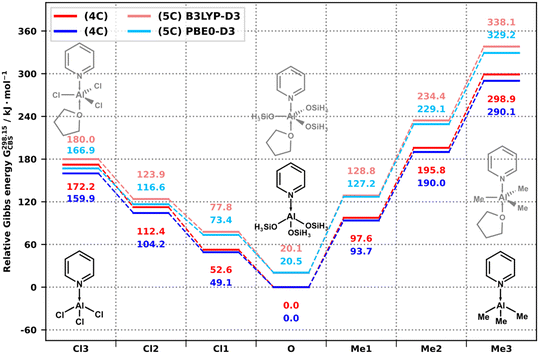 |
| | Fig. 6 Relative Gibbs energy of the condensation of py–AlCl3/py–AlMe3 (dark, 4C) and py–AlCl3(THF)/py–AlMe3(THF) (light, 5C) with model A of CUBE at 298.15 K, as calculated by B3LYP-D3/CBS (red) and PBE0-D3/CBS (blue). | |
The results show that while the additional coordination of THF is favored at 0 K (for py–AlCl3 and py–Al(OSiH3)3 by 50 kJ mol−1), it is disfavored at 298.15 K for all states. This agrees with our recent experimental observations, where no evidence for 5- or 6-coordinated Al species was observed in 27Al TQ/MAS NMR spectra of dried products prepared in THF.14 While the results are completely realistic for the initial precursors, model A falls short of representing the steric demands of CUBE, therefore, in reality, the coordination of THF to py–AlMe3−x(OCUBE)x (x = 1–3, equivalent to states Me2, Me1, and O in Fig. 5 and 6) and py–AlCl3−x(OCUBE)x (x = 1–3, equivalent to states Cl2, Cl1, and O) can be expected to be progressively more disfavored with the increasing number of CUBEs in the coordination sphere of Al, even at 0 K. The interaction of the incoming CUBE with the coordinated THF will likely result in an increased reaction barrier. The comparison of the energy difference between the 4-(4C) and 5-coordinated (5C) states (equivalent to the Gibbs energy change of coordination of THF to the 4-coordinated Al species) shows that the dative coordination is most favored by py–AlCl3 and least by py–AlMe3. The final aluminosilicate site is comparable to py–AlCl3 at low temperatures and it assumes a behavior intermediate between the two precursors at higher temperatures. This has the minor effect of generally decreasing ΔG of the condensation steps starting from py–AlCl3(THF) and increasing it for py–AlMe3(THF).
The conclusion is that although electronically favored, the coordination of weak ligands to Al precursors, resulting in pentacoordinate states, is a minor effect, which does not significantly affect the thermodynamics of the condensation, but it may significantly increase its activation barriers if the reactions are conducted at low temperatures. In any case, if pentacoordinate aluminosilicate species remain in the reaction mixtures upon reaching room temperature, the coordination is lost with heating and solvent removal.
In the case of ZnEt2/ZnCl2 precursors, 2-, 3-, and 4-coordinated states were studied, where 0 (2C), 1 (3C-THF), or 2 (4C-THF) molecules of THF can coordinate to both precursors. For ZnCl2, the coordination of a free Cl−, resulting in [ZnCl3]− (3C–Cl), was also envisioned. Thus, reactions (16A)–(22A) were added together to form a system with total composition ZnEt2 + ZnCl2 + 2 Me3SnOSiH3 + 2 THF + Cl−, and the total Gibbs free energy was plotted in Fig. 7–9, for 0, 298.15, and 373.15 K, respectively. Much like in the case of Al above, starting from left and right, the original precursors, denoted as states Cl2 and Et2, can undergo two steps of condensation towards the common zincosilicate products in the center – Zn(OSiH3)2(THF)x for ZnEt2(THF)x/ZnCl2(THF)x precursors and [ZnCl(OSiH3)2]− for [ZnCl3]−. Likewise, vertical transitions among 2C, 3C-THF, and 4C-THF series involve association or dissociation of THF, while a transition between any one of these states and the 3C–Cl series involves the replacement of any coordinated THF for a single Cl− or vice versa. The energy scale is referenced with respect to the state with the most stable uncharged zincosilicate species Zn(OSiH3)2(THF)2.
 |
| | Fig. 7 Relative Gibbs energy of the condensation of ZnCl2/ZnEt2 (black/gray, 2C), ZnCl2(THF)/ZnEt2(THF) (light, 3C-THF), ZnCl2(THF)2/ZnEt2(THF)2 (dark, 4C-THF), and [ZnCl3]− (orange/pink, 3C–Cl) with model A of CUBE at 0 K, as calculated by B3LYP-D3/CBS (gray/red/orange) and PBE0-D3/CBS (black/blue/pink). | |
 |
| | Fig. 8 Relative Gibbs energy of the condensation of ZnCl2/ZnEt2 (black/gray, 2C), ZnCl2(THF)/ZnEt2(THF) (light, 3C-THF), ZnCl2(THF)2/ZnEt2(THF)2 (dark, 4C-THF), and [ZnCl3]− (orange/pink, 3C–Cl) with model A of CUBE at 298.15 K, as calculated by B3LYP-D3/CBS (gray/red/orange) and PBE0-D3/CBS (black/blue/pink). | |
 |
| | Fig. 9 Relative Gibbs energy of the condensation of ZnCl2/ZnEt2 (black/gray, 2C), ZnCl2(THF)/ZnEt2(THF) (light, 3C-THF), ZnCl2(THF)2/ZnEt2(THF)2 (dark, 4C-THF), and [ZnCl3]− (orange/pink, 3C–Cl) with model A of CUBE at 373.15 K, as calculated by B3LYP-D3/CBS (gray/red/orange) and PBE0-D3/CBS (black/blue/pink). | |
The results show that the whole dataset exhibits the same monotonic trend hinted at in the previous sections by reactions (18A)/(14B) and (21A)/(15B), where alkyl zinc precursors tend to condense with CUBE to zincosilicates, but these tend to decompose in the presence of SnMe3Cl to produce ZnCl2 and CUBE. The only anomaly is in the case of uncoordinated ZnEt2, where the first condensation is spontaneous but the second is not, unless additional stabilization is provided by at least one ligand – a possible sign of the presence of hyperconjugation effects between Zn and Et, which is therefore energetically expensive to lose. This would also explain the much milder ΔG of condensation from uncoordinated states Et2 to Et1 compared to their counterparts with coordinated THF. Analogously to the case of Al, the Zn–Cl structures show greater affinity towards THF coordination compared to their Zn–Et counterparts. At 0 K, coordination of THF is universally preferred, but with increasing temperature, the states with higher coordination numbers are gradually more disfavored to the point where at 373.15 K even the coordination to the zincosilicate site Zn(OSiH3)2 is in equilibrium. The association of a free Cl− ion with the Zn site is already strongly preferred over the coordination of two THF molecules by 90.3/104.2 kJ mol−1 at 0 K, by B3LYP-D3 and PBE0-D3, respectively, and it only increases with temperature. Therefore, the Zn/CUBE system will aggressively abstract Cl− from available sources, and heating will only thermodynamically promote the process.
Summarized, the coordination of THF has very little effect on the thermodynamics of the condensation of ZnCl2, while it has a harmonizing effect on ZnEt2, where it increases the driving force and evens out the differences between the first and the second step of the condensation pathway. The coordination of a free Cl− ion always dominates over ligands such as THF.
General trends
The computed data show several trends across the spectrum of different elements, oxidation states, and computational methods (Table 2). First, the exoergicity of the condensation decreases from light elements down in the groups, which is the primary ordering of Table 2, and it is a natural result of the decreasing ionization energies and electron affinities of heavier elements. There is very little correspondence between the values of the thermodynamic parameters and the Pauling electronegativities of the elements. However, there is a crude correspondence with the oxophilicity scale developed by Kepp.34 Early d-block elements are oxophilic, and coincidentally, all of the reported experimentally used transition metal precursors fall into groups 4–6 (Ti to W). Our calculations showed that Zn (group 12) represents the other edge of this presumed “CUBE gap” in the middle of the periodic table. Also, in general, precursors suitable for condensation with CUBE exhibit the covalent character of their bonding to O and the leaving group (Cl, Me, Et).
Table 2 Summary of the thermodynamic parameters for the first step condensation of all the studied precursors and their comparison to the properties of the central metal atoms
| M |
Site precursor |
TD parameters (1st step, model B, kJ mol−1) |
Metal properties |
| B3LYP-D3 |
PBE0-D3 |
Δ (B3LYP–PBE0) |
Pauling electronegativity |
Oxophilicity34 |
| ΔE |
ΔG298.15 |
ΔE |
ΔG298.15 |
ΔΔE |
ΔΔG |
| B |
py–BCl3 |
−88.83 |
−86.69 |
−82.42 |
−80.09 |
−6.41 |
−6.60 |
2.04 |
1.0 |
| Al |
py–AlMe3 |
−113.71 |
−102.43 |
−108.44 |
−98.82 |
−5.27 |
−3.62 |
1.61 |
0.8 |
| py–AlCl3 |
−62.45 |
−59.96 |
−56.29 |
−53.76 |
−6.16 |
−6.19 |
| [AlCl4]− |
−65.58 |
−68.33 |
−62.40 |
−64.57 |
−3.18 |
−3.76 |
| Si |
SiCl4 |
−89.87 |
−98.52 |
−83.95 |
−92.18 |
−5.92 |
−6.35 |
1.90 |
0.8 |
| Me3SiCl |
−59.37 |
−60.17 |
−55.03 |
−54.95 |
−4.34 |
−5.23 |
| P |
PCl3 |
−80.61 |
−87.60 |
−75.65 |
−81.30 |
−4.96 |
−6.31 |
2.19 |
0.7 |
| POCl3 |
−50.28 |
−61.83 |
−48.55 |
−61.14 |
−1.72 |
−0.69 |
| Ti |
TiCl4 |
−62.31 |
−77.07 |
−60.88 |
−74.29 |
−1.43 |
−2.77 |
1.54 |
1.0 |
| Cp2TiCl2 |
−43.11 |
−45.32 |
−37.05 |
−42.41 |
−6.06 |
−2.92 |
| V |
VCl4 |
−58.35 |
−70.53 |
−56.24 |
−62.56 |
−2.11 |
−7.97 |
1.63 |
0.8 |
| VOCl3 |
−50.28 |
−61.83 |
−48.55 |
−61.14 |
−1.72 |
−0.69 |
| Zn |
ZnEt2(THF)2 |
−66.60 |
−63.48 |
−69.00 |
−57.27 |
2.39 |
−6.21 |
1.65 |
0.2 |
| ZnCl2(THF)2 |
8.95 |
15.28 |
9.55 |
12.72 |
−0.60 |
2.56 |
| [ZnCl3]− |
−0.04 |
−4.47 |
−0.48 |
−3.82 |
0.44 |
−0.65 |
| Sn |
SnCl4 |
−8.67 |
−15.31 |
−6.93 |
−13.33 |
−1.74 |
−1.97 |
1.96 |
0.4 |
| Sb |
SbCl3 |
−25.57 |
−30.07 |
−23.54 |
−24.95 |
−2.04 |
−5.12 |
1.82 |
0.3 |
| Ph3SbCl2 |
−32.34 |
−30.41 |
−27.04 |
−23.34 |
−5.30 |
−7.08 |
Second, the condensation is generally more spontaneous and energetic for alkyl metals than for the corresponding metal chlorides. Third, the presence of electron-donating groups on the central metal decreases the driving force (increases ΔG) for the condensation.
Concerning computational characteristics, most of the differences in the driving force come from electronic effects (comparison of ΔE to ΔG298.15). The match between the datasets calculated by B3LYP-D3 and PBE0-D3 is remarkable, with the latter predicting systematically higher ΔG298.15. The differences are attributable to both electronic energy and thermodynamic corrections. Examination of the CBS extrapolation parameters B (eqn (2)) and α (eqn (3)) for both datasets (ESI,† Table S47) shows that both parameters assume systematically lower values with PBE0-D3 compared to B3LYP-D3. This means that the CBS convergence for PBE0-D3 is flatter, and the functional is less sensitive to the size of the basis set.
Conclusions
This study used quantum chemistry DFT methods to estimate the thermodynamic parameters of model reactions in vacuum, representing the steps of the real-world, experimentally reported condensation reactions of the CUBE building block with metal chlorides and alkyl metals conducted in aprotic solvents. The main concerns were the irreversibility of the condensation of the already experimentally reported precursors and the computational screening of other potential precursors for future use.
Our investigation found that the previously reported and experimentally used precursors, AlCl3, [AlCl4]−, Si–Cl compounds, PCl3, TiCl4, and VOCl3, should undergo sufficiently irreversible condensation reactions with CUBE. The untested precursors BCl3, VCl4, and POCl3 are predicted to behave similarly. AlMe3 is almost twice as exoergic as AlCl3. Cp2TiCl2 reacts readily in the first step, but the second step may be partially reversible. SbCl3 and Ph3SbCl2 are borderline cases; all steps are similar and spontaneous, but reversibility might pose a problem. SnCl4 was found to be unsuitable as it is near equilibrium. Zn was found to be an interesting case. While it is possible to prepare zincosilicates from ZnEt2, it is not feasible to use ZnCl2. Moreover, the equilibrium is shifted towards ZnCl2, and the affinity of Zn for Cl− is so high that we predict that once a source of Cl−, such as SnMe3Cl, is introduced, even zincosilicate structures prepared from ZnEt2 will inevitably dissolve back to CUBE and ZnCl2.
The condensation of CUBE, in general, appears to be driven mainly by the oxophilicity of the metal in the precursor, which is the primary factor limiting the use of certain elements with CUBE. The driving force is higher for alkyl metals than for the corresponding metal chlorides, and it also decreases for heavy elements. The preference of [SnMe3]+ to bind to Cl− over CUBE has a supporting effect, where at low temperatures, the condensation is slightly disfavored, while at high temperatures (100 °C), this process contributes over 20 kJ mol−1 of the additional driving force, helping to complete the condensation.
This study demonstrated a sound, computationally cheap method for the screening of potential precursors for the CUBE-based synthesis of porous metallosilicates. It also showed that the behavior of B3LYP-D3 and PBE0-D3, together with the CBS extrapolation scheme, is stable and reliable enough that in the future, calculations by a single method can be trusted.
Data availability
The data supporting this article has been included as part of the ESI.†
Author contributions
MK: methodology; computation; writing – original draft preparation; visualization; data curation. HS: methodology; writing – review and editing; AS: writing – review and editing; JP: conceptualization; writing – review and editing; funding acquisition; supervision.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90254) – the computational resources provided by the IT4Innovations OPEN-24-63 project and the OP JAK project Quantum materials for applications in sustainable technologies (QM4ST) CZ.02.01.01/00/22_008/0004572, program Johannes Amos Comenius, call Excellent Research.
References
- V. Smeets, A. Styskalik and D. P. Debecker, J. Sol-Gel Sci. Technol., 2021, 97, 505–522, DOI:10.1007/s10971-021-05486-1
 .
.
- A. Shimojima and K. Kuroda, Molecules, 2020, 25, 524, DOI:10.3390/molecules25030524
 .
.
- T. Engel and G. Kickelbick, Eur. J. Inorg. Chem., 2015, 1226–1232, DOI:10.1002/ejic.201402551
 .
.
- M. Kikuchi, T. Hayashi, T. Matsuno, K. Kuroda and A. Shimojima, Dalton Trans., 2024, 53, 6256–6263, 10.1039/D4DT00215F
 .
.
- J. Jamoul, S. Smet, S. Radhakrishnan, C. V. Chandran, J. A. Martens and E. Breynaert, Chem. Mater., 2024, 36, 1385–1394, DOI:10.1021/acs.chemmater.3c02546
 .
.
- F. J. Feher and K. J. Weller, Inorg. Chem., 1991, 30, 880–882, DOI:10.1021/ic00005a003
 .
.
- F. J. Feher and K. J. Weller, Chem. Mater., 1994, 6, 7–9, DOI:10.1021/cm00037a002
 .
.
- N. N. Ghosh, J. C. Clark, G. T. Eldridge and C. E. Barnes, Chem. Commun., 2004, 856–857, 10.1039/b316184f
 .
.
- J. C. Clark, S. Saengkerdsub, G. T. Eldridge, C. Campana and C. E. Barnes, J. Organomet. Chem., 2006, 691, 3213–3222, DOI:10.1016/j.jorganchem.2006.03.028
 .
.
- M.-Y. Lee, J. Jiao, R. Mayes, E. Hagaman and C. E. Barnes, Catal. Today, 2011, 160, 153–164, DOI:10.1016/j.cattod.2010.06.029
 .
.
- J. C. Clark and C. E. Barnes, Chem. Mater., 2007, 19, 3212–3218, DOI:10.1021/cm070038b
 .
.
- C. E. Barnes, K. Sharp, A. A. Albert, M. E. Peretich, P. Fulvio, P. F. Ciesielski and B. S. Donohoe, J. Nanosci. Lett., 2015, 5, 1–7 CrossRef
 .
.
- A. Styskalik, J. G. Abbott, M. C. Orick, D. P. Debecker and C. E. Barnes, Catal. Today, 2019, 334, 131–139, DOI:10.1016/j.cattod.2018.11.079
 .
.
- M. Kejik, J. Brus, L. Jeremias, L. Simonikova, Z. Moravec, L. Kobera, A. Styskalik, C. E. Barnes and J. Pinkas, Inorg. Chem., 2024, 663, 2679–2694, DOI:10.1021/acs.inorgchem.3c04035
 .
.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Aust. J. Chem., 2012, 4, 17, DOI:10.1186/1758-2946-4-17
 .
.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363, DOI:10.1002/jcc.540141112
 .
.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102, DOI:10.1063/5.0005188
 .
.
- J. Baker, A. Kessi and B. Delley, J. Chem. Phys., 1996, 105, 192–212, DOI:10.1063/1.471864
 .
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913
 .
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789, DOI:10.1103/PhysRevB.37.785
 .
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170, DOI:10.1063/1.478522
 .
.
- C. Adamo, G. E. Scuseria and V. Barone, J. Chem. Phys., 1999, 111, 2889–2899, DOI:10.1063/1.479571
 .
.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023, DOI:10.1063/1.456153
 .
.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371, DOI:10.1063/1.464303
 .
.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820, DOI:10.1021/acs.jcim.9b00725
 .
.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112, DOI:10.1063/1.1622923
 .
.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569, DOI:10.1063/1.1305880
 .
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344
 .
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465, DOI:10.1002/jcc.21759
 .
.
- R. Peverati and K. K. Baldridge, J. Chem. Theory Comput., 2008, 4, 2030–2048, DOI:10.1021/ct800252z
 .
.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446, DOI:10.1016/S0009-2614(99)00179-7
 .
.
- A. Vegas, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1985, 41, 1689–1690, DOI:10.1107/S0108270185009052
 .
.
- E. Hayashi, Y. Takahashi, H. Itoh and N. Yoneda, Bull. Chem. Soc. Jpn., 1993, 66, 3520–3521, DOI:10.1246/bcsj.66.3520
 .
.
- K. P. Kepp, Inorg. Chem., 2016, 55, 9461–9470, DOI:10.1021/acs.inorgchem.6b01702
 .
.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Hugo
Semrad
,
Hugo
Semrad
 ,
Ales
Styskalik
,
Ales
Styskalik
 and
Jiri
Pinkas
and
Jiri
Pinkas
 *
*






.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.






