Noble gas bonds facilitate anion⋯anion supramolecular assemblies: insights from CSD and DFT analysis

Abstract

Noble gas bonding (NgB) is a noncovalent interaction where noble gases, such as xenon or krypton, function as Lewis acids. These interactions arise from regions of positive electrostatic potential, known as σ-holes or π-holes, which form on the noble gas atom and interact with electron-rich sites, such as lone pairs or anions. Although recently discovered, NgBs have demonstrated considerable potential in supramolecular chemistry, with their strength—especially in the case of heavier noble gases like xenon—comparable to that of hydrogen bonds. Anion⋯anion interactions, which are typically hindered by electrostatic repulsion, can occur through attractive forces like σ-hole and π-hole interactions. While these interactions are increasingly observed in biological and synthetic systems, particularly in solid-state and polar environments, their stabilization via NgBs remains largely unexplored. In this study, we present a computational and experimental analysis of noble gas bonds (NgBs) facilitating anion⋯anion interactions, emphasizing the unique role of xenon as a σ-hole donor. Through a combination of Cambridge Structural Database (CSD) inspection and density functional theory (DFT) calculations, we reveal the novel contribution of NgBs in dispersing electrostatic charge, allowing for the stabilization of anion⋯anion dimers. Our findings suggest that, while the concept of counterion-mediated anion⋯anion attraction is well known, the use of noble gas bonding offers a distinct and previously unexplored mechanism for enabling such interactions. These results open new possibilities for designing supramolecular assemblies with unconventional bonding motifs.

---

Introduction

Noble gas bonding (also known as aerogen bonding) is a noncovalent interaction involving a Group 18 element, such as xenon or krypton, acting as an electron acceptor.¹ This interaction is mediated by a region of positive electrostatic potential, commonly referred to as a σ-hole or π-hole, which forms between the noble gas atom and an electron-rich site, such as a lone pair of a Lewis base or an anion.^1,2 Noble gas bonds are analogous to other σ- and π-hole interactions, such as halogen, chalcogen, and pnictogen bonding, but are generally less directional due to the weaker anisotropy around the noble gas atom.³

Despite their relatively recent discovery, noble gas bonds have been shown to play a significant role in supramolecular chemistry and crystal engineering. Studies have demonstrated that these interactions can rival the strength of hydrogen bonds and other σ-hole interactions, particularly when involving heavier noble gases like xenon. Theoretical investigations, employing molecular electrostatic potential (MEP) surfaces and quantum theory of atoms in molecules (QTAIM), have revealed that these bonds are driven by a combination of electrostatic, dispersion, and polarization effects.^1–4

Anion⋯anion interactions, though seemingly counterintuitive due to the electrostatic repulsion between like charges, are possible through attractive forces such as σ-hole and π-hole bonds.⁵ These interactions can overcome coulombic repulsion, enabling the formation of stable anion⋯anion adducts under specific conditions. σ- and π-Hole bonds occur when regions of depleted electron density (σ-holes or π-holes) on one anion attract regions of excess electron density, such as lone pairs, on another anion.^6–9

Such interactions have been observed in various biological systems and synthetic compounds.¹⁰ For example, hydrogen bonds (HBs) have long been known to facilitate anion⋯anion self-assembly, as seen in systems like phosphate dimerization.^11,12 Moreover, σ- and π-hole interactions extend this phenomenon to other anions, such as halides and oxoanion complexes, enabling their self-assembly into one-, two-, or three-dimensional supramolecular architectures.^13,14

Anion⋯anion interactions are particularly influential in the solid state and polar solvents, where they are stabilized by polarization and dispersion forces, allowing the formation of discrete adducts or complex supramolecular structures.^13,14 Recent examples include anion⋯anion interactions in perrhenate anions assisted by hydrogen^13b and chalcogen bonds.

The stabilization of anion⋯anion self-assembly through noble gas bonding (NgB) remains largely unexplored. As far as we know, only one example has been described by Scheiner and coworkers,^13f who detailed anion⋯anion interactions in tetramethylammonium pentafluoroxenate(IV) (CSD code SOBWAH).¹⁵ In this system, the XeF₅⁻ anions adopt a planar pentagonal geometry and form NgB-mediated infinite chains through the antiparallel pairing of one Xe–F bond with a symmetrically equivalent Xe–F bond from a neighboring anion (Fig. 1). These infinite 1D chains are further stabilized by hydrogen bonds with the adjacent tetramethylammonium counterions.

Fig. 1 Partial view of the X-ray structure of SOBWAH. Hydrogen atoms are omitted for clarity. NgBs are represented by dashed lines. Distances are given in Å.

The concept of counterions enabling anion⋯anion interactions has been previously established,⁵ primarily in the context of electrostatic interactions that mitigate the inherent repulsion between like charges. The novelty in this manuscript is that we present the first evidence of an anion⋯anion dimer mediated by noble gas bonds (NgBs), a phenomenon that, to the best of our knowledge, has not been previously explored in the literature. Additionally, DFT calculations performed in the solid state (using periodic boundary conditions), in solution, and in the gas phase show that NgBs involving xenon as a σ-hole donor can promote the formation of anion⋯anion interactions. The physical nature of these interactions has been further analyzed using a wide range of computational tools.

Theoretical methods

Calculations were carried out using the Turbomole program (version 7.7)¹⁶ at the BP86 (ref. 17)-D3BJ¹⁸/def2-TZVP¹⁹ level of theory. The geometries were fully optimized using either periodic boundary conditions or solvent effects using the COSMO continuum dielectric model.²⁰ MEP surfaces were plotted on a 0.001 a.u. isosurface. QTAIM²¹ and NCIPlot²² analyses were conducted using the Multiwfn program,²³ with visualizations generated through VMD software.²⁴ For the NCIPlot representations in the figures, the following settings were applied: RDG = 0.45, ρ_cut-off = 0.04 a.u., and a color scale of −0.04 a.u. ≤ (sign λ₂)ρ ≤ 0.04 a.u.

Energy decomposition analysis (EDA) was performed using the Kitaura–Morokuma method,²⁵ as implemented in Turbomole (version 7.7). The electron localization function (ELF)²⁶ was computed at the same level of theory using Multiwfn.²³ Additionally, chemical bonding analysis was conducted by combining the extended transition state (ETS) method with natural orbitals for chemical valence (NOCV) theory, known as the ETS-NOCV approach introduced by Ziegler et al.,²⁷ and implemented in the Multiwfn program.²³

Results and discussion

CSD search

We began by manually inspecting all organo-xenon structures available in the Cambridge Structural Database (CSD, version 5.45, November 2023),²⁸ identifying a total of 40 structures (see Table S1† for the full list). Among these, two structures lacked crystallographic coordinates. Out of the remaining 38 structures, 20 are salts where xenon is part of the cationic species, making the anions susceptible to forming anion⋯anion adducts. However, some of these structures feature very bulky anions, such as hexakis(penta-fluorotellurolato)antimony (COGTUR), tetrakis(perfluorophenyl)-borate (MOFJAT), and difluoro-bis(pentafluorophenyl)borate (KEDMUB), where the observed anion⋯anion contacts cannot be rationalized as the result of directional σ- or π-hole interactions.

In other cases, the anions are octahedral, such as AsF₆⁻ (e.g., DAMROY, ESOSIQ, JAQCOT, ZOGPIV), which lack the σ-holes necessary for establishing directional anion⋯anion interactions. Additionally, several structures (KAZLUV, KAZMAC, KAZMEG, KAZMIK) contain spherical monoatomic halides like Br⁻ or Cl⁻, which also lack anisotropy in their electron density and are therefore incapable of forming directional interactions.

To illustrate this behaviour, we examined the X-ray packing of two AsF₆⁻ salts (ZOGPIV and DAMROY) (Fig. 2). In ZOGPIV,²⁹ the anion is surrounded by four pentafluorophenyl-2,6-difluoropyridyl-xenon(II) cations, establishing two bifurcated Xe₂⋯F NgB contacts and two anion⋯π interactions with the pentafluorophenyl rings. Similarly, in the DAMROY structure³⁰ (Fig. 2b), the anion is surrounded by four (μ²-chloro)-bis(pentafluorophenyl)-xenon(II) cations, forming multiple NgBs and anion–π contacts. These examples show that AsF₆⁻ salts are not prone to forming anion⋯anion dimers or higher-dimensional assemblies.

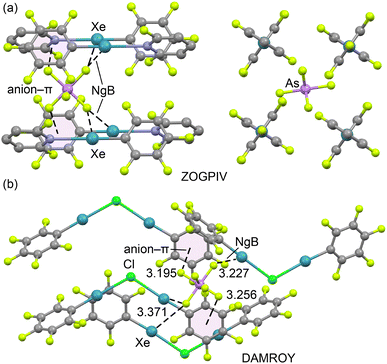Fig. 2 Partial views of the X-ray structures of ZOGPIV (a, two different views) and DAMROY (b). Hydrogen atoms have been omitted for clarity; NgBs are represented as dashed lines. Distances in Å.

Our initial inspection of the CSD revealed that out of the 20 possible structures, 11 have anions that lack the σ- or π-holes necessary for establishing directional contacts. The remaining structures feature tetrahedral anions, which, in principle, could form anion⋯anion adducts. Upon closer examination, we found that some of these structures exhibit the expected alternation of anions and cations, rather than the formation of anion⋯anion dimers, as shown in Fig. 3. For example, in the QOYRED³¹ structure, the T-shaped difluoro-(pentafluorophenyl)-xenon(IV) cation interacts with one tetrafluoroborate anion via a σ-hole and with two additional anions via π-holes, propagating the ion pairs into 1D supramolecular polymers. Similarly, in the 2,6-difluorophenyl-xenon(II) trifluoromethanesulfonate salt (ROQQET),³² the NgB ion pairs are connected via anion–π interactions, without any evidence of anion⋯anion interactions.

Fig. 3 Partial views of the X-ray structures of QOYRED (a) and ROQQET (b). Hydrogen atoms have been omitted for clarity; NgBs and anion–π interactions are represented as dashed lines. Distances in Å.

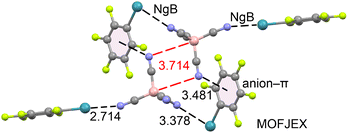
Finally, we identified one structure that forms anion⋯anion interactions: MOFJEX,³³ which consists of pentafluorophenyl-xenon(II) tetracyanoborate. As shown in Fig. 4, two tetracyanoborate anions are positioned close to each other, forming an antiparallel dimer. In this arrangement, the nitrogen atom of one anion is located opposite the B–CN bond of the adjacent anion, and vice versa (N⋯B–C angle = 170.7°). This anion⋯anion dimer is stabilized by the counterions through two different contacts: Xe⋯N NgBs and anion–π interactions. Both types of NgB contacts exhibit distances shorter than the sum of Alvarez's van der Waals radii (∑R_vdw = 3.72 Å).³⁴ The anion⋯anion B⋯N distance is 3.714 Å, which is 0.144 Å longer than ∑R_vdw(B + N) = 3.57 Å. Measuring the distance from the nitrogen atom to the nearest carbon atom gives 3.345 Å (not shown in figure), which is shorter than ∑R_vdw(C + N) = 3.43 Å.

Fig. 4 Partial view of the X-ray structure of MOFJEX. NgBs and anion–π interactions are represented as black dashed lines, while anion⋯anion contacts are represented as red dashed lines. Distances in Å.

Thus, this anion⋯anion interaction can be interpreted as a B⋯N triel bond,³⁵ based on its linear directionality, or as a C⋯N tetrel bond,³⁶ depending on whether we consider the shortest distance. The energetic and physical nature of this interaction is further analyzed in the next section.

DFT calculations

We first analyzed the anisotropy in the electron density distribution within the tetracyanoborate anion and investigated how this distribution is affected by the presence of the noble gas bonding (NgB) interaction. Fig. 5 shows the molecular electrostatic potential (MEP) surfaces of isolated tetracyanoborate in the gas phase and pentafluorophenyl-xenon(II) tetracyanoborate salt. The isolated anion exhibits an anisotropic distribution with four negative σ-holes located opposite the B–CN bonds. Notably, in the presence of the counterion, the negative value of the σ-hole is significantly reduced from −69.5 kcal mol⁻¹ to −0.5 kcal mol⁻¹.

Fig. 5 MEP surfaces of tetracyanoborate (a) and pentafluorophenyl-xenon(II) tetracyanoborate salt (b). The energies at selected points of the surface are given in kcal mol⁻¹.

The significant reduction in negative charge when the counterion is present suggests that the anion⋯anion repulsion is likely negligible, with other attractive forces such as dispersion or correlation playing a dominant role in the formation of anion⋯anion interactions.

We optimized the structure of MOFJEX in the solid state using periodic boundary conditions (PBC) and found that the resulting architecture closely matches the experimental packing (Fig. 6). The anion⋯anion distance is slightly shorter than the experimental value (3.616 Å), and the Xe⋯N NgB is also reduced to 2.673 Å, suggesting that these interactions are intrinsic to the system and not merely a consequence of packing effects. Interestingly, while the anion⋯anion and NgB distances shorten, the anion⋯π distance increases slightly. The QTAIM/NCIPlot analysis of the ion-pair dimer retrieved from the optimized structure confirms the presence of NgBs and the [B(CN)₄]⁻⋯[B(CN)₄]⁻ interaction. Each NgB is characterized by a bond critical point (BCP, red sphere) and bond path connecting the Xe to the N-atom, with a pronounced blue reduced density gradient (RDG) isosurface at the BCP, indicating the strongly attractive nature of the NgB interaction.

Fig. 6 (a) RI-BP86-D3BJ/def2-TZVP optimized geometry of pentafluorophenyl-xenon(II) tetracyanoborate salt using PBC. Distances in Å. (b) QTAIM/NCIPlot analysis of an ion-pair dimer. Only intermolecular interactions are represented. BCPs are shown as red spheres and bond paths as orange lines. RDG = 0.45, color code −0.04 a.u. ≤ (sign λ₂)ρ ≤ 0.04 a.u. Only BCPs are shown for clarity.

Interestingly, the anion⋯anion interaction is characterized by five BCPs symmetrically distributed. Notably, the N-atom of one anion is connected to two C-atoms of the cyano groups rather than the B-atom of the adjacent anion, suggesting the formation of tetrel bonds instead of triel bonds. However, a green RDG isosurface envelops the entire region between the anions, including the boron atom, indicating its potential participation in the binding mechanism. It is important to note that BCPs in noncovalent interactions involving tetrahedral anions often link lone pair donor atoms to substituents rather than the central σ-hole donor atom.³⁷ Additionally, in some cases, boron triel bonds have been shown to lack electron-density descriptors.³⁸

We further explored the behaviour of the anion⋯anion dimer in solution, using water as the solvent. As expected, the optimization of the dimer in the gas phase resulted in the monomers separating to infinity. However, optimization in solution yielded two distinct minima, labelled A and B (Fig. 7). In dimer A, the monomers adopt an antiparallel orientation with a BCP and bond path distribution similar to the experimentally observed structure. This dimer is only 0.23 kcal mol⁻¹ higher in energy than the separate monomers, indicating that the polar water solvent effectively lowers the electrostatic repulsion between the like charges.¹⁴ Additionally, the B⋯N distance is shorter in the solution-optimized dimer than in the crystal structure, suggesting that electrostatic repulsion is more effectively mitigated in solution than in the solid state. In dimer B, the N-atom of one anion points toward the B-atom of the adjacent anion along a C₃ axis. This minimum has a slightly longer B⋯N distance and is 0.8 kcal mol⁻¹ less favourable. QTAIM analysis of dimer B shows that the N-atom is linked to three C-atoms of the cyano groups, suggesting the formation of three C⋯N tetrel bonds instead of a triel bond. The NCIPlot analysis, however, indicates participation of both the C- and B-atoms in the interaction, showing that the RDG isosurface embraces both the B and C-atoms. When considering the effect of the counterion (C₆F₅Xe⁺) in water, the dimerization energy of adduct A shifts from slightly positive to negative (−1.38 kcal mol⁻¹), confirming that NgBs facilitate anion⋯anion interactions in solution.

Fig. 7 QTAIM/NCIPlot analysis of two minima of the tetracyanoborate anion⋯anion dimer (a and b), the NgB ion pair (c), the ion-pair dimer (d) and the ion pair substituting C₆F₅Xe⁺ by K⁺ (e), all optimized in water. BCPs are shown as red spheres and bond paths as orange lines. RDG = 0.45, color code −0.04 a.u. ≤ (sign λ₂)ρ ≤ 0.04 a.u. Only BCPs are shown for clarity.

For completeness, we also analyzed the NgB dimer C to compare the anion⋯anion dimers A and B with the anion⋯cation NgB dimer. This interaction is characterized by a blue disk-shaped RDG isosurface coinciding with the BCP, indicative of strong interactions. This is corroborated by the dimerization energy, which is −11.9 kcal mol⁻¹ (Fig. 7c). Interestingly, the Xe⋯N distance in dimer C is longer than that in the ion-pair dimer (Fig. 7d), suggesting that the NgB contact is strengthened by the presence of the [B(CN)₄]⁻⋯[B(CN)₄]⁻ interaction.

It is worth noting that previous studies have demonstrated that the presence of cations on opposite sides of a dianionic dimer can significantly alter interaction energies between two π-stacked TCNE radical anions, shifting them from repulsive (positive) to attractive (negative) values.³⁹ Inspired by this observation, we investigated whether introducing a different cation, such as K⁺ (as used in ref. 39), positioned behind the tetracyanoborates, would have a similar effect as the noble-gas bonded difluoro(pentafluorophenyl)-xenon (C₆F₅Xe⁺).

The fully optimized assembly is shown in Fig. 7e, illustrating that the K⁺ ions occupy positions nearly coinciding with the xenon atom in MOFJEX, albeit with slightly longer distances (2.791 Å). Additionally, the B⋯N distances in the K⁺ ion-pair dimer are longer than those in the C₆F₅Xe⁺ assembly, suggesting that K⁺ exerts a smaller stabilizing effect on the anion⋯anion interactions. Indeed, the ion-pair dimerization energy is slightly lower for the K⁺ assembly compared to that of C₆F₅Xe⁺. Nevertheless, these results confirm that a different cation, such as K⁺, can still induce a shift from positive to negative interaction energies, though with reduced efficacy compared to the noble-gas bonded system.

To better understand the forces responsible for the stability of these dimers, we performed an energy decomposition analysis (EDA). The interaction energy (E_tot) was partitioned into electrostatic (E_el), exchange repulsion (E_ex-rep), orbital (E_orb), dispersion (E_disp), and correlation (E_cor) terms (Fig. 8). In both dimers A and B, the electrostatic term is repulsive, as expected. However, the attractive contributions from the orbital, dispersion, and correlation terms are sufficient to overcome the E_ex-rep repulsive force. Notably, dimer A exhibits significantly larger attractive terms than dimer B, which aligns with its antiparallel pairing (featuring two B⋯N contacts). At the same time, dimer A also has a larger exchange-repulsion term, which compensates for the attractive interactions.

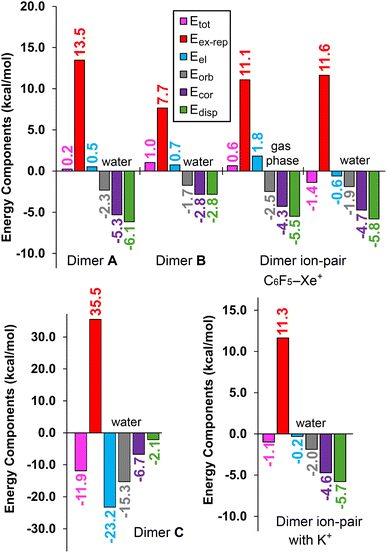Fig. 8 Energy decomposition analysis (EDA) for dimers A, B, C and the two ion-pair dimers represented in Fig. 7. The total interaction energy (E_tot), electrostatic (E_el), exchange repulsion (E_ex-rep), orbital (E_orb), dispersion (E_disp), and correlation (E_cor) terms are shown in kcal mol⁻¹.

In dimer C, the electrostatic term is dominant, followed by the orbital contribution. This is attributed to the short Xe⋯N distance, which suggests some degree of covalency in the interaction. In contrast to dimers A, B, and ion-pair dimers, the dispersion contribution in dimer C is relatively small, as the π-system of the cyano groups is not significantly involved in the noble-gas bond (NgB).

Finally, the EDA analysis of ion-pair dimers involving K⁺ is comparable to that of C₆F₅Xe⁺ (see Fig. 8, bottom-right). In both cases, the dispersion and correlation terms are dominant, followed by orbital contributions, with the electrostatic term being nearly negligible for K⁺ (−0.2 kcal mol⁻¹). This analysis confirms that C₆F₅Xe⁺ exhibits a superior ability to dissipate the negative charge of the anion compared to K⁺, thereby more effectively promoting the formation of anion⋯anion dimers.

The dispersion term (E_disp) dominates in dimer A and ion-pair dimers, indicating significant participation of the π-electrons. This suggests that the binding mode in dimer A can be characterized as antiparallel π-stacking of the cyano groups, which aligns with the findings from the QTAIM and NCIPlot analyses.

Additionally, we computed the EDA for the ion-pair dimer in both solution and the gas phase. While the total interaction energy (E_tot) is positive in the gas phase, it becomes negative in solution. This shift is primarily driven by the electrostatic term (E_el), which is negative in solution but positive in the gas phase, further highlighting the crucial role of the dielectric environment in stabilizing the interaction.

As discussed earlier, while QTAIM analysis shows that the bond critical points (BCPs) connect the N-atom of one anion to the C-atoms of the other anion, without involving the boron atom, NCIPlot analysis reveals that the B-atom also participates in the interaction. To explore this aspect further, we analyzed both dimers using the natural orbitals for chemical valence (ETS-NOCV) method. This computational approach provides valuable insights into electron density rearrangements during the interaction. The eigenvectors of the NOCV deformation density matrix represent the primary channels of electron flow, while the corresponding eigenvalues quantify the magnitude of this flow.

Table 1 lists the most significant interaction pairs for dimers A and B. Pairs with interaction energies smaller than −0.5 kcal mol⁻¹ were included in the calculation of total interaction energies (shown in the last column of Table 1) but are not listed individually. Notably, the total ETS-NOCV energy values are comparable to the orbital contributions (E_orb) obtained from the energy decomposition analysis (EDA) in Fig. 8. Both methods (Kitaura–Morokuma and NOCV) reveal that the total orbital contribution is smaller in dimer B compared to dimer A. The NOCV density isosurfaces for the pairs listed in Table 1 are shown in Fig. 9. In dimer A, two equivalent NOCV pairs indicate electron displacement from the N-atom of one CN group to two CN groups on the other monomer, and vice versa. The total transferred electron density is 0.14 e, with an associated stabilization energy of −1.04 kcal mol⁻¹. The contribution of the B-atom is modest, as depletion of electron density at the B-atom is observed in comparison to the C-atoms.

Table 1 Pair energy contributions <−0.5 kcal mol⁻¹ for dimers A and B, and electron transfer in e. The total energies of all pairs are also indicated. Energies are in kcal mol⁻¹

Dimer	Electron flow	e transfer	Pair energy	Total pair energies
a Sum of the two equivalent electron transfers.
A	N → C,B	0.14	−1.04^a	−2.70
B	N → C,B	0.08	−0.75	−2.11

---

Fig. 9 Isosurfaces of NOCV pair density for the electron flows in anion⋯anion dimers A (a) and B (b) corresponding to the pairs listed in Table 1.

In dimer B, electron donation from the N-atom to both the boron and three carbon atoms is clearly visible. The electron displacement is similar across these four atoms, consistent with the NCIPlot analysis, suggesting a tetrafurcated N⋯C,B interaction in this case. The total transferred electron density is smaller at 0.08 e, with an associated stabilization energy of −0.75 kcal mol⁻¹.

The combined QTAIM and NOCV results suggest that dimer A is predominantly stabilized by N⋯C contacts, with minimal involvement of the B-atom, while in dimer B, the participation of both C- and B-atoms is more balanced. To further support this interpretation, we computed the Laplacian of the electron density (∇²ρ), electron localization function (ELF), and reduced density gradient (RDG) 2D plots, representing them in planes containing the interacting atoms. These properties offer complementary perspectives on the nature of the anion⋯anion contacts. The ∇²ρ 2D plot provides insights into the covalent nature of the noncovalent interactions (NCI), while the RDG maps are effective for pinpointing regions where noncovalent interactions occur. Additionally, the ELF 2D map is useful for distinguishing Lewis base and acid regions within the anion⋯anion dimers.

For dimer A, we selected the plane containing the B–CN antiparallel pair. The ELF plot shows a clear σ-hole at the B-atom and a large region of electron density at the N-atom corresponding to the lone pair (LP). However, the LP is not directed toward the σ-hole, explaining the limited involvement of the B-atom, in agreement with the NOCV analysis. The ELF plot also reveals π-holes at the C-atoms due to polarization of the C≡N bond. These π-holes align with regions of accumulated electron density from the π-electrons of the C≡N bond (Fig. 10a). Consequently, dimer A can be interpreted as an antiparallel π-stacking interaction between the B–C≡N groups. This is further supported by the 2D plot of the Laplacian overlaid with the RDG map, showing a large blue region between the B–C≡N groups, consistent with antiparallel π-stacking.

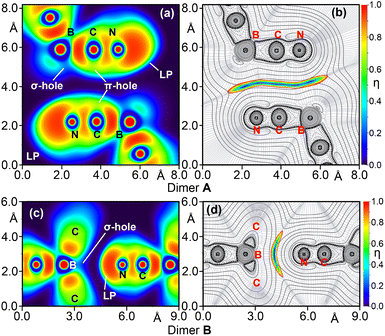Fig. 10 2D plots of the ELF and overlapped Laplacian and RDG for anion⋯anion dimers A (a and b) and B (c and d).

In contrast, the ELF plot for dimer B shows a large LP on the N-atom directed toward the σ-hole on the B-atom, suggesting that dimer B is primarily stabilized by a σ-hole interaction. The 2D RDG map displays a blue region located between the N- and B-atoms, extending to the C-atoms. This combined ELF/RDG analysis for dimer B indicates that a triel bond interaction is predominant, which aligns with the NOCV results, although it somewhat contradicts the QTAIM analysis that suggested a trifurcated N⋯C,C,C interaction.

Conclusion

In this study, we have demonstrated the unique role that noble gas bonds (NgBs), particularly those involving xenon, can play in facilitating anion⋯anion interactions. Through a combination of Cambridge Structural Database (CSD) inspection and extensive DFT calculations in various environments (solid-state, solution, and gas phase), we have provided the first evidence of NgB-mediated anion⋯anion dimers. This work highlights the importance of considering NgBs as a novel counterion mechanism in supramolecular chemistry, expanding the scope of anion⋯anion interactions beyond traditional electrostatic frameworks. Future studies could explore how NgBs can be combined with other directional bonding interactions to design more complex and functional.

The computational analysis, including energy decomposition analysis (EDA), QTAIM, and ETS-NOCV methods, further elucidates the nature of these interactions, showing a significant contribution from dispersion forces and electron density redistribution, particularly in antiparallel π-stacking and tetrel bonding arrangements. This research opens new avenues in understanding anion⋯anion interactions, where NgBs can be leveraged to stabilize unconventional interactions and build complex molecular assemblies.

Data availability

The data supporting the findings of this study are available within the article and its ESI.† All programs used in this work as commercially available.

Author contributions

R. M. G.: investigation, validation, visualization. A. F.: conceptualization, writing – original draft, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank financial support from the Spain Ministry of Science, Innovation and Universities (MICIU/AEI of Spain; projects PID2020-115637GB-I00 and PID2023-148453NB-I00, FEDER funds).

Notes and references

1. A. Bauzá and A. Frontera, Angew. Chem., Int. Ed., 2015, 54, 7340–7343.
2. (a) M. Gao, J. Cheng, W. Li, B. Xiao and Q. Li, Chem. Phys. Lett., 2016, 651, 50–55; (b) L. M. Azofra, J. Elguero and I. Alkorta, Phys. Chem. Chem. Phys., 2020, 22, 11348–11353; (c) D. Quinonero, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2016, 18, 27939–27950; (d) G. Wang, Z. Chen, Z. Xu, J. Wang, Y. Yang, T. Cai, J. Shi and W. Zhu, J. Phys. Chem. B, 2016, 120, 610–620.
3. (a) M. D. Esrafili, F. Mohammadian-Sabet and M. Solimannejad, Chem. Phys. Lett., 2016, 659, 196–202; (b) M. D. Esrafili and E. Vessally, Chem. Phys. Lett., 2016, 662, 80–85; (c) W. Zierkiewicz, M. Michalczyk and S. Scheiner, Phys. Chem. Chem. Phys., 2018, 20, 4676–4687; (d) J. J. Miao, Z. H. Xiong and Y. Gao, J. Phys.: Condens. Matter, 2018, 30, 444001; (e) J. Miao, B. Song and Y. Gao, Chem. – Asian J., 2015, 10, 2615–2618.
4. (a) A. Bauzá and A. Frontera, Phys. Chem. Chem. Phys., 2015, 17, 24748–24753; (b) R. M. Gomila and A. Frontera, Front. Chem., 2020, 8, 395.
5. A. Pizzi, A. Dhaka, R. Beccaria and G. Resnati, Chem. Soc. Rev., 2024, 53, 6654.
6. (a) Y. V. Nelyubina, M. Y. Antipin and K. A. Lyssenko, Russ. Chem. Rev., 2010, 79, 167–187; (b) V. Y. Kotov and S. L. Gorei'sky, Russ. Chem. Bull., 1999, 48, 823–830.
7. S. R. Kass, J. Am. Chem. Soc., 2005, 127, 13098–13099.
8. R. Barbas, R. Prohens, A. Bauza, A. Franconetti and A. Frontera, Chem. Commun., 2019, 55, 115–118.
9. M. O. Miranda, D. J. R. Duarte and I. Alkorta, ChemPhysChem, 2020, 21, 1052–1059.
10. (a) R. Billing and D. E. Khoshtariya, Inorg. Chem., 1994, 33, 4038–4040; (b) Y. V. Nelyubina, K. A. Lyssenko, V. Yu. Kotov and M. Y. Antipin, J. Phys. Chem. A, 2008, 112, 8790–8796.
11. T. Beke-Somfai, P. Lincoln and B. Nordén, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4828–4833.
12. (a) W. Zhao, A. H. Flood and N. G. White, Chem. Soc. Rev., 2020, 49, 7893–7906; (b) N. G. White, CrystEngComm, 2019, 21, 4855–4858.
13. (a) M. Calabrese, A. Pizzi, R. Beccaria, A. Frontera and G. Resnati, ChemPhysChem, 2023, 24, e202300298; (b) A. Daolio, A. Pizzi, G. Terraneo, A. Frontera and G. Resnati, ChemPhysChem, 2021, 22, 2281–2285; (c) A. Daolio, A. Pizzi, G. Terraneo, M. Ursini, A. Frontera and G. Resnati, Angew. Chem., Int. Ed., 2021, 60, 14385–14389; (d) R. Beccaria, A. Dhaka, M. Calabrese, A. Pizzi, A. Frontera and G. Resnati, Chem. – Eur. J., 2024, 30, e202303641; (e) A. Grabarz, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Molecules, 2021, 26, 2116; (f) W. Zierkiewicz, M. Michalczyk, T. Maris, R. Wysokiński and S. Scheiner, Chem. Commun., 2021, 57, 13305–13308.
14. A. A. Kazakova, A. S. Kubasov, A. O. Chizhov, A. P. Novikov, M. A. Volkov, A. V. Borisov, V. G. Nenajdenko, E. A. Dukhnovsky, A. E. Bely, M. M. Grishina, A. S. Kritchenkov, R. M. Gomila, A. Frontera and A. G. Tskhovrebov, Inorg. Chim. Acta, 2024, 563, 121929.
15. K. O. Christe, E. C. Curtis, D. A. Dixon, H. P. Mercier, J. C. P. Sanders and G. J. Schrobilgen, J. Am. Chem. Soc., 1991, 113, 3351.
16. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
17. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
18. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
19. (a) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
20. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 2, 799–805.
21. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
22. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
23. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
24. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
25. K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340.
26. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
27. (a) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10; (b) A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939.
28. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
29. H. J. Frohn, T. Schroer and G. Henkel, Z. Naturforsch., B: J. Chem. Sci., 1995, 50, 1799.
30. H.-J. Frohn, T. Schroer and G. Henkel, Angew. Chem., Int. Ed., 1999, 38, 2554.
31. K. Koppe, J. Haner, H. P. A. Mercier, H.-J. Frohn and G. J. Schrobilgen, Inorg. Chem., 2014, 53, 11640.
32. D. Naumann, W. Tyrra, R. Gnann, D. Pfolk, T. Gilles and K.-F. Tebbe, Z. Anorg. Allg. Chem., 1997, 623, 1821.
33. K. Koppe, H.-J. Frohn, H. P. A. Mercier and G. J. Schrobilgen, Inorg. Chem., 2008, 47, 3205.
34. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
35. (a) S. J. Grabowski, Coord. Chem. Rev., 2020, 407, 213171; (b) S. J. Grabowski, Molecules, 2020, 25, 2703.
36. (a) A. Bauzá and A. Frontera, Angew. Chem., Int. Ed., 2015, 54, 7340–7343; (b) A. Bauzá, S. K. Seth and A. Frontera, Coord. Chem. Rev., 2019, 384, 107–125.
37. (a) S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 5702–5717; (b) S. Scheiner, Phys. Chem. Chem. Phys., 2020, 22, 16606–16614; (c) R. Wysokiński, M. Michalczyk, W. Zierkiewicz and S. Scheiner, Phys. Chem. Chem. Phys., 2019, 21, 10336–10346; (d) S. Scheiner, J. Phys. Chem. A, 2017, 121, 5561–5568.
38. E. C. Escudero-Adán, A. Bauzá, C. Lecomte, A. Frontera and P. Ballester, Phys. Chem. Chem. Phys., 2018, 20, 24192–24200.
39. Y. Jung and M. Head-Gordon, Phys. Chem. Chem. Phys., 2004, 26, 2008–2011.

---

Footnote

† Electronic supplementary information (ESI) available: Table S1 and Cartesian coordinated of optimized compounds. See DOI: https://doi.org/10.1039/d4ce01175a

---