Crystal/magnetic structure and cation inversion in hydrothermally synthesized MnFe₂O₄, CoFe₂O₄, NiFe₂O₄, and ZnFe₂O₄ nanoparticles: a neutron powder diffraction study

Abstract

The crystal and magnetic structures of MnFe₂O₄, CoFe₂O₄, NiFe₂O₄ and ZnFe₂O₄ nanocrystallites are reported based on joint structural modelling of powder X-ray diffraction and neutron powder diffraction data. The nanoparticle samples were prepared using equivalent precursor preparation routes (co-precipitation of transition metal hydroxides using NH₄OH) and identical hydrothermal synthesis conditions (steel autoclave, 200 °C, 1 hour), allowing the isolated effect of the divalent cation to be evaluated. The study uncovers how variations in cation site preferences, spinel inversion degree, and crystallite size, which are challenging to discern using conventional characterization techniques, distinctly influence the magnetic structures. Diffraction peak profile analysis and scanning transmission electron microscopy images show how MnFe₂O₄ forms the largest crystallites (17.13(2) nm), followed by NiFe₂O₄ (10.31(1) nm) and CoFe₂O₄ (7.92(1) nm), while ZnFe₂O₄ forms ultrafine nanoparticles of only 3.70(1) nm. The transition metal ions have different affinities for the tetrahedral and octahedral crystallographic sites as evident from the obtained spinel inversion degrees, x, [M²⁺_1−xFe³⁺_x]^tet[M²⁺_xFe³⁺_2−x]^octO₄. The MnFe₂O₄ and CoFe₂O₄ nanocrystallites exhibit mixed/semi-inverse spinel structures with x = 0.87(3) and 0.954(6), respectively, while NiFe₂O₄ is fully inverse (x = 1.00) and ZnFe₂O₄ is closer to a normal spinel (x = 0.138(4)). The combination of neutron diffraction and magnetic measurements illustrates how cation identity impacts site occupancy, crystallite size, and magnetization, providing new insights into the design of ferrite-based nanomaterials for magnetic applications.

---

Introduction

The spinel-structured ferrite compounds (MFe₂O₄, M = Mn, Fe, Co, Ni, Zn, etc.) are important magnetic materials, as their low cost, excellent resistance to corrosion and good magnetic performance make them crucial in a variety of applications, such as electromagnetic machinery (transformers/motors/generators), power supplies, high-frequency chokes and antennae, and microwave devices.¹ Furthermore, nanostructured spinel ferrite particles are currently being studied for uses in e.g. magnetic exchange-spring nanocomposites,^2,3 drug delivery,^4,5 neuromorphic spintronics,^6,7 magnetically recoverable nanocatalysts,^8,9 MRI contrast agents,^10,11 hyperthermia cancer treatment^12,13 and many more applications.¹⁴ In all applications, the performance of the spinel ferrite particles can be optimized by tuning or maximizing their magnetic properties, which are directly determined by the complex interplay between the crystal-, magnetic-, and micro-structure of the nanoparticles.^15,16

The spinel ferrites crystallize in the spinel structure (space group Fd3̄m), which consists of a face centered cubic (fcc) lattice of cubic close packed oxygen atoms within which 1/8 of the tetrahedral sites and 1/2 of the octahedral sites are occupied by the transition metal ions (see Fig. 1). Notably, the different divalent cations can exhibit different affinities for the specific crystallographic sites resulting in formation of normal spinel structures (all M²⁺ occupying all tetrahedral 8a Wyckoff sites), inverse spinel structures (all M²⁺ occupying half the octahedral 16d Wyckoff sites) or mixed spinels with a fraction, x, of the Fe³⁺ ions (called the inversion degree) occupying the tetrahedral sites, [M²⁺_1−xFe³⁺_x]^tet[M²⁺_xFe³⁺_2−x]^octO₄. For larger/bulk crystallites, the thermodynamically stable cation distribution is normal in ZnFe₂O₄, mixed in MnFe₂O₄, and inverse in CoFe₂O₄ and NiFe₂O₄,¹⁷ while nanosized crystallites have been reported to exhibit a variety of inversion degrees.^16,18–25

Fig. 1 Illustration of a mixed spinel structure in which both octahedral and tetrahedral sites are occupied by stoichiometric amounts of cations, i.e. 1/3 M²⁺ and 2/3 Fe³⁺. Illustration made with VESTA.²⁶

The magnetic properties of spinel ferrites are closely linked to the type and distribution of cations between tetrahedral and octahedral sites, which determine the net magnetization and anisotropy. At room temperature, the spinel ferrite compositions mentioned above (except for the paramagnetic ZnFe₂O₄) display a ferrimagnetic ordering, which is governed by a relatively strong antiparallel super-exchange-coupling between the neighbouring ions on the tetrahedral and octahedral sites.²⁷ As there are twice as many octahedrally as tetrahedrally coordinated transition metal ions in the structure, the net magnetisation generally lies along the octahedral moment direction. Consequently, the intrinsic magnetic properties of MFe₂O₄ nanoparticles are determined by the choice of divalent cation, M²⁺, and the distribution of the cationic species, M²⁺ and Fe³⁺, between the crystallographic sites in the spinel structure. At room temperature, bulk CoFe₂O₄ is a hard magnet (first uniaxial magneto-crystalline anisotropy constant, K₁, of 290 kJ m⁻³ and saturation magnetisation, M_s, of 75 Am² kg⁻¹), MnFe₂O₄ and NiFe₂O₄ are soft magnets (M_s = 83 Am² kg⁻¹ and 50 Am² kg⁻¹, respectively), and ZnFe₂O₄ is paramagnetic (antiferromagnet with Néel temperature, T_N, of 10 K).^27,28 Notably, we have previously demonstrated how hydrothermally synthesized Zn_xCo_1−xFe₂O₄ (0 ≤ x ≤ 1) nanocrystallites can be trapped in a meta-stable mixed spinel cation configuration with higher saturation magnetisation compared to the thermodynamically stable bulk configuration.²⁹

For nano-sized particles, variations in crystallite size can also have a particularly large influence on their magnetic behaviour, i.e. coercivity and susceptibility. In larger ferri-/ferromagnetic crystals, the build-up of magnetostatic energy in the structure drives a division of the crystal into distinct magnetic domains with different directions of magnetisation resulting in zero net magnetization.²⁷ These magnetic domains are separated by domain walls in which a gradual reorientation of the spins takes place across the domain wall thickness. When an external magnetic field is applied, the spin reorientation easily progresses in the material by gradual movement of magnetic domain walls. However, below a certain size threshold, domain formation is no longer energetically favourable compared to the magnetostatic energy of the uniformly magnetized body. Consequently, the crystallite can sustain a single magnetic domain and a coherent rotation of all spins is necessary to reverse the magnetisation of the crystallite. This leads to a substantial increase in the magnetic coercivity.²⁷ However, reducing the crystallite size further, below a certain limit, results in the particle entering a superparamagnetic state, in which a constant thermal flipping of the spins takes place, resulting in a loss of long-range magnetic order. In addition, very small nanoparticles have a considerable fraction of the magnetic atoms situated in the surface region where defects and dangling bonds cause their net magnetic moment to be reduced.^30,31 Consequently, the atomic- and nano-structural features discussed above directly determine the magnetic performance, i.e. coercive field, Curie/Neél temperature and saturation magnetisation of the materials.¹⁷ In this context, understanding and controlling the relationship between spinel ferrite synthesis, nanocrystallite size, crystal structure and magnetic properties is key to optimizing their performance.

In the present study, the crystal and magnetic structures of hydrothermally synthesized nanosized spinel ferrite crystallites with compositions MnFe₂O₄, CoFe₂O₄, NiFe₂O₄ and ZnFe₂O₄, are determined and compared. The selected ferrites represent a range of spinel systems with distinct cation distributions and magnetic behaviors, enabling a systematic evaluation of how divalent cations influence structural and magnetic properties. These compositions also span typical bulk spinel configurations from normal to inverse, making them ideal candidates for studying how cation site preferences affect nanoscale magnetic properties. To isolate the effect of the individual divalent ions on the obtained crystallite size and structure, the samples were prepared using the same precursor preparation procedures (co-precipitation of transition metal hydroxides), and applying identical hydrothermal reaction conditions (steel autoclave, 200 °C, 1 hour) for all four compositions. Notably, this is made possible by using 25% NH₄OH, a relatively weak precipitating base (compared to the 12–16 M NaOH from our previous studies), since Mn oxidation and hematite (α-Fe₂O₃) impurity formation are known to occur in MnFe₂O₄ synthesis at high pH.³² The structural analysis is carried out by joint Rietveld refinement of powder X-ray diffraction (PXRD) and neutron powder diffraction (NPD) data. Here, the NPD technique is particularly advantageous as the scattering length of neutrons varies erratically with atomic number, giving much higher contrast between neighbouring elements in the periodic table than provided from conventional X-ray diffraction.³³ The magnetic structures of the ferrites are evaluated by implementation of a magnetic structural model in the NPD data refinements and related to the macroscopic magnetic properties observed using vibrating sample magnetometry (VSM).

Experimental

Sample preparation

Precursor preparation route. An aqueous 0.6 M iron(III) hydroxide dispersion was prepared by dropwise addition of 25% NH₄OH to a solution of FeCl₃·6H₂O (Sigma-Aldrich, ≥98% purity) under constant magnetic stirring until a pH of 10 was reached. The FeOOH dispersion was repeatedly washed with demineralized water, centrifuged (3 minutes, 2000 rpm) and decanted until the supernatant pH was under 8. Subsequently, the prepared 0.6 M FeOOH dispersion was mixed with 2.0 M aqueous MCl₂ solution (M = Mn, Co, Ni, or Zn depending on the desired product) in the desired nominal molar amount. Then, 25% NH₄OH was added dropwise under constant magnetic stirring until a pH of 10 was reached. Under these moderately alkaline aqueous conditions, Fe precipitates as the trivalent oxyhydroxide (FeOOH) while Mn, Co, Ni and Zn form divalent hydroxides (M(OH)₂).^34,35 Notably, particular care was taken in the case of Mn to not increase pH above 10, as it forms trivalent Mn(OH)₃ or may precipitate as mixed valence Mn₃O₄ under highly alkaline conditions.^34,36

Autoclave synthesis. Gram-scale preparation of powders for neutron powder diffraction was carried out using 180 ml Teflon lined steel autoclaves as the reaction vessels, loaded with approximately 70 ml precursor. The autoclaves were placed in a convection oven preheated to 200 °C for 1 h. After the synthesis, the autoclaves were taken out of the oven and allowed to cool down at ambient temperature. Subsequently, the aqueous nanoparticle suspensions were washed with demineralized water and separated from the supernatant by centrifuging (3 minutes, 2000 rpm). The washing was repeated three times before the product was left to dry at 60 °C in a vacuum oven for >24 hours.

Characterisation

Laboratory PXRD. In-house powder X-ray diffraction patterns of the samples were collected at room temperature using a Rigaku SmartLab diffractometer (Rigaku, Japan) configured with cross beam optics in Bragg–Brentano geometry and equipped with a DteX/Ultra detector. The instrument was equipped with a cobalt anode (λ₁ = 1.7892 Å, λ₂ = 1.7931 Å). Data were collected in a 2θ-range of 15° to 125° (Q_max ≈ 6.2 Å⁻¹) with an angular resolution of 0.021°.

Neutron powder diffraction. Neutron powder diffraction experiments were carried out at the Cold Neutron Powder Diffractometer (DMC) instrument at the Swiss Spallation Neutron Source (SINQ), Paul Scherrer Institute (PSI), Villigen, Switzerland at room temperature using a wavelength of 2.459 Å.³⁷ Data collection was carried out on approximately 2 g of powder loaded into a vanadium can. The DMC instrument is equipped with a linear position sensitive BF₃ multidetector consisting of 400 detector channels at an angular separation of 0.21° covering a total angular range of 79.81° (Q_max ≈ 3.7 Å⁻¹). The detector was moved between two positions to attain an angular resolution of 0.11°.

Co-refinement of PXRD and NPD data. Co-refinement of PXRD and NPD data using a constrained structural model was carried out using the Fullprof Suite software package.³⁸ The model was based on the spinel structures of the given MFe₂O₄ (M = Mn, Co, Ni, Zn) composition in the cubic Fd3̄m space group. Linear restraints were imposed to avoid unphysical over- or under-population on the tetrahedral 8a and octahedral 16d Wyckoff sites while keeping a nominal stoichiometric ratio of 1 : 2 between M²⁺ and Fe³⁺. The lattice parameters, crystallite size, atomic position of oxygen on the 32e Wyckoff site and an overall isotropic atomic displacement parameter (B_iso) were refined in a constrained manner, while scale factor, zero shift (or sample displacement in the case of the NPD) and background (Chebyshev polynomial) were refined for the individual patterns. The peak profiles were modelled using the Thompson–Cox–Hastings formulation of the pseudo-Voigt function.³⁹ The instrumental contribution to the peak profiles were determined by Rietveld refinement of data from a NIST LaB₆ 660B line profile standard (PXRD) and a Na₂Ca₃Al₂F₁₄ standard (NPD), measured in the same instrumental configurations as the samples, and deconvoluted from the data in the refinements. The crystallite sizes (i.e. mean volume-averaged isotropic dimensions of coherently scattering crystalline domains), 〈D〉, were estimated from the refined peak broadening parameters by the Scherrer equation, 〈D〉 = (K·λ)/(H·cos(θ)),⁴⁰ where λ is the wavelength, θ is the Bragg angle, H is the full width at half the maximum intensity, and K is the shape factor (here set to 0.829 assuming isotropic crystallite morphology).⁴¹

Magnetic structure refinement. For the NPD data, the contribution from the magnetic scattering was described using a collinear ferrimagnetic model with antiparallel magnetic moments on the tetrahedral and octahedral sites.¹⁵ Notably, the magnetic easy axis in a cubic lattice is determined by the composition- and temperature-dependent magnetocrystalline anisotropy of the specific material. The magnetic easy axis of a cubic structure is along the 〈100〉 direction for materials with a positive first anisotropy constant (K₁ > 0), and along the 〈111〉 direction for materials with a negative first anisotropy constant (K₁ < 0).¹⁷ Therefore, CoFe₂O₄ (K₁ = 290 kJ m⁻³) at room temperature has its easy magnetization axis along 〈100〉, while the easy axes of MnFe₂O₄ (K₁ = −3 kJ m⁻³) and NiFe₂O₄ (K₁ = −7 kJ m⁻³) lie along the 〈111〉 crystallographic direction.^27,28 However, the symmetry of cubic structures prevents discrimination between the different axis options by structural refinement of powder neutron diffraction data,⁴²i.e. changing the direction of the refined Cartesian magnetic moment components, between 〈100〉 and 〈111〉 produces no difference in the obtained fit quality and refined magnetic moment magnitudes. Consequently, the theoretical magnetic easy axes, i.e. 〈100〉 for CoFe₂O₄ and 〈111〉 for MnFe₂O₄ and NiFe₂O₄, were employed in the refinements, with the 〈111〉 axis also being employed for the magnetic modelling of ZnFe₂O₄ (paramagnetic in theory) data.

STEM and STEM-EDS. The nanoparticles were suspended in pure (99.9%) ethanol and sonicated for ∼4 min before they were drop-casted onto an Au 300 mesh grid with an ultrathin (approx. 3 nm) carbon film on lacey carbon. Scanning transmission electron microscopy (STEM) images and STEM energy-dispersive X-ray spectroscopy (EDS) datasets were collected using a Talos FX-200 operated at an acceleration voltage of 200 keV. The beam convergence angle was 10.5 mrad. The collection angle of the high angle annular dark field (HAADF) detector was 60–200 mrad. STEM-EDS data was collected using the installed Bruker ChemiSTEM system. The total collection time of each EDS dataset differed between ∼3 min and ∼25 min depending on a trade-off between optimizing signal-to-noise and minimizing contamination build-up. The latter was quite significant for the ZnFe₂O₄ sample, which made long data collection times impossible.

Size distributions were determined manually using the software FIJI.⁴³ It was assumed that the particles were spherical. Between 165 and 770 particles were counted for the four different samples. The STEM images were plotted using the python libraries HyperSpy,⁴⁴ Pandas,⁴⁵ numpy,⁴⁶ and Matplotlib.⁴⁷

For the analysis of the EDS dataset, the automated quantification of the atomic fraction implemented to the Velox software used to control the ChemiSTEM system was used to obtain the averaged atomic ratios between the elements, no absorption correction was used. The EDS element maps were plotted using the python library HyperSpy.⁴⁴ For this, the background around the relevant elemental peaks were subtracted using a linear background interpolation prior to integration over the elemental peak, as implemented in HyperSpy.⁴⁴ The individual count maps were smoothed using a Gaussian kernel of 1 pixel and plotted using the python libraries SciPy,⁴⁸ and Matplotlib.⁴⁷

Magnetic properties. Magnetic hysteresis curves were measured using a Quantum Design Physical Property Measurement System (PPMS) equipped with a Vibrating Sample Magnetometer (VSM). The field dependent magnetisation of the samples was measured at 300 K on cold pressed pellets (diameter = 2.7 mm, mass = 5–20 mg) by scanning the external field between ±1592 kA m⁻¹ (±2 T). The measurements were conducted at a frequency of 40 Hz and an averaging time of 2 seconds.

Results and discussion

Crystal-, magnetic- and microstructure of MnFe₂O₄ nanocrystallites

Fig. 2a and b show the PXRD and NPD data with Rietveld refined fits obtained from the MnFe₂O₄ nanoparticle sample. The diffraction patterns show no indication of any secondary crystalline phases, as all reflections can be attributed to the spinel ferrite structure. The refined atomic structure is illustrated in Fig. 2c and the structural parameters are summarized in Table 1. A relatively good fit is obtained for the PXRD data; however, the model struggles to fully describe the NPD data. In particular, the (400) Bragg reflection at Q ≈ 3 Å⁻¹ in the NPD data, which has a significant contribution from both the nuclear and magnetic scattering, shows a considerable misfit. Since, Mn²⁺ and Fe³⁺ have the same electron configuration (3d⁵), and therefore very similar X-ray scattering form factors,⁴⁹ their respective content and position in the structure cannot be accurately determined from PXRD data alone, as equivalent PXRD fit quality will be obtained irrespective of cation distribution.⁵⁰ Thus, the obtained distribution of cations relies on the fit to the NPD data, which for the MnFe₂O₄ sample studied here exhibits a considerable contribution from the magnetic structure. Considering that the misfit is mainly observed for the NPD data, the cause can be several factors including: 1) incorrect cation distribution between tetrahedral (8a) and octahedral (16d) sites; 2) incorrect assumption of stoichiometric sample composition, i.e. Mn/Fe ratio erroneously fixed in the refinement; 3) oxidation of Mn²⁺ to Mn³⁺ and introduction of cation vacancies in the spinel structure (similar to the ambiguous cases in the maghemite (γ-Fe₂O₃) and magnetite (Fe₃O₄) systems);⁵¹ 4) incorrect or oversimplified model for the magnetic structure, which is assumed to be isostructural to the nuclear structure (same unit cell), with antiparallel moments on the 8a and 16d site aligned along the 〈111〉 crystallographic direction.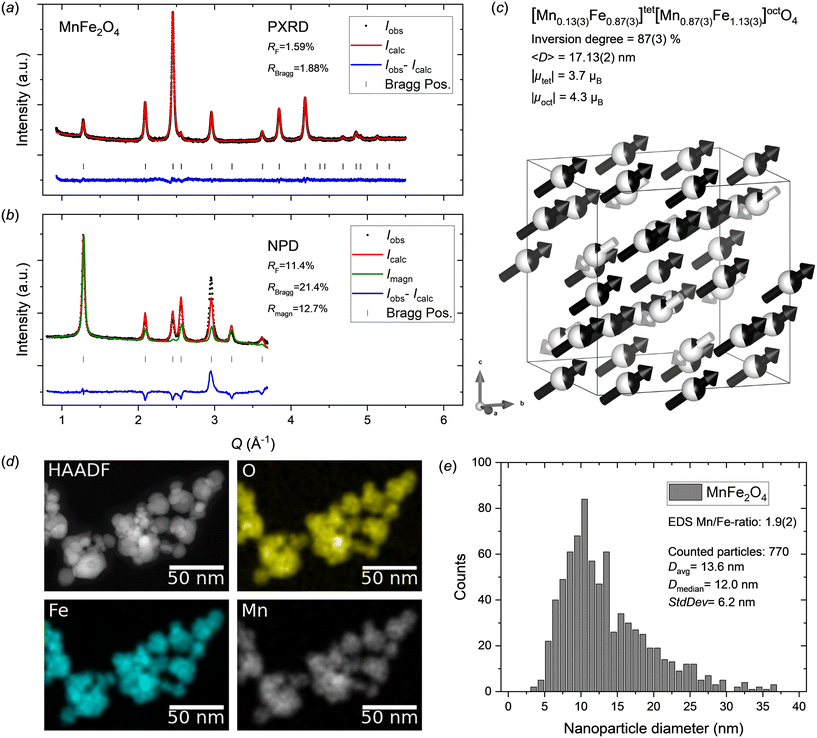

Fig. 2 a) PXRD and b) NPD data for MnFe₂O₄ nanocrystallites with jointly refined Rietveld fits. c) Illustration of the refined crystal and magnetic structure of the MnFe₂O₄ sample. The white and black arrows indicate the relative magnitudes and orientations of the refined magnetic moment components on tetrahedral and octahedral sites, respectively. The refined atomic site occupation fractions of Mn²⁺ (black) and Fe³⁺ (white) are illustrated on the spheres. Illustration made with VESTA.²⁶ d) STEM-HAADF image and EDS elemental maps for the MnFe₂O₄ nanoparticle sample. e) MnFe₂O₄ nanoparticle size analysis from STEM data.

Table 1 Atomic structure parameters for the MnFe₂O₄ nanocrystallite sample

MnFe2O4
Space group: Fd3̄m (#227)
Unit cell: a = b = c = 8.49637(9) Å, α = b = γ = 90°
Fit quality PXRD: RBragg = 1.88%, RF = 1.59%
Fit quality NPD: RBragg = 21.4%, RF = 11.4%, Rmagn = 12.7%
Atom	Wyckoff site	x	y	z	B iso (Å^2)	sof	R x (μB)
Note: the numbers in parentheses indicate the errors on the last significant digit of the refined parameters.a Site occupation fraction (sof).b The magnetic moment vector component (Rx = Ry = Rz) refined along the 〈111〉 direction.c The atomic displacement parameters (Biso) were constrained to be equal.d Linear restraints were imposed on the tetrahedral (8a) and octahedral (16d) site occupancies to avoid unphysical over-population and constrain to nominal composition.
Mn	8a	0.125	0.125	0.125	1.24(1)^c	0.13(3)^d	−2.1
Fe	8a	0.125	0.125	0.125	1.24(1)^c	0.87(3)^d	−2.1
Mn	16d	0.5	0.5	0.5	1.24(1)^c	0.44(2)^d	2.5
Fe	16d	0.5	0.5	0.5	1.24(1)^c	0.56(2)^d	2.5
O	32e	0.25695(9)	0.25695(9)	0.25695(9)	1.24(1)^c	1	0

---

To evaluate these potential causes, various changes to the structural model were tested (see Supporting Information). Notably, free refinement of cation occupancies (Mn²⁺, Mn³⁺, Fe²⁺, Fe³⁺) and vacancy concentrations on the tetrahedral and octahedral sites is impossible due to heavy correlations leading to refinement divergence. Thus, a stable refinement can only be achieved by implementing linear restraints on composition and site occupancies (as described in the experimental section) or fixing certain parameters. The tested models include: 1) free refinement of Mn-content (site occupation fractions linearly restrained to 1.0). 2) Magnetite, i.e. Mn-deficient structure (Fe₃O₄). 3) Maghemite, i.e. Mn-deficient structure with disordered vacancies (γ-Fe₂O₃). 4) Maghemite-like structure with disordered vacancies and nominal stoichiometric Mn : Fe ratio (γ-Mn_0.67Fe_1.33O₃). 5) Changing from divalent to trivalent Mn in the magnetic structure. However, significantly poorer fits were obtained for options 1–4 and option 5 yielded no noticeable improvement compared to the initially employed MnFe₂O₄ model (see ESI†). Notably, STEM-EDS maps (see Fig. 2d) show a homogeneous elemental distribution in the MnFe₂O₄ nanoparticles confirming the single-phase nature of the sample, and the 1 : 2 metal ion stoichiometry was confirmed by quantitative analysis of EDS spectra. Furthermore, in a previous study, we employed X-ray absorption spectroscopy (XAS) to confirm the oxidation states in spinel ferrite nanoparticles, including analogously prepared MnFe₂O₄ nanocrystallites, which confirmed divalent Mn and trivalent Fe.¹⁵ In addition, the refined cell parameter of 8.49637(9) Å is in good agreement with previous reports for stoichiometric MnFe₂O₄ (typically ∼8.5 Å)^52,53 rather than those generally reported for Fe₃O₄ or γ-Fe₂O₃ (typically ∼8.35–8.40 Å),^18,54,55 indicating that the assumptions of nominal MnFe₂O₄ composition in the sample, Mn²⁺ and Fe³⁺ oxidation states and no vacancies in the structure are likely correct. Consequently, despite the shortcoming of the employed model, the cause for the misfit could not be identified, and no better description could be achieved here.

The peak profile analysis yielded a mean MnFe₂O₄ crystallite dimension, 〈D〉, of 17.13(2) nm. The atomic structure refinement yielded an inversion degree of 87(3)%, which is significantly different from the value for bulk MnFe₂O₄, which is generally reported to have around 20–25% inversion.^56,57 However, disordered cation distributions (inversion degrees of ∼60–70%, i.e. near-stoichiometric and disordered Mn/Fe occupancy on each site) have previously been reported for fine nanocrystallites (<10 nm).^18,19

The contribution from magnetic scattering to the NPD data was modelled by implementing a collinear ferrimagnetic structure with antiparallel moments on the 8a and 16d site aligned along the 〈111〉 crystallographic direction. Concurrent and unconstrained refinement of the Mn²⁺ and Fe³⁺ Cartesian magnetic moment components on both tetrahedral and octahedral sites (together with site occupancies) introduced too many degrees of freedom and excessive parameter correlations, thereby causing refinement divergence. Consequently, the magnetic orientations were fixed to lie along the 〈111〉 direction (i.e. R_x = R_y = R_z constraint) and average moments (i.e. R_Mn = R_Fe constraint) were refined for each of the tetrahedral and octahedral sites, yielding net magnetic moments, μ = (R_x² + R_y² + R_z²)^1/2, of |μ_tet| = 3.7μ_B and |μ_oct| = 4.3μ_B.

As mentioned earlier, the STEM-EDS maps show a homogeneous elemental distribution in the MnFe₂O₄ nanoparticles (see Fig. 2d) and EDS spectra collected in several different regions yielded an average Mn/Fe ratio of 1.9(2), which agrees with the formal 1 : 2 ratio. The STEM images (see Fig. 2d and ESI†) confirm the nanocrystalline nature and isotropic morphology of the nanoparticles. Particle size analysis was carried out by manual measurement of 770 individual particles across representative STEM micrographs taken different places on the grids. The resulting particle size distribution is shown in Fig. 2e. The obtained average particle size of 13.6 ± 6.2 nm, although somewhat smaller, is compatible with the crystallite size from the diffraction data analysis (17.13(2) nm). The discrepancy can be ascribed to the relatively broad and skewed lognormal-like size distribution, which enhances the difference between the average number weighted size from STEM analysis and volume-weighted size that is inherently obtained from diffraction data.

Crystal-, magnetic- and microstructure of CoFe₂O₄ nanocrystallites

Fig. 3a and b show the PXRD and NPD patterns and corresponding jointly refined Rietveld fits for the hydrothermally synthesized CoFe₂O₄ nanocrystallite sample. All reflections could be attributed to the spinel ferrite structure and the data show no indication of any secondary crystalline phases. Relatively good fits were obtained to both the PXRD and NPD data, however, like the MnFe₂O₄ sample discussed above, a considerable misfit is observed for the (400) reflection at ∼3 Å⁻¹. The refined atomic and magnetic structure is shown in Fig. 3c and the structural parameters are provided in Table 2. The obtained cell parameter of 8.3901(1) Å is in good agreement with previously reported values for CoFe₂O₄ nanocrystallites, further supporting that nominal stoichiometry and phase purity have been achieved.^15,18,58,59 The peak profile analysis yields a mean crystallite size of 7.92(1) nm and the atomic structure refinement indicates an almost fully inverse spinel structure with an inversion degree of 95.4(6)%. This value is in agreement with the known bulk preference for the inverse configuration,¹⁷ although nanosized CoFe₂O₄ crystallites have been reported to adopt mixed spinel structures.^18,59 This could indicate a size- and/or synthesis method-dependent nature of the cation configuration in CoFe₂O₄. The collinear ferrimagnetic structure was refined along the 〈100〉 crystallographic direction given the hard magnetic properties of the compound (see experimental section), with net magnetic moments of 3.5 and 3.6μ_B obtained for the tetrahedral and octahedral sites, respectively.

Fig. 3 a) PXRD and b) NPD data for CoFe₂O₄ nanocrystallites with jointly refined Rietveld fits. c) Illustration of the refined crystal and magnetic structure of the CoFe₂O₄ sample. The white and black arrows indicate the relative magnitudes and orientations of the refined magnetic moment components on tetrahedral and octahedral sites, respectively. The refined atomic site occupation fractions of Co²⁺ (red) and Fe³⁺ (white) are illustrated on the spheres. Illustration made with VESTA.²⁶ d) STEM-HAADF image and EDS elemental maps for the CoFe₂O₄ nanoparticle sample. e) CoFe₂O₄ nanoparticle size analysis from STEM data.

Table 2 Atomic structure parameters for the CoFe₂O₄ nanocrystallite sample

CoFe2O4
Space group: Fd3̄m (#227)
Unit cell: a = b = c = 8.3901(1) Å, α = b = γ = 90°
Fit quality PXRD: RBragg = 4.09%, RF = 4.25%
Fit quality NPD: RBragg = 10.4%, RF = 6.22%, Rmagn = 6.09%
Atom	Wyckoff site	x	y	z	B iso (Å^2)	sof	R x (μB)
Note: the numbers in parentheses indicate the errors on the last significant digit of the refined parameters.a Site occupation fraction (sof).b The magnetic moment vector component (Rx) refined along the 〈100〉 direction.c The atomic displacement parameters (Biso) were constrained to be equal.d Linear restraints were imposed on the tetrahedral (8a) and octahedral (16d) site occupancies to avoid unphysical over-population and constrain to nominal composition.
Co	8a	0.125	0.125	0.125	1.09(1)^c	0.046(6)^d	−3.5
Fe	8a	0.125	0.125	0.125	1.09(1)^c	0.954(6)^d	−3.5
Co	16d	0.5	0.5	0.5	1.09(1)^c	0.477(3)^d	3.6
Fe	16d	0.5	0.5	0.5	1.09(1)^c	0.523(3)^d	3.6
O	32e	0.25634(8)	0.25634(8)	0.25634(8)	1.09(1)^c	1	0

---

The elemental mapping by STEM-EDS shows a homogeneous distribution of the metal ions in the CoFe₂O₄ nanoparticles (see Fig. 3d), which is consistent with a single-phase sample. Quantitative analysis of EDS spectra collected in several different regions yielded an average Co/Fe ratio of 2.2(3), which agrees well with the formal 1 : 2 metal ion stoichiometry. The nanocrystalline nature and isotropic morphology of the nanoparticles were confirmed by the STEM images (see Fig. 3d and ESI†). Particle size analysis was carried out by manual measurement of 528 individual particles across representative STEM micrographs taken different places on the grids. The resulting particle size distribution is shown in Fig. 3e. The average particle size of 8.8 ± 3.2 nm agrees well with the nanocrystallite size obtained from the diffraction data analysis (7.92(1) nm).

Crystal-, magnetic- and microstructure of NiFe₂O₄ nanocrystallites

Fig. 4a and b show the jointly refined PXRD and NPD patterns collected on the NiFe₂O₄ nanocrystallites. The diffraction data show no indications of secondary crystalline phases and relatively good fits were obtained for both the PXRD and NPD patterns, including the (400) peak of the NPD data, which was not fully described for the MnFe₂O₄ and CoFe₂O₄ samples. The refined crystal- and magnetic structure is illustrated in Fig. 4c and the structural parameters are provided in Table 3. A cubic cell parameter of 8.3574(1) Å was obtained, which is in good agreement with previously reported values for NiFe₂O₄ (∼8.33–8.36 Å).^60–63 In the bulk, NiFe₂O₄ is an inverse spinel,¹⁷ however, both inverse and mixed spinel structures have been reported for nanosized crystallites,^18,20–22 indicating a potential dependence on particle size or synthesize route. Here, the initial linearly restrained refinement of the site occupancies led to a slight unphysical overpopulation of Ni²⁺ on the 16d site and under population on the 8a site, indicating a strong preference for the inverse spinel configuration. Therefore, the site occupations were fixed to the fully inverse distribution in the final refinement. The peak profile analysis yielded a mean crystallite size of 10.31(1) nm. Given that NiFe₂O₄ is a soft magnetic material, the atomic magnetic moment components were refined along the theoretically preferred space diagonal of the cubic unit cell (〈111〉 direction). Net moments of 3.6 and 3.1μ_B were obtained for the 8a and 16d sites, respectively.

Fig. 4 a) PXRD and b) NPD data for NiFe₂O₄ nanocrystallites with jointly refined Rietveld fits. c) Illustration of the refined crystal and magnetic structure of the NiFe₂O₄ sample. The white and black arrows indicate the relative magnitudes and orientations of the refined magnetic moment components on tetrahedral and octahedral sites, respectively. The atomic site occupation fractions of Ni²⁺ (blue) and Fe³⁺ (white) are illustrated on the spheres. Illustration made with VESTA.²⁶ d) STEM-HAADF image and EDS elemental maps for the NiFe₂O₄ nanoparticle sample. e) NiFe₂O₄ nanoparticle size analysis from STEM data.

Table 3 Atomic structure parameters for the NiFe₂O₄ nanocrystallite sample

NiFe2O4
Space group: Fd3̄m (#227)
Unit cell: a = b = c = 8.3574(1) Å, α = b = γ = 90°
Fit quality PXRD: RBragg = 6.68%, RF = 5.17%
Fit quality NPD: RBragg = 3.29%, RF = 1.87%, Rmagn = 2.88%
Atom	Wyckoff site	x	y	z	B iso (Å^2)	sof	R x (μB)
Note: the numbers in parentheses indicate the errors on the last significant digit of the refined parameters.a Site occupation fraction (sof).b The magnetic moment vector component (Rx = Ry = Rz) refined along the 〈111〉 direction.c The atomic displacement parameters (Biso) were constrained to be equal.
Ni	8a	0.125	0.125	0.125	0.66(1)^c	0	−2.1
Fe	8a	0.125	0.125	0.125	0.66(1)^c	1	−2.1
Ni	16d	0.5	0.5	0.5	0.66(1)^c	0.5	1.8
Fe	16d	0.5	0.5	0.5	0.66(1)^c	0.5	1.8
O	32e	0.25841(9)	0.25841(9)	0.25841(9)	0.66(1)^c	1	0

---

The STEM-EDS maps of the NiFe₂O₄ nanoparticles show an even homogeneous distribution of Ni and Fe in the sample (see Fig. 4d) corroborating the single-phase nature. The 1 : 2 metal ion stoichiometry of the Ni spinel ferrite compound was confirmed by quantitative analysis of EDS spectra collected in several different regions yielding an average Ni/Fe ratio of 2.1(2). The STEM images (see Fig. 4d and ESI†) confirm the nanocrystalline nature and isotropic morphology of the nanoparticles. Particle size analysis was carried out by manual measurement of 394 individual particles across representative TEM micrographs taken different places on the grids. The resulting particle size distribution is shown in Fig. 4e. The obtained average particle size of 9.4 ± 3.2 nm is agreement with crystallite dimension from the diffraction data analysis (10.31(1) nm).

Crystal-, magnetic- and microstructure of ZnFe₂O₄ nanocrystallites

The PXRD and NPD patterns of the ZnFe₂O₄ nanocrystallite sample and the corresponding Rietveld fits are shown in Fig. 5a and b. As evident from the highly broadened diffraction peaks, the ZnFe₂O₄ sample consists of ultrafine crystallites (〈D〉 = 3.70(1) nm). The diffraction data do not show any additional crystalline phases to be present in the sample as all peaks are well described by the spinel structure model. The refined crystal- and magnetic structure is illustrated in Fig. 5c and the structural parameters are provided in Table 4. A cell parameter of 8.4588(4) is obtained, which agrees with the relatively large variety of previously reported values for ZnFe₂O₄ nanoparticles (∼8.39–8.45 Å), when considering the very small particles size, which often causes some cell expansion due to the increased surface/bulk ratio.^18,23,64,65 A spinel inversion of 13.8(4)% is obtained from the refinement, which differs from the thermodynamically stable normal spinel configuration,¹⁷ but falls within the various degrees of inversion between 0 and 0.6 that have been reported for nanosized crystallites in the literature.^18,23,24 At first glance, the combination of an almost completely normal spinel structure, with the majority of non-magnetic Zn²⁺ on the tetrahedral site, could be expected to yield a highly optimized intrinsic magnetic performance. However, the very low amount of a magnetic species (Fe³⁺) on the tetrahedral site leads to a destabilization of the magnetic structure due to the weak antiferromagnetic tetrahedral–octahedral superexchange coupling. This causes the material to be paramagnetic at room temperature (as evident from the magnetization data discussed later) and is the reason for the very weak magnetic scattering observed. At very low temperature (<10 K), ZnFe₂O₄ forms a long-range antiferromagnetic structure, as the low thermal energy allows extended antiferromagnetic superexchange coupling between the octahedral Fe³⁺ moments.⁶⁶ Here, despite the largely paramagnetic nature of the sample, the small magnetic scattering contribution was modelled based on a collinear ferrimagnetic structure along the 〈111〉 crystallographic direction, yielding small net moments of 1.9 and 1.5μ_B on the tetrahedral and octahedral sites, respectively. The small amount of long-range magnetic diffraction signal present can be ascribed to a slight magnetic ordering induced by the small amount of tetrahedral Fe³⁺, which results in regions with sufficient coherently scattering magnetic ordering.

Fig. 5 a) PXRD and b) NPD data for ZnFe₂O₄ nanocrystallites with jointly refined Rietveld fits. c) Illustration of the refined crystal and magnetic structure of the ZnFe₂O₄ sample. The refined magnetic moment components on tetrahedral and octahedral sites are too small to be illustrated. The refined atomic site occupation fractions of Zn²⁺ (green) and Fe³⁺ (white) are illustrated on the spheres. The displayed arrows have been scaled ×2 compared to the other structural illustrations to make them visible. Illustration made with VESTA.²⁶ d) STEM-HAADF image and EDS elemental maps for the ZnFe₂O₄ nanoparticle sample. e) ZnFe₂O₄ nanoparticle size analysis from STEM data.

Table 4 Atomic structure parameters for the ZnFe₂O₄ nanocrystallite sample

ZnFe2O4
Space group: Fd3̄m (#227)
Unit cell: a = b = c = 8.4588(4) Å, α = b = γ = 90°
Fit quality PXRD: RBragg = 1.48%, RF = 1.41%
Fit quality NPD: RBragg = 4.20%, RF = 2.37%, Rmagn = 5.01%
Atom	Wyckoff site	x	y	z	B iso (Å^2)	sof	R x (μB)
Note: the numbers in parentheses indicate the errors on the last significant digit of the refined parameters.a Site occupation fraction (sof).b The magnetic moment vector component (Rx = Ry = Rz) refined along the 〈111〉 direction.c The atomic displacement parameters (Biso) were constrained to be equal.d Linear restraints were imposed on the tetrahedral (8a) and octahedral (16d) site occupancies to avoid unphysical over-population and constrain to nominal composition.
Zn	8a	0.125	0.125	0.125	0.51(2)^c	0.862(4)^d	0
Fe	8a	0.125	0.125	0.125	0.51(2)^c	0.138(4)^d	−8.1
Zn	16d	0.5	0.5	0.5	0.51(2)^c	0.069(2)^d	0
Fe	16d	0.5	0.5	0.5	0.51(2)^c	0.931(2)^d	0.9
O	32e	0.2489(3)	0.2489(3)	0.2489(3)	0.51(2)^c	1	0

---

Fig. 5d shows a representative STEM-EDS map illustrating the homogeneous elemental distribution in the ZnFe₂O₄ nanoparticles. The expected 1 : 2 metal ion stoichiometry was confirmed by quantitative analysis of EDS spectra collected in several different regions yielding an average Zn/Fe ratio of 2.3(4). The nanocrystalline nature and isotropic morphology of the nanoparticles are confirmed by the TEM images (see Fig. 5d and ESI†). Particle size analysis was carried out by manual measurement of 165 individual particles across representative STEM micrographs taken different places on the grids. The resulting particle size distribution is shown in Fig. 5e. The obtained average particle size of 5.1 ± 1.6 nm is compatible with the crystallite size from the diffraction data analysis (3.70(1) nm).

Magnetic properties

The magnetic hysteresis curves of the four samples collected by VSM are shown in Fig. 6a, illustrating their distinct magnetic behaviour as a result of their different atomic- and nano-structural natures. The MnFe₂O₄ (M_s = 63.0(1) Am² kg⁻¹), CoFe₂O₄ (M_s = 64.2(1) Am² kg⁻¹) and NiFe₂O₄ (M_s = 50.2(1) Am² kg⁻¹) nanocrystallite samples exhibit magnetic responses characteristic of soft magnets, while the ZnFe₂O₄ (M_s = 6.1(1) Am² kg⁻¹) sample is paramagnetic. Notably, bulk CoFe₂O₄ is known to exhibit semi-hard magnetic properties with an effective magnetocrystalline anisostropy constant, K₁, of 290 kJ m⁻³ and a Curie temperature, T_C, of 790 °C.²⁷ Thus, the lack of a coercive field indicates that the dimensions of the synthesized CoFe₂O₄ particles are below the superparamagnetic limit. The spin reversal time, τ, for superparamagnetic nanoparticles can be estimated by the Néel–Brown law, τ = τ₀ exp(K₁V/k_BT), where τ₀ is the attempt time (∼1 ns), k_B is the Boltzmann constant, V is the crystallite volume, and T is the temperature.^28,67 For isotropic crystallites, the critical superparamagnetic threshold diameter D_sp can be obtained from the Néel–Brown law as follows: D_sp = [6k_BT ln[τ/τ₀]/(πK₁)]^1/3. By setting the spin reversal time equal to the VSM measurement averaging time (2 s), a critical dimension of ∼8.4 nm is obtained for CoFe₂O₄ at 300 K. The average crystallite size of 7.92(1) nm obtained from peak profile analysis of the diffraction data is therefore below the superparamagnetic limit and in agreement with the observed lack of magnetic hysteresis. The slight opening of the hysteresis loop for the CoFe₂O₄ sample illustrated in the insert of Fig. 6a (H_c = 13.2(2) kA m⁻¹) can be attributed to polydispersity with a minor part of the crystallites having sizes above the critical dimension.

Fig. 6 a) Room temperature field dependent magnetisation curves of the MnFe₂O₄, CoFe₂O₄, NiFe₂O₄, and ZnFe₂O₄ nanoparticles with saturation magnetisations, M_s, (determined by law of approach to saturation) indicated. b) Comparison of intrinsic magnetizations estimated from the magnetic structure refinement of the NPD data (M_NPD) and the macroscopic saturation magnetizations from the VSM data (M_s).

The magnetic properties of spinel ferrites depend on a combination of factors, including the type of divalent ion, the spinel inversion degree, and the crystallite size.¹⁷ As demonstrated in our previous studies, the inversion degree of spinel ferrite nanoparticles may differ significantly from their bulk counterparts and may vary considerably depending on employed synthesis conditions and/or with thermal history.^15,29,68Fig. 6b compares the saturation magnetizations calculated from the refinements of structure and magnetic moment in the NPD, M_NPD, to the observed macroscopic saturation magnetizations, M_s, from the VSM data. The M_NPD value may be used as an estimate for the upper-limit intrinsic saturation magnetization permitted by the structure for a fully crystalline sample. Although the magnetizations from the two methods follow similar trends, the plot also illustrates the somewhat limited agreement between the two approaches and the relatively poor predictive capability of the M_NPD value. This may be due to several factors, including the very high uncertainties of the magnetic structure refinement, reduced crystallinity of the sample, and the influence of microstructural and finite-size effects.^30,31

Discussion

All of the ferrite samples studied here (MnFe₂O₄, CoFe₂O₄, NiFe₂O₄, and ZnFe₂O₄) were confirmed to be spinel structured, nanosized and phase pure (i.e. no crystalline impurities observed). To ensure the formation of phase-pure spinel ferrites without impurities such as hematite (α-Fe₂O₄) or manganese oxides, several key parameters were carefully controlled. A precise stoichiometry of the metal ions was maintained to match the target spinel compositions, ensuring a balanced cation distribution. Uniform mixing of the precursor species was achieved through constant magnetic stirring during the dropwise addition of 25% NH₄OH, which provided a moderately basic environment (pH ≈ 10). This pH was critical for promoting the precipitation of homogeneous FeOOH and M(OH)₂ gels, especially for MnFe₂O₄, where excessive alkalinity could lead to manganese oxide impurities.^34,35 The presence of divalent transition metal species in the precursor mixture further ensured spinel phase formation, as highlighted by our earlier study showing their role in preventing α-Fe₂O₃ crystallization.⁶⁹

The obtained crystallite sizes, unit cell lengths, cation inversion degrees and saturation magnetisations of the samples from this study are summarised in Table 5, where they are compared to values from our previous studies employing different precursor routes and/or synthesis conditions.^15,29 Variations in cell parameters (PXRD peak positions) and crystallite/particle size (PXRD peak widths and STEM analysis) caused by the distinct chemistries of the different divalent transition metal ions are observed. In the present study, all precursors were equivalently prepared by the NH₄OH method described earlier, and treated at identical physical reaction conditions, i.e. in an autoclave reactor at 200 °C for 1 h. However, in the previous studies various adjustments to the procedure were done, as indicated for the specific cases below, to promote certain product characteristics. The stronger NaOH base is often used as the precipitating agent in hydrothermal spinel ferrite synthesis, however, the NH₄OH precursor preparation route was used for the preparation of MnFe₂O₄ nanocrystallites in both this and our previous study. This is because the NaOH route does not yield phase pure MnFe₂O₄ samples, but instead leads to formation of a considerable amount of α-Fe₂O₃ impurity. Here, a higher synthesis temperature of 200 °C was used, which is found to cause formation of larger MnFe₂O₄ crystallites of 17.13(2) nm compared to 13.5(2) nm obtained at 150 °C. In addition, the higher temperature yields a higher inversion degree of 0.87(3) compared to the 0.643(3) obtained at 150 °C. A small increase in M_s is also observed. Since Mn²⁺ and Fe³⁺ ions have identical ground state 3d⁵ electron configurations, the increased M_s is likely a result of the larger crystallite size.

Table 5 Summary of hydrothermally synthesized spinel ferrite nanoparticle characteristics obtained in the present study compared to our previous studies employing different precursor routes and/or synthesis conditions

Compound	Study	Base type	Synthesis conditions	Crystallite size (nm)	Unit cell length (Å)	Inversion deg.	M s (Am^2 kg^−1)
a Weighted average from bimodal size model.
MnFe2O4	This study	25% NH4OH (pH = 10)	AC, 200 °C, 1 h	17.13(2)	8.49637(9)	0.87(3)	63.0(1)
	Study 1 (ref. 15)	25% NH4OH (pH = 10)	AC, 150 °C, 1 h	13.5(2)^a	8.46(12)	0.643(3)	60.5(1)
CoFe2O4	This study	25% NH4OH (pH = 10)	AC, 200 °C, 1 h	7.92(1)	8.3901(1)	0.954(6)	64.2(1)
	Study 1 (ref. 15)	12 M NaOH (pH > 14)	AC, 200 °C, 1 h	13.4(1)	8.4018(1)^a	0.660(6)	71.7(2)
	Study 2 (ref. 29)	16 M NaOH (pH > 14)	AC, 240 °C, 2 h	17.6(1)	8.3897(2)	0.72(1)	74.0(2)
NiFe2O4	This study	25% NH4OH	AC, 200 °C, 1 h	10.31(1)	8.3574(1)	1	50.2(1)
	Study 1 (ref. 15)	12 M NaOH (pH > 14)	AC, 200 °C, 1 h	23.7(17)^a	8.36(12)^a	1	47.1(1)
ZnFe2O4	This study	25% NH4OH	AC, 200 °C, 1 h	3.70(1)	8.4588(4)	0.138(4)	6.1(1)
	Study 1 (ref. 15)	12 M NaOH (pH > 14)	Flow (250 bar), 390 °C	9.8(1)	8.4376(3)	0.166(10)	10.8(1)
	Study 2 (ref. 29)	16 M NaOH (pH > 14)	AC, 240 °C, 2 h	11.0(1)	8.4515(2)	0.24(1)	20.5(1)

---

For CoFe₂O₄, the NaOH precursor route was used in two previous studies with different base concentrations of 12 M and 16 M, respectively. The syntheses were carried out with identical physical reaction conditions in Study 1 (200 °C for 1 h) and at higher temperature and for longer time in Study 2 (240 °C for 2 h). The NH₄OH route yields much smaller crystallites of 7.92(1) nm compared to the 13.4(1) nm obtained using the 12 M NaOH route at identical synthesis conditions (200 °C, 1 h) and 17.6(1) nm using the stronger 16 M NaOH route for longer time and at higher temperature (240 °C, 2 h). This is consistent with observations in a previous in situ PXRD study of hydrothermal CoFe₂O₄ nanoparticle formation, where changing precursor pH or precursor concentration at the time of adding the precipitating base, proved to be a more efficient handle for changing particle sizes compared to varying synthesis temperature.⁶⁹ In the bulk, CoFe₂O₄ adopts a fully inverse spinel structure, i.e. Co²⁺ occupying half the octahedral sites. However, our structural studies of hydrothermally synthesised CoFe₂O₄ nanocrystallites consistently indicate that metastable mixed spinel cation configurations are obtained.^15,29 Interestingly, the smaller crystallites from the NH₄OH route exhibit a higher inversion degree of 0.954(6), which is closer to the thermodynamically stable fully inverse structure of the bulk compound, compared to the almost random/disordered distribution of 0.660(6) and 0.72(1) from the NaOH routes. Using a softer base may thus be less likely to induce formation of metastable cation configurations. The CoFe₂O₄ nanoparticles prepared through the NH₄OH route yield a lower M_s of 64.2(1) Am² kg⁻¹ compared to the 71.7(2) and 74.0(2) Am² kg⁻¹ produced by the NaOH routes. The M_s drop can be attributed to the higher inversion degree (i.e. a larger amount of the less magnetic 3d⁷ Co²⁺ ions replacing 3d⁵ Fe³⁺ on the octahedral site) along with the smaller crystallite size.

In the case of NiFe₂O₄, identical physical reaction conditions (i.e. autoclave reactor at 200 °C for 1 h) were used for the two different precursors of the present and previous study. As for CoFe₂O₄, a considerable difference in the obtained crystallite sizes is observed, with the NH₄OH precursor route yielding smaller 10.31(1) nm NiFe₂O₄ crystallites compared to 23.7(17) nm from the NaOH route. As in our previous studies using the NaOH route, refining the cation occupancies in the modelling of the diffraction data led to unphysical excess occupation by Ni on the octahedral site indicating a fully inverse structure.^15,68 Consequently, NiFe₂O₄ seemingly has a very strong affinity for the fully inverse spinel structure even for small crystallites of ∼10 nm. Interestingly, despite the smaller crystallite size, a slightly larger M_s of 50.2(1) Am² kg⁻¹ is obtained for the NH₄OH synthesized particles compared to 47.1(1) Am² kg⁻¹ for the larger particles from the NaOH synthesis.

For ZnFe₂O₄, our two previous studies both used the NaOH precursor preparation route. In one case, 12 M NaOH was employed and the synthesis was carried out under supercritical hydrothermal conditions (390 °C, 250 bar) in a continuous flow reactor.^15,70 In the other case, the precursor preparation was done using a stronger 16 M NaOH solution and the synthesis carried out in an autoclave reactor at 240 °C for 2 h.²⁹ Here, the combination of using a softer NH₄OH base in the precursor preparation and carrying out the synthesis at a lower reaction temperature of 200 °C yields very fine ZnFe₂O₄ crystallites with an average diameter of 3.70(1) nm. For the NaOH studies, larger crystallites of 9.8(1) and 11.0(1) nm were obtained. In the bulk, ZnFe₂O₄ adopts a normal spinel structure, i.e. with Zn²⁺ exclusively occupying the tetrahedral site. However, for the nanosized crystallites a metastable mixed spinel configuration is consistently obtained. As for the CoFe₂O₄ samples, it seems that using a softer base causes a more bulk-like cation configuration with an inversion degree of 0.138(4) compared to the 0.24(1) obtained from the 16 M NaOH route. Since Zn²⁺ ions (3d¹⁰ electron configuration) are non-magnetic, bulk ZnFe₂O₄ in the thermodynamically stable normal spinel configuration adopts an antiferromagnetic structure with a Néel temperature, T_N, of 10 K, i.e. paramagnetic at room temperature.^28,66 However, deviations from the normal spinel configuration undoes the perfect cancellation of the antiparallel 3d⁵ Fe³⁺ magnetic moments on the octahedral sites. Consequently, the nanocrystallites from our previous studies, with a higher degree of cation disorder, exhibit a higher saturation magnetisation than the crystallites with a more “normal” cation configuration.

Conclusion

The crystal and magnetic structures of hydrothermally synthesized MnFe₂O₄, CoFe₂O₄, NiFe₂O₄ and ZnFe₂O₄ nanocrystallites have been examined using joint structural modelling of PXRD and NPD data. By using weak 25% NH₄OH as the precipitating base in the precursor preparations it was possible to prepare phase-pure MnFe₂O₄, CoFe₂O₄, NiFe₂O₄ and ZnFe₂O₄ nanocrystallites employing identical hydrothermal synthesis conditions. This, in turn, allowed us to isolate and study the effect of the individual divalent ions on the obtained crystallite size and structure. The data reveals a substantial effect of the type of cation on the resulting nanocrystallite size, spinel cation configurations and magnetic structure/properties. The study highlights how a detailed fundamental understanding of the synthesis-structure–property relationship is essential for accurately predicting, designing, and tailoring spinel ferrite materials with specific or optimized properties.

Data availability

The data supporting this article are included in the article and ESI.†

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

The authors are grateful for the obtained beamtime at the Cold Neutron Powder Diffractometer (DMC) instrument at the Swiss Spallation Neutron Source (SINQ), Paul Scherrer Institute (PSI), Villigen, Switzerland. Lukas Keller and Emmanuel Canévet are thanked for their support during the beamtime. This work was financially supported by the Danish National Research Foundation (Center for Materials Crystallography, DNRF93), Innovation Fund Denmark (Green Chemistry for Advanced Materials, GCAM-4107-00008B), Independent Research Fund Denmark (Small and Smart Magnet Design), Danish Center for Synchrotron and Neutron Science (DanScatt), and Comunidad de Madrid, Spain, through an “Atracción de Talento Investigador” fellowship (2020-T2/IND-20581). C. G.-M. acknowledges financial support from grant RYC2021–031181-I funded by MCIN/AEI/10.13039/501100011033 and by the “European Union NextGenerationEU/PRTR”. This project has received funding from the European Union's Horizon Europe research and innovation programme under grant agreement No 101063369 (OXYPOW) and No 101109595 (MAGWIRE). Affiliation with the Center for Integrated Materials Research (iMAT) at Aarhus University is gratefully acknowledged. EDB and RK acknowledge funding from the Carlsberg Foundation (CF18-0705), Aarhus University Centre for Integrated Materials Research and the Interdisciplinary Nanoscience Center.

References

1. J. M. D. Coey, J. Magn. Magn. Mater., 2002, 248, 441–456.
2. Q. Song and Z. J. Zhang, J. Am. Chem. Soc., 2012, 134, 10182–10190.
3. A. Quesada, C. Granados-Miralles, A. Lopez-Ortega, S. Erokhin, E. Lottini, J. Pedrosa, A. Bollero, A. M. Aragon, F. Rubio-Marcos, M. Stingaciu, G. Bertoni, C. D. J. Fernandez, C. Sangregorio, J. F. Fernandez, D. Berkov and M. Christensen, Adv. Electron. Mater., 2016, 2, 1500365.
4. Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167–R181.
5. C. C. Berry and A. S. G. Curtis, J. Phys. D: Appl. Phys., 2003, 36, R198–R206.
6. M. de h-Óra, A. Nicolenco, P. Monalisha, T. Maity, B. Zhu, S. Lee, Z. Sun, J. Sort and J. MacManus-Driscoll, APL Mater., 2023, 11, 051105.
7. Y. Yang, Z. Xi, Y. Dong, C. Zheng, H. Hu, X. Li, Z. Jiang, W.-C. Lu, D. Wu and Z. Wen, ACS Appl. Mater. Interfaces, 2020, 12, 56300–56309.
8. D. Guin, B. Baruwati and S. V. Manorama, Org. Lett., 2007, 9, 1419–1421.
9. R. Abu-Reziq, H. Alper, D. S. Wang and M. L. Post, J. Am. Chem. Soc., 2006, 128, 5279–5282.
10. J. H. Lee, Y. M. Huh, Y. Jun, J. Seo, J. Jang, H. T. Song, S. Kim, E. J. Cho, H. G. Yoon, J. S. Suh and J. Cheon, Nat. Med., 2007, 13, 95–99.
11. H. B. Na, I. C. Song and T. Hyeon, Adv. Mater., 2009, 21, 2133–2148.
12. J. T. Jang, H. Nah, J. H. Lee, S. H. Moon, M. G. Kim and J. Cheon, Angew. Chem., Int. Ed., 2009, 48, 1234–1238.
13. C. A. Quinto, P. Mohindra, S. Tong and G. Bao, Nanoscale, 2015, 7, 12728–12736.
14. A. H. Lu, E. L. Salabas and F. Schuth, Angew. Chem., Int. Ed., 2007, 46, 1222–1244.
15. H. L. Andersen, M. Saura-Múzquiz, C. Granados-Miralles, E. Canévet, N. Lock and M. Christensen, Nanoscale, 2018, 10, 14902–14914.
16. K. R. Sanchez-Lievanos, J. L. Stair and K. E. Knowles, Inorg. Chem., 2021, 60, 4291–4305.
17. S. S. Chikazumi and C. D. Graham, Physics of ferromagnetism, Oxford University Press, Oxford, New York, 2nd edn, 2009.
18. E. Solano, C. Frontera, T. Puig, X. Obradors, S. Ricart and J. Ros, J. Appl. Crystallogr., 2014, 47, 414–420.
19. C. Liu, B. S. Zou, A. J. Rondinone and Z. J. Zhang, J. Phys. Chem. B, 2000, 104, 1141–1145.
20. J. Jacob and M. A. Khadar, J. Appl. Phys., 2010, 107, 114310.
21. S. M. Patange, S. E. Shirsath, G. S. Jangam, K. S. Lohar, S. S. Jadhav and K. M. Jadhav, J. Appl. Phys., 2011, 109, 053909.
22. Z. Z. Lazarevic, C. Jovalekic, A. Milutinovic, D. Sekulic, V. N. Ivanovski, A. Recnik, B. Cekic and N. Z. Romcevic, J. Appl. Phys., 2013, 113, 187221.
23. T. Slatineanu, A. R. Iordan, M. N. Palamaru, O. F. Caltun, V. Gafton and L. Leontie, Mater. Res. Bull., 2011, 46, 1455–1460.
24. V. Blanco-Gutierrez, E. Climent-Pascual, M. J. Torralvo-Fernandez, R. Saez-Puche and M. T. Fernandez-Diaz, J. Solid State Chem., 2011, 184, 1608–1613.
25. Á. Gallo-Cordova, A. Espinosa, A. Serrano, L. Gutiérrez, N. Menéndez, M. del Puerto Morales and E. Mazarío, Mater. Chem. Front., 2020, 4, 3063–3073.
26. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
27. J. M. D. Coey, Magnetism and magnetic materials, Cambridge University Press, Cambridge, 2010.
28. R. Skomski, J. Phys.: Condens. Matter, 2003, 15, R841–R896.
29. H. L. Andersen, C. Granados-Miralles, M. Saura-Múzquiz, M. Stingaciu, J. Larsen, F. Søndergaard-Pedersen, J. V. Ahlburg, L. Keller, C. Frandsen and M. Christensen, Mater. Chem. Front., 2019, 3, 668–679.
30. B. Xavier and L. Amílcar, J. Phys. D: Appl. Phys., 2002, 35, 201.
31. S. Linderoth, P. V. Hendriksen, F. Bødker, S. Wells, K. Davies, S. W. Charles and S. Mørup, J. Appl. Phys., 1994, 75, 6583–6585.
32. B. Zhang, G. Tang, Z. Yan, Z. Wang, Q. Yang and J. Cui, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2007, 22, 514–517.
33. W. Clegg, Crystal structure analysis: principles and practice, International Union of Crystallography; Oxford University Press, Chester, England, New York, 2001.
34. Z. Wang, X. Guo, J. Montoya and J. K. Nørskov, npj Comput. Mater., 2020, 6, 160.
35. J. B. Gerken, J. G. McAlpin, J. Y. C. Chen, M. L. Rigsby, W. H. Casey, R. D. Britt and S. S. Stahl, J. Am. Chem. Soc., 2011, 133, 14431–14442.
36. W. Sun, D. A. Kitchaev, D. Kramer and G. Ceder, Nat. Commun., 2019, 10, 573.
37. J. Schefer, P. Fischer, H. Heer, A. Isacson, M. Koch and R. Thut, Nucl. Instrum. Methods Phys. Res., Sect. A, 1990, 288, 477–485.
38. J. Rodriguez-Carvajal, Phys. B, 1993, 192, 55–69.
39. P. Thompson, D. E. Cox and J. B. Hastings, J. Appl. Crystallogr., 1987, 20, 79–83.
40. P. Scherrer, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 1918, vol. 1918, pp. 98–100.
41. J. I. Langford and A. J. C. Wilson, J. Appl. Crystallogr., 1978, 11, 102–113.
42. G. Shirane, Acta Crystallogr., 1959, 12, 282–285.
43. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld and B. Schmid, Nat. Methods, 2012, 9, 676–682.
44. F. de la Peña, E. Prestat, V. T. Fauske, P. Burdet, J. Lähnemann, P. Jokubauskas, T. Furnival, M. Nord, T. Ostasevicius, K. E. MacArthur, D. N. Johnstone, M. Sarahan, J. Taillon, T. Aarholt, V. Migunov, A. Eljarrat, J. Caron, C. Francis, T. Nemoto, T. Poon, S. Mazzucco, N. Tappy, N. Cautaerts, S. Somnath, T. Slater, M. Walls, F. Winkler and H. W. Ånes, hyperspy/hyperspy: Release v1.7.3 (v1.7.3), Zenodo, 2022,  DOI:10.5281/zenodo.7263263.
45. Pandas-developement-team.
46. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. Del Rio, M. Wiebe, P. Peterson, P. Gerard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
47. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
48. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272.
49. V. Valvoda, International Tables for Crystallography, Volume C: Mathematical, Physical and Chemical Tables, Kluwer Acedemic Publishers, Dordrecht/Boston/London, 3rd edn, 2004, ch. 4.
50. A. J. Blake and W. Clegg, Crystal structure analysis: principles and practice, Oxford University Press, Oxford, New York, 2nd edn, 2009.
51. H. L. Andersen, B. A. Frandsen, H. P. Gunnlaugsson, M. R. V. Jorgensen, S. J. L. Billinge, K. M. O. Jensen and M. Christensen, IUCrJ, 2021, 8, 33–45.
52. B. Antic, A. Kremenović, A. S. Nikolic and M. Stoiljkovic, J. Phys. Chem. B, 2004, 108, 12646–12651.
53. C. Wende, K. Olimov, H. Modrow, F. E. Wagner and H. Langbein, Mater. Res. Bull., 2006, 41, 1530–1542.
54. M. E. Fleet, J. Solid State Chem., 1986, 62, 75–82.
55. J. E. Jørgensen, L. Mosegaard, L. E. Thomsen, T. R. Jensen and J. C. Hanson, J. Solid State Chem., 2007, 180, 180–185.
56. R. Nepal, M. Saghayezhian, J. Zhang and R. Jin, J. Magn. Magn. Mater., 2020, 497, 165955.
57. J. M. Hastings and L. M. Corliss, Phys. Rev., 1956, 104, 328–331.
58. S. Yanez-Vilar, M. Sanchez-Andujar, C. Gomez-Aguirre, J. Mira, M. A. Senaris-Rodriguez and S. Castro-Garcia, J. Solid State Chem., 2009, 182, 2685–2690.
59. C. Liu, A. J. Rondinone and Z. J. Zhang, Pure Appl. Chem., 2000, 72, 37–45.
60. R. Borah and S. Ravi, J. Magn. Magn. Mater., 2021, 538, 168276.
61. Z. Li, J. Dai, D. Huang and X. Wen, J. Alloys Compd., 2022, 907, 164386.
62. I. H. Gul and E. Pervaiz, Mater. Res. Bull., 2012, 47, 1353–1361.
63. K. Raju and D. H. Yoon, J. Supercond. Novel Magn., 2014, 27, 1285–1292.
64. R. Kalia, R. Pushpendra, R. K. Kunchala, S. N. Achary and B. S. Naidu, J. Alloys Compd., 2021, 875, 159905.
65. N. Pailhé, A. Wattiaux, M. Gaudon and A. Demourgues, J. Solid State Chem., 2008, 181, 1040–1047.
66. A. Kremenovic, B. Antic, P. Vulic, J. Blanusa and A. Tomic, J. Magn. Magn. Mater., 2017, 426, 264–266.
67. S. Blundell, Magnetism in condensed matter, Oxford University Press, Oxford; New York, 2001.
68. J. Hölscher, H. L. Andersen, M. Saura-Múzquiz, P. G. Garbus and M. Christensen, CrystEngComm, 2020, 22, 515–524.
69. H. L. Andersen and M. Christensen, Nanoscale, 2015, 7, 3481–3490.
70. P. Hald, J. Becker, M. Bremholm, J. S. Pedersen, J. Chevallier, S. B. Iversen and B. B. Iversen, J. Solid State Chem., 2006, 179, 2674–2680.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ce01001a

---