Halogen–copper redox chemistry as a driving force for spherical Janus microswimmers

Abstract

Most Janus particle microswimmers use catalytic reaction mechanisms, including hydrogen peroxide or hydrazine degradation, to generate gradients for self-propulsion. However, several alternative reaction mechanisms can also lead to activity, including the redox reactions of noble metals, enzymes and glucose, often using spherical Cu@SiO₂ Janus particles. Copper, as a very versatile metal, is involved in reactions, as an oxidant or as an electrode, for example in dilute halogen solutions. This so-called nanobattery system works well for rod-shaped bimetallic and shape-asymmetric rods. To allow comparability with simulations, we present the adaptation of this propulsion reaction for Janus colloids. Altogether, this study provides an overview of the chemical process and swimming behaviour of spherical Cu@SiO₂ Janus particles in dilute halogen solutions. We combine an experimental approach that includes the determination of the effect of particle size and cap thickness, supported by simulations of these systems.

---

The propulsion of artificial active matter has been dominated by H₂O₂ degradation since its first discovery.¹ Given that the degradation of this strongly oxidising chemical provides an excellent and reliable fuel for microscale motion, the combination Pt@SiO₂ Janus particle has become a widely used model system to study behaviors. However, continuously expanding applications require more flexibility in fuel selection in order to use more sustainable or biocompatible fuels. Since Sen and his team studied the reaction of copper with halogens using a Pt–Cu bimetallic rod and their self-electrophoretic movement as nanobatteries,² it is known that suitable reactions are not restricted to catalytic systems. Recent examples include galvanophoretic movement while reacting with noble metal acids,^3,4 different enzyme substrates,^5,6 and also glucose,⁷ expanding on the range of potential microswimmer systems. Since the Janus morphology allows better comparison with simulations and theory, this spherical particle type dominates experimental studies. Therefore, in this work we introduce Cu@SiO₂ Janus particles in halogen fuels to explore the ‘hydrogen atom’ of active particles in this fuel combination, which allows the study of interesting chemical influences: the interplay between the established gradient, the ionic strength and the superimposed chemical equilibria. We compare microscopic behaviour, chemical analysis and finite element simulation to improve our ability to classify the system under investigation in the ever-expanding field of fuel options. Halogens and copper react to form copper halides, which can be either Cu(I) or Cu(II) halides, depending on the halogen and the reaction conditions. The overall reactivity decreases from fluorine towards iodine, which is the least reactive homologue and frequently forms insoluble CuI. Nevertheless, the halogen is permanently reduced during the reaction while the Cu is continuously oxidised due to its lower electronegativity. Since the reaction of fluorine and chlorine is very vigorous and potentially explosive, which is not ideal in a microscope setup, we restrict our experiments to the less reactive bromine and iodine, highlighting the interesting difference of a soluble product for bromine, while obtaining a highly insoluble precipitating product for iodine. Bromine (Br₂) is a reddish brown liquid at room temperature with a strong, pungent odor. It has limited solubility in water and undergoes a self-disproportionation reaction (see eqn (1)).

Br₂⁺H₂O ⇌ HBrO + Br⁻ + H⁺ K_eq = 3.5 × 10⁻⁹ M² (298 K) (1)

This process leads to two reactive species, HBrO and Br₂. Looking at the equilibrium constant for bromine hydrolysis of 3.5 × 10⁻⁹ M² at 298 K indicates the disproportionation of Br₂ in water which results in an initially acidic solution (see Fig. S2, ESI†). In the presence of Cu, the pH increases significantly over time, indicating the development of the reaction.

On this basis, we assume that HBrO is used as a higher oxidant to reduce Cu, acting as a reactive species and shifting the dissociation reaction of Br₂ to the side of its disproportionate ions.

HBrO + H⁺ + Br⁻ + Cu ⇌ CuBr₂(aq) + H₂O ΔE = 0.98 V (2)

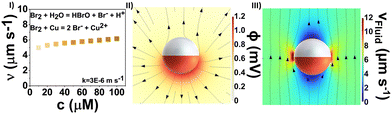
In Fig. 1(I), this reaction is schematically illustrated. For simplification, the Br₂ is assumed to dissociate fully into its ions.

Fig. 1 (I) Reaction scheme of Cu with dissociated Br₂ (II) mean velocity at different concentrations of Br₂ fuel (III) MSD at different concentrations of Br₂ solutions.

During the oxidation of the solid Cu surface, the highly soluble CuBr₂(aq) is formed (see eqn (2)), releasing ions into the solution. The release of ions creates a concentration gradient that drives the motion of particles through a process known as ionic self-diffusiophoresis. This mechanism is similar to other systems, such as Ag-,⁸ AgCl-,⁹ and Ag₃PO₄ motors.¹⁰ However, the halogen fuel system stands out because it exhibits ionic diffusiophoresis at much lower concentrations and does not utilize hydrogen peroxide as a fuel. Additionally, the halogen–copper system operates without the need for an additional power source, such as light, apart from the chemical fuel. Following this, we introduce another type of ionic diffusiophoretic system for spherical Cu@SiO₂ microswimmers. Due to the slower diffusion of Cu²⁺ ions (0.714 × 10⁻⁹ m² s⁻¹) compared to Br⁻ ions (2.08 × 10⁻⁹ m² s⁻¹),¹¹ an outward electric field is established to maintain electroneutrality. This electric field propels the negatively charged particle, causing it to move toward the Cu cap direction. The production of Cu²⁺ ions during the motion is proven by the conversion with NH₃ forming the highly coloured complex of Cu(NH₃)₄²⁺ and followed by UV-Vis analysis. Fig. S3 (ESI†) depicts the UV-Vis measurement results of the sample with NH₃ added after the reaction of Cu@SiO₂ with Br₂, including samples examining NH₃-complexed CuSO₄ at varied concentrations.

As copper is consumed during the reaction and the product diffuses into the surrounding liquid, the SEM images of Br₂-reacted Cu@SiO₂ exhibit no noticeable changes across concentrations from 10 to 250 μM (see Fig. S4, ESI†). At higher concentrations of 500 μM, the copper cap is completely dissolved. Looking at the swimming behaviour of the moving particle in Fig. 1(II) and (III), the shown velocity and MSD curves do not reveal any particular trend from 10 to 100 μM. At 10 μM, the mean velocity of roughly 3 μm s⁻¹ can be attributed to Brownian motion, which is solidified with the linear MSD curve, displaying Brownian diffusivity (MSD(t) ∝ 1).¹² A maximum velocity of 6.5 μm s⁻¹ is reached at 25 μM, with an MSD curve indicating super diffusion. However, at higher concentrations, the velocity remains constant around 5 μm s⁻¹, with a lower rise in MSD curve. In contrast, at even higher concentrations of 150 μM, the particles become immediately immobilised due to the large number of ions produced (see Video S1, ESI†), which is related to how these ions affect double-layer interactions and van der Waals forces, as described by the Derjaguin–Landau–Verwey–Overbeek theory.^4,13

To understand the correlation between the increasing concentration of Br₂ fuel and the increasing ion content, leading to roughly constant swimming speeds, finite element method simulations (COMSOL) were performed. In the simulation of the Br₂ system, two major reactions mentioned above were considered: the reaction of Br₂ with H₂O (eqn (1)) and the reaction of Cu and HOBr (eqn (2)). Since Br₂ reacts with H₂O to produce HOBr and HOBr will be consumed further by Cu, the overall reaction at the Cu surface was simplified to Cu and Br₂ forming CuBr₂, which will further dissociate to Cu²⁺ and Br⁻ (Fig. 2I). We assumed a first order reaction with a constant reaction rate of 3 × 10⁻⁶ m s⁻¹ adapted from Sen's work.² For more details, please refer to the simulation section.

Fig. 2 (I) Calculated velocities of 5 μm Cu@SiO₂ Janus particles at different concentrations of Br₂ solution at a constant reaction rate (3 × 10⁻⁶ m s⁻¹) (II) theoretical electric potential around the Janus particle in a solution of 50 μM Br₂ (III) computed fluid flow around the particle in a 50 μM Br₂ fuel.

The simulated velocities, as shown in Fig. 2(I), exhibit comparable values ranging from 4 to 6 μm s⁻¹ for Br₂ at concentrations between 10 and 100 μM compared to the experimental data. The positive velocity values denote particle propulsion with the Cu cap forward, aligning well with experimental observations. Fig. 2(II) presents the electric potential and electric field lines at a Br₂ concentration of 50 μM. In the near field, a slightly higher potential is shown near the Cu surface, along with outward electric field lines extending from Cu to SiO₂. These electric field lines, coupled with the negatively charged SiO₂, generate a fluid flow, as depicted in Fig. 2(III), moving from the Cu side to the SiO₂ side. The velocity does not increase as observed in other chemically active microswimmers at higher fuel concentrations because of the influence of the background ions. At higher concentrations, although more Cu²⁺ and Br⁻ ions are produced, which would typically generate stronger propulsion, the reaction of Br₂ with H₂O introduces a significant excess of Br⁻ ions and protons into the solution. These background ions significantly slow down the electrokinetic swimmer due to the increased conductivity of the solution. This occurs in multiple ways, but the primary reason is that the induced electric field E (which is responsible for the propulsion) scales inversely with the solution conductivity δ, as described by Ohm's law: E = i/δ, where i is the current density.¹⁴ At higher fuel concentrations, more ions are produced, leading to an increase in the current density i, as it is proportional to the ion concentration. However, the fuel also generates more background ions, causing the solution conductivity δ, to increase proportionally. As a result, the electric field E, remains relatively stable despite the increased ion concentration, which explains why the micromotor speed remains stable even at higher fuel concentrations.

In addition to the Br₂ solution, the swimming behavior of Cu@SiO₂ Janus particles is observed in I₂ fuel, which undergoes an analogous redox reaction with Cu but is less reactive than Br₂.

I₂(aq) + 2Cu(s) ⇌ 2CuI(s) (3)

At 298 K, the equilibrium constant for the self-disproportion reaction

I₂ + H₂O ⇌ HIO + I⁻ + H⁺ K_eq = 5.4 × 10⁻¹³ M² (298 K) (4)

is 5.4 × 10⁻¹³ M²,¹⁵ which is 10⁴ times lower than for Br₂, which results in low ion dissociation. Moreover, Sen's group identified I₂ as the active species responsible for oxidising the solid Cu from their measured reaction potential. For simplicity, just the reactive species are represented in the schematic illustration of the reaction (see Fig. 3). During the reaction on the metal surface, insoluble CuI is produced, resulting in cubic crystals on the particle. The production of cubic CuI with the space group F4̄3m is further confirmed by XRD (see Fig. S7, ESI†). The formation of insoluble CuI crystals removes most ions from the solution. Nevertheless, the particles swim cap forward, similar to their motion in a Br₂ solution. We attribute this propulsion to the presence of intermediate ions, Cu⁺ and I⁻, prior to the formation of CuI. Similar to the mechanism in the Br₂ system, I⁻ (2.045 × 10⁻⁹ m² s⁻¹) diffuses much faster than Cu⁺ (0.73 × 10⁻⁹ m² s⁻¹),¹¹ creating an electric field directed from the Cu side to the SiO₂ side. This electric field propels the particle forward with the Cu cap leading. Considering the data in Fig. 3(II) and (III) it becomes clear that at a concentration of 10 μM, the movement can be attributed to Brownian motion. At 25 μM, the MSD curve and increased velocity of 5.8 μm s⁻¹ indicate swimming particles, without detectable CuI crystals in SEM and EDX measurements. With increasing fuel concentration, the mean velocities show considerable growth. As a result, the mean velocity with 100 μM I₂ is 4 μm s⁻¹ greater than with the same concentration of Br₂. Furthermore, the absence of new ion generation in the solution prevents particles from being stuck to the substrate.

Fig. 3 (I) Reaction scheme (II) mean velocity at different concentrations of I₂ (III) MSD at different concentrations (IV) SEM and EDX analysis of particles at different I₂ concentrations.

To validate the experimental results, we also implemented COMSOL simulations. For the I₂ system only one reaction was considered (eqn (3)), since I₂ reacts minimally with H₂O compared to Br₂. The intermediate ions, Cu⁺ and I⁻, were considered the major ionic species in the system. The reaction rate constant was set to 1 × 10⁻⁷ m s⁻¹, as adapted from Sen et al.² The simulated velocities mirror the experimental trend, with increasing velocity as the I₂ concentration increases from 10 to 100 μM. The lower values observed in the experiments can be attributed to the formation of CuI crystals on the Cu surface, which partially cover the Cu cap and slow down the reaction rate. The distinction between the I₂ and Br₂ systems can also be understood by examining the generation of background ions. Unlike Br₂, I₂ does not react with water to produce excess ions. As a result, at higher I₂ concentrations, more Cu⁺ and I⁻ ions are produced in the near field, but the far-field conductivity of the solution remains unchanged (Fig. 4(II)).

Fig. 4 (I) Calculated velocities of 5 μm Cu@SiO₂ Janus particles at different concentrations of I₂ solution and a constant reaction rate (1 × 10⁻⁷ m s⁻¹) (II) theoretical electric potential around the Janus particle in a solution of 50 μM I₂ (III) computed fluid flow around the particle in a 50 μM I₂ fuel.

Compared to the electric field generated in the Br₂ system, the direction of the electric field with I₂ is similar. However, the electric potential near the active side of the particle with I₂ is significantly higher compared to the Br₂ system, which indicates a more vigorous electric field intensity for I₂, resulting in a more substantial fluid flow shown in Fig. 4(III). In comparison to a Br₂ solution as fuel for the spherical Janus particles, I₂ as a fuel exhibits significantly better swimming behavior with increasing fuel concentrations due to the formation of barely soluble CuI crystals rather than ions.

To complete the study we performed experiments to analyse the influence of morphological characteristics of the Janus particle on the swimming. Thus we examined the velocity data for both halogen fuels at a concentration of 50 mM, varying the particle size from 2, to 3, and 5 μm with a constant copper cap thickness of 30 nm and for 5 μm particles we analyse different copper cap thicknesses of 5, 30, and 50 nm, showing the results in Fig. 5.

Fig. 5 Influences of (I) particle size and (II) Cu cap thickness to velocity.

The smallest particles of 2 μm show for Br₂ slightly higher speed (7.7 μm s⁻¹) than for the larger particles, which aligns with studies on the correlation between swimmer diameter and speed, noting that larger particles produce more ions, resulting in a higher screening length.^16,17 However, the decrease is not very significant. The data for 50 μM I₂ fuel, which show mean velocities in the range of 4 to 7 μm s⁻¹, confirm these findings. The comparison of different layer thicknesses for 5 μm particles shows more interesting tendencies: in a Br₂ solution there is no significant difference for the speeds obtained for 5 nm and 30 nm layers (3.7 μm s⁻¹ and 4.9 μm s⁻¹, respectively). However, with a 50 nm cap, the particles become stuck to the substrate immediately after adding the fuel. For the I₂ solutions, we observe no apparent trapping even for the thickest layers and their velocities range from 3.8 to 6.4 μm s⁻¹, confirming the crucial importance of the precipitation of CuI.

In conclusion, using a halogen–copper redox fuel system, we investigate the effects of overlaid secondary equilibria on the active motion of spherical Janus particle microswimmers. Our findings reveal that swimming speeds vary with different fuels, showing a peak velocity of 6.5 μm s⁻¹ for Br₂ at 25 μM. In contrast, at higher concentrations, the velocity remains approximately constant due to particle-surrounded ions. In contrast, I₂ displays a continuous increase in velocity with concentration, driven by the precipitation of insoluble CuI. Simulations support our experimental data, giving insights into the reaction mechanisms and fluid dynamics involved. The differing swimming behaviours are attributed to the distinct disproportionation reactions of the halogens in water and product solubility. This study gives us a clearer perspective on this specific system while also facilitating comparisons with other fuel systems.

JS acknowledges funding from the Cottrell Foundation. Zuyao Xiao acknowledges a CSC PhD fellowship. This work was supported by the Free State of Saxony and by the European Union (ESF Plus) by funding of the research group ‘MultiMOD’.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. J. R. Howse, R. A. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102.
2. R. Liu and A. Sen, J. Am. Chem. Soc., 2011, 133, 20064–20067.
3. L. Feuerstein, C. G. Biermann, Z. Xiao, C. Holm and J. Simmchen, J. Am. Chem. Soc., 2021, 143, 17015–17022.
4. J. Bastos-Arrieta, C. Bauer, A. Eychmüller and J. Simmchen, J. Chem. Phys., 2019, 150, 144902.
5. X. Ma, A. Jannasch, U.-R. Albrecht, K. Hahn, A. Miguel-López, E. Schaffer and S. Sánchez, Nano Lett., 2015, 15, 7043–7050.
6. X. Ma and S. Sánchez, Tetrahedron, 2017, 73, 4883–4886.
7. F. Fessler, M. Wittmann, J. Simmchen and A. Stocco, Soft Matter, 2024, 20, 5904–5914.
8. Z. H. Shah, S. Wang, L. Xian, X. Zhou, Y. Chen, G. Lin and Y. Gao, Chem. Commun., 2020, 56, 15301–15304.
9. C. Zhou, H. Zhang, J. Tang and W. Wang, Langmuir, 2018, 34, 3289–3295.
10. D. Wentao, L. Ran and S. Ayusman, J. Am. Chem. Soc., 2013, 135(4), 1280–1283.
11. J. Rumble, CRC Handbook of Chemistry and Physics, Abingdon, 2020.
12. V. Briane, M. Vimond and C. Kervrann, Briefings Bioinf., 2020, 21, 1136–1150.
13. O. Malysheva, T. Tang and P. Schiavone, J. Colloid Interface Sci., 2008, 327, 251–260.
14. J. L. Moran and J. D. Posner, Annu. Rev. Fluid Mech., 2017, 49, 511–540.
15. I. Lengyel, I. R. Epstein and K. Kustin, Inorg. Chem., 1993, 32, 5880–5882.
16. A. T. Brown, W. C. Poon, C. Holm and J. De Graaf, Soft Matter, 2017, 13, 1200–1222.
17. S. Ebbens, M.-H. Tu, J. R. Howse and R. Golestanian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 020401.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cc00405e

---