The golden goal of entatic state model design: lowering the internal reorganization energy leads to exponential increase in electron transfer rate

Abstract

We report a novel guanidine quinolinyl entatic state model system with an electron transfer rate on the order of 10⁵ M⁻¹ s⁻¹ and remarkably little internal reorganization. Comparison between this system and previously reported TMGqu systems reveals an exponential correlation between the internal reorganization energy and the electron transfer rate.

---

Copper containing proteins are found in many living organisms where they serve vital functions.¹ Of them, type I copper proteins facilitate electron transfer reactions in several organisms via a bound Cu ion.² These proteins are characterized by high electron self-exchange rates k₁₁ between 10³ and 10⁸ M⁻¹ s⁻¹ which are observed in spite of the different preferred stereochemistry of the Cu^I/II redox pair; having Cu^I prefer tetrahedral coordination geometries and Cu^II tetragonal ones.^3,4 Therefore, a full rearrangement of the Cu centre during a redox event would lead to high reorganization energies λ₁₁ and should thus decrease k₁₁. To explain how electron transfer copper proteins avoid this limitation, Vallee and Williams proposed the entatic state concept in 1968, focused on the coordination geometry of the active site.⁵ According to it, the copper of type I proteins is bound in a distorted geometry that lies between the preferred geometries of either Cu^I or Cu^II and energizes both oxidation states, in turn lowering the kinetic barrier between them. The protein framework is also theorized to be rigid, experiencing only very little structural change upon electron transfer, further lowering the required reorganization energy. The concept of the entatic state has been popular over the past decades.^6,7 While the actual presence of the entatic state in type I copper proteins is disputed,⁸ the connection between distorted coordination environments, minimal reorganization energies and enhanced electron transfer properties is well documented.^6,9,10 The reported range of model systems for electron transfer proteins is not only limited to the entatic state concept and demonstrates a wide array of different ligand geometries and employed donors. The fastest known electron transfer systems reach self-exchange rates of 10⁵ to 10⁶ M⁻¹ s⁻¹ and are mostly comprised of systems with a mixture of N- and S-donors, sometimes accompanied by Cl-donors.^9,11 Pure N-donor models, however, have shown to be able to achieve fast electron transfer rates as well, with McMillin et al. reporting [Cu(TAAB)]^2+/+ and its k₁₁ of 10⁵ M⁻¹ s⁻¹ and the redox pair [Cu(L7)]^+/2+ by Himmel et al. with a k₁₁ of 10⁶ M⁻¹ s⁻¹.¹² These, however, lack mechanistic insight or do not follow the entatic state, leaving detailed principles to build a perfect entatic state model as of yet unaccounted for.

In this study, we use an inverse design approach to assemble all features used for the perfect entatic state model and report a novel guanidine quinolinyl (TMGqu) based entatic state model system that exhibits a rapid electron transfer rate on the order of 10⁵ M⁻¹ s⁻¹. The complex pair exists in two discrete conformers in the solid state and favors one conformer when in solution. Correlating the reorganization energies of all 2-substituted TMGqu systems (Fig. 1) against their electron self-exchange rates reveals an exponential interrelation between the internal reorganization energy and k₁₁.‡

Fig. 1 Illustration of the herein reported correlation between the employed ligand systems for copper entatic state models, their internal reorganization energy λ₁₁ and the resulting electron self-exchange rate k₁₁. The substituent in brackets shows slight deviations from the trend.

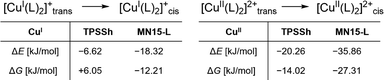
Designing the ligand TMG2Phqu was done with the desired structural parameters for the ideal entatic state model in mind (a difference in τ₄ between Cu(I/II): Δτ₄ = 0 and an average τ₄ of Øτ₄ = 0.50), utilizing the previously reported ligand TMG2^cHexqu as a basis to improve upon (Fig. 2).^3,6 The ligand was combined with either [Cu^I(MeCN)₄]PF₆ or [Cu^II(MeCN)₄](OTf)₂ to yield the corresponding copper complexes [Cu^I(TMG2Phqu)₂]PF₆·CH₂Cl₂ (C1-PF₆) and [Cu^II(TMG2Phqu)₂](OTf)₂·0.5 H₂O (C2-OTf). The molecular structures in the solid state are depicted in Fig. 3, selected bond lengths, angles and structural parameters of both complexes in Table S4 (ESI†).

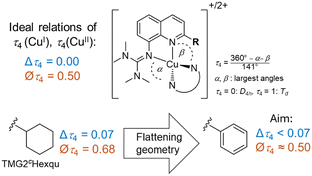Fig. 2 Ideal relations of τ₄ parameters expected in a perfect entatic state (above) and rationale behind the design of the herein reported TMG2Phqu (below) utilizing data from previous studies.^3,6 Δτ₄: difference of τ₄ of Cu(I) and Cu(II) species. ∅τ₄: Average τ₄ of Cu(I) and Cu(II) species.

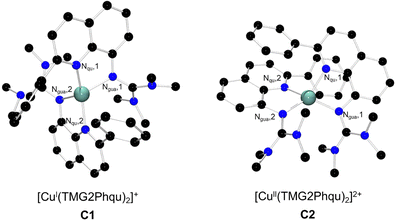Fig. 3 Molecular structures of the Cu^I and Cu^II complex cations C1 and C2 in the solid state. H atoms, non-coordinating anions and solvent molecules have been omitted for clarity.

The depicted complex cations C1 and C2, jointly referred to as redox pair R1, are conformational isomers of each other, with the N_Qu donors being arranged opposite of each other in a trans configuration in C1-PF₆, while being cis configured in C2-OTf (see angles in Table 1). The stark difference in conformations could possibly originate from packing effects. However, crystallization of C1-PF₆ from different solvent systems proved unsuccessful which is why the structures were computationally assessed. Besides the molecular structures in solid state of C1-PF₆ and C2-OTf, each oxidation state was further optimized with density functional theory (DFT) calculations in the trans conformer (conformer T) and the cis conformer (conformer C), to assess the relative stability of each conformer in each oxidation state. Selected bond lengths and structural parameters of both conformers are listed in  Table 1.

Table 1 Computationally obtained key bond lengths, bond angles and structure parameters of the complex cations C1_T,DFT, C2_T,DFT, C1_C,DFT and C2_C,DFT (TPSSh, def2-TZVP, GD3BJ, PCM (MeCN))

	C1T,DFT	C2T,DFT	C1C,DFT	C2C,DFT
a .^3
Bond lengths [Å]
Cu–Ngua,1	2.076	1.994	2.073	1.999
Cu–Ngua,2	2.093	2.037	2.073	1.999
Cu–Nqu,1	2.024	1.999	2.039	1.999
Cu–Nqu,2	2.026	1.966	2.039	1.999
Bond angles [°]
Ngua,1–Cu–Ngua,2	116.3	122.8	116.7	118.0
Ngua,1–Cu–Nqu,2	110.5	106.2	137.9	141.5
Ngua,1–Cu–Nqu,1	82.6	83.8	82.0	83.3
Ngua,2–Cu–Nqu,1	121.6	111.7	137.9	141.5
Ngua,2–Cu–Nqu,2	81.5	82.6	82.0	83.3
Nqu,1–Cu–Nqu,2	146.2	155.0	109.9	99.5
Structural parameters
τ 4	0.65	0.58	0.60	0.55
Δτ4	0.07		0.05
∅τ4	0.62		0.57
∡ (CuN2, CuN2′) [°]	79.2	66.9	66.1	57.1
Δ∡ [°]	12.3		9.0
∅∡ [°]	73.1		61.6
RMSD [Å]	0.232		0.320

---

The corresponding redox pairs of each conformer, R1_T,DFT and R1_C,DFT, show a generally high structural similarity among each other, with a remarkably strong structural similarity between C1_C,DFT and C2_C,DFT. The difference in τ₄-values of only 0.05 is the smallest reported for any optimized geometry of any tetracoordinate TMGqu system.‡ This small difference is paired with a mean τ₄-value of 0.57, close to the ideal of 0.50. To determine the preferred conformer of each oxidation state, isodesmic reactions were computed utilizing geometries optimized via TPSSh and MN15-L (see Fig. 4). For C2_DFT, these calculations yield a noticeable preference across the board for the flatter conformer C. For C1_DFT, this preference is less pronounced but still present and further supported by computations conducted with CREST (ESI,† Section S8). The results at hand therefore indicate that C1 and C2 both exist predominantly in cis conformation when in solution.

Fig. 4 Electronic energy and Gibbs free enthalpy differences upon conformational change from trans to cis by both C1_DFT and C2_DFT as obtained by the given functional. Calculation with def2-TZVP and PCM (MeCN) for both functionals, TPSSh computations were additionally performed with GD3BJ.

To experimentally validate that no possible conformational rearrangements impede the electron transfer processes, both the cyclic voltammetry (CV) measurements as well as the stopped-flow UV/Vis spectroscopic experiments were carried out twice for both “directions”, starting once from C1-PF₆ and C2-OTf, each. The cyclic voltammograms, as can be seen in Table S5 (ESI†), show good reversibility and similar potentials, with the only stark difference being the I_ox/I_red ratio obtained for the CV initiated with C2-OTf. Notably, this peak-to-peak ratio of 0.80 remains constant independent of scan rate, indicating that it might not be linked to a possible decay or inactivation of the Cu^I species but is of a different origin.¹³ Since the measurements otherwise indicate good reversibility, it can be concluded that the redox process beginning from any of both starting points is not subjected to a sufficiently large kinetic barrier to be measurably impeded. The electron self-exchange rates k₁₁ were obtained via application of the Marcus cross-relation (eqn (1)), which is derived from the Marucs theory describing the outer-sphere mechanism of electron transfer reactions (the method is given a detailed explanation in Sections 1.3.10 and 8 of the ESI†).^14,15

The cross-relation allows to determine the self-exchange rate k₁₁ of a complex by measuring the reaction rate k₁₂ of its redox reaction with a so-called counter complex. The reactions were monitored by stopped-flow UV/Vis spectroscopy and the cross-reaction rates k₁₂ were determined via linear regression of obtained k_app of varying counter complex concentrations. For the oxidation of C1-PF₆, we employed [Co(bpy)₃](PF₆)₃, with its k₂₂ as reported in acetonitrile at 298 K.¹⁶ For the reduction of C2-OTf, we employed the novel [Cu(TMG2NMe₂qu)₂]PF₆ (C3-PF₆), whose k₂₂ is reported in the ESI† (Section S6 and S8).The most important data points pertaining to the kinetic measurements, as well as the k₁₁, are listed in Table 2. The obtained k₁₁ are both at an order of 10⁵ M⁻¹ s⁻¹. These rates exceed the previously fastest TMGqu systems of our group by two orders of magnitude and are in the range of the fastest reported k₁₁ of any reported Cu-based model system to date.¹² The near identical rates for both observed reactions further indicate that no stark conformational changes can occur during any of both redox reactions and that a unitary reaction pathway is likely. These findings render the cis conformer a plausible active species, since it is the only plausible conformer of C2. The rapid electron transfer kinetics can be explained with the low amount of structural change seen for R1_C,DFT. This is stressed by the low reorganization energies λ_11,I which were computed using Nelsen's four-point method, and λ_11,S,cont, computed using the continuum method (Table 3).^6,14,17 Further plotting the k₁₁ of all 2-substituted guanidine quinolinyl systems against their λ_11,I and λ_11,S,cont reveals an exponential correlation between the reaction rates and the reorganization energies (Fig. 5).‡ This correlation is especially clear for the internal reorganization energies. The rapid self-exchange rates of R1 can therefore be explained in accordance with the rigid coordination sphere of the entatic state model and the resulting low degree of reorganization. Hence, the employed inverse design approach for the ligand proved successful in yielding a significantly improved entasis. Aside from the flattened substituent, the rigid geometry during the redox process could further be linked to London dispersion interactions between the phenyl-substituent and the quinolinyl system. The ligands in the cis conformers are oriented in parallel to each other, with a distance of about twice the van-der-Waals radius of carbon (Fig. S5, ESI†),¹⁸ pointing towards a possible attractive interaction that works against the adoption of a more tetrahedral geometry for C1_C.

Table 2 Employed counter complex, redox potentials E_1/2, differences between the redox potentials of the starting compound and the counter complex ΔE_1/2, equilibrium constants K₁₂, reaction rates k₁₂ and self-exchange rates k₁₁ of the given starting compound

Starting compound	Counter complex	E 1/2 vs. Fc/Fc^+ [V]	ΔE1/2 [V]	K 12 [ ]	k 12 [M^−1 s^−1]	k 11 [M^−1 s^−1]
C1-PF6	[Co(bpy)3](PF6)3	−0.239	0.183	1.23 × 10^3	(1.31 ± 0.07) × 10^4	(1.15 ± 0.12) × 10^5
C2-OTf	[Cu(TMG2NMe2qu)2]PF6	−0.220	0.115	8.79 × 10^1	(4.29 ± 0.24) × 10^4	(1.51 ± 0.17) × 10^5

---

Table 3 Reorganization energies and selected structural parameters for the listed guanidine quinolinyl systems (TPSSh, def2-TZVP, GD3BJ, PCM (MeCN))^‡

	λ11,I [kJ mol^−1]	λ 11,S,cont [kJ mol^−1]	λ 11,T [kJ mol^−1]	Δτ4^a	∅τ4^a
a Values stem from DFT optimized structures. b Values as reported by Herres-Pawlis et al.^6
[Cu(TMG2Phqu)2]^+/2+R1	45.6	60.9	106.5	0.05	0.58
[Cu(TMGqu)2]^+/2+^b	66.6	65.1	131.7	0.20	0.53
[Cu(TMG2Mequ)2]^+/2+^b	55.2	63.7	118.9	0.13	0.59
[Cu(TMG2^cHexqu)2]^+/2+^b	52.7	60.5	113.2	0.07	0.68
[Cu(TMG2NMe2qu)2]^+/2+	68.4	62.7	133.0	0.07	0.54

---

Fig. 5 Semi-logarithmic plots of the inner (λ_11,I) and outer (λ_11,S,cont) reorganization energies against the obtained self-exchange rates k₁₁ of 2-substituted TMGqu systems.‡ The labels refer to the ligand system employed in the corresponding Cu^I/II redox pair.

To conclude, herein we present the results of our inversely designed entatic state model and report the synthesis of the novel TMG2Phqu ligand systems and its Cu^I/II complexes which were structurally investigated using XRD, DFT and XTB. Stopped-flow UV/Vis spectroscopic experiments show that the new redox pair exhibits an electron self-exchange rate on the order of 10⁵ M⁻¹ s⁻¹, ranking it as the fastest known TMGqu-system and one of the fastest pure N-donor systems to date. Correlations between k₁₁ and computed internal reorganization energies of all 2-substituted TMGqu systems were able to reveal an exponential interrelation of both parameters, highlighting the key role of the internal reorganisation energy. The reported system therefore represents the logical evolution of entatic state model systems by having a rigid coordination sphere with minimal change during a redox reaction and paves the way to even faster electron transfer systems.

S. H.-P. acknowledges financial support by the Deutsche Forschungsgemeinschaft (DFG, 413524714) and the Nakatani Foundation. We thank the Regional Computing Center of the University of Cologne (RRZK) for providing computing time on the DFG-funded High Performance Computing (HPC) system CHEOPS as well as support. Moreover, we thank NFDI4Chem for support with data sharing in the Chemotion and RADAR4Chem repositories.

Data availability

Synthetic Information is available in the ESI.† The obtained analytical stopped-flow-UV/Vis spectroscopic data and cyclic voltammetry data, as well as the optimized coordinates from DFT computations are provided in the RADAR4Chem repository. DOI: https://doi.org/10.22000/ab0bmuwhdgfs0tqq. Experimental data like NMR-, mass- and IR-spectra can be viewed in the Chemotion repository. https://dx.doi.org/10.14272/collection/ToS_2024-11-28.

Conflicts of interest

There are no conflicts of interest to declare.

Notes and references

1. E. I. Solomon, M. J. Baldwin and M. D. Lowery, Chem. Rev., 1992, 92, 521–542.
2. M. R. Redinbo, T. O. Yeates and S. Merchant, J. Bioenerg. Biomembr., 1994, 26, 49–66; J. Liu, S. Chakraborty, P. Hosseinzadeh, Y. Yu, S. Tian, I. Petrik, A. Bhagi and Y. Lu, Chem. Rev., 2014, 114, 4366–4469; E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659–3853.
3. L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964.
4. C. Buning, G. W. Cantersm, P. Comba, C. Dennsion, L. Jeuken, M. Melter and J. Sanders-Loejhr, J. Am. Chem. Soc., 2000, 122, 204–211; S. Suzuki, K. Kataoaka, K. Yamaguchi, T. Inoue and Y. Kai, Coord. Chem. Rev., 1999, 190–192, 245–265; R. R. Conry, Encyclopedia of Inorganic Chemistry, 2005 DOI:10.1002/0470862106.ia052.
5. B. L. Vallee and R. J. P. Williams, Proc. Natl. Acad. Sci. U. S. A., 1968, 59, 609–614.
6. J. Heck, F. Metz, S. Buchenau, M. Teubner, B. Grimm-Lebsanft, T. P. Spaniol, A. Hoffmann, M. A. Rubhausen and S. Herres-Pawlis, Chem. Sci., 2022, 13, 8274–8288.
7. B. G. Karlsson, R. Aasa, B. G. Malmström and L. G. Lundberg, FEBS Lett., 2001, 253, 99–102; B. G. Malmstrom, Eur. J. Biochem., 1994, 223, 711–718; K. Pierloot, M. H. Olsson, U. Ryde, B. O. Roos, B. Xie, T. Elder, L. J. Wilson and D. M. Stanbury, Inorg. Chem., 1999, 38, 12–19; B. Xie, L. J. Wilson and D. M. Stanbury, Inorg. Chem., 2001, 40, 3606–3614; E. W. Dahl and N. K. Szymczak, Angew. Chem., Int. Ed., 2016, 55, 3101–3105; A. Hoffmann, J. Stanek, B. Dicke, L. Peters, B. Grimm-Lebsanft, A. Wetzel, A. Jesser, M. Bauer, M. Gnida, W. Meyer-Klaucke, M. Rübhausen and S. Herres-Pawlis, Eur. J. Inorg. Chem., 2016, 4731–4743; D. F. Schrempp, S. Leingang, M. Schnurr, E. Kaifer, H. Wadepohl and H. J. Himmel, Chemistry, 2017, 23, 13607–13611; E. Falcone and C. Hureau, Chem. Soc. Rev., 2023, 52, 6595–6600; L. Garcia, F. Cisnetti, N. Gillet, R. Guillot, M. Aumont-Nicaise, J. P. Piquemal, M. Desmadril, F. Lambert and C. Policar, J. Am. Chem. Soc., 2015, 137, 1141–1146; P. Comba, Coord. Chem. Rev., 2003, 238–239, 21–29; P. Comba, M. Kerscher and A. Roodt, Eur. J. Inorg. Chem., 2004, 4640–4645; G. D. Stroscio, R. D. Ribson and R. G. Hadt, Inorg. Chem., 2019, 58, 16800–16817.
8. W. R. Hagen, Metallomics, 2019, 11, 1768–1778.
9. G. Chaka, J. L. Sonnenberg, H. B. Schlegel, M. J. Heeg, G. Jeaeger, T. J. Nelson, L. A. Ochrymowycz and D. B. Rorabacher, J. Am. Chem. Soc., 2007, 129, 5217–5227.
10. D. K. Coggin, J. A. González, A. M. Kook, C. Bergman, T. D. Brennan, W. R. Scheldt, D. M. Stanbury and L. J. Wilson, Inorg. Chem., 1991, 30, 1125–1134.
11. E. A. Ambundo, M. Deydler, A. J. Grall, N. Aguera-Vega, L. T. Dressel, T. H. Cooper, M. J. Heeg, L. A. Ochrymowycz and D. B. Rorabacher, Inorg. Chem., 1999, 38, 4233–4242; A. M. Vande Linde, K. L. Juntunen, O. Mols, M. B. Ksebati, L. Ochrymowycz and D. Rorabacher, Inorg. Chem., 1991, 30, 5037–5042; A. M. Vande Linde, B. C. Westerby, L. Ochrymowycz and D. Rorabacher, Inorg. Chem., 1993, 32, 251–257; K. Krylova, C. P. Kulatilleke, M. J. Heeg, C. A. Salhi, L. Ochrymowycz and D. Rorabacher, Inorg. Chem., 1999, 38, 4322–4328; P. J. Griffin and L. Olshansky, J. Am. Chem. Soc., 2023, 145, 20158–20162; E. W. Dahl and N. K. Szymczak, Angew. Chem., Int. Ed., 2016, 55, 3101–3105.
12. E. J. Pulliam and D. R. McMillin, Inorg. Chem., 1984, 23, 1172–1175; S. Holzmann, J. Osterbrink, O. Hübner, M. Schulz, A. Poddelskii, E. Kaifer and H.-J. Himmel, Eur. J. Inorg. Chem., 2024, e202400597.
13. P. Zanello and N. G. Connelly, Inorganic Electrochemistry, The Royal Society of Chemistry, 2003.
14. R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322.
15. L. H. Gade, Koordinationschemie, John Wiley & Sons, 2012.
16. B. C. Dunn, L. Ochrymowycz and D. Rorabacher, Inorg. Chem., 1995, 34, 1954–1956.
17. J. Heck, A. Kucenko, A. Hoffmann and S. Herres-Pawlis, Dalton Trans., 2024, 53, 12527–12542.
18. A. V. Bondi, J. Phys. Chem., 1964, 68, 441–451; R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental data of the methods and details of the synthesis with characterization (NMR and IR spectroscopy and mass spectrometry), crystallographic information, UV/Vis-spectra, CVs and stopped-flow UV/Vis spectra, DFT details, NMR spectra, additional plots and further discussions. See DOI: https://doi.org/10.1039/d4cc06406b

‡ The redox couple [Cu(TMG2Meequ)₂]^+/2+ was excluded from the comparisons since the additional O-donors and the resulting 4+2 coordination motif make it unsuited for structural comparison with tetracoordinate guanidine quinolinyl systems.

---