Manipulating metal–ligand binding in allosteric coordination complexes through ring strain

Abstract

The weak-link approach (WLA) to organometallic complexes offers a powerful method to create allosteric shape-shifting coordination complexes. However, chemically tuning the metal–ligand interactions entails challenging syntheses. This study explores the influence of ring strain on the lability of the platinum–sulfur interaction within WLA complexes, providing a simpler alternative to chemical modifications. We study the relationship of ring size, and subsequent reactivity within 4- to 8-membered WLA cyclic Pt coordination complexes through solution and solid-state studies. These results show that strain can direct the energetic preference for the desired allosteric states and therefore, the choice of small molecule effectors required to facilitate such interconversions.

---

Coordination complexes have been used extensively in catalysis,^1–3 energy storage,^4,5 sensing,^6,7 and drug discovery.^8,9 One interesting subset of such structures are complexes that can be allosterically regulated with anionic and small molecule effectors, giving rise to shape-shifting molecules with stoichiometric and catalytic properties. Specifically, the weak-link approach (WLA),¹⁰ a synthetic method that constructs organometallic macrocycles with appropriate metal precursors (Rh(I),¹⁰ Ir(I),¹¹ Pd(II),¹² Pt(II)¹³) from hemilabile ligands^14,15 (bidentate ligands with one strong-binding atom and one weak-binding atom), allows access to structures that can be deliberately toggled between different forms (e.g. tweezers,^16–18 triple decker,^19,20 and macrocycle structures,^10,11,21Scheme 1). The types of small molecules or elemental anions to initiate such shape-shifting transformations often depend on the types of hetero-atoms that form the weak-link (S, O, N, Se)^22–24 and the electronic and steric considerations of their substituents.^24–28 Therefore, tailoring the hemilability of these weak-link ligands can often demand elaborate and time-consuming syntheses.^25,27 Ideally, tuning metal–ligand interactions without significantly altering weak chemical links and R groups simplifies synthesis and preserves customization potential for enhancing applications of allosteric organometallic complexes.

Scheme 1 Shape-shifting WLA complexes. Prior chemical approaches and a ring strain approach proposed by this paper to tune metal–ligand interactions in organometallic complexes.

The introduction of ring strain in WLA complexes offers a potentially simpler alternative to controlling the binding affinity of the weak-links of the complexes and the types of effectors they will react with.²⁹ Ring strain and geometry has been used in many systems to control complex reactivity,^30,31 for example in the types of substrates in ring-opening metathesis polymerization,³² yet in the case of the WLA, it has yet to be studied.

Herein, we report the synthesis of a series of WLA complexes assembled from hemilabile ligands of varying linker lengths and thus, varying degrees of ring strain (Scheme 1). Their solid-state structures have been confirmed by single-crystal X-ray diffraction (SCXRD). Competitive binding experiments involving Cl⁻ and MeCN against the Pt–S weak-links were conducted to determine the coordination environment around Pt(II), thereby understanding how ring strain impacts metal–ligand interactions. Notably, Cl⁻, an anionic effector, unanimously displaces the weaker metal–ligand coordination, either opening the WLA complexes (5- to 7-membered rings) or substituting the weaker effector on open complexes. In contrast, MeCN, a more weakly binding small molecule effector, selectively displaces the weak-links in cyclic complexes depending on the extent of destabilization by ring strain. To thoroughly evaluate how ring strain influences hemilability in the series of WLA complexes, DFT calculations were performed to understand the stability of the highly strained 4- and 8- membered rings.

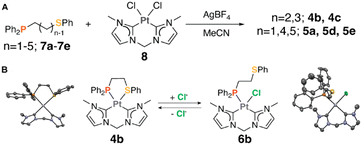
To investigate the effects of ring strain on metal–ligand interactions, a series of hemilabile ligands with varied alkyl chain lengths was employed. Both coordinating atoms (P and S) and their substituent groups were kept unchanged to focus exclusively on the impact of ring strain. To begin, a series of ligands with 1 to 5 methylene spacer units, 7a–7e, were synthesized and fully characterized by ¹H and ³¹P{¹H} NMR spectroscopy (Fig. S11–S14, ESI†). These ligands allow the conceptualization of a series of 4- to 8-membered cyclic organometallic complexes with varied ring strain: Pt(II) precursor, 8, was activated by chloride abstraction with AgBF₄ and reacted with hemilabile ligands, 7a–7e. The resulting Pt(II) WLA complexes consist of one asymmetric hemilabile P,S (phosphino-thioether) ligand and one symmetric non-labile bis-carbene ligand (Fig. 1A).

Fig. 1 (A) Synthesis of bis-carbene hemilabile ligand Pt(II) complexes. (B) Reversible Cl⁻-promoted structural interconversion of 4b and 6b and their crystal structures drawn with 50% probability ellipsoids. Counterions, hydrogens, and solvent molecules are omitted for clarity (C: gray, P: orange, S: yellow, N: purple, Pt: white, Cl: green).

The advantage of using this series of bis-carbene complexes as opposed to the complexes with two asymmetric P,S ligands, 1–3 (Scheme 1), is that only two structural states are possible. Compared to complexes 1–3, which exhibit three possible structural states, complexes 4a–4e are either closed or open, depending on whether the weak-link or the effector is bound. Moreover, characterization is simplified because a single ³¹P{¹H} NMR resonance associated with each structural state allows easy discernment of the two states using ³¹P{¹H} NMR spectroscopy.³³

Coordination complexes 4b, 4c, 5a, 5d, and 5e were characterized by ¹H, ³¹P{¹H}, and ¹⁹⁵Pt NMR spectroscopy, high-resolution mass spectrometry in solution and by SCXRD in the solid state (Fig. S1–S5 and S15–S25, ESI†). The ³¹P{¹H} and ¹⁹⁵Pt NMR spectra of these complexes each show a single resonance, indicating that the complexes are consistently in either a closed or open state. SCXRD studies were conducted to determine their exact states, revealing that 4b and 4c were formed in the closed state with Pt–S bound, while 5a, 5d, and 5e were formed in the open state with Pt bound to MeCN (Fig. S10, ESI†).

In previous WLA studies, the weak-link atom (S), a stronger coordination moiety than MeCN, preferentially binds to the metal center.^24–27 However, the observed 5a, 5d, and 5e structures showed unusual behavior in which the weaker MeCN effector outcompetes the S heteroatom for the available coordination site. This behavior is a direct consequence of the ring strain introduced in 4-, 7-, and 8-membered rings, which weakens the Pt–S interaction in these three complexes.

To realize further shape transformations in the as-synthesized open complexes, 5a, 5d, and 5e were subjected to vacuum overnight in an attempt to remove MeCN and produce the closed complexes.³⁴ The open complex 5d was converted into the corresponding closed structure, 4d, as evidenced by ³¹P{¹H} and ¹⁹⁵Pt NMR spectroscopy in solution (Fig. 3A), and SCXRD in the solid state (Fig. S7, ESI†). The displacement of MeCN by thioether resulted in a downfield shift in the ³¹P{¹H} resonance from 7.57 ppm in 5d to 17.03 ppm in 4d, along with an increased ¹J_P–Pt coupling constant from 2394 to 2466 Hz (Fig. S7, ESI†). To facilitate the transition of the open state 5d to the closed state 4d, specific conditions (applying vacuum to remove MeCN) are required, indicating that 4d is not the lowest energy configuration but is instead stabilized by the removal of the small molecule effector MeCN. Conversely, when MeCN was reintroduced, 4d rapidly reverted back to 5d, highlighting the thermodynamic preference for the more stable open state. The quick transition underscores that the open state has lower free energy and is therefore thermodynamically favored.³⁵

Despite the vacuum treatment, 5e retained its open state, as evidenced by the unchanged ³¹P{¹H} NMR resonance at 7.51 ppm (Fig. S8, ESI†). Unlike 4d and 5d, 5e might not exhibit a thermodynamic-kinetic dilemma, as it does not undergo structural transformations under conditions that typically induce such changes. In contrast, the ³¹P{¹H} spectrum for 5a showed an additional minor resonance at −55.17 ppm, suggesting the formation of a new Pt(II) species, potentially forming a closed 4-membered chelate or an 8-membered dimer.³⁶ Upon reintroducing MeCN, this new species reverted to the open configuration, suggesting that the MeCN-bound open complex 5a is more thermodynamically stable than other structural states (Fig. S6, ESI†). These results differ from those of 4b and 4c, where the closed state is thermodynamically favored, supporting our hypothesis that chelate ring sizes significantly affect structural stability.

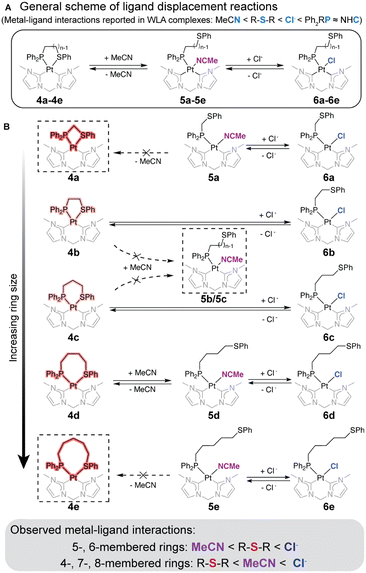
As summarized in Fig. 2, reversible structural interconversion studies on WLA complexes were conducted using ligands of varying binding affinities, ranked as MeCN < thioether < Cl⁻. The strongest effector, Cl⁻, can replace all coordination moieties to form 6a–6e, regardless of ring size. Interestingly, the binding competition between MeCN and thioether is dependent on the ring size of the complex. In the 5- and 6-membered cyclic complexes 4b and 4c, thioether preferentially binds over MeCN, consistent with the coordination patterns observed in previous WLA studies.³⁷ However, in 4-, 7-, and 8-membered acyclic complexes 5a, 5d, and 5e, MeCN preferentially chelates over thioether. Notably, the 7-membered complex can reversibly toggle between a thioether-bound closed state (4d) and a MeCN-bound open state (5d).

Fig. 2 (A) Scheme depicting ligand displacement reactions with MeCN and Cl⁻ against the Pt–S weak-links. (B) Summary of ligand displacement experiments. Structures outlined with dashed-line boxes were not experimentally obtained.

To understand the varied binding preferences among complexes with different ring sizes, we examined their ring strain in single crystals and DFT-calculated solid-state structures (Fig. 3B–D and Table S1, ESI†). Ring strain is defined as an energy difference between open acyclic structures and their closed cyclic analogs.²⁹ To establish a ring strain baseline from acyclic structures, open, unstrained complexes (5a, 6b, 6c, 5d, and 5e) were first examined: similar P–Pt–L bond angles are observed, ranging from 87° to 90°, regardless of ring size. This range served as a strain-free baseline (Fig. 3B). In contrast, the closed complexes (4a–4e) display P–Pt–S angles from 73° to 97°, which increase with ring size from 4- to 8-membered rings.²⁹

Fig. 3 (A) Reaction scheme for ligand displacement; an example interconversion between 4d and 5d, with highlighted closed (P–Pt–S) and open (P–Pt–L) bond angles. (B) Line plots showing closed (P–Pt–S) and open (P–Pt–L) bond angles for 4- to 8-membered rings. Bond angles are based on data from DFT calculations (4a, 4e, 5c) or single crystal structures (the rest). (C) Differences in bond angles between closed and open states, derived from Fig. 3B. (D) Energy differences between closed and open state.

Through pairwise comparisons, 5- and 6-membered cyclic complexes show nearly identical bond angles in both open and closed states, indicating minimal ring strain in these closed structures. Conversely, closed complexes with 4-, 7- and 8-membered rings exhibit larger ring strain, as evidenced by the P–Pt–S/L bond angle differences between the two states (Fig. 3C). For example, the angle difference sharply decreases from 16° in the 4-membered ring to nearly 0° in the 5- and 6-membered rings, then gradually increases to 10° in the 8-membered ring. This indicates that 4a has the largest ring strain due to its 4-membered ring, followed by 4e (8-membered) and 4d (7-membered). Ring strain energies between open and closed states, quantified using DFT-calculated models (Table S1, ESI†), align with the trend that complexes with 5- and 6-membered chelates have the least ring strain, followed by the remaining three complexes (Fig. 3D). For context, the ring strain introduced (<10 kcal mol⁻¹) is significantly smaller than that of strong covalent bonds (50–150 kcal mol⁻¹) and comparable to weak hydrogen bonding (2–10 kcal mol⁻¹).

Solid-state analyses and DFT calculations collectively explain the binding preferences between thioether and MeCN in different cyclic coordination complexes. The 5- and 6-membered rings show negligible ring strain, favoring the stronger thioether binder over MeCN to form the closed complexes 4b and 4c. In comparison, the 4- and 8-membered complexes have substantial strain energy, favoring the weaker binder MeCN over thioether to form the open complexes 5a and 5e. The 7-membered ring in 4d results in a smaller ring strain than 4a and 4e, allowing MeCN dissociation and thioether association upon applying vacuum.

This work is significant because the structures described and characterized here represent a series of WLA coordination complexes systematically designed to incorporate varying degrees of ring strain. This design allows researchers to understand how such strain translates to strength of metal–ligand interactions and sensitivity to ligand displacement reactions. By finetuning these interactions through ring strain, researchers can deliberately modulate allosteric reactivity and target preferred coordination states. This capability is critical for designing shape-shifting organometallic catalysts^18,20 and chemical sensors¹⁷ with enhanced sensitivity.

This material is based upon work supported by the following awards: the National Science Foundation DMR-2104353 and CHE-1709888, the Air Force Office of Scientific Research FA9550-22-1-0300, and the Sherman Fairchild Foundation. F. Y. W acknowledges the financial support from academic year research grant (No. 17652) from Northwestern University. This work made use of the IMSERC Physical Characterization facility at Northwestern University; We thank Dr Noel Leon for helpful discussions and manuscript preparation.

Data availability

The data supporting this article, including synthetic procedures, spectral data, and crystallographic and computational information have been included as part of the ESI.† Crystallographic data for 5a, 4b, 6b, 4c, 4d, 5d, and 5e has been deposited at CCDC under 2295740–2295741, 2295745–2295749, respectively.

Conflicts of interest

There are no conflicts to declare.

References

1. J. Dupont, R. F. de Souza and P. A. Z. Suarez, Chem. Rev., 2002, 102(10), 3667–3692.
2. R. H. Crabtree, Organometallics, 2011, 30(1), 17–19.
3. L. Alig, M. Fritz and S. Schneider, Chem. Rev., 2019, 119(4), 2681–2751.
4. N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96(2), 877–910.
5. D.-Y. Wang, R. Liu, W. Guo, G. Li and Y. Fu, Coord. Chem. Rev., 2021, 429, 213650.
6. O. S. Wenger, Chem. Rev., 2013, 113(5), 3686–3733.
7. J. W. Steed, Chem. Soc. Rev., 2009, 38(2), 506–519.
8. S. Gutiérrez, M. Tomás-Gamasa and J. L. Mascareñas, Chem. Sci., 2022, 13(22), 6478–6495.
9. M. Patra and G. Gasser, ChemBioChem, 2012, 13(9), 1232–1252.
10. J. R. Farrell, C. A. Mirkin, I. A. Guzei, L. M. Liable-Sands and A. L. Rheingold, Angew. Chem., Int. Ed., 1998, 37(4), 465–467.
11. M. V. Ovchinnikov, B. J. Holliday, C. A. Mirkin, L. N. Zakharov and A. L. Rheingold, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(8), 4927–4931.
12. A. H. Eisenberg, F. M. Dixon, C. A. Mirkin, C. L. Stern, C. D. Incarvito and A. L. Rheingold, Organometallics, 2001, 20(10), 2052–2058.
13. P. A. Ulmann, A. M. Brown, M. V. Ovchinnikov, C. A. Mirkin, A. G. DiPasquale and A. L. Rheingold, Chem. – Eur. J., 2007, 13(16), 4529–4534.
14. J. C. Jeffrey and T. B. Rauchfuss, Inorg. Chem., 1979, 18(10), 2658–2666.
15. C. S. Slone, D. A. Weinberger and C. A. Mirkin, The Transition Metal Coordination Chemistry of Hemilabile Ligands, Inorg. Chem., 1999, 233–350.
16. N. C. Gianneschi, S.-H. Cho, S. T. Nguyen and C. A. Mirkin, Angew. Chem., Int. Ed., 2004, 43(41), 5503–5507.
17. J. Mendez-Arroyo, J. Barroso-Flores, A. M. Lifschitz, A. A. Sarjeant, C. L. Stern and C. A. Mirkin, J. Am. Chem. Soc., 2014, 136(29), 10340–10348.
18. C. M. McGuirk, C. L. Stern and C. A. Mirkin, J. Am. Chem. Soc., 2014, 136(12), 4689–4696.
19. Y.-M. Jeon, J. Heo, A. M. Brown and C. A. Mirkin, Organometallics, 2006, 25(11), 2729–2732.
20. H. J. Yoon, J. Kuwabara, J.-H. Kim and C. A. Mirkin, Science, 2010, 330(6000), 66–69.
21. B. J. Holliday, J. R. Farrell, C. A. Mirkin, K.-C. Lam and A. L. Rheingold, J. Am. Chem. Soc., 1999, 121(26), 6316–6317.
22. I. V. Kourkine, C. S. Slone, C. A. Mirkin, L. M. Liable-Sands and A. L. Rheingold, Inorg. Chem., 1999, 38(12), 2758–2759.
23. X. Liu, C. L. Stern and C. A. Mirkin, Organometallics, 2002, 21(6), 1017–1019.
24. M. S. Rosen, A. M. Spokoyny, C. W. Machan, C. Stern, A. Sarjeant and C. A. Mirkin, Inorg. Chem., 2011, 50(4), 1411–1419.
25. A. M. Spokoyny, C. W. Machan, D. J. Clingerman, M. S. Rosen, M. J. Wiester, R. D. Kennedy, C. L. Stern, A. A. Sarjeant and C. A. Mirkin, Nat. Chem., 2011, 3(8), 590–596.
26. R. D. Kennedy, C. W. Machan, C. M. McGuirk, M. S. Rosen, C. L. Stern, A. A. Sarjeant and C. A. Mirkin, Inorg. Chem., 2013, 52(10), 5876–5888.
27. B. J. Holliday, P. A. Ulmann, C. A. Mirkin, C. L. Stern, L. N. Zakharov and A. L. Rheingold, Organometallics, 2004, 23(8), 1671–1679.
28. Y. Liu, Z. S. Kean, A. I. d’Aquino, Y. D. Manraj, J. Mendez-Arroyo and C. A. Mirkin, Inorg. Chem., 2017, 56(10), 5902–5910.
29. T. Dudev and C. Lim, J. Am. Chem. Soc., 1998, 120(18), 4450–4458.
30. R. D. Hancock and A. E. Martell, Supramol. Chem., 1996, 6(3–4), 401–407.
31. R. D. Hancock, J. Chem. Educ., 1992, 69(8), 615.
32. A. R. Hlil, J. Balogh, S. Moncho, H.-L. Su, R. Tuba, E. N. Brothers, M. Al-Hashimi and H. S. Bazzi, J. Polym. Sci., Part A: Polym. Chem., 2017, 55(18), 3137–3145.
33. P. E. Garrou, Chem. Rev., 1981, 81(3), 229–266.
34. A. M. Lifschitz, R. M. Young, J. Mendez-Arroyo, V. V. Roznyatovskiy, C. M. McGuirk, M. R. Wasielewski and C. A. Mirkin, Chem. Commun., 2014, 50(52), 6850–6852.
35. P. D. Branco, G. Yablonsky, G. B. Marin and D. Constales, Comput. Chem. Eng., 2019, 125, 606–611.
36. G. K. Anderson and R. Kumar, J. Organomet. Chem., 1988, 342(2), 263–268.
37. A. M. Spokoyny, M. S. Rosen, P. A. Ulmann, C. Stern and C. A. Mirkin, Inorg. Chem., 2010, 49(4), 1577–1586.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2295740–2295741 and 2295745–2295749. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc06135g

‡ These authors contributed equally.

---