Chiral recognition of amino acids through homochiral metallacycle [ZnCl₂L]₂

Abstract

Chiral recognition holds tremendous significance in both life science and chemistry. The ability to differentiate between enantiomers is crucial because one enantiomer typically holds greater biological relevance while its counterpart is often not only unnecessary but also potentially harmful. In this regard, homochiral metallacycle [ZnCl₂L]₂ is used in this study to understand and differentiate between the R and S enantiomers of amino acids (alanine, proline, serine, and valine). The electronic, geometric, and thermodynamic stabilities of the amino acid enantiomers inside the metallacycle are determined through various analyses. The greater interaction energy (E_int) is obtained for the ser@metallacycle complexes i.e., −33.03 and −30.75 kcal mol⁻¹, respectively for the S and R enantiomers. The highest chiral discrimination energy of 3.11 kcal mol⁻¹ is achieved for ala@metallacycle complexes. Regarding the electronic properties, the frontier molecular orbital (FMO) analysis indicates that the energy gap decreases after complexation, which is confirmed through density of states (DOS) analysis. Moreover, natural bond orbital (NBO) analysis determines the amount and direction of charge transfer i.e., from metallacycle towards amino acids. The maximum NBO charge transfer is observed for S-pro@metallacycle complex i.e., −0.291 |e|. Electron density difference (EDD) analysis further proves the direction of charge transfer. Noncovalent interaction index (NCI) and quantum theory of atoms in molecules (QTAIM) analyses demonstrate that the noncovalent interactions present between the host and guest are the weak van der Waals forces and hydrogen bonding. The results of NCI and QTAIM analyses for all the complexes are in alignment with those of the interaction energy (E_int) and chiral discrimination energy (E_chir) analyses, i.e., significantly greater non-bonding interactions are observed for the complexes with greater E_chir, i.e., for ala@metallacycle. Overall, our analyses demonstrate the excellent chiral discrimination ability of metallacycle towards chiral molecules, i.e., for enantiomers of amino acids through host–guest supramolecular chemistry.

---

1. Introduction

The identification and determination of enantiomeric excess for chiral species are of utmost importance, particularly in clinical applications, owing to the unique functionalities exhibited by their enantiomers.¹ Up till now, various methods have been employed for this purpose, including chiral chromatography,² chiral electrophoresis,³ spectroscopic⁴ and enzymatic methods⁵etc. In recent years, substantial progress has been made to understand the enantioselectivity of proteins and nucleic acids’ active sites.⁶ In this regard, the phenomenon of chiral recognition is of great significance. Chiral recognition serves as a comprehensive term covering diverse properties of chiral systems, including difference in energy between the R and S enantiomers in chiral environment, or the differences in intramolecular energies between the R–R and S–R pairs.⁷ The prevailing strategy for chiral recognition involves creating a chiral environment using chiral host molecules. This environment facilitates the recognition of target chiral guests through weak supramolecular interactions.⁸ Cyclodextrins are well recognized hosts for the encapsulation of various hosts molecules inside their cavities.⁹ Various supramolecular materials, including macrocyclic compounds and porous organic cages, have gathered significant attention due to their intriguing molecular structures and excellent host–guest recognition capabilities.¹⁰ Vladimir et al. used self-assembled melamine and cyanuric acid to determine their chiral recognition abilities.¹¹ Furthermore, Schulte et al. studied chiral recognition in helicene-based coordination cages.¹²

In previous eras, most of the chiral drugs were employed as the mixture of enantiomers, i.e., as racemates, as it was a challenging task to obtain enantiomerically pure ones.¹³ In pharmaceuticals, one enantiomer is often more efficient than the other, the other being less efficient or even poisonous. After the thalidomide tragedy in the late 1950s, Blaschke et al. discovered that only the S enantiomer of this drug exhibits teratogenic effects.¹⁴ On the contrary, S enantiomer of a well-known drug ibuprofen is biologically active, whereas its R enantiomer is not.⁹ Moreover, D-sugars are the primary source of energy for cells, and L-amino acids are utilized for protein synthesis. Amino acids serve as prominent chiral compounds in nature. It's widely acknowledged that L-amino acids are natural constituents of biological systems, whereas D-amino acids may exhibit toxicity or metabolic irregularities in living organisms. In this regard, the chiral discrimination of the enantiomers of drugs, carbohydrates and amino acids is fundamental for understanding various biological processes, as well as for the development of safer pharmaceuticals etc. The chiral recognition of amino acids stands as a crucial and challenging field.¹⁵

Thus far, significant developments have been made, including the design and synthesis of chiral nanomaterials as hosts for the chiral recognition, including porous organic cages, covalent organic frameworks,¹⁶etc. which represent key approaches for achieving chiral recognition of amino acids. Previously, researchers have also examined the chiral recognition of chiral molecules, specifically amino acids through various systems, such as chiral metal complexes,^17,18 crown ethers,^19–21 chiral gas chromatography,²² high-performance liquid chromatography,²³ cyclodextrin derivatives^24–26 and so on.²⁷ Moreover, Asghar et al. used CC2 porous organic cages for the chiral recognition of amino acids enantiomers.²⁸ The results demonstrated the highest chiral discrimination energy for the enantiomers of proline, i.e., 2.78 kcal mol⁻¹. Chen and co-workers determine the chiral recognition of cysteine enantiomers through fluorescent nanoprobe.¹⁵ But still more competent chiral hosts are required for effective and selective separation of enantiomers of amino acids. In this regard, the metallacycles function efficiently as suitable candidates for chiral recognition. Metallacycles represent a novel category of supramolecular materials formed by combining appropriate metal ions with organic ligands acquiring several binding sites.¹⁰

Herein, a homochiral metallacycle [ZnCl₂L]₂ is used for the chiral recognition of amino acids enantiomers (see Fig. 2). This metallacycle [ZnCl₂L]₂ was synthesized by a reaction of (S)-(1-isonicotinoylpyrrolidin-2-yl)methyl-isonicotinate (L) with ZnCl₂¹⁰ and to the best of our knowledge has not been used for the chiral recognition of amino acids through host–guest supramolecular chemistry. The homochiral nature and a remarkable cavity inside the metallacycle makes it a better choice for the chiral recognition of the guests (i.e., amino acids), through host–guest interactions. The oxygen atoms and the pyridine rings located along the four walls of the metallacycle, play a major role in host–guest non-covalent interactions (specifically hydrogen bonding and van der Waals interactions), thus making it an ideal host for the chiral recognition. The amino acids selected for chiral recognition are alanine, proline, serine, and valine (see Fig. 1). Two of these are non-essential amino acids i.e., alanine and serine, playing significant roles in protein synthesis.²⁹ Thus, chiral recognition of their enantiomers is crucial. Likewise, the chiral recognition of the enantiomers of valine is important as it is an essential amino acid and found in various tissues.³⁰ Moreover, the chiral recognition of the enantiomers of proline is also significant as it is a conditionally essential amino acid and one of its enantiomers play a signaling function in modulating mitochondrial activities and initiating targeted gene expression.³¹

Fig. 1 Molecular structures of amino acids.

Fig. 2 Optimized structure of metallacycle.

In this research work, DFT simulations are carried out for the chiral recognition of amino acids enantiomers by chiral metallacycle. Since our bodies exclusively recognize S enantiomers of amino acids, this highlights the importance of chiral recognition of enantiomers. This study examines chiral recognition mechanisms and intramolecular interactions between the chiral host and guest, through various analyses, including frontier molecular orbital (FMO), natural bond orbital (NBO), electron density difference (EDD), density of states (DOS), non-covalent interaction index (NCI) and quantum theory of atoms in molecules (QTAIM).

2. Computational methodology

The DFT calculations are carried out using Gaussian 09 software,³² while for structural visualization, GaussView 5.0³³ and Chemcraft software are used. The DFT functional and basis set employed for the geometry optimization and frequency calculations are ωB97XD/6-31G(d,p). Through this combination of functional and basis set, the ground state optimized geometries of the complexes are attained, along with the confirmation of the presence of structures at potential energy minima.^34,35 The electronic properties such as FMO, DOS and NBO analysis are also performed at ωB97XD/6-31G(d,p) level of theory. The wB97XD functional, with its long-range corrected hybrid exchange–correlation and dispersion correction, is particularly well-suited for calculation of electronic properties, as it provides more accurate HOMO and LUMO energies compared to standard hybrid functionals. This is due to its inclusion of 100% asymptotic exchange at long ranges, which improves the reliability of the HOMO–LUMO gap.^36–38 Furthermore, for the calculation of interaction energies of the complexes, the following equation is used,

E_int = E_complex − (E_metallacycle + E_{amino acid}) (1)

Here, E_int is the interaction energy of the designed complexes, whereas E_complex, E_metallacycle, and E_{amino acid} are the energies associated with the complexes (host–guest), metallacycle and amino acids, respectively. The calculations are also performed in two different solvents i.e., water and dichloromethane, employing polarizable continuum model (PCM) in order to study the effect of solvent on the stability of amino acid@metallacycle complexes. The values of interaction energies in these two solvents are given in Table 1.

Table 1 Interaction energies (E_int) with interacting atoms (A_ad), interacting distance (D_int), and chiral discrimination energy (E_chir) between R and S enantiomers of amino acids@metallacycle

Complexes	A ad (Ana-surface)	D int (Å)	E int (kcal mol^−1)	E chir (kcal mol^−1)	E int in H20 (kcal mol^−1)	E int in DCM (kcal mol^−1)	BSSE	ΔG
R-ala@metallacycle	H1⋯C4	2.53	−28.38	3.11	−23.84	−24.21	−18.74	−13.32
	O5⋯H2	1.81
	H3⋯O6	2.12
S-ala@metallacycle	O1⋯H2	2.07	−31.49		−24.87	−25.70	−22.72	−19.86
	H3⋯C5	2.69
	H4⋯C6	2.62
R-pro@metallacycle	H1⋯O4	1.73	−30.23	1.94	−27.62	−27.80	−21.22	−14.68
	H2⋯O4	2.57
	H3⋯O5	2.46
S-pro@metallacycle	H1⋯O4	2.39	−32.17		−29.82	−29.98	−24.11	−16.75
	H2⋯O5	2.49
	H3⋯O6	1.76
R-ser@metallacycle	H1⋯O4	1.76	−30.75	2.28	−26.17	−26.86	−20.46	−15.12
	H2⋯O5	2.41
	H3⋯O6	2.31
S-ser@metallacycle	C1⋯H4	2.95	−33.03		−26.46	−27.02	−22.52	−16.24
	O2⋯H5	1.78
	O3⋯H6	2.18
R-val@metallacycle	H1⋯O4	1.76	−30.27	2.49	−25.76	−26.32	−21.30	−12.40
	H2⋯C5	2.41
	H3⋯C6	2.97
S-val@metallacycle	H1⋯O4	1.71	−27.78		−25.34	−25.66	−17.06	−11.18
	H2⋯C5	2.56
	H3⋯C6	2.73

---

In the systems where two fragments or units form a complex, there are chances of basis set superposition error (BSSE). So, to ensure the reliability and accuracy of results, it becomes essential to include corrections for such type of errors.³⁹ Hence, BSSE corrected interaction energies are also calculated for the designed complexes. In order to check whether the host–guest encapsulation is thermodynamically feasible or not, Gibbs free energy is calculated employing eqn (2).

ΔrG°(298 K) = ∑(ε₀ + G_corr)_products − ∑(ε₀ + G_corr)_reactants (2)

For the further evaluation of the electronic properties and interactions between amino acid and metallacycle in the designed complexes, various analyses are performed, including, NBO (to analyze charge transfer), EDD (to understand the regions of charge accumulation and depletion), FMO and DOS (to study change in electronic properties, HOMO, LUMO levels and E_gap). The E_gap in the designed complexes is determined by taking the difference of energies between HOMO and LUMO, i.e.,

E_gap = E_LUMO − E_HOMO (3)

Here, E_gap, represents the energy gap between the HOMO and LUMO of the designed complexes, E_LUMO is the energy of lowest unoccupied molecular orbital, whereas E_HOMO is the energy of highest occupied molecular orbital. The FMOs are visualized through VMD software. Moreover, in the formation of the host–guest complexes, noncovalent interactions play a crucial role. The strength and nature of noncovalent interactions (repulsive, van der Waals and electrostatic) is determined by reduced density gradient (RDG) or noncovalent interaction index analysis (NCI). Multiwfn 3.8 software⁴⁰ is used for the generation of 2D RDG maps and 3D RDG isosurfaces. For the visualization of 3D isosurfaces, VMD software⁴¹ is employed. The 2D RDG maps depend on electron density (ρ) as well as the reduced density gradient,⁴²i.e.,

The nature of non-bonding interactions is determined through different colors presented in 3D RDG isosurfaces, i.e., red, blue, and green colors illustrating the presence of repulsive, electrostatic and van der Waals interactions. To further elaborate the nature of non-bonding interactions, QTAIM analysis is performed. The topological parameters determined through QTAIM analysis are Laplacian of electron density ∇²ρ(r), total electron density ρ(r), total energy density H(r), local potential energy G(r), and local kinetic energy V(r), representing the nature of interaction at bond critical points (BCPs).^43,44 The total energy density H(r) is found through the addition of local kinetic and potential energies i.e., V(r) and G(r), respectively.

H(r) = V(r) + G(r) (5)

Additionally, one other parameter i.e., interaction energy (E_int) of individual bonds is evaluated in order to further confirm the nature of non-bonding interactions. The interaction energy of the individual bonds is evaluated through Espinosa approach. The equation for the calculation of E_int is as follows,

If the value of E_int lies in the range of 3–10 kcal mol⁻¹, the electrostatic interactions (hydrogen bonding) are expected between the host–guest complexes,^45,46 whereas the value less than 3 kcal mol⁻¹, demonstrate the presence of weak van der Waals forces.

3. Results and discussion

3.1. Geometric parameters

In this research work, we have selected a chiral metallacycle [ZnCl₂L]₂ as a host molecule for the chiral discrimination of amino acid enantiomers, i.e., alanine, proline, serine, and valine. All the amino acids (including both enantiomers) are encapsulated inside the cavity of the metallacycle, with several orientations, and the most stable complexes are then selected for further analyses i.e., one with highest interaction energy. The values of interaction energies (E_int), interaction distances (D_int), and chiral discrimination energies (E_chir) of all the complexes are computed and reported in Table 1, whereas the stable optimized geometries are shown in Fig. 3. The total of eight amino acid@metallacycle complexes are formed. In comparison between the E_int of all the complexes, the comparatively greater E_int is found for the ser@metallacycle complexes i.e., −33.03 and −30.75 kcal mol⁻¹, respectively for the S and R enantiomers. So, it can be concluded that the enantiomers of amino acid serine show stronger interaction with the metallacycle. This is because, the serine is stabilized through the OH group (present on carbon number 3), directing towards the side wall of the metallacycle.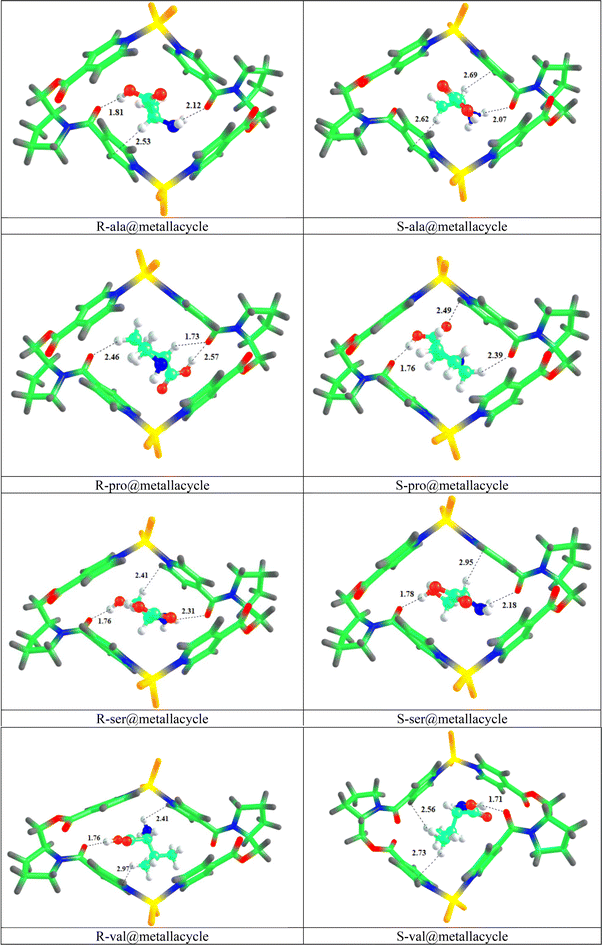

Fig. 3 Optimized geometries of R and S amino acid@metallacycle complexes showing interacting distances (D_int).

In comparison between R and S-pro@metallacycle, S-pro@metallacycle exhibits greater E_int and greater stability. This conclusion aligns with the experimental data, which demonstrates a greater elution time for S-proline, indicating stronger interactions with the metallacycle (i.e., stationary phase) in gas chromatography.¹⁰ The enhanced stability of S-proline is attributed to the more favorable interactions with the metallacycle, corroborating the experimental observations.

Overall, in comparison between the R and S enantiomers of all the complexes, S enantiomers of ala@metallacycle, pro@metallacycle and ser@metallacycle show the greater E_int, whereas the R enantiomers of val@metallacycle shows the higher E_int. The reason behind the greater E_int of S enantiomeric complexes is that the S configuration of metallacycle is taken for the analyses throughout the manuscript. It is a general observation that the homochiral complexes (i.e., SS) exhibit greater interaction energies and are thus more stable.⁴⁷ However, this may not always be the case, as demonstrated in a chiral recognition study by Asghar et al., where the heterochiral complex of proline with the CC2 cage is preferred. Considering the interaction distances of the complexes into account, the least D_int are observed for the enantiomeric complexes of proline, followed by R and S-ser@metallacycle (see Table 1). The lesser D_int is observed for the complexes having greater E_int.

In order to check the effect of solvent on chiral recognition, E_int of the complexes (amino acid@metallacycle) are computed in two solvents, i.e., H₂O and DCM. The values of E_int in water range from −23.84 to −29.82 kcal mol⁻¹, while the values in DCM range from −24.21 to −29.88 kcal mol⁻¹, indicating the stability of the complexes in solvents. It is observed that the values of E_int in solvents are somewhat less than that observed in gas phase, but the difference is not quite significant. Overall, the trend of chiral recognition is similar for all the complexes in solvents as observed in gas phase, i.e., the greater E_int is observed for S enantiomeric complexes of alanine, proline, and serine, and R enantiomeric complex of valine. Moreover, the basis set superposition error (BSSE) corrected interaction energies are also reported in Table 1. The greater negative values ranging from −17.06 to −24.11 kcal mol⁻¹ indicate the stability of the designed complexes. To check the thermodynamic feasibility of the host–guest formation, Gibbs free energy is calculated (using eqn (2)). The negative values of Gibbs free energy ranging from −11.18 to −19.86 kcal mol⁻¹ (see Table 1) reveal that the host–guest encapsulation is a spontaneous (exergonic) process. Additionally, the amino acids in zwitterionic forms are encapsulated inside the cavity of the host. The interaction energies of the resulting complexes are calculated in gas phase, and in solvents (i.e., in water and DCM). The values of interaction energies of the complexes affirm that the resulting complexes have higher stability, even when the amino acids are taken as zwitterions (see Table S2 of ESI†).

The chiral discrimination energy (E_chir) is the ability of a chiral molecule to show different intermolecular interactions than its enantiomer.⁴⁸ It is calculated by taking the difference in interaction energies of the two enantiomeric complexes. Here, E_chir is basically the ability of the metallacycle to differentiate between the two enantiomers.

E_chir = E^{(S-a.a@metallacycle)}_int − E^{(R-a.a@metallacycle)}_int (7)

In the eqn (7), E_chir is the chiral recognition or chiral discrimination energy, E^{(S-a.a@metallacycle)}_int and E^{(R-a.a@metallacycle)}_int are the interaction energies of S and R enantiomers of amino acid with the metallacycle, respectively. The enantiomeric complexes of ala@metallacycle exhibit the highest values of E_chir (i.e., 3.11 kcal mol⁻¹), followed by val@metallacycle (2.49 kcal mol⁻¹), ser@metallacycle (2.28 kcal mol⁻¹) and pro@metallacycle (1.94 kcal mol⁻¹). The highest value of E_chir for ala@metallacycle, can be attributed the smallest size of alanine, hence ideal encapsulation suitability (i.e., its enantiomers fit best inside the cavity of the host metallacycle). Conversely, in a study conducted by Asghar et al. where CC2 porous organic cages were used for the chiral recognition of amino acids enantiomers,²⁸ it can be seen that the highest chiral discrimination energy is obtained for the enantiomers of proline, i.e., 2.78 kcal mol⁻¹. The lowest value of E_chir for the pro@metallacycle might be due to its position inside the host, as it is projected a little outside from the inner cavity of the metallacycle, ultimately resulting in a reduced E_chir.

3.2. DOS spectra analysis

The DOS spectra are computed to verify the results of FMO analysis. The DOS spectra for R and S enantiomeric complexes are reported in Fig. S1 of ESI,† with the black, red, and blue curves, representing the total density of states (TDOS), amino acid and metallacycle DOS, respectively. In all the graphs, the vertical dotted line represents the position of HOMO, whereas after the HOMO level, the first short line pointing upwards on the horizontal axis (i.e., x-axis), represents the position of LUMO. The difference between the HOMO and LUMO energies is marked as E_gap. In the spectra of R and S-ala@metallacycle, the contribution of the HOMO of both the species towards the HOMO of the complex (i.e., in TDOS) is visible, as both the red and blue curves are visible at the HOMO level. The dotted lines for HOMO levels exactly touch the x-axes at energies of −8.68 and −8.92 eV, for R and S-ala@metallacycle, respectively. The short lines on x-axes are observed at −0.75 and −0.87 eV, respectively for R and S-ala@metallacycle, specifying the positions of LUMOs. Only the blue curve is prominent on the LUMO, whereas the red curve nearly diminishes, elaborating the major participation of only the LUMO of metallacycle towards the LUMO of the complex. On the other hand, the LUMO of the amino acid does not take part in formation of LUMO of the complexes. The energy gap for R and S-ala@metallacycle found through FMO analysis is 7.93 and 8.04 eV, which is also visible in the DOS spectra i.e., the difference of energy between the HOMO and LUMO of the complexes. For R and S-pro@metallacycle complexes, again both the red and blue curves are visualized in the position of HOMO, while for LUMO, only the blue curve is notable. The energy of the HOMO, LUMO and the energy gap for R and S-pro@metallacycle, observed through FMO is also justified by the DOS spectra. Similarly, for the enantiomeric complexes of ser@metallacycle and val@metallacycle, the results of FMO are verified by the DOS analysis.

3.3. NBO analysis

NBO analysis is carried out to accurately predict the direction of charge transfer between the host and guest molecules upon complexation. For all the complexes, NBO charges are calculated by adding the magnitude of charge present on every single atom of amino acid. The magnitude of the resulting NBO charge is negative for all the complexes, demonstrating the charge transfer from the metallacycle towards the amino acids, resulting in an increase in charge on amino acids. The values of NBO charges are reported in Table S4.† The NBO charges range from −0.012 to −0.291 |e|, for all the complexes. The maximum NBO charge transfer is seen in for S-pro@metallacycle i.e., −0.291 |e|, followed by R-ala@metallacycle complex i.e., −0.058 |e| and −0.052 |e| for R-val@metallacycle, whereas the minimum value of −0.012 |e| is obtained for S-ala@metallacycle. While comparing the results of NBO with FMO, it can be seen that except for S-pro@metallacycle, the lesser E_gap and greater NBO charges are observed for the complexes, containing R enantiomers of amino acids. The difference in the NBO charge transfer between R and S enantiomeric complexes, is also calculated and the results indicate a greater difference for ala@metallacycle and pro@metallacycle complexes i.e., one complex with the greater chiral discrimination energy and the other with lowest E_gap, respectively. Among all the enantiomeric complexes, the least difference of NBO charge transfer is observed for the ser@metallacycle, due to the lesser difference between the energy gaps of the two enantiomeric complexes. Overall, NBO charge transfer is justified by the values of E_chir and E_gap.

Further insights into the direction of charge transfer can be obtained through the stabilization energy (E(2)). E(2) quantifies the donor–acceptor interactions within the complexes. NBO charges indicate that the charge has been transferred from the metallacycle towards the amino acids. E(2) provides additional information about this interaction from an energetic perspective. Out of the many possible interactions, the most significant donor–acceptor interactions between the metallacycle and amino acids are compiled in Table S4.† The higher values of E(2) or donor–acceptor interaction energies (ranging from 5.53–27.49) are in corroboration with the greater interaction energies reported for all the complexes. It is evident that for four of the designed complexes (i.e., R-ala@metallacycle, S-pro@metallacycle, R-ser@metallacycle and R-ser@metallacycle), the charge is being transferred from lone pair orbital (LP) of oxygen atom (of host metallacycle) towards the antibonding orbital (BD*) of O–H of amino acids. Similarly for S-ala@metallacycle, R-val@metallacycle and S-val@metallacycle, charge transferred is observed from lone pair orbital (LP) of oxygen of the host towards antibonding orbital (LP*) of H. Moreover, for S-ala@metallacycle, NBO charge transfer is from LP of oxygen towards the BD* of N–H.

3.4. EDD analysis

For the visual illustration of the NBO charge transfer between the amino acids and the metallacycle, EDD analysis is performed. The NBO analysis predicted the direction of charge transfer mainly from metallacycle towards the amino acids. The 3D representation of EDD isosurfaces verifies these findings. The red and blue colored isosurfaces are present over all the designed complexes. The patches with red color show the charge depletion, whereas those with blue color indicate the charge accumulation. For R and S-ala@metallacycle, the patches appear on the pyridine units located along the four walls (sides) of the metallacycle. Some of these patches are blue, while the others are red colored. The blue patches show that some charge is being accumulated on the pyridine, whereas the red patches show evidence of charge depletion. Similarly, the encapsulated alanine exhibits both colored patches, representing the electron density donation and back donation. Overall, the blue colored isosurfaces are dominantly present on the amino acid i.e., alanine. On the contrary, the red patches are mostly seen on the metallacycle. This conclusion is in correspondence with the results of NBO charge transfer, where the direction of charge transfer is seen from metallacycle towards the alanine. Among all the complexes, the greater blue colored patches are visible on R-proline in R-pro@metallacycle complex (i.e., the complex with maximum NBO charge). In comparison between the R and S-ala@metallacycle, the greater number of patches are observed for the former, which is an added justification of greater NBO charge transfer in case of R-ala@metallacycle. The similar pattern of electron density accumulation and depletion is observed for all the other complexes, thus verifying the results of NBO charge transfer for all the complexes (Fig. 4).

Fig. 4 3D representation of EDD isosurfaces of R and S amino acid@metallacycle.

3.5. NCI analysis

NCI analysis, also known as RDG analysis i.e., reduced density gradient analysis, is performed to determine the nature as well as the strength of non-bonding interactions present between the amino acids and the metallacycle in the reported host–guest complexes. The repulsive, weak van der Waals and electrostatic forces are represented by the red, green, and blue colors, respectively. The results of NCI analysis are in the form of both the 2D and 3D representations. The 2D graphs and 3D isosurfaces for the reported complexes can be visualized in Fig. 5 and S3 (of ESI†). Here, the 3D isosurfaces show the green colored patches predominantly, signifying the existence of weak van der Waals forces as the major non-bonding interactions. The 2D graphs show RDG as a function of λ₂(ρ). The values of λ₂(ρ) ranges from −0.05 to 0.05 a.u., along the horizontal axis. Overall, in the 2D scattered RDG graph, the repulsive interactions (in red) range from 0.05 to 0.015 a.u., whereas this range for van der Waals (in green) and electrostatic interactions (in blue) is 0.015 to −0.02 a.u. and −0.02 to −0.05 a.u., respectively.

Fig. 5 Visual illustration of 3D isosurfaces and 2D RDG graphs of R and S amino acids@metallacycle.

For R-ala@metallacycle, the green colored patches are prevalent, while only two blue colored patches are observed. One is localized between the hydrogen of COOH group of alanine and oxygen of the metallacycle, while the other one is present between the H of NH₂ group of alanine and the O of metallacycle. Likewise, some red colored patches are noticed in the pyridine rings of the metallacycle. In the 2D RDG graph of R-ala@metallacycle, red, green, and blue colored spikes are evident, justifying the results of 3D analysis. For S-ala@metallacycle, the green colored patches are present in most of the places between the alanine and metallacycle. There is only one blue colored patch, which is localized between the N of NH₂ and the O of metallacycle. In the 2D RDG map of the complex, the green colored spikes are denser compared to R-ala@metallacycle complex, demonstrating the presence of greater non-bonding interactions in the complex. The results of RDG analysis for R and S enantiomeric complexes of alanine are in alignment with the results of interaction energies, i.e., the greater non-bonding interactions are observed for the complex with greater E_int value.

In comparison between the R and S-pro@metallacycle complexes, comparatively greater number of green colored patches are observed for the later in the 3D isosurfaces, with one blue patch for both the complexes, i.e., present between the H of COOH group of proline and O of the metallacycle. Additionally, a greater number of spikes are observed for S-pro@metallacycle. So, the results of RDG for the R and S-pro@metallacycle are also in correspondence with E_int. Among R and S-ser@metallacycle, the greater patches are shown by the later complex. Also, the later complex exhibits two blue patches, one present between the H of COOH group of serine and the O of metallacycle, whereas the other is present between the H of NH₂ group of serine and the O atom of the metallacycle. Only one such patch is seen in the R-ser@metallacycle, i.e., present between the H of COOH group and the O of metallacycle. Similarly, denser spikes are also observed (in 2D map) for the complex with greater number of patches (in 3D isosurface). For R and S-val@metallacycle, the patches observed are almost comparable, with a little greater for the former complex. Both the complexes also show only one H bond, between the H of COOH of valine and O atom of the metallacycle. The 2D RDG maps are also similar, with somewhat denser spikes for the R-val@metallacycle. Overall, the greater non-covalent interactions are observed for the enantiomeric complexes of ser@metallacycle, i.e., having greater interaction energies. Hence, the results of NCI analysis for all the complexes are in close agreement with those of the interaction energy analysis, i.e., significantly greater non-bonding interactions are observed for the complexes with greater E_int.

3.6. QTAIM analysis

The QTAIM analysis is carried out to further evaluate the nature of non-bonding interactions present between the amino acids and the metallacycle. QTAIM analysis involves various topological parameters, including the bond critical points (BCPs), electron density ρ(r), Laplacian of electron density ∇²ρ(r), local potential energy G(r), local kinetic energy V(r) and total electron energy density H(r). The values of these parameters are crucial in determining the strength as well as nature of the interactions present between the amino acids and the metallacycle.

In comparison between the bond critical points of R and S-ala@metallacycle complexes, the greater number of BCPs are observed for S-ala@metallacycle i.e., 11, while 9 BCPs are found for R-ala@metallacycle, signifying the greater host–guest interaction in the former complex. This is in correspondence with the results of interaction energies, i.e., comparatively greater interaction energies are observed for the S-ala@metallacycle. Similarly, the number of BCPs present in R-pro@metallacycle and S-pro@metallacycle are 16 each. Moreover, the BCPs observed for R and S-ser@metallacycle are 10 and 11, respectively, whereas the BCPs for R and S-val@metallacyle are 14 each. The number of BCPs are in alignment with the values of E_int, where the greater BCPs are observed for the complexes with greater E_int. Additionally, the greater difference in the number of BCPs is observed for the enantiomeric complexes of ala@metallacycle i.e., 2. This can be compared with the chiral discrimination energies, where the greatest E_chir is found for ala@metallacycle complexes.

While considering the other parameters of QTAIM analysis, it is observed that both the energy density H(r) and Laplacian ∇²ρ are positive for all the complexes, elaborating the involvement of van der Waals interactions in the complex formation. Moreover, the values of electron density (ρ) for all the complexes range from 0.0025–0.0411 a.u. i.e., positive and less than 0.1 a.u., specifying the presence of weak van der Waals forces in all the reported complexes. Furthermore, the ratio of −V/G for all the complexes is less than 2 (i.e., ranging from 0.16–1.07 a.u.), which further validates the existence of weak van der Waals forces in the designed complexes. The E_int calculated through QTAIM, range from 0.31–9.73 kcal mol⁻¹, justifying the nature of noncovalent interactions as the van der Waals forces and hydrogen bonding.

While comparing the E_int (topological parameter calculated through QTAIM analysis) of individual bonds of R and S enantiomeric complexes of ala@metallacycle, it is found that the value of E_int for R-ala@metallacycle range from 0.66–7.94 kcal mol⁻¹, whereas 0.31–4.99 kcal mol⁻¹ for S-ala@metallacycle. Most of these values are below 3 kcal mol⁻¹, indicating the presence of weak van der Waals forces between the alanine and the metallacycle. The two values of E_int are greater than 3 for R-ala@metallacycle and one value is greater than 3 for S-ala@metallacycle, affirming the presence of two and one hydrogen bonds in the said complexes. These hydrogen bonds are evident in the 3D representations of NCI analysis, which shows that for R-ala@metallacycle, one hydrogen bond is present between the H of COOH group of alanine and the O of the metallacycle, whereas the other one is present between the H of NH₂ group of alanine and the O atom of metallacycle. Similarly, for S-ala@metallacycle, NCI shows the H bond of the hydrogen atom of COOH (of alanine) with the O of metallacycle. Furthermore, for R and S enantiomers of pro@metallacycle, the values of E_int range from 0.66–8.53 and 0.50–7.81 kcal mol⁻¹, with only one hydrogen bond observed in both the complexes. The presence of one blue colored patch for both these enantiomeric complexes in the 3D illustrations of NCI i.e., between the H of COOH of proline with O of the metallacycle confirm the formation of hydrogen bond there. Along with the hydrogen bond, the major nonbonding interactions operating there are the van der Waals interactions (as most of the values of E_int are less than 3).

Moreover, the range of E_int (of individual bonds) obtained for R and S-ser@metallacycle is 1.04–8.78 and 0.75–8.35 kcal mol⁻¹, respectively. The two values correspond to the hydrogen bond in the later complex, whereas one such value is found for the former complex. The presence of these H bonds is well justified by the appearance of one and two blue colored patches in the R and S-ser@metallacycle. Likewise, 0.31–8.47 and 0.53–9.73 kcal mol⁻¹ are the ranges of E_int for R and S-val@metallacycle complexes, along with the presence of one H bond in each. Again, the presence of the H bond in both these complexes is justified by the NCI analysis. Overall, the results of QTAIM analysis are analogous to the results obtained through NCI analysis.

The QTAIM analysis is an analytical method which supports the chiral discrimination. QTAIM analysis explains the range of interaction energies of individual bonds for all the R and S enantiomeric complexes. It is observed that the complex, ala@metallacycle has the highest value of E_chir, followed by val@metallacycle, ser@metallacycle and pro@metallacycle. It is believed that the reason behind the highest E_chir for ala@metallacycle is not only the smaller size of alanine, but also the difference in the number of bond critical points (BCPs) between R and S enantiomeric complexes of alanine in the QTAIM analysis (i.e., 11 for S-ala@metallacycle and 9 for R-ala@metallacycle). Moreover, the interaction energy of individual bonds in QTAIM analysis shows that there is only one hydrogen bond for S-ala@metallacycle (i.e., E_int = 4.99), whereas two hydrogen bonds for R-ala@metallacycle (i.e., E_int = 4.49 and 7.94). Overall, the range of E_int for the bonds of S-ala@metallacycle and R-ala@metallacycle complexes is 0.31–4.99 and 0.66–794, respectively (i.e., the greater difference between S and R-val@metallacycle, leading to greater E_chir). For val@metallacycle complexes, QTAIM analysis predicts that E_int for S and R enantiomeric complexes range from 0.53–9.73 and 0.31–8.47, respectively, i.e., the higher values are observed for the S-val@metallacycle, compared to R-val@metallacycle. This difference in E_int contributes to higher values of E_chir. Furthermore, for ser@metallacycle, the E_int ranges from 0.75–8.35 for S-ser@metallacycle complex, and 1.04–8.78 for R-ser@metallacycle complex, i.e., the difference in E_int for S and R enantiomeric complexes, leading to E_chir, i.e., 2.28. Additionally, the least E_chir is observed for pro@metallacycle complexes. The reason can be attributed to the lesser difference in the range of E_int for both the complexes, i.e., 0.50–7.81 for S-pro@metallacycle and 0.66–8.53 for R-pro@metallacycle complex, along with only one bond having E_int in the range of hydrogen bonding, and a total of 16 BCPs for both the complexes (Fig. 6).

Fig. 6 QTAIM analysis for R and S amino acids@metallacycle, showing BCPs.

4. Conclusions

In this study, the chiral recognition ability of the homochiral metallacycle is investigated based on host–guest supramolecular chemistry. The molecules encapsulated inside the metallacycle as guests are the R and S enantiomers of amino acid alanine, proline, serine, and valine. All the designed complexes are thermodynamically stable, as revealed by the results of their interaction energies. In comparison between all the complexes, comparatively greater E_int is found for the ser@metallacycle complexes i.e., −33.03 and −30.75 kcal mol⁻¹, for the S and R enantiomers respectively, indicating their greater stability among all. The highest chiral discrimination energy of 3.11 kcal mol⁻¹ is obtained for ala@metallacycle complexes, which is justified via QTAIM. In the context of electronic properties, the FMO analysis indicates that the energy gap decreases after complexation, as compared to bare metallacycle or amino acids. The results of FMO analysis are confirmed via DOS spectra analysis, illustrating the position of HOMO, LUMO and the E_gap of the complexes. Moreover, NBO analysis determines the amount and direction of charge transfer i.e., from metallacycle towards amino acids. The maximum NBO charge transfer is seen for S-pro@metallacycle complex i.e., −0.291 |e|. EDD analysis confirms the direction of charge transfer. NCI and QTAIM analyses demonstrate the nature of noncovalent interactions between the host and guest as the van der Waals forces and hydrogen bonding. The results of these analyses for all the complexes are in alignment with those of the interaction energy analysis, i.e., significantly greater non-bonding interactions are observed for the complexes with greater E_int. Overall, based on the results of all these analyses, it can be concluded that the metallacycle is a good choice for the efficient chiral discrimination of amino acids. Moreover, the metallacycle can potentially be used with different peptides as well. It is expected that the future research might explore the binding interactions and reactivity of the metallacycle with a variety of peptides, potentially expanding its applications in biochemical and pharmaceutical fields.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

References

1. F. Feizi, M. Shamsipur, A. Barati, M. B. Gholivand and F. Mousavi, Chiral recognition and quantitative analysis of tyrosine enantiomers using L-cysteine capped CdTe quantum dots: Circular dichroism, fluorescence, and theoretical calculation studies, Microchem. J., 2020, 158, 105168.
2. B. Chankvetadze, Polysaccharide-based chiral stationary phases for enantioseparations by high-performance liquid chromatography: an overview, in Chiral separations: methods and protocols, 2019, pp. 93–126.
3. M. Liu, L. Chen, T. Tian, Z. Zhang and X. Li, Identification and quantitation of enantiomers by capillary electrophoresis and circular dichroism independent of single enantiomer standard, Anal. Chem., 2019, 91(21), 13803–13809.
4. F. Copur, N. Bekar, E. Zor, S. Alpaydin and H. Bingol, Nanopaper-based photoluminescent enantioselective sensing of L-Lysine by L-Cysteine modified carbon quantum dots, Sens. Actuators, B, 2019, 279, 305–312.
5. X. Li, C. Meng, Q. Chen, H. Tan, T. Chen and H. Liu, Combining enzymatic hydrolysis with magnetic nanoparticles for resolution of chiral substances, Colloids Surf., A, 2019, 564, 101–107.
6. J. C. Lang and D. W. Armstrong, Chiral surfaces: The many faces of chiral recognition, Curr. Opin. Colloid Interface Sci., 2017, 32, 94–107.
7. N. Nandi, Chiral discrimination in the confined environment of biological nanospace: reactions and interactions involving amino acids and peptides, Int. Rev. Phys. Chem., 2009, 28(2), 111–167.
8. J. Yang, Q. Zeng and L. Wang, Electrochemical polymerization induced chirality fixation of crystalline pillararene-based polymer and its application in interfacial chiral sensing, Anal. Chem., 2021, 93(29), 9965–9969.
9. Y. Zeng, Y. Wang, Z. Liang and Z. Jiao, The study of chiral recognition on ibuprofen enantiomers by a fluorescent probe based on β-cyclodextrin modified ZnS: Mn quantum dots, Spectrochim. Acta, Part A, 2021, 246, 119002.
10. B. Huang, K. Li, Q.-Y. Ma, T.-X. Xiang, R.-X. Liang, Y.-N. Gong, B.-J. Wang, J.-H. Zhang, S.-M. Xie and L.-M. Yuan, Homochiral metallacycle used as a stationary phase for capillary gas chromatographic separation of chiral and achiral compounds, Anal. Chem., 2023, 95(35), 13289–13296.
11. V. Y. Gus’kov, D. A. Sukhareva, Y. Y. Gainullina, E. M. Hamitov, Y. G. Galkin and V. N. Maistrenko, Chiral recognition capabilities of melamine and cyanuric acid supramolecular structures, Supramol. Chem., 2018, 30(11), 940–948.
12. T. R. Schulte, J. J. Holstein and G. H. Clever, Chiral self–discrimination and guest recognition in helicene–based coordination cages, Angew. Chem., Int. Ed., 2019, 58(17), 5562–5566.
13. J. Shen and Y. Okamoto, Efficient separation of enantiomers using stereoregular chiral polymers, Chem. Rev., 2016, 116(3), 1094–1138.
14. G. Blaschke, H. P. Kraft, K. Fickentscher and F. Kohler, Chromatographic separation of racemic thalidomide and teratogenic activity of its enantiomers, Arzneim.-Forsch., 1979, 29, 1640–1642.
15. A. Chen, Y. Zhong, X. Yin, R. Li, Q. Deng and R. Yang, A novel achiral fluorescent nanoprobe for the chiral recognition of cysteine enantiomers, Sens. Actuators, B, 2023, 393, 134262.
16. S. Zhuo, X. Wang, L. Li, S. Yang and Y. Ji, Chiral carboxyl-functionalized covalent organic framework for enantioselective adsorption of amino acids, ACS Appl. Mater. Interfaces, 2021, 13(26), 31059–31065.
17. J. R. Aldrich-Wright, R. S. Vagg and P. A. Williams, Design of chiral picen-based metal complexes for molecular recognition of α-aminoacids and nucleic acids, Coord. Chem. Rev., 1997, 166, 361–389.
18. J. Chin, S. S. Lee, K. J. Lee, S. Park and D. H. Kim, A metal complex that binds α-amino acids with high and predictable stereospecificity, Nature, 1999, 401(6750), 254–257.
19. J. R. n. Avilés-Moreno, M. M. Quesada-Moreno, J. J. López-González and B. Martínez-Haya, Chiral recognition of amino acid enantiomers by a crown ether: chiroptical IR-VCD response and computational study, J. Phys. Chem. B, 2013, 117(32), 9362–9370.
20. Y. Machida, H. Nishi, K. Nakamura, H. Nakai and T. Sato, Enantiomer separation of amino compounds by a novel chiral stationary phase derived from crown ether, J. Chromatogr., A, 1998, 805(1–2), 85–92.
21. M. Karakaplan and T. Aral, Synthesis of new chiral crown ethers containing a (p-methoxyphenoxy) methyl moiety and their chiral recognition ability towards amino acid esters, Tetrahedron: Asymmetry, 2005, 16(12), 2119–2124.
22. V. Schurig, Chiral separations using gas chromatography, TrAC, Trends Anal. Chem., 2002, 21(9–10), 647–661.
23. A. Cavazzini, L. Pasti, A. Massi, N. Marchetti and F. Dondi, Recent applications in chiral high performance liquid chromatography: a review, Anal. Chim. Acta, 2011, 706(2), 205–222.
24. J. M. Alexander, J. L. Clark, T. J. Brett and J. J. Stezowski, Chiral Discrimination in Cyclodextrin Complexes of Amino Acid Derivatives: β-cyclodextrin/N-acetyl-L-phenylalanine and N-acetyl-D-phenylalanine Complexes, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(8), 5115–5120.
25. P. Shahgaldian and U. Pieles, Cyclodextrin derivatives as chiral supramolecular receptors for enantioselective sensing, Sensors, 2006, 6(6), 593–615.
26. C. J. Easton and S. F. Lincoln, Chiral discrimination by modified cyclodextrins, Chem. Soc. Rev., 1996, 25(3), 163–170.
27. M. Maqbool, M. Aetizaz and K. Ayub, Chiral discrimination of amino acids by Möbius carbon belt, Diamond Relat. Mater., 2024, 146, 111227.
28. M. Asghar, A. Lakhani, M. Asif, N. S. Sheikh, M. A. Hashmi, R. Ludwig, H. H. Hammud and K. Ayub, Chiral Recognition of Amino Acids Using CC2 Porous Organic Cages, J. Phys. Chem. A, 2023, 4245–4258.
29. Q. Zhao, J. Yang, J. Zhang, D. Wu, Y. Tao and Y. Kong, Single-template molecularly imprinted chiral sensor for simultaneous recognition of alanine and tyrosine enantiomers, Anal. Chem., 2019, 91(19), 12546–12552.
30. Y. Nagata, T. Akita, C. Ishii, M. Oyaide, M. Mita, T. Ide and K. Hamase, Development of an enantioselective three-dimensional HPLC system for the determination of alanine, valine, isoleucine, allo-isoleucine and leucine in human plasma and urine, J. Pharm. Biomed. Anal. Open, 2023, 100013.
31. L. Szabados and A. Savouré, Proline: a multifunctional amino acid, Trends Plant Sci., 2010, 15(2), 89–97.
32. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision D. 01, Gaussian, Inc., Wallingford CT. 2009. See also: URL: https://www.gaussian.com.
33. Gaussian, GaussView 5 Manual, Semichem Inc., Shawnee Mission, KS, 09, 2009, pp. 1–25.
34. M. Sohaib, M. Maqbool, H. Sajid and K. Ayub, Superalkalides based on stacked janus molecule with improved optical nonlinearity, Mater. Sci. Semicond. Process., 2024, 179, 108513.
35. T. Abu-Izneid, A. Rauf, Z. Ahmad, A. Wadood, K. Ayub, N. Muhammad, Y. S. Al-Awthan, M. Maqbool, O. S. Bahattab and H. A. Hemeg, Density functional theory (DFT), molecular docking, and xanthine oxidase inhibitory studies of dinaphthodiospyrol S from Diospyros kaki L, Saudi Pharm. J., 2024, 32(2), 101936.
36. A. Kumar, R. Schweitzer-Stenner and B. M. Wong, A new interpretation of the structure and solvent dependence of the far UV circular dichroism spectrum of short oligopeptides, Chem. Commun., 2019, 55(40), 5701–5704.
37. B. M. Wong and T. H. Hsieh, Optoelectronic and excitonic properties of oligoacenes: substantial improvements from range-separated time-dependent density functional theory, J. Chem. Theory Comput., 2010, 6(12), 3704–3712.
38. M. E. Foster and B. M. Wong, Nonempirically tuned range-separated DFT accurately predicts both fundamental and excitation gaps in DNA and RNA nucleobases, J. Chem. Theory Comput., 2012, 8(8), 2682–2687.
39. M. Aetizaz, F. Ullah, S. Sarfaraz, T. Mahmood and K. Ayub, Robust and facile detection of formaldehyde through transition metals doped olympicene sensors: a step forward DFT investigation, RSC Adv., 2023, 13(42), 29231–29241.
40. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592.
41. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38.
42. S. Pan, R. Saha, S. Mandal, S. Mondal, A. Gupta, M. A. Fernandez-Herrera, G. Merino and P. K. Chattaraj, Selectivity in gas adsorption by molecular cucurbit [6] uril, J. Phys. Chem. C, 2016, 120(26), 13911–13921.
43. S. Sarfaraz, M. Yar, A. A. Khan, R. Ahmad and K. Ayub, DFT investigation of adsorption of nitro-explosives over C2N surface: Highly selective towards trinitro benzene, J. Mol. Liq., 2022, 352, 118652.
44. Y. S. Al-Faiyz, S. Sarfaraz, M. Yar, S. Munsif, A. A. Khan, B. Amin, N. S. Sheikh and K. Ayub, Efficient Detection of Nerve Agents through Carbon Nitride Quantum Dots: A DFT Approach, Nanomaterials, 2023, 13(2), 251.
45. E. Espinosa, E. Molins and C. Lecomte, Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities, Chem. Phys. Lett., 1998, 285(3–4), 170–173.
46. I. Mata, I. Alkorta, E. Espinosa and E. Molins, Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields, Chem. Phys. Lett., 2011, 507(1–3), 185–189.
47. M. Asghar, A. Lakhani, M. Asif, N. S. Sheikh, M. A. Hashmi, R. Ludwig, H. H. Hammud and K. Ayub, Chiral Recognition of Amino Acids Using CC2 Porous Organic Cages, J. Phys. Chem. A, 2023, 127(19), 4245–4258.
48. R. Hemmati and K. Patkowski, Ab Initio Study of Chiral Discrimination in the Glycidol Dimer, J. Phys. Chem. A, 2020, 124(45), 9436–9450.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4bm01119h

---