Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Characterizing nanoparticle size and composition using microfluidic Raman diffusion-ordered spectroscopy
Robert W.
Schmidt†
 ab,
Giulia
Giubertoni†
*b,
Paul
Kolpakov
c,
Noushine
Shahidzadeh
c,
Freek
Ariese
ab,
Giulia
Giubertoni†
*b,
Paul
Kolpakov
c,
Noushine
Shahidzadeh
c,
Freek
Ariese
 *a and
Sander
Woutersen
*a and
Sander
Woutersen
 *b
*b
aLaserLaB Amsterdam, Department of Physics and Astronomy, Vrije Universiteit Amsterdam, De Boelelaan 1081, 1081 HV Amsterdam, the Netherlands. E-mail: f.ariese@vu.nl
bVan ’t Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098XH Amsterdam, the Netherlands. E-mail: g.giubertoni@uva.nl; s.woutersen@uva.nl
cVan der Waals-Zeeman Institute (WZI), Institute of Physics, University of Amsterdam, Science Park 904, 1098XH Amsterdam, The Netherlands
First published on 21st October 2025
Abstract
We show that microfluidic Raman Diffusion-Ordered SpectroscopY (Raman-DOSY) can be used to simultaneously characterize the size and the chemical composition of nanoparticles in solution. In these experiments, we inject a solution of nanoparticles into one half of a microfluidic channel, and solvent into the other. After the injection, the nanoparticles diffuse from the solution-filled part into the solvent-filled part of the channel, at a rate determined by their diffusion coefficient. By analyzing the time-dependent Raman spectrum in the initially solvent-filled part of the channel, we determine the size (from the diffusion coefficient) and characterize the chemical composition (from the corresponding Raman spectra) of the nanoparticles. Within about 1 hour we obtain both the size and chemical-structure information of polystyrene beads with diameters of 20, 50, and 100 nm. We further demonstrate that this method can distinguish nanoparticles of varying sizes in mixed samples. These results show that microfluidic Raman-DOSY is a promising method for combined size- and composition analysis of nanoparticles.
Introduction
Characterizing the chemical structure and determining the size of nanoparticles in solution is essential in many industrial and academic applications, including nanoparticle-based advanced materials, drugs, and biomedical diagnostics.1–6 Among the available techniques to characterize the chemical structure of nanoparticles, Raman spectroscopy is particularly valued for its label-free detection capabilities. It can provide chemical identification,7–9 and does not require any special preparation or labeling of the sample, making it highly versatile and non-destructive. Crystals and synthetic polymers often exhibit distinct and intense Raman signals, allowing for the precise identification and analysis of nanocrystals10 and nanoplastics.11–13 However, for nanoparticles that are smaller than the optical-diffraction limit, Raman spectroscopy provides no information about the particle size.To add size sensitivity to Raman spectroscopy, we have recently developed Raman Diffusion-Ordered Spectroscopy (Raman-DOSY), an analytical method that simultaneously measures the Raman spectrum and the diffusion coefficient of molecules (or particles) in a fluid, using the Stokes–Einstein relation to determine their sizes. We applied this technique to cytochrome-c, micelles, and acetonitrile, demonstrating its capability to characterize both biological and synthetic systems across a broad range of sizes.14 Inspired by NMR-DOSY,15–29 Raman-DOSY differs in its practical implementation while retaining the core concept of diffusion-based size estimation. Previous studies have explored diffusion mechanisms in polymer blends using confocal Raman microscopy and surface-enhanced Raman spectroscopy (SERS), particularly in polystyrene/polystyrene bilayer systems.30–33
In Raman-DOSY, the sample solution and the pure solvent are injected in parallel into a Y-shaped flow cell (Fig. 1A). The flow is laminar, resulting in a well-defined interface between the solution- and solvent-filled halves of the channel. The injection is stopped at t = 0, and subsequently a time series of Raman spectra is measured at the far edge of the solvent-filled half of the channel (Raman-laser focus indicated by the green spot in Fig. 1A). At t = 0, the Raman spectrum shows only the peaks of the solvent (and of the flow-cell substrate), but as time progresses, the Raman peaks of the diffusing solute molecules or particles appear with a time dependence that is determined by their diffusion coefficient. When analyzing a mixture of molecules/particles with different sizes, the smaller particles quickly diffuse into the laser spot (t = t1), whereas the larger particles have a longer lag phase (t = t2 > t1), see Fig. 1B. From a global analysis of the two-dimensional frequency- and time-dependent data set, we obtain a two-dimensional DOSY plot,14 which has Raman frequency on the x axis and the diffusion coefficient (or equivalently, size) on the y-axis (Fig. 1C).
So far, we have applied Raman-DOSY only to small molecules and micelles, using a comparatively wide (4 mm) channel.14 However, for larger particles diffusion over such a distance takes prohibitively long: a Raman-DOSY measurement would require several days for particles of 100 nm size in a channel of 4 mm width. However, the time required for an optical DOSY experiment scales with the square of the channel width (L2), and therefore can be reduced by decreasing the channel width. Here, we go to the extreme limit of this idea by using a microfluidic approach to Raman-DOSY, with a 300 μm wide channel that enables us to determine the size and characterize the chemical structure of nanoparticles within a reasonable measurement time: approximately 2 hours for 100-nm particles, and less than 20 minutes for 20-nm particles in water.
Methods
Experiment
Data analysis
The Raman spectral pre-processing and data analysis were performed in MATLAB R2021b (The MathWorks Inc., Natick). Pre-processing included correcting spectral offsets by estimating a baseline (1-order polynomial and asymmetric truncated quadratic cost function),35 and removing the Raman peaks associated with the water and flow-cell substrate by averaging the first three spectra of a time series to create a blank spectrum and subtracting that from the entire dataset.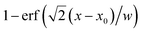 , where x0 is the position of the interface and w is the radius (1/e2) of the estimated Gaussian laser spot. The diffusion distance was calculated from the interface location including the radius to the laser location.
, where x0 is the position of the interface and w is the radius (1/e2) of the estimated Gaussian laser spot. The diffusion distance was calculated from the interface location including the radius to the laser location.
The method for calculating the diffusion coefficient is described in detail elsewhere.14,36 In short, the diffusion is described by the diffusion equation:
 | (1) |
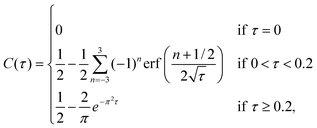 | (2) |
The time- and frequency-dependent Raman spectra S were measured at the far edge (y = L/2) of the channel and were globally fitted to the following function to obtain the diffusion coefficients and associated spectra:
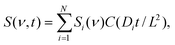 | (3) |
To obtain a 2D DOSY spectrum I(ν, D) from the global-fit result, we multiply the spectral amplitude Si(ν) by the appropriate probability distribution for Di:37
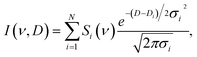 | (4) |
Results
Microfluidic Raman DOSY on monodisperse nanoparticles
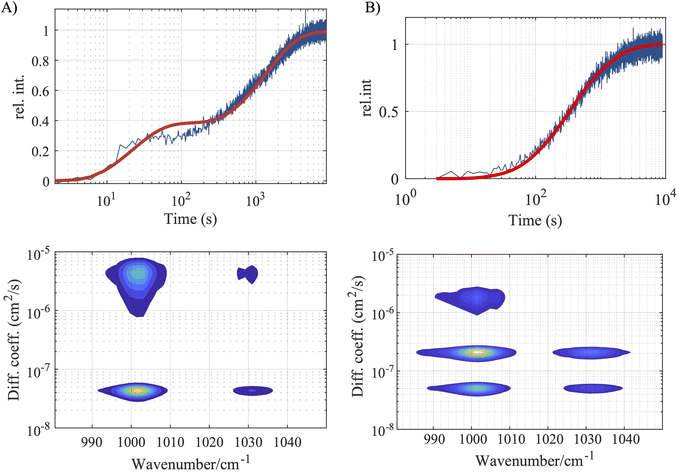
We use polystyrene beads to investigate the capability of microfluidic Raman DOSY for characterizing nanoplastic particle size and composition. Polystryene has a pronounced Raman peak at 1001 cm−1 (due to the trigonal phenyl-ring breathing mode) and a less intense peak at 1031 cm−1 (due to the CH2-rocking mode).38,39Fig. 2A shows the time series of Raman spectra observed upon injecting a suspension of 51-nm polystyrene beads into the microfluidic DOSY cell (substrate and water Raman signals subtracted), with the spectral curves transitioning in color from blue (first spectrum) to red (last spectrum). Fig. 2B and C (top panels, blue curves) shows the spectrally integrated Raman intensity as a function of time (spectral integration range 993–1010 cm−1). The time dependence mirrors the diffusion of the nanoparticles into the top part of the channel, which occurs much more slowly for the larger particles (note the different axis ranges). The red curves in the plots are least-squares fits of eqn (2) to the data. From a global least-squares fit of eqn (3) to the data we obtain Raman-DOSY spectra, shown in the bottom panels of Fig. 2. These spectra show the two characteristic Raman peaks of polystyrene (1001 and 1031 cm−1), together with the diffusion coefficients (the standard deviations in the latter were obtained by performing three independent measurements; the separate measurements are shown in Fig. S3), from which we can estimate the particle size.From the Raman-DOSY measurement, we obtain a diffusion coefficient of 1.86 ± 0.1·10−7 cm2 s−1 for the 22-nm polystyrene beads, which is slightly lower than the expected diffusion coefficient of 1.96·10−7 cm2, but within the uncertainty range. From the observed diffusion coefficient, we estimate the size to be 23.6 ± 1.1 nm (1σ), which is within the error margin of the certified size of 22 ± 2 nm. The 51-nm Raman-DOSY measurements yielded a diffusion coefficient of 7.58 ± 0.06·10−8 cm2 s−1, which is slightly lower than the expected diffusion coefficient of 8.45·10−8 cm2 s−1. The size estimated from the Raman-DOSY measurement is 58 ± 3 nm (the individual time-dependent plots of the triplicate measurement used to determine the uncertainties in the diffusion constant and the size are shown in Fig. S4).
Microfluidic Raman DOSY on mixed nanoparticle solutions
We have also investigated the suitability of microfluidic Raman DOSY to characterize samples containing nanoparticles of more than one size. For this purpose, we prepared a mixture of 20 nm and 100 nm polystyrene beads. Interestingly, from our Raman-DOSY measurement on the pure standards we found that the 100 nm polystyrene standard contained an impurity with a much smaller size: the time-dependent Raman signal of the 100 nm polystyrene standard, shown in the top panel of Fig. 3A, is a sum of two sigmoidal curves, indicating the presence of two very different sizes in the sample. The smaller particles diffuse within about 15 s, after which the Raman signal curve rises further until it reaches a plateau level at around 5000 s. We could fit the time-dependent Raman signal of the 100 nm standard using a sum of two components (eqn (3) with N = 2; the data could not be described by a single-component fit, see Fig. S10. From five independent measurements (see SI), we estimate a mean diffusion coefficient for the smaller compound of 4.35 ± 1.93·10−6 cm2 s−1, while for the larger it was 4.34 ± 0.66·10−8 cm2 s−1, which corresponds to a mean size of 1.0 ± 0.4 nm and 101 ± 15 nm, respectively; see Table S1 and Fig. S5. The corresponding DOSY plot (Fig. 3A, bottom) also shows the two compounds, which have an identical Raman spectrum but very different diffusion coefficients (y-coordinates). Since the initial diffusing impurity in the 100 nm standard was not specified in the polystyrene standard, we aimed to identify it. The Raman spectra of both compounds exhibited peaks at 622, 1001, 1030, 1159, and 1602 cm−1, which matched the Raman spectra of polystyrene used in the nanosphere standard. Additionally, we applied Principal Component Analysis (PCA) to illustrate the variance during the diffusion of the compounds (see Fig. S8). To this purpose, we divided the entire spectral time series dataset into two subsets, one for each compound, and applied PCA to these datasets. The plots of the principal components for the impurity and the 100-nm beads dataset were nearly identical, except for the noise. The absence of missing or shifted peaks suggests that the impurity is a polystyrene oligomer, with a diameter of 1.0 ± 0.4 nm (corresponding to ∼351 Da, using ρ = 1.05 g cm−3). The 1 nm sized impurity was not observed in the 50 nm and 20 nm polystyrene standards (Fig. S9).We then analyzed a (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) mixture of polystyrene beads with specified diameters of 22 nm and 101 nm. The time-dependent Raman signal is shown in Fig. 3B (triplicate measurement shown in Fig. S6). From a global least-squares fit of eqn (3) to the time- and frequency dependent data, in which we include the abovementioned contamination as the third component, we obtain diffusion coefficients 2.1 ± 0.3·10−7 cm2 s−1 for the nominally 20-nm beads and 5.1 ± 0.6·10−8 cm2 s−1 for the nominally 100 nm beads (these values are averages and standard deviations obtained from three independent measurements), from which we estimate diameters of 20.6 ± 2.6 nm and 84 ± 10 nm. These estimated diameters are somewhat smaller than the specified sizes of 22 and 101 nm, possibly due to cross-correlation between the two size parameters in the global least-squares fit: the overlapping diffusion curves of the two particles make it challenging for the fitting algorithm to accurately separate and fit the data for each compound. We are currently working on improved algorithms based on NMR-DOSY methods40–43 to improve the accuracy of our data analysis.
1 v/v) mixture of polystyrene beads with specified diameters of 22 nm and 101 nm. The time-dependent Raman signal is shown in Fig. 3B (triplicate measurement shown in Fig. S6). From a global least-squares fit of eqn (3) to the time- and frequency dependent data, in which we include the abovementioned contamination as the third component, we obtain diffusion coefficients 2.1 ± 0.3·10−7 cm2 s−1 for the nominally 20-nm beads and 5.1 ± 0.6·10−8 cm2 s−1 for the nominally 100 nm beads (these values are averages and standard deviations obtained from three independent measurements), from which we estimate diameters of 20.6 ± 2.6 nm and 84 ± 10 nm. These estimated diameters are somewhat smaller than the specified sizes of 22 and 101 nm, possibly due to cross-correlation between the two size parameters in the global least-squares fit: the overlapping diffusion curves of the two particles make it challenging for the fitting algorithm to accurately separate and fit the data for each compound. We are currently working on improved algorithms based on NMR-DOSY methods40–43 to improve the accuracy of our data analysis.
Discussion
The above results show that microfluidic Raman DOSY can be used for characterizing the size (from the diffusion coefficients) and chemical structure (from the associated Raman spectra) of nanoparticles. Thus microfluidic Raman DOSY forms a simple and affordable complement to the existing methods for nanoparticle analysis, the most important of which we will now discuss briefly.NMR-DOSY efficiently measures the diffusion coefficient of particles and simultaneously provides their NMR spectrum,25,37,44–46 but also has some drawbacks: for large particles, line broadening makes it difficult to record NMR-DOSY spectra, and moreover, NMR requires the use of deuterated solvents. Electron microscopy (SEM) is another commonly used method to determine particle sizes. The size resolution is about 1 nm, rendering it very suitable for nanoparticles but rather impractical to precisely determine the dimensions of small polymers or oligomeric contaminations. When combined with energy-dispersive X-ray spectroscopy, it can identify compounds based on their elemental composition. Although effective for analyzing nanoplastics, it is time-consuming, and it only provides a local size distribution.
Chromatography methods such as size exclusion chromatography (SEC) and field flow fractionation (FFF) are also often used to determine particle sizes.47,48 Different types of detectors can be combined with SEC, but in general they provide rather limited information on the chemical composition of the particles.
FFF combined with a multi-angle light scattering detector can measure colloids down to 50 nm but does not provide chemical identification.49,50 Using SEC and FFF combined with mass spectrometry has shown success in characterizing proteins and biopharmaceuticals,51 although accessibility may vary depending on laboratory infrastructure. Other size-sensitive methods are dynamic light scattering (DLS) and nanoparticle tracking analysis (NTA).52–54 These purely size-sensitive methods can determine accurate size distributions across the sample but need to be combined with another technique to identify the chemical structure of particles.
Raman-DOSY probes the size and chemical structure simultaneously, and thus offers a reliable and non-invasive method to investigate and characterize nanoparticles. Unlike chromatography or NMR-DOSY, Raman-DOSY does not require calibration with standards of well-defined sizes, or the use of deuterated solvents. However, the limited sensitivity of Raman spectroscopy to detect molecules at low concentrations restricts the current application of Raman-DOSY. This low sensitivity is primarily due to the inherently weak Raman scattering, which is further reduced because the compounds of interest are diluted by a factor of two by the solvent channel in the cell during the measurement. An effective solution to this problem is to enhance the signal using resonance Raman spectroscopy.55,56 This technique involves tuning the excitation wavelength to match an electronic transition of the molecule, significantly amplifying the Raman signal. Additionally, targeting specific vibrational modes, such as the CH stretches of the polymer backbone, can further improve the sensitivity. For molecules with inherently weak Raman cross section, techniques such as Stimulated Raman Scattering (SRS) spectroscopy can be employed to enhance sensitivity.57 In cases where particles exhibit no detectable Raman signal, such as exosomes or metal oxide nanospheres, an alternative strategy might be to monitor the solvent. By measuring the reduction in the Raman signal of the solvent, one can in principle infer the presence of non-Raman-active particles, as they displace the solvent within the detection volume. However, in such cases other (UV/vis, IR) optical DOSY methods36,58 might be more efficient.
Samples containing a large number of components, or a continuous size distribution, will be less easy to analyze than the test samples investigated here, but we believe that many data analysis methods that have been developed for NMR-DOSY measurements of such complicated samples15,40,59–61 can also be used (after minor modifications) to analyze optical-DOSY measurements.
The applicability of microfluidic Raman-DOSY for nanoparticle analysis is currently limited somewhat by the window material (olefin polymer) used in our microfluidic DOSY cell and the analysis algorithm. Raman peaks of the particles may overlap with signals from the microfluidic window, making it difficult to distinguish between the sample and the cell material. Cell designs with glass, quartz or CaF2 top or bottom windows will solve these issues. To improve the data analysis, we want to apply the advanced data-analysis methods that have been developed previously for NMR-DOSY, and that make it possible to characterize the size distribution of polydisperse samples in a robust manner.40–43
Conclusions and outlook
We have investigated solutions containing nanoplastic particles of different sizes using microfluidic Raman DOSY. By using a small channel width, we can investigate nanoparticles in a competitive timeframe, as demonstrated by the Raman-DOSY spectra of polystyrene beads with diameters of 20, 50, and 100 nm. At the same time, we can detect smaller impurities in the polystyrene standard, demonstrating that the method can be used to analyze samples with a wide particle size distribution. We found that this method can successfully characterize the size and the chemical structure of the tested nano-plastic samples, with an accuracy of ∼10%. We believe that Raman-DOSY offers a noninvasive and label-free method to characterize simultaneously the chemical structure and the size of nanoparticles/aggregates, which constitutes an easy-to-use and affordable addition to the existing methods for nanoparticle size and structure characterization.Conflicts of interest
G. Giubertoni and S. Woutersen are co-founders and shareholders of InspectT, a spin-off commercializing optical-DOSY technology. The remaining authors declare no competing interests.Data availability
The data for this article are available at Zenodo at https://doi.org/10.5281/zenodo.15798911.Supplementary information is available. See DOI: https://doi.org/10.1039/d5ay01250c.
Acknowledgements
This research received funding from The Netherlands Organization for Scientific Research (NWO) in the framework of the ENW PPP Fund for the top sectors (Grant 741.018.202 “Soft Advanced Materials”) and from the Ministry of Economic Affairs in the framework of the “PPS-Toeslagregeling”. GG is supported by NWO under project number VI.Veni.212.240.Notes and references
- V. Mailänder and K. Landfester, Biomacromolecules, 2009, 10, 2379–2400 CrossRef PubMed.
- E. Busseron, Y. Ruff, E. Moulin and N. Giuseppone, Nanoscale, 2013, 5, 7098–7140 RSC.
- P. D. Howes, R. Chandrawati and M. M. Stevens, Science, 2014, 346, 1247390 CrossRef PubMed.
- M. Kopp, S. Kollenda and M. Epple, Acc. Chem. Res., 2017, 50, 1383–1390 CrossRef CAS PubMed.
- S. Mourdikoudis, R. M. Pallares and N. T. K. Thanh, Nanoscale, 2018, 10, 12871–12934 RSC.
- M. Epple, V. M. Rotello and K. Dawson, Acc. Chem. Res., 2023, 56, 3369–3378 CrossRef CAS PubMed.
- E. Smith and G. Dent, Modern Raman Spectroscopy, Wiley, 2019 Search PubMed.
- L. Ettema, B. Lochocki, J. J. M. Hoozemans, J. F. de Boer and F. Ariese, J. Opt., 2022, 24, 054005 CrossRef CAS.
- P. Larkin, Infrared and Raman Spectroscopy, Elsevier, 2011, vol. 44, p. 085201 Search PubMed.
- M. Testa-Anta, M. A. Ramos-Docampo, M. Comesana-Hermo, B. Rivas-Murias and V. Salgueirino, Nanoscale Adv., 2019, 1, 2086–2103 RSC.
- L. Zada, H. A. Leslie, A. D. Vethaak, G. H. Tinnevelt, J. J. Jansen, J. F. de Boer and F. Ariese, J. Raman Spectrosc., 2018, 49, 1136–1144 CrossRef CAS.
- J. R. Ferraro, K. Nakamoto and C. W. Brown, Introductory Raman Spectroscopy, Elsevier, 2nd edn, 2003 Search PubMed.
- J. Toporski, T. Dieing and O. Hollricher, Confocal Raman Microscopy, Springer International Publishing, Cham, 2nd edn, 2018, vol. 66 Search PubMed.
- R. W. Schmidt, G. Giubertoni, F. Caporaletti, P. Kolpakov, N. Shahidzadeh, F. Ariese and S. Woutersen, J. Phys. Chem. A, 2023, 127, 7638–7645 CrossRef CAS PubMed.
- K. F. Morris and C. S. Johnson Jr, J. Am. Chem. Soc., 1992, 114, 3139–3141 CrossRef CAS.
- C. S. Johnson Jr, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 34, 203–256 CrossRef.
- L. Avram and Y. Cohen, Angew. Chem., Int. Ed., 2005, 44, 520–554 CrossRef PubMed.
- D. Li, I. Keresztes, R. Hopson and P. Williard, Acc. Chem. Res., 2008, 42, 270–280 CrossRef PubMed.
- G. A. Morris, in Encyclopedia of Magnetic Resonance, ed. R. K. Harris and R. E. Wasylishen, Wiley, Chichester, UK, 2009 Search PubMed.
- K. Salorinne, T. Lahtinen, J. Koivisto, E. Kalenius, M. Nissinen, M. Pettersson and H. Häkkinen, Anal. Chem., 2013, 85, 3489–3492 CrossRef CAS PubMed.
- L. Avram and Y. Cohen, Chem. Soc. Rev., 2014, 44, 586–602 RSC.
- M. Foroozandeh, L. C. nar, L. G. Martins, D. Sinnaeve, G. D. Poggetto, C. F. Tormena, R. W. Adams, G. A. Morris and M. Nilsson, Angew. Chem., Int. Ed., 2016, 55, 15579–15582 CrossRef CAS PubMed.
- R. Evans and I. J. Day, RSC Adv., 2016, 6, 47010–47022 RSC.
- G. Pagès, V. Gilard, R. Martino and M. Malet-Martino, Analyst, 2017, 142, 3771–3796 RSC.
- P. Groves, Polym. Chem., 2017, 8, 6700–6708 RSC.
- G. D. Poggetto, L. Castañar, M. Foroozandeh, P. Kiraly, R. W. Adams, G. A. Morris and M. Nilsson, Anal. Chem., 2018, 90, 13695–13701 CrossRef PubMed.
- M. Urbańczyk, Y. Kharbanda, O. Mankinen and V.-V. Telkki, Anal. Chem., 2020, 92, 9948–9955 CrossRef PubMed.
- K. Kristinaityte, A. Mames, M. Pietrzak, F. F. Westermair, W. Silva, R. M. Gschwind, T. Ratajczyk and M. Urbańczyk, J. Am. Chem. Soc., 2022, 144, 13938–13945 CrossRef CAS PubMed.
- E. Ruzicka, P. Pellechia and B. C. Benicewicz, Anal. Chem., 2023, 95, 7849–7854 CrossRef CAS PubMed.
- A. C. D. Luca, G. Rusciano, G. Pesce, S. Caserta, S. Guido and A. Sasso, Macromolecules, 2008, 41, 5512–5514 CrossRef.
- C. D. Mana, G. A. Torchia and J. P. Tomba, Soft Matter, 2018, 14, 3315–3323 RSC.
- R. Demoor, V. Guarepi, A. Cisilino, V. Alvarez and J. P. Tomba, J. Raman Spectrosc., 2021, 52, 1022–1031 CrossRef CAS.
- A. P. Cisilino, C. D. D. Monno and J. P. Tomba, Soft Matter, 2024, 20, 7535–7545 RSC.
- F. M. White, Fluid Mechanics, McGraw-Hill, 7th edn, 2009 Search PubMed.
- V. Mazet, C. Carteret, D. Brie, J. Idier and B. Humbert, Chemom. Intell. Lab. Syst., 2005, 76, 121–133 CrossRef CAS.
- G. Giubertoni, G. Rombouts, F. Caporaletti, A. Deblais, R. van Diest, J. N. H. Reek, D. Bonn and S. Woutersen, Angew. Chem., Int. Ed., 2023, 62, e202213424 CrossRef CAS PubMed.
- K. F. Morris and C. S. Johnson, J. Am. Chem. Soc., 1992, 114, 3139–3141 CrossRef CAS.
- A. Palm, J. Phys. Chem., 1951, 55, 1320–1324 CrossRef CAS.
- C. H. Choi and M. Kertesz, J. Phys. Chem. A, 1997, 101, 3823–3831 CrossRef CAS.
- M. A. Delsuc and T. E. Malliavin, Anal. Chem., 1998, 70, 2146–2148 CrossRef CAS.
- T. Buffeteau, L. Ducasse, L. Poniman, N. Delsuc and I. Huc, Chem. Commun., 2007, 2714–2716 Search PubMed.
- M. Urbanćzyk, D. Bernin, W. Koz&macute;inśki and K. Kazimierczuk, J. Phys. Chem. Lett., 2013, 85, 1828–1833 Search PubMed.
- A. Cherni, E. Chouzenoux and M.-A. Delsuc, Analyst, 2017, 142, 772–779 RSC.
- X.-X. Zhang, S. L. Brantley, S. A. Corcelli and A. Tokmakoff, Nat. Commun. Biol., 2020, 3, 525 CrossRef CAS PubMed.
- M. S. Ullah, V. V. Zhivonitko, A. Samoylenko, A. Zhyvolozhnyi, S. Viitala, S. Kankaanpää, S. Komulainen, L. Schröder, S. J. Vainio and V.-V. Telkki, Chem. Sci., 2021, 12, 8311–8319 RSC.
- N. Wolff, C. Beuck, T. Schaller and M. Epple, Nanoscale Adv., 2024, 6, 3285–3298 RSC.
- H. G. Barth, C. Jackson and B. E. Boyes, Anal. Chem., 1994, 66, 595–620 CrossRef PubMed.
- A. M. Striegel, Chromatographia, 2022, 85, 307–313 CrossRef CAS PubMed.
- M. Baalousha, F. V. Kammer, M. Motelica-Heino, H. S. Hilal and P. Le Coustumer, J. Chromatogr. A, 2006, 1104, 272–281 CrossRef CAS PubMed.
- J. Gigault, H. El Hadri, S. Reynaud, E. Deniau and B. Grassl, Anal. Bioanal. Chem., 2017, 409, 6761–6769 CrossRef CAS PubMed.
- C. Contado, Anal. Bioanal. Chem., 2017, 409, 2501–2518 CrossRef CAS PubMed.
- M. Kaszuba, D. McKnight, M. T. Connah, F. K. McNeil-Watson and U. Nobbmann, J. Nanopart. Res., 2008, 10, 823–829 CrossRef CAS.
- J. Stetefeld, S. A. McKenna and T. R. Patel, Biophys. Rev., 2016, 8, 409–427 CrossRef CAS PubMed.
- H. Jans, X. Liu, L. Austin, G. Maes and Q. Huo, Anal. Chem., 2009, 81, 9425–9432 CrossRef CAS PubMed.
- S. Chadha, E. Ghiamati, R. Manoharan and W. H. Nelson, Appl. Spectrosc., 1992, 46, 1176–1181 CrossRef CAS.
- A. H. Kuptsov and G. N. Zhizhin, Handbook of Fourier Transform Raman and Infrared Spectra of Polymers, Elsevier, 1998, vol. 45 Search PubMed.
- L. van Haasterecht, L. Zada, R. W. Schmidt, E. de Bakker, E. Barbé, H. A. Leslie, A. D. Vethaak, S. Gibbs, J. F. de Boer, F. B. Niessen, P. P. M. van Zuijlen, M. L. Groot and F. Ariese, J. Biophot., 2020, 13, 1–10 Search PubMed.
- G. Giubertoni, M. G. Rachid, C. Moll, M. Hilbers, S. Samanipour and S. Woutersen, Anal. Chem., 2024, 96, 15168–15176 CAS.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 213–227 CrossRef.
- M. Nilsson and G. A. Morris, Anal. Chem., 2008, 80, 3777–3782 CrossRef CAS PubMed.
- A. A. Colbourne, S. Meier, G. A. Morris and M. Nilsson, Chem. Commun., 2013, 49, 10510–10512 RSC.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |