Open Access Article
Open Access ArticleNIRS-based fresh grape ripeness prediction with SPA-LASSO spectral feature selection
Jia-Yue
Hu
a,
Zhuo-Kang
Wang
a,
Yu-Yu
Wang
d,
Yu-Hao
Wu
a,
Hai-Cheng
Wei
 *c,
Jing
Zhao
*b,
Liu
Yang
a,
Yu-zhe
Tan
a,
Zi-Long
Deng
a,
Zhi-Jie
Xiang
a,
Zi-Yi
Wang
a and
Xin-Tong
Zhao
a
*c,
Jing
Zhao
*b,
Liu
Yang
a,
Yu-zhe
Tan
a,
Zi-Long
Deng
a,
Zhi-Jie
Xiang
a,
Zi-Yi
Wang
a and
Xin-Tong
Zhao
a
aSchool of Electrical and Information Engineering, North Minzu University, No. 204 North Wenchang Street, Yinchuan, Ningxia 750021, China. E-mail: wei_hc@nun.edu.cn
bSchool of Information Engineering, Ningxia University, Yinchuan 750021, China
cSchool of Medical Technology, North Minzu University, Yinchuan 750021, Ningxia, China
dDepartment of Lab Construction & Administration, North Minzu University, Yinchuan 750021, Ningxia, China
First published on 22nd May 2025
Abstract
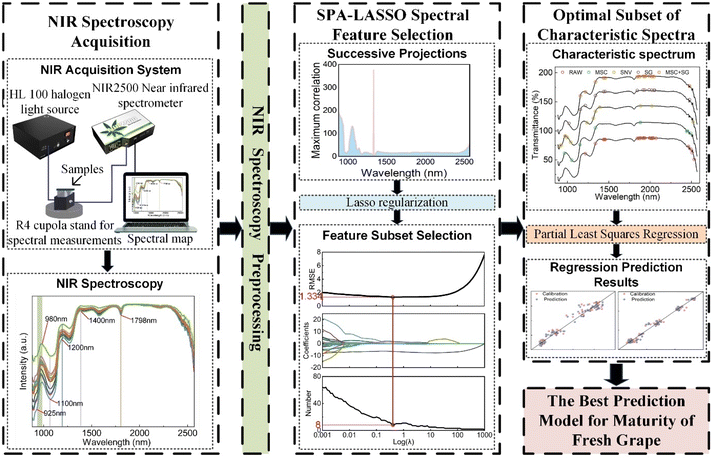
A rapid and non-destructive maturity evaluation model based on Near-Infrared Spectroscopy (NIRS) is proposed for monitoring quality parameter changes during the ripening process of fresh grapes and determining the optimal harvest period. Initially, physicochemical parameter variations of Cabernet Sauvignon grapes across twelve growth stages were studied to support predictions. Subsequently, SPA-LASSO was used to select feature wavelengths from five preprocessed full spectra, and Partial Least Squares Regression (PLSR) was employed to establish models predicting Soluble Solid Content (SSC) and Total Acid (TA) levels. Based on experimental results, the best-performing model for maturity prediction was selected. Results indicate that SSC increases and TA decreases from fruit enlargement to ripening stages. In late maturity, SSC slightly decreases and TA slightly increases. The SG + SPA-LASSO + PLSR model performed best for both SSC and TA, with SSC prediction model coefficients of determination (RC2 and RP2) at 0.982 and 0.983 respectively, and root mean square errors (RMSEC and RMSEP) of 1.010 and 0.978. TA prediction model coefficients were RC2 = 0.954, RP2 = 0.944, RMSEC = 2.347, and RMSEP = 2.618. Overall, SPA-LASSO proved effective in feature selection, enhancing model generalization for spectroscopic screening in non-destructive grape maturity assessment.
1 Introduction
Grapes play a crucial role as a primary ingredient in winemaking, holding significant importance in both agricultural and food industries.1 Soluble solid content (SSC) and total acids (TA) of grapes are pivotal factors influencing the flavor and mouthfeel of wine. Optimal ripeness ensures the ideal sugar-to-acid ratio in grapes.2 SSC and TA are two crucial indicators for assessing grape ripeness.3 Traditionally, their measurement relies on chemical detection methods, which are invasive, labor-intensive, and prone to interference from other components in the sample.4,5 Spectral detection technology offers a new approach for non-destructive, rapid analysis, and real-time monitoring of parameters such as SSC and TA during fruit growth.6 Minas et al. developed predictive models based on multivariate Near-Infrared Spectroscopy (NIRS), allowing accurate prediction of internal dry matter content and soluble solid concentration in peaches through a single scan. This enables non-destructive assessment of internal quality and ripeness of peaches.7 Li et al. combined high spatial resolution hyperspectral imaging technology with machine learning methods to accurately predict anthocyanin content in mulberry fruits and applied this to map the distribution of anthocyanins within mulberry fruits.8 Fluorescence spectra are emitted when a substance returns from its excited state to its ground state, and their wavelengths and intensities provide information about the substance's properties and the environment. Scalisi et al. collected fluorescence spectra of four different varieties of yellow peaches, establishing a model to predict fruit ripeness based on parameters such as fruit firmness and SSC (soluble solid content). The predictive models built using LDA demonstrated high accuracy, with F1 scores ≥ 0.85 across all maturity stages.9 Despite the numerous advantages of using various spectra for substance content prediction, these techniques face challenges such as noise, baseline drift, and spectral overlap.10 These issues complicate the processing and analysis of spectral data,11 particularly when aiming for a single target variable. Spectra inherently contain a large number of irrelevant variables, especially in near-infrared spectra, which can lead to lower accuracy in spectral prediction models and difficulties in interpreting spectral analysis results.12 Therefore, selecting appropriate methods for feature spectrum selection is crucial based on the specific data characteristics and analysis goals.Common methods for feature spectrum selection can be broadly categorized into three main types based on their principles: statistical,13,14 machine learning,15 and informatics.16,17 For example, Tian et al. used the CARS algorithm to optimize the improved iPLS to select a subset of near-infrared spectral features. They selected 14 effective feature wavelengths between 1160 nm and 1338 nm and established a prediction model for crude protein content in brown rice based on near-infrared spectroscopy technology, with a validation set correlation coefficient of 0.8876.18 Dharmawan et al. used PCA technology to compress the near-infrared spectral information of Arabica coffee, selected PC variables based on contribution rate, and used an ANN model based on a multi-layer perceptron to classify Arabica coffee from different origins. The accuracy achieved in internal cross validation, training, and testing sets ranged from 90% to 100%. The error in the classification process shall not exceed 10%.19 With the rise of deep learning, there have been numerous methods for feature spectral selection based on deep learning. Zhou et al. proposed a spectral feature selector based on convolutional neural networks to select features from the near-infrared hyperspectral data of over 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 wheat grains. 60 channels were selected from 200 channels as feature subsets, and combined with a convolutional neural network classifier with an attention mechanism, automatic lossless classification of a single wheat grain was achieved with a classification accuracy of 90.2%.20 Kuo et al. modified the one-dimensional spectrogram power network and constructed a 1D ResGC Net with embedded residual global context, which can automatically identify near-infrared spectral feature bands and extract spectral feature information. However, deep learning is difficult to deploy on portable handheld devices due to their large size and high hardware resource requirements. In addition, most deep learning models are called “black box models”, and the internal data processing process of the model is difficult to explain, resulting in highly extracted data features.21
000 wheat grains. 60 channels were selected from 200 channels as feature subsets, and combined with a convolutional neural network classifier with an attention mechanism, automatic lossless classification of a single wheat grain was achieved with a classification accuracy of 90.2%.20 Kuo et al. modified the one-dimensional spectrogram power network and constructed a 1D ResGC Net with embedded residual global context, which can automatically identify near-infrared spectral feature bands and extract spectral feature information. However, deep learning is difficult to deploy on portable handheld devices due to their large size and high hardware resource requirements. In addition, most deep learning models are called “black box models”, and the internal data processing process of the model is difficult to explain, resulting in highly extracted data features.21
Therefore, in order to solve the problem of damaging the detection of SSC and TA content in fresh grapes by traditional methods, accurately select characteristic wavelengths, reduce redundant spectral information, and establish the best prediction model for the maturity and quality of fresh grapes, this study collected samples of fresh grapes at twelve growth stages, used near-infrared spectroscopy technology to capture the quality index parameters of fresh grapes at different maturity stages, and used the SPA-LASSO algorithm for spectral feature selection. At the same time, the partial least squares regression method was used to establish SSC and TA content prediction models with various feature spectral sets. By comparing the prediction results, the best prediction model was selected for evaluating the maturity of fresh grapes.
2 Materials and methods
2.1 Sample collection
The fresh table grape samples used in the experiment were all Cabernet Sauvignon grapes, collected by experienced growers from June 18, 2023, to September 25, 2023, at Legacy Peak Estate (38°26′49.7544′′N, 106°0′27.67464′′E, Yinchuan, China). The sampling covered four growth stages (berry enlargement, veraison, maturity, and post-maturity), with three independent sampling batches per stage (totaling 4 stages × 3 batches = 12 batches), and 300 berries were collected per batch. During each sampling event, grape clusters were randomly selected from a pre-designated row of vines. Using the five-point sampling method,22 five undamaged and disease-free berries were randomly picked from the upper, middle, and lower positions of each cluster. All sampling procedures were completed between 9:00 AM and 10:00 AM on the respective sampling days.From each batch of 300 berries, a group of 10 berries with the most similar physiological traits was selected. The skins and seeds were removed, and the juice was extracted. The juice was then centrifuged at 1500 rpm for 10 minutes, filtered through a 0.45 μm microporous membrane, and used for subsequent experiments.
2.2 Acquisition of NIRS data and measurement of physicochemical parameters
The near-infrared transmission spectroscopy platform was constructed using an NIR2500 near-infrared spectrometer (Ideaoptics Instruments Co., Ltd, China), HL100 halogen light source, RIB-600-NIR direct-pass fiber optic cable, R4 cuvette holder for spectral measurements, and Morpho Spectral Acquisition Software (Version 3.2 12.2).During near-infrared transmission spectroscopy of Cabernet Sauvignon grape juice samples, 5 mL of liquid was extracted into a cuvette. The scanning wavelength range was set from 900 nm to 2500 nm, with a wavelength resolution of 3.2 nm and integration time of 10 ms. Each sample was measured three times, and the average was calculated to obtain the final spectral data used for establishing prediction models. After completing the near-infrared transmission spectroscopy, each sample was immediately retrieved for the measurement of SSC and total acids.
The SSC content of the samples was measured using an SN-DR3205 digital refractometer (Shanghai Shangpu Instrument Equipment Co., Ltd, Shanghai, China), while the TA content was determined by the acid–base titration method23 (expressed as tartaric acid equivalents). SSC and TA contents for each period were measured three times, and the average values were calculated as the final reference content.
3 Data analysis and model development
3.1 Preprocessing of spectral data
During NIRS collection, factors such as instrument vibration, environmental interference, and sample scattering effects can reduce the accuracy and reliability of the spectra.24 Therefore, it is necessary to select appropriate preprocessing methods to correct the raw spectra, minimizing the influence of these interfering factors and enhancing the prediction accuracy of the models.Four preprocessing methods, namely Savitzky–Golay smoothing (S–G smoothing), Multiplicative Scatter Correction (MSC), Standard Normal Variate (SNV), and MSC–S–G, were employed to process the spectra. The best preprocessing method was selected based on the prediction results.
3.2 Feature wavelength selection (SPA-LASSO)
Spectral data typically contain a vast amount of information. Through feature wavelength selection, it is possible to reduce the influence of redundant information and noise,25 thereby improving the predictive performance of the model, simplifying its structure, and reducing computational complexity.SPA is a forward iterative feature selection method commonly used for spectral data.26 It gradually reduces the feature space by iteratively selecting the most relevant subsets of features to lower dimensions while retaining essential information. The main steps of the algorithm are as follows:
(1) Initialization: select an initial wavelength as the starting wavelength, add it to the set of selected features, and set the maximum number of variables.
(2) Stepwise selection: calculate the correlation between each unselected wavelength point and all wavelength points in the selected feature set sequentially. Retain the wavelength with the highest correlation and add it to the selected feature set.
(3) Termination and output: repeat step (2) until the number of wavelength points in the selected feature set reaches the predetermined maximum number of variables. Output all wavelength points in the feature set as the final set of selected feature wavelengths.
The LASSO algorithm is a widely used linear regression method in machine learning. This algorithm automatically selects features that significantly impact the target variable by introducing L1 regularization, while compressing the coefficients of other features to zero, thereby achieving model sparsity.27 Its optimization objective is shown as eqn (1):
| (1/(2 × M)) × sum(yi − θ0 − ∑(θj × xji))2 + λ × sum(|θj|) | (1) |
The SPA-LASSO method combines SPA with LASSO. It utilizes SPA to select a subset of spectral variables that are highly correlated with the target variable, and then applies the LASSO algorithm to further refine this variable set, producing the final set of spectral feature variables.
The significant advantage of the SPA-LASSO method lies in: (1) reducing computational complexity. The runtime of the LASSO algorithm is dependent on the number of features. By employing the SPA algorithm for preliminary screening, the SPA-LASSO method can handle a smaller feature set in the LASSO algorithm, saving computational resources and feature selection time. (2) Enhanced feature selection accuracy and interpretability. The SPA algorithm can eliminate features with poor correlation with the target variable, reducing interference from less useful features in the LASSO algorithm. This improves the accuracy and stability of feature selection. By passing a more relevant set of features to the LASSO algorithm, the model can be further refined to select features that provide better explanatory power for the target variable. (3) Avoiding local optima and reducing feature redundancy. The LASSO algorithm, with its L1 regularization, tends to produce sparse coefficient estimates. This allows it to globally consider the correlation of all features with the target variable, thereby avoiding local optima and reducing feature redundancy. The technical roadmap is shown in Fig. 1.
3.3 Building predictive models and performance evaluation
Partial Least Squares Regression (PLSR) is a commonly used predictive modeling method suitable for handling multivariate regression problems.28 PLSR can effectively handle high-dimensional data and multicollinearity by extracting latent variables or factors, reducing dimensionality, lowering computational complexity, and avoiding the curse of dimensionality. This enhances the stability and accuracy of the model. Therefore, in this study, PLSR is applied to establish predictive models based on NIRS analysis.3.4 Model performance evaluation
Calculate RC2, RP2, RMSEC, RMSEP, and mean absolute errors (MAEC, MAEP) separately for the calibration and prediction sets to evaluate the performance of the predictive model. Their calculation methods are shown as follows: | (2) |
 | (3) |
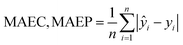 | (4) |
RMSE is used to measure the average error between predicted values and actual values. A smaller RMSE indicates that the predicted values are closer to the actual values. Mean Absolute Error (MAE) represents the average absolute difference between predicted values and actual values. It measures the average prediction bias of the model; a smaller MAE indicates higher prediction accuracy of the model. R2 is used to measure the model's explanatory power over the observed data. A value closer to 1 indicates stronger explanatory power of the model.
The spectral preprocessing, feature wavelength selection, and PLSR model establishment in the experiment were all carried out in Matlab 2022a, and the t-test was performed using SPSS 19.0 software.
4 Results and discussion
4.1 Physical and chemical parameters analysis using NIRS
The physicochemical indicators and their trends during sampling of Cabernet Sauvignon grapes are presented in Fig. 2 respectively. The SSC quality score shows a gradual increase throughout the entire grape growth and development process, while the TA quality score exhibits an overall decreasing trend. During the first to fifth sampling periods, SSC and TA show slow growth with some fluctuations. This is because the grapes are in the fruit enlargement stage, primarily undergoing cell division, which results in relatively less sugar accumulation.29 At this stage, grape enlargement requires substantial water support for growth. Absorption and loss of water can dilute or concentrate the TA in the fruit, leading to fluctuations in the total acid content.From the 6th to the 9th sampling period, the grapes are in the veraison stage. During this period, grapes begin to accumulate sugars, resulting in an increase in SSC content, while acidic substances start to degrade, leading to a gradual decrease in TA content.30 This trend continues until the 11th sampling period when the grapes reach maturity. The SSC quality score peaks at 26.2°Bx, while the TA quality score reaches its minimum at 5.02 mg L−1. In the 12th harvesting period, the SSC quality score shows a slight decrease. This is likely due to post-maturity processes such as respiration, conversion of sugars into other substances like alcohol, and loss of moisture in the grapes. The TA content increases, possibly indicating stress on the fruit due to drought conditions, leading to the production of more organic acids.31
Fig. 3 shows the average spectra of grape samples collected over twelve periods. Although there are significant differences in absorption peaks, the overall trends are consistent. The spectral distribution between 900 and 970 nm is likely due to absorption by phenolic compounds, anthocyanins, cellulose, and sucrose.32 The wavelength range from 925 nm to 980 nm may relate to carbohydrates and O–H groups in water.33 The peak at 1200 nm corresponds to the second overtone of C–H stretching in sugars and organic acids, while the trough at 1798 nm is due to the C–O stretching in sugars and organic acids.34 Absorption peaks at 1100 nm and 1410 nm are attributed to the combination bands of O–H in water.35 Beyond 2400 nm, the spectral signals exhibit significant noise, necessitating preprocessing of the raw spectral signals to enhance the signal-to-noise ratio and improve spectral quality.
4.2 Development of the prediction model
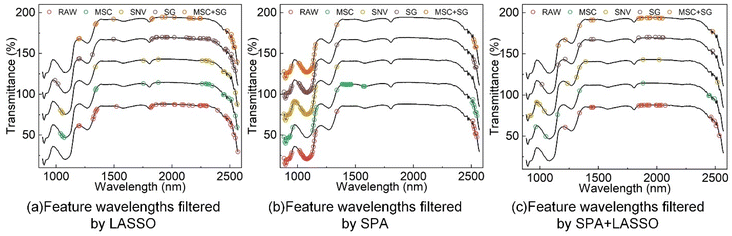
The original spectral data contain 256 wavelength points. To eliminate redundant information, the original spectra were processed using three feature wavelength selection methods: LASSO, SPA, and SPA-LASSO.When applying the LASSO algorithm to perform feature wavelength selection from the original spectral data of grape samples, we evaluated the model's performance and selected the optimal regularization parameter λ. This was done using 10-fold cross-validation, where the optimal λ value was determined by minimizing the root mean square error based on the cross-validation results. The final selected feature wavelengths are depicted in Fig. 4(a). When using the SPA algorithm for spectral feature selection, the choice of starting wavelength is crucial. Selecting an appropriate starting wavelength not only helps preserve key information in the selected feature wavelengths but also reduces the risk of overfitting. In this case, the 70th wavelength point was set as the starting wavelength, with a maximum iteration of 255 times. The algorithm retained the top 40 wavelength points that correlated most strongly with the starting wavelength as the final set of feature wavelengths, as shown in Fig. 4(b).
The feature wavelengths selected by the SPA algorithm are concentrated more densely between 880 nm and 1150 nm, while wavelengths between 1630 nm and 2400 nm have not been chosen as feature wavelengths. This may be because the SPA algorithm places greater emphasis on the spatial distribution among the feature wavelengths, thereby preferring feature sets that exhibit spatial continuity or consistency. Among the five preprocessing methods used, a significant number of identical wavelength points are selected as feature wavelengths, predominantly ranging from 900 nm to 1200 nm. This is because the SPA algorithm primarily considers the correlations among the feature wavelengths and their correlations with the target variable during the feature selection process, independent of the data preprocessing methods applied to the features. As a result, the selected set of feature wavelengths demonstrates statistical significance and interpretability.
When improving the feature wavelength selection using the LASSO algorithm on top of the SPA algorithm, the process starts by using the SPA algorithm to select the 70th wavelength point as the starting wavelength. The SPA algorithm retains the top 100 wavelength points with the highest correlations as the intermediate set of feature wavelengths. Subsequently, the LASSO algorithm is applied to further refine this intermediate set of feature wavelengths. The selection of the optimal regularization parameter is determined based on 10-fold cross-validation results to minimize the RMSE. This process finalizes the selection of the feature wavelength set, as depicted in Fig. 4(c).
Compared to the SPA algorithm, the LASSO algorithm, due to its inclusion of L1 regularization, selects feature wavelengths that are more spatially sparse and evenly distributed. After applying MSC and SNV preprocessing to the spectra, the number of selected feature wavelengths is minimal and highly consistent. This is likely because these preprocessing methods eliminate nonlinear and linear offsets in the spectral data, enhancing data reliability and signal-to-noise ratio. The total number of feature wavelengths selected by SPA-LASSO is significantly fewer than those selected by the former two methods. While the SPA algorithm emphasizes spatial sparsity, the LASSO algorithm considers inter-variable correlations to a greater extent.
Predictive models were established using PLSR for the full spectra and each set of selected feature wavelengths from five preprocessing types. Prior to model construction, the dataset was randomly split into training (80%) and testing (20%) sets, with an additional 25% split from the training set for validation. The PLS model results based on the full spectra with different preprocessing methods are shown in Table 1.
| Substance | Selection spectra | Calibration set | Prediction set | ||||
|---|---|---|---|---|---|---|---|
| R2C | RMSEC | MAEC | R2P | RMSEP | MAEP | ||
| SSC | Raw spectra | 0.806 | 3.287 | 2.639 | 0.715 | 4.090 | 3.370 |
| MSC | 0.877 | 2.598 | 2.318 | 0.880 | 2.584 | 2.294 | |
| SG | 0.898 | 2.398 | 2.119 | 0.869 | 2.689 | 2.366 | |
| SNV | 0.861 | 2.807 | 2.306 | 0.849 | 2.902 | 2.435 | |
| MSC + SG | 0.913 | 2.334 | 1.936 | 0.915 | 2.402 | 2.035 | |
| TA | Raw spectra | 0.799 | 5.016 | 4.102 | 0.788 | 5.091 | 4.379 |
| MSC | 0.855 | 4.126 | 3.421 | 0.829 | 4.475 | 3.765 | |
| SG | 0.889 | 3.892 | 2.847 | 0.885 | 3.921 | 2.791 | |
| SNV | 0.835 | 4.453 | 3.654 | 0.804 | 4.922 | 3.980 | |
| MSC + SG | 0.898 | 3.661 | 2.592 | 0.892 | 3.761 | 2.889 | |
From Table 1 it can be observed that the PLSR models established using different preprocessing methods for full spectra yield varying prediction results. Overall, predictions for the SSC content are better than those for the TA content, likely due to larger errors when measuring TA data using titration methods. Specifically for SSC or TA prediction models individually, models built using raw spectra yield the poorest results. Models using MSC + SG preprocessing consistently achieve the highest prediction accuracies (RC2, RP2 > 0.910 for SSC content; RC2, RP2 > 0.890 for TA content). This could be attributed to MSC + SG effectively correcting spectral baseline drift and reducing noise interference, thus emphasizing data stability and signal-to-noise ratio. Therefore, among the four preprocessing methods evaluated for predicting SSC and TA contents based on full spectra, MSC + SG proves to be the most suitable. However, despite this, the prediction results are still not entirely satisfactory, highlighting the necessity for feature wavelength selection to eliminate redundant information and enhance prediction model accuracy.
The PLS model results for the SSC content and TA content based on respective feature wavelength sets are shown in Tables 2 and 3, respectively.
| Substance | Selection spectra | Wavelengths | Calibration set | Prediction set | ||||
|---|---|---|---|---|---|---|---|---|
| R C 2 | RMSEC | MAEC | R P 2 | RMSEP | MAEP | |||
| a Bold values indicate the best-performing models for current prediction results. | ||||||||
| SSC | Raw spectra + LASSO | 35 | 0.972 | 1.286 | 0.972 | 0.969 | 1.335 | 1.007 |
| MSC + LASSO | 20 | 0.968 | 1.349 | 1.052 | 0.967 | 1.375 | 0.995 | |
| SNV + LASSO | 16 | 0.960 | 1.504 | 1.061 | 0.945 | 1.754 | 1.208 | |
| SG + LASSO | 37 | 0.969 | 1.328 | 0.924 | 0.964 | 1.443 | 1.132 | |
| MSC + SG + LASSO | 23 | 0.970 | 1.274 | 0.946 | 0.966 | 1.384 | 0.996 | |
| Raw spectra + SPA | 40 | 0.963 | 1.436 | 0.935 | 0.966 | 1.404 | 1.086 | |
| MSC + SPA | 40 | 0.965 | 1.401 | 0.989 | 0.961 | 1.481 | 1.051 | |
| SNV + SPA | 40 | 0.959 | 1.521 | 0.953 | 0.958 | 1.552 | 1.090 | |
| SG + SPA | 40 | 0.963 | 1.460 | 1.077 | 0.946 | 1.760 | 1.421 | |
| MSC + SG + SPA | 40 | 0.939 | 1.891 | 1.484 | 0.931 | 1.986 | 1.550 | |
| Raw spectra + SPA-LASSO | 22 | 0.977 | 1.168 | 0.926 | 0.980 | 1.074 | 0.848 | |
| MSC + SPA-LASSO | 8 | 0.979 | 1.101 | 0.861 | 0.971 | 1.305 | 0.888 | |
| SNV + SPA-LASSO | 13 | 0.981 | 1.056 | 0.859 | 0.979 | 1.107 | 0.905 | |
| SG + SPA-LASSO | 14 | 0.982 | 1.010 | 0.687 | 0.983 | 0.978 | 0.716 | |
| MSC + SG + SPA-LASSO | 17 | 0.981 | 1.048 | 0.881 | 0.982 | 1.040 | 0.780 | |
| Substance | Selection spectra | Wavelengths | Calibration set | Prediction set | ||||
|---|---|---|---|---|---|---|---|---|
| R C 2 | RMSEC | MAEC | R P 2 | RMSEP | MAEP | |||
| a Bold values indicate the best-performing model for the current prediction results. | ||||||||
| TA | Raw spectra + LASSO | 35 | 0.930 | 2.930 | 2.305 | 0.927 | 3.009 | 2.417 |
| MSC + LASSO | 20 | 0.905 | 3.394 | 2.702 | 0.908 | 3.309 | 2.730 | |
| SNV + LASSO | 16 | 0.911 | 3.256 | 2.694 | 0.900 | 3.466 | 2.879 | |
| SG + LASSO | 37 | 0.928 | 2.903 | 2.248 | 0.917 | 3.049 | 2.302 | |
| MSC + SG + LASSO | 23 | 0.934 | 2.793 | 2.181 | 0.928 | 2.875 | 2.156 | |
| Raw spectra + SPA | 40 | 0.910 | 3.254 | 2.614 | 0.897 | 3.589 | 2.938 | |
| MSC + SPA | 40 | 0.928 | 2.925 | 2.348 | 0.918 | 3.115 | 2.378 | |
| SNV + SPA | 40 | 0.923 | 2.978 | 2.329 | 0.930 | 2.887 | 2.289 | |
| SG + SPA | 40 | 0.919 | 3.050 | 2.301 | 0.904 | 3.334 | 2.721 | |
| MSC + SG + SPA | 40 | 0.939 | 2.774 | 2.222 | 0.928 | 2.952 | 2.329 | |
| Raw spectra + SPA-LASSO | 22 | 0.942 | 2.686 | 2.151 | 0.934 | 2.734 | 2.073 | |
| MSC + SPA-LASSO | 8 | 0.918 | 3.182 | 2.534 | 0.904 | 3.426 | 2.852 | |
| SNV + SPA-LASSO | 13 | 0.941 | 2.609 | 1.952 | 0.934 | 2.795 | 2.200 | |
| SG + SPA-LASSO | 14 | 0.954 | 2.347 | 1.846 | 0.944 | 2.618 | 2.046 | |
| MSC + SG + SPA-LASSO | 17 | 0.943 | 2.624 | 2.056 | 0.944 | 2.538 | 1.969 | |
By comparing the prediction data from Tables 1–3, it is evident that the predictive models established using feature spectra significantly outperform those using full spectra. This indicates that feature spectra selected by specific wavelengths have better interpretability. Moreover, the number of wavelengths after feature selection is reduced by 84% compared to the full spectra, indicating a substantial reduction in redundant information in the spectra. Among the feature selection methods, SPA-LASSO identifies the fewest feature wavelengths, further streamlining the predictive models. Specifically, the MSC + SPA-LASSO method reduces the number of feature wavelengths by over 96% compared to the full spectra.
Comparing the SSC prediction models established with various feature wavelengths from Table 2, the model built using the MSC + SG + SPA method yielded the poorest results, with R2C and R2P both exceeding 0.931, albeit significantly better than the full spectrum model. The SG + SPA-LASSO method performed optimally on both the calibration and prediction sets (RC2 = 0.982, RP2 = 0.983), with the prediction set's coefficient of determination slightly higher than that of the calibration set, indicating strong generalization ability and mitigating overfitting. While the prediction model established using the MSC + SPA-LASSO method (RC2 = 0.979, RP2 = 0.971) slightly underperformed compared to the SG + SPA-LASSO method, its feature wavelength set, composed of only 8 wavelengths, significantly reduced model complexity. This reduction is crucial for minimizing the size of portable handheld devices and improving the operational speed of deployed hardware infrastructure.
Comparing the results of various TA prediction models in Table 3, the model established using the MSC + LASSO method performed the poorest, with R2C and R2P both exceeding 0.905. The SG + SPA-LASSO method exhibited the best performance in the calibration set (R2C = 0.954). Meanwhile, the MSC + SG + SPA-LASSO method performed best in the prediction set, with both models achieving (R2P = 0.944), but MSC + SG + SPA-LASSO had a smaller RMSEP, indicating lower average prediction error and higher accuracy on the prediction set. However, the MSC + SPA-LASSO model, which has the smallest feature wavelength set, showed poor performance ((RC2 = 0.918), (RP2 = 0.904)). This could be attributed to the model excessively reducing the number of features, thereby losing some spectroscopic information that, while less correlated, still holds value for total acid prediction, consequently lowering the model's performance.
After a thorough analysis of the PLS model results, a comprehensive conclusion was drawn: prediction models based on feature spectra outperform those based on full spectra, especially when utilizing the SPA-LASSO method to select fewer but more accurate feature variables. Fig. 5 depicts scatter plots of measured and predicted values of SSC and TA for both calibration and prediction sets, with solid regression lines illustrating the correlation between measured and predicted values. Notably, Fig. 5(c) demonstrates excellent fitting performance for SSC. Conversely, Fig. 5(e) indicates slightly poorer predictions for TA, particularly at higher values. This variation may relate to the physiological maturity of grape samples and the stability of TA content.36 These results indicate that PLS models accurately predict SSC and TA levels during grape ripening. The SPA-LASSO feature wavelength selection method effectively identifies optimal subsets of wavelengths with the best predictive ability in spectral data, reducing redundant information and thereby enhancing modeling effectiveness and generalization capability.
 | ||
| Fig. 5 Individual prediction scatter plots ((a)–(c) for SSC predictions, (d)–(f) for TA predictions). | ||
Data availability
The datasets generated and/or analyzed during the current study are not publicly available due to further investigation running on the same project for futuristic solutions but are available from the corresponding author on reasonable request.Author contributions
Jia-Yue Hu: data curation, formal analysis, writing – original draft. Zhuo-Kang Wang: methodology, software, visualization. Yu-Yu Wang: investigation, resources. Yu-Hao Wu: conceptualization, project administration. Hai-Cheng Wei: conceptualization, supervision, funding acquisition. Jing Zhao: writing – review & editing, validation. Liu Yang: data collection, methodology. Yu-zhe Tan: software, formal analysis. Zi-Long Deng: resources, writing – review & editing. Zhi-Jie Xiang: data curation, visualization. Zi-Yi Wang: investigation, methodology. Xin-Tong Zhao: writing – original draft, funding acquisition.Conflicts of interest
The authors of this review paper declare that there are no conflicts of interest in relation to the subject matter of this paper. No financial or personal relationships with any organizations or products that may have influenced the review have been disclosed. All sources used in the review have been appropriately cited, and the review has been conducted objectively and without bias.Acknowledgements
This research was funded by the Ningxia Higher Education Industry-Academia Cooperation and Collaborative Talent Cultivation Project titled “Construction and Exploration of an Integrated Practical Platform under the New Engineering Context” (Project No. cxy2021017), and the Research and Practice on Education and Teaching Reform in Ordinary Undergraduate Universities in Ningxia (Project No. bjg2024006). Support was also provided by the Key Project of Ningxia Natural Science Foundation (2024AAC02036), and the National Natural Science Foundation of China (No. 62361001).Notes and references
- L. L. D. R. Osorio, E. Flórez-López and C. D. Grande-Tovar, The potential of selected agri-food loss and waste to contribute to a circular economy: Applications in the food, cosmetic and pharmaceutical industries, Molecules, 2021, 26(2), 515 CrossRef PubMed.
- M. I. Rouxinol, M. R. Martins and J. M. Barroso, et al., Wine grapes ripening: A review on climate effect and analytical approach to increase wine quality, Appl. Biosci., 2023, 2(3), 347–372 CrossRef.
- A. Benelli, C. Cevoli and A. Fabbri, In-field Vis/NIR hyperspectral imaging to measure soluble solids content of wine grape berries during ripening[C], 2020 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), IEEE, 2020, pp. 99–103 Search PubMed.
- S. Xu, Y. Guo and X. Liang, et al., Intelligent Rapid Detection Techniques for Low-Content Components in Fruits and Vegetables: A Comprehensive Review, Foods, 2024, 13(7), 1116 CrossRef CAS PubMed.
- S. A. Jaywant, H. Singh and K. M. Arif, Sensors and instruments for brix measurement: A review, Sensors, 2022, 22(6), 2290 CrossRef PubMed.
- Z. Guo, M. M. Wang and A. A. Agyekum, et al., Quantitative detection of apple watercore and soluble solids content by near infrared transmittance spectroscopy, J. Food Eng., 2020, 279, 109955 CrossRef CAS.
- I. S. Minas, F. Blanco-Cipollone and D. Sterle, Accurate non-destructive prediction of peach fruit internal quality and physiological maturity with a single scan using near infrared spectroscopy, Food Chem., 2021, 335, 127626 CrossRef CAS PubMed.
- X. Li, Z. Wei and F. Peng, et al., Non-destructive prediction and visualization of anthocyanin content in mulberry fruits using hyperspectral imaging, Front. Plant Sci., 2023, 14, 1137198 CrossRef PubMed.
- A. Scalisi, D. Pelliccia and M. G. O'Connell, Maturity prediction in yellow peach (Prunus persica L.) cultivars using a fluorescence spectrometer, Sensors, 2020, 20(22), 6555 CrossRef CAS PubMed.
- Z. Dong and J. Xu, Baseline estimation using optimized asymmetric least squares (O-ALS), Measurement, 2024, 233, 114731 CrossRef.
- K. J. Szekeres, S. Vesztergom and M. Ujvári, et al., Methods for the Determination of Valid Impedance Spectra in Non-stationary Electrochemical Systems: Concepts and Techniques of Practical Importance, Chemelectrochem, 2021, 8(7), 1233–1250 CrossRef CAS.
- D. Xiao, J. Huang and J. Li, et al., Inversion study of cadmium content in soil based on reflection spectroscopy and MSC-ELM model, Spectrochim. Acta, Part A, 2022, 283, 121696 CrossRef CAS PubMed.
- Y. Qin, K. Song and N. Zhang, et al., Robust NIR quantitative model using MIC-SPA variable selection and GA-ELM, Infrared Phys. Technol., 2023, 128, 104534 CrossRef CAS.
- M. Kamruzzaman, D. Kalita and M. T. Ahmed, et al., Effect of variable selection algorithms on model performance for predicting moisture content in biological materials using spectral data, Anal. Chim. Acta, 2022, 1202, 339390 CrossRef CAS PubMed.
- J. Wang, H. Zhang and J. Wang, et al., Feature selection using a neural network with group lasso regularization and controlled redundancy, IEEE Transact. Neural Networks Learn. Syst., 2020, 32(3), 1110–1123 Search PubMed.
- H. Fu, G. Sun and J. Ren, et al., Fusion of PCA and segmented-PCA domain multiscale 2-D-SSA for effective spectral-spatial feature extraction and data classification in hyperspectral imagery, IEEE Trans. Geosci. Rem. Sens., 2020, 60, 1–14 Search PubMed.
- M. P. Uddin, M. A. Mamun and M. I. Afjal, et al., Information-theoretic feature selection with segmentation-based folded principal component analysis (PCA) for hyperspectral image classification, Int. J. Rem. Sens., 2021, 42(1), 286–321 CrossRef.
- Y. Tian, L. Sun and H. Bai, et al., Quantitative detection of crude protein in brown rice by near-infrared spectroscopy based on hybrid feature selection, Chemom. Intell. Lab. Syst., 2024, 247, 105093 CrossRef CAS.
- A. Dharmawan, R. E. Masithoh and H. Z. Amanah, Development of PCA-MLP model based on visible and shortwave near infrared spectroscopy for authenticating Arabica coffee origins, Foods, 2023, 12(11), 2112 CrossRef CAS PubMed.
- L. Zhou, C. Zhang and M. F. Taha, et al., Wheat kernel variety identification based on a large near-infrared spectral dataset and a novel deep learning-based feature selection method, Front. Plant Sci., 2020, 11, 575810 CrossRef PubMed.
- C. E. Kuo, Y. K. Tu and S. L. Fang, et al., Early detection of drought stress in tomato from spectroscopic data: A novel convolutional neural network with feature selection, Chemom. Intell. Lab. Syst., 2023, 239, 104869 CrossRef CAS.
- L. Wu, Y. Jiang and F. Zhao, et al., Increased organic fertilizer application and reduced chemical fertilizer application affect the soil properties and bacterial communities of grape rhizosphere soil, Sci. Rep., 2020, 10(1), 9568 CrossRef CAS PubMed.
- D. Pierre, Acid-base titration, Undergraduate Journal of Mathematical Modeling: One+ Two, 2019, 10(1), 8 Search PubMed.
- C. Pasquini, Near infrared spectroscopy: A mature analytical technique with new perspectives–A review, Anal. Chim. Acta, 2018, 1026, 8–36 CrossRef CAS PubMed.
- D. F. Barbin, A. L. S. M. Felicio and D. W. Sun, et al., Application of infrared spectral techniques on quality and compositional attributes of coffee: An overview, Food Res. Int., 2014, 61, 23–32 CrossRef CAS.
- M. C. U. Araújo, T. C. B. Saldanha and R. K. H. Galvao, et al., The successive projections algorithm for variable selection in spectroscopic multicomponent analysis, Chemometr. Intell. Lab. Syst., 2001, 57(2), 65–73 CrossRef.
- V. Fonti and E. Belitser, Feature selection using lasso, VU Amsterdam Research Paper in Business Analytics, 2017, vol. 30, pp. 1–25 Search PubMed.
- J. H. Cheng and D. W. Sun, Partial least squares regression (PLSR) applied to NIR and HSI spectral data modeling to predict chemical properties of fish muscle, Food Eng. Rev., 2017, 9, 36–49 CrossRef CAS.
- H. Ezura and K. Hiwasa-Tanase, Fruit development, Plant Developmental Biology-Biotechnological Perspectives, Springer Berlin Heidelberg, Berlin, Heidelberg, 2009, vol. 1: 301–318 Search PubMed.
- B. W. Du Plessis, Cellular Factors that Affect Table Grape Berry Firmness, Stellenbosch University, Stellenbosch, 2008 Search PubMed.
- T. R. Thomas, M. A. Matthews and K. A. Shackel, Direct in situ measurement of cell turgor in grape (Vitis vinifera L.) berries during development and in response to plant water deficits, Plant Cell Environ., 2006, 29(5), 993–1001 CrossRef PubMed.
- H. Schulz, A. Krähmer, A. Naumann, et al., Infrared and Raman spectroscopic map** and imaging of plant materials, Infrared and Raman Spectroscopic Imaging: Second, Completely Revised and Updated Edition, 2014, pp. 225–294 Search PubMed.
- P. H. G. D. Diniz, A. A. Gomes and M. F. Pistonesi, et al., Simultaneous classification of teas according to their varieties and geographical origins by using NIR spectroscopy and SPA-LDA, Food Anal. Methods, 2014, 7, 1712–1718 Search PubMed.
- S. Chen, F. Zhang and J. Ning, et al., Predicting the anthocyanin content of wine grapes by NIR hyperspectral imaging, Food Chem., 2015, 172, 788–793 CrossRef CAS PubMed.
- B. G. Coombe, Growth stages of the grapevine: adoption of a system for identifying grapevine growth stages, Aust. J. Grape Wine Res., 1995, 1(2), 104–110 CrossRef.
- F. Ping, J. Yang and X. Zhou, et al., Quality Assessment and Ripeness Prediction of Table Grapes Using Visible–Near-Infrared Spectroscopy, Foods, 2023, 12(12), 2364 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2025 |